Further Discussions of the Complex Dynamics of a 2D Logistic Map: Basins of Attraction and Fractal Dimensions

Abstract

In this paper, we study the complex dynamic characteristics of a simple nonlinear logistic map. The map contains two parameters that have complex influences on the map’s dynamics. Assuming different values for those parameters gives rise to strange attractors with fractal dimensions. Furthermore, some of these chaotic attractors have heteroclinic cycles due to saddle-fixed points. The basins of attraction for some periodic cycles in the phase plane are divided into three regions of rank-1 preimages. We analyze those regions and show that the map is noninvertible and includes $Z_0,Z_2$ and $Z_4$ regions.

1. Introduction

In 1976, the first version of the 1D logistic map was introduced and modeled by May [1]. The model was used to study the behavior of some biological species in each generation. However, the mathematical model of this map was simple, but May detected some complex dynamic characteristics about its trajectories. It was described by the following first-order difference equation,

$$x_{t+1}=\mu x_t(1-x_t)$$

(1)

where x must lie in the interval $(0,1)$ otherwise some disadvantages such as population distinction may exist. The parameter $\mu$ has a significant impact on the dynamics of this equation and has been restricted in the interval $\left(0,4\right)$. Some of these dynamics are flip bifurcation, open periodic windows and chaos. These complex dynamics were examined in [1]. That work opened the gate to several studies on logistic systems that can be used to simulate other complex systems in nature. Indeed, there are many phenomena in different disciplines that have been modeled by logistic systems such as economy, biology, physics and chemistry. For instance, a 2D coupled logistic system was studied in [2]. In [3], a symmetrical coupled nonlinear logistic system was investigated and adopted in an encryption process. A simple coupled logistic system was used to examine the influences of spatial heterogeneity on population dynamics [4]. Heterogeneity and the impact of spatial structure on population dynamics were analyzed in [5]. The complex dynamics of a kicked logistic map were investigated in [6]. In [7], a multimodal family of a logistic map that possesses a single parameter was introduced. Other studies on such systems and their complex dynamic characteristics can be found in the literature ([8,9,10,11,12,13,14]). Some interesting works that have studied hyperchaotic properties have been reported. For instance, in [15] a 2D hyperchaotic map with a simple algebraic structure was introduced and studied. In order to enhance chaos complexity in 2D maps, a chaotic 2D map was proposed in [16]. Other interesting results that give more insights about the analysis carried out in this paper have been reported (see [17,18,19,20]).

In the current paper, we study the 2D nonsymmetrical logistic map given in [21]. Even though the mathematical expression of the model is simple, it possesses some periodic cycles and strange attractors with complex attractive basins and some of those attractors have fractal dimensions. They are some transient dynamic behaviors that have not been previously detected in the literature. The map contains two parameters that are restricted in two different intervals, as we show later. Studying the influence of each parameter separately while the other parameter is fixed gives rise to periodic cycles with simple attractive basins; however, it also results in some strange chaotic attractors that have not been reported before. The second parameter seems to have a great influence on the dynamics of the map. The phase plane of the map according to varying this parameter while keeping the first parameter fixed contains several bifurcated points that were not reported in the literature. Interestingly, the influences of those parameters give rise to different attracting behaviors when they take different values in the intervals. Those attracting behaviors include periodic cycles with complex attractive basins and strange attractors whose dimensions are fractals. Furthermore, the phase plane of the map is divided into many regions where preimages coexist, and as a result, the noninvertibility of the map is discussed. Briefly, the main contribution in this paper is the fractal dimension detected for some strange attractors in this simple 2D logistic map. Heteroclinic cycles are detected for some chaotic attractors. There are many approaches to find a numerical approximation of heteroclinic cycle. In this paper, we apply the procedures given in [22] for that purpose. Furthermore, there are three different types of some periodic cycles found under certain parameter values. For instance, the numerical simulation shown later detects three different types of period 2-cycle. The first one consists of two periodic points lying in a straight line parallel to the x-axis, the second one lies in a line parallel to y-axis, and the third one lies in the diagonal. The basins of attraction of the first type seem to be more complex as they contain holes that formed due to points from the divergent and nonconvergent points.

The paper is summarized as follows. In Section 2, we present the model and the stability of its fixed points. Section 3 studies the local and global analysis using some numerical simulations by which different periodic cycles with their basins and chaotic attractors are analyzed. In Section 4, the critical curves for the noninvertible map are obtained. Finally, we present our conclusion.

2. 2D Logistic Map

In this section, we study the complex dynamic characteristics of the following 2D logistic map [21].

$$\begin{array}{c}{x}_{t+1}={\mu }_1{x}_t(1-x_t),\hfill \\ y_{t+1}={\mu }_2{x}_t{y}_t(1-y_t)\hfill \end{array}$$

(2)

where the parameters ${\mu }_1$ and ${\mu }_2$ are restricted in the intervals $\left(0,4\right]$ and $\left(0,5.745\right]$, respectively. These parameters are of great importance when studying the complex dynamic features of the map (2). They represent the bifurcation parameters of the map. Biologically, $\left(x_t,y_t\right)$ represents two species that evolve logistically. On varying time the interaction between those two species depends on the growth rate represented by ${\mu }_1(y_t)$ and ${\mu }_2(x_t)$. The interaction between those species represented by the coupled logistic (2) simulates the predator-prey interaction on which we assume ${\mu }_1(y_t)={\mu }_1$ that is constant and ${\mu }_2(x_t)={\mu }_2{x}_t$ that is an increasing linear growth rate. The map (2) belongs to the group of unidirectional coupled maps; however, these growth rates are simple but they give interesting chaotic behaviors for the map (2). Our restrictions on these parameters differ from those in [1] on the second parameter ${\mu }_2$. This restriction on the second parameter comes from numerical simulations performed in laboratory in the next section. The map (2) admits three fixed points, $e_1=(0,0),e_2=\left(\frac{{\mu }_1-1}{{\mu }_1},0\right)$ and $e_3=\left(\frac{{\mu }_1-1}{{\mu }_1},\frac{{\mu }_1{\mu }_2-{\mu }_1-{\mu }_2}{{\mu }_2({\mu }_1-1)}\right)$. These points are obtained by setting $x_{t+1}=x_t=\overline{x}$ and $y_{t+1}=y_t=\overline{y}$.

Proposition 1.

(1) The fixed point $e_1$ is locally stable provided that $0<{\mu }_1<1$ otherwise it is unstable. (2) The fixed point $e_2$ is locally stable provided that $1<{\mu }_1<3$ and $-1<\frac{\left({\mu }_1-1\right){\mu }_2}{{\mu }_1}<1$. (3) The fixed point $e_3$ is locally stable provided that $1<{\mu }_1<3$ and $-1<\frac{{\mu }_2-{\mu }_1\left({\mu }_2-2\right)}{{\mu }_1}<1$.

Proof. 

(1) The Jacobian at this point becomes $J_{e_1}=\left(\begin{array}{cc}{\mu }_1& 0\\ 0& 0\end{array}\right)$. It has only two eigenvalues ${\lambda }_1={\mu }_1$ and ${\lambda }_2=0$. It is locally stable if $0<{\mu }_1<1$. (2) The Jacobian at this point becomes $J_{e_2}=\left(\begin{array}{cc}2-{\mu }_1& 0\\ 0& \frac{\left({\mu }_1-1\right){\mu }_2}{{\mu }_1}\end{array}\right)$. The eigenvalues are, ${\lambda }_1=2-{\mu }_1$ and ${\lambda }_2=\frac{\left({\mu }_1-1\right){\mu }_2}{{\mu }_1}$. The condition $\left|{\lambda }_{1,2}\right|<1$ completes the proof. (3) It is similar to the previous one. □

Proposition 2.

The map undergoes the following types of bifurcations at the fixed point $e_3$:

• A transcritical or fold bifurcation if ${\mu }_1=1$ or ${\mu }_1=\frac{{\mu }_2}{{\mu }_2-1}$.
• A flip bifurcation if ${\mu }_1=3$ or ${\mu }_1=\frac{{\mu }_2}{{\mu }_2-3}$.

Proof. 

A transcritical or fold bifurcation can occur when $1-\tau +\delta =0$ where $\tau$ and $\delta$ are the trace and determinant of the Jacobian matrix at the point $e_3$. Solving $1-\tau +\delta =0$ completes part 1 of the proof. A flip bifurcation can occur when $1+\tau +\delta =0$ and this completes the proof of the second part. □

3. Local and Global Analysis

Let us assume the following parameters, $\left({\mu }_1,{\mu }_2\right)=\left(3,4\right)$ with the initial datum $\left(x_0,y_0\right)=\left(0.11,0.12\right)$. At this set we have $e_3=\left(\frac{2}{3},\frac{5}{8}\right)$. The Jacobian matrix at this point becomes $\left(\begin{array}{cc}-1& 0\\ \frac{15}{16}& \frac{-2}{3}\end{array}\right)$ and hence the eigenvalues become ${\zeta }_1=-1$ and ${\zeta }_2=\frac{-2}{3}$. It is clear that $\left|{\zeta }_2\right|<1$ and $\left|{\zeta }_1\right|=1$, which means that $e_3$ is a nonhyperbolic point; therefore, the second condition in the stability triangle $\left\{\left(\tau ,\delta \right):1-\tau +\delta >0,1+\tau +\delta =0,1-\delta >0\right\}$ where $\tau$ and $\delta$ are the trace and determinant of the Jacobian matrix, respectively, equals 0. This means that at this point the period 2-cycle is born as one of the eigenvalues will equal −1 then further increasing in the parameter ${\mu }_1$ gives rise to a series of period-doubling cycles and thus the nonhyperbolic fixed point $e_3$ loses its stability. Figure 1a shows the bifurcation diagrams on varying both parameters. The simulation shows that both parameters have a complex impact on each other and on the map’s dynamic that enters chaotic region as confirmed by largest Lyapunov exponent given in Figure 1b. In order to see that, we separately study the influences of ${\mu }_1$ on the dynamics of the map while the other parameter is fixed. Increasing the bifurcation parameter ${\mu }_1$ to $3.1$, a period-2 cycle emerges due to flip bifurcation. Its basins of attraction is plotted in Figure 1c along with the fixed point $e_3$. The fixed point $e_3$ in all figures in this paper is denoted by a circle whereas the periodic cycle points are denoted by squares. At ${\mu }_1=3.5$ the period 4-cycle appears and is plotted in Figure 1d with its basins of attraction. Increasing this parameter further gives rise to higher periodic cycles as shown in Figure 1e (period 8-cycle) and Figure 1f (period 16-cycle).

At ${\mu }_1=3.59$ and ${\mu }_2=3.74$, the behavior of the map becomes chaotic as it enters chaos region. This chaotic behavior consists of four disconnected chaotic areas as displayed in Figure 2a. Increasing the parameter ${\mu }_1$ further makes the four chaotic areas gather into two chaotic areas. The phase plane given in Figure 2b shows these two disconnected chaotic areas at ${\mu }_1=3.66$ and ${\mu }_2=3.74$. These two areas continue to appear until ${\mu }_1=3.68$, where only one piece of chaotic attractor takes place as presented in Figure 2c. This is because there are heteroclinic cycles connecting those two chaotic areas via the saddle point $e_3$. In Figure 2d, this chaotic attractor becomes more complex as the parameter increases.

On the other hand, we study the influences of the parameter ${\mu }_2$ on the dynamics of the map while fixing the other parameter. Assuming $\left({\mu }_1,{\mu }_2\right)=\left(3,5.05\right)$ we get a dynamic situation of the map consisting of two similar forks (or one can say, transient dynamic behaviors) as shown in Figure 2e. This is because the parameter’s value ${\mu }_1=3$ is a period-doubling bifurcation point; therefore, the map’s behavior at those parameters’ values is divided into two parts just like the 1D bifurcation diagram. Such transient dynamics are due to the fact that the first variable shows endless damped oscillations because ${\mu }_1=3$ is a bifurcation point. Oscillations of $x_t$ through the term ${\mu }_2(x_t)={\mu }_2{x}_t$ affect the second equation $y_{t+1}={\mu }_2(x_t)y_t(1-y_t)$. At high values of ${\mu }_2(x_t)$ the dynamics of $y_t$ tend towards chaotic dynamics while low ${\mu }_2(x_t)$ makes the dynamics tend toward a stable regime; however, when ${\mu }_2(x_t)$ becomes constant, there is a steady-state dynamical regime. Increasing ${\mu }_2$ further makes these two forks become larger as displayed in Figure 2f. This behavior changes into four transient dynamics parts as ${\mu }_2$ increases to $5.25$—these are displayed in Figure 3a. As ${\mu }_2$ increases, the transient dynamics diagrams in the phase plane are doubled. Figure 3b shows eight parts of the transient dynamics at ${\mu }_2=5.33$. At ${\mu }_2=5.416$, the transient dynamics become large. A further increase in this parameter gives rise to different chaotic behaviors of the map as given in Figure 3d,e. This numerical simulation shows interesting behaviors of the 2D logistic map that have not been reported in the literature. This leads us to investigate the influence of those parameters together. 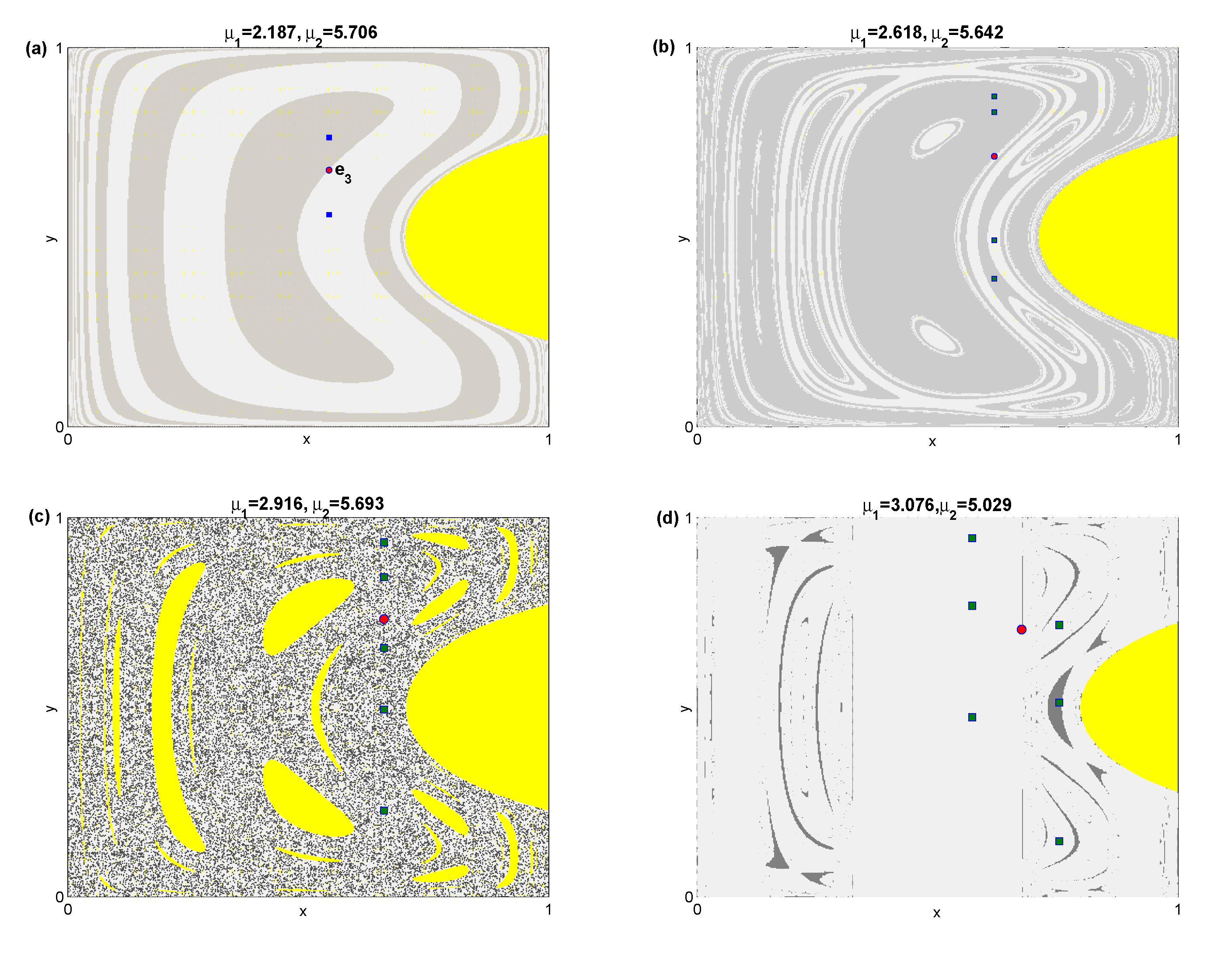Figure 3f shows the 2D bifurcation diagram for both parameters and presents the regions in the phase plane where different periodic cycles coexist when varying both parameters. The shaded region represents the stable region of the point $e_3$ and the other colors refer to different types of period cycles as shown in the figure and its caption.

Now, we study the situation when both parameters are different and give rise to periodic cycles with basins of attraction that include holes from divergent or nonconvergent points in the phase plane. The numerical simulation shows that there are three types of period 2-cycles. The first one consists of two points located vertically on the same line; the second one lies horizontally; the third one is located on a line parallel to the diagonal. In Figure 4a we display the period 2-cycle with its basins of attraction. The yellow color refers to the divergent points in the phase plane, the dark and light gray denote the period-2 basins of attraction. This cycle is born at the parameters’ values, ${\mu }_1=2.187$ and ${\mu }_2=5.706$. In Figure 4b we give the basins of attraction of the period 4-cycle around the fixed point at the parameters’ values, ${\mu }_1=2.618$ and ${\mu }_2=5.642$. It is obvious that the attractive basins are more complex than period 2-cycle. The basins of attraction become more complex due to the increasing numbers of divergent holes when the period 5-cycle coexists. Furthermore, the region of divergent points in the phase plane increased. It is clear in Figure 4c that the points of the period 5-cycle and the fixed point $e_3$ lie in a perpendicular line. Another interesting periodic cycle is period-6 which has six periodic points distributed on two sides around the fixed point $e_3$. Figure 4d displays this cycle with its basins of attraction. The period 7-cycle emerges at the parameters’ values, ${\mu }_1=2.813$ and ${\mu }_2=5.744$. It has complex basins like the period 5-cycle, as shown in Figure 4e. It has seven periodic points located on the same line where $e_3$ exists. It is worth mentioning here that the numerical experiments carried out have shown three different types of period 7-cycle. We have focused only on the one with the complex basins of attraction that have more yellow holes from the divergent points. In Figure 4f, the basins of attraction for period 8-cycle are given. In addition, all the types of period-3 and period 9-cycles have no complex basins of attraction. They have the same basins as those plotted in Figure 1. In Figure 4g, we depict the basins of period 10-cycles, which also have complex basins. It should be noted that there are some chaotic attractors of the map, which are born for different values of the parameters ${\mu }_1$ and ${\mu }_2$. In Figure 4h,I we give two different chaotic attractors that take place at $\left({\mu }_1,{\mu }_2\right)=\left(3.72,2.234\right)$ and $\left({\mu }_1,{\mu }_2\right)=\left(3.969,3.74\right)$, respectively. Interestingly, the results obtained so far have made us to detect the fractal dimension for some strange attractors for the map. For the strange attractor given in Figure 2c, the two Lyapunov exponents are $L{E}_1=0.3395323392$ and $L{E}_2=-0.4634481402$ and according to [23], it has the fractal dimension $FD=1.7326$, whereas for the strange attractor given in Figure 4h one gets $L{E}_1=0.3667508805$ and $L{E}_2=-0.5252798980$ and then $FD=1.6982$. The above numerical experiments for the basins of attraction for different periodic cycles and chaotic attractors lead us to investigate some of the geometric properties of the map. Even though the map has a simple form, it has complex basins of attraction due to the coexistence of holes of divergent points and some strange chaotic attractors that deserve to be studied. The next section analyzes the noninvertibility and critical curves of the current 2D logistic map.

4. Noninvertible Map and Critical Curves

It is clear that the map (2) is trapped to the origin point $(0,0)$. This means that setting $x_t=0$ or $y_t=0$ makes $x_{t+1}=0$ or $y_{t+1}=0$, respectively. This point can be used to identify the boundaries of the basins of attraction of any attracting set for the map (2). In order to discuss the structure of the basins we put $x_{t+1}=\acute{x}$ and $y_{t+1}=\acute{y}$ in (2). It means that the time evolution of the map is attained by the iteration of the map $T:(x,y)\to (\acute{x},\acute{y})$ as follows

$$T:\left\{\begin{array}{c}\acute{x}={\mu }_{1}x(1-x),\hfill \\ \acute{y}={\mu }_{2}xy(1-y)\hfill \end{array}\right.$$

(3)

The map T is called invertible [24] if there exists an inverse $T^{-1}$ such that $T^{-1}:(\acute{x},\acute{y})\to (x,y)$ is unique in each point in the range. The point $(\acute{x},\acute{y})\in {\mathbb{R}}^2$ is called a rank-1 image while the set $\left\{X:X^{\prime }=TX\right\}$ is called the rank-1 preimages where $X\in {\mathbb{R}}^2$. Now, the map T is called a noninvertible map if an image $(\acute{x},\acute{y})$ has at least two rank-1 preimages. To investigate that, the following proposition is raised.

Proposition 3.

(1) The origin point $e_1=(0,0)$ has four real rank-1 preimages. (2) Any point in the form $(p,0),p\ne 0$ that lies in the invariant x-axis has four real rank-1 preimages if $p<\frac{{\mu }_1}{4}$ otherwise it has no real rank-1 preimages. (3) Any point in the form $(0,q),q\ne 0$ that lies in the invariant y-axis has two real rank-1 preimages if $q<\frac{{\mu }_2}{4}$ otherwise it has no real rank-1 preimages. (4) Any point in the form $(\acute{x},\acute{y})\ne (0,0)$ has four real rank-1 preimages provided that $\acute{x}<\frac{{\mu }_1}{4}$ and $\acute{y}<\frac{{\mu }_2}{4}\left(\frac{1}{2}+\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}}\right)$ otherwise it has no real preimages.

Proof. 

(1) Setting $\acute{x}=\acute{y}=0$ in (3) gives the four points $O_{-1}^{(0)}=(0,0),O_{-1}^{(1)}=(1,0),O_{-1}^{(2)}=(0,1)$ and $O_{-1}^{(3)}=(1,1)$. (2) Setting $\acute{x}=p$ and $\acute{y}=0$ in (3) then solving it algebraically completes the proof. (3) The proof is the same as the previous one. (4) Solving (3) algebraically with respect to x and y we get,

$$\begin{array}{c}{\xi }_1=\left(\frac{1}{2}+\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}},\frac{1}{2}+\frac{1}{2}\sqrt{1-\frac{4\acute{y}}{{\mu }_2\left(\frac{1}{2}+\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}}\right)}}\right),\\ {\xi }_2=\left(\frac{1}{2}+\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}},\frac{1}{2}-\frac{1}{2}\sqrt{1-\frac{4\acute{y}}{{\mu }_2\left(\frac{1}{2}+\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}}\right)}}\right),\\ {\xi }_3=\left(\frac{1}{2}-\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}},\frac{1}{2}+\frac{1}{2}\sqrt{1-\frac{4\acute{y}}{{\mu }_2\left(\frac{1}{2}-\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}}\right)}}\right),\\ {\xi }_4=\left(\frac{1}{2}-\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}},\frac{1}{2}-\frac{1}{2}\sqrt{1-\frac{4\acute{y}}{{\mu }_2\left(\frac{1}{2}-\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}}\right)}}\right)\end{array}$$

(4)

These points are real if $\acute{x}<\frac{{\mu }_1}{4}$ and $\acute{y}<\frac{{\mu }_2}{4}\left(\frac{1}{2}+\frac{1}{2}\sqrt{1-\frac{4\acute{x}}{{\mu }_1}}\right)$ otherwise they are complex. The proof is completed. □

Now we conclude that the map T may have $0,2$ or 4 real rank-1 preimages and hence it is a noninvertible map. Furthermore, the boundaries of any attracting set of the map (3) will be represented by the line segments ${\omega }_1=O{O}_{-1}^{(1)},{\omega }_2=O{O}_{-1}^{(2)}$ and their preimages ${\omega }_1^{-1}$ and ${\omega }_2^{-1}$, respectively.

Proposition 4.

Let ${\omega }_1=O{O}_{-1}^{(1)}$ and $,{\omega }_2=O{O}_{-1}^{(2)}$ then

$$\Im =\left({}_{n=0}^{\infty }{T}^{-n}({\omega }_1)\right)\cup \left({}_{n=0}^{\infty }{T}^{-n}({\omega }_2)\right),$$

forms the set of all rank-n preimages.

Using (3), one can get ${\omega }_1^{-1}$:$y=0$ or $y=1$ and ${\omega }_2^{-1}:x=0$ or $x=1$. Hence, any attracting set will have basins of attraction that are bounded by these line segments and their preimages. The phase plane of the map T can be divided into many regions denoted by $Z_i$ where the index i refers to the number of real rank-1 preimages under the map T. In order to identify these regions we should calculate the critical curve $LC$ that requires to first get $L{C}_{-1}$ and hence $LC=T(L{C}_{-1})$. Since T is continuous and differentiable then $L{C}_{-1}$ is obtained by vanishing the determinant of the Jacobian of T. It is represented by the following union $L{C}_{-1}=L{C}_{-1}^{(a)}\cup L{C}_{-1}^{(b)}\cup L{C}_{-1}^{(c)}$ where,

$$L{C}_{-1}^{(a)}:x=0,L{C}_{-1}^{(b)}:x=\frac{1}{2},L{C}_{-1}^{(c)}:y=\frac{1}{2}$$

(5)

It is clear that $L{C}_{-1}$ does not depend on ${\mu }_1$ and ${\mu }_2$. Using (3) and (5) $LC$ is represented by the union $LC=L{C}^{(a)}\cup L{C}^{(b)}\cup L{C}^{(c)}$ where,

$$\begin{array}{c}L{C}^{(a)}:x=0\mathrm{or}x=1,\hfill \\ L{C}^{(b)}:x=\frac{1}{2}\pm \frac{1}{2}\sqrt{1-\frac{2}{{\mu }_1}};{\mu }_1\ge 2\hfill \\ L{C}^{(c)}:{\mu }_{2}xy(1-y)=\frac{1}{2}\hfill \end{array}$$

(6)

Both $LC$ and $L{C}_{-1}$ are plotted in Figure 5. It is clear that $L{C}_c$ separates the region $Z_4$ whose points have four real rank-1 preimages from the region $Z_2$ whose points have two distinct rank-1 preimages. $L{C}_b$ separates at some intervals the region $Z_2$ from the $Z_4$ region [24]. In addition, all the corner points $(1,0),(0,1)$ and $(1,1)$ have no preimages and hence they belong to $Z_0$ region. Any points in the form $(\frac{{\mu }_1}{4},0)$ and $(0,\frac{{\mu }_2}{4})$ belong to $Z_2$ region.

5. Conclusions

The current work investigates some complex dynamic characteristics of a simple 2D logistic map. We have shown that the map’s fixed point becomes unstable due to the coexistence of some complex dynamic behaviors resulted in flip bifurcation; however, although the map is simple, it possesses different types of periodic cycles that have complex attractive basins that include holes of divergent points in the phase plane. We discussed the noninvertibility of the map and have confirmed that the phase plane of the map can be divided into three regions $Z_0,Z_2$ and $Z_4$. Furthermore, we calculated the critical curves of the map and show that any attracting set will have basins of attraction that have been bounded by the box $\left[0,1\right]\times \left[0,1\right]$. Our contribution in this paper has been focused on detecting some new complex dynamic characteristics for some periodic cycles including heteroclinic cycles and strange attractors with fractal basins. Though the map is simple, it possesses high periodic cycles whose basins are more complex due to the increasing number of holes represented by divergent points beside some strange attractors whose basins are fractal. Our future studies are to investigate such complex dynamic characteristics on 3D logistic map.