Interaction Patterns for Staggered Assembly of Fibrils from Semiflexible Chains
Abstract
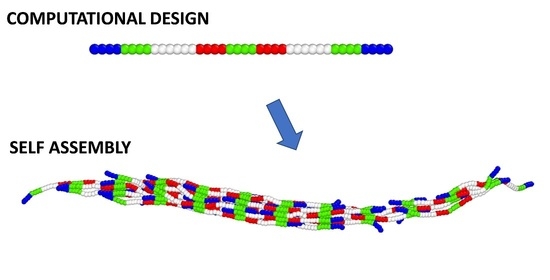
1. Introduction
2. Materials and Methods
3. Results
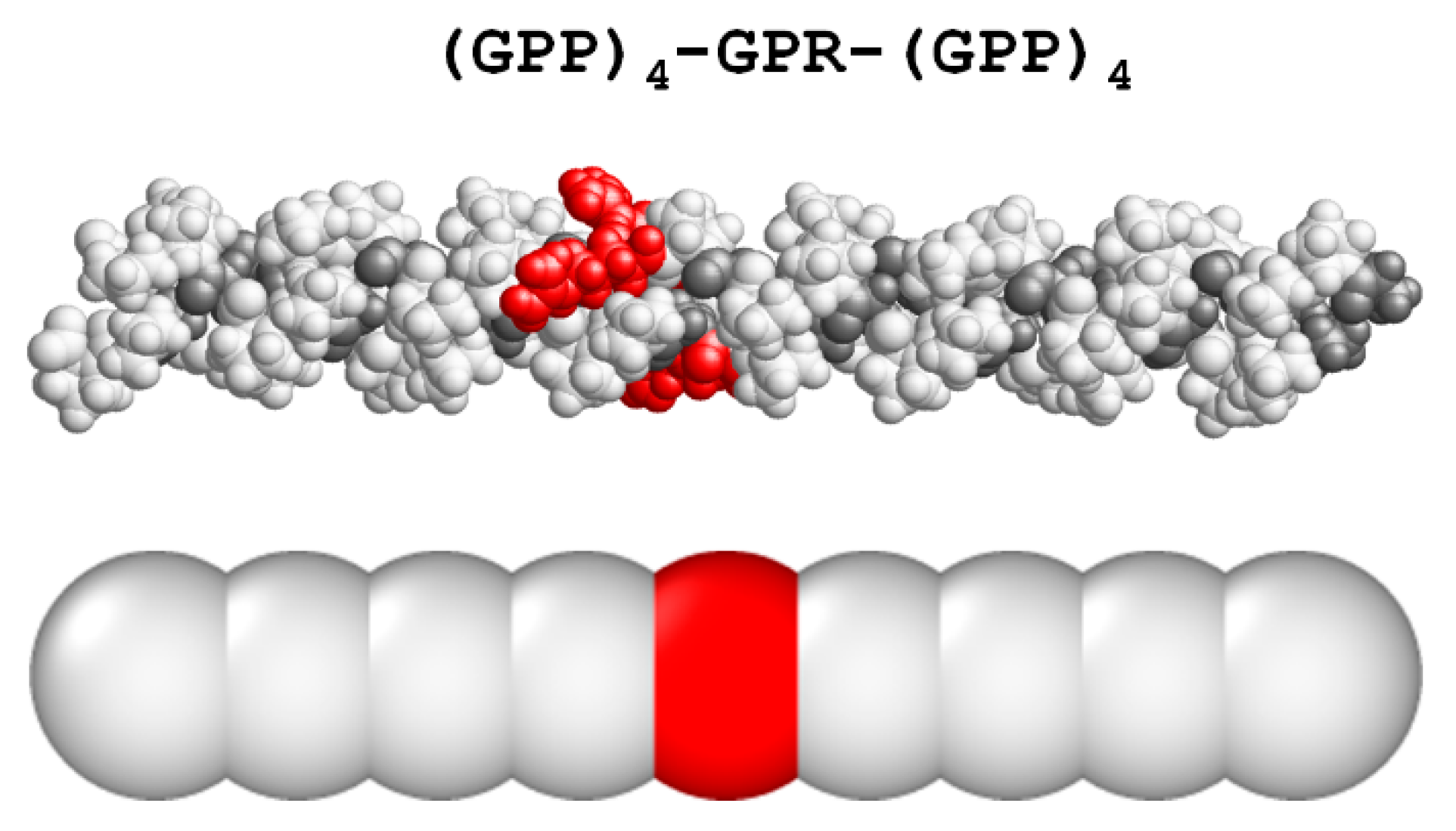
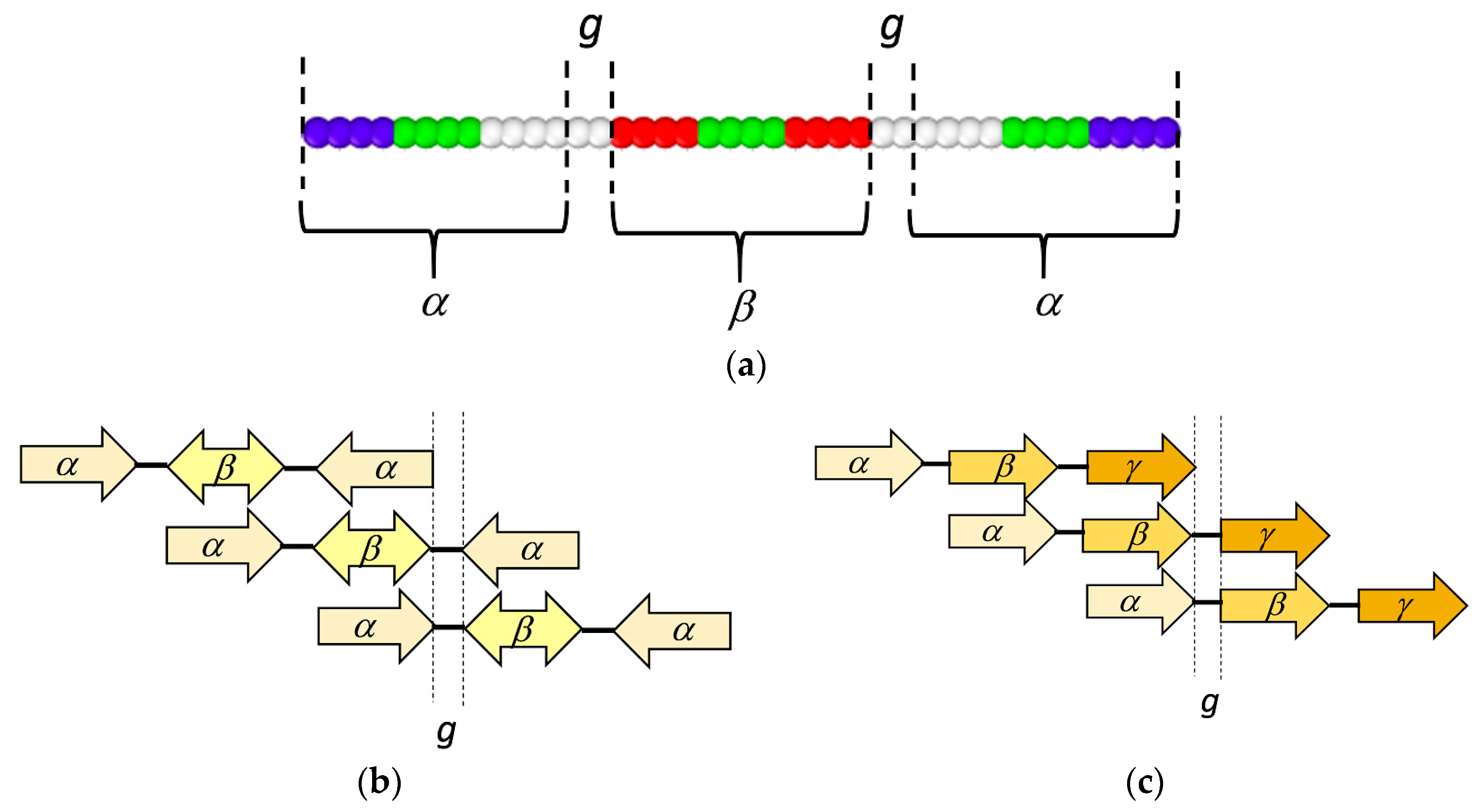
3.1. Coarse-Grained Model for Patterned Semiflexible Chains
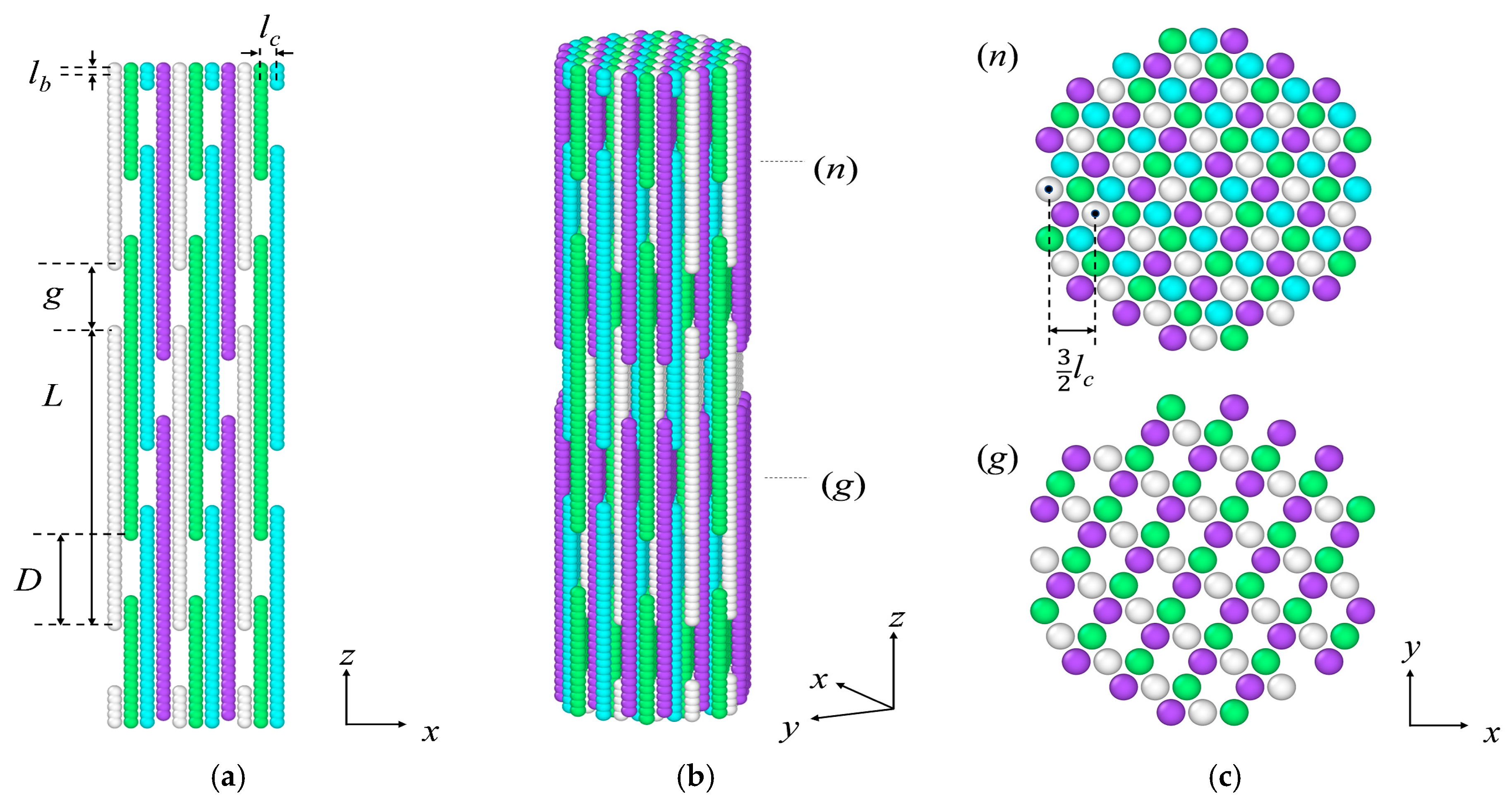
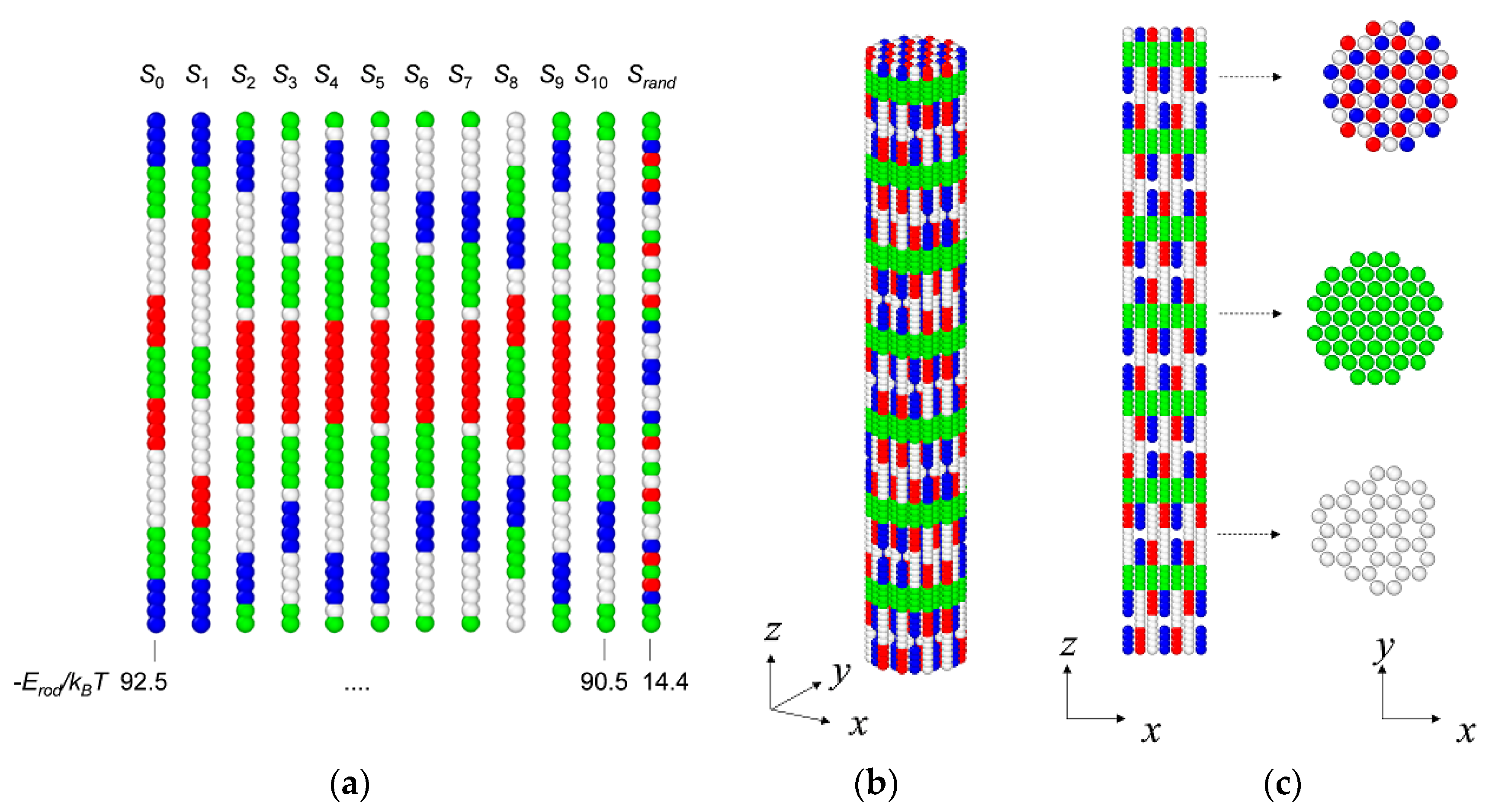
3.2. Target-Staggered Crystalline Arrangements
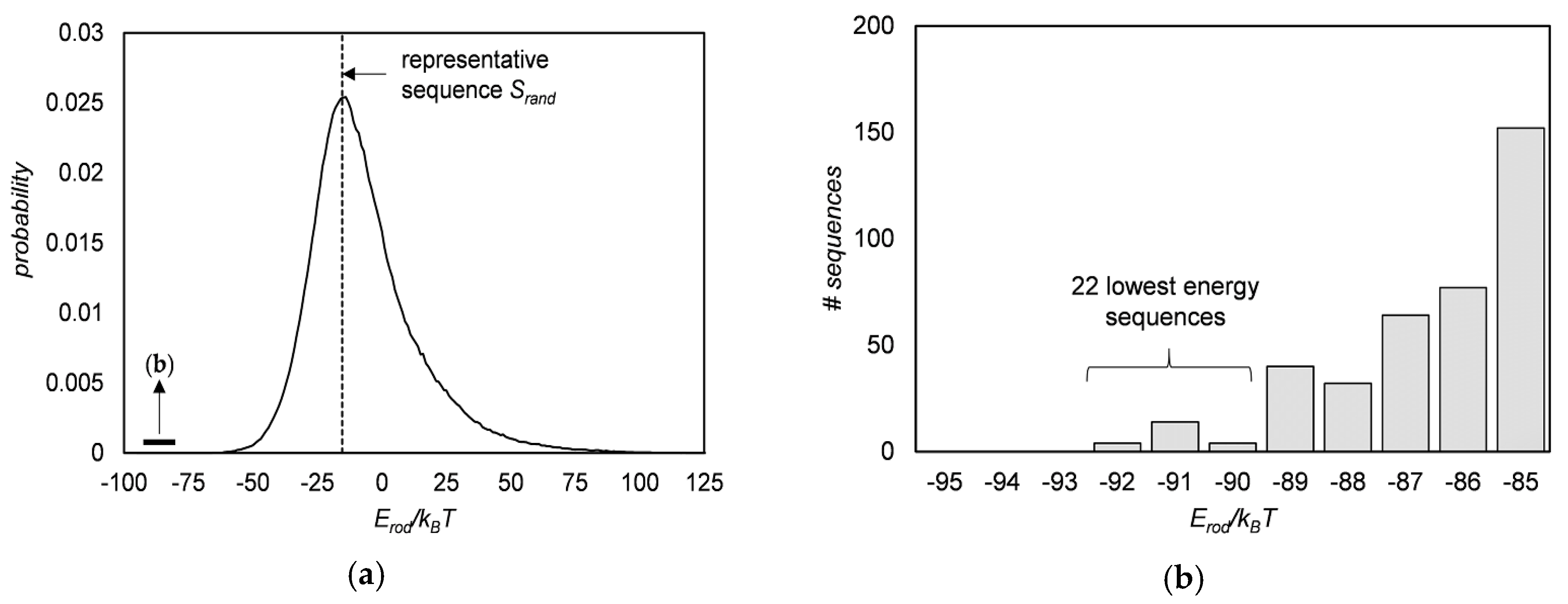
3.3. Sequence Optimization
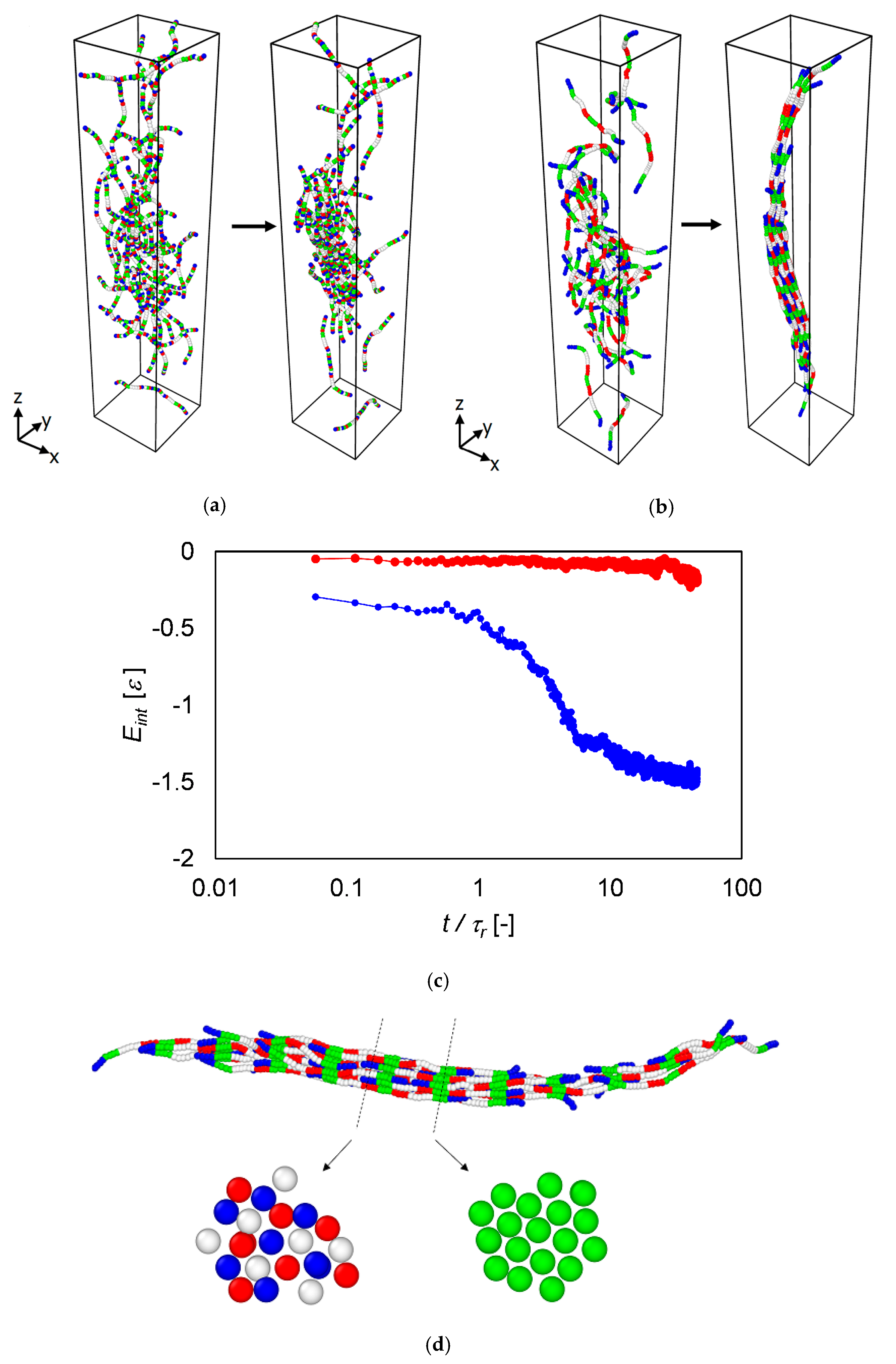
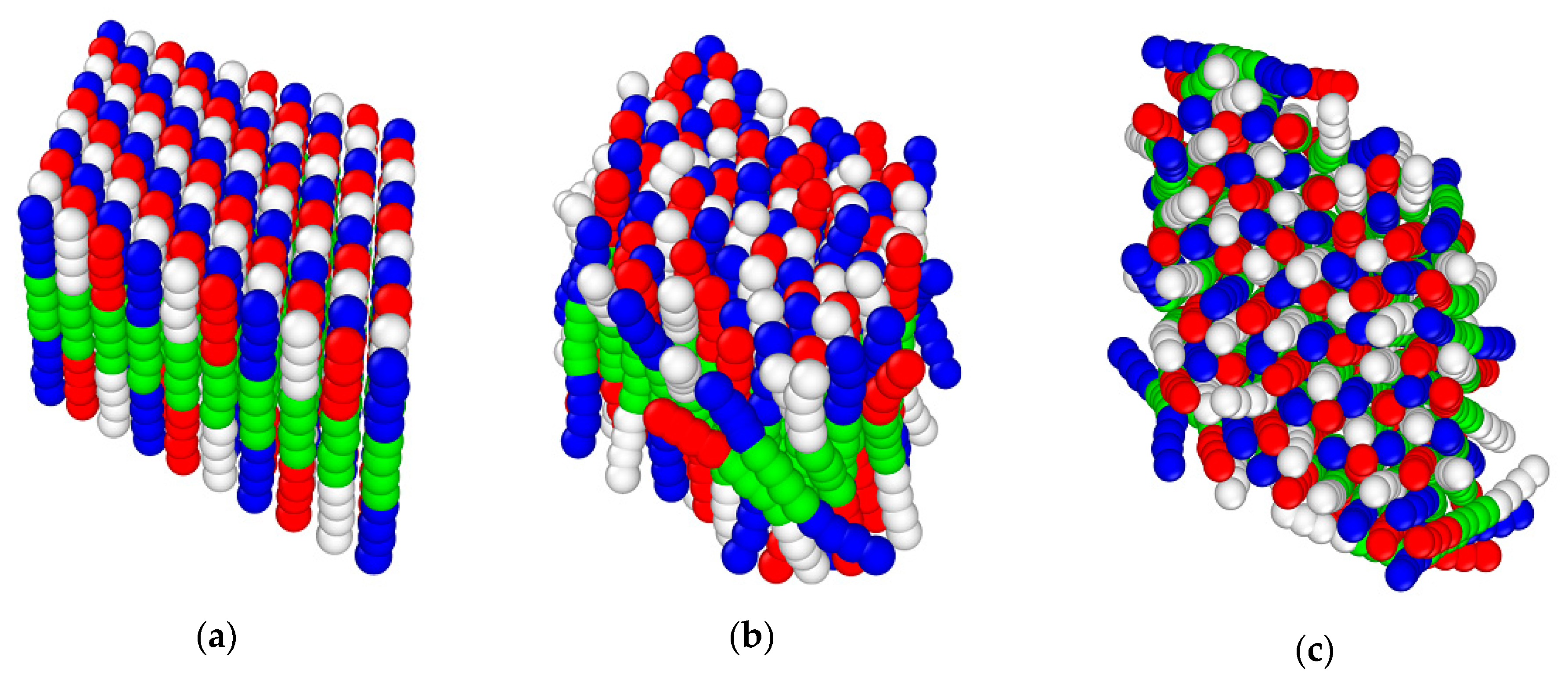
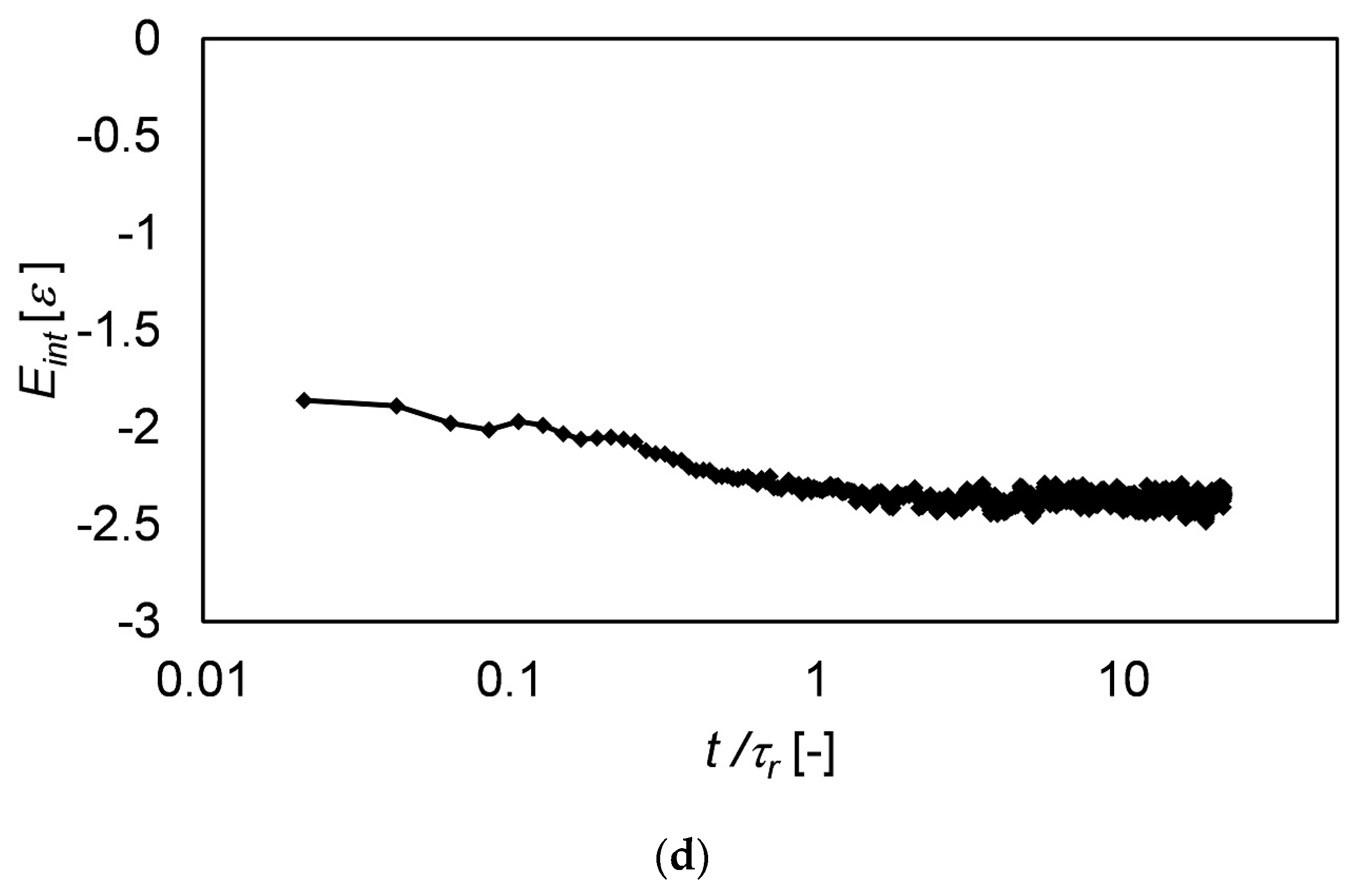
3.4. Langevin Dynamics Simulations
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seeman, N.C.; Sleiman, H.F. DNA nanotechnology. Nat. Rev. Mater. 2017, 3, 1–23. [Google Scholar]
- Huang, P.-S.; Boyken, S.E.; Baker, D. The coming of age of de novo protein design. Nat. Cell Biol. 2016, 537, 320–327. [Google Scholar] [CrossRef]
- Torquato, S. Inverse optimization techniques for targeted self-assembly. Soft Matter 2009, 5, 1157–1173. [Google Scholar] [CrossRef]
- Engel, M.; Damasceno, P.F.; Phillips, C.L.; Glotzer, S.C. Computational self-assembly of a one-component icosahedral quasicrystal. Nat. Mater. 2015, 14, 109–116. [Google Scholar] [CrossRef]
- Wilber, A.W.; Doye, J.P.K.; Louis, A.A.; Noya, E.G.; Miller, M.A.; Wong, P. Reversible self-assembly of patchy particles into monodisperse icosahedral clusters. J. Chem. Phys. 2007, 127, 085106. [Google Scholar] [CrossRef] [PubMed]
- Romano, F.; Sciortino, F. Patterning symmetry in the rational design of colloidal crystals. Nat. Commun. 2012, 3, 975–976. [Google Scholar] [CrossRef] [PubMed]
- Hulmes, D.J.S.; Miller, A.; Parry, D.A.D.; Piez, K.A.; Woodhead-Galloway, J. Analysis of the primary structure of collagen for the origins of molecular packing. J. Mol. Biol. 1973, 79, 137–148. [Google Scholar] [CrossRef]
- Doyle, B.B.; Hukins, D.W.L.; Hulmes, D.J.S.; Miller, A.; Rattew, C.J.; Woodhead-Galloway, J. Origins and implications of the D stagger in collagen. Biochem. Biophys. Res. Commun. 1974, 60, 858–864. [Google Scholar] [CrossRef]
- Meng, J.J.; Khan, S.; Ip, W. Charge interactions in the rod domain drive formation of tetramers during intermediate filament assembly. J. Biol. Chem. 1994, 269, 18679–18685. [Google Scholar]
- Eikenberry, E.F.; Brodsky, B. X-ray diffraction of reconstituted collagen fibers. J. Mol. Biol. 1980, 144, 397–404. [Google Scholar] [CrossRef]
- Kaur, P.J.; Strawn, R.; Bai, H.; Xu, K.; Ordas, G.; Matsui, H.; Xu, Y. The Self-assembly of a Mini-fibril with Axial Periodicity from a Designed Collagen-mimetic Triple Helix. J. Biol. Chem. 2015, 290, 9251–9261. [Google Scholar] [CrossRef] [PubMed]
- Strawn, R.; Chen, F.; Haven, P.J.; Wong, S.; Park-Arias, A.; De Leeuw, M.; Xu, Y. To achieve self-assembled collagen mimetic fibrils using designed peptides. Biopolymers 2018, 109, e23226. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Strawn, R.; Xu, Y. The predominant roles of the sequence periodicity in the self-assembly of collagen-mimetic mini-fibrils. Protein Sci. 2019, 28, 1640–1651. [Google Scholar] [CrossRef] [PubMed]
- Kouwer, P.H.J.; Koepf, M.; Le Sage, V.A.A.; Jaspers, M.; Van Buul, A.M.; Eksteen-Akeroyd, Z.H.; Woltinge, T.; Schwartz, E.; Kitto, H.J.; Hoogenboom, R.; et al. Responsive biomimetic networks from polyisocyanopeptide hydrogels. Nat. Cell Biol. 2013, 493, 651–655. [Google Scholar] [CrossRef]
- Włodarczyk-Biegun, M.K.; Slingerland, C.J.; Werten, M.W.T.; Van Hees, I.A.; De Wolf, F.A.; De Vries, R.; Stuart, M.A.C.; Kamperman, M. Heparin as a Bundler in a Self-Assembled Fibrous Network of Functionalized Protein-Based Polymers. Biomacromolecules 2016, 17, 2063–2072. [Google Scholar] [CrossRef] [PubMed]
- Freeman, R.; Han, M.; Álvarez, Z.; Lewis, J.A.; Wester, J.R.; Stephanopoulos, N.; McClendon, M.T.; Lynsky, C.; Godbe, J.M.; Sangji, H.; et al. Reversible self-assembly of superstructured networks. Science 2018, 362, 808–813. [Google Scholar] [CrossRef]
- Rele, S.; Song, Y.; Apkarian, R.P.; Qu, Z.; Conticello, V.P.; Chaikof, E.L. D-Periodic Collagen-Mimetic Microfibers. J. Am. Chem. Soc. 2007, 129, 14780–14787. [Google Scholar] [CrossRef]
- Sharp, T.H.; Bruning, M.; Mantell, J.; Sessions, R.B.; Thomson, A.R.; Zaccai, N.R.; Brady, R.L.; Verkade, P.; Woolfson, D.N. Cryo-transmission electron microscopy structure of a gigadalton peptide fiber of de novo design. Proc. Natl. Acad. Sci. USA 2012, 109, 13266–13271. [Google Scholar] [CrossRef]
- Rosenbaum, D.M.; Liu, D.R. Efficient and Sequence-Specific DNA-Templated Polymerization of Peptide Nucleic Acid Aldehydes. J. Am. Chem. Soc. 2003, 125, 13924–13925. [Google Scholar] [CrossRef]
- Vesentini, S.; Redaelli, A.; Gautieri, A. Nanomechanics of collagen microfibrils. Muscles Ligaments Tendons J. 2013, 3, 23–34. [Google Scholar] [CrossRef]
- Kirkness, M.W.; Lehmann, K.; Forde, N.R. Mechanics and structural stability of the collagen triple helix. Curr. Opin. Chem. Biol. 2019, 53, 98–105. [Google Scholar] [CrossRef] [PubMed]
- LAMMPS Molecular Dynamics Simulator. Available online: https://lammps.sandia.gov/ (accessed on 1 September 2020).
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Grønbech-Jensen, N.; Farago, O. A simple and effective Verlet-type algorithm for simulating Langevin dynamics. Mol. Phys. 2013, 111, 983–991. [Google Scholar] [CrossRef]
- Grønbech-Jensen, N.; Hayre, N.R.; Farago, O. Application of the G-JF discrete-time thermostat for fast and accurate molecular simulations. Comput. Phys. Commun. 2014, 185, 524–527. [Google Scholar] [CrossRef]
- Ramshaw, J.A.M.; Shah, N.K.; Brodsky, B. Gly-X-Y Tripeptide Frequencies in Collagen: A Context for Host–Guest Triple-Helical Peptides. J. Struct. Biol. 1998, 122, 86–91. [Google Scholar] [CrossRef]
- Bromley, E.H.C.; Channon, K.; Moutevelis, E.; Woolfson, D.N. Peptide and Protein Building Blocks for Synthetic Biology: From Programming Biomolecules to Self-Organized Biomolecular Systems. ACS Chem. Biol. 2008, 3, 38–50. [Google Scholar] [CrossRef]
- Reinke, A.W.; Grant, R.A.; Keating, A.E. A Synthetic Coiled-Coil Interactome Provides Heterospecific Modules for Molecular Engineering. J. Am. Chem. Soc. 2010, 132, 6025–6031. [Google Scholar] [CrossRef]
- Fletcher, J.M.; Harniman, R.L.; Barnes, F.R.H.; Boyle, A.L.; Collins, A.; Mantell, J.; Sharp, T.H.; Antognozzi, M.; Booth, P.J.; Linden, N.; et al. Self-Assembling Cages from Coiled-Coil Peptide Modules. Science 2013, 340, 595–599. [Google Scholar] [CrossRef]
- Gradišar, H.; Božič, S.; Doles, T.; Vengust, D.; Hafner-Bratkovič, I.; Mertelj, A.; Webb, B.S.; Šali, A.; Klavžar, S.; Jerala, R. Design of a single-chain polypeptide tetrahedron assembled from coiled-coil segments. Nat. Chem. Biol. 2013, 9, 362–366. [Google Scholar] [CrossRef]
- Locardi, E.; Kwak, J.; Scheraga, H.A.; Goodman, M. Thermodynamics of Formation of the Triple Helix from Free Chains and from Template-Constrained Chains of Collagen-like Monodisperse Poly(Gly-Pro-Hyp) Structures. J. Phys. Chem. A 1999, 103, 10561–10566. [Google Scholar] [CrossRef]
- Persikov, A.V.; Ramshaw, J.A.M.; Brodsky, B. Prediction of Collagen Stability from Amino Acid Sequence. J. Biol. Chem. 2005, 280, 19343–19349. [Google Scholar] [CrossRef] [PubMed]
- Doig, A.J. Statistical Thermodynamics of the Collagen Triple-Helix/Coil Transition. Free Energies for Amino Acid Substitutions within the Triple-Helix. J. Phys. Chem. B 2008, 112, 15029–15033. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Brodsky, B.; Inouye, M. Dissecting a Bacterial Collagen Domain fromStreptococcus pyogenes: Sequence and length-dependent variations in triple helix stability and folding. J. Biol. Chem. 2011, 286, 18960–18968. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; An, B.; Ramshaw, J.A.M.; Brodsky, B. Bacterial collagen-like proteins that form triple-helical structures. J. Struct. Biol. 2014, 186, 451–461. [Google Scholar] [CrossRef]
- Alford, R.F.; Leaver-Fay, A.; Jeliazkov, J.R.; O’Meara, M.J.; DiMaio, F.P.; Park, H.; Shapovalov, M.V.; Renfrew, P.D.; Mulligan, V.K.; Kappel, K.; et al. The Rosetta All-Atom Energy Function for Macromolecular Modeling and Design. J. Chem. Theory Comput. 2017, 13, 3031–3048. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Value | Unit |
|---|---|---|
| κ | 1.5 | σ−1 |
| lB | 0.47 | σ |
| q | 2.0 | − |
| 2.0 | ||
| 0.1 | ||
| lb | 0.57 | σ |
| ks | 100 | |
| kb | 10 |
| Packing | L/lb | D/lb | g/lb | |
|---|---|---|---|---|
| P1 | 40 | 14 | 3 | 2 |
| P2 | 40 | 15 | 3 | 5 |
| P3 | 40 | 16 | 3 | 8 |
| P4 | 40 | 11 | 4 | 4 |
| P5 | 40 | 12 | 4 | 8 |
| P6 | 40 | 9 | 5 | 5 |
| P7 | 40 | 8 | 6 | 8 |
| P8 | 40 | 7 | 6 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jongeling, A.; Svaneborg, C.; Vries, R.d. Interaction Patterns for Staggered Assembly of Fibrils from Semiflexible Chains. Symmetry 2020, 12, 1926. https://doi.org/10.3390/sym12111926
Jongeling A, Svaneborg C, Vries Rd. Interaction Patterns for Staggered Assembly of Fibrils from Semiflexible Chains. Symmetry. 2020; 12(11):1926. https://doi.org/10.3390/sym12111926
Chicago/Turabian StyleJongeling, Arnoud, Carsten Svaneborg, and Renko de Vries. 2020. "Interaction Patterns for Staggered Assembly of Fibrils from Semiflexible Chains" Symmetry 12, no. 11: 1926. https://doi.org/10.3390/sym12111926
APA StyleJongeling, A., Svaneborg, C., & Vries, R. d. (2020). Interaction Patterns for Staggered Assembly of Fibrils from Semiflexible Chains. Symmetry, 12(11), 1926. https://doi.org/10.3390/sym12111926