Complete Quantum Information in the DNA Genetic Code

Abstract

We find that the degeneracies and many peculiarities of the DNA genetic code may be described thanks to two closely related (fivefold symmetric) finite groups. The first group has signature $G={\mathbb{Z}}_5⋊H$ where $H={\mathbb{Z}}_2.S_4\cong 2O$ is isomorphic to the binary octahedral group $2O$ and $S_4$ is the symmetric group on four letters/bases. The second group has signature $G={\mathbb{Z}}_5⋊GL(2,3)$ and points out a threefold symmetry of base pairings. For those groups, the representations for the 22 conjugacy classes of G are in one-to-one correspondence with the multiplets encoding the proteinogenic amino acids. Additionally, most of the 22 characters of G attached to those representations are informationally complete. The biological meaning of these coincidences is discussed.

1. Introduction

La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi a gli occhi (io dico l’universo), ma non si può intendere se prima non s’impara a intender la lingua, e conoscer i caratteri, ne’ quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi, ed altre figure geometriche, senza i qualimezi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro laberinto.

(Galileo Galilei (1564–1642), Il Saggiatore, cap. 6).

Until now, deciphering the code of life [1,2,3,4,5,6,7,8]—the genetic code—has not been fully successful although theories have been proposed before [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. How is our new attempt different from earlier trials? Our mathematical approach lies at the crossroads of finite group theory and quantum information in line with other papers mainly devoted to quantum computing [33] but also focused on elementary particles [34].

Life cells need a macromolecule called deoxyribonucleic acid (or DNA) to be packed in a chromosome during cell mitosis. DNA unwinds when it is copied during DNA replication or when its code is used to make proteins. DNA is a helix consisting of two parallel polynucleotide chains carrying genetic instructions in 4 nitrogeneous bases for the growth and reproduction of all living organisms. The genetic code is organized in triples of bases called codons. There are $4^3=64$ codons but only 20 standard amino acids, meaning a high redundancy of the code. In our approach, we use the characters and corresponding representations of a well-defined finite group G to explain the mapping of the nitrogeneous bases to amino acids. The group characters may be used to build minimal and informationally complete quantum measurements, one for each character and corresponding amino acid.

Section 2.1 details the discovery and main properties of DNA and the genetic code. Section 2.2 reports the main efforts already accomplished towards the understanding and origin of the genetic code. Section 3 recalls how minimal informationally complete quantum measurements are performed and the necessary elements of character theory of finite groups. In Section 4, the assignment of characters of the small group $G=(240,105)$ to amino acids is detailed. In Section 5, we provide a justification for the fact that minor and major grooves in the DNA double helix have periods whose ratio approximates the golden ratio. This is based on the study of points over a hyperelliptic curve occuring in the character table.

2. DNA and the Genetic Code

In this section, we summarize the main aspects of DNA from a historical perspective (in Section 2.1) and some previous attempts to explain the degeneracies in the mapping of codons to proteins (in Section 2.2).

2.1. Main Properties of DNA and the Genetic Code

The discovery of DNA is attributed to Watson and Crick in 1953 [1]. However, the phosphorous-containing substance now called DNA was first isolated by F. Miescher in 1869 in the nuclei of white blood cells under the name of ‘nuclein’ (a nucleic acid) paving the way for its recognition as the carrier of inheritance [2]. In 1909, P. Levene found that DNA contains the pentoses (A), guanine (G), thymine (T), cytosine (C), a deoxyribose, and a phosphate group. At that time, it was still believed that the protein component of chromosomes was the true basis of heredity. The recognition that DNA rather than proteins could be the genetic material was suggested by the E. Chargaff’s rules, which proposed in 1940 that the four bases are present in the percentages: $A\approx T\approx 30\%$ and $G\approx C\approx 20\%$ for all species [3]. Subsequent X-ray crystallography work by English researchers R. Franklin and M. Wilkins contributed to Watson and Crick’s derivation of the three-dimensional, double-helical model for the structure of DNA [4].

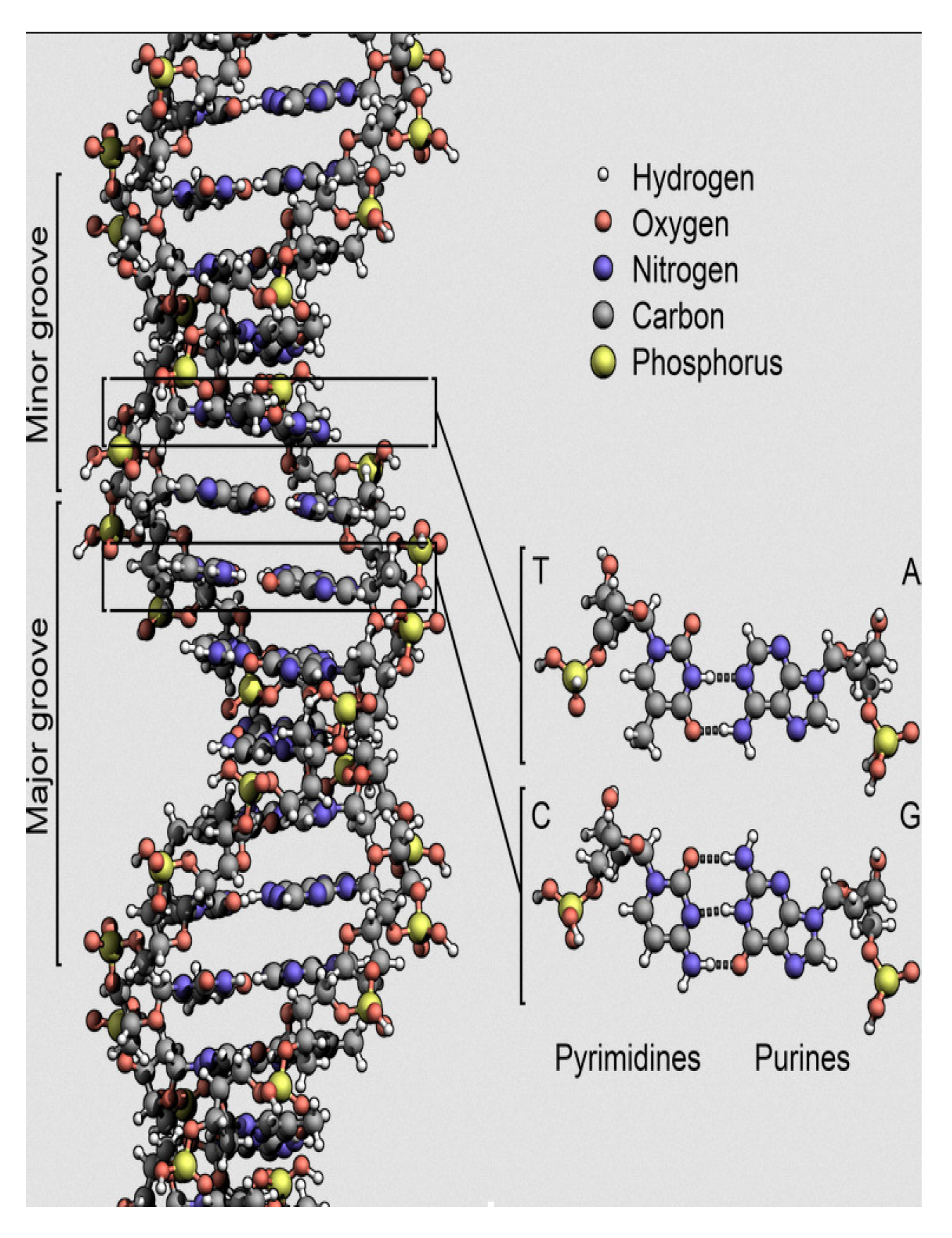
As shown in Figure 1, DNA is a double helix, with the two strands connected by hydrogen bonds. In the most current form of DNA (called B-DNA), the ratio of the diameter $D\approx 21$ to the period $l+L$ and the ratio between the minor groove $l\approx 13$ and major groove $L\approx D\approx 21$ are both close to the golden ratio $\varphi =(\sqrt{5}-1)/2\approx 0.618$ [35].

G. Gamow (also a cosmologist) observed that the $4^3=64$ possible permutations of the four DNA bases A, T, G, and C, taken three at a time (as codons), could be reduced to 20 distinct combinations and might code for the 20 amino acids which, he suggested, might well be the sole constituents of all proteins [5]. However the lack of overlapping of codons (not assumed by Gamow) and the demonstration that the genetic code is made up of a series of three base pair codons, which code for individual amino acids, dates back to 1961 with the Crick, Brenner et al. experiment [6]. Now we know that the peculiar non ambiguous and non overlapping assignment of all 64 codons to the 20 amino acids is nearly universal [7].

The ‘genetic code’ is the set of rules used by living cells to translate information encoded within genetic material (DNA or messenger RNA sequences of nucleotide triplets, or codons) into proteins. Translation is accomplished by the ribosome, which links amino acids in an order specified by messenger RNA (mRNA), using transfer RNA (tRNA) molecules to carry amino acids, and to read the mRNA, three nucleotides at a time.

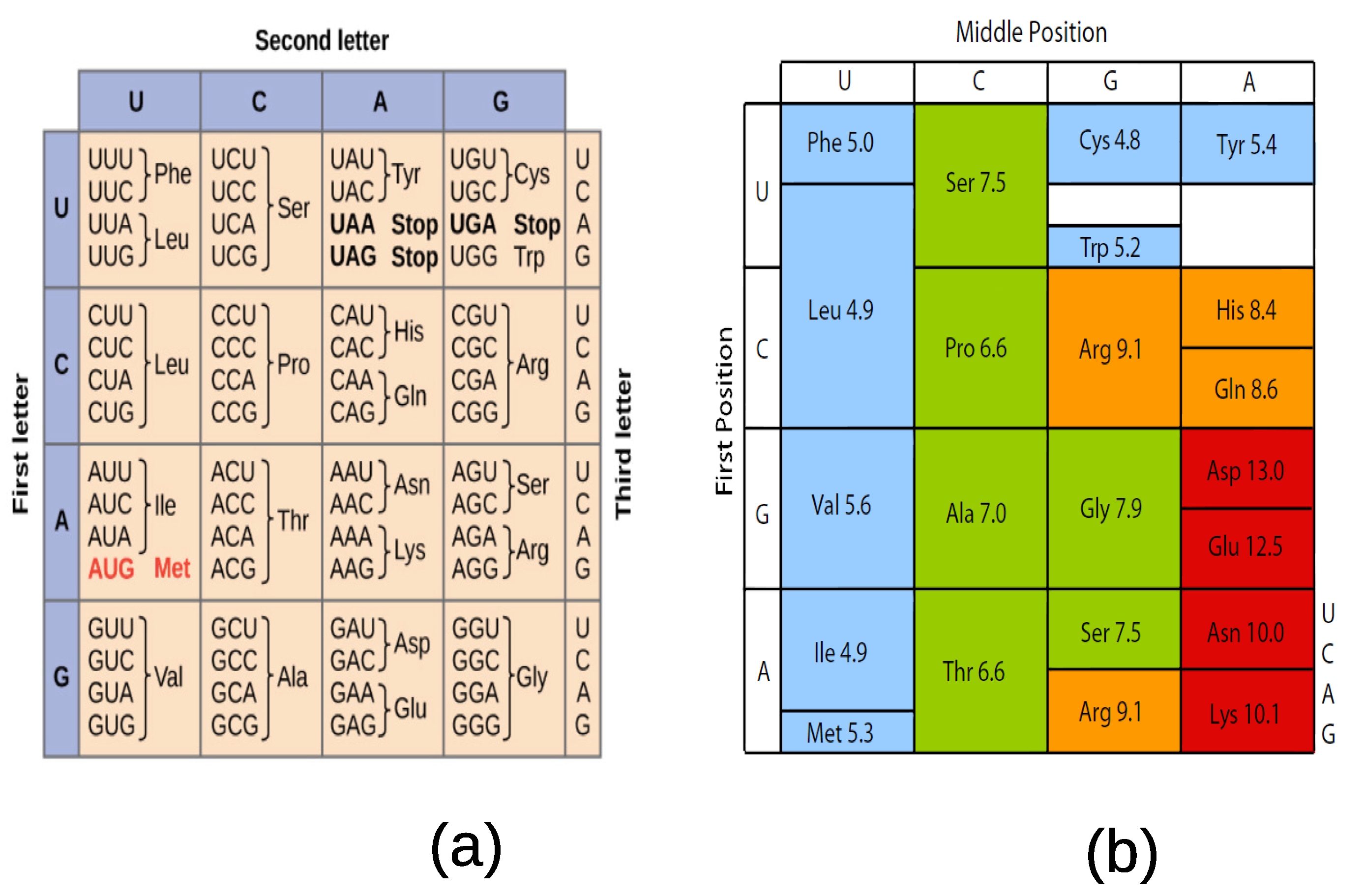
The codons which code for the same amino acids form multiplets and are organized as:

• Met, Trp: 2 singlets;
• Asn, Asp, Cys, Gln, Glu, His, Lys, Phe, Tyr: 9 doublets;
• Ile, Term: 2 triplets;
• Ala, Gly, Pro, Thr, Val: 5 quadruplets;
• Arg, Leu, Ser: 3 sextets.

A 21st proteinogenic amino acid Selenocysteine (symbol Sec) was found present in some enzymes and a 22st amino acid Pyrrolysine (Symbol Pyl) in some archaea and bacteria.

The assignment of three-letter codons to the standard 20 amino acids is shown in Figure 2a. It is clearly seen in this table that the assignment of codons to amino acids is not random but follows underlying rules to be discovered.

2.2. Theories about the Degeneracies within the Genetic Code

Woese and collaborators introduced the concept of polar requirement to express stereochemical associations between amino acids and nucleobases in solution [8,9]. Taking dimethylpyridine (or DMP) as a solvant, the polar requirement is found as in Figure 2b [11,12]. For more recent predictors of the stereochemical associators the reader may read reference [13]. While the polar requirement is correlated with the organization of the codon table, it does not provide a clue about the type of degeneracies selected almost universally in extant organisms.

It is common to distinguish several levels in DNA structure. The primary structure consists of the sequence of amino acids, the secondary structure consists of the base pairings and can be decomposed into stems, loops, or their combinations and the tertiary structure corresponds to their three-dimensional embedding. As a last resort, the symmetries of the tertiary structure are responsible for the structure of the genetic code.

The physical link between messenger RNA (mRNA) and the amino acid sequence of proteins is a transfer RNA (tRNA). Corresponding to the three bases of an mRNA codon is an anticodon. Each tRNA has a distinct anticodon triplet sequence that can form three complementary base pairs to one or more codons for an amino acid. Some anticodons pair with more than one codon due to so-called wobble base pairing. Considering the secondary and tertiary structure of tRNA, as well as the fact that the third position in the codon is not strictly read by the anticodon according to Watson–Crick pairing rules, Crick hypothesized that codon translation into a proteins is mainly due to the first two positions of the codon [14,15]. There are 16 groups of codons specified by the first two codonic positions and the level of degeneracy can be dermined by them according to Lagerkvist’s rules [16,17].

In the same line of thoughts, doublet codings may have been associated to reverse recognition in earlier times of life organisms [18,19]. This prompted the authors of [21,22] to propose a model of the genetic code and its degeneracy distribution based on a boolean number system and/or a tessera code. See also [23] about the ribosomal translation and [24,25] about the hypothesis that life on earth and the genetic code evolved around tRNA and the corresponding anticodons.

A completely different approach of the genetic code has been based on a Lie group G and a chain of subgroups derived by a symmetry breaking process [26,27]. This view is reminiscent of the one used to explain the periodic table of chemical elements as well as the multiplet structure of massive elementary particles such as quarks. The most satisfactorily theory of the genetic code would result from the symplectic algebra $\mathrm{sp}\left(6\right)$ through the appropriate symmetry breaking chain. A similar program has been proposed for finite simple groups [28,29].

Finally, there exist many other attempts to map the codons to multiplets of the genetic code thanks to an appropriate algebraic geometric object. Let us mention [30], which describes the genetic code thanks to an hypercube ${\mathbb{Z}}_2^6$, Ref. [31] which makes use of the symmetries of the polyhedral symmetries of a quasi-28-gon, and [32] which parametrizes the codons in terms of integer quaternions.

3. Symmetries and Quantum Information from the Characters of a Finite Group

There are two important ingredients in our approach. One topic follows from our earlier work on ‘magic state’ quantum computing [33] and consists of performing a generalized quantum measurement while keeping complete information in the process, as explained in Section 3.1. The second (more recent) topic consists of finding the ‘magic states’ in the bank of characters of a selected finite group. The latter approach recalled in Section 3.2 was found successful in the context of symmetries of elementary matter particles [34].

3.1. Minimal Informationally Complete Quantum Measurements

Let ${\mathcal{H}}_d$ be a d-dimensional complex Hilbert space and $\{E_1,\dots ,E_m\}$ be a collection of positive semi-definite operators (POVM) that sum up to the identity. Taking the unknown quantum state as a rank 1 projector $\rho =\left|\psi \right.〉\left.〈\psi \right|$ (with ${\rho }^2=\rho$ and $\mathrm{tr}\left(\rho \right)=1$), the i-th outcome is obtained with a probability given by the Born rule $p\left(i\right)=\mathrm{tr}\left(\rho E_i\right)$. A minimal and informationally complete POVM (or MIC) requires $d^2$ one-dimensional projectors ${\Pi }_i=\left|{\psi }_i\right.〉\left.〈{\psi }_i\right|$, with ${\Pi }_i=d{E}_i$, such that the rank of the Gram matrix with elements $\mathrm{tr}\left({\Pi }_i{\Pi }_j\right)$, is precisely $d^2$.

With a MIC, the complete recovery of a state $\rho$ is possible at a minimal cost from the probabilities $p\left(i\right)$. In the best case, the MIC is symmetric and called a SIC with a further relation ${\left|〈{\psi }_i|{\psi }_j〉\right|}^2=\mathrm{tr}\left({\Pi }_i{\Pi }_j\right)=\frac{d{\delta }_{ij}+1}{d+1}$ so that the density matrix $\rho$ can be made explicit [37].

In our earlier references, starting with [33], a large collection of MICs are derived. They correspond to Hermitian angles ${\left|〈{\psi }_i|{\psi }_j〉\right|}_{i\ne j}\in A=\{a_1,\dots ,a_l\}$ belonging to a discrete set of values of small cardinality l. They arise from the action of a Pauli group ${\mathcal{P}}_d$ [38] on an appropriate magic state pertaining to the coset structure of subgroups of index d of a free group with relations.

Let us illustrate our topic with the derivation of a 3-dimentional MIC. The qutrit Pauli group is generated by the shift (X) and clock (Z) operators as follows:

$$X\left|j\right.〉=\left|j+1mod3\right.〉,Z\left|j\right.〉={\omega }^j\left|j\right.〉,$$

(1)

with $\omega =exp(2i\pi /3)$ and j takes the three values 0, 1, and 2. The generators are:

$$X=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right),\mathrm{and}Z=\left(\begin{array}{ccc}1& 0& 0\\ 0& \omega & 0\\ 0& 0& {\omega }^2\end{array}\right).$$

(2)

It is not difficult to check that a qutrit magic state can be taken as:

$$\left|m\right.〉=(0,1,\pm 1)=\left(\left|1\right.〉\right)\pm \left|2\right.〉)/\sqrt{2}.$$

(3)

The nine qutrit Pauli matrices are:

$$I,Z,Z^2,X,X^2,XZ,X{Z}^2,\left(X{Z}^2\right),{\left(X{Z}^2\right)}^2,{\left(XZ\right)}^2.$$

(4)

Taking the action of Pauli matrices, one arrives at the so-called Hesse SIC [33] (Figure 1).

Similarly, the generalized Pauli group for a d-dimensional qudit is generated by shift (X) and clock (Z) operators:

$$X\left|j\right.〉=\left|j+1modd\right.〉,Z\left|j\right.〉={\omega }^j\left|j\right.〉,$$

(5)

with $\omega =exp(2i\pi /d)$ and j takes the values from 0 to $d-1$. The challenge is to find an appropriate d-dimensional magic state $\left|m\right.〉$ so that a MIC results from the action of the Pauli group on the projector $\left|m\right.〉\left.〈m\right|$.

In [33] (

Table 1. The character table for the symmetric group $G=S_4$. There are five conjugacy classes of elements of dimensions 1, 1, 2, 3, and 3, respectively. The size and the order of an element in the class is as shown. The last five rows of the table are the irreducible characters ${\kappa }_i$, $i=1,\dots ,5$, of G. To each of them is associated the rank of the Gram matrix defined in Section 3.1.

Class	1	2	3	4	5	Class
Size	1	3	6	8	6	Size
Order	1	2	2	3	4	Order
Char	dim					Gram
${\kappa }_1$	1	1	1	1	1	5
${\kappa }_2$	1	1	−1	1	− 1	21
${\kappa }_3$	2	2	0	−1	0	$d^2$
${\kappa }_4$	3	−1	−1	0	1	$d^2$
${\kappa }_5$	3	−1	1	0	−1	$d^2$

) and later references of the first author, e.g., [39], a number of cases are provided with $d\ge 3$ obtained from permutation groups. In reference [34], an entirely new class of MICs in the Hilbert space ${\mathcal{H}}_d$, relevant for the lepton and quark mixing patterns, is obtained by taking fiducial/magic states as characters of a finite group G possessing d conjugacy classes and using the action of a Pauli group ${\mathcal{P}}_d$ on them. The same approach is used in this paper.

3.2. The Character Table of a Finite Group and Quantum Information

Let G be a finite group, V a finite-dimensional vector space over a field F, and let $r:G\to GL\left(V\right)$ be a representation of G on V. The character ${\kappa }_r\left(g\right)$ associates to an element $g\in G$ the trace of the corresponding matrix $r\left(g\right)$. A character ${\kappa }_r$ is called irreducible if r is an irreducible representation. The degree of the character $\kappa$ is called the dimension of the representation.

Assume that G is made of d conjugacy classes of elements. One introduces class functions on G from the ring of complex-valued functions on G that are constant on conjugacy classes. In fact we restrict ourselves to functions with values in cyclotomic fields [40].

The table of irreducible characters of G, or character table for short, is a way to summarize the properties of irreducible representations of elements g of G.

Let us take the case of the symmetric group $S_4$, also called the small group $(24,12)$ (number 12 in the range of 15 groups of order 24). The character table is in Table 1. It makes explicit the five irreducible characters of G, the corresponding dimension $\dim$ of the representation, as well as the size and order of an element in each class. For each class, we added the calculation of the rank of the Gram matrix that corresponds to the POVM obtained by the action of the 5-dit Pauli group over the irreducible character ${\kappa }_i$ of the class. For the classes 3 to 5, the rank of the Gram matrix is $d^2=25$ so that the POVM is a MIC.

As a second example, one takes the binary octahedral group $2O$ also called the small group $(48,28)$ (number 28 in the range of 52 groups of order 48). Group $2O$ is an important ingredient of our model of the genetic code, as shown in Section 4. The character table is shown in

Table 2. The character table for the symmetric group $G=2O=(48,28)$. There are eight conjugacy classes of elements of dimensions $1(\times 2)$, $2(\times 3)$, $3(\times 2)$, and 4. The size and the order of an element in the class is as shown. The last five rows of the table are the irreducible characters ${\kappa }_i$, $i=1,\cdots ,8$, of G. To each of them is associated the rank of the Gram matrix defined in Section 3.1.

Class	1	2	3	4	5	6	7	8	Class
Size	1	1	8	6	12	8	6	6	Size
Order	1	2	3	4	4	6	8	8	Order
Char	dim								Gram
${\kappa }_1$	1	1	1	1	1	1	1	1	8
${\kappa }_2$	1	1	1	1	− 1	1	−1	−1	45
${\kappa }_3$	2	2	−1	2	0	−1	0	0	56
${\kappa }_4$	2	−2	−1	0	0	1	$\sqrt{2}$	$-\sqrt{2}$	59
${\kappa }_5$	2	−2	−1	0	0	1	$-\sqrt{2}$	$\sqrt{2}$	59
${\kappa }_6$	3	3	0	−1	1	0	−1	−1	59
${\kappa }_7$	3	3	0	−1	−1	0	1	1	59
${\kappa }_8$	4	−4	1	0	0	−1	0	0	59

. It makes explicit the eight irreducible characters of G, the corresponding dimension of the representation, as well as the size and order of an element in each class. At the right hand side of the column, one finds the rank of the Gram matrix that corresponds to the POVM obtained by the action of the 8-dit Pauli group over the irreducible character ${\kappa }_i$ of the class. None of the characters of the group $2O$ is informationally complete.

4. Symmetries and Quantum Information in the Genetic Code

As shown in the previous section, there may exist several representations of a given dimension in a finite group. Does a group G exist whose multiplets map to the multiplets of the genetic code in a satisfactorily way? We shall impose the constraint that there are enough n-plets to embed the mappings to the proteinogenic amino acids for dimensions $n=1$, 2, 3, and 4 and that there are at least 2 sextuplets. Small groups $(240,105)$ and $(240,106)$ (with 22 conjugacy classes) and $(240,107)$ and $(240,108)$ (with 28 conjugacy classes) are the group candidates with the smallest cardinality. All of them have two 6-dimensional representations. We could not find another candidate group of a higher cardinality. The most economical groups are thus the former two groups and the latter two are different only in the sense that there are 6 one-dimensional representations instead of two.

The first group $(240,105)$ has signature $G={\mathbb{Z}}_5⋊H$ where $H={\mathbb{Z}}_2.S_4\cong 2O$ is isomorphic to the binary octahedral group $2O$ and $S_4$ is the symmetric group on four letters/bases. The second group $(240,106)$ has signature $G={\mathbb{Z}}_5⋊GL(2,3)$ and points out a threefold symmetry of base pairings. For those groups, the representations for the 22 conjugacy classes of G are almost in one-to-one correspondence with the multiplets encoding the proteinogenic amino acids. The assignment is not perfect in the sense that there are only two representations of dimension 6 while there are three sextuplets in the genetic code.

The 22 characters of the group $G=(240,105)$ are investigated in Section 5. A sketch of the character properties of G is in

Table 3. For the group $G=(240,105)\cong {\mathbb{Z}}_5⋊2O$, the table provides the dimension of the representation, the rank of the Gram matrix obtained under the action of the 22 -dimensional Pauli group, the order of a group element in the class and a good assignment to an amino acid according to its polar requirement value. Bold characters are for faithful representations. There is an ‘exception’ for the assignment of the sextet ‘Leu’ that is assumed to occupy two 4-dimensional slots. All characters are informationally complete except for the ones assigned to ‘Stop’, ‘Leu’, ‘Pyl’, and ‘Sec’.

(240,105)	dimension	1	1	2	2	2	2	2	2	2	2	2
${\mathbb{Z}}_5⋊({\mathbb{Z}}_2.S_4)$	d-dit, d = 22	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$
$\cong {\mathbb{Z}}_5⋊2O$	amino acid	Met	Trp	Cys	Phe	Tyr	His	Gln	Asn	Lys	Glu	Asp
	order	1	2	3	4	4	5	5	6	8	8	10
	polar req.	5.3	5.2	4.8	5.0	5.4	8.4	8.6	10.0	10.1	12.5	13.0
(240,105)	dimension	3	3	4	4	4	4	4	4	4	6	6
	d-dit, d = 22	$d^2$	475	483	480	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$
	amino acid	Ile	Stop	Leu,Pyl,Sec	Leu	Val	Pro	Thr	Ala	Gly	Ser	Arg
	order	10	15	15	15	15	20	20	30	30	30	30
	polar req.	4.9			4.9	5.6	6.6	6.6	7.0	7.9	7.5	9.1

. It includes the dimension of the representation associated to each character, the order of an element in each class, and additionally the rank of the Gram matrix when one builds a POVM based on the character as a magic/fiducial state as in Section 3.1. Table 3 proposes a one-to-one assignment of the representations of G to amino acids. A given degeneracy of an amino acid in the genetic code corresponds to the dimension of the selected representations of G. The amino acids of a given degeneracy/dimension in the table are ordered according to their increasing polar requirement value (given in Figure 2b) and thus follows the order of a group element in the corresponding class. Most representations are informationally complete with the rank of the Gram matrix equal to $d^2$. The exceptions are for the 3-dimensional slot for the Stop codon and the 4-dimensional slot that we associate to the amino-acid Leu and the 2 extra amino acids Pyl and Sec. There is an ambiguity in the assignment of codons UAG and UGA that code for Stop, and for Pyl (with the codon UAG) and Sec (with the codon UGA). Thus the slight ambiguity of nature in coding the amino acids is recovered in our approach. The assignments to codons is displayed in detail in

Table 4. Excerpt of Table 3 with the assignment of codons to amino acids according to the standard genetic code. There is no ambiguity in such assignments except for codons UAG and UGA that code for ‘Stop’, as well as for ‘Pyl’ and ‘Sec’, respectively. According to our approach, this ambiguity is reflected in the characters being non informationally complete for the corresponding two slots. Bold characters are for faithful representations.

(240,105)

dimension

1

1

2

2

2

2

2

2

2

2

2

$\cong {\mathbb{Z}}_5⋊2O$

amino acid

Met

Trp

Cys

Phe

Tyr

His

Gln

Asn

Lys

Glue

Asp

bases

AUG

UGG

UGU

UUU

UAU

CAU

CAA

AAU

AAA

GAA

GAU

UGC

UUC

UAC

CAC

CAG

AAC

AAG

GAG

GAC

(240,105)

dimension

3

3

4

4

4

4

4

4

4

6

6

amino acid

Ile

Stop

Leu

Leu

Val

Pro

Thr

Ala

Gly

Ser

Arg

Pyl,Sec

bases

AUU

UAA

UUA

CUU

GUU

CCU

ACU

CGU

GGU

UCU

CGU

AUC

UAG

UUG

CUC

GUC

CCC

ACC

GCC

GGC

UCC

CGC

AUA

UGA

UAG

CUA

GUA

CCA

ACA

GCA

GGA

UCA

GGA

UGA

CUG

GUG

CCG

ACG

GCG

GGG

UCG

CGG

AGU

AGA

AGC

AGG

. According to our approach, this ambiguity is reflected into three characters being non informationally complete.

Another possible assignment of amino acids to the representations of group $(240,106)$ is possible. This group has similar dimensions of representations than group $(240,105)$ with slight differences in the order of an element in each class and the rank of the Gram matrix for the corresponding POVM, as shown in

Table 5. The group $(240,106)\cong {\mathbb{Z}}_5⋊GL(2,3)$ as another candidate for the assignments of amino acids. It has the same dimensions of representations and closely related group orders. One may postulate that the group $(240,106)$ encodes D-amino acids while the group $(240,105)$ encodes L-amino acids. For most naturally-occurring amino acids, the carbon alpha to the amino group has the L-configuration. Bold characters are for faithful representations.

(240,106)	dimension	1	1	2	2	2	2	2	2	2	2	2
$\cong {\mathbb{Z}}_5⋊GL(2,3)$	order	1	2	2	3	4	5	5	6	8	8	10
	d-dit, d = 22	$d^2$	$d^2$	483	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$
(240,106)	dimension	3	3	4	4	4	4	4	4	4	6	6
	order	10	15	15	15	15	20	20	30	30	30	30
	d-dit, d = 22	482	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	$d^2$	440	440

. One may postulate that it encodes the D-amino acids while the group $(240,105)$ encodes proteinogenic L-amino acids. For most naturally-occurring amino acids, the carbon alpha to the amino group has the L-configuration. D-amino acids are most occasionally found in nature as residues in proteins.

Normal subgroups $(48,28)\cong 2O$ of the group $(240,105)$ and $GL(2,3)\cong (48,29)$ of the group $(240,106)$ may be used to encode some of the so-called essential amino-acids in humans as shown in

Table 6. The assignment of representations of groups $2O$ or $GL(2,3)$ to most essential amino acids in humans. There are two extra essential amino acids Val and Leu but they are not strictly essential from a metabolic perspective. Strictly indispensable amino acids are Trp, Lys, and Thr which cannot be submitted to transamination. Bold characters are for faithful representations.

	dimension	1	1	2	2	2	3	3	4
	order	1	2	3	4	4	6	8	8
(48,28) = 2O	d-dit, d = 8	8	45	56	59	59	59	59	59
(48,29) = GL(2,3)	d-dit, d = 8	56	58	59	$d^2$	$d^2$	63	63	61
	amino acid	Met	Trp	Phe	His	Lys	Ile	Stop	Thr
	polar req.	5.3	5.2	5.0	8.4	10.1	4.9		6.6

[41]. The distinction between essential and non-essential amino acid is of course non universal. While humans lack metabolic pathways to synthesize Trp, Lys, and Thr, it is known that bacteria can synthesize all 20 amino acids. One observes that apart from two exceptions for the 4-dimensional slots of $GL(2,3)$, the characters of these groups are not informationally complete.

5. Symmetries of the Genetic Code, the Golden Ratio, and a Hyperelliptic Curve

If one accepts the validity of the aforementioned group theoretical model of the genetic code, one can provide clues why nature selected these particular symmetries. One clue is contained in the detailed structure of the characters of the group $(240,105)$ and its cousin group $(240,106)$. The golden ratio is playing a role in accordance with the DNA structure.

The list of 22 characters for the group $(240,105)$ is in

Table 7. The character table for the group $G=(240,105)\cong {\mathbb{Z}}_5⋊2O$. The two right hand side columns are for the rank of the Gram matrix (with $d=22$) for the corresponding character and the assignment of an amino acid of the genetic code, respectively (see also Table 3 and Table 4 for further details). The notation in the entries is as follows: $z_1=-(\sqrt{5}+1)/2$, $z_2=\sqrt{5}-1$, $z_3=3(1+\sqrt{5})/2$, $z_4=\sqrt{2}$, the exponent * means the algebraic conjugation, e.g., $z_1^{*}=(\sqrt{5}-1)/2$, the $r_i$’s are the four real roots of the quartic curve $x^4-x^3-4x^2+4x+1=0$, i.e., $r_1\approx -1.956295$, $r_2\approx 1.338261$, $r_3\approx -0.209056$, and $r_4\approx 1.827091$.

${\kappa }_1$	1	1	1	1	1	1	1	1	1	1	1	1
${\kappa }_2$	1	1	1	1	−1	1	1	1	−1	−1	1	1
${\kappa }_3$	2	2	−1	2	0	2	2	−1	0	0	2	2
${\kappa }_4$	2	2	2	2	0	$z_1$	$z_1^{*}$	2	0	0	$z_1$	$z_1^{*}$
${\kappa }_5$	2	2	2	2	0	$z_1^{*}$	$z_1$	2	0	0	$z_1^{*}$	$z_1$
${\kappa }_6$	2	−2	−1	0	0	2	2	1	$z_4$	$-z_4$	−2	−2
${\kappa }_7$	2	−2	−1	0	0	2	2	1	$-z_4$	$z_4$	−2	−2
${\kappa }_8$	2	2	−1	2	0	$z_1$	$z_1^{*}$	−1	0	0	$z_1$	$z_1^{*}$
${\kappa }_9$	2	2	−1	2	0	$z_1^{*}$	$z_1$	−1	0	0	$z_1^{*}$	$z_1$
${\kappa }_{10}$	2	2	−1	2	0	$z_1$	$z_1^{*}$	−1	0	0	$z_1$	$z_1^{*}$
${\kappa }_{11}$	2	2	−1	2	0	$z_1^{*}$	$z_1$	−1	0	0	$z_1^{*}$	$z_1$
${\kappa }_{12}$	3	3	0	−1	−1	3	3	0	1	1	3	3
${\kappa }_{13}$	3	3	0	−1	1	3	3	0	−1	−1	3	3
${\kappa }_{14}$	4	−4	1	0	0	4	4	−1	0	0	−4	−4
${\kappa }_{15}$	4	−4	−2	0	0	$z_2$	$z_2^{*}$	2	0	0	$-z_2$	$-z_2^{*}$
${\kappa }_{16}$	4	−4	−2	0	0	$z_2^{*}$	$z_2$	2	0	0	$-z_2^{*}$	$-z_2$
${\kappa }_{17}$	4	−4	1	0	0	$z_2$	$z_2^{*}$	−1	0	0	$-z_2$	$-z_2^{*}$
${\kappa }_{18}$	4	−4	1	0	0	$z_2$	$z_2^{*}$	−1	0	0	$-z_2$	$-z_2^{*}$
${\kappa }_{19}$	4	−4	1	0	0	$z_2^{*}$	$z_2$	−1	0	0	$-z_2^{*}$	$-z_2$
${\kappa }_{20}$	4	−4	1	0	0	$z_2^{*}$	$z_2$	−1	0	0	$-z_2^{*}$	$-z_2$
${\kappa }_{21}$	6	6	0	−2	0	$z_3$	$z_3^{*}$	0	0	0	$z_3$	$z_3^{*}$
${\kappa }_{22}$	6	6	0	−2	0	$z_3^{*}$	$z_3$	0	0	0	$z_3^{*}$	$z_3$
→	1	1	1	1	1	1	1	1	1	1	$d^2$	Met
→	1	1	1	1	1	1	1	1	1	1	$d^2$	Trp
→	−1	−1	−1	−1	2	2	−1	−1	−1	− 1	$d^2$	Cys
→	$z_1^{*}$	$z_1^{*}$	$z_1$	$z_1$	$z_1$	$z_1^{*}$	$z_1$	$z_1$	$z_1^{*}$	$z_1^{*}$	$d^2$	Phe
→	$z_1$	$z_1$	$z_1^{*}$	$z_1^{*}$	$z_1^{*}$	$z_1$	$z_1^{*}$	$z_1^{*}$	$z_1$	$z_1$	$d^2$	Tyr
→	−1	−1	−1	−1	0	0	1	1	1	1	$d^2$	His
→	−1	−1	−1	−1	0	0	1	1	1	1	$d^2$	Gln
→	$r_4$	$r_3$	$r_1$	$r_2$	$z_1^{*}$	$z_1$	$r_1$	$r_2$	$r_3$	$r_4$	$d^2$	Lys
→	$r_2$	$r_1$	$r_4$	$r_3$	$z_1$	$z_1^{*}$	$r_4$	$r_3$	$r_1$	$r_2$	$d^2$	Glu
→	$r_3$	$r_4$	$r_2$	$r_1$	$z_1^{*}$	$z_1$	$r_2$	$r_1$	$r_4$	$r_3$	$d^2$	Asp
→	0	0	0	0	−1	−1	0	0	0	0	$d^2$	Ile
→	0	0	0	0	−1	−1	0	0	0	0	475	Stop
→	1	1	1	1	0	0	−1	−1	−1	−1	483	Leu, Pyl, Sec
→	$-z_1$	$-z_1$	$-z_1^{*}$	$-z_1^{*}$	0	0	$z_1^{*}$	$z_1^{*}$	$z_1$	$z_1$	480	Leu
→	$-z_1^{*}$	$-z_1^{*}$	$-z_1$	$-z_1$	0	0	$z_1$	$z_1$	$z_1^{*}$	$z_1^{*}$	$d^2$	Val
→	$-r_3$	$-r_4$	$-r_2$	$-r_1$	0	0	$r_2$	$r_1$	$r_4$	$r_3$	$d^2$	Pro
→	$-r_4$	$-r_3$	$-r_1$	$-r_2$	0	0	$r_1$	$r_2$	$r_3$	$r_4$	$d^2$	Thr
→	$-r_1$	$-r_2$	$-r_3$	$-r_4$	0	0	$r_3$	$r_4$	$r_2$	$r_1$	$d^2$	Ala
→	$-r_2$	$-r_1$	$-r_4$	$-r_3$	0	0	$r_4$	$r_3$	$r_1$	$r_2$	$d^2$	Gly
→	0	0	0	0	$-z_1$	$-z_1^{*}$	0	0	0	0	$d^2$	Ser
→	0	0	0	0	$-z_1^{*}$	$-z_1$	0	0	0	0	$d^2$	Arg

. A closely related table (not shown) is found for the group $(240,106)$. The entries in the character table are shown to be either rational numbers, quadratic irrationalities such as $z_1=-(\sqrt{5}+1)/2$, $z_2=\sqrt{5}-1$, $z_3=3(1+\sqrt{5})/2$, $z_4=\sqrt{2}$ and their algebraic conjugates, or $\pm r_i$ where $r_i$ is one of the four roots $r_i$ of the quartic polynomial $x^4-x^3-4x^2+4x+1=0$, where $r_1=-2cos(\pi /15)\approx -1.956295$, $r_2=-2cos(11\pi /15)\approx 1.338261$, $r_3=-2cos(7\pi /15)\approx -0.209056$, and $r_4=-2cos(13\pi /15)\approx 1.827091$.

It is known that such a quartic contains the golden ratio $\varphi =z_2/2$ and the irrational $\sqrt{2}$ in its structure. Following [42] (Section 3), the inflection secant S has segments whose length ratio is $\varphi$. In addition, the double tangent, the inflection secant, and the straight line passing through the third tangent point and parallel to them separate areas whose ratio is $\sqrt{2}$.

It may be that some other clues in the mystery of the genetic code (and a possible connection to the present approach) are in a concept introduced under the name of Boerdijk–Coxeter (BC) helix—an helix made of contiguous tetrahedra—more or less at the same time than the discovery of DNA [43]. The concept was revisited to arrive at a BC helix exhibiting a connection to aperiodicity and the golden ratio [44,45].

From now, we consider the (genus one) hyperelliptic curve $\mathcal{C}$:

$$\mathcal{C}:y^2=x^4-x^3-4x^2+4x+1,$$

(6)

as a potential model of many features of DNA double helix.

The characters responsible of the quadratic irrationalities and roots of the quartic are defined over the cyclotomic fields $\mathbb{Q}\left({\zeta }_5\right)$ and $\mathbb{Q}\left({\zeta }_{15}\right)$, respectively, where ${\zeta }_n$ is a primitive n-th complex root of unity. Thus we focus on $\mathcal{C}$ with points over such cyclotomic fields.

5.1. Points of $\mathcal{C}$ over Cyclotomic Fields

As usual for elliptic and hyperelliptic curves of genus g, $\mathcal{C}$ is embedded in a weighted projective plane, with weights 1, $g+1$, and 1, respectively on coordinates x, y, and z. Therefore, point triples are such that $(x:y:z)=(\mu x:\mu y:\mu z)$, $\mu$ in the field of definition, and the points at infinity take the form $(1:y:0)$. Below, the software Magma is used for the calculation of points of $\mathcal{C}$ [40]. For the points of $\mathcal{C}$, there is a parameter called ‘bound’ that loosely follows the heights of the x-coordinates found by the search algorithm.

Let us start with points on $\mathcal{C}$ with entries over the cyclotomic field $\mathbb{Q}\left({\zeta }_5\right)$.

For points whose entries are bounded by modulus 1, one gets 8 cases $(1:\pm 1:0)$ (the points at infinity), $(0:\pm 1:1)$, $(1:\pm 1:1)$ and $(2+\varphi :\pm (3+\varphi ):1)$. For points whose entries are bounded by modulus 2, one gets 10 extra cases $(\pm 2:-1:0)$, $(\pm 2:1:1)$, $(2\varphi :\pm (3-4\varphi ):1)$, $(-2(1+\varphi ):\pm (7+4\varphi ):1)$, and $(1-\varphi :\pm (4+\varphi ):1)$. For points whose entries are bounded by modulus 10, one gets 8 extra cases $(4/3:\pm 1/9:1)$, $(6:\pm 31:1)$, $(4/5:\pm 31/25:1)$, and $(-1/7:\pm 29/49:1)$.

Let us continue with points on $\mathcal{C}$ with entries over $\mathbb{Q}\left({\zeta }_{15}\right)$. Points with integer entries are as those given over $\mathbb{Q}\left({\zeta }_5\right)$. In addition, the points whose entries are bounded by modulus 1 are $(r_1:0:1)$, $(r_2:0:1)$, $(r_3:0:1)$, $(r_4:0:1)$ (where $r_i$ is one of the four roots of the quartic polynomial above), $(2+\varphi :\pm (3+\varphi ):1)$ [the latter 2 points are on $\mathbb{Q}\left({\zeta }_5\right)$] The non rational points whose entries are bounded by modulus 2 are $(2\varphi :\pm (3-4\varphi ):1)$, $(-2(1+\varphi ):\pm (7+4\varphi ):1)$ [the latter 2 points are on $\mathbb{Q}\left({\zeta }_5\right)$], and $({\varphi }^2:\pm (1+{\varphi }^2):1$. For non rational points whose entries are bounded by modulus 7, one gets 8 extra cases and no more up to bound 10. The entries could not be found related to simple irrationalities and are approximated as $(3.02234:\pm 5.69063:1)$, $(0.90536:\pm 1.12804:1)$, $(0.50552:\pm 1.39140:1)$, and $(11.56677:\pm 125.95399)$.

Over both cyclotomic fields, there are plenty of extra points where the entries have higher modulus but we do not list them here.

5.2. The Group Law on the Jacobian J of the Hyperelliptic Curve $\mathcal{C}$

There exists a group law on the Jacobian J of a hyperelliptic curve [46]. Using Magma we provide some results for the operations in $J\left(\mathcal{C}\right)$ defined over $\mathbb{Q}\left({\zeta }_5\right)$.

Let focus on the 8 elements $a_i$ of bound 1 in the Jacobian. In the Mumford representation of Jacobian elements, $a_1=(1,0,0)$, $a_2=(x^2-15/8,-x^2+49/16,2)$, $a_3=(x-4/5,-x^2-3/5,2)$, $a_4=(x-4/3,-x^2+5/3,2)$, $a_5=(x+1/7,-x^2-4/7,2)$, $a_6=(x-1,-x^2+2,2)$, $a_7=(x-(2+\varphi ),-x^2+2(1+\varphi ),2)$, and $a_8=(x+2.25123,-x^2+8.03750,2).$ In

Table 8. The inverse of the 8 elements $a_i$ of bound 1 in the Jacobian J of the hyperelliptic curve $\mathcal{C}$ over $\mathbb{Q}\left({\zeta }_5\right)$. One gets $-a_2=(1,-x^2+x/2,2)$, $-a_3=(x,-x^2-1,2)$, $-a_4=(x,-x^2+1,2)$ and $-a_5=(x-1,-x^2,2)$ of bounds 4, 5, 15, and 7, respectively.

points of J	$a1$	$a2$	$a3$	$a4$	$a_5$	$a_6$	$a_7$	$a_8$
inverse	$a1$	4	5	15	7	$a_6$	$a_7$	?

, the inverses or elements $a_i$ are shown. In

Table 9. The addition table between the 8 elements $a_i$ of bound 1 in the Jacobian J of the hyperelliptic curve $\mathcal{C}$ over $\mathbb{Q}\left({\zeta }_5\right)$. The 10 elements with bound 2 in the Jacobian are denoted $b_i$. For entries with bound not 1 or 2, only the bound is given. The points of the Jacobian with bounds 2 used in the table are $b_1=(x+2,-x^2+3,2)$, $b_6=(x-70/31,-x^2+221/31,2)$, $b_8=(x-6,-x^2+5,2)$, $b_2\approx (x+0.19821,-x^2+0.28285,2)$, $b_9\approx (x-1.30757,-x^2-2.47363,2)$, and $b_{10}\approx (x-2.00889,-x^2-1.01292,2)$.

sum	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$	$a_7$	$a_8$
$a_1$	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$	$a_7$	$a_8$
$a_2$	.	15	5	4	7	$a_5$	$a_8$	?
$a_3$	.	.	$b_6$	$a_2$	6	$b_8$	$b_{10}$	54
$a_4$	.	.	.	$b_8$	$b_6$	$b_1$	$b_2$	14
$a_5$	.	.	.	.	15	$a_2$	$b_9$	?
$a_6$	.	.	.	.	.	$a_1$	$b_4$	$b_9$
$a_7$	.	.	.	.	.	.	$a_1$	$a_2$
$a_8$	.	.	.	.	.	.	.	15

, one explicits the sums $a_i+a_j$ between two elements of bound 1 in the Jacobian.

A similar group law exists for $\mathcal{C}$ defined over $\mathbb{Q}\left({\zeta }_{15}\right)$ but it is more difficult to explicit the points and we do not give details here.

6. Conclusions

We unveiled part of the machinery of DNA in building the genetic code thanks to the representations of a distinguished finite group of signature $G={\mathbb{Z}}_5⋊2O$, where $2O$ is the binary octahedral group. The group characters $\kappa$ of G are found to map to the proteinogenic amino acids and this is performed by almost keeping complete quantum information when the $\kappa$’s are seen as magic states, as in quantum computing. Moreover, there exists a unique quartic and a related hyperelliptic curve $\mathcal{C}$ behind the DNA scene which gives sense to the irrationalities found in the character table (and in the real biological world). It is still too early to conclude that DNA calculates on points of $\mathcal{C}$ or on points of the Jacobian $J\left(\mathcal{C}\right)$ but it is tempting to work in this direction in future papers. It may be that other finite groups and their attached hyperelliptic curve are governing the secondary and tertiary structure of proteins such that the alpha helix, the symmetries in the spliceosome, and the DNA packing into chromatin and chromosomes.