Abstract
An object is 3D centro-symmetrical if the object can be segmented into two halves and the relationship between them can be represented by a combination of reflection about a plane and a rotation through 180° about an axis that is normal to the plane. A 2D orthographic image of the 3D centro-symmetrical object is always 2D rotation-symmetrical. Note that the human visual system is known to be sensitive to 2D rotational symmetry. This human sensitivity to 2D rotational symmetry might also be used to detect 3D centro-symmetry. If it is, can this detection of 3D centro-symmetry be helpful for the perception of 3D? In this study, the geometrical properties of 3D centro-symmetry and its 2D orthographic and perspective projections were examined to find out whether 3D centro-symmetry plays any role in the perception of 3D. I found that, from a theoretical point-of-view, it is unlikely that 3D centro-symmetry can be used by the human visual system to organize a 2D image of an object in a way that makes it possible to recover the 3D shape of an object from its 2D image.
1. Introduction
The human visual system is particularly sensitive to a number of 2D configurations that are composed of local image features in a retinal image [1,2,3,4,5,6,7,8]. Examples of such 2D image features are parallelism, collinearity, perpendicularity, and symmetry. Two-dimensional symmetry is one of the most important of these configurations (see [9,10,11,12] for reviews).
Symmetry can be defined as an invariant under a group of transformations [13,14,15]. For example, 2D mirror symmetry is invariant under reflection, and 2D N-fold rotational symmetry is invariant under rotation for 360/N° where N is an integer larger than 1. These two types of 2D symmetry are unique, because only they can form a compact 2D figure. A mirror-symmetrical figure can be segmented into two halves by a line, called the “symmetry-axis” that makes the halves reflections of one another. An N-fold rotation-symmetrical figure can be segmented into N parts in which any part is always a rotation of another part for 360/N°.
The human visual system is sensitive to both 2D mirror and 2D rotational symmetry [16,17,18,19,20]. This high sensitivity to 2D mirror symmetry is often explained by the 3D mirror symmetry of many objects in our everyday life (e.g., [21]). However, a 2D retinal image of a 3D mirror-symmetrical object is 2D mirror-symmetrical on a spherical retina only if the symmetry plane of the object passes the center of projection of the eye under a perspective projection. Such a view of this kind of a mirror-symmetrical object is degenerate. This sensitivity to 2D mirror symmetry can be explained by its property as a model-based invariant of a 3D shape [22,23]. The 2D image of a surface-of-revolution in a 3D scene is always mirror-symmetrical under an orthographic projection to an image plane and under a perspective projection to a spherical retina [23,24,25,26].
Two-dimensional rotational symmetry can be also regarded as a model-based invariant of a 3D shape. A boundary contour of a 2D orthographic projection of a 3D centro-symmetrical shape (Figure 1) is always 2D rotational-symmetrical with 2 folds (Figure 2). A centro-symmetrical shape has a central point. Line segments connecting symmetrical pairs of points of the shape intersect with one another at the central point and are bisected by the point. In this study, this point is referred to as the “symmetry point” and line segments connecting the individual symmetrical pair of points are referred to as the “symmetry line segments”. A centro-symmetrical shape can be segmented into two symmetrical halves by a plane with an arbitrary orientation that passes the symmetry point. The relation between these two halves can be represented by a combination of reflection about the plane and rotation for 180° about an axis that is normal to the plane and that passes the symmetry point.
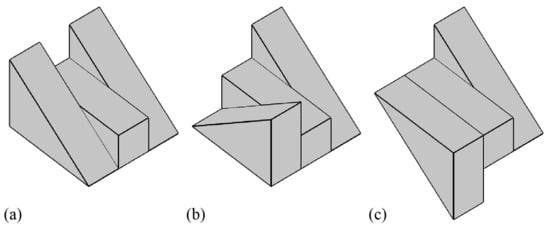
Figure 1.
Objects with 3 types of 3D symmetry: (a) a 3D mirror-symmetrical object, (b) a 3D rotation-symmetrical object, and (c) a 3D centro-symmetrical object.
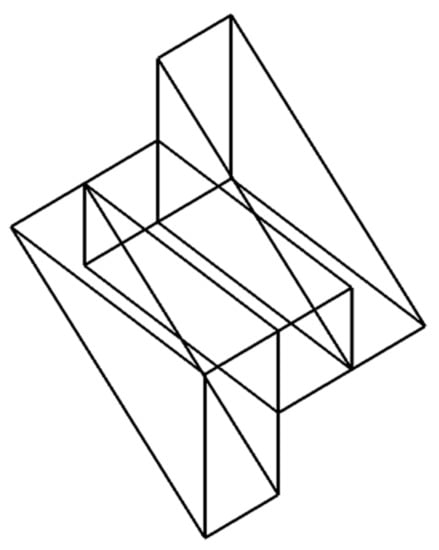
Figure 2.
An orthographic image of a 3D centro-symmetrical object (Figure 1c) with its surface transparent. The 2D image of the 3D centro-symmetrical shape itself is 2D rotational symmetrical with 2 folds, once we ignore the occlusion by the opaque surface of the shape.
Three-dimensional centro-symmetry has been studied in crystallography but not in vision science, despite its potential relevance for understanding human beings’ sensitivity to 2D rotational symmetry. In this study, the geometrical properties of 3D centro-symmetry and its 2D orthographic and perspective projections were studied to make it possible to discuss (i) the potential sensitivity of the human visual system to 3D centro-symmetry and (ii) whether this kind of sensitivity can actually aid the perception of 3D.
2. Theorems and Proofs
2.1. A 2D Orthographic Projection of 3D Centro-Symmetry
Consider a 3D centro-symmetrical object with an arbitrary orientation in a 3D scene. Set the 3D Cartesian coordinate system of the scene so that the origin of the 3D system is at the symmetry point of the object. Now consider a symmetrical pair of points and of the object. Their relation can be represented as , because a midpoint between Pi and Qi is at the symmetry point .
Next, consider a 2D orthographic projection of the 3D centro-symmetrical object. The image plane for the orthographic projection is set so that it passes the origin of the 3D coordinate system. The 2D Cartesian coordinate system is set so that the x- and y-axes of the 2D coordinate system coincide with the X- and Y-axes of the 3D coordinate system of the scene. The Z-axis of the 3D coordinate system is normal to the image plane.
The 2D orthographic projection of the 3D centro-symmetrical object is always 2D rotation-symmetrical with 2-folds. The orthographic projections of Pi and Qi can be written as:
where pi is the projection of Pi and qi is the projection of Qi. The relation between pi and qi can be represented as . It is equivalent with a 2D rotation for 180° around to which the symmetry point O3D is projected. This implies that a 2D orthographic image of a 3D centro-symmetrical object is always 2D 2-fold rotation-symmetrical around a projection of the symmetry center of the object. This means that the image is invariant when it rotates 180° around the projection of the symmetry center.
2.2. Recovering a 3D Centro-Symmetrical Shape from Its 2D Orthographic Image
It has been shown that a one-parameter family of 3D shapes can be recovered from a single 2D orthographic image of an object if the object is 3D mirror- or rotation-symmetrical [27,28,29]. Starting with an image of an object, another image of the object can be generated, virtually, from a different viewpoint by using the symmetry of the object (Figure 3). A point in the object can be projected to both the original and a virtual image. The 3D position of such a point can be computed by finding the intersection of two lines of projection of the point from the original and virtual images. The parameter of this family represents the relative orientation between the two views of the original and virtual images [25,30,31]. The veridical 3D shape of the object is included in this family.
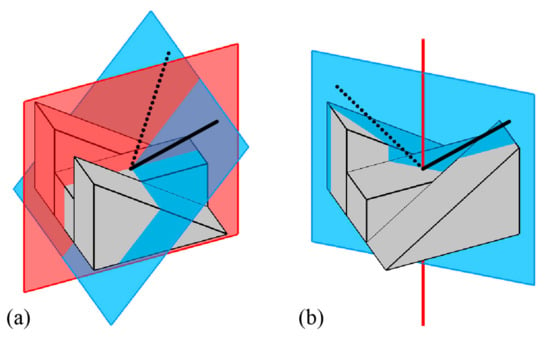
Figure 3.
(a) The 3D mirror- and (b) the 3D rotation-symmetrical objects in Figure 1 viewed from different directions. Thick black lines represent the viewing directions for images in Figure 1, and the dotted lines represent the viewing directions of their virtual images that were generated from the images in Figure 1.
It is also possible to generate a virtual image of a 3D centro-symmetrical object from its 2D orthographic image, but, here, the virtual image based on 3D centro-symmetry does not facilitate the recovery of the 3D shape of the object. The viewing direction of the virtual image is opposite to the viewing direction of the original image. This means that that the two lines of projection to each point of the object from the two views of the images coincide perfectly with one another.
Note that a 2D orthographic image of a 3D centro-symmetrical object is always 2D 2-fold rotation-symmetrical. Under an orthographic projection, any 2D 2-fold rotation-symmetrical image has an infinite number of 3D centro-symmetrical interpretations. Now, set the 2D Cartesian coordinate system of the image so that its origin is at the symmetry point of the rotation-symmetrical image. Next, set the 3D Cartesian coordinate system of a 3D scene in which the 3D interpretation is constructed so that the X- and Y-axes of the 3D coordinate system coincide with the x- and y-axes of the 2D coordinate system of the image. The Z-axis of the 3D coordinate system is normal to the image plane. The relation between a 2D rotation-symmetrical pair of points and in the image can be represented by a rotation for 180° around : . The 3D centro-symmetrical interpretations of bi and di can be constructed as:
where Bi is the 3D interpretation of bi, Di is the 3D interpretation of di, and Zi is an arbitrary real number. The midpoint between Bi and Di is at . This construction process can be applied to all 2D rotation-symmetrical pairs of points in the image. For each pair of points, the Z coordinates of their constructed 3D points can be set independently from the other pairs of points. When this is done, the set of pairs of constructed 3D points is 3D centro-symmetrical about O3D. Each pair of the constructed points can be connected by a symmetry line segment that is bisected by O3D.
2.3. A 2D Perspective Projection of 3D Centro-Symmetry
A 2D perspective projection of a 3D centro-symmetrical object is not 2D rotation-symmetrical unless the object is planar and frontoparallel. Symmetry line segments connecting symmetrical pairs of points in the objects are projected to line segments that intersect with one another at a point to which the symmetry center of the object is projected. The projection of the symmetry point is not at the midpoints of the projection of the symmetry line segments unless the symmetry line segments are frontoparallel.
A model-based invariant of 3D centro-symmetry under a 2D perspective projection is only a common intersection of line segments that connect corresponding pairs of points. This can be proven by showing that a 3D centro-symmetrical interpretation can always be constructed from a 2D image that satisfies this constraint (see also [25,32,33,34] for analogous theorems of 3D mirror and rotational symmetry). A common intersection in a 2D image is a projection of the symmetry point of the constructed 3D centro-symmetrical interpretation and its symmetry line segments are projected to the line segments that connect the corresponding pairs of points in a 2D image.
Setting the 2D Cartesian coordinate system of a 2D image and the 3D Cartesian coordinate system of a 3D scene in which the 3D interpretation can be constructed as follows: (i) the origin of the 3D coordinate system is at the center of the projection, (ii) the Z-axis of the 3D coordinate system coincides with the principal axis and it is perpendicular to the image plane Z = f, where f is the focal distance, (iii) the Z-axis passes the origin of the 2D coordinate system, and (iv) the X- and Y-axes of the 3D coordinate system are parallel to the x- and y-axes of the 2D coordinate system.
Now, consider constructing a 3D centro-symmetrical interpretation from a given 2D image that is composed of corresponding pairs of points. Line segments connecting the individual pairs of points in the 2D image pass a point . The point cs appears between points of these individual pairs. These line segments and cs are projections of the symmetry line segments and of the symmetry point of the 3D interpretation.
Next, consider one of the corresponding pairs (pi, qi). A line segment connecting pi and qi passes cs. This pair of points can be written as:
where θi is the orientation of the line segment connecting pi and qi, and and are the distance of pi and qi from cs. Note that the line segment connecting pi and qi is a projection of a symmetry line segment, and cs is a projection of the symmetry point. The symmetry line segment is parallel to a vector Si connecting the center of projection [0 0 0]t and the vanishing point vi of the symmetry line segment. The vanishing point vi of the symmetry line segment should be collinear with pi, qi, and cs, and it can be written as:
where and is the distance of vi from cs. The endpoints of the symmetry line segment and the symmetry point bisecting the symmetry line segment are projected to pi, qi, and cs. Then, the relation between pi, qi, cs, and vi can be represented by the following equation (see [25,35]):
From Equation (5):
The symmetry line segment is parallel to a vector Si connecting the center of projection [0 0 0]t and its vanishing point vi in the 2D image:
Let the 3D centro-symmetrical construction of pi and qi be Pi and Qi and the symmetry point be Cs:
where Δs is a free parameter representing the distance of Cs from the center of projection. Note that Pi and Qi in the 3D scene are connected by the symmetry line segment that is bisected by Cs:
where |Δi| is the length of the symmetry line segment. From Equations (3) and (7)–(9), we have:
From Equations (6) and (10), Δi can be computed as:
The free parameter Δs is the distance of the symmetry point Cs from the center of projection. It determines the size of the constructed 3D centro-symmetrical interpretation. This construction process can be applied to all of the corresponding pairs of points in the 2D image. Δs should be the same among all of the pairs of points. When this has been done, the set of pairs of constructed 3D points is 3D centro-symmetrical about Cs. Each pair of constructed points can be connected by a symmetry line segment that is bisected by Cs.
2.4. Model-Based Invariant of 3D Centro-Symmetry with Planar Contours
Consider a 3D mirror-symmetrical pair of curves. It has been suggested that the planarity of these individual contours can play an important role when the human visual system detects the 3D mirror symmetry from the 2D image of its contours. This can be explained by introducing a model-based invariant into the 2D image by using 3D mirror symmetry along with the planarity of contours [32,33,36]. Under an orthographic projection, the relationship between the images of the curves can be represented by a sub-group of the 2D affine transformation. Under a perspective projection, the relationship can also be represented by a transformation that includes the same sub-group of the 2D affine transformation.
An analogous model-based invariant can be introduced into the 2D image by using 3D rotational symmetry along with the planarity of contours [25]. Under an orthographic projection, the relationship between the images of planar curves that are 3D rotation-symmetrical to one another can be represented by a sub-group of the 2D affine transformation. Under a perspective projection, the relationship can also be represented by a transformation that includes the same sub-group of the 2D affine transformation. Note that the sub-group of the 2D affine transformation for 3D rotational symmetry is different from the sub-group for 3D mirror symmetry. In the next two sections, the same approach to 3D centro-symmetry will be discussed under both orthographic and perspective projections.
2.4.1. Model-Based Invariant of 3D Centro-Symmetry with Planar Contours under a 2D Orthographic Projection
Under an orthographic projection, the planarity of contours does not play any role. Note that a 2D orthographic image of a 3D centro-symmetrical object is always 2D rotational symmetry and that a 3D centro-symmetrical interpretation can always be constructed from a 2D rotation-symmetrical image (see Section 2.1. A 2D orthographic projection of 3D centro-symmetry). It is always possible to construct a 3D centro-symmetric pair of planar curves from a pair of 2D rotation-symmetrical curves with an orthographic projection.
Consider a pair of curves ϕ and ψ that are 2D rotation-symmetrical around the origin in a 2D image and a corresponding pair of points on ϕ and on ψ. Their relation can be represented as . From Equation (1), their 3D centro-symmetrical interpretations can be constructed as and , where Pi is the 3D interpretation of pi and Qi is the 3D interpretation of qi. The parameter Zi is computed as:
where NX, NY, NZ, and kΦ are free parameters. This construction process can be applied to all corresponding pairs of points on ϕ and ψ. NX, NY, NZ, and kΦ should be the same among all of the pairs of points. When this is done, a 3D centro-symmetrical pair of planar curves Φ and Ψ can be constructed from ϕ and ψ. Equation (12) represents a plane of Φ. The plane of Φ is parallel to a plane of Ψ.
2.4.2. Model-Based Invariant of 3D Centro-Symmetry with Planar Contours under a 2D Perspective Projection
Under a perspective projection, a model-based invariant can be introduced into the 2D image by 3D centro-symmetry used along with the planarity of contours. Now, consider a 3D centro-symmetrical pair of planar contours Φ and Ψ and their 2D perspective projections φ and ψ. Plane ΠΦ of Φ and plane ΠΨ of Ψ are parallel to one another. Set the 2D Cartesian coordinate system of a 2D image and the 3D Cartesian coordinate system of a 3D scene in which the 3D interpretation will be constructed as follows: (i) the origin of the 3D coordinate system is at the center of projection, (ii) the Z-axis of the 3D coordinate system coincides with the principal axis and it is perpendicular to the image plane Z = f, where f is the focal distance, (iii) the Z-axis passes the origin of the 2D coordinate system, and (iv) the X- and Y-axes of the 3D coordinate system are parallel to the x- and y-axes of the 2D coordinate system.
First, consider for simplicity, a case in which ΠΦ and ΠΨ are frontoparallel:
where kΦ, kΨ are constants. Let the symmetry center of Φ and Ψ be . From Equation (13), . Now, consider a corresponding pair of points Pi on Φ and Qi on Ψ. Pi and Qi can be written as: and . Their perspective projections can be written as:
From Equation (14), the relation between pi and qi is:
where is a perspective projection of CS. This shows that the relation between φ and ψ can be represented by a sub-group of the 2D affine transformation, namely scaling by a factor of −kΨ/kΦ around cs.
If a pair of curves β and δ in the 2D image satisfy Equation (15), their 3D centro-symmetrical interpretations are a pair of planar contours in the 3D scene. Now, consider n corresponding pairs of points (b1, b2, … bn) on β and (d1, d2, … dn) on δ where n ≥ 3. They satisfy Equation (15): (bi – cβδ) = −kβδ(di – cβδ), where i is an integer (1 ≤ i ≤ n), kβδ is a constant, and cβδ is an intersection of line segments connecting the corresponding pairs of points between β and δ. From Equation (3), bi and di can be written as bi = cβδ + lbi[cosθi sinθi]t and di = cβδ + ldi[cosθi sinθi]t, where θi is the orientation of the line segment connecting bi and di, and and are the distance of bi and di from cβδ. Note that lbi/ldi is kβδ for all of the corresponding pairs of points, because β and δ satisfy Equation (15). Let Bi and Di be the 3D centro-symmetrical interpretations of bi and di and ZBi and DBi be their Z-coordinates. From Equations (7)–(11), the Z-coordinates of Bi and Di are:
where Δs is a free parameter representing the distance of the symmetry point from the center of projection. It should be the same among all of the pairs of points. Note that is also the same among all of the pairs of points, because lbi/ldi is constant (kβδ). Equation (16) shows that the 3D centro-symmetrical interpretations of β and δ are a pair of contours that are individually frontoparallel and planar.
Next, consider a general case in which planes ΠΦ and ΠΨ are not frontoparallel:
where kΦ, kΨ, NX, NY, and NZ are constants, and NX2 + NY2 = 1. Note that [NX NY NZ]t is normal to ΠΦ and ΠΨ. Let CS = [XC, YC, ZC]t be their symmetry center. Note that a line connecting two of the points Pi and Pj of Φ, and a line connecting their corresponding points Qi and Qj of Ψ, are parallel to one another. Let φ, ψ, and cs be 2D perspective projections of Φ, Ψ, and CS. This general case can be transformed to a simple case in which ΠΦ and ΠΨ are frontoparallel by rotating the principal axis and the image plane around the center of projection [0 0 0]t. The perspective image after this rotation can be computed by using Kanatani’s transformation [37].
Now consider n corresponding pairs of points (p1, p2, … pn) on φ and (q1, q2, … qn) on ψ where n ≥ 3 (Figure 4). They are projections of points (P1, P2, … Pn) on Φ and (Q1, Q2, … Qn) on Ψ. Draw a line connecting two of the points pi and pj on φ and a line connecting their corresponding points qi and qj on ψ (the dashed gray lines in Figure 4). The intersection hij of these two lines is a vanishing point of two parallel lines connecting Pi and Pj and connecting Qi and Qj. These lines are on the planes ΠΦ and ΠΨ individually, and they are parallel to one another. It follows that hij is on a line Hs (the solid red line in Figure 4) that is a common horizon of ΠΦ and ΠΨ. Another vanishing point can be found by drawing a line connecting different points on φ and by drawing a line connecting their corresponding points on ψ. An additional corresponding pair of points on φ and ψ can be determined by drawing a line (the dotted green line in Figure 4) passing cs and finding its intersection with φ and ψ if necessary.
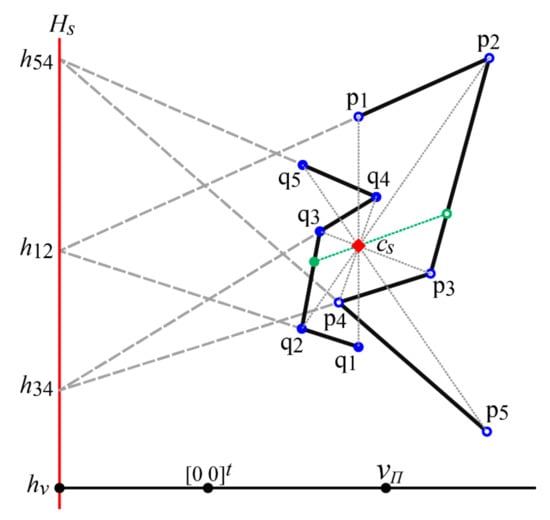
Figure 4.
A pair of 2D curves ϕ and ψ satisfying the following two conditions: (i) line segments connecting the corresponding pairs of points on ϕ and ψ (the dotted gray line) intersect with one another at a point cs (the red diamond), (ii) a line connecting two of the points on φ and a line connecting their corresponding points on ψ always intersect on Hs.
This vanishing point is also on Hs. Hs can be determined by finding a line that connects these vanishing points.
By using the horizon Hs of ΠΦ and ΠΨ, a vanishing point of a line normal to ΠΦ and ΠΨ can be found. Now, draw a line that passes the principal point [0 0]t in the image and that is perpendicular to Hs. Let hv be an intersection of this line with Hs. Next, find a point vΠ on this line such that the visual angle between hv and vΠ from the center of projection is perpendicular. The line connecting vΠ and the center of projection is normal to ΠΦ and ΠΨ and it is parallel to [NX NY NZ]t (Equation (17)).
Now, rotate the principal axis and the image plane together in the 3D scene to make the principal axis normal to ΠΦ and ΠΨ and ΠΦ and ΠΨ become frontoparallel. This rotation is around a vector [NY − NX 0]t and the degree of the rotation is .
A matrix RΠ representing this rotation can be formulated by using Rodrigues’ rotation formula:
where cθ = cosθ, sθ = sinθ, and rθ = 1−cosθ. After the rotation RΠ, a point [x y]t in the original image is transformed to [x′ y′]t [37]:
Note that ΠΦ and ΠΨ become frontoparallel after RΠ. With this done, the transformed image satisfies Equation (15). From Equations (15) and (19), the relation between φ and ψ is:
where pi′, qi′, and cs′ are the transformations of pi, qi, and cs by using Equation (19). This shows that the relation between φ and ψ can be represented by the transformation of Equation (19) and by a sub-group of the 2D affine transformation that is scaling.
3. General Discussion
This study examined how, from a theoretical point of view, 3D centro-symmetry can be used to organize a 2D image of an object and to recover its 3D shape from the 2D image. My study showed that 3D centro-symmetry has the following properties: (i) a 2D orthographic image of a 3D centro-symmetrical shape is always 2D rotation-symmetrical, (ii) a 3D centro-symmetrical shape can be recovered from its single 2D perspective projection but not from its 2D orthographic projection, (iii) any pair of 2D curves is consistent with a 3D centro-symmetrical interpretation under a perspective projection, and (iv) additional model-based invariants of 3D rotational symmetry can be introduced under a perspective projection if the 3D centro-symmetrical set of curves are planar, individually.
This study was motivated by the fact that the human visual system is known to be sensitive to 2D rotational symmetry, which is a model-based invariant of 3D centro-symmetry under an orthographic projection but not under a perspective projection. It raises two questions: (i) which 3D centro-symmetry or 3D rotational symmetry is actually inferred from 2D rotational symmetry in the human visual system and (ii) can any sensitivity to 3D centro-symmetry be helpful for the perception of 3D? The first question can be addressed by testing the human sensitivity to 2D rotation-symmetrical patterns with a 3D centro-symmetrical or with a 3D rotation-symmetrical depth distribution (see Figure 5, see also [38,39,40,41] for studies of the perception of 2D mirror symmetry from a dotted pattern with a depth distribution). Note, however, even if the human visual system is sensitive to 3D centro-symmetry, it is unclear how 3D centro-symmetry can be of any help in the perception of 3D. Note that this study showed that 3D centro-symmetry can be theoretically helpful for the 3D perception with a perspective projection but not with an orthographic projection. This inconsistency is inconvenient for the human visual system, because it prevents it from making effective use of 3D centro-symmetry. When the retinal image of a 3D centro-symmetrical object is small, the image can be approximated well by an orthographic projection, and the human visual system can detect 3D centro-symmetry of the object on the basis of 2D rotational symmetry. However, here, the 3D centro-symmetry is not helpful in perceiving the 3D shape of the object, because the image is too small. When the retinal image of an object is sufficiently large, 3D centro-symmetry is helpful in perceiving the 3D shape of the object from this large image, but the 3D centro-symmetry cannot be detected on the basis of 2D rotational symmetry. Therefore, this theoretical study suggests that 3D centro-symmetry cannot be used by the human visual system to organize a 2D image of an object to make it possible to recover its 3D shape from the 2D image.

Figure 5.
Stereoscopic images of random dot patterns with 2D rotational symmetry (for both crossed and uncrossed fusion). The depth distributions of the patterns were (a) 3D centro-symmetrical and (b) 3D rotation-symmetrical.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Biederman, I. Recognition-by-components: A theory of human image understanding. Psychol. Rev. 1987, 94, 115–147. [Google Scholar] [CrossRef]
- Feldman, J. Formation of visual “objects” in the early computation of spatial relations. Percept. Psychophys. 2007, 69, 816–827. [Google Scholar] [CrossRef]
- Koffka, K. Principles of Gestalt Psychology; Harcourt, Brace, & World: New York, NY, USA, 1935. [Google Scholar]
- Kubilius, J.; Sleurs, C.; Wagemans, J. Sensitivity to nonaccidental configurations of two-line stimuli. i-Perception. 2017, 8, 1–12. [Google Scholar] [CrossRef]
- Leeuwenberg, E.; van der Helm, P.A. Structural Information Theory: The Simplicity of Visual Form; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Metzger, W. Laws of Seeing Translated by L Spillman & S Lehar; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Wagemans, J. Perceptual use of nonaccidental properties. Can. J. Psychol. 1992, 46, 236–279. [Google Scholar] [CrossRef] [PubMed]
- Witkin, A.P.; Tenenbaum, J.M. On the Role of Structure in Vision. In Human and Machine Vision; Beck, J., Hope, B., Rosenfeld, A., Eds.; Academic Press: New York, NY, USA, 1983; pp. 481–543. [Google Scholar]
- van der Helm, P.A.; Leeuwenberg, E.L.J. Goodness of visual regularities: A nontransformational approach. Psychol. Rev. 1996, 103, 429–456. [Google Scholar] [CrossRef] [PubMed]
- Swaddle, J. Visual signaling by asymmetry: A review of perceptual processes. Philos. Trans. Biol. Sci. 1999, 354, 1383–1393. [Google Scholar] [CrossRef] [PubMed]
- Treder, M.S. Behind the looking-glass: A review on human symmetry perception. Symmetry 2010, 2, 1510–1543. [Google Scholar] [CrossRef]
- Wagemans, J. Detection of visual symmetries. Spat. Vis. 1995, 9, 9–32. [Google Scholar] [CrossRef]
- Liu, Y.; Hel-Or, H.; Kaplan, C.S. Computational symmetry in computer vision and computer graphics. Found. Trends Comput. Graph. Vis. 2010, 5, 1–195. [Google Scholar] [CrossRef]
- Stewart, I.; Golubitsky, M. Fearful Symmetry: Is God a Geometer? Penguin Books: London, UK, 1993. [Google Scholar]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Kahn, J.I.; Foster, D.H. Horizontal-vertical structure in the visual comparison of rigidly transformed patterns. J. Exp. Psychol. Hum. Percept. Perform. 1986, 12, 422–433. [Google Scholar] [CrossRef]
- Mach, E. The Analysis of Sensations and the Relation of the Physical to the Psychical; Dover: New York, NY, USA, 1959. [Google Scholar]
- Makin, A.D.J.; Rampone, G.; Pecchinenda, A.; Bertamini, M. Eletrophysiological responses to visuospatial regularity. Psychophysiology 2013, 50, 1045–1055. [Google Scholar] [PubMed]
- Makin, A.D.J.; Wilton, M.M.; Pecchinenda, A.; Bertamini, M. Symmetry perception and affective responses: A combined EEG/EMG study. Neuropsychologia 2012, 50, 3250–3261. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J.; Van Gool, L.; Swinnen, V.; Van Horebeek, J. Higher-order structure in regularity detection. Vis. Res. 1993, 33, 1067–1088. [Google Scholar] [CrossRef]
- Funk, C.; Liu, Y. Beyond planar symmetry: Modeling human perception of reflection and rotation symmetries in the wild. In Proceedings of the IEEE International Conference on Computer Vision 2017, Venice, Italy, 22–29 October 2017; pp. 793–803. [Google Scholar]
- Rothwell, C.A. Object Recognition through Invariant Indexing; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Sawada, T.; Li, Y.; Pizlo, Z. Shape Perception. In Oxford Handbook of Computational and Mathematical Psychology; Busemeyer, J., Townsend, J., Wang, Z.J., Eidels, A., Eds.; Oxford University Press: New York, NY, USA, 2015; pp. 255–276. [Google Scholar]
- Horaud, R.; Brady, M. On the geometric interpretation of image contours. Artif. Intell. 1988, 37, 333–353. [Google Scholar] [CrossRef]
- Sawada, T.; Zaidi, Q. Rotational symmetry in a 3D scene and its 2D image. J. Math. Psychol. 2018, 87, 108–125. [Google Scholar] [CrossRef]
- Wong, K.K.; Mendoça, P.R.S.; Cipolla, R. Reconstruction of surfaces of revolution from single uncalibrated views. Image. Vis. Comput. 2004, 22, 829–836. [Google Scholar] [CrossRef]
- Hong, W.; Yang, A.Y.; Huang, K.; Ma, Y. On symmetry and multiple-view geometry: Structure, pose, and calibration from a single image. International J. Comput. Vis. 2004, 60, 241–265. [Google Scholar] [CrossRef]
- Vetter, T.; Poggio, T. Symmetric 3D objects are an easy case for 2D object recognition. Spat. Vis. 1994, 8, 443–453. [Google Scholar]
- Yang, A.Y.; Huang, K.; Rao, S.; Hong, W.; Ma, Y. Symmetry-based 3-D reconstruction from perspective images. Comput. Vis. Image Underst. 2005, 99, 210–240. [Google Scholar] [CrossRef]
- Pizlo, Z.; Li, Y.; Sawada, T.; Steinman, R. Making a Machine that Sees Like Us; Oxford University Press: New York, NY, USA, 2014. [Google Scholar]
- Sawada, T. Visual detection of symmetry of 3D shapes. J. Vis. 2010, 10, 4. [Google Scholar] [CrossRef]
- Hong, W.; Ma, Y.; Yu, Y. Reconstruction of 3-D deformed symmetric curves from perspective images without discrete features. In Lecture Notes in Computer Science: Computer Vision-ECCV; Pajdla, T., Matas, J., Eds.; Springer-Verlag: Berlin, Germany, 2004; Volume 3023, pp. 533–545. [Google Scholar]
- Sawada, T.; Li, Y.; Pizlo, Z. Any pair of 2D curves is consistent with a 3D symmetric interpretation. Symmetry 2011, 3, 365–388. [Google Scholar] [CrossRef]
- Sugihara, K. Anomalous mirror symmetry generated by optical illusion. Symmetry 2016, 8, 21. [Google Scholar] [CrossRef]
- Erkelens, C.J. Equidistant intervals in perspective photographs and paintings. i-Perception 2016, 7, 4. [Google Scholar] [CrossRef] [PubMed]
- Sawada, T.; Li, Y.; Pizlo, Z. Detecting 3-D mirror symmetry in a 2-D camera image for 3-D shape recovery. Proc. IEEE 2014, 102, 1588–1606. [Google Scholar] [CrossRef]
- Kanatani, K. Constraints on length and angle. Comput. Vis. Graph. Image Process 1988, 41, 28–42. [Google Scholar] [CrossRef]
- Chen, C.C.; Sio, L.T. 3D surface configuration modulates 2D symmetry detection. Vis. Res. 2015, 107, 86–93. [Google Scholar] [CrossRef]
- Farell, B. The perception of symmetry in depth: Effect of symmetry plane orientation. Symmetry 2015, 7, 336–353. [Google Scholar] [CrossRef]
- Locher, P.; Smets, G. The influence of stimulus dimensionality and viewing orientation on detection of symmetry in dot patterns. Bull. Psychon. Soc. 1992, 30, 43–46. [Google Scholar] [CrossRef]
- Treder, M.S.; van der Helm, P.A. Symmetry versus repetition in cyclopean vision: A microgenetic analysis. Vis. Res. 2007, 47, 2956–2967. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).