Analogy between Thermodynamic Phase Transitions and Creeping Flows in Rectangular Cavities
Abstract
1. Introduction
2. Renormalization Group Theory of Critical Phenomena and Phase Transitions
3. Numerical Modeling
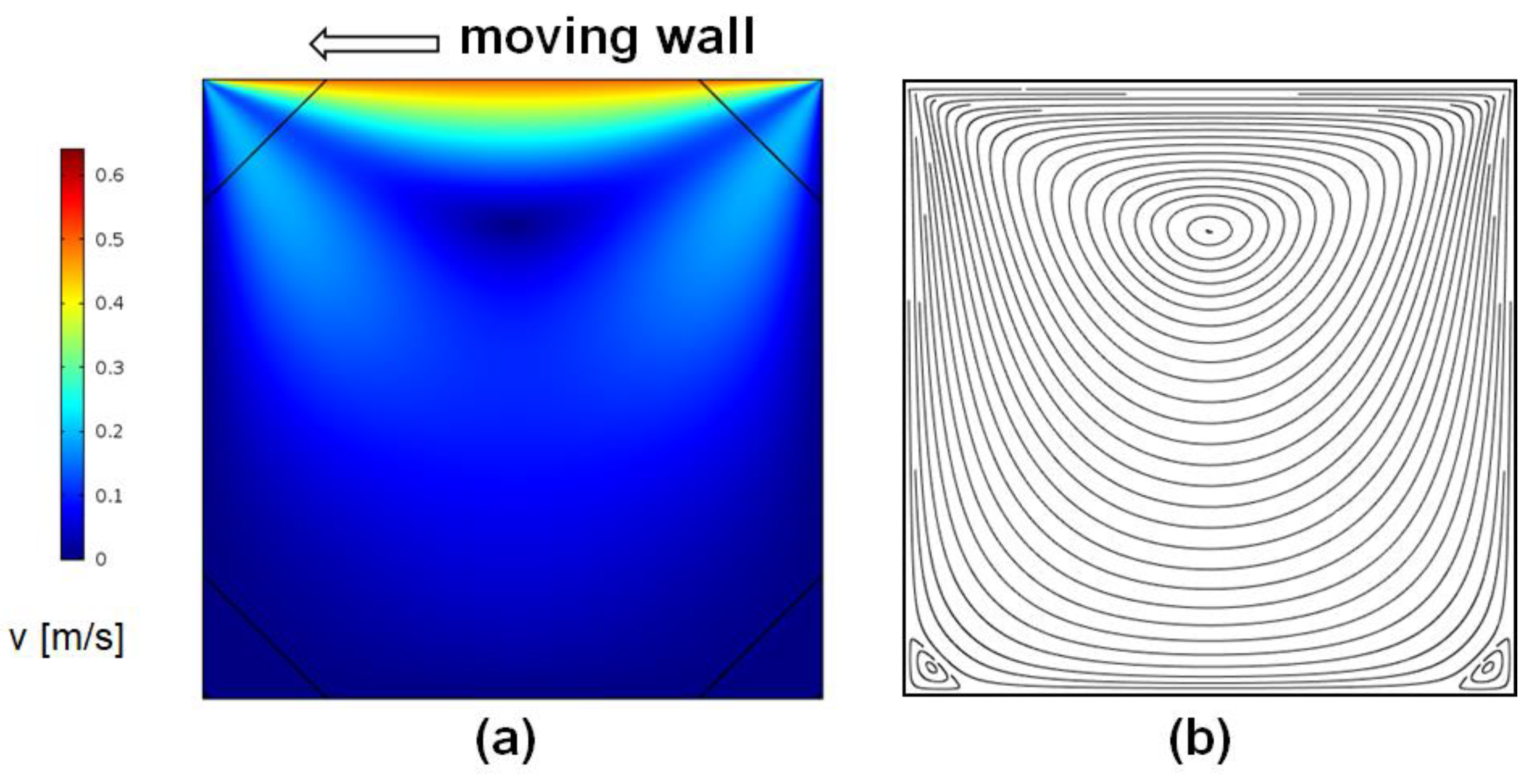
4. Cavity Fluid Mechanics
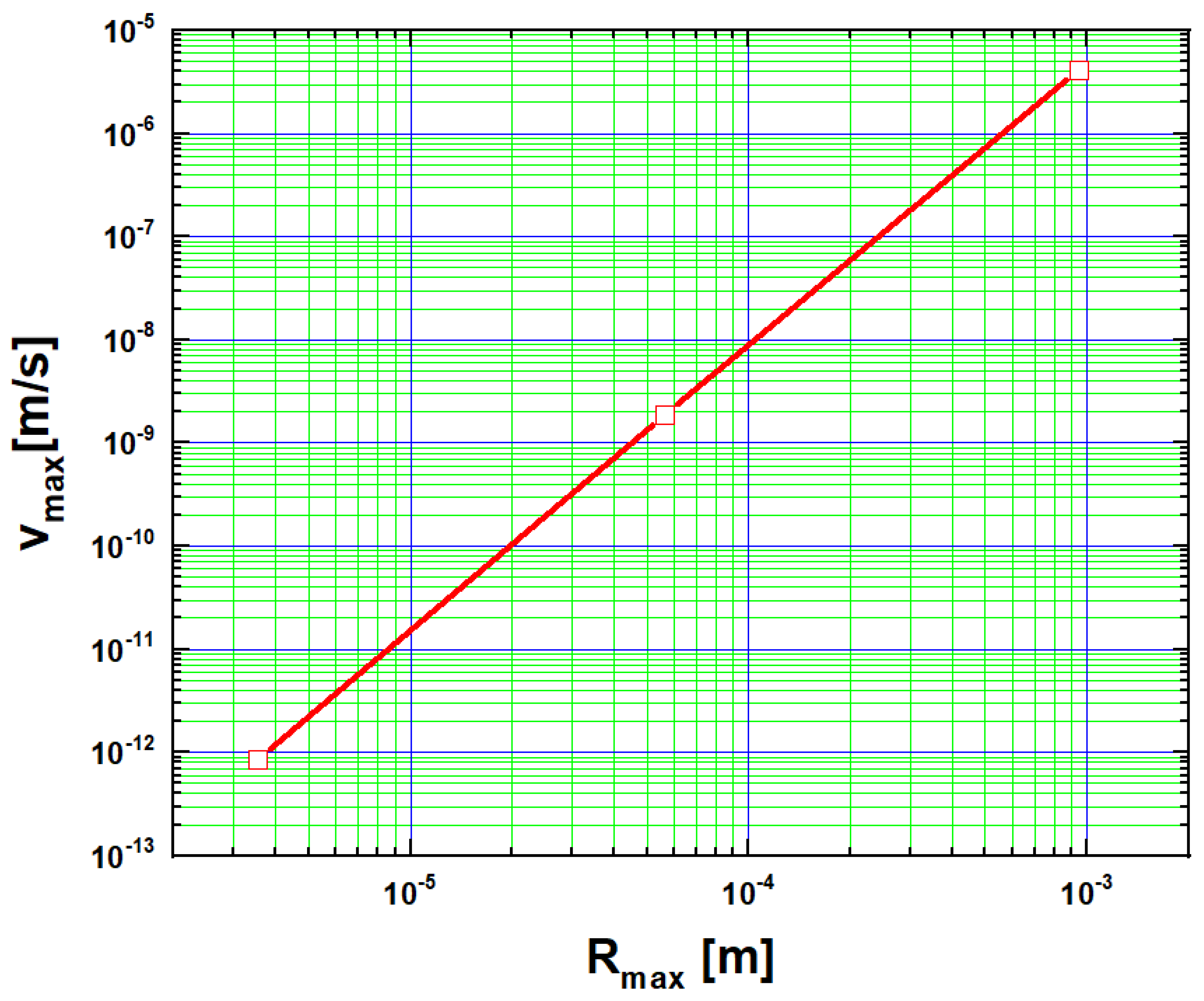
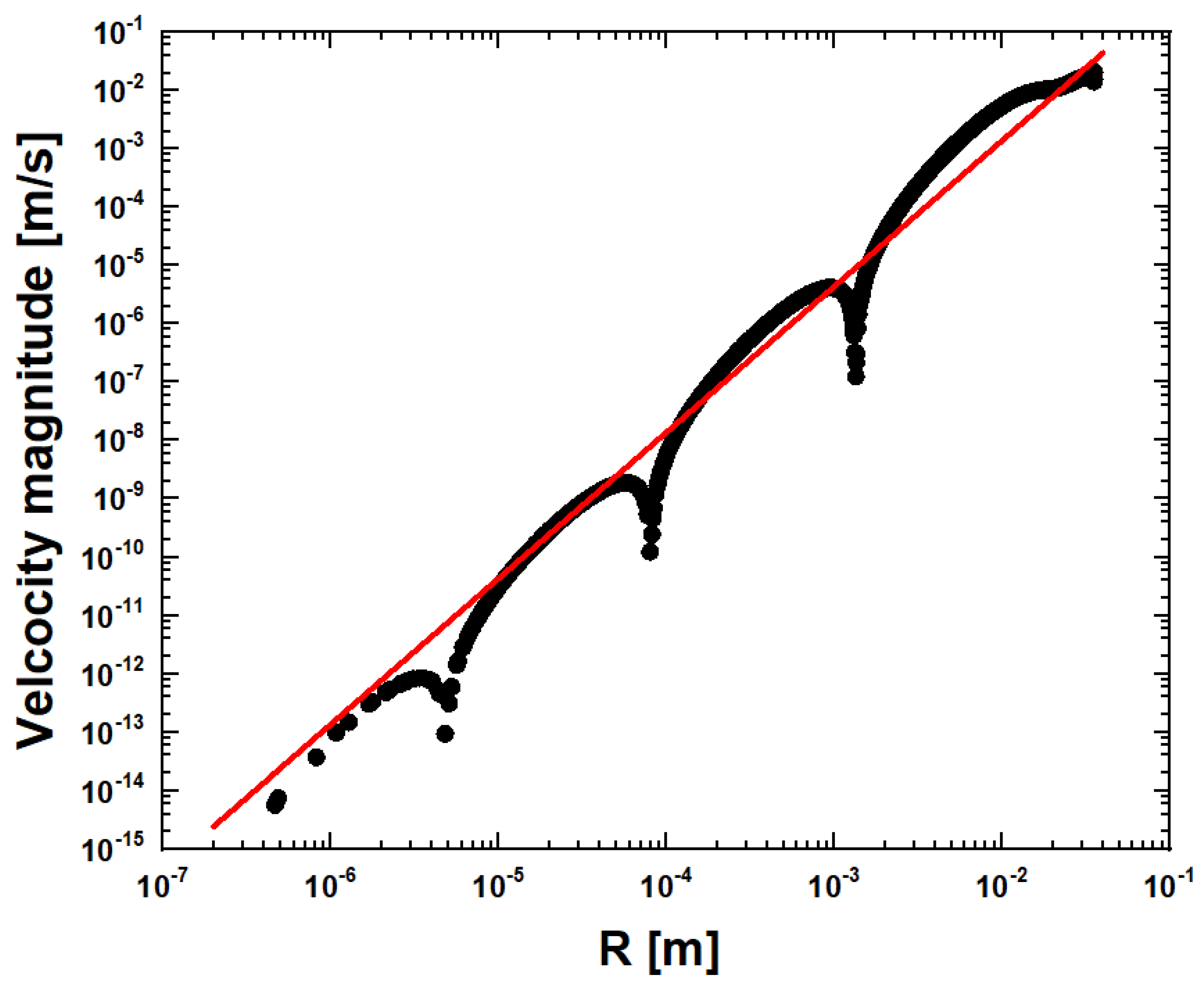
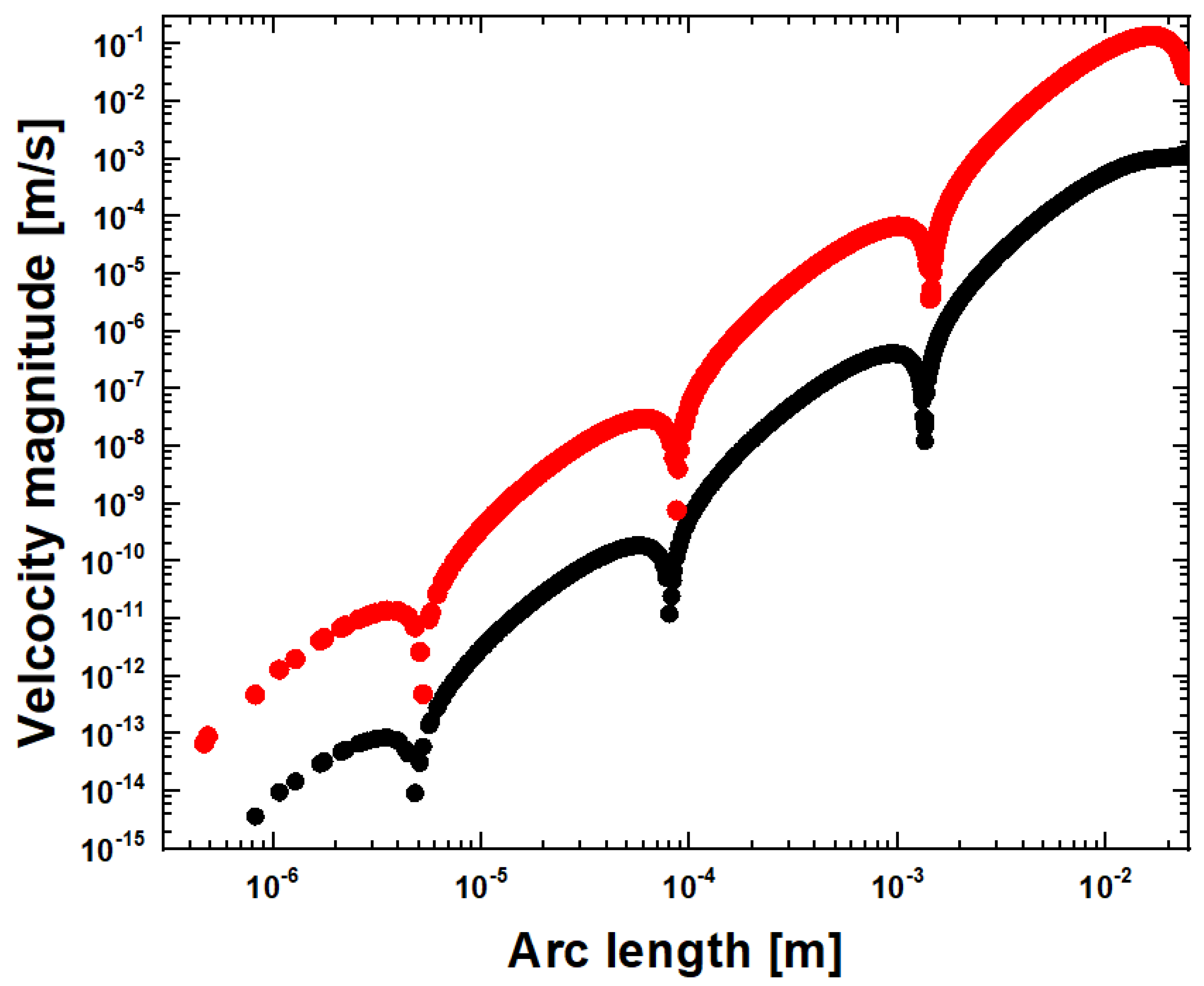
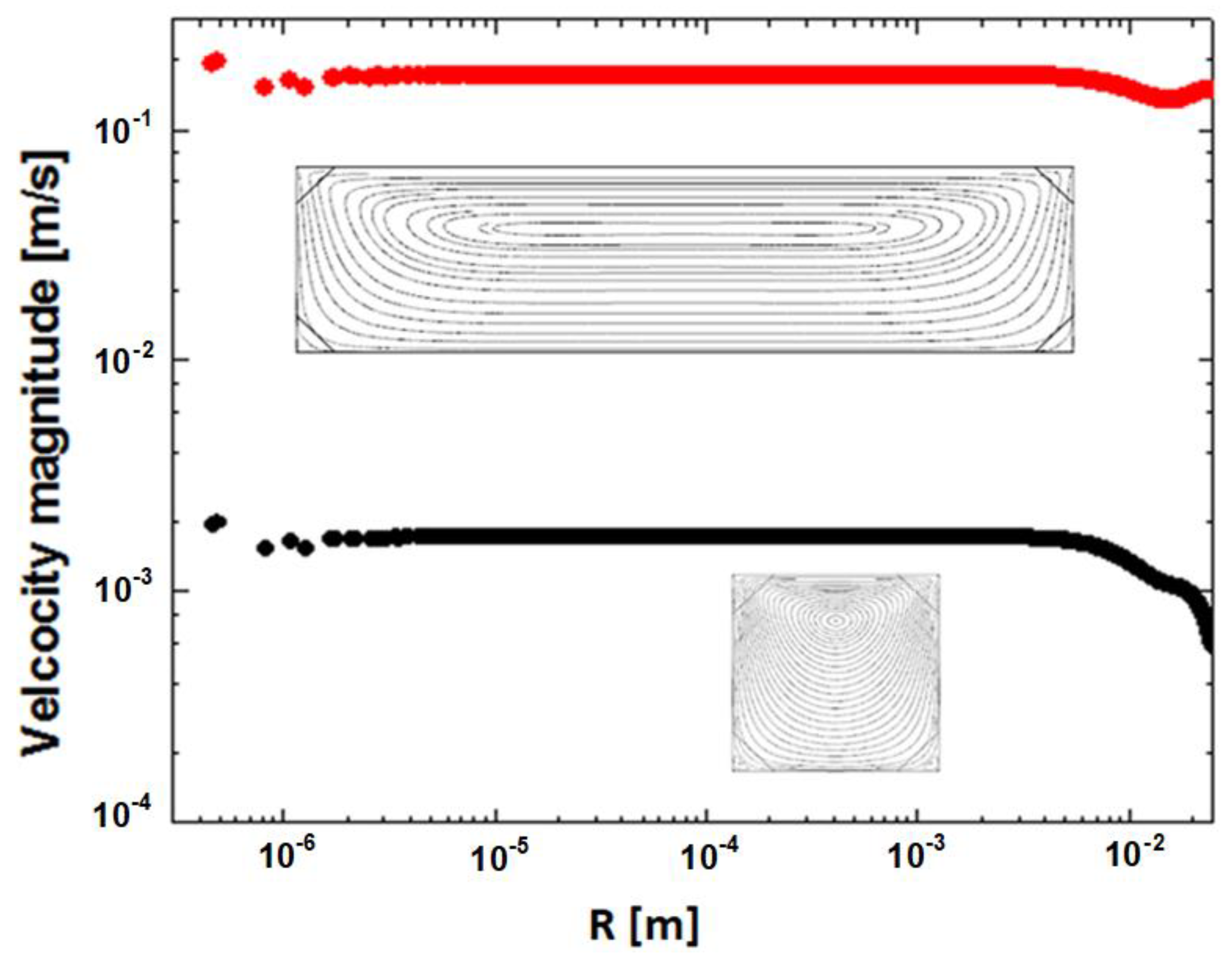
5. Critical Point Analog
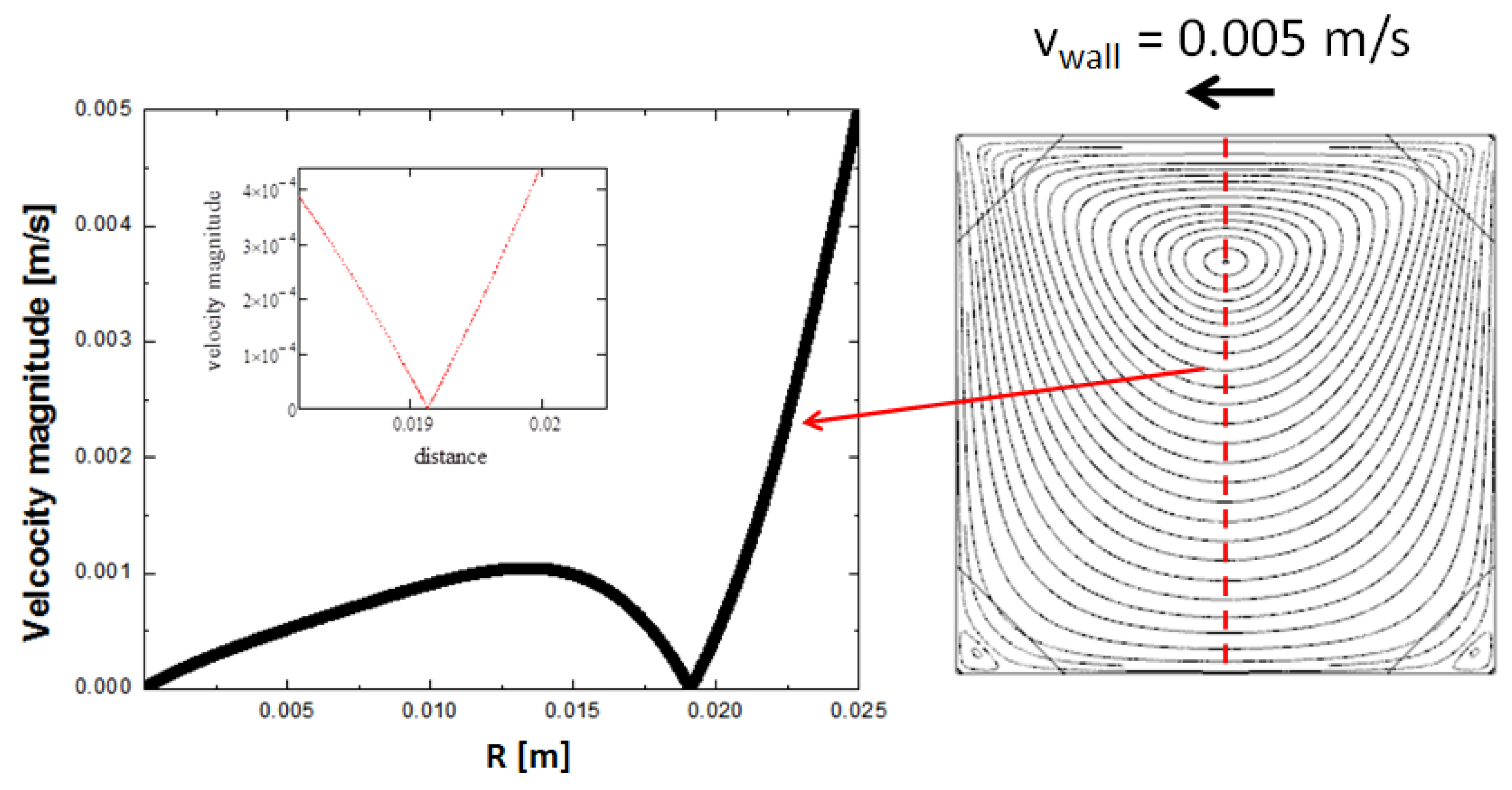
6. Discontinuity Point Analog
7. High Temperature Point Analog
8. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Kaufman, M.; Fodor, P.S. Fluid mechanics in rectangular cavities—Analytical model and numerics. Phys. A Stat. Mech. Appl. 2010, 389, 2951–2955. [Google Scholar] [CrossRef]
- Tadmor, Z.; Gogos, G. Principles of Polymer Processing, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Fodor, P.S.; Kaufman, M. The evolution of mixing in the staggered herringbone micromixer. Mod. Phys. Lett. B 2011, 25, 1111. [Google Scholar] [CrossRef]
- Moffatt, H.K. Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 1964, 18, 1–18. [Google Scholar] [CrossRef]
- Moffatt, H.K. Singularities in Fluid Dynamics and their Resolution. In Lectures on Topological Fluid Mechanics; Ricca, R.L., Ed.; Springer: Berlin, Germany, 1973; pp. 157–166. [Google Scholar]
- Barenblatt, G.I. Scaling, Self-Similarity, and Intermediate Asymptotics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Goldenfeld, N.; Kadanoff, L.P. Simple Lessons from Complexity. Science 1999, 284, 87–89. [Google Scholar] [CrossRef] [PubMed]
- Fodor, P.S.; Kaufman, M. Moffatt eddies in the single screw extruder: Numerical and analytical study. AIP Conf. Proc. 2015, 1664, 50010. [Google Scholar]
- Derrida, B.; Giacomin, G. Log-periodic Critical Amplitudes: A Perturbative Approach. J. Stat. Phys. 2013, 154, 286–304. [Google Scholar] [CrossRef]
- Berker, A.N.; Ostlund, S. Renormalisation-group calculations of finite systems: Order parameter and specific heat for epitaxial ordering. J. Phys. C Solid State Phys. 1979, 12, 4961–4975. [Google Scholar] [CrossRef]
- Griffiths, R.B.; Kaufman, M. Spin systems on hierarchical lattices. Introduction and thermodynamic limit. Phys. Rev. B 1982, 26, 5022–5032. [Google Scholar] [CrossRef]
- Kaufman, M.; Griffiths, R.B. Spin systems on hierarchical lattices. II. Some examples of soluble models. Phys. Rev. B 1984, 30, 244–249. [Google Scholar] [CrossRef]
- Fisher, M.E.; Berker, A.N. Scaling for first-order phase transitions in thermodynamic and finite systems. Phys. Rev. B 1982, 26, 2507–2513. [Google Scholar] [CrossRef]
- Diep, H.T. Statistical Physics; World Scientific: Singapore, 2015. [Google Scholar]
- Fisher, M.E. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 1967, 30, 615–730. [Google Scholar] [CrossRef]
- Ottino, J.M. The Kinematics of Mixing: Stretching, Chaos, and Transport; Cambridge University Press: New York, NY, USA, 1989. [Google Scholar]
- Kaufman, M.; Griffiths, R.B. Convexity of the free energy in some real-space renormalization-group approximations. Phys. Rev. B 1983, 28, 3864–3865. [Google Scholar] [CrossRef]
- Riedel, E.K.; Wegner, F.J. Effective critical and tricritical exponents. Phys. Rev. B 1974, 9, 294–315. [Google Scholar] [CrossRef]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; Informa UK Limited: Colchester, UK, 2018. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaufman, M.; Fodor, P.S. Analogy between Thermodynamic Phase Transitions and Creeping Flows in Rectangular Cavities. Symmetry 2020, 12, 1859. https://doi.org/10.3390/sym12111859
Kaufman M, Fodor PS. Analogy between Thermodynamic Phase Transitions and Creeping Flows in Rectangular Cavities. Symmetry. 2020; 12(11):1859. https://doi.org/10.3390/sym12111859
Chicago/Turabian StyleKaufman, Miron, and Petru S. Fodor. 2020. "Analogy between Thermodynamic Phase Transitions and Creeping Flows in Rectangular Cavities" Symmetry 12, no. 11: 1859. https://doi.org/10.3390/sym12111859
APA StyleKaufman, M., & Fodor, P. S. (2020). Analogy between Thermodynamic Phase Transitions and Creeping Flows in Rectangular Cavities. Symmetry, 12(11), 1859. https://doi.org/10.3390/sym12111859





