Local Super Antimagic Total Labeling for Vertex Coloring of Graphs

Abstract

Let $G=(V,E)$ be a graph with vertex set V and edge set E. A local antimagic total vertex coloring f of a graph G with vertex-set V and edge-set E is an injective map from $V\cup E$ to $\{1,2,\dots ,|V|+|E\left|\right\}$ such that if for each $uv\in E\left(G\right)$ then $w\left(u\right)\ne w\left(v\right)$, where $w\left(u\right)={\sum }_{uv\in E\left(G\right)}f\left(uv\right)+f\left(u\right)$. If the range set f satisfies $f\left(V\right)=\{1,2,\dots ,|V\left|\right\}$, then the labeling is said to be local super antimagic total labeling. This labeling generates a proper vertex coloring of the graph G with the color $w\left(v\right)$ assigning the vertex v. The local super antimagic total chromatic number of graph G, ${\chi }_{lsat}\left(G\right)$ is defined as the least number of colors that are used for all colorings generated by the local super antimagic total labeling of G. In this paper we investigate the existence of the local super antimagic total chromatic number for some particular classes of graphs such as a tree, path, cycle, helm, wheel, gear, sun, and regular graphs as well as an amalgamation of stars and an amalgamation of wheels.

1. Introduction

Vertex coloring is an assignment of colors to every vertex of graph G such that any two adjacent vertices receive different colors and the number of colors used for such coloring is made as minimal as possible. The vertex coloring problem has many applications such as a scheduling system [1] and frequency allocation.

Formally the vertex coloring in a graph is defined as follows. The k-coloring of graph G is a map of $c:V\to \{1,2,\cdots ,k\}$ where V is the set of vertices of G and $c\left(v\right)$ is a color of vertex v such that $c\left(u\right)\ne c\left(v\right)$ whenever vertices u and v are adjacent. The smallest positive integer of k is such that G satisfies the k-coloring and is called the chromatic number of G, denoted by $\chi \left(G\right)$ [2].

The vertex coloring of graphs is then approached by using the local antimagic total labeling of a graph. In 2017, Arumugam, Premalatha, Bača, and Semaničová-Feňovčíková [3] introduced this concept and defined it as follows. The local antimagic total labeling on a graph G with $\left|V\right|$ vertices and $\left|E\right|$ edges is defined as a bijection $f:E\to \{1,2,\cdots ,m\}$ such that the weights of any two adjacent vertices are different, that is, $w\left(u\right)\ne w\left(v\right)$ where $w\left(u\right)={\Sigma }_{e\in E\left(u\right)}f\left(e\right)$ and $E\left(u\right)$ is the set of edges incident to u. Thus, any local antimagic total labeling of a graph G induces a proper vertex coloring of G where the weight $w\left(u\right)$ is assigned as the color of vertex u. The local antimagic chromatic number of G, denoted by ${\chi }_{la}\left(G\right)$, is the minimum number of colors taken over all colorings induced by local antimagic total labelings of G.

The local antimagic chromatic number of some families of graphs are presented in the paper [3]. These include the complete graph $K_n$ for $n\ge 3$, the star $K_{1,n}$ for $n\ge 2$, the path $P_n$ for $n\ge 3$, the cycle on n for $n\ge 3$, the friendship graph $F_n$ for $n\ge 2$, the complete bipartite graph $K_{m,n}$ for $m,n\ge 2$, and the wheel $W_n$ for $n\ge 3$. Nazula, Slamin, and Dafik [4] determined the local antimagic chromatic number of uni cyclic graphs. Arumugam, Yi-Chun, Premalatha, and Tao-Ming [5] discovered the local antimagic chromatic number of the corona product of two graphs such as paths, cycles, and complete graphs with other graphs.

Recently, Putri, Dafik, Agustin, and Alfarisi [6] extended this notion by labeling the vertices and edges of a graph G to establish a vertex coloring. The local vertex antimagic total labeling on a graph G with $\left|V\right|$ vertices and $\left|E\right|$ edges is defined to be an injective assignment $f:V\cup E\to \{1,2,\cdots ,|V|+|E\left|\right\}$ so that the weights of any two adjacent vertices u and v are distinct, that is, $w\left(u\right)\ne w\left(v\right)$ where $w\left(u\right)=f\left(u\right)+{\Sigma }_{e\in E\left(u\right)}f\left(e\right)$ and $E\left(u\right)$ is the set of edges incident to u. For local antimagic total labeling, any local vertex antimagic total labeling of a graph G induces a proper vertex coloring of G where the vertex u is assigned by the color $w\left(u\right)$. The local antimagic total chromatic number, denoted by ${\chi }_{lat}\left(G\right)$, is the minimum number of colors taken over all colorings induced by local vertex antimagic total labelings of G. It is easy to see that for any graph G, ${\chi }_{la}\left(G\right)\ge {\chi }_{lat}\left(G\right)\ge \chi \left(G\right)$. The local antimagic total chromatic number for some family of graphs have been established by several authors such as prisms and Möbius ladders [7], brooms [8], stars [6], wheels, fans, and friendship graphs [9].

In the local antimagic total labeling of graph G, if the vertices of G receive the smallest labels, that is, $\{1,2,...,|V\left|\right\}$, then it is called local super antimagic total labeling. Any local super antimagic total labeling also induces a proper vertex coloring of G where the vertex u is assigned the color $w\left(u\right)$. The local super antimagic total chromatic number, denoted by ${\chi }_{lsat}\left(G\right)$, is the minimum number of colors taken over all colorings induced by local super antimagic total labelings of G. Again it is easy to see that for any graph G, ${\chi }_{lat}\left(G\right)\ge {\chi }_{lsat}\left(G\right)\ge \chi \left(G\right)$. Pratama, Setiawani, and Slamin [10] determined the local super antimagic total vertex coloring of some wheel-related graphs such as fans, even gear graphs, and sun flower graphs. In this paper, we determine the local super antimagic total chromatic number of some families of graphs such as stars, double stars, paths, cycles, gears, suns, helms, wheels and, some graphs obtained from an amalgamation product.

2. Results

We start this section with the upper bound on the chromatic number of the local super antimagic total of a tree as described in the following theorem.

Theorem 1.

If T is a tree on $n\ge 2$ vertices with k leaves, then ${\chi }_{lsat}\left(T\right)\le n-k+1$.

Proof. 

Let T be a tree on $n\ge 2$ vertices with k leaves. Let $v_i$ be some vertices in T that are adjacent to $nl\left(v_i\right)$ leaves, namely, $l_i^j$, where $1\le i\le r$, $1\le j\le nl\left(v_i\right)$, $nl\left(v_1\right)\ge nl\left(v_2\right)\ge \dots \ge nl\left(v_r\right)$. Label the leaves $l_i^j$ for $1\le j\le nl\left(v_i\right)$ by $f\left(l_i^j\right)=j$ if $i=1$ and $f\left(l_i^j\right)=j+{\sum }_{t=1}^{i-1}nl\left(v_t\right)$ if $i=2,3,...,r$ and label the edges $e_i=v_i{l}_i^j$ with $n+1,n+2,\dots ,n+k$ using formula $f\left(e_i\right)=n+k+1-f\left(l_i^j\right)$ to obtain $w\left(l_1^j\right)=w\left(l_2^j\right)=\dots =w\left(l_r^j\right)$. The rest of the edges are labeled by $\{n+k+1,n+k+2,\dots ,2n-1\}$ such that $s_e\left(v_i\right)\le s_e\left(v_j\right)$, for each $i\ne j$ and $1\le i,j\le n-k$ where $s_e\left(v_i\right)$ is the sum of all labels of edges that are incident to the vertex $v_i$. Label vertex $v_i$ by x and vertex $v_j$ by y, where $x<y$ for $x,y\in \{k+1,k+2,\dots ,n\}$. The weight of leaves are obtained from the smallest labels of vertices and edges. Thus, the total labeling of f produces $w\left(l_i^j\right)<w\left(v_i\right)<w\left(v_j\right)$ for each $i\ne j$, where $1\le i,j\le n-k$. It is clear that the weight of vertices are different whenever they are adjacent. Therefore the local super antmagic total labeling f gives ${\chi }_{lsat}\left(T\right)\le n-k+1$. □

Star, denoted by $S_{n+1}$, is a special class of tree of order $n+1$ with n leaves. By using Theorem 1 and the fact that ${\chi }_{lsat}\left(G\right)\ge 2$ for any connected graph G of order of at least 2, we obtain the local super antimagic total chromatic number of the star as follows.

Corollary 1.

If $S_{n+1}$ is a star, then ${\chi }_{lsat}\left(S_{n+1}\right)=2$.

Double star, denoted by $S_{k,n-k}$, is another special class of tree of order $n+2$ with n leaves and two central vertices that are adjacent to k and $n-k$ leaves, respectively. By using Theorem 1 and a local super antimagic total labeling, we obtain the local super antimagic total chromatic number of the double star as follows.

Corollary 2.

If $S_{k,n-k}$, for $n\ge 2$ and $k\ge 1$, is a double star, then ${\chi }_{lsat}\left(S_{k,n-k}\right)=3$.

Proof. 

Let $S_{k,n-k}$, for $n\ge 2$ and $k\ge 1$, be a double star of order $n+2$ with n leaves. Let $u_1$ and $u_2$ be two central vertices of the double star $S_{k,n-k}$, where $u_1$ is adjacent to k leaves, say $u_1^1,u_1^2,...,u_1^k$, and $u_2$ is adjacent to $n-k$ leaves, say $u_2^1,u_2^2,...,u_2^{n-k}$. For $n=2$ and $k=1$, the double star $S_{k,n-k}$ or $S_{1,1}$ is isomorphic to path $P_4$. It is easy to check that ${\chi }_{lsat}\left(P_4\right)\ne 2$, so ${\chi }_{lsat}\left(P_4\right)\ge 3$. Combined with Theorem 1, it implies that ${\chi }_{lsat}\left(S_{1,1}\right)={\chi }_{lsat}\left(P_4\right)=3$. We now suppose that ${\chi }_{lsat}\left(S_{k,n-k}\right)=2$ for $n\ge 3$ and $k\ge 1$. Then there must be two vertices of distance two with the same weight. Without loss of generality, suppose that $w\left(u_1\right)=w\left(u_2^j\right)$ for any $j=1,2,\dots ,n-k$ and $d\left(u_1\right)\ge 3$ where $d\left(u_1\right)$ is the degree of central vertex $u_1$. Since the smallest labels are used for $n+2$ vertices and the three smallest edge labels are $n+3$, $n+4$, and $n+5$, it implies that $w\left(u_1\right)\ge 1+(n+3)+(n+4)+(n+5)=3n+13$. However, the weight of $u_2^j$ for any $j=1,2,\dots ,n-k$ is obtained from the sum of one vertex label and one edge label, which can be the largest ones, that is, $w\left(u_2^j\right)\le (n+2)+(2n+3)=3n+5$. Thus $w\left(u_1\right)>w\left(u_2^j\right)$, which is a contradiction. So ${\chi }_{lsat}\left(S_{k,n-k}\right)\ge 3$. Again combined with Theorem 1, we obtain ${\chi }_{lsat}\left(S_{k,n-k}\right)=3$. □

In the next theorem, we present the local super antimagic total chromatic number of a cycle $C_n$ on $n\ge 3$ vertices.

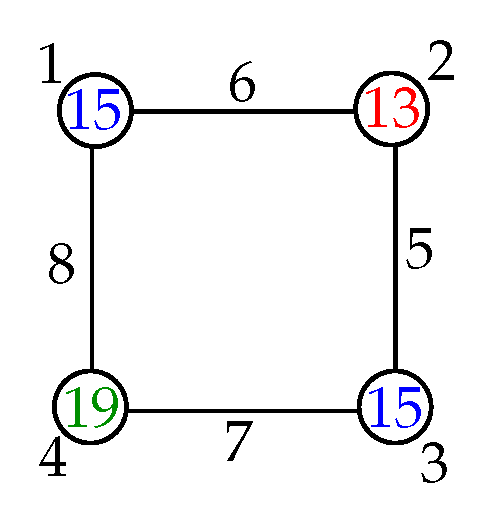
Theorem 2.

If $C_n$ is a cycle on $n\ge 3$ vertices, then:

$${\chi }_{lsat}\left(C_n\right)=\left\{\begin{array}{c}3,\mathrm{if}n\mathrm{is}\mathrm{odd}\mathrm{or}n=4\hfill \\ 2,\mathrm{otherwise}.\hfill \end{array}\right.$$

Proof. 

Let $C_n$ be a cycle on $n\ge 3$ vertices with vertex set $V\left(C_n\right)=\{x_i:1\le i\le n\}$ and edge set $E\left(C_n\right)=\{x_i{x}_{i+1}:1\le i\le n-1\}\cup \left\{x_n{x}_1\right\}$. To obtain the upper bound on ${\chi }_{lsat}\left(C_n\right)$, we divide into five cases.

Case i. For $n=4$.

Let $\{x_1,x_2,x_3,x_4\}$ be the vertex set of $C_4$. Suppose that ${\chi }_{lsat}\left(C_4\right)=2$ and the weights are y and z. Then there are two pair of vertices of distance two in $C_4$ with the same weight, without loss of generality, let $w\left(x_1\right)=w\left(x_3\right)=y$ and $w\left(x_2\right)=w\left(x_4\right)=z$. in this total labeling, the labels of vertices are used once, while the labels of edges are used twice. Thus, the total weight of all 4 vertices are $2y+2z=(1+2+3+4)+2(5+6+7+8)$, that is, $y+z=31$. There are 4 possible solutions (pairs of weight) for $\{y,z\}$, namely, {12,19}, {13,18}, {14,17}, and {15,16}. Each weight corresponds to two independent triple labels (one vertex label and two edges labels). Table A1 shows all possible local super antimagic total labelings of $C_4$. It can be seen that the sum of the first two independent triple labels is 15 and the second one is 16. However, it is also impossible because weight 15 and 16 share two edge labels. Thus ${\chi }_{lsat}\left(C_4\right)\ge 2$. Figure A1 shows the local super antimagic total labeling of $C_4$ with 3 different weights. This implies that ${\chi }_{lsat}\left(C_4\right)\le 3$. Therefore ${\chi }_{lsat}\left(C_4\right)=3$.

Case ii. For odd $n\ge 3$.

Label the vertices and edges of cycle $C_n$ using the following formula.

$$\begin{array}{ccc}\hfill f_1\left(x_i\right)& =& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=1,\hfill \\ i-1,\hfill & \mathrm{for}\mathrm{odd}i\ne 1,\hfill \\ i+1,\hfill & \mathrm{for}\mathrm{even}i,\hfill \end{array}\right.\hfill \\ \hfill f_1\left(x_i{x}_{i+1}\right)& =& \left\{\begin{array}{c}\frac{4n-i+1}{2},\mathrm{for}\mathrm{odd}i,\hfill \\ \frac{3n-i+1}{2},\mathrm{for}\mathrm{even}i,\hfill \end{array}\right.\hfill \\ \hfill f_1\left(x_n{x}_1\right)& =& \frac{3n+1}{2}.\hfill \end{array}$$

This labeling gives any two adjacent vertices with different weights, that is,

$$\begin{array}{ccc}\hfill w\left(x_i\right)& =& \left\{\begin{array}{cc}\frac{7n+1}{2},\hfill & \mathrm{for}\mathrm{odd}i\ge 3,\hfill \\ \frac{7n+3}{2},\hfill & \mathrm{for}\mathrm{i}=1,\hfill \\ \frac{7n+5}{2},\hfill & \mathrm{for}\mathrm{even}i.\hfill \end{array}\right.\hfill \end{array}$$

Thus ${\chi }_{lsat}\left(C_n\right)\le 3$ for odd $n\ge 3$.

Case iii. For $n\equiv 2,6$ (mod 8).

Label the vertices and edges of cycle $C_n$ using the following formula.

$$\begin{array}{ccc}\hfill f_2\left(x_i\right)& =& \left\{\begin{array}{cc}\frac{n}{2}+i,\hfill & \mathrm{for}\mathrm{odd}i\le \frac{n}{2},\hfill \\ i,\hfill & \mathrm{for}\mathrm{even}i\le \frac{n}{2},\hfill \\ i-\frac{n}{2},\hfill & \mathrm{for}\mathrm{even}i>\frac{n}{2},\hfill \\ i,\hfill & \mathrm{for}\mathrm{odd}i>\frac{n}{2},\hfill \end{array}\right.\hfill \\ \hfill f_2\left(x_i{x}_{i+1}\right)& =& \left\{\begin{array}{cc}\frac{4n-i+1}{2},\hfill & \mathrm{for}\mathrm{odd}i,\hfill \\ \frac{7n-2i+2}{4},\hfill & \mathrm{for}\mathrm{even}i>\frac{n}{2},\hfill \\ \frac{5n-2i+2}{4},\hfill & \mathrm{for}\mathrm{even}i<\frac{n}{2},\hfill \end{array}\right.\hfill \\ \hfill f_2\left(x_n{x}_1\right)& =& \frac{5n+2}{4}.\hfill \end{array}$$

This labeling also gives any two adjacent vertices with different weights, that is,

$$\begin{array}{ccc}\hfill w\left(x_i\right)& =& \left\{\begin{array}{cc}\frac{15n+2}{4}+1,\hfill & \mathrm{for}\mathrm{odd}i,\hfill \\ \frac{13n+2}{4}+1,\hfill & \mathrm{for}\mathrm{even}i.\hfill \end{array}\right.\hfill \end{array}$$

Therefore ${\chi }_{lsat}\left(C_n\right)\le 2$ for $n\equiv 2,6$ (mod 8).

Case iv. For $n\equiv 0$ (mod 8).

Label the vertices and edges of cycle $C_n$ using the following formula.

$$\begin{array}{ccc}\hfill f_3\left(x_i\right)& =& \left\{\begin{array}{cc}\frac{3n+i+2}{4}-(1+{(-1)}^{\frac{i}{2}})\frac{n-4}{16},\hfill & \mathrm{for}\mathrm{even}\frac{n}{2}+4\le i\le n,\hfill \\ \frac{3n+4}{4},\hfill & \mathrm{for}i=\frac{n}{2}+2\hfill \\ \frac{2n+i+1}{4}-(1-{(-1)}^{\frac{i+1}{2}})\frac{n-4}{16},\hfill & \mathrm{for}\mathrm{odd}\frac{n}{2}+3\le i\le n-1,\hfill \\ \frac{2n-i+8}{4}-(1-{(-1)}^{\frac{i}{2}})\frac{n+4}{16},\hfill & \mathrm{for}\mathrm{even}2\le i\le \frac{n}{2},\hfill \\ \frac{n-i+7}{4}-(1-{(-1)}^{\frac{i+1}{2}})\frac{n+4}{16},\hfill & \mathrm{for}\mathrm{odd}1\le i\le \frac{n}{2}+1,\hfill \end{array}\right.\hfill \\ \hfill f_3\left(x_i{x}_{i+1}\right)& =& \left\{\begin{array}{cc}\frac{8n-i+1}{4}-(1+{(-1)}^{\frac{i+1}{2}})\frac{n+4}{16},\hfill & \mathrm{for}\mathrm{odd}1\le i\le \frac{n}{2}+3,\hfill \\ \frac{4n-i+1}{2},\hfill & \mathrm{for}\mathrm{odd}\frac{n}{2}+5\le i\le n-1,\hfill \\ \frac{5n+2i}{4},\hfill & \mathrm{for}\mathrm{even}2\le i\le \frac{n}{2},\hfill \\ \frac{7n+2i+4}{8}+(1+{(-1)}^{\frac{i}{2}})\frac{n-4}{16},\hfill & \mathrm{for}\mathrm{even}\frac{n}{2}+2\le i\le n-2,\hfill \end{array}\right.\hfill \\ \hfill f_3\left(x_n{x}_1\right)& =& \frac{5n}{4}.\hfill \end{array}$$

This labeling also gives any two adjacent vertices with different weights, that is,

$$\begin{array}{ccc}\hfill w\left(x_i\right)& =& \left\{\begin{array}{cc}\frac{27n}{8}+1,\hfill & \mathrm{for}\mathrm{odd}i,\hfill \\ \frac{29n}{8}+2,\hfill & \mathrm{for}\mathrm{even}i.\hfill \end{array}\right.\hfill \end{array}$$

Therefore ${\chi }_{lsat}\left(C_n\right)\le 2$ for $n\equiv 0$ (mod 8).

Case v. For $n\equiv 4$ (mod 8).

Label the vertices and edges of cycle $C_n$ using the following formula.

$$\begin{array}{ccc}\hfill f_4\left(x_i\right)& =& \left\{\begin{array}{cc}\frac{n}{2},\hfill & \mathrm{for}i=1,\hfill \\ n,\hfill & \mathrm{for}i=3,\hfill \\ \frac{7n-4}{8},\hfill & \mathrm{for}i=\frac{n}{2}+1,\hfill \\ \frac{3n+4}{8},\hfill & \mathrm{for}i=\frac{n}{2}+3,\hfill \\ \frac{9n-2i+2}{8},\hfill & \mathrm{for}\frac{n}{2}+5\le i\le n-1,i\equiv 3\left(\mathrm{mod}4\right),\hfill \\ \frac{4n-i+1}{4},\hfill & \mathrm{for}\frac{n}{2}+7\le i\le n-3,i\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{7n-2i+8}{8},\hfill & \mathrm{for}\frac{n}{2}+4\le i\le n-2,i\equiv 2\left(\mathrm{mod}4\right),\hfill \\ \frac{3n-i+4}{4},\hfill & \mathrm{for}\frac{n}{2}+2\le i\le n,i\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{3n+2i-2}{8},\hfill & \mathrm{for}7\le i\le \frac{n}{2}-3,i\equiv 3\left(\mathrm{mod}4\right),\hfill \\ \frac{2n+2i-2}{8},\hfill & \mathrm{for}5\le i\le \frac{n}{2}-1,i\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{n+2i+4}{8},\hfill & \mathrm{for}4\le i\le \frac{n}{2}-2,i\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{i+2}{4},\hfill & \mathrm{for}2\le i\le \frac{n}{2},i\equiv 2\left(\mathrm{mod}4\right),\hfill \end{array}\right.\hfill \\ \hfill f_4\left(x_i{x}_{i+1}\right)& =& \left\{\begin{array}{cc}2n,\hfill & \mathrm{for}i=1,\hfill \\ \frac{11n+4}{8},\hfill & \mathrm{for}i=2,\hfill \\ n+1,\hfill & \mathrm{for}i=\frac{n}{2}+1,\hfill \\ \frac{4n+2-i}{2},\hfill & \mathrm{for}\mathrm{even}4\le i\le \frac{n}{2}+2,\hfill \\ \frac{5n+2i-2}{4},\hfill & \mathrm{for}\mathrm{odd}\frac{n}{2}+3\le i\le n-1,\hfill \\ \frac{11n+2i+2}{8},\hfill & \mathrm{for}5\le i\le \frac{n}{2}-1,i\equiv 1\left(\mathrm{mod}4\right),\hfill \\ \frac{5n+i+1}{4},\hfill & \mathrm{for}3\le i\le \frac{n}{2}-3,i\equiv 3\left(\mathrm{mod}4\right),\hfill \\ \frac{11n-2i+12}{8},\hfill & \mathrm{for}\frac{n}{2}+6\le i\le n-4,i\equiv 0\left(\mathrm{mod}4\right),\hfill \\ \frac{5n-i+6}{4},\hfill & \mathrm{for}\frac{n}{2}+4\le i\le n-2,i\equiv 2\left(\mathrm{mod}4\right),\hfill \end{array}\right.\hfill \\ \hfill f_4\left(x_n{x}_1\right)& =& \frac{9n+12}{8}.\hfill \end{array}$$

This labeling also gives any two adjacent vertices with different weights, that is,

$$\begin{array}{ccc}\hfill w\left(x_i\right)& =& \left\{\begin{array}{cc}\frac{29n+12}{8},\hfill & \mathrm{for}\mathrm{odd}i,\hfill \\ \frac{29n+12}{8}-\frac{n}{4},\hfill & \mathrm{for}\mathrm{even}i.\hfill \end{array}\right.\hfill \end{array}$$

Therefore ${\chi }_{lsat}\left(C_n\right)\le 2$ for $n\equiv 4$ (mod 8).

Combining all cases with the fact that ${\chi }_{lsat}\left(C_n\right)\ge \chi \left(C_n\right)=3$ for odd n and ${\chi }_{lsat}\left(C_n\right)\ge \chi \left(C_n\right)=2$ for even $n\ne 4$, we conclude that:

$${\chi }_{lsat}\left(C_n\right)=\left\{\begin{array}{c}3,\mathrm{if}n\mathrm{is}\mathrm{odd}\mathrm{or}n=4,\hfill \\ 2,\mathrm{otherwise}.\hfill \end{array}\right.$$

 □

The local super antimagic total labeling of the cycle $C_n$ for even $n\ge 6$ can be used for labeling a path $P_n$ for even $n\ge 6$ by removing an edge of $C_n$ as described in the following corollary.

Corollary 3.

If $P_n$ is a path of order even $n\ge 6$, then $3\le {\chi }_{lsat}\left(P_n\right)\le 4$.

Proof. 

Let $P_n$ be the path of order even $n\ge 6$ with the vertex set $\{x_1,x_2,\cdots ,x_n\}$. Suppose that there exists a labeling $f^{*}$ such that ${\chi }_{lsat}\left(P_n\right)=2$. Then for odd i,

$$\begin{array}{c}\hfill w\left(x_i\right)\ge \frac{min\left\{{\sum }_{i=1}^{\frac{n}{2}}{f}^{*}\left(x_{2i-1}\right)\right\}+{\sum }_{e\in E\left(P_n\right)}{f}^{*}\left(e\right)}{\frac{n}{2}}=\frac{\left(\genfrac{}{}{0pt}{}{\frac{n}{2}+1}{2}\right)+\left(\genfrac{}{}{0pt}{}{2n}{2}\right)-\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)}{\frac{n}{2}}=\frac{13n-10}{4}.\end{array}$$

However we know that for an end vertex, without loss of generality say $x_1$, we have $w\left(x_1\right)\le max\left\{f\left(x_i\right)\right\}+max\left\{f\left(e\right)\right\}=n+2n-1=3n-1$. So, $\frac{13n-10}{4}<3n-1$. This implies that $n<6$, contradiction with $n\ge 6$. Therefore, ${\chi }_{lsat}\ge 3$.

The upper bound can be obtained by labeling in Teorema 2 for even n by removing edge $uv\in E\left(C_n\right)$ that satisfies $f\left(uv\right)=2n$. Then $w\left(u\right)<w\left(v\right)<w\left(x_i\right)<w\left(x_{i+1}\right)$. Thus, ${\chi }_{lsat}\left(P_n\right)\le 4$. This concludes the proof that for even $n\ge 6$, $3\le {\chi }_{lsat}\left(P_n\right)\le 4$. □

Although for the even case, the local super antimagic total chromatic number of path is not fixed, we have fixed the value for the odd case as presented in the following theorem.

Theorem 3.

If $P_n$ is a path of order odd $n\ge 5$, then ${\chi }_{lsat}\left(P_n\right)=3$.

Proof. 

Let $P_n$ be the path of order odd $n\ge 5$ with the vertex set $\{x_1,x_2,\cdots ,x_n\}$. Suppose that there exists a labeling $f^{*}$ such that ${\chi }_{lsat}\left(P_n\right)=2$, that is, $w\left(x_1\right)=w\left(x_3\right)=\dots =w\left(x_n\right)=a$ and $w\left(x_2\right)=w\left(x_4\right)=\dots =w\left(x_{n-1}\right)=b$ for some positive integers a and b. Then,

$$\begin{array}{ccc}\hfill \sum _{v\in V\left(P_n\right)}{f}^{*}\left(v\right)+2\sum _{e\in E\left(P_n\right)}{f}^{*}\left(e\right)& =& \left(\frac{n+1}{2}\right)a+\left(\frac{n-1}{2}\right)b\hfill \\ \hfill \frac{n(7n-5)}{2}& =& \left(\frac{n+1}{2}\right)a+\left(\frac{n-1}{2}\right)b\hfill \end{array}$$

which is diophantine equations with the initial condition $a_0=\frac{n(7n-5)}{2}$ and $b_0=-\frac{n(7n-5)}{2}$. Thus the general solution is $a=\frac{n(7n-5)}{2}-\left(\frac{n-1}{2}\right)t$ and $b=-\frac{n(7n-5)}{2}+\left(\frac{n+1}{2}\right)t$, where t is an integer. Since a and b are positive integers, then:

$$\begin{array}{ccc}\hfill \frac{n(7n-5)}{2}-\left(\frac{n-1}{2}\right)t>0& \Rightarrow & t<\frac{n(7n-5)}{n-1}=7n+2+\frac{2}{n-1}\hfill \\ \hfill -\frac{n(7n-5)}{2}+\left(\frac{n+1}{2}\right)t<0& \Rightarrow & t>\frac{n(7n-5)}{n+1}=7n-12+\frac{12}{n+1}\hfill \end{array}$$

which imply that $7n-11\le t\le 7n+2$. This solution equivalent to $a=\frac{(14-k)n+(k-12)}{2}$ and $b=\frac{kn+(k-12)}{2}$ for $k=1,2,\dots ,14$. We know that for even i,

$$\begin{array}{c}\hfill w\left(x_i\right)\ge \frac{min\left\{{\sum }_{i=1}^{\frac{n-1}{2}}{f}^{*}\left(x_{2i}\right)\right\}+{\sum }_{e\in E\left(P_n\right)}{f}^{*}\left(e\right)}{\frac{n-1}{2}}=\frac{\left(\genfrac{}{}{0pt}{}{\frac{n+1}{2}}{2}\right)+\left(\genfrac{}{}{0pt}{}{2n}{2}\right)-\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)}{\frac{n-1}{2}}=\frac{13n+1}{4}.\end{array}$$

However, this bound is impossible to be satisfied by $k=1,2,\dots ,6$. Since such a value of k implies that $b<\frac{13n+1}{4}$. If we consider the upper bound of $w\left(x_i\right)$ for even i, that is,

$$\begin{array}{ccc}\hfill w\left(x_{even}\right)& \le & \frac{max\left\{{\sum }_{i=1}^{\frac{n-1}{2}}{f}^{*}\left(x_{2i}\right)\right\}+{\sum }_{e\in E\left(P_n\right)}{f}^{*}\left(e\right)}{\frac{n-1}{2}}=\frac{\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)-\left(\genfrac{}{}{0pt}{}{\frac{n+3}{2}}{2}\right)+\left(\genfrac{}{}{0pt}{}{2n}{2}\right)-\left(\genfrac{}{}{0pt}{}{n+1}{2}\right)}{\frac{n-1}{2}}\hfill \\ & =& \frac{\left(\genfrac{}{}{0pt}{}{2n}{2}\right)-\left(\genfrac{}{}{0pt}{}{\frac{n+3}{2}}{2}\right)}{\frac{n-1}{2}}=\frac{15n+3}{4}.\hfill \end{array}$$

Again, this bound is impossible to be satisfied by $k=8,9,\dots ,14$ as it implies that $b>\frac{15n+3}{4}$. Furthermore, $k=7$ is also impossible as it implies $a=b$ which is contradiction for $f^{*}$ as a local super antimagic total labeling of $P_n$. Thus, there are no values of a and b that satisfy the condition. So, ${\chi }_{lsat}\left(P_n\right)\ge 3$.

To prove the upper bound, we label the vertices and edges of $P_n$ by using the following formula.

$$\begin{array}{ccc}\hfill f\left(x_i\right)& =& \left\{\begin{array}{cc}1,\hfill & \mathrm{for}i=2,\hfill \\ n-1,\hfill & \mathrm{for}i=1,\hfill \\ n,\hfill & \mathrm{for}i=n,\hfill \\ n-i,\hfill & \mathrm{for}\mathrm{odd}i=3,5,\cdots ,n-2,\hfill \\ n+2-i,\hfill & \mathrm{for}\mathrm{even}i=4,6,\cdots ,n-1,\hfill \end{array}\right.\hfill \\ \hfill f\left(x_i{x}_{i+1}\right)& =& \left\{\begin{array}{cc}2n-1,\hfill & \mathrm{for}i=1,\hfill \\ \frac{2n+i-1}{2},\hfill & \mathrm{for}\mathrm{odd}i=3,5,\cdots ,n-2,\hfill \\ \frac{3n+i-3}{2},\hfill & \mathrm{for}\mathrm{even}i=2,4,\cdots ,n-1.\hfill \end{array}\right.\hfill \end{array}$$

It is easy to see that the labeling f gives different vertex weights, namely, $w\left(x_1\right)=w\left(x_n\right)=3n-2$, $w\left(x_i\right)=\frac{7n-1}{2}$ for odd $i=3,5,\cdots ,n-2$ and $w\left(x_i\right)=\frac{7n-1}{2}-2$ for even $i=2,4,\cdots ,n-1$. Thus ${\chi }_{lsat}\left(P_n\right)\le 3$. Combined with the lower bound, we conclude that ${\chi }_{lsat}\left(P_n\right)=3$ for odd $n\ge 5$. □

Gear, denoted by $G_n$, is a graph of order $2n+1$ that is obtained from a cycle on $2n$ vertices $C_{2n}$ by adding one central vertex and connecting half of rim vertices alternately to the central vertex. If the vertex set $C_n$ is $\{x_1,x_2,\dots ,x_{2n}\}$ and the central vertex is c, then the vertex set of $G_n$ is $\{c,x_1,x_2,\dots ,x_{2n}\}$ and the edge set of $G_n$ is $\{c{x}_1,c{x}_3,\dots ,c{x}_{2n-1}\}\cup \{x_1{x}_2,x_2{x}_3,\dots ,x_{2n}{x}_1\}$. For the case odd $n\ge 5$, the local super antimagic total chromatic number of the gear $G_n$ can be obtained from the local super antimagic total labeling of a cycle $C_{2n}$ as follows.

Corollary 4.

If $G_n$ for odd $n\ge 5$ is a gear, then ${\chi }_{lsat}\left(G_n\right)=3$.

Proof. 

Let $G_n$ for odd $n\ge 5$ be a gear with the vertex set $\{c,x_1,x_2,\dots ,x_{2n}\}$ and the edge set $\{c{x}_1,c{x}_3,\dots ,c{x}_{2n-1}\}\cup \{x_1{x}_2,x_2{x}_3,\dots ,x_{2n}{x}_1\}$. We will use the local super antimagic total labeling of a cycle $C_{2n}$ given in Theorem 2 and then apply a labeling $f^{+}$ with formula $f^{+}\left(c\right)=2n+1$ for the central vertex of $G_n$, $f^{+}\left(e\right)=f\left(e\right)+1$ for the edges of $G_n$ and $f^{+}\left(x_i\right)=f\left(x_i\right)$ for the rim vertices of $G_n$ where i is even. When i is odd, label the rim vertices of $G_n$ using $f^{+}\left(x_i\right)$ by permuting labels $f\left(x_1\right),f\left(x_3\right),\dots ,f\left(x_{2n-1}\right)$ according to a rule given in Table A2. This labeling gives any two adjacent vertices of $G_n$ with different weights, that is,

$$\begin{array}{ccc}\hfill w\left(x_i\right)& =& \left\{\begin{array}{cc}12n+5,\hfill & \mathrm{for}\mathrm{odd}i,\hfill \\ \frac{13n+7}{2},\hfill & \mathrm{for}\mathrm{even}i,\hfill \end{array}\right.\hfill \\ \hfill w\left(c\right)& =& \frac{1}{2}(9n^2+7n+2).\hfill \end{array}$$

Thus ${\chi }_{lsat}\left(G_n\right)\le 3$.

We now prove the lower bound on the local super antimagic total chromatic number of $G_n$. Suppose that ${\chi }_{lsat}\left(G_n\right)=2$. Then there must exist $x_i$ for some even $2\le i\le 2n$ such that $w\left(x_i\right)=w\left(c\right)$. The largest $w\left(x_i\right)$ at most is the sum of the largest vertex labels and the two largest edge labels, that is, $w\left(x_i\right)\le (2n+1)+(5n+1)+5n=12n+2$. While the weight of the central vertex must be at least the sum of the smallest vertex labels and smallest n edge labels, that is, $w\left(c\right)\ge 1+{\sum }_{i=1}^n(2n+1+i)=\frac{5n^2+3n}{2}+1$. It is easy to see that $12n+2<\frac{5n^2+3n}{2}+1$ for any $n\ge 5$ which is a contradiction. So, ${\chi }_{lsat}\left(G_n\right)\ge 3$. Combined with the upper bound above, we obtain ${\chi }_{lsat}\left(G_n\right)=3$ for odd $n\ge 5$. □

The following theorem presents the local super antimagic total chromatic number of a special class of cubic graphs, so called a cubic bipartite graph. The cubic bipartite graph, denoted by $C{B}_n$ for even $n\ge 6$, is a regular 2-colorable connected graph of degree 3 that can be constructed from a cycle $C_n$ with vertex set $\{v_1,v_2,\cdots ,v_{2k}\}$ by connecting $v_i$ to $v_j$ where i is odd and $j=i+k-\frac{1+{(-1)}^k}{2}$ mod $2k$.

Theorem 4.

If $C{B}_n$ for even $n\ge 6$ is a cubic bipartite graph, then ${\chi }_{lsat}\left(C{B}_n\right)=2$.

Proof. 

Let $C{B}_n$ for even $n\ge 6$ be the circulant cubic graph with the vertex set $V\left(C{B}_n\right)=\left\{x_i\right|1\le i\le 2k\}$ and the edge set $E\left(C{B}_n\right)=\left\{x_i{x}_{i+1}\right|1\le i\le 2k-1\}\cup \left\{x_{2k}{x}_1\right\}\cup \left\{x_i{x}_j\right|i$ is odd and $j=i+k-\frac{1+{(-1)}^k}{2}$ mod $2k\}$. Label the vertices and edges of cycle $C_n$ using the following formula.

$$\begin{array}{ccc}\hfill f\left(x_i\right)& =& \left\{\begin{array}{cc}k,\hfill & \mathrm{for}i=1,\hfill \\ \frac{i-1}{2},\hfill & \mathrm{for}\mathrm{odd}i=3,...,2k-1,\hfill \\ \frac{3k+i+1}{2},\hfill & \mathrm{for}\mathrm{odd}k\mathrm{and}\mathrm{even}i=2,...,k-1,\hfill \\ \frac{k+i+1}{2},\hfill & \mathrm{for}\mathrm{odd}k\mathrm{and}\mathrm{even}i=k+1,....,2k,\hfill \\ \frac{3k+i+2}{2},\hfill & \mathrm{for}\mathrm{even}k\mathrm{and}\mathrm{even}i=2,....,k-2,\hfill \\ \frac{k+i+2}{2},\hfill & \mathrm{for}\mathrm{even}k\mathrm{and}\mathrm{even}i=k,...,2k.\hfill \end{array}\right.\hfill \\ \hfill f\left(x_i{x}_{i+1}\right)& =& \left\{\begin{array}{cc}2k+\frac{i+1}{2},\hfill & \mathrm{for}\mathrm{odd}i,\hfill \\ 4k+1-\frac{i}{2},\hfill & \mathrm{for}\mathrm{even}i,\hfill \end{array}\right.\hfill \\ \hfill f\left(x_{2k}{x}_1\right)& =& 3k+1,\hfill \\ \hfill f\left(x_i{x}_j\right)& =& 5k-\frac{i-1}{2},\mathrm{for}\mathrm{odd}i,\hfill \end{array}$$

This labeling gives different weights for any two adjacent vertices,

$$\begin{array}{ccc}\hfill w\left(x_i\right)& =& \left\{\begin{array}{cc}11k+2,\hfill & \mathrm{for}\mathrm{odd}i,\hfill \\ 12k+2,\hfill & \mathrm{for}\mathrm{even}i.\hfill \end{array}\right.\hfill \end{array}$$

Thus ${\chi }_{lsat}\left(C{B}_n\right)\le 2$. Since $C{B}_n$ is 2-colorable, then ${\chi }_{lsat}\left(C{B}_n\right)\ge \chi \left(C{B}_n\right)=2$. Combining these two bounds, we conclude that ${\chi }_{lsat}\left(C{B}_n\right)=2$. □

The joint product of two graphs generates a graph that consists of the union of the two graphs with additional edges connecting all vertices of the first graph to each vertex of the second graph. In the next theorems, we present the local super antimagic total chromatic number of graphs produced by a joint product of two isomorphic cycles and a joint product of two isomorphic cubic bipartite graphs.

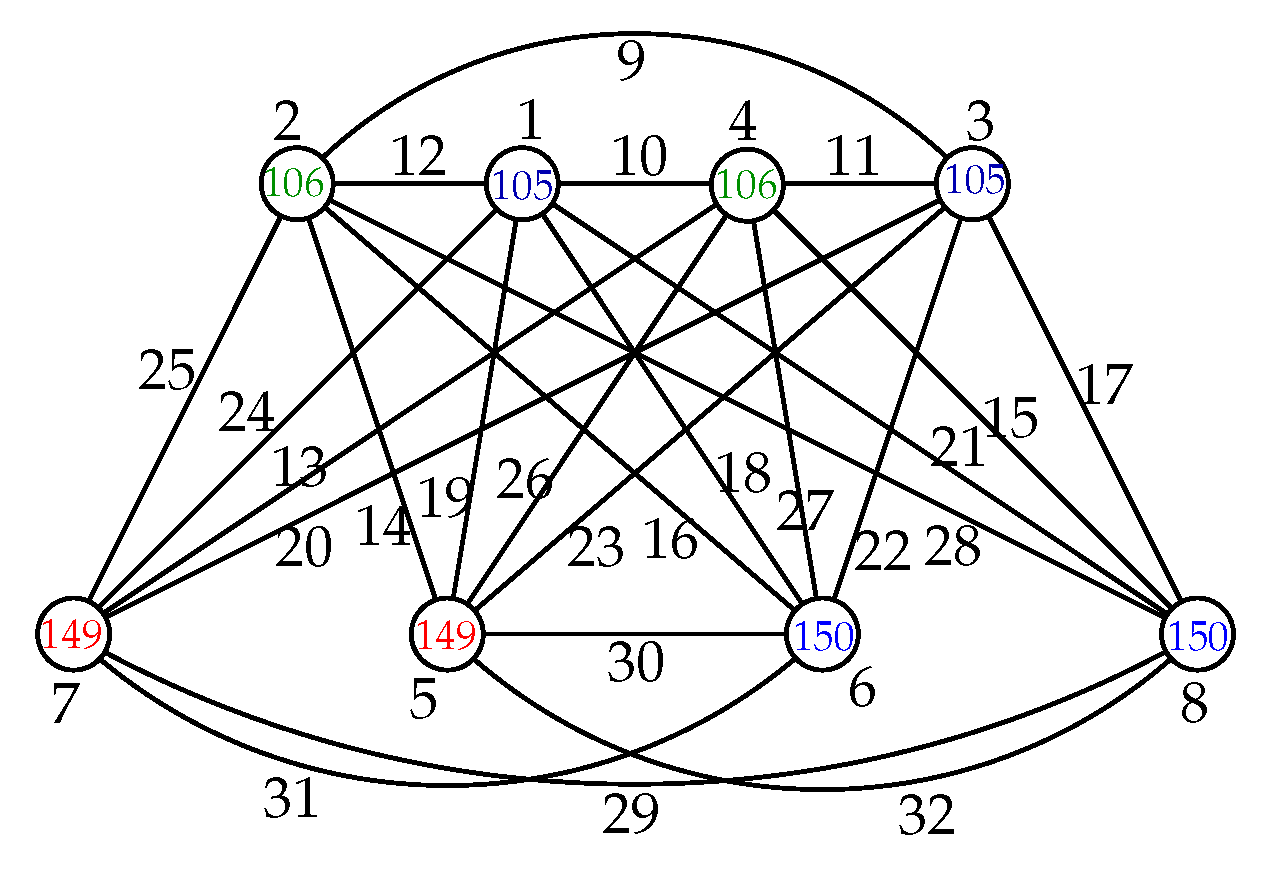
Theorem 5.

If $C_n+C_n$ is a joint product of two isomorphic cycles $C_n$ for $n\ge 3$, then

$$\begin{array}{c}\hfill {\chi }_{lsat}(C_n+C_n)=\left\{\begin{array}{c}4,\mathrm{for}\mathrm{even}n,\hfill \\ 6,\mathrm{for}\mathrm{odd}n.\hfill \end{array}\right.\end{array}$$

Proof. 

Let $C_n+C_n$ be the joint product of two isomorphic cycles $C_n$ for $n\ge 3$ with the vertex set $V(C_n+C_n)=\{x_i,y_i|1\le i\le n\}$ and edge set $E(C_n+C_n)=\{x_i{x}_{i+1},y_i{y}_{i+1}|1\le i\le n-1\}\cup \{x_n{x}_1,y_n{y}_1\}\cup \left\{x_i{y}_j\right|1\le i,j\le n\}$. We first show the lower bound of ${\chi }_{lsat}(C_n+C_n)$. Since $x_i$ and $y_i$ are adjacent, for each $1\le i\le n$, any vertex $x_i$ cannot use the color of vertex $y_i$. Thus $\chi \left(C_n+C_n\right)=2\chi \left(C_n\right)$. We know that ${\chi }_{lsat}(C_n+C_n)\ge \chi (C_n+C_n)$. Consequently, ${\chi }_{lsat}(C_n+C_n)\ge 2\chi \left(C_n\right)$.

To show the upper bound of ${\chi }_{lsat}(C_n+C_n)$, we use the following labeling. For $n=4$, we obtain ${\chi }_{lsat}(C_n+C_n)\le 4$ by using the labeling as shown in Figure A2.

While for $n\ne 4$, we will use the labeling f in the proof of Theorem 2 as follows.

$$\begin{array}{ccc}\hfill f^{+}\left(x_i\right)& =& f\left(x_i\right),\hfill \\ \hfill f^{+}\left(y_i\right)& =& f\left(y_i\right)+n,\hfill \\ \hfill f^{+}\left(e_i\right)& =& f\left(e_i\right)+n,\mathrm{for}{e}_i=x_i{x}_{i+1},\hfill \\ \hfill f^{+}\left(x_i{y}_j\right)& =& r(i,j)+3n,\hfill \\ \hfill f^{+}\left(e_j\right)& =& f\left(e_j\right)+(n+2)n,\mathrm{for}{e}_j=y_j{y}_{j+1}.\hfill \end{array}$$

where $r(i,j)$ is the number in the ith row and the jth column of rectangle $R(m,n)$ given by Hagedorn [11] for $m=n$.

The labeling $f^{+}$ gives different weights for any two adjacent vertices in $C_n+C_n$, that is,

$$\begin{array}{ccc}\hfill w^{+}\left(x_i\right)& =& w\left(x_i\right)+2n+\frac{{\sum }_i^{n^2}(3n+i)}{n},\hfill \\ \hfill w^{+}\left(y_i\right)& =& w\left(y_i\right)+n+2n(n+2)+\frac{{\sum }_i^{n^2}(3n+i)}{n}.\hfill \end{array}$$

Thus ${\chi }_{lsat}(C_n+C_n)\le 2{\chi }_{lsat}\left(C_n\right)$ for $n\ne 4$. Combined with the lower bound, we conclude that ${\chi }_{lsat}(C_n+C_n)=4$ for even n and ${\chi }_{lsat}(C_n+C_n)=6$ for odd n. □

Using similar arguments as in the proof of Theorem 5, we present the local super antimagic total chromatic number of graphs produced by a joint product of two isomorphic cubic bipartite graphs as follows.

Theorem 6.

If ${CB}_n+C{B}_n$ is a joint product of two isomorphic $C{B}_n$ for $n\ge 6$, then ${\chi }_{lsat}(C{B}_n+C{B}_n)=4$.

The following theorems presents the local super antimagic total chromatic number of graphs produced by the corona product of two graphs. The corona product of two graphs $G_1$ and $G_2$ generates a graph by taking one copy of $G_1$ and $\left|V\right(G_1\left)\right|$ copies of $G_2$ and joining the ith vertex of $G_1$ to each vertex in the ith copy of $G_2$.

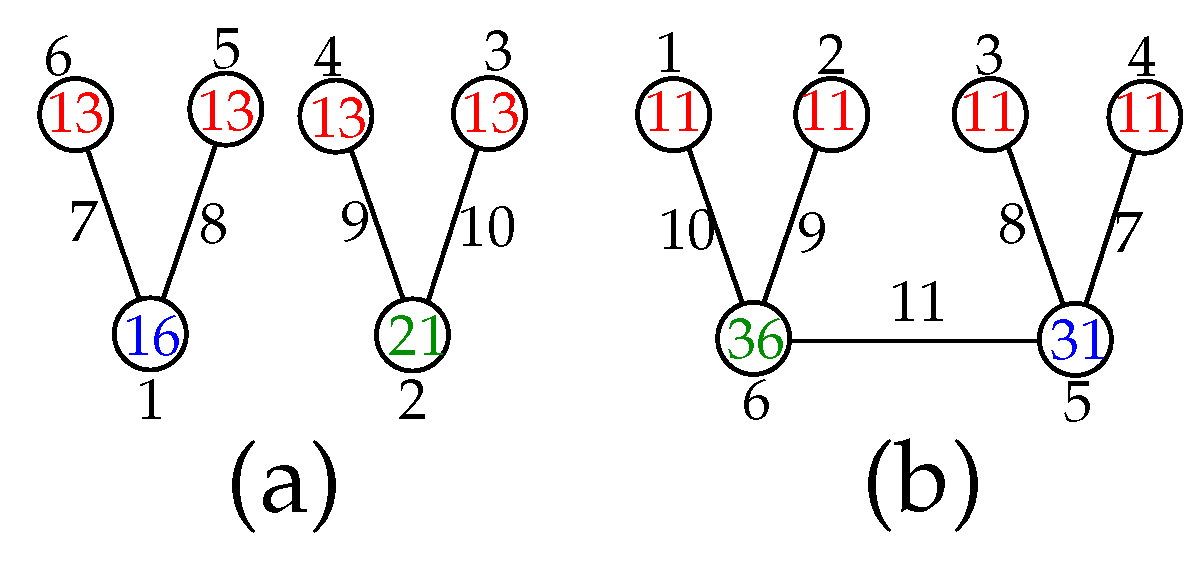
Theorem 7.

If H is a regular graph of order $n\ge 2$ and $\overline{K_m}$ is a null graph of order $m\ge 2$, then ${\chi }_{lsat}(H\odot \overline{K_m})\le {\chi }_{lsat}\left(H\right)+1,$ where $(m,n)\ne (odd,even)$.

Proof. 

Let H be a regular graph of order $n\ge 2$ and $\overline{K_m}$ be the null graph of order $m\ge 2$. Then $H\odot \overline{K_m}$ has the vertex set $V=\{v_j,x_j^i|v_j\in V\left(H\right),1\le j\le n,1\le i\le m\}$ and the edge set $E=\{e,v_j{x}_j^i|e\in E\left(H\right),v_j\in V\left(H\right),1\le i\le m,1\le j\le n\}$. We assume that f is a local super antimagic total labeling for H such that f provides t different vertex weights. We divide the proof into three cases.

Case i. For $(m,n)=(2,2)$.

There are two possible subcases to consider, that is, $H=K_2$ and $H=\overline{K_2}$. The labeling which is illustrated in Figure A3 shows that ${\chi }_{lsat}(H\odot \overline{K_2})\le {\chi }_{lsat}\left(H\right)+1$ for both subcases.

Case ii.For $m\equiv nmod2$, $(m,n)\ne (2,2)$, and $m\ge 2$.

We consider the rectangle $R(m,n)$ that consists of m rows and n columns where $m\equiv nmod2$ containing $mn$ first natural numbers such that the sum of entries in each row and each column is the same constant. This condition always occur unless $(m,n)=(2,2)$ as given by Hagedorn [11]. Label every vertex of $H\odot \overline{K_m}$ by $f^{+}\left(v_j\right)=mn+f\left(v_j\right)$ and every edge of $H\odot \overline{K_m}$ by $f^{+}\left(e\right)=2mn+f\left(e\right)$ for all $v_j,e\in H$, where f is the local super antimagic total labeling of H such that ${\chi }_{lsat}\left(H\right)=t$. Let $r(i,j)$ be the number in the ith row and the jth column of rectangle $R(m,n)$. Label the edge $v_j{x}_j^i$ by $r(i,j)+n+mn$ for $1\le i\le m,1\le j\le n$ and the pendant vertex by $f^{+}\left(x_j^i\right)=mn+n+1-f\left(v_j{x}_j^i\right)$. Thus the weight of vertices are:

$$\begin{array}{ccc}\hfill w^{+}\left(v_j\right)& =& w\left(v\right)+2kmn+mn+\frac{m(mn+1)}{2}+(mn+n)m,\hfill \\ \hfill w^{+}\left(x_j^i\right)& =& mn+n+1.\hfill \end{array}$$

Case iii.For even m and odd n.

Label the pendant edge by $f^{+}\left(v_j{x}_j^i\right)=n(m+i)+j$ for odd i and $f^{+}\left(v_j{x}_j^i\right)=n(m+i+1)-j+1$ for even i. Label then the pendant vertex by $f^{+}\left(x_j^i\right)=mn+n+1-f\left(v_j{x}_j^i\right)$. This labeling also gives the the same weights of vertices in Case ii.

From the three cases, we conclude that ${\chi }_{lsat}(H\odot \overline{K_m})\le {\chi }_{lsat}\left(H\right)+1$. □

The corona product $C_n\odot \overline{K_m}$ is a generalized sun $S_n^m$. The generalized sun $S_n^m$ has n vertices of degree $m+2$ and $mn$ vertices of degree 1. The following corollary present the local super antimagic chromatic number of the generalized sun.

Corollary 5.

If $S_n^m=C_n\odot \overline{K_m}$ for $n\ge 3$ and $m\ge 1$ is a generalized sun, then:

$${\chi }_{lsat}\left(S_n^m\right)=\left\{\begin{array}{c}4,\mathrm{for}\mathrm{odd}n,\hfill \\ 3,\mathrm{for}\mathrm{even}n.\hfill \end{array}\right.$$

Proof. 

Let $S_n^m=C_n\odot \overline{K_m}$ for $n\ge 3$ and $m\ge 1$ be a generalized sun with the vertex set $V\left(S_n^m\right)=\{x_i,y_i^j|1\le i\le n,1\le j\le m\}$ and the edge set $E\left(S_n^m\right)=\left\{x_i{x}_{i+1}\right|1\le i\le n-1\}\cup \left\{x_n{x}_1\right\}\cup \left\{x_i{y}_i^j\right|1\le i\le n,1\le j\le m\}$. Suppose that ${\chi }_{lsat}\left(S_n^m\right)=\chi \left(S_n^m\right)$. Then there is a condition that $w\left(x_i\right)=w\left(y_k^j\right)$ with $d\left(x_i\right)\ge 3$ and $d\left(y_k^j\right)=1$. Of course, $w\left(y_k^j\right)\le 3(m+1)n$, however, $w\left(x_i\right)\ge 3(m+1)n+7$. This implies that $w\left(y_k^j\right)<w\left(x_i\right)$, which is a contradiction as they have the same weight. Thus, ${\chi }_{lsat}\left(S_n^m\right)\ge \chi \left(S_n^m\right)+1$.

To show the upper bound of ${\chi }_{lsat}\left(S_n^m\right)$, we divide the proof into four cases.

Case i.For even m and $n=4$.

Label the vertices and edges of the generalized sun $S_n^m$ using the following formula.

$$\begin{array}{ccc}\hfill f_1(x_1,x_2,x_3,x_4)& =& (3,1,4,2)\hfill \\ \hfill f_1(x_1{y}_1^1,x_2{y}_2^1,x_3{y}_3^1,x_4{y}_4^1)& =& (8m+2,8m-1,8m,8m-3)\hfill \\ \hfill f_1(x_1{y}_1^2,x_2{y}_2^2,x_3{y}_3^2,x_4{y}_4^2)& =& (8m+3,8m+1,8m+4,8m-2)\hfill \\ \hfill f_1(y_1^1,y_2^1,y_3^1,y_4^1)& =& (7,10,9,12)\hfill \\ \hfill f_1(y_1^2,y_2^2,y_3^2,y_4^2)& =& (6,8,5,11)\hfill \\ \hfill f_1\left(y_i^j\right)& =& \left\{\begin{array}{cc}4j+1+i,\hfill & \mathrm{for}\mathrm{even}j\ge 4,1\le i\le 4,\hfill \\ 4j+3-i,\hfill & \mathrm{for}\mathrm{odd}j\ge 3,1\le i\le 4,\hfill \end{array}\right.\hfill \\ \hfill f_1\left(x_i{y}_i^j\right)& =& \left\{\begin{array}{cc}8m+8-4j-i,\hfill & \mathrm{for}\mathrm{even}j\ge 4,1\le i\le 4,\hfill \\ 8m-4-4j+i,\hfill & \mathrm{for}\mathrm{odd}j\ge 3,1\le i\le 4.\hfill \end{array}\right.\hfill \end{array}$$

The labeling $f_1$ gives the vertex weights $w\left(x_i^j\right)=8m+9$ for $1\le i\le 4$, $1\le j\le m$, $w\left(x_1\right)=w\left(x_3\right)=32m+21+\frac{{\sum }_{i=1}^{m-2}8m-5+i}{4}$ and $w\left(x_2\right)=w\left(x_4\right)=32m+12+\frac{{\sum }_{i=1}^{m-2}8m-5+i}{4}$. Thus ${\chi }_{lsat}\left(S_4^m\right)\le 3$.

Case ii. For odd m and even $n\ge 4$.

Theorems 2 and 7 imply that ${\chi }_{lsat}\left(S_n^m\right)={\chi }_{lsat}(C_n\odot \overline{K_m})\le 3$ for even n and ${\chi }_{lsat}\left(S_n^m\right)\le 4$ for odd n.

Case iii. For $m=1$.

Label the vertices and edges of the generalized sun $S_n^m$ using the following formula.

$$\begin{array}{ccc}\hfill f_2\left(y_i^1\right)& =& \left\{\begin{array}{cc}n,\hfill & \mathrm{for}i=1,\hfill \\ i-1,\hfill & \mathrm{for}2\le i\le n,\hfill \end{array}\right.\hfill \\ \hfill f_2\left(x_i\right)& =& \left\{\begin{array}{cc}2n-i,\hfill & \mathrm{for}i\equiv n-1mod2,\hfill \\ 2n+2-i,\hfill & \mathrm{for}i\equiv nmod2,\hfill \\ 2n,i=1,\hfill & \mathrm{for}n\equiv 1mod2,\hfill \end{array}\right.\hfill \\ \hfill f_2\left(x_i{y}_i^1\right)& =& \left\{\begin{array}{cc}2n+1,\hfill & \mathrm{for}i=1,\hfill \\ 3n+2-i,\hfill & \mathrm{for}2\le i\le n,\hfill \end{array}\right.\hfill \\ \hfill f_2\left(x_i{x}_{i+1}\right)& =& 3n+1,\mathrm{for}1\le i\le n-1,\hfill \\ \hfill f_2\left(x_n{x}_1\right)& =& 4n.\hfill \end{array}$$

The labeling $f_2$ gives the vertex weights $w\left(y_i^1\right)=3n+1$, $w\left(x_1\right)=11n+2$ for odd n, $w\left(x_i\right)=11n+3$ for even i, $w\left(x_i\right)=11n+1$ for odd i and $i\ne n$ where n is odd. Thus, ${\chi }_{lsat}\left(S_n^1\right)\le 3$ for even n and ${\chi }_{lsat}\left(S_n^1\right)\le 4$ for odd n.

Case iv. For odd m and even $n\ge 3$.

Label the vertices and edges of the generalized sun $S_n^m$ using the following formula.

$$\begin{array}{ccc}\hfill f_3\left(y_i^j\right)& =& \left\{\begin{array}{cc}n,\hfill & \mathrm{for}i=1,j=1,\hfill \\ i-1,\hfill & \mathrm{for}2\le i\le n,j=1,\hfill \\ (j-1)n+i,\hfill & \mathrm{for}1\le i\le n,2\le j\le m-1,j\equiv 0mod2,\hfill \\ jn+1-i,\hfill & \mathrm{for}1\le i\le n,3\le j\le m,j\equiv 1mod2,\hfill \end{array}\right.\hfill \\ \hfill f_3\left(x_i\right)& =& \left\{\begin{array}{cc}(m+1)n-i,\hfill & \mathrm{for}1\le i\le n,i\equiv 1mod2,\hfill \\ (m+1)n+2-i,\hfill & \mathrm{for}1\le i\le n,i\equiv 0mod2,\hfill \end{array}\right.\hfill \\ \hfill f_3\left(x_i{y}_i^j\right)& =& \left\{\begin{array}{cc}(2m+1)n+1,\hfill & \mathrm{for}i=1,j=1,\hfill \\ 2(m+1)n+2-i,\hfill & \mathrm{for}2\le i\le n,j=1,\hfill \\ (2m+3-j)n+1-i,\hfill & \mathrm{for}1\le i\le n,2\le j\le m-1,j\equiv 0mod2,\hfill \\ (2m+2-j)n+i,\hfill & \mathrm{for}1\le i\le n,3\le j\le m,j\equiv 1mod2,\hfill \end{array}\right.\hfill \\ \hfill f_3\left(x_i{x}_{i+1}\right)& =& (2m+1)n+i,\mathrm{for}1\le i\le n,\hfill \\ \hfill f_3\left(x_n{x}_1\right)& =& 2(m+1)n.\hfill \end{array}$$

The labeling $f_3$ gives the vertex weights $w\left(y_i^j\right)=2(m+1)n+1$, $w\left(x_i\right)=11n+3+\frac{{\sum }_{i=1}^{(m-1)n}(n+i)}{n}$ for even i, $w\left(x_i\right)=11n+1+\frac{{\sum }_{i=1}^{(m-1)n}(n+i)}{n}$ for odd i. Thus, ${\chi }_{lsat}\left(S_n^m\right)\le 3$ for odd m and even $n\ge 3$.

From the four cases above, we conclude that ${\chi }_{lsat}\left(S_n^m\right)=3$ for even n and ${\chi }_{lsat}\left(S_n^m\right)=4$ for odd n. □

The next theorem presents the upper bound of the local super antimagic chromatic number of a regular graph H whose each vertex is joined to one central vertex c and to m pendant vertices for $m\ge 1$.

Theorem 8.

If G is a graph obtained from a regular graph H of order $n\ge 2$ by joining each vertex to one center vertex and m pendant vertices for $m\ge 1$, then:

(i)

${\chi }_{lsat}\left(G\right)\le {\chi }_{lsat}(H+K_1)+1,\mathrm{for}m\ge 2\mathrm{and}(m,n)\ne (odd,even)$;

(ii)

${\chi }_{lsat}\left(G\right)\le {\chi }_{lsat}\left(H\right)+2,\mathrm{for}(m,n)=(odd,even)$;

(iii)

${\chi }_{lsat}\left(G\right)\le {\chi }_{lsat}\left(H\right)+2,\mathrm{for}m=1$.

Proof. 

Let G be the graph obtained from a regular graph H of order $n\ge 2$ by joining each vertex to one central vertex c and m pendant vertices for $m\ge 1$. Then G has the vertex set $V\left(G\right)=\{v_i,x_i|v_i\in V\left(H\right),1\le i\le n\}\cup \left\{c\right\}$ and the edge set $E\left(G\right)=\left\{e\right|e\in E\left(H\right)\}\cup \{c{v}_i,v_i{x}_i|v_i\in V\left(H\right),1\le i\le n\}$. It is easy to prove parts (i) and (ii). We now prove part (iii) as follows. Suppose that ${\chi }_{lsat}\left(H\right)=t$ is obtained from local super antimagic total labeling f for H. Label the vertices of G by $f^{+}\left(x_i\right)=i$ for $1\le i\le n$, $f^{+}\left(v_i\right)=f\left(v_i\right)+n$ for each $v_i\in V\left(H\right)$ and $f^{+}\left(c\right)=2n+1$. Label then the edges of G by $f^{+}\left(v_i{x}_i\right)=3n+2-i$ for each $v_i\in V\left(H\right)$ and $1\le i\le n$, $f^{+}\left(e\right)=f\left(e\right)+2n+1$ for each $e\in E\left(H\right)$, $f^{+}\left(c{v}_i\right)=3n+1+kn/2+i$ where $1\le i\le n$. The labeling $f^{+}$ gives $t+2$ different vertex weights, that is, $w^{+}\left(x_i\right)=3n+2$, $w^{+}\left(v\right)=k(2n+1)+7n+kn/2+3+w\left(v\right)$ and $w^{+}\left(c\right)=2n+1+{\sum }_{i=1}^n(3n+1+kn/2+i)$. Thus, ${\chi }_{lsat}\left(G\right)\le {\chi }_{lsat}\left(H\right)+2$. □

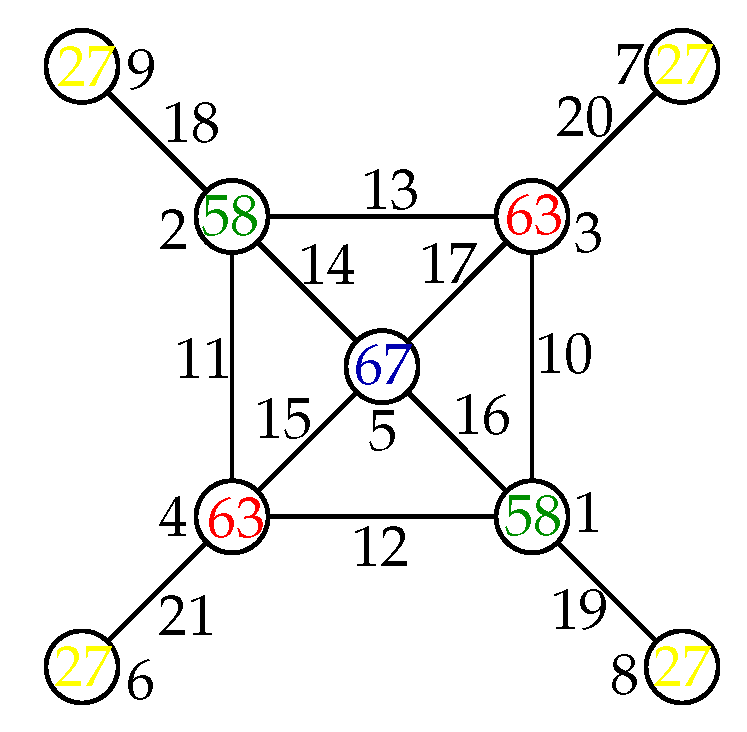
Helm, denoted by $H_n$, is a graph obtained from a regular graph H where $H=C_n$ by joining each vertex of H or $C_n$ to one vertex c called center and to a pendant vertex. The local super antimagic chromatic number of the helm $H_n$ for $n\ge 3$ is presented in the following corollary.

Corollary 6.

If $H_n$ for $n\ge 3$ is a helm, then:

$${\chi }_{lsat}\left(H_n\right)=\left\{\begin{array}{c}4,\mathrm{for}\mathrm{even}n,\hfill \\ 5,\mathrm{for}\mathrm{odd}n.\hfill \end{array}\right.$$

Proof. 

Let $H_n$ for $n\ge 3$ is the helm. Since $H_n$ is a graph obtained from $C_n$ by joining each vertex of $C_n$ to center c and to a pendant vertex, then $H_n$ has the vertex set $V\left(H_n\right)=V(C_n\odot K_1)\cup \left\{c\right\}=\left\{x_i\right|\le i\le n\}\cup \left\{y_i\right|1\le i\le n\}\cup \left\{c\right\}$ and the edge set $E\left(H_n\right)=E(C_n\odot K_1)\cup \left\{c{x}_i\right|x_i\in V\left(C_n\right)\}=\left\{x_i{x}_{i+1}\right|1\le i\le n-1\}\cup \left\{x_n{x}_1\right\}\cup \left\{c{x}_i\right|1\le i\le n\}\cup \left\{x_i{y}_i\right|1\le i\le n\}$. For $i=1,2,\dots ,n$, the degree of $x_i$ is 4 and the degree of $y_i$ is 1, while the degree of c is n. For $n=3$, it is easy to see that $w\left(c\right)\ge 28$ and $w\left(y_i\right)\le 23$. It is impossible to have $w\left(c\right)=w\left(y_i\right)$ or $w\left(x_j\right)=w\left(y_i\right)$. Thus ${\chi }_{lsat}\left(H_3\right)>\chi \left(H_3\right)$. For $n>3$, we have $w\left(x_i\right)\ge 8n+15$ and $w\left(y_i\right)\le 7n+2$. This also implies that ${\chi }_{lsat}\left(H_n\right)>\chi \left(H_n\right)$ for any $n>3$. The upper bound of ${\chi }_{lsat}\left(H_n\right)$ for $n=4$ can be obtained from the labeling as shiwn in Figure A4, that is, ${\chi }_{lsat}\left(H_4\right)\le 4$. While for other n the upper bound of ${\chi }_{lsat}\left(H_n\right)$ is obtained from Theorem 8(iii) and Theorem 2. Combining the lower bound and the upper bound of ${\chi }_{lsat}\left(H_n\right)$, we conclude that:

$${\chi }_{lsat}\left(H_n\right)=\left\{\begin{array}{c}4,\mathrm{for}\mathrm{even}n,\hfill \\ 5,\mathrm{for}\mathrm{odd}n.\hfill \end{array}\right.$$

 □

The vertex amalgamation of n copies of graph G at a fix vertex $v\in V\left(G\right)$, denoted $Amal(G,v,n)$ for $n\ge 2$ is a graph obtained by identifying n copies of graph G at the vertex v. Thus $Amal(G,v,n)={\bigcup }_{i=1}^n{G}_i$ and ${\bigcap }_{i=1}^n{G}_i=\left\{v\right\}$. The following theorem presents the local super antimagic total labeling of amalgamation of n copies stars $S_{m+2}$

Theorem 9.

If $Amal(S_{m+2},v,n)$ for $m,n\ge 2$ is a graph obtained from amalgamation of n copies of stars $S_{m+2}$ at the pendant vertex v, then ${\chi }_{lsat}\left(Amal(S_{m+2},v,n)\right)=3$.

Proof. 

Let $Amal(S_{m+2},v,n)$ for $m,n\ge 2$ be the graph obtained from amalgamation of n copies of stars $S_{m+2}$ at the pendant vertex v. Then $Amal(S_{m+2},v,n)$ has the vertex set $V\left(Amal(S_{m+2},v,n)\right)=\{x_i^j,c_i|1\le i\le n,1\le j\le m\}\cup \left\{c\right\}$ and the edge set $E\left(Amal(S_{m+2},v,n)\right)=\{c{c}_i,c_i{x}_i^j|1\le i\le n,1\le j\le m\}$. By Corollary 1 and Theorem 8(i), we have the upper bound ${\chi }_{lsat}\left(Amal(S_{m+2},v,n)\right)\le 3$ for $(m,n)\ne (odd,even)$. For $(m,n)=(odd,even)$, label the vertices and edges of $Amal(S_{m+2},v,n)$ using the following formula:

$$\begin{array}{ccc}\hfill f\left(x_i^j\right)& =& \left\{\begin{array}{cc}(m-j+1)n+1-i,\hfill & \mathrm{for}\mathrm{odd}j=1,3,\cdots ,m-2,\hfill \\ (m-j)n+i,\hfill & \mathrm{for}\mathrm{even}j=2,4,\cdots ,m-1,\hfill \\ i,\hfill & \mathrm{for}j=m,\hfill \end{array}\right.\hfill \\ \hfill f\left(c_i\right)& =& \left\{\begin{array}{cc}mn+\frac{n}{2}+1-i,\hfill & \mathrm{for}i\le \frac{n}{2},\hfill \\ mn+\frac{3n}{2}+2-i,\hfill & \mathrm{for}i>\frac{n}{2},\hfill \end{array}\right.\hfill \\ \hfill f\left(c\right)& =& mn+\frac{n}{2}+1,\hfill \\ \hfill f\left(c{c}_i\right)& =& \left\{\begin{array}{cc}(2m+1)n+2i+1,\hfill & \mathrm{for}i\le \frac{n}{2},\hfill \\ 2mn+2i,\hfill & \mathrm{for}i>\frac{n}{2},\hfill \end{array}\right.\hfill \\ \hfill f\left(c_i{x}_i^j\right)& =& \left\{\begin{array}{cc}(j+m)n+1+i,\hfill & \mathrm{for}\mathrm{odd}j=1,3,\cdots ,m-2,\hfill \\ (j+m+1)n+2-i,\hfill & \mathrm{for}\mathrm{even}j=2,4,\cdots ,m-1,\hfill \\ (2m+1)n+2-i,\hfill & \mathrm{for}j=m.\hfill \end{array}\right.\hfill \end{array}$$

This labeling gives the local super antimagic total labeling with different vertex weights, namely,

$$\begin{array}{ccc}\hfill w\left(x_i^j\right)& =& (2n+1)m+2,\hfill \\ \hfill w\left(c_i\right)& =& \left(5m+\frac{5}{2}\right)n+2+\frac{{\sum }_{i=1}^{(m-1)n}\left(\right(m+1)n+1+i)}{n},\hfill \\ \hfill w\left(c\right)& =& mn+\frac{n}{2}+1+\sum _{i=1}^n(2m+1)n+i.\hfill \end{array}$$

Thus ${\chi }_{lsat}\left(Amal(S_{m+2},v,n)\right)\le 3$. Since the degree of c is at least 3 and the degree of $x_i^j$ is 1 when $n\ge 3$. The possibility are $w\left(c\right)\ge 3(m+1)n+10$ and $w\left(x_i^j\right)<3(m+1)n+1$. Thus $w\left(c\right)\ne w\left(x_i^j\right)$. For $n=2$, suppose that ${\chi }_{lsat}\left(Amal(S_{m+2},v,n)\right)=2$, that is, $w\left(c\right)=w\left(x_i^j\right)$ for each $i\in \{1,2\}$, $j\in \{1,2,\dots ,m\}$. We know that $w\left(c\right)\ge 4m+10$ since the degree of c is 2. However, the maximum weighs of c and $x_i^j$ are $\frac{{\sum }_{i=3}^{4m+5}i}{2m+1}<4m+10$, a contradiction. Thus ${\chi }_{lsat}\left(Amal(S_{m+2},v,n)\right)\ge 3$ for every $n\ge 2$. Combining the lower bound and upper bound, we obtain ${\chi }_{lsat}\left(Amal(S_{m+2},v,n)\right)=3$, for every $m,n\ge 2$. □

The following theorem presents the local super antimagic total labeling of the amalgamation of m copies wheels $W_n$ at the central vertex v.

Theorem 10.

If $Amal(W_n,v,m)$ for $n\ge 3$ and $m\ge 2$ is a graph obtained from amalgamation of m copies of wheels $W_n$ at the central vertex v, then:

$${\chi }_{lsat}\left(Amal(W_n,v,m)\right)=\left\{\begin{array}{c}3,\mathrm{for}\mathrm{even}n,\hfill \\ 4,\mathrm{for}\mathrm{odd}n.\hfill \end{array}\right.$$

Proof. 

Let $Amal(W_n,v,m)$ for $n\ge 3$ and $m\ge 2$ be the graph obtained from amalgamation of m copies of wheels $W_n$ at the central vertex v. Then $Amal(W_n,v,m)$ has the vertex set $V\left(Amal(W_n,v,m)\right)=\left\{x_i^j\right|1\le i\le n,1\le j\le m\}\cup \left\{c\right\}$ and the edge set $E\left(Amal(W_n,v,m)\right)=\{x_i^j{x}_{i+1}^j,c{x}_i^j|1\le i\le n-1,1\le j\le m\}\cup \{x_n^j{x}_1^j,c{x}_n^j|1\le j\le m\}$. Label the vertices and edges of $Amal(W_n,v,m)$ using the following formula.

$$\begin{array}{ccc}\hfill f\left(x_i^j\right)& =& \left\{\begin{array}{cc}m(i-1)+j+1,\hfill & \mathrm{for}i\equiv n(mod2),\hfill \\ m(i-3)+j+1,\hfill & \mathrm{for}i\equiv n-1(mod2),\hfill \\ 3mn+j+1,\hfill & \mathrm{for}i=2,n\equiv 1(mod2),\hfill \end{array}\right.\hfill \\ \hfill f\left(c\right)& =& 1,\hfill \\ \hfill f\left(x_i^j{x}_{i+1}^j\right)& =& m(3n-i+1)-j+2,\mathrm{for}1\le i\le n-1,1\le j\le m,\hfill \\ \hfill f\left(x_n^j{x}_1^j\right)& =& m(2n+1)-j+2,\mathrm{for}1\le j\le m,\hfill \\ \hfill f\left(c{x}_i^j\right)& =& m(n+i-1)+j+1,\mathrm{for}1\le i\le n,1\le j\le m.\hfill \end{array}$$

This labeling gives local super antimagic total labeling with different vertex weights, namely,

$$\begin{array}{ccc}\hfill w\left(x_i\right)& =& \left\{\begin{array}{cc}m(7n+1)+6,\hfill & \mathrm{for}i\equiv n-1(mod2),\hfill \\ m(7n-1)+6,\hfill & \mathrm{for}i\equiv n(mod2),\hfill \\ 7mn+6,\hfill & \mathrm{for}i=2,n\equiv 1(mod2),\hfill \end{array}\right.\hfill \\ \hfill w\left(c\right)& =& \frac{mn(3mn+3)}{2}+1.\hfill \end{array}$$

Thus ${\chi }_{lsat}\left(Amal(W_n,v,m)\right)\le 3$ for even n and ${\chi }_{lsat}\left(Amal(W_n,v,m)\right)\le 4$ for odd n. We know that ${\chi }_{lsat}\left(Amal(W_n,v,m)\right)\ge 3$ for even n and ${\chi }_{lsat}\left(Amal(W_n,v,m)\right)\ge 4$ for odd n. Therefore, ${\chi }_{lsat}\left(Amal(W_n,v,m)\right)=3$ for even n and ${\chi }_{lsat}\left(Amal(W_n,v,m)\right)=4$ for odd n. □

The local super antimagic total chromatic number of a wheel $W_n$ for $n\ge 3$ is implied by Theorem 10 when $m=1$ as follows.

Corollary 7.

If $W_n$ for $n\ge 3$ is a wheel, then:

$${\chi }_{lsat}\left(W_n\right)=\left\{\begin{array}{c}3,\mathrm{for}\mathrm{even}n,\hfill \\ 4,\mathrm{for}\mathrm{odd}n.\hfill \end{array}\right.$$

3. Conclusions

We conclude this paper with some open problems. Some classes of graphs have a condition that ${\chi }_{lsat}\left(G\right)-\chi \left(G\right)=k$ where $k=0$ or $k=1$. Consequently, we have the following open problem.

Problem 1.

Characterize the family of graphs that satisfies ${\chi }_{lsat}\left(G\right)=\chi \left(G\right)+k$, for $k\ge 2$.

We have determined the local super antimagic total chromatic number of cubic bipartite graph that is a regular 2-colorable connected graph of degree 3. In general, the local super antimagic total chromatic number of cubic graphs have not been discovered. So, we have:

Problem 2.

Determine the local super antimagic total chromatic number of cubic graphs of order $n\ge 8$.

Some particular classes of tree such as path, star, double star, and amalgamation of stars have determined their local super antimagic total chromatic numbers. However, the local super antimagic total chromatic number of tree in general has not been discovered. Thus,

Problem 3.

Determine the local super antimagic total chromatic number of tree $T_n$ of order $n\ge 5$.