Existence of Three Solutions for a Nonlinear Discrete Boundary Value Problem with ϕ_c-Laplacian

Abstract

In this paper, based on critical point theory, we mainly focus on the multiplicity of nontrivial solutions for a nonlinear discrete Dirichlet boundary value problem involving the mean curvature operator. Without imposing the symmetry or oscillating behavior at infinity on the nonlinear term f, we respectively obtain the sufficient conditions for the existence of at least three non-trivial solutions and the existence of at least two non-trivial solutions under different assumptions on f. In addition, by using the maximum principle, we also deduce the existence of at least three positive solutions from our conclusion. As far as we know, our results are supplements to some well-known ones.

1. Introduction

Let $\mathbb{Z}$ and $\mathbb{R}$ denote all integers and real numbers, respectively. Let N be a fixed positive integer. Define $\mathbb{Z}(a,b)=\{a,a+1,\cdots ,b\}$ with $a\le b$ for any $a,b\in \mathbb{Z}$.

Difference equations are widely used in various research fields, such as computer science, discrete optimization, economics and biological neural networks [1,2,3,4]. On the existence and multiplicity of solutions for the boundary value problems of difference equations, many authors have come to important conclusions by exploiting various methods, including the method of upper and lower solutions, Brouwer degree and invariant sets of descending flow [5,6,7]. Critical point theory was used largely to explore differential equations much earlier on in history. In 2003, Guo and Yu in [8] used critical point theory for the first time to obtain sufficient conditions for the existence of periodic solutions and subharmonic solutions of difference equations. This crucial breakthrough inspired many scholars to use critical point theory to study the dynamics of difference equations and many meaningful and interesting results have been obtained, especially in periodic solutions [9,10,11], homoclinic solutions [12,13,14,15,16] and boundary value problems [17,18,19,20,21,22,23].

In [24], Agarwal, Perera and O’Regan employed the critical point theory to establish the existence of at least two positive solutions of the following second order discrete boundary value problem

$$\left\{\begin{array}{c}-{\Delta }^{2}x(k-1)=f(k,x\left(k\right)),k\in \mathbb{Z}(1,N),\hfill \\ x\left(0\right)=x(N+1)=0,\hfill \end{array}\right.$$

where $\Delta x\left(k\right)=x(k+1)-x\left(k\right)$, ${\Delta }^{2}x\left(k\right)=\Delta (\Delta x\left(k\right))$ and $f:\mathbb{Z}(1,N)\times \mathbb{R}\to \mathbb{R}$ is a continuous function. In [18], by using the three critical point theorems proposed by Bonanno [25], Jiang and Zhou obtained sufficient conditions for the existence of at least three solutions of the following Dirichlet boundary value problem with ${\varphi }_p$-Laplacian

$$\left\{\begin{array}{c}-\Delta \left({\varphi }_p(\Delta u(k-1))\right)=\lambda f(k,u\left(k\right)),k\in \mathbb{Z}(1,N),\hfill \\ u\left(0\right)=u(N+1)=0,\hfill \end{array}\right.$$

where ${\varphi }_p$ is the p-Laplacian defined by ${\varphi }_p\left(u\right)={\left|u\right|}^{p-2}u(p>1)$ with $u\in \mathbb{R}$ and $\lambda >0$ is a positive parameter. Different from the conclusion of [18], Bonanno in [26] obtained the existence of three positive solutions without the asymptotic condition of the nonlinear function f. In particular, Bonanno obtained the sufficient conditions for the existence of at least four nontrivial solutions when f satisfies the growth condition at zero and infinity [26], which improved the result in [18].

In [27], by using critical point theory, Nastasi and Vetro obtained the existence of at least two positive solutions to the following Dirichlet boundary value problem with $(p,q)$-Laplacian

$$\left\{\begin{array}{c}-\Delta \left({\varphi }_p(\Delta u(z-1))\right)-\Delta \left({\varphi }_q(\Delta u(z-1))\right)+\alpha \left(z\right){\varphi }_p\left(u\left(z\right)\right)+\beta \left(z\right){\varphi }_q\left(u\left(z\right)\right)=\lambda g(z,u\left(z\right)),z\in \mathbb{Z}(1,N),\hfill \\ u\left(0\right)=u(N+1)=0,\hfill \end{array}\right.$$

where $1<q<p<+\infty$, $\alpha ,\beta :\mathbb{Z}(1,N)\to \mathbb{R}$ and $g:[1,N+1]\times \mathbb{R}\to \mathbb{R}$ are a continuous function with $g(N+1,t)=0$ for all $t\in \mathbb{R}$.

It is well known that the differential equation with ${\varphi }_c$-Laplacian (${\varphi }_c$ is the mean curvature operator defined by ${\varphi }_c\left(s\right)=s/\sqrt{1+s^2}$ for $s\in \mathbb{R}$) was studied by many scholars in the past decades [28,29,30,31]. It is usually regarded as a variant of the Liouville–Bratu–Gelfand problem, which is used to study the dynamic model of combustible gases. As mentioned above, we find that the research on the difference equation largely focuses on the case with ${\varphi }_p$-Laplacian. However, there are only a few results on the boundary value problems involving ${\varphi }_c$-Laplacian [32]. Recently, Zhou and Ling in [33] considered the existence of multiple solutions of the following discrete Dirichlet boundary value problem with ${\varphi }_c$-Laplacian.

Problem 1

$$\left\{\begin{array}{c}-\Delta \left(\frac{\Delta u(k-1)}{\sqrt{1+{(\Delta u(k-1))}^2}}\right)=\lambda f(k,u\left(k\right)),k\in \mathbb{Z}(1,N),\hfill \\ u\left(0\right)=u(N+1)=0.\hfill \end{array}\right.$$

The authors in [33] found that the properties of the nonlinear term $F(k,u)={\int }_0^{u}f(k,t)dt$ plays an important role on the existence of multiple solutions. When $F(k,u)$ has oscillating behavior at infinity, there are infinite solutions to the boundary value (Problem 1) [33]. Naturally, we would like to ask: What will happen if $F(k,u)$ does not oscillate at infinity?

To address this problem, in this paper, we will study the existence of solutions for the boundary value (Problem 1) without oscillating nonlinear terms. In fact, based on the theorems of G. Bonanno (Theorem 4.1 in [22] and Theorem 2.1 in [23]), we will give the conditions of the existence of at least three nontrivial solutions for (Problem 1), when $F(k,u)$ does not have oscillation property at infinity. In addition, when $f(k,0)>0$, we obtain the sufficient conditions for the existence of at least three positive solutions of (Problem 1). Moveover, we give two examples to illustrate our main results.

For convenience, we end this section by recalling some classical definitions and two well-known lemmas, which are the main tools of this paper.

Let $(X,\parallel ·\parallel )$ be a real Banach space. We say that $I:X\to \mathbb{R}$ is coercive on X if ${lim}_{\parallel u\parallel \to +\infty }I\left(u\right)=+\infty$. If I is a continuously Gâteaux differentiable functional, we say that I satisfies the Palais–Smale condition ((PS)-condition in short), if any sequence $u_n\subset X$ such that $\left\{I\left(u_n\right)\right\}$ is bounded and $\left\{I^{\prime }\left(u_n\right)\right\}$ is convergent to 0 in $X^{*}$, has a convergent subsequence in X.

$\left(H\right)$ Let $(X,\parallel ·\parallel )$ be a real finite dimensional Banach space and let Φ, $\Psi :X\to \mathbb{R}$ be two continuously Gâteaux differentiable functionals with Φ coercive and such that

$$\underset{X}{inf}\Phi =\Phi \left(0\right)=\Psi \left(0\right)=0.$$

Lemma 1.

([22]) Assume that (H) holds and there exist $r>0$ and $\overline{x}\in X$, with $0<r<\Phi \left(\overline{x}\right)$, such that:

($a_1$)

$\frac{\underset{\Phi \left(x\right)\le r}{sup}\Psi \left(x\right)}{r}<\frac{\Psi \left(\overline{x}\right)}{\Phi \left(\overline{x}\right)};$

($a_2$)

for each $\lambda \in {\Lambda }_r:=\left(\frac{\Phi \left(\overline{x}\right)}{\Psi \left(\overline{x}\right)},\frac{r}{\underset{\Phi \left(x\right)\le r}{sup}\Psi \left(x\right)}\right),$ the functional $\Phi -\lambda \Psi$ is coercive.

Then, for each $\lambda \in {\Lambda }_r$, the functional $I_{\lambda }=\Phi -\lambda \Psi$ has at least three distinct critical points in X.

Lemma 2.

([23]) Let X be a real Banach space and let Φ, Ψ:$X\to \mathbb{R}$ be two continuously Gâteaux differentiable functionals such that $\underset{X}{inf}\Phi =\Phi \left(0\right)=\Psi \left(0\right)=0.$ Assume that there are $r>0$ and $\tilde{u}\in X$, with $0<\Phi \left(\tilde{u}\right)<r$, such that

$$\frac{\underset{\Phi \left(u\right)\le r}{sup}\Psi \left(u\right)}{r}<\frac{\Psi \left(\tilde{u}\right)}{\Phi \left(\tilde{u}\right)}$$

(1)

for each $\lambda \in \left(\frac{\Phi \left(\tilde{u}\right)}{\Psi \left(\tilde{u}\right)},\frac{r}{\underset{\Phi \left(u\right)\le r}{sup}\Psi \left(u\right)}\right)$, and the functional $I_{\lambda }=\Phi -\lambda \Psi$ satisfies (PS)-condition and it is unbounded from below. Then, for each $\lambda \in \left(\frac{\Phi \left(\tilde{u}\right)}{\Psi \left(\tilde{u}\right)},\frac{r}{\underset{\Phi \left(u\right)\le r}{sup}\Psi \left(u\right)}\right)$, the functional $I_{\lambda }$ admits at least two non-zero critical points $u_{\lambda ,1},$$u_{\lambda ,2}$ such that $I_{\lambda }\left(u_{\lambda ,1}\right)<0<I_{\lambda }\left(u_{\lambda ,2}\right).$

2. Preliminaries

In this section, we recall some definitions, notations and properties. Consider the N-dimensional Banach space

$$S=\{u:[0,N+1]\to \mathbb{R}:u(0)=u(N+1)=0\}$$

endowed with the norm

$$\parallel u\parallel ={\left({\displaystyle \sum _{k=1}^{N+1}}{|\Delta u(k-1)|}^2\right)}^{\frac{1}{2}}.$$

We define the functional $\Phi ,\Psi :S\to \mathbb{R}$ in the following way

$$\Phi \left(u\right)={\displaystyle \sum _{k=1}^{N+1}}\left(\sqrt{1+{(\Delta u(k-1))}^2}-1\right),\Psi \left(u\right)={\displaystyle \sum _{k=1}^N}F(k,u\left(k\right))$$

(2)

for each $u\in S$, where

$$F(k,\xi ):={\int }_0^{\xi }f(k,t)dt,\xi \in \mathbb{R}.$$

It is easy to check that $\Phi ,\Psi \in C^1(S,R)$ and we have

$${\Phi }^{\prime }\left(u\right)\left(v\right)=-{\displaystyle \sum _{k=1}^N}\Delta \left({\varphi }_c\left(\Delta u(k-1)\right)\right)v\left(k\right)$$

and

$${\Psi }^{\prime }\left(u\right)\left(v\right)=-{\displaystyle \sum _{k=1}^N}f(k,u\left(k\right))v\left(k\right).$$

By a standard argument, it can be shown that the critical points of the functional

$$I_{\lambda }=\Phi -\lambda \Psi$$

are the solutions of (Problem 1).

Let

$${\parallel u\parallel }_{\infty }=max\left\{\left|u\right(k\left)\right|:k\in \mathbb{Z}(1,N)\right\}.$$

We see that ${\parallel ·\parallel }_{\infty }$ is another norm in S. From Lemma 2.2 of [18], we have

Lemma 3.

([18]) For any $u\in S$, the following relation holds

$${\parallel u\parallel }_{\infty }\le \frac{\sqrt{N+1}}{2}\parallel u\parallel .$$

From (2.1) and (2.3) in [22], we have

Lemma 4.

([22]) For any $u\in S$, one has

$$\frac{1}{\sqrt{N{\lambda }_N}}\parallel u\parallel \le {\parallel u\parallel }_{\infty }\le \frac{1}{\sqrt{{\lambda }_1}}\parallel u\parallel ,$$

where ${\lambda }_1=4{sin}^2\frac{\pi }{2(N+1)}$ and ${\lambda }_N=4{sin}^2\frac{N\pi }{2(N+1)}$.

Finally, in order to obtain the positive solutions of (Problem 1), we need the following strong maximum principle, which can be found in Theorem 2.1 of [33].

Lemma 5.

([33]) Assume $u\in S$ such that either

$$u\left(k\right)>0or\Delta \left({\varphi }_c(\Delta u(k-1))\right)\le 0,$$

for all $k\in \mathbb{Z}(1,N).$ Then, either $u>0$ in $\mathbb{Z}(1,N)$ or $u\equiv 0$.

3. Main Results

For convenience, set

$$F_t:={\displaystyle \sum _{k=1}^N}F(k,t),\mathrm{for}\mathrm{all}t>0.$$

Our first result is the following theorem.

Theorem 1.

Assume that there exist two positive constants c and d with

$$2\sqrt{1+d^2}>1+\sqrt{1+\frac{4c^2}{N+1}}$$

(3)

such that

(i) 

$f(k,\xi )>0$ for each $k\in \mathbb{Z}(1,N)$ and $\xi \in [-c,c]$;

(ii) 

$\frac{F_d}{2(\sqrt{1+d^2}-1)}>\frac{F_c}{-1+\sqrt{1+\frac{4c^2}{N+1}}};$

(iii) 

$\underset{\left|\xi \right|\to +\infty }{lim\; sup}\frac{F(k,\xi )}{\left|\xi \right|}<\frac{2F_c}{N(\sqrt{4c^2+N+1}-\sqrt{N+1})}$.

Then, for every $\lambda \in \Lambda :=\left(\frac{2(\sqrt{1+d^2}-1)}{F_d},\frac{-1+\sqrt{1+\frac{4c^2}{N+1}}}{F_c}\right)$, (Problem 1) has at least three nontrivial solutions.

Proof. 

We take $X=S$, $\Phi$ and $\Psi$ as in (2). Clearly, $\Phi$ and $\Psi$ are two continuously Gâteaux differentiable functionals. Now, we prove the coercivity of $\Phi$. In fact, one has

$$\begin{array}{cc}\hfill \Phi \left(u\right)& ={\displaystyle \sum _{k=1}^{N+1}}\left(\sqrt{1+{(\Delta u(k-1))}^2}-1\right)\hfill \\ & \ge {\left({\displaystyle \sum _{k=1}^{N+1}}\left[1+{(\Delta u(k-1))}^2\right]\right)}^{\frac{1}{2}}-{\displaystyle \sum _{k=1}^{N+1}}1\hfill \\ & \ge \parallel u\parallel -N-1.\hfill \end{array}$$

This means $\underset{\parallel u\parallel \to +\infty }{lim}\Phi \left(u\right)=+\infty$ and verifies the coercivity of $\Phi$. Moreover, by the definition of $\Phi$ and $\Psi$, we can obtain

$$\underset{X}{inf}\Phi =\Phi \left(0\right)=\Psi \left(0\right)=0.$$

To summarize, condition $\left(H\right)$ in Lemma 1 holds.

According to Lemma 1, it is clear that Theorem 1 holds if we can verify $\left(a_1\right)$ and $\left(a_2\right)$ of Lemma 1.

Put

$$r=-1+\sqrt{1+\frac{4c^2}{N+1}}.$$

If $\Phi \left(u\right)\le r$, let

$$v\left(k\right)=\sqrt{1+{(\Delta u\left(k\right))}^2}-1\mathrm{for}k\in \mathbb{Z}(0,N).$$

Then, we have ${\displaystyle \sum _{k=0}^N}v\left(k\right)\le r$ and

$${\displaystyle \sum _{k=0}^N}{(\Delta u\left(k\right))}^2={\displaystyle \sum _{k=0}^N}\left(v{\left(k\right)}^2+2v\left(k\right)\right)\le {\left({\displaystyle \sum _{k=0}^N}v\left(k\right)\right)}^2+2{\displaystyle \sum _{k=0}^N}v\left(k\right)\le r^2+2r=\frac{4c^2}{N+1}.$$

Thus, ${\parallel u\parallel }_{\infty }\le \frac{\sqrt{N+1}}{2}\parallel u\parallel \le c$ by Lemma 3.

By (i), we see that $F(k,\xi )$ is increasing in $\xi \in [-c,c]$. Thus

$$\frac{\underset{\Phi \left(u\right)\le r}{sup}\Psi \left(u\right)}{r}\le \frac{\underset{{\parallel u\parallel }_{\infty }\le c}{sup}{\displaystyle \sum _{k=1}^N}F(k,u\left(k\right))}{-1+\sqrt{1+\frac{4c^2}{N+1}}}\le \frac{{\displaystyle \sum _{k=1}^N}\underset{\left|\xi \right|\le c}{max}F(k,\xi )}{-1+\sqrt{1+\frac{4c^2}{N+1}}}=\frac{F_c}{-1+\sqrt{1+\frac{4c^2}{N+1}}}.$$

(4)

Then, it is easy to get

$$\frac{\underset{\Phi \left(u\right)\le r}{sup}\Psi \left(u\right)}{r}<\frac{1}{\lambda }.$$

(5)

Now, let $\overline{u}\in S$ be defined by

$$\overline{u}\left(k\right)=\left\{\begin{array}{c}d,\mathrm{if}k\in \mathbb{Z}(1,N),\hfill \\ 0,\mathrm{if}k=0\mathrm{or}k=N+1.\hfill \end{array}\right.$$

Then, we see from (3) that

$$\Phi \left(\overline{u}\right)=2(\sqrt{1+d^2}-1)>\sqrt{1+\frac{4c^2}{N+1}}-1=r.$$

Moreover, it holds that

$$\frac{\Psi \left(\overline{u}\right)}{\Phi \left(\overline{u}\right)}=\frac{{\displaystyle {\displaystyle \sum _{k=1}^N}}F(k,\overline{u}\left(k\right))}{2(\sqrt{1+d^2}-1)}=\frac{F_d}{2(\sqrt{1+d^2}-1)}.$$

(6)

Therefore, we have

$$\frac{\Psi \left(\overline{u}\right)}{\Phi \left(\overline{u}\right)}>\frac{1}{\lambda }.$$

(7)

Hence, condition $\left(a_1\right)$ of Lemma 1 follows by combining $\left(5\right)$ with $\left(7\right).$

Next, we prove the coercivity of the functional $I_{\lambda }$. From $\left(iii\right)$, there is an $\epsilon >0$ such that

$$\underset{\left|\xi \right|\to +\infty }{lim\; sup}\frac{F(k,\xi )}{\left|\xi \right|}<\epsilon <\frac{2F_c}{N(\sqrt{4c^2+N+1}-\sqrt{N+1})}.$$

Then, there is a positive constant h such that

$$F(k,\xi )\le \epsilon \left|\xi \right|+h$$

for each $\xi \in \mathbb{R}$ and $k\in \mathbb{Z}(1,N)$. By Lemma 3 and $\lambda <\frac{-1+\sqrt{1+\frac{4c^2}{N+1}}}{F_c}$, one has

$$\begin{array}{cc}\hfill \lambda {\displaystyle \sum _{k=1}^N}F(k,u\left(k\right))& \le \lambda {\displaystyle \sum _{k=1}^N}\left[\epsilon \left|u\right(k\left)\right|+h\right]\hfill \\ & \le \lambda \frac{\epsilon N\sqrt{N+1}}{2}\parallel u\parallel +\lambda Nh\hfill \\ & \le \frac{\epsilon N\left(\sqrt{N+1+4c^2}-\sqrt{N+1}\right)}{2F_c}\parallel u\parallel +\frac{\left(-1+\sqrt{1+\frac{4c^2}{N+1}}\right)Nh}{F_c},\hfill \end{array}$$

for each $u\in S$. Therefore, it is true that

$$\begin{array}{cc}\hfill I_{\lambda }\left(u\right)& =\Phi \left(u\right)-\lambda \Psi \left(u\right)\hfill \\ \hfill & ={\displaystyle \sum _{k=1}^{N+1}}\left[\sqrt{1+{(\Delta u(k-1))}^2}-1\right]-\lambda {\displaystyle \sum _{k=1}^N}F(k,u\left(k\right))\hfill \\ & \ge {\left[{\displaystyle \sum _{k=1}^{N+1}}\left[1+{(\Delta u(k-1))}^2\right]\right]}^{\frac{1}{2}}-N-1-\lambda {\displaystyle \sum _{k=1}^N}F(k,u\left(k\right))\hfill \\ & \ge \left[1-\frac{\epsilon N\left(\sqrt{N+1+4c^2}-\sqrt{N+1}\right)}{2F_c}\right]\parallel u\parallel -N-1-\frac{\left(-1+\sqrt{1+\frac{4c^2}{N+1}}\right)Nh}{F_c}.\hfill \end{array}$$

Thus, we get that $I_{\lambda }$ is coercive, and condition $\left(a_2\right)$ of Lemma 1 is verified. In summary, all assumptions of Lemma 1 are proved, and so the functional $I_{\lambda }$ has at least three distinct critical points in X for each $\lambda \in \Lambda$. Since $u\equiv 0$ is not a solution to the (Problem 1), the proof is completed. □

Remark 1.

It is obvious that the mean curvature operator ${\varphi }_c$ is odd symmetric (${\varphi }_c(-s)=-{\varphi }_c\left(s\right)$, $s\in \mathbb{R}$). When the nonlinear term f is also odd symmetric ($f(·,-s)=-f(·,s)$), the variational functional $I_{\lambda }$ is even symmetric ($I_{\lambda }(-u)=I_{\lambda }\left(u\right)$, $u\in S$). In this case, it is easy to obtain multiple solutions to (Problem 1) by using the critical point theory with symmetries. However, in this paper, we obtain multiple solutions to (Problem 1) without the symmetry on f.

Now, let

$$F^{+}(k,\xi )={\int }_0^{\xi }f(k,t^{+})dt,(k,\xi )\in \mathbb{Z}(1,N)\times \mathbb{R},$$

where $t^{+}=max\{0,t\}$ and define $I_{\lambda }^{+}=\Phi -\lambda {\Psi }^{+}$, with $\Phi$ defined in (2) and

$${\Psi }^{+}\left(u\right):={\displaystyle \sum _{k=1}^N}{F}^{+}(k,u\left(k\right)).$$

It is well known that $I_{\lambda }^{+}\in C^1(S,\mathbb{R})$ and the critical points of $I_{\lambda }^{+}$ are precisely the solutions of the following problem.

Problem 2

$$\left\{\begin{array}{c}-\Delta \left({\varphi }_c\left(\Delta u(k-1)\right)\right)=\lambda f(k,u^{+}\left(k\right)),k\in \mathbb{Z}(1,N),\hfill \\ u\left(0\right)=u(N+1)=0.\hfill \end{array}\right.$$

We have the following corollary.

Corollary 1.

Assume that there exist two positive constants c and d with

$$2\sqrt{1+d^2}>1+\sqrt{1+\frac{4c^2}{N+1}}$$

such that

(i) 

$f(k,\xi )>0$ for each $k\in \mathbb{Z}(1,N)$ and $\xi \in [0,c]$;

(ii) 

$\frac{F_d}{2(\sqrt{1+d^2}-1)}>\frac{F_c}{-1+\sqrt{1+\frac{4c^2}{N+1}}};$

(iii) 

$\underset{\xi \to +\infty }{lim\; sup}\frac{F(k,\xi )}{\xi }<\frac{2F_c}{N(\sqrt{4c^2+N+1}-\sqrt{N+1})}$.

Then, for every $\lambda \in \Lambda$, (Problem 1) has at least three positive solutions.

Proof. 

For each $k\in \mathbb{Z}(1,N)$, consider (Problem 2) with

$$f^{+}(k,\xi )=\left\{\begin{array}{c}f(k,\xi ),\mathrm{if}\xi >0,\hfill \\ f(k,0),\mathrm{if}\xi \le 0.\hfill \end{array}\right.$$

One has that condition $\left(i\right)$ of Theorem 1 holds. Besides, we have

$$\underset{\xi \to -\infty }{lim\; sup}\frac{F^{+}(k,\xi )}{\left|\xi \right|}=\underset{\xi \to -\infty }{lim\; sup}\frac{\xi f(k,0)}{\left|\xi \right|}=-f(k,0)<\frac{2F_c}{N(\sqrt{4c^2+N+1}-\sqrt{N+1})}.$$

So, all conditions of Theorem 1 are true. Moreover, since $u\equiv 0$ is not a solution of problem $\left(P_{\lambda ,f}^{+}\right)$, we can get that (Problem 2) has at least three nontrivial solutions. Assume $u=\left\{u\right(k\left)\right\}$ is one of the nontrivial solution, for any $k\in \mathbb{Z}(1,N)$, one has either $u\left(k\right)>0$ or

$$-\Delta \left({\varphi }_c\left(\Delta u(k-1)\right)\right)=\lambda f(k,u^{+}\left(k\right))=\lambda f(k,0)>0.$$

Then, we have $u>0$ for all $k\in \mathbb{Z}(1,N)$ by Lemma 5, i.e., u is a positive solution. In addition, if u is a positive solution of (Problem 2), then u is a positive solution of (Problem 1) obviously and Corollary 1 is proved. □

Next, we will use Lemma 2 to obtain another conclusion of this paper.

Theorem 2.

Assume that there exist two positive constants c and d with

$$2\sqrt{1+d^2}<1+\sqrt{1+\frac{4c^2}{N+1}}$$

(8)

such that

($T_1$)

$f(k,\xi )>0$ for each $k\in \mathbb{Z}(1,N)$ and $\xi \in [-c,c]$;

($T_2$)

$max\left\{\frac{2(\sqrt{1+d^2}-1)}{F_d},\frac{2\sqrt{N(N+1)}sin\frac{N\pi }{2(N+1)}}{\beta }\right\}<\frac{-1+\sqrt{1+\frac{4c^2}{N+1}}}{F_c};$

($T_3$)

there exist a positive constant β such that

$$\underset{\left|t\right|\to +\infty }{lim\; inf}\frac{F(k,t)}{\left|t\right|}>\beta$$

for each $k\in \mathbb{Z}(1,N).$

Then, for every $\lambda \in \left(max\left\{\frac{2(\sqrt{1+d^2}-1)}{F_d},\frac{2\sqrt{N(N+1)}sin\frac{N\pi }{2(N+1)}}{\beta }\right\},\frac{-1+\sqrt{1+\frac{4c^2}{N+1}}}{F_c}\right)$, (Problem 1) has at least two non-zero critical points $u_{\lambda ,1},$$u_{\lambda ,2}$ such that $I_{\lambda }\left(u_{\lambda ,1}\right)<0<I_{\lambda }\left(u_{\lambda ,2}\right).$

Proof. 

Clearly, $\Phi$, $\Psi$ are two continuously Gâteaux differentiable functionals and

$$\underset{X}{inf}\Phi =\Phi \left(0\right)=\Psi \left(0\right)=0.$$

Let $\overline{u}$ and r be the same as the ones defined in the proof of Theorem 1. Then we have

$$\frac{\underset{\Phi \left(u\right)\le r}{sup}\Psi \left(u\right)}{r}\le \frac{F_c}{-1+\sqrt{1+\frac{4c^2}{N+1}}}<\frac{1}{\lambda }$$

and

$$\frac{\Psi \left(\overline{u}\right)}{\Phi \left(\overline{u}\right)}=\frac{F_d}{2(\sqrt{1+d^2}-1)}>\frac{1}{\lambda }.$$

So inequality (1) in Lemma 2 holds. Besides, form $\left(T_3\right)$ and Lemma 4, there is a constant h such that, for any $u\in S$ and $k\in \mathbb{Z}(1,N)$,

$$\begin{array}{cc}\hfill \lambda {\displaystyle \sum _{k=1}^N}F(k,u\left(k\right))& \ge \lambda {\displaystyle \sum _{k=1}^N}\left(\beta \right|u\left(k\right)|-h)\hfill \\ & \ge {\lambda \beta \parallel u\parallel }_{\infty }-\lambda Nh\hfill \\ & \ge \frac{\lambda \beta }{\sqrt{N{\lambda }_N}}\parallel u\parallel -\lambda Nh.\hfill \end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill I_{\lambda }\left(u\right)& =\Phi \left(u\right)-\Psi \left(u\right)\hfill \\ & ={\displaystyle \sum _{k=1}^{N+1}}\left[\sqrt{1+{(\Delta u(k-1))}^2}-1\right]-\lambda {\displaystyle \sum _{k=1}^N}F(k,u\left(k\right))\hfill \\ & \le {\displaystyle \sum _{k=1}^{N+1}}\left[1+\sqrt{{(\Delta u(k-1))}^2}-1\right]-\frac{\lambda \beta }{\sqrt{N{\lambda }_N}}\parallel u\parallel +\lambda Nh\hfill \\ & \le {\left({\displaystyle \sum _{k=1}^{N+1}}{1}^2\right)}^{\frac{1}{2}}{\left({\displaystyle \sum _{k=1}^{N+1}}{(\Delta u(k-1))}^2\right)}^{\frac{1}{2}}-\frac{\lambda \beta }{\sqrt{N{\lambda }_N}}\parallel u\parallel +\lambda Nh\hfill \\ & \le \left(\sqrt{N+1}-\frac{\lambda \beta }{\sqrt{N{\lambda }_N}}\right)\parallel u\parallel +\lambda Nh\hfill \\ & =\left(\sqrt{N+1}-\frac{\lambda \beta }{2\sqrt{N}sin\frac{N\pi }{2(N+1)}}\right)\parallel u\parallel +\lambda Nh.\hfill \end{array}$$

Thus, we see that $\underset{\parallel u\parallel \to +\infty }{lim}{I}_{\lambda }\left(u\right)=-\infty$, which means that the functional $I_{\lambda }$ is unbounded from below. Moreover, we can get that $-I_{\lambda }$ is coercive. Therefore, $I_{\lambda }$ satisfies the (PS)-condition and the proof is completed. □

4. Examples

Example 1.

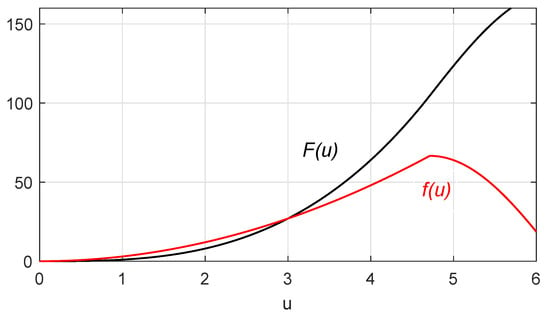
Fix $N\in \mathbb{Z}(1,20)$ and consider the boundary value (Problem 1) with

$$f(k,u)=f\left(u\right)=\left\{\begin{array}{c}3u^2+\frac{1}{4}cosu,\mathit{if}u\le \frac{3\pi }{2},\hfill \\ \frac{27{\pi }^2}{4}cos(u+\frac{\pi }{2}),\mathit{if}u>\frac{3\pi }{2},\hfill \end{array}\right.$$

for $k\in \mathbb{Z}(1,N)$. Then, we have

$$F(k,\xi )=F\left(\xi \right)=\left\{\begin{array}{c}{\xi }^3+\frac{1}{4}sin\xi ,\mathit{if}\xi \le \frac{3\pi }{2},\hfill \\ \frac{27{\pi }^3}{8}-\frac{1}{4}+\frac{27{\pi }^2}{4}sin(\xi +\frac{\pi }{2}),\mathit{if}\xi >\frac{3\pi }{2}.\hfill \end{array}\right.$$

Let $c=\frac{1}{2}$ and $d=4$. Then one has

$$2\sqrt{1+d^2}=2\sqrt{17}>1+\sqrt{1+\frac{1}{N+1}}=1+\sqrt{1+\frac{4c^2}{N+1}}.$$

In addition, as shown in Figure 1, $f(k,\xi )>0$ for each $\xi \in [0,\frac{1}{2}]$. Thus condition $\left(i\right)$ of Corollary 1 follows. Moreover, we have

$$\frac{F_c}{-1+\sqrt{1+\frac{4c^2}{N+1}}}=\frac{N(1+2sin\frac{1}{2})}{8\left(-1+\sqrt{1+\frac{1}{N+1}}\right)}\le \frac{N(1+2sin\frac{1}{2})}{8\left(-1+\sqrt{\frac{21}{20}}\right)}\approx 9.915N$$

(9)

and

$$\frac{F_d}{2(\sqrt{1+d^2}-1)}=\frac{N(256+sin4)}{8(\sqrt{17}-1)}\approx 10.216N.$$

(10)

Figure 1. The images of $f\left(u\right)$ and $F\left(u\right)$ in Example 1.

Since

$$\frac{256+sin4}{8(\sqrt{17}-1)}-\frac{1+2sin\frac{1}{2}}{8\left(-1+\sqrt{\frac{21}{20}}\right)}>0,$$

by combining (9) and (10), condition $\left(ii\right)$ of Corollary 1 holds.

We can further verify condition $\left(iii\right)$ of Corollary 1, since

$$\underset{\xi \to +\infty }{lim\; sup}\frac{F(k,\xi )}{\xi }=\underset{\xi \to +\infty }{lim\; sup}\frac{\frac{27{\pi }^3}{8}-\frac{1}{4}+\frac{27{\pi }^2}{4}sin(\xi +\frac{\pi }{2})}{\xi }=0<\frac{2F_c}{N(\sqrt{4c^2+N+1}-\sqrt{N+1})}.$$

To sum up, all the conditions of Corollary 1 are satisfied. Hence, for

$$\lambda \in \mathsf{\Lambda }=\left(\frac{8(\sqrt{17}-1)}{N(256+sin4)},\frac{8\left(-1+\sqrt{1+\frac{1}{N+1}}\right)}{N(1+2sin\frac{1}{2})}\right),$$

the boundary value problem admits at least three positive solutions.

Example 2.

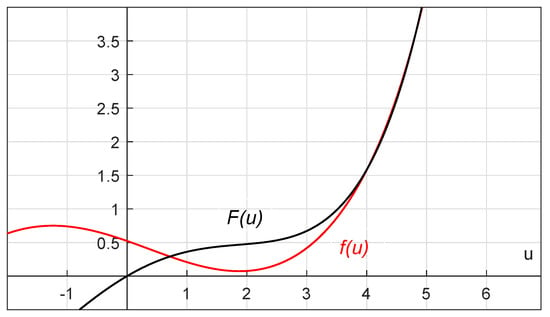
Let $N=3$ and $\beta =10$, consider the boundary value (Problem 1) with

$$f(k,u)=f\left(u\right)=\left\{\begin{array}{c}\frac{1}{6}\left[(3-2u)cos\frac{u}{2}+e^{u-2}\right],\mathit{if}u\le 2\pi ,\hfill \\ \frac{1}{6}\left(4\pi -3+e^{2\pi -2}\right),\mathit{if}u>2\pi ,\hfill \end{array}\right.$$

for each $k\in \mathbb{Z}(1,N).$ Then, we have

$$F(k,\xi )=F\left(\xi \right)=\left\{\begin{array}{c}\frac{1}{3}\left[(3-2\xi )sin\frac{\xi }{2}+4\left(1-cos\frac{\xi }{2}\right)\right]+\frac{e^{-2}}{6}\left(e^{\xi }-1\right),\mathit{if}\xi \le 2\pi ,\hfill \\ \frac{1}{6}\left(4\pi -3+e^{2\pi -2}\right)\xi -\frac{\pi }{3}(4\pi -3+e^{2\pi -2})+\frac{e^{-2}}{6}\left(e^{2\pi -1}\right)+\frac{8}{3},\mathit{if}\xi >2\pi .\hfill \end{array}\right.$$

Moreover, the images of $f\left(u\right)$ and $F\left(u\right)$ are shown in Figure 2.

Figure 2. The images of $f\left(u\right)$ and $F\left(u\right)$ in Example 2.

Letting $c=\sqrt{N+1}=2$ and $d=\frac{1}{2}$, we have

$$2\sqrt{1+d^2}=\sqrt{5}<1+\sqrt{5}=1+\sqrt{1+\frac{4c^2}{N+1}}.$$

Now, we prove $f\left(u\right)>0$ for each $u\in [-2,2]$. Let

$$f_1\left(u\right)=(3-2u)cos\frac{u}{2}and{f}_2\left(u\right)=e^{u-2}.$$

Then $f\left(u\right)=\frac{1}{6}\left(f_1\left(u\right)+f_2\left(u\right)\right)$ for $u\le 2\pi$. Besides, it is obvious that $f_2\left(u\right)>0$ on $[-2,2]$ and $f_1\left(u\right)\ge 0$ on $\left[-2,\frac{3}{2}\right]$. When $u\in \left[\frac{3}{2},2\right]$, we have

$$f_1^{\prime }\left(u\right)=\frac{1}{2}\left[(2u-3)sin\frac{u}{2}-4cos\frac{u}{2}\right]\le \frac{1}{2}(sin1-4cos1)<0.$$

Thus $f_1\left(u\right)$ is decreasing on $[\frac{3}{2},2]$. Since $f_2\left(u\right)$ is an increasing function and $f_1\left(2\right)+f_2\left(\frac{3}{2}\right)=-cos1+e^{-\frac{1}{2}}>0$, we can get $f\left(u\right)>0$ on $[-2,2]$.

In addition, we have

$$F_d={\displaystyle \sum _{k=1}^N}F(k,d)=N{\int }_0^d\frac{1}{6}\left[(3-2u)cos\frac{u}{2}+e^{u-2}\right]du\approx 0.663$$

and

$$F_c={\displaystyle \sum _{k=1}^N}F(k,c)=N{\int }_0^c\frac{1}{6}\left[(3-2u)cos\frac{u}{2}+e^{u-2}\right]du\approx 1.430.$$

It follows that

$$\frac{2(\sqrt{1+d^2}-1)}{F_d}=\frac{\sqrt{5}-2}{F_d}\approx 0.356,$$

and

$$\frac{-1+\sqrt{1+\frac{4c^2}{N+1}}}{F_c}=\frac{\sqrt{5}-1}{F_c}\approx 0.865.$$

The above together with

$$\frac{2\sqrt{N(N+1)}sin\frac{N\pi }{2(N+1)}}{\beta }=\frac{4\sqrt{3}sin\frac{3\pi }{8}}{10}\approx 0.640$$

confirms condition $\left(T_2\right)$ of Theorem 2.

Besides,

$$\begin{array}{cc}\hfill \underset{\left|\xi \right|\to +\infty }{lim\; inf}\frac{F(k,\xi )}{\xi }& =\underset{\xi \to +\infty }{lim\; inf}\frac{\frac{1}{6}\left(4\pi -3+e^{2\pi -2}\right)\xi -\frac{\pi }{3}(4\pi -3+e^{2\pi -2})+\frac{e^{-2}}{6}\left(e^{2\pi -1}\right)+\frac{8}{3}}{\xi }\hfill \\ & =\frac{1}{6}\left(4\pi -3+e^{2\pi -2}\right)\hfill \\ & \approx 13.673>\beta \hfill \end{array}$$

for each $k\in \mathbb{Z}(1,N)$. We can see from Theorem 2 that the boundary value problem has at least two non-zero solutions for each $\lambda \in \left(\frac{4\sqrt{3}sin\frac{3\pi }{8}}{10},\frac{\sqrt{5}-1}{3{\int }_0^2\frac{1}{6}\left[(3-2u)cos\frac{u}{2}+e^{u-2}\right]du}\right)\approx \left(0.640,0.865\right)$.

5. Conclusions

A discrete Dirichlet boundary value problem involving the mean curvature operator is studied in this paper. Unlike the existing result in [33], we obtained different sufficient conditions of the existence of multiple solutions without assuming that the nonlinear term oscillates at infinity, as shown in Theorems 1 and 2. First, according to the research results of Bonanno in [22], we obtain at least three non-trivial solutions in Theorem 1. In addition, as a supplement to Theorem 1, we prove the existence of at least three positive solutions through the maximum principle. Note that inequality (3) plays an important role in the proof of Theorem 1. For the situation that inequality (3) is not satisfied, under another suitable assumption on the nonlinear term, we still can obtain the existence of at least two non-trivial solutions based on Theorem 2.1 in [23]. It seems that the method used in this paper can be adapted to discuss the existence of homoclinic solutions or periodic solutions of difference equations with ${\varphi }_c$-Laplacian. This will be left as our future work.