Modified Jacobi-Gradient Iterative Method for Generalized Sylvester Matrix Equation
Abstract
1. Introduction
(AS): The sequence of approximated solutions converges to the exact solution, no matter the initial value is.
2. A Modified Jacobi-Gradient Iterative Method for the Generalized Sylvester Equation
| Algorithm 1: Modified Jacobi-gradient based iterative (MJGI) algorithm |
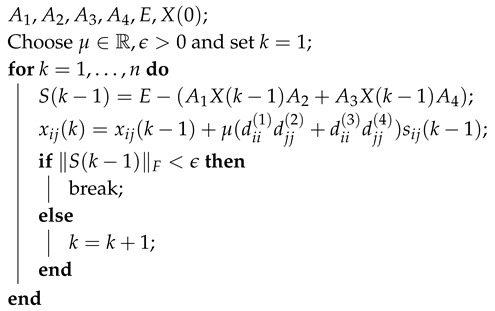 |
3. Convergence Analysis of the Proposed Method
3.1. Convergence Criteria
- (1)
- Then, (AS) holds if and only if.
- (2)
- Iffor all, then (AS) holds if and only if
- (3)
- Iffor all, then (AS) holds if and only if
- (4)
- If H is symmetric, then (AS) holds if and only ifandhave the same sign, and μ is chosen so that
- (i)
- for any initial value .
- (ii)
- System (11) has an asymptotically-stable zero solution.
- (iii)
- The iteration matrix has spectral radius less than 1.
- (i)
- and for all ;
- (ii)
- and for all .
- Case 1
- for all j. In this case, if and only if
- Case 2
- for all j. In this case, if and only if
- Case 1
- If then the condition (16) is equivalent to
- Case 2
- If then the condition (16) is equivalent to
- Case 3
- If , thenwhich is a contradiction.
3.2. Convergence Rate and Error Estimate
3.3. Optimal Parameter
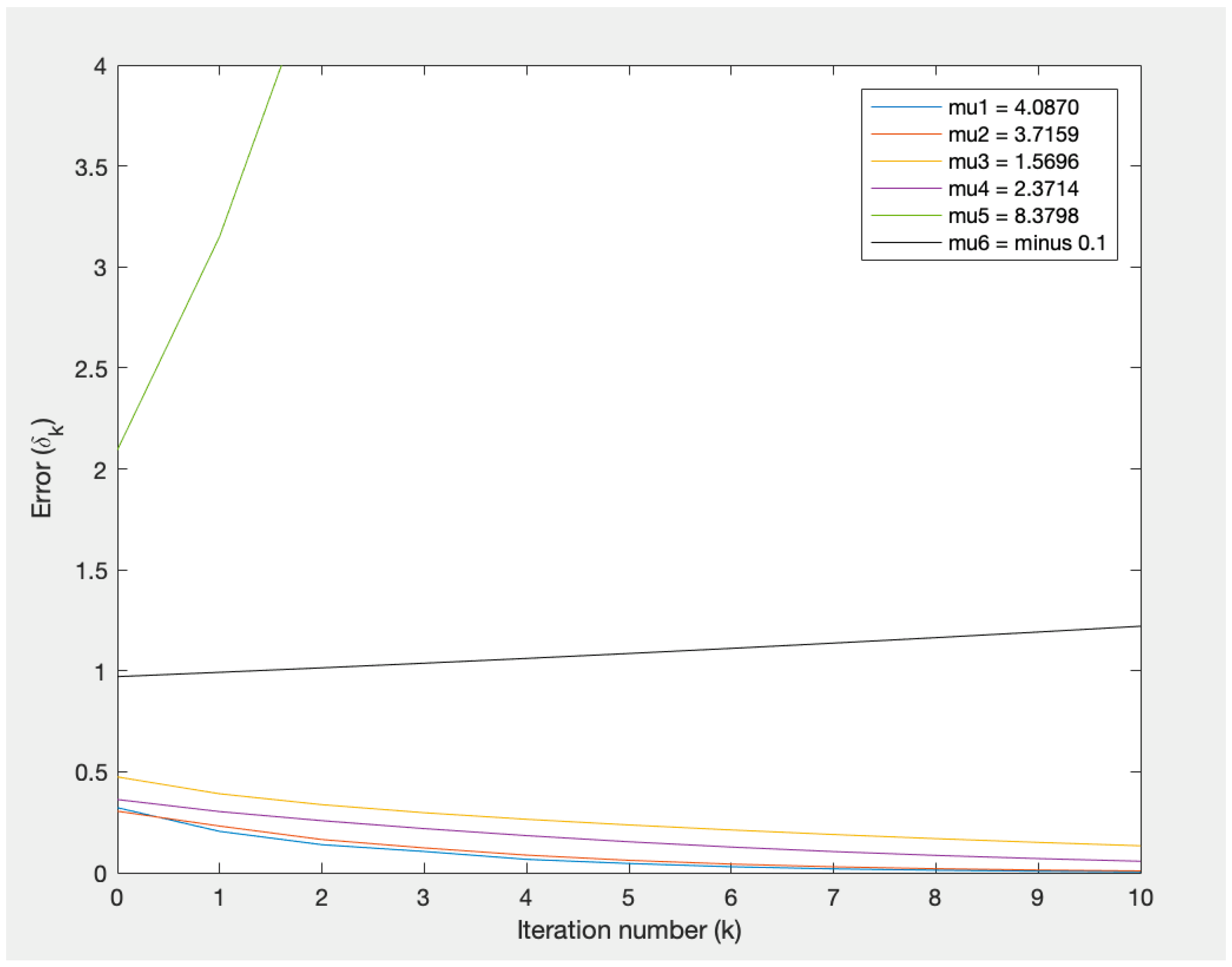
4. Numerical Simulations
4.1. Numerical Simulation for the Generalized Sylvester Matrix Equation
4.2. Numerical Simulation for Sylvester Matrix Equation
| Algorithm 2: Modified Jacobi-gradient based iterative (MJGI) algorithm for Sylvester equation |
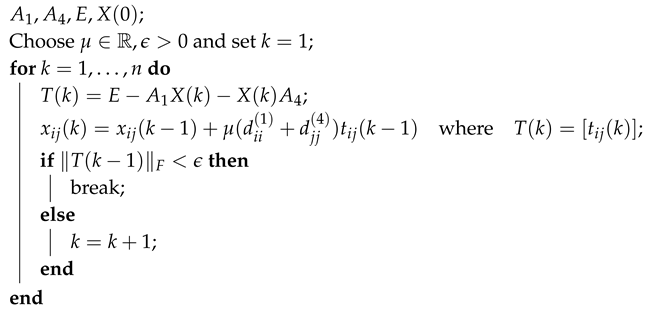 |
5. Conclusions and Suggestion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shang, Y. Consensus seeking over Markovian switching networks with time-varying delays and uncertain topologies. Appl. Math. Comput. 2016, 273, 1234–1245. [Google Scholar] [CrossRef]
- Shang, Y. Average consensus in multi-agent systems with uncertain topologies and multiple time-varying delays. Linear Algebra Appl. 2014, 459, 411–429. [Google Scholar] [CrossRef]
- Golub, G.H.; Nash, S.; Van Loan, C.F. A Hessenberg-Schur method for the matrix AX + XB = C. IEEE Trans. Automat. Control. 1979, 24, 909–913. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. Hierarchical least squares identification methods for multivariable systems. IEEE Trans. Automat. Control 1997, 42, 408–411. [Google Scholar] [CrossRef]
- Benner, P.; Quintana-Orti, E.S. Solving stable generalized Lyapunov equations with the matrix sign function. Numer. Algorithms 1999, 20, 75–100. [Google Scholar] [CrossRef]
- Starke, G.; Niethammer, W. SOR for AX − XB = C. Linear Algebra Appl. 1991, 154–156, 355–375. [Google Scholar] [CrossRef]
- Jonsson, I.; Kagstrom, B. Recursive blocked algorithms for solving triangular systems—Part I: One-sided and coupled Sylvester-type matrix equations. ACM Trans. Math. Softw. 2002, 28, 392–415. [Google Scholar] [CrossRef]
- Jonsson, I.; Kagstrom, B. Recursive blocked algorithms for solving triangular systems—Part II: Two-sided and generalized Sylvester and Lyapunov matrix equations. ACM Trans. Math. Softw. 2002, 28, 416–435. [Google Scholar] [CrossRef]
- Kaabi, A.; Kerayechian, A.; Toutounian, F. A new version of successive approximations method for solving Sylvester matrix equations. Appl. Math. Comput. 2007, 186, 638–648. [Google Scholar] [CrossRef]
- Lin, Y.Q. Implicitly restarted global FOM and GMRES for nonsymmetric matrix equations and Sylvester equations. Appl. Math. Comput. 2005, 167, 1004–1025. [Google Scholar] [CrossRef]
- Kressner, D.; Sirkovic, P. Truncated low-rank methods for solving general linear matrix equations. Numer. Linear Algebra Appl. 2015, 22, 564–583. [Google Scholar] [CrossRef]
- Dehghan, M.; Shirilord, A. A generalized modified Hermitian and skew-Hermitian splitting (GMHSS) method for solving complex Sylvester matrix equation. Appl. Math. Comput. 2019, 348, 632–651. [Google Scholar] [CrossRef]
- Dehghan, M.; Shirilord, A. Solving complex Sylvester matrix equation by accelerated double-step scale splitting (ADSS) method. Eng. Comput. 2019. [Google Scholar] [CrossRef]
- Li, S.Y.; Shen, H.L.; Shao, X.H. PHSS iterative method for solving generalized Lyapunov equations. Mathematics 2019, 7, 38. [Google Scholar] [CrossRef]
- Shen, H.L.; Li, Y.R.; Shao, X.H. The four-parameter PSS method for solving the Sylvester equation. Mathematics 2019, 7, 105. [Google Scholar] [CrossRef]
- Hajarian, M. Generalized conjugate direction algorithm for solving the general coupled matrix equations over symmetric matrices. Numer. Algorithms 2016, 73, 591–609. [Google Scholar] [CrossRef]
- Hajarian, M. Extending the CGLS algorithm for least squares solutions of the generalized Sylvester-transpose matrix equations. J. Frankl. Inst. 2016, 353, 1168–1185. [Google Scholar] [CrossRef]
- Dehghan, M.; Mohammadi-Arani, R. Generalized product-type methods based on Bi-conjugate gradient (GPBiCG) for solving shifted linear systems. Comput. Appl. Math. 2017, 36, 1591–1606. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. Gradient based iterative algorithms for solving a class of matrix equations. IEEE Trans. Automat. Control 2005, 50, 1216–1221. [Google Scholar] [CrossRef]
- Niu, Q.; Wang, X.; Lu, L.-Z. A relaxed gradient based algorithm for solving Sylvester equation. Asian J. Control 2011, 13, 461–464. [Google Scholar] [CrossRef]
- Zhang, X.D.; Sheng, X.P. The relaxed gradient based iterative algorithm for the symmetric (skew symmetric) solution of the Sylvester equation AX + XB = C. Math. Probl. Eng. 2017, 2017, 1624969. [Google Scholar] [CrossRef]
- Xie, Y.J.; Ma, C.F. The accelerated gradient based iterative algorithm for solving a class of generalized Sylvester-transpose matrix equation. Appl. Math. Comput. 2012, 218, 5620–5628. [Google Scholar] [CrossRef]
- Ding, F.; Chen, T. Iterative least-squares solutions of coupled Sylvester matrix equations. Syst. Control Lett. 2005, 54, 95–107. [Google Scholar] [CrossRef]
- Fan, W.; Gu, C.; Tian, Z. Jacobi-gradient iterative algorithms for Sylvester matrix equations. In Proceedings of the 14th Conference of the International Linear Algebra Society, Shanghai University, Shanghai, China, 16–20 July 2007. [Google Scholar]
- Tian, Z.; Tian, M.; Gu, C.; Hao, X. An accelerated Jacobi-gradient based iterative algorithm for solving Sylvester matrix equations. Filomat 2017, 31, 2381–2390. [Google Scholar] [CrossRef]
- Ding, F.; Liu, P.X.; Chen, T. Iterative solutions of the generalized Sylvester matrix equations by using the hierarchical identification principle. Appl. Math. Comput. 2008, 197, 41–50. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]

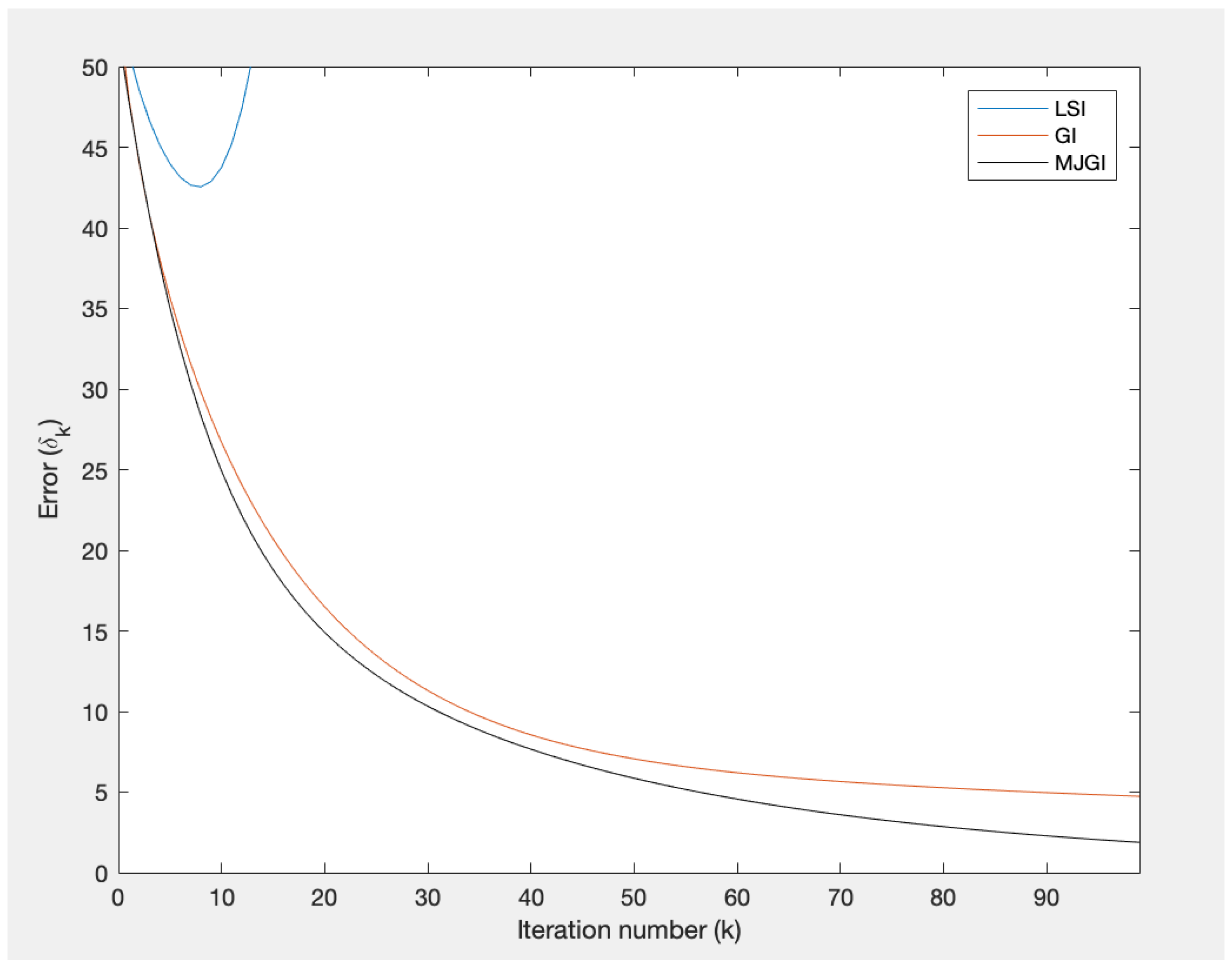

| Method | IT | CT | Error: |
|---|---|---|---|
| Direct | - | 0.0364 | - |
| LSI | 75 | 0.0125 | 1.1296 × 105 |
| GI | 75 | 0.0049 | 1.4185 |
| MJGI | 75 | 0.0022 | 0.5251 |
| Method | IT | CT | Error: |
|---|---|---|---|
| Direct | - | 34.6026 | - |
| LSI | 100 | 0.1920 | 2.7572 × 104 |
| GI | 100 | 0.0849 | 4.7395 |
| MJGI | 100 | 0.0298 | 1.8844 |
| Method | IT | CT | Error: |
|---|---|---|---|
| Direct | - | 0.0118 | - |
| GI | 100 | 0.0051 | 2.5981 |
| RGI | 100 | 0.0061 | 3.4741 |
| AGBI | 100 | 0.0051 | 7.3306 |
| JGI | 100 | 0.0038 | 17.2652 |
| MJGI | 100 | 0.0028 | 0.4281 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sasaki, N.; Chansangiam, P. Modified Jacobi-Gradient Iterative Method for Generalized Sylvester Matrix Equation. Symmetry 2020, 12, 1831. https://doi.org/10.3390/sym12111831
Sasaki N, Chansangiam P. Modified Jacobi-Gradient Iterative Method for Generalized Sylvester Matrix Equation. Symmetry. 2020; 12(11):1831. https://doi.org/10.3390/sym12111831
Chicago/Turabian StyleSasaki, Nopparut, and Pattrawut Chansangiam. 2020. "Modified Jacobi-Gradient Iterative Method for Generalized Sylvester Matrix Equation" Symmetry 12, no. 11: 1831. https://doi.org/10.3390/sym12111831
APA StyleSasaki, N., & Chansangiam, P. (2020). Modified Jacobi-Gradient Iterative Method for Generalized Sylvester Matrix Equation. Symmetry, 12(11), 1831. https://doi.org/10.3390/sym12111831






