Central Splitting of A2 Discrete Fourier–Weyl Transforms
Abstract
1. Introduction
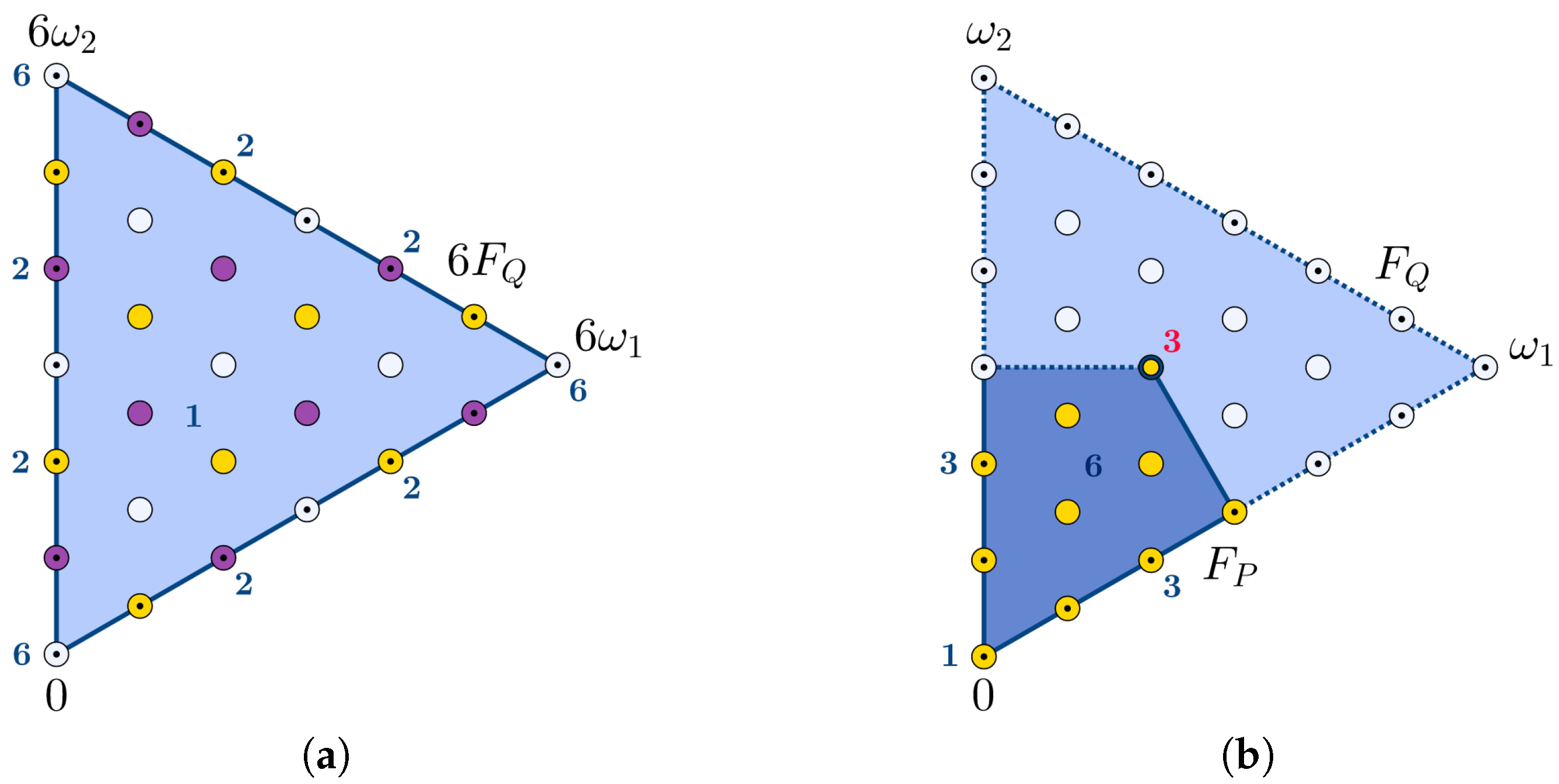
2. Splitting Weight and Point Sets
2.1. Root and Weight Lattices
2.2. Splitting Weight Sets
2.3. Splitting Point Sets
3. Weight Lattice Fourier–Weyl Transforms
3.1. C- and S-Functions
3.2. Discrete Orthogonality
3.3. Splitting Transforms
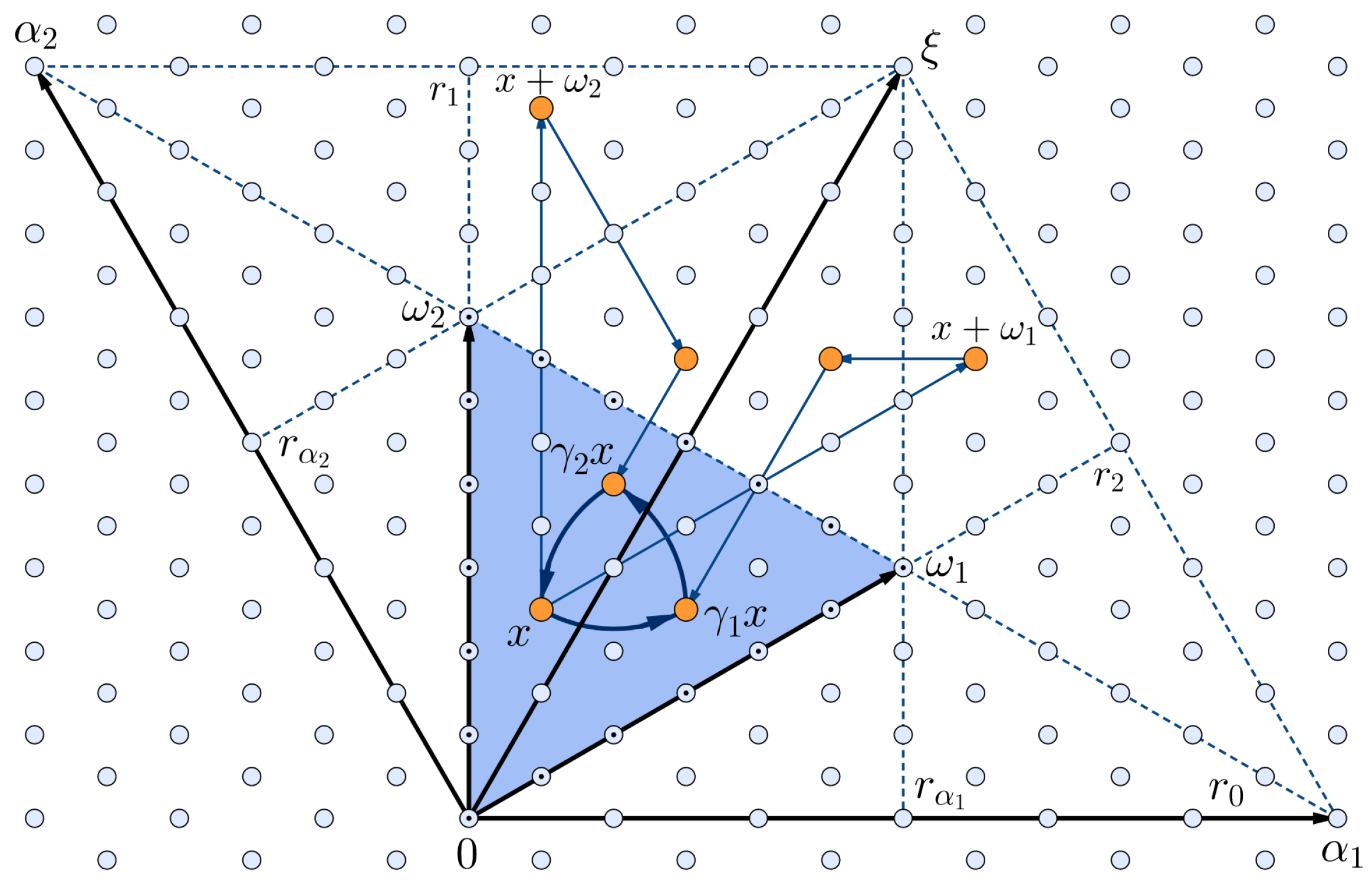
4. Central Splitting
4.1. Central Splitting of Discrete Transforms
4.2. Decompositions of Unitary Transform Matrices
4.3. Decompositions of Transform Matrices and
5. Concluding Remarks
- The decompositions of the weight lattice Fourier–Weyl transforms into the splitting transforms are considered as a point of departure in exploring the fast bivariate discrete Fourier transforms involving the (anti)symmetric orbit functions of the Weyl group . The central splitting method offers an advantageous approach to computational efficiency, using the reduction of the initial weight lattice Fourier–Weyl transform into three smaller-weight lattice splitting transforms. Even though the recursive method to determine the further splitting of currently developed two-variable cosine and sine transforms has not been determined yet, the demonstrated reduced weight transform is considered as a stepping stone towards the fast discrete transforms. Moreover, analogously to the interpolation tests conducted for cosine and sine discrete transforms [2,17,18], the developed discrete splitting transforms also manifest excellent interpolation properties.
- For the crystallographic reflection group , repeatedly using the central splitting of one-variable discrete cosine and sine transforms produces the standard versions of the fast split-radix transforms [4]. In this case, the possibility of rearranging the splitting point sets into the original format governed by the affine Weyl group ensures the central splitting method’s recursive behavior. The decompositions of the transform matrices, similar to the formulated unitary matrix decompositions in Theorem 2, have been rigorously proven for the one-dimensional sine and cosine transforms in [30]. However, in the case of the group, since a further splitting of the points in the kite-shaped domain has not been formulated yet, the recursive central splitting method remains an unsolved problem.
- Given the importance of multi-dimensional digital data processing [16,37,38,39,40], a central-splitting mechanism could be potentially developed for other compact simple Lie groups with non-trivial elements of the center, such as with its center provided by a cyclic group of elements, , and with the center given by a cyclic group of order 2, whose center contains 4 elements, that equivalently to has 3 elements of the center. Such an approach would be considered as a first step to a general multidimensional fast transform. Since a similar behavior of the central splitting in the case of the finite reflection group is expected, the extension of the developed Fourier–Weyl transforms to higher-dimensional cases should be treated independently.
- Another family of orbit functions, known as E-functions, is obtained by symmetrizing multivariate exponential terms over even subgroups of a considered Weyl group. Such functions are developed in [13], and their corresponding Fourier–Weyl transforms together with continuous interpolations are examined in detail [41]. There is one type of the E-functions for the root systems with the roots of one length [3]. For the root systems with two lengths of simple roots, the six types of E-functions, together with their even complex-valued dual weight lattice Fourier–Weyl transforms, are formulated in [14]. Hence, instead of the discrete transforms based on the C- and S-functions, the central splitting of the transforms developed by means of the E-functions represents an open problem. Furthermore, the Fourier–Weyl transforms with their kernel represented by the combinations of different types of Weyl orbit functions have not been previously explored.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hrivnák, J.; Patera, J. On discretization of tori of compact simple Lie groups. J. Phys. A Math. Theor. 2009, 42, 385208. [Google Scholar] [CrossRef]
- Patera, J.; Zaratsyan, A. Discrete and Continuous Cosine Transform Generalized to Lie Groups SU(3) and G(2). J. Math. Phys. 2005, 46, 113506. [Google Scholar] [CrossRef]
- Moody, R.V.; Patera, J. Orthogonality within the families of C-, S-, and E-functions of any compact semisimple Lie group. SIGMA 2006, 2, 076. [Google Scholar] [CrossRef]
- Britanak, V.; Rao, K.; Yip, P. Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations; Elsevier/Academic Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Moody, R.V.; Patera, J. Computation of character decompositions of class functions on compact semisimple Lie groups. Math. Comp. 1987, 48, 799–827. [Google Scholar] [CrossRef]
- Moody, R.V.; Patera, J. Characters of elements of finite order in simple Lie groups. SIAM. J. Algebr. Discret. Methods 1984, 5, 359–383. [Google Scholar] [CrossRef]
- Hrivnák, J.; Walton, M.A. Weight-Lattice Discretization of Weyl-Orbit Functions. J. Math. Phys. 2016, 57, 083512. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L.; Patera, J. On discretization of tori of compact simple Lie groups II. J. Phys. A 2012, 45, 255201. [Google Scholar] [CrossRef]
- Czyżycki, T.; Hrivnák, J.; Motlochová, L. Generalized Dual-Root Lattice Transforms of Affine Weyl Groups. Symmetry 2020, 12, 1018. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L. Dual-root lattice discretization of Weyl orbit functions. J. Fourier Anal. Appl. 2019, 25, 2521–2569. [Google Scholar] [CrossRef]
- Klimyk, A.U.; Patera, J. Orbit functions. SIGMA 2006, 2, 006. [Google Scholar] [CrossRef]
- Klimyk, A.U.; Patera, J. Antisymmetric orbit functions. SIGMA 2007, 3, 023. [Google Scholar] [CrossRef]
- Klimyk, A.U.; Patera, J. E-orbit functions. SIGMA 2008, 4, 002. [Google Scholar] [CrossRef]
- Hrivnák, J.; Juránek, M. On E-Discretization of Tori of Compact Simple Lie Groups. II. J. Math. Phys. 2017, 58, 103504. [Google Scholar] [CrossRef]
- Moody, R.V.; Motlochová, L.; Patera, J. Gaussian cubature arising from hybrid characters of simple Lie groups. J. Fourier Anal. Appl. 2014, 20, 1257–1290. [Google Scholar] [CrossRef]
- Li, H.; Sun, J.; Xu, Y. Discrete Fourier analysis, cubature and interpolation on a hexagon and a triangle. SIAM J. Numer. Anal. 2008, 46, 1653–1681. [Google Scholar] [CrossRef]
- Patera, J.; Zaratsyan, A. Discrete and Continuous Cosine Transform Generalized to Lie Groups SU(2) × SU(2) and O(5). J. Math. Phys. 2005, 46, 053514. [Google Scholar] [CrossRef]
- Patera, J.; Zaratsyan, A. Discrete and continuous sine transform generalized to the semisimple Lie groups of rank two. J. Math. Phys. 2006, 47, 043512. [Google Scholar] [CrossRef]
- Hrivnák, J.; Motlochová, L. Discrete cosine and sine transforms generalized to honeycomb lattice. J. Math. Phys. 2018, 59, 063503. [Google Scholar] [CrossRef]
- Flamant, J.; Le Bihan, N.; Chainais, P. Time frequency analysis of bivariate signals. Appl. Comput. Harmon. Anal. 2019, 46, 351–383. [Google Scholar] [CrossRef]
- Püschel, M.; Moura, J.M.F. Algebraic signal processing theory: Foundation and 1-D time. IEEE Trans. Signal Process. 2008, 56, 3572–3585. [Google Scholar] [CrossRef]
- Zheng, Y.; Guo, B.; Chen, Z.; Li, C. A Fourier Descriptor of 2D Shapes Based on Multiscale Centroid Contour Distances Used in Object Recognition in Remote Sensing Images. Sensors 2019, 19, 486. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Guo, C.; Sheridan, J.T. A review of optical image encryption techniques. Opt. Laser Technol. 2014, 57, 327–342. [Google Scholar] [CrossRef]
- Rasheed, M.H.; Salih, O.M.; Siddeq, M.M.; Rodrigues, M.A. Image compression based on 2D Discrete Fourier Transform and matrix minimization algorithm. Array 2020, 6, 100024. [Google Scholar] [CrossRef]
- Irarrazaval, P.; Lizama, C.; Parot, V.; Sing-Long, C.; Tejos, C. The fractional Fourier transform and quadratic field magnetic resonance imaging. Comput. Math. Appl. 2011, 62, 1576–1590. [Google Scholar] [CrossRef]
- Lahav, A.; Chernyakova, T.; Eldar, Y.C. FoCUS: Fourier-Based Coded Ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1828–1839. [Google Scholar] [CrossRef]
- Hernández, J.R.; Amado, M.; Pérez-González, F. DCT-Domain Watermarking Techniques for Still Images: Detector Performance Analysis and a New Structure. IEEE Trans. Image Process. 2000, 9, 55–68. [Google Scholar] [CrossRef]
- Kahlessenane, F.; Khaldi, A.; Euschi, S. A robust blind color image watermarking based on Fourier transform domain. Optik 2020, 208, 164562. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Plonka, G.; Tasche, M. Fast and numerically stable algorithms for discrete cosine transforms. Linear Algebra Appl. 2005, 394, 309–345. [Google Scholar] [CrossRef]
- Püschel, M. Cooley-Tukey FFT like algorithms for the DCT. In Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ’03), Hong Kong, China, 6–10 April 2003; pp. 501–504. [Google Scholar] [CrossRef]
- Püschel, M.; Moura, J.M.F. The Algebraic Approach to the Discrete Cosine and Sine Transforms and Their Fast Algorithms. SIAM J. Comput. 2003, 32, 1280–1316. [Google Scholar] [CrossRef]
- Bourbaki, N. Groupes et Algèbres de Lie, Chapiters IV, V, VI; Hermann: Paris, France, 1968. [Google Scholar]
- Humphreys, J.E. Reflection Groups and Coxeter Groups; Cambridge Studies in Advanced Mathematics 29; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar] [CrossRef]
- McKay, W.G.; Patera, J. Tables of Dimensions, Indices, and Branching Rules for Representations of Simple Lie Algebras; Marcel Dekker, Inc.: New York, NY, USA, 1981. [Google Scholar]
- Bodner, M.; Patera, J.; Szajewska, M. Decomposition matrices for the special case of data on the triangular lattice of SU(3). Appl. Comput. Harmon. Anal. 2017, 43, 346–353. [Google Scholar] [CrossRef]
- Atoyan, A.; Patera, J. Properties of continuous Fourier extension of the discrete cosine transform and its multidimensional generalization. J. Math. Phys. 2004, 45, 2468–2491. [Google Scholar] [CrossRef]
- Klimyk, A.U.; Patera, J. (Anti)symmetric multivariate trigonometric functions and corresponding Fourier transforms. J. Math. Phys. 2007, 48, 093504. [Google Scholar] [CrossRef]
- Li, H.; Xu, Y. Discrete Fourier analysis on fundamental domain and simplex of Ad lattice in d-variables. J. Fourier Anal. Appl. 2010, 16, 383–433. [Google Scholar] [CrossRef]
- Nesterenko, M.; Patera, J. Three dimensional C-, S-, and E-transforms. J. Phys. A 2008, 41, 475205. [Google Scholar] [CrossRef][Green Version]
- Hrivnák, J.; Patera, J. On E-discretization of tori of compact simple Lie groups. J. Phys. A Math. Theor. 2010, 43, 165206. [Google Scholar] [CrossRef]

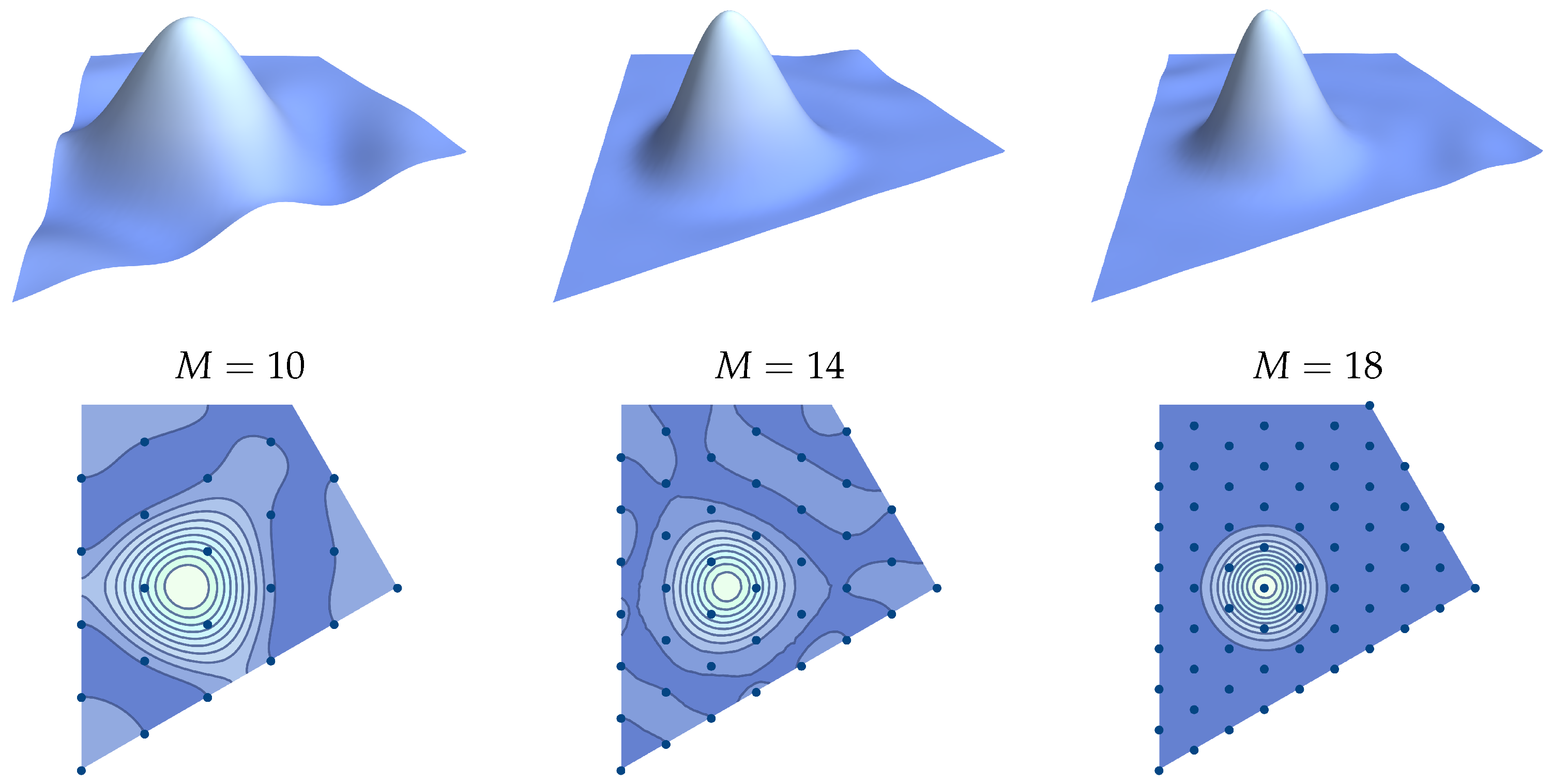
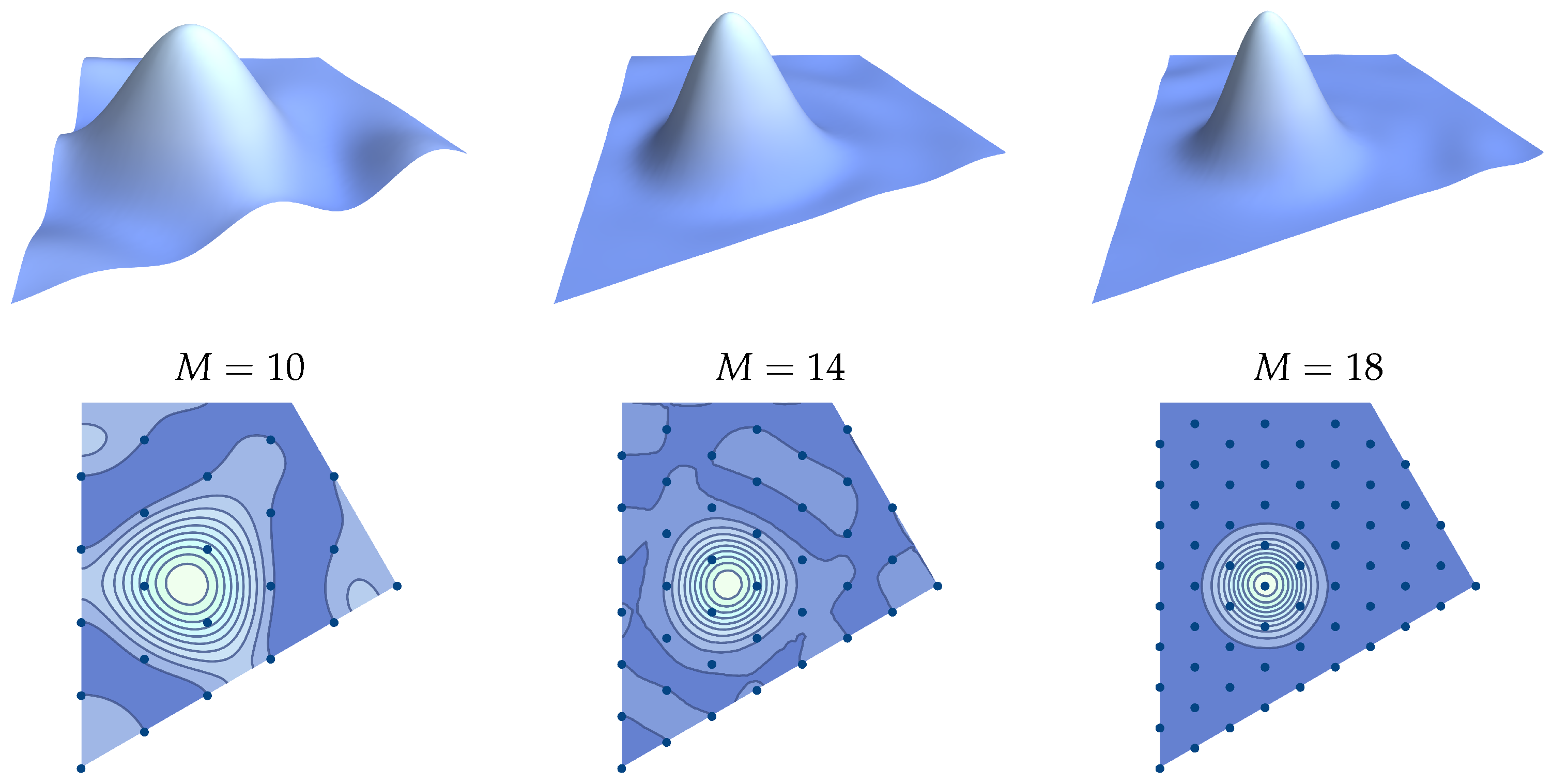
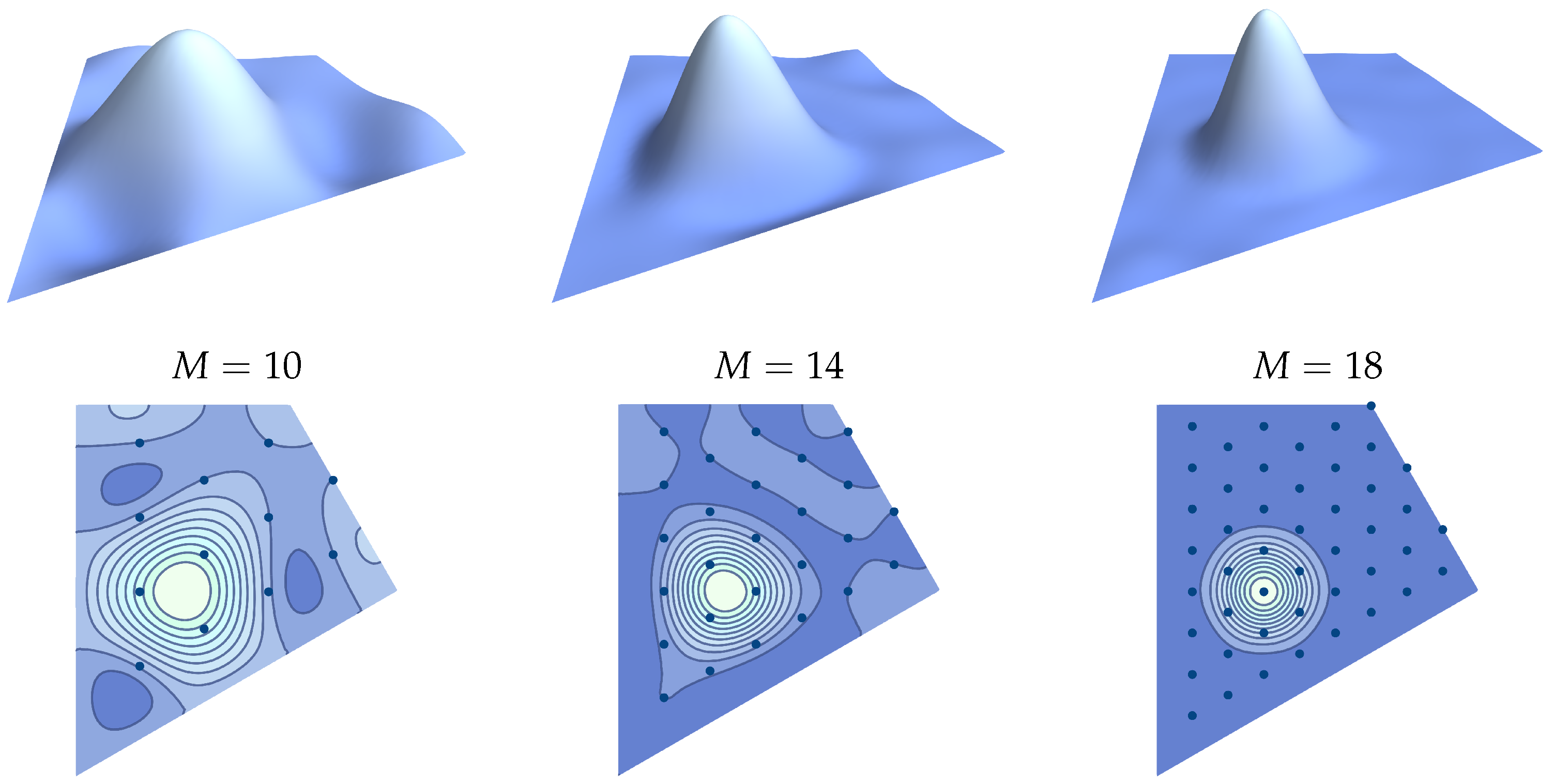
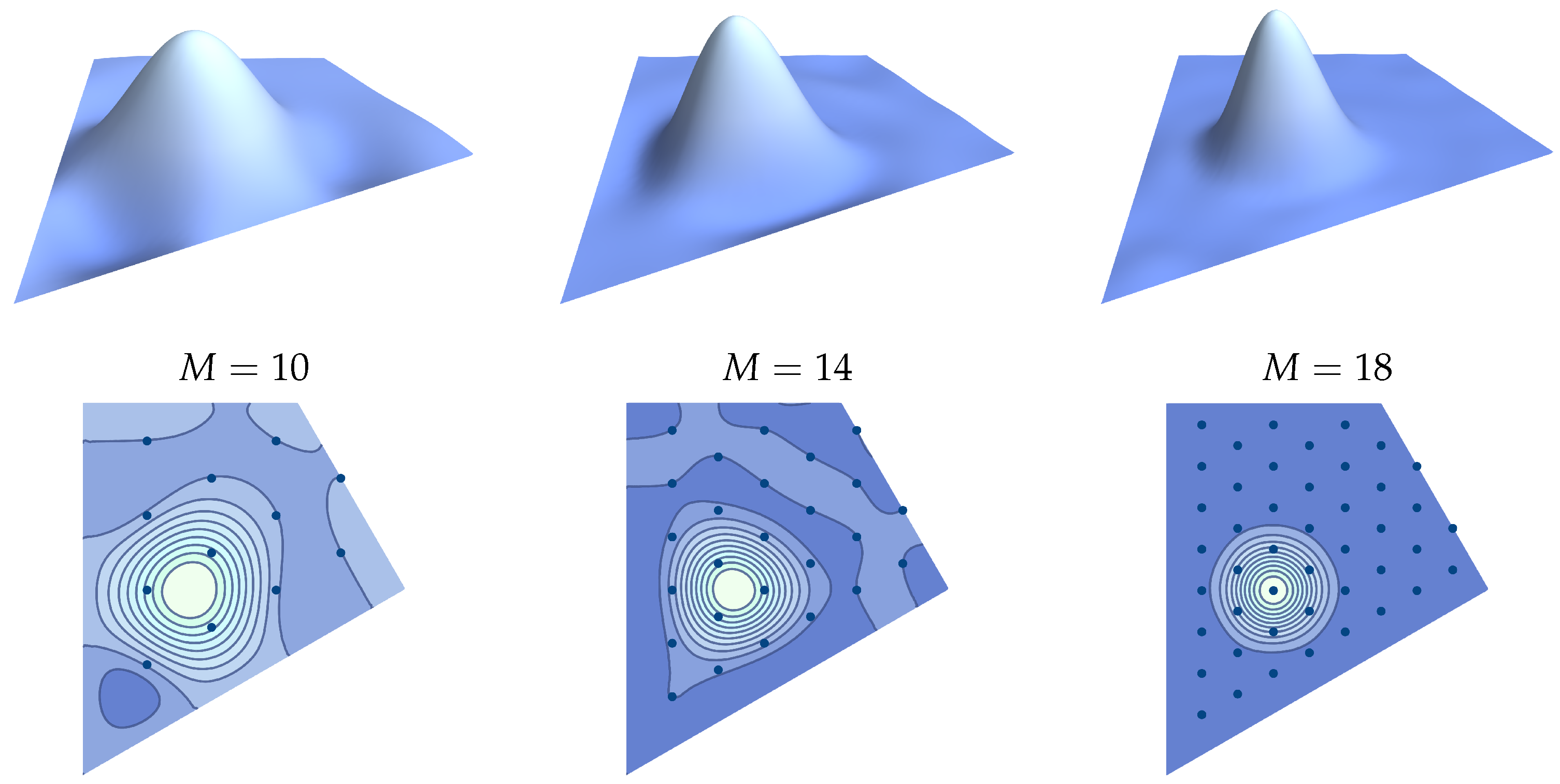
| M | 10 | 12 | 14 | 16 | 18 |
|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hrivnák, J.; Myronova, M.; Patera, J. Central Splitting of A2 Discrete Fourier–Weyl Transforms. Symmetry 2020, 12, 1828. https://doi.org/10.3390/sym12111828
Hrivnák J, Myronova M, Patera J. Central Splitting of A2 Discrete Fourier–Weyl Transforms. Symmetry. 2020; 12(11):1828. https://doi.org/10.3390/sym12111828
Chicago/Turabian StyleHrivnák, Jiří, Mariia Myronova, and Jiří Patera. 2020. "Central Splitting of A2 Discrete Fourier–Weyl Transforms" Symmetry 12, no. 11: 1828. https://doi.org/10.3390/sym12111828
APA StyleHrivnák, J., Myronova, M., & Patera, J. (2020). Central Splitting of A2 Discrete Fourier–Weyl Transforms. Symmetry, 12(11), 1828. https://doi.org/10.3390/sym12111828





