Abstract
In 1977, Nourein (Intern. J. Comput. Math. 6:3, 1977) constructed a fourth-order iterative method for finding all zeros of a polynomial simultaneously. This method is also known as Ehrlich’s method with Newton’s correction because it is obtained by combining Ehrlich’s method (Commun. ACM 10:2, 1967) and the classical Newton’s method. The paper provides a detailed local convergence analysis of a well-known but not well-studied generalization of Nourein’s method for simultaneous finding of multiple polynomial zeros. As a consequence, we obtain two types of local convergence theorems as well as semilocal convergence theorems (with verifiable initial condition and a posteriori error bound) for the classical Nourein’s method. Each of the new semilocal convergence results improves the result of Petković, Petković and Rančić (J. Comput. Appl. Math. 205:1, 2007) in several directions. The paper ends with several examples that show the applicability of our semilocal convergence theorems.
1. Introduction
This paper deals with the convergence of two iterative methods for finding all zeros of a polynomial simultaneously. The first one is due to Nourein [1] and it has quartic convergence when all zeros of the polynomial are simple and has linear convergence otherwise. The second one is a generalization of Nourein’s method for simultaneously finding all zeros of an arbitrary polynomial that has at least one multiple zero. To our knowledge, Nourein’s method for multiple zeros appears for the first time in the book of Sendov, Andreev and Kjurkchiev [2].
Throughout this paper, stands for a valued field with absolute value and denotes the ring of polynomials over .
Weierstrass’ method and elementary symmetric functions. Historically, the first iterative method for simultaneous finding all zeros of a polynomial was constructed by Weierstrass [3] in 1891. Let
be a polynomial in of degree . Furthermore, let us define the elementary symmetric functions , as follows:
It is well-known that a vector is a solution of the symmetric system
if and only if are all zeros of the polynomial f. Using this fact, Weierstrass [3] derived an iterative algorithm for solving the symmetric system (2). Weierstrass’s method is defined by the following iteration:
where the so-called Weierstrass correction is defined by
and is the set of all vectors in with pairwise distinct coordinates. Weierstrass’s method (3) has quadratic convergence when all zeros of f are simple and has linear convergence otherwise. For historical notes and advanced results for Weierstrass’s method, we refer to [4,5].
Ehrlich’s method. In 1967, Ehrlich [6] introduced a third-order simultaneous method defined by the following iteration:
where the iteration function is defined by with
In 1975, Börsch-Supan [7] presented another third-order simultaneous method. In 1982, Werner [8] proved that both Ehrlich’s and Börsch-Supan’s methods are identical. For historical notes and advanced results for Ehrlich’s method, we refer to [9,10,11].
Local and semilocal convergence analysis. Recently, a general convergence theory of iterative methods of the type , where is an iteration function of a metric space X, was developed in [12,13]. Central to this theory is the concept of the function of initial approximations (see ([13], Section 3)). Roughly speaking, this is a real-valued function that sets the initial conditions. The initial condition of any convergence theorem of an iterative method can be represented in the form
where J is an interval on of the form , or , where R is a positive number.
Convergence analysis of an iterative method always is done with respect to a function of the initial conditions E. The goal of convergence is to find initial guesses that guarantees convergence of the iteration sequence to to a fixed point of the iteration function T.
Definition 1.
A convergence analysis is called semilocal when the function of initial conditions E does not depend on the fixed point ξ and is local otherwise.
Semilocal convergence theorems have great practical applications because their initial conditions are computer-verifiable. In general, local convergence theorems have mainly theoretical significance. However, very recently in [14], it was proved that two kinds of local convergence theorems for iterative methods for simultaneous approximation of polynomial zeros can be transformed into semilocal convergence results.
Nourein’s method for simple zeros. There are different ways to increase the convergence order of an iterative method for simultaneous computation of polynomial zeros. In 1977, Nourein [1,15] constructed three simultaneous methods that increase the convergence order of Weierstrass’s, Ehrlich’s and Börsch-Supan’s methods. Each of these three methods was constructed as a combination of two already known iterative methods. In particular, combining Ehrlich’s method and the classical Newton’s method, Nourein [1] constructed in the following fourth-order iterative method (for simple zeros):
where the iteration function is defined by with
Nourein’s method (7) is also known as Ehrlich’s method with Newton’s corrections. As it is shown in Milovanović and Petković [16] and in Petković and Herceg [17], the iterative method (7) is one of the most efficient and powerful simultaneous methods with globally convergent performance.
In 1998, Petković, Herceg and Ilić [18] proved that the method (7) is convergent under the initial condition
where the function is defined by
In 2007, Petković, Petković and Rančić [19] (see also ([20], Theorem 3.10)) established the following improvement of this result.
Theorem 1
(Petković, Petković and Rančić [19]). Suppose is a polynomial of degree with simple zeros. If an initial approximation with distinct coordinates satisfies the condition
then Nourein’s iteration (7) is convergent with an order of convergence of four.
Nourein’s method for multiple zeros. Nourein’s method (7) has a well-known but not well-studied generalization for the simultaneous finding of multiple polynomial zeros. Let be a polynomial of degree which splits in , and let (s is a positive integer such that ) be all distinct zeros of f with multiplicity , respectively.
In what follows, we use a binary relation # on defined by
where .
Let us define Nourein’s method for polynomials that has at least one multiple zero. First, we define the Schröder’s iteration function by [21]:
where the domain of N is the set
Now the generalized Nourein’s method for simultaneously finding all the zeros of f is defined in by the following fixed-point iteration (see, e.g., ([2], Section 20) and ([22], Section 7.2)):
where the iteration function is defined by
and the domain of is the set
Contributions. In this paper, we present a detailed local convergence analysis for generalized Nourein’s method (11) for multiple zeros. As a consequence of these results, we obtain two types of local convergence theorems as well as semilocal convergence theorems (with verifiable initial condition and a posteriori error bound) for the classical Nourein’s method (7). Each of the new semilocal convergence results improves Theorem 1 in several directions.
The paper is structured as follows: Section 2 gives some notations that are used throughout the paper without specific quoting. In Section 3, we study the local convergence of generalized Nourein’s iteration (11) with respect to a function of initial conditions of the first kind. In this section, the main new result is Theorem 3. In Section 4, we study the convergence of generalized Nourein’s iteration (11) with respect to a function of initial conditions of the second kind. The main new result of this section is Theorem 5, which plays an important role in Section 7 for obtaining new semilocal convergence results for the classical Nourein’s method (7).
In Section 5, we present two new local convergence results of the first kind (Theorem 6 and Corollary 1) for the classical Nourein’s method (7). In Section 6, we obtain three new local convergence results of the second kind (Theorems 7 and 8 and Corollary 3) for the classical Nourein’s method (7).
To the best of authors’ knowledge, the theorems given in Section 3, Section 4, Section 5 and Section 6 are the first local convergence results in the literature about both Nourein’s methods (for simple or multiple zeros).
In Section 7, we provide three new semilocal convergence results for polynomials with simple zeros (Theorems 11 and 12 and Corollary 5). Each of these semilocal convergence results improves the result of Petković, Petković and Rančić [19] in several directions. Note that these results are based on some results given in [14] and some local convergence results obtained in the previous sections. Section 8 provides several numerical examples that show the applicability of our semilocal convergence theorems. Finally, the paper ends with a conclusion section.
2. Notations
In this short section, we give some notations that are used throughout the paper without specific quoting. We denote by and the real and the nonnegative numbers, respectively.
Let be equipped with partial coordinate-wise ordering defined by
and let the vector space be equipped with the norm
and with a vector norm (with values in ) defined by
Let and be two vectors. We denote by a vector in defined by
if y has only nonzero coordinates. We define a function by
Also, we define a function by
We assume by definition that . For two integers and , we define the quantity by
and if . In the short, we write
Throughout the paper, J denotes an interval on containing 0, that is, an interval of the form , or , where R is a positive number.
Definition 2
([13]). A function is said to be quasi-homogeneous of degree if
3. Local Convergence Theorem of the First Kind for Multiple Zeros
Let be a polynomial of degree which splits in , and let be all distinct zeros of f with multiplicity , respectively. In this section, we investigate the local convergence of Nourein’s iteration (11) with respect to a function of initial conditions defined as follows:
where . The function of initial conditions (15) has been used in [23,24,25] for studying the local convergence of the first kind of some iterative methods for simultaneous approximation of multiple polynomial zeros.
We define the quantities , and as follows:
where is defined by
We begin this section with some useful inequalities in which play an important role in the proofs of our results.
Lemma 1
Lemma 2.
Let and be three vectors such that
If is a vector with pairwise distinct coordinates, then for all , we have
where is defined by (15).
Proof.
From the triangle inequality in and the inequality (17), we obtain
which completes the proof. □
The following general convergence theorem plays a substantial role in our paper.
Theorem 2
(Proinov [26]). Let be an iteration function, and let be a vector with pairwise distinct coordinates, and let a function be defined by (15). Suppose is a quasi-homogeneous function of degree such that, for every vector with , the following conditions hold:
Let be an initial guess such that
Then the Picard iteration is well-defined and converges to ξ with order and with error estimates
where .
Before formulating the main result of this section, we need a few more lemmas.
Lemma 3
Lemma 4.
Let be a polynomial of degree which splits in , and let be all distinct zeros of f with multiplicity , respectively. Suppose a vector is such that for some i. Then
where the iteration function is given by (12) and is given by
Proof.
In this and the next section, we use the following polynomial functions:
where m, a and b are given by (16).
It is easy to show that each of the functions A and B strictly decreases on and has a unique zero which lies in the interval . If is the unique solution of the equation , then it can be shown that
Lemma 5.
Proof.
First we prove that . It follows from (25) that , which according to Lemma 3 shows that . We can apply Lemma 3 with since the inequality (17) holds with
Then by Lemma 2 and (25), we obtain
for all . Consequently, . Now suppose . According to (13), it remains to prove that
Using (20), we get that (30) holds true if and only if , where is given by (19). By the triangle inequality, Lemma 3, the second part of Lemma 1, the inequality (29), Hölder’s inequality and condition (25), we obtain for the following estimate:
which yields . Hence, . To prove (26), we have to show that
If , then and so (32) becomes an equality. Suppose . From Lemma 4 and the triangle inequality, we obtain
which completes the proof. □
We are ready now to state the first main result of this paper.
Theorem 3.
Let be a polynomial of degree which splits in , and let be all distinct zeros of f with multiplicity , respectively. Suppose is an initial guess satisfying the following condition:
where the functions E and B are defined by (15) and (22), respectively. Then Nourein’s iteration (11) is well-defined and converges with fourth-order to the root vector with the following error estimates:
where and the function ϕ is defined by (27).
Proof.
We shall apply Theorem 2 to the iteration function defined by (12). Let be the unique solution of the equation . The function is quasi-homogeneous of degree on . It follows from Lemma 5 that, for every vector with , we have and that the inequality (26) holds. Then it follows from Theorem 2 that, under the initial condition
the iteration (11) is well-defined and converges to with order and with error estimates (34). It is easy to see that the above initial condition is equivalent to (33). This completes the proof. □
4. Local Convergence Theorem of the Second Kind for Multiple Zeros
Let be a polynomial of degree which splits in , and let be all distinct zeros of f with multiplicity , respectively. In this section, we investigate the local convergence of Nourein’s iteration (11) with respect to the function of initial conditions defined as follows:
where . Recall that denotes the set of all vectors in with pairwise distinct coordinates. We note that the function of initial conditions (35) has been used in [23,24,25] to study the local convergence of the second kind of some iterative methods for finding simultaneously multiple polynomial zeros.
Lemma 6
([5], Lemma 7.1). Let . If x has pairwise distinct coordinates, then for all , the following inequalities hold:
where is defined by (35).
Lemma 7
Theorem 4
(Proinov [26]). Let be an iteration function, be a vector, and let a function be defined by (35). Suppose is a nonzero quasi-homogeneous function of degree such that, for any with , we have
Let be an initial guess such that
where the function is defined by
Then the Picard iteration is well-defined and converges to ξ with error estimates
where , , and the functions ψ and ϕ are defined by
Besides, if the inequality in (36) is strict, then the order of convergence is at least r.
Now, we define the real functions as follows:
where a, b and m are defined by (16). Let be the unique zero of the function A, where A is defined by (21). It is easy to show that strictly increases on and that it is quasi-homogeneous of degree on . The function strictly decreases and it has a unique zero on because and . On the other hand, for every , where the functions A and Q are defined by (21) and (23). Thus, we conclude that the function Q has a unique zero on too.
Analogously to Lemma 3, we can prove the following lemma:
Lemma 8.
Proof.
The first part of (40) follows from the first part of Lemma 3. The second part of (40) is equivalent to
for every . If , then (41) holds trivially. Suppose that . Then it is easy to show that
where
From the triangle inequality and Lemma 6, we obtain
From (43), we obtain the following estimate:
From (42) and the estimates (43) and (44), we get (41), which completes the proof. □
Lemma 9.
Proof.
The proof is carried out in the same way as the proof of Lemma 5 using Lemma 6, Lemma 7 and Lemma 9 instead of Lemma 1, Lemma 2 and Lemma 3, respectively. □
Now, we are ready to state and prove the main result in this section.
Theorem 5.
Let be a polynomial of degree which splits in , and let be all distinct zeros of f with multiplicity , respectively. Suppose is an initial guess with distinct coordinates which satisfies the following conditions:
where the functions E, A and Q are defined by (35), (21) and (23), respectively. Then the iteration (11) is well-defined and converges to ξ with error estimates
where , , and ψ is defined by (39). Moreover, if the second inequality in (47) is strict, then the convergence order is at least four.
Proof.
We shall apply Theorem 4 to the iteration function defined by (12). Let be the unique positive solution of the equation . The function is quasi-homogeneous of degree on . It follows from Lemma 9 that, for every vector with , we have and the inequality (46) holds. Then it follows from Theorem 4 that under the initial condition
the iteration (11) is well-defined and converges to with order and with error estimates (48). Taking into account that , we can see that the initial conditions (47) and (49) are equivalent. This completes the proof. □
5. Local Convergence Theorem of the First Kind for Simple Zeros
Let be a polynomial of degree which has n simple zeros in , and let be a root vector of the polynomial f. In this section, we study the local convergence of the classical Nourein’s method (7) with respect to the function of initial conditions defined by
Now the real functions A, B, Q and , considered in Section 3, take the following forms:
where a and b are defined by
As a consequence of Theorem 3, we get the following two convergence results for simple zeros.
Theorem 6.
Let be a polynomial of degree which has n simple zeros in , and let be a root vector of f. Suppose that is an initial guess satisfying the following condition:
where the functions E and B are defined by (50) and (52), respectively. Then Nourein’s iteration (7) is well-defined and converges with fourth-order to ξ with the following error estimates:
where and the function ϕ is defined by (54).
Corollary 1.
Let be a polynomial of degree that has n simple zeros in , and let be a root vector of f. If is an initial guess satisfying
then Nourein’s iteration (7) is well-defined and converges with fourth-order to ξ with error estimates
where the real function ϕ is defined by
Proof.
The following convergence result is an immediate consequence of Corollary 1.
Corollary 2.
Remark 1.
For the first time, an initial condition of the type (58) was presented by Dochev [28]. He has proved that, if is a polynomial of degree and has only simple zeros, then Weierstrass’s iteration (3) is well-defined and convergent quadratically to a root vector of f under the initial condition
where the function δ is defined by (14).
For other local convergence theorems of the first kind for other simultaneous iterative methods, we refer to [5,9,29,30,31,32,33].
6. Local Convergence Theorem of the Second Kind for Simple Zeros
Let be a polynomial of degree that has n simple zeros in and let be a root vector of f. We study the convergence of the classical Nourein’s method (7) with respect to a function of initial conditions defined by
Applying Theorem 5 to the polynomials with simple zeros, we get the following convergence theorem.
Theorem 7.
Let be a polynomial of degree that has n simple zeros in , and let be a root vector of f. Suppose that is an initial guess with distinct coordinates which satisfies the following condition:
where the functions E and Q are defined by (59) and (53), respectively. Then Nourein’s iteration (7) is well-defined and converges to ξ with error estimates
where , and the functions ϕ and ψ are defined by (62). Moreover, if the second inequality in (63) is strict, then the rate of convergence is of order four.
In the case , as a consequence of Theorem 5, we obtain the next two results. Now, we define the function of initial conditions by
Theorem 8.
Let be a polynomial of degree that has n simple zeros in , and let be a root vector of f. Suppose that is an initial guess with distinct coordinates which satisfies the following condition:
where the function E is defined by (65) and the function Q is defined by
Proof.
According to Theorem 7, we have to prove that . It can be proved that Q strictly decreases on , and . Hence, Q has a unique zero R on . Then it follows from (66) that
On the other hand, we have mentioned above that the function Q has a unique zero on . Consequently, . Then we deduce that , which yields . This completes the proof. □
Corollary 3.
Let be a polynomial of degree that has n simple zeros in , and let be a root vector of f. Suppose that is an initial guess with distinct coordinates which satisfies the following initial condition:
where the function E is defined by (65). Then Nourein’s iteration (7) is well-defined and converges to ξ with order of convergence four and with error estimates (64).
Proof.
In view of Theorem 8, we have to show that satisfies the initial condition (66). We shall prove the second inequality in (66) because the first one is trivial. From condition (68) and the fact that Q defined by (67) strictly decreases on , we obtain
Hence, the condition (66) is satisfied, which completes the proof. □
From Corollary 3, we immediately obtain the following convergence result.
Corollary 4.
Let be a polynomial of degree that has n simple zeros and let be a root vector of f. Suppose is a vector with distinct coordinates satisfying the initial condition
where the function δ is defined by (14). Then Nourein’s iteration (7) is well-defined and converges to ξ with order of convergence four.
Remark 2.
For the first time, an initial condition of the type (69) was presented by Wang and Zhao [34]. They proved that, if is a polynomial of degree and has only simple zeros, then Ehrlich’s iteration (5) is well-defined and convergent cubically to a root vector of f under the initial condition
where the function δ is defined by (14).
For local convergence of the second kind for other iterative method, we refer to [5,9,27,29,31,32,35].
7. Semilocal Convergence Analysis for Simple Zeros
In this section, we establish three semilocal convergence theorems for the classical Nourein’s method (7). Each of these results improves Theorem 1 in several directions.
Let be a polynomial of degree . We study the convergence of the method (7) with respect to the function of initial conditions defined by
where the operator is defined by (4). We define a relation of equivalence ≡ on by if there exists a permutation of the indexes such that
Now, we can define a distance between two vectors as follows [32,33]:
For proof of the main theorem of this section, we need two results from [14]. In order to make the paper self-contained, we include recall of these results.
Theorem 9
([14], Theorem 5.1). Let be an algebraically closed field and let be a polynomial of degree . Suppose that is a vector with distinct coordinates satisfying
where a is defined by (55). Then f has only simple zeros and there exists a root vector of f such that
where the distance function ρ is defined by (71) and the real functions are defined by
We note that the functions and h strictly increase on , where is defined by (72).
Theorem 10
([14], Theorem 5.2). Let be algebraically closed field, and let be a polynomial of degree . Suppose that is a vector with distinct coordinates such that
and , where is defined by (4) and a is defined by (55). Then polynomial f has only simple zeros in and there exists a root vector of f such that
where the function α is defined by (74).
Now, we can state and prove the main results of this paper.
Theorem 11.
Let be an algebraically closed field. and let be a polynomial of degree . Suppose that is an initial guess with distinct coordinates satisfying
where a is defined by (55) and the functions , A, Q and h are defined by (70), (51), (53) and (74), respectively. Then f has only simple zeros in and Nourein’s iteration (7) is well-defined and converges to a root vector ξ of f with order of convergence four and with a posteriori error estimate
where the distance function ρ is defined by (71), τ is defined by (72) and the real function α is defined by (74).
Proof.
First, we note that the function h is defined on by (74), where is defined by (72). It follows from the first inequality of (77) that
Then by Theorem 9, it follows that f has n simple zeros in and there exists a root vector of f such that
where the function is defined by (59). From the second inequality of (77), we conclude that , where is the unique solution of the equation . Now from (79), we conclude that , which yields the inequality
Define the real function on by (61). From the inequality (79), taking into account that the functions strictly decreases on , we obtain which implies
since and for every . Hence, the initial guess satisfies the condition (63). Now, it follows from Theorem 7 that the iteration (7) is well-defined and converges to with order of convergence four. The error estimate (78) follows from Theorem 9. □
Furthermore, we shall consider two semilocal convergence results in the case . In this case, the function of initial conditions is defined by
and the functions and h are defined on by
where is defined by
The distance function is defined on by
Let us define a real function as follows
where Q and h are defined by (67) and (81), respectively.
Theorem 12.
Let be an algebraically closed field, and let be a polynomial of degree . Suppose that is an initial guess with distinct coordinates satisfying
where the functions and Ω are defined by (80) and (84), respectively. Then f has only simple zeros in and Nourein’s iteration (7) is well-defined and converges to a root vector ξ of f with order of convergence four and with a posteriori error estimate
where the distance function ρ is defined by (83), τ is defined by (82) and the real function α is defined by (81).
Proof.
It follows from the first inequality of (85) that , where is defined by (82). By Theorem 9, we conclude that f has only simple zeros and there exists a root vector of f such that where the function is defined by (65). Then by monotonicity of h, we get
From this and the second inequality in (77), taking into account that Q is strictly decreasing on , we obtain
It follows from Theorem 8 that the iteration (7) is well-defined and converges to with order of convergence four. The error estimate (86) follows from the Theorem 9. □
Using Corollary 3 and Theorem 10, we obtain the next semilocal result.
Corollary 5.
Let be an algebraically closed field and be a polynomial of degree . Suppose that is an initial guess with distinct coordinates satisfying
where the function E is defined by (80). Then f has only simple zeros in and Nourein’s iteration (7) is well-defined and converges to a root vector ξ of f with order of convergence four and with a posteriori error estimate (86).
Proof.
The initial condition (87) can be represented in the form (75) with R defined by
It is easy to check that . Then it follows from Theorem 10 that f has only simple zeros in and there exists a root vector of f such that
where the function is defined by (65). Now, Corollary 3 implies that Nourein’s iteration (7) converges to with order of convergence four. As we have mentioned in the proof of the previous theorem, the error estimate (86) follows from the Theorem 9. This ends the proof. □
Remark 3.
We note that each of our semilocal convergence results (Theorems 11 and 12 and Corollary 5) improves and complements (with a posteriori error estimate) the result of Petković, Petković and Rančić [19] (see Theorem 1 above). In particular, they give larger convergence domains than Theorem 1 and they do not require in advance the simplicity of the zeros of f. For instance, let us prove that Corollary 5 is an improvement of Theorem 1. Let an initial vector satisfies the initial condition (8). Then,
which shows that the initial condition (87). Hence, it follows from Corollary 5 that the conclusion of Theorem 1 holds.
Semilocal convergence of the same kind as above results can be found in [5,27,31,32,33,35,36].
8. Numerical Examples
In this section, we present three numerical examples to show the applicability of Theorem 12. Let be a polynomial of degree , and let be an initial guess. Starting from the vector , we generate Nourein’s iterative sequence for the polynomial f. Each of our semilocal convergence results (Theorem 11 and 12 and Corollary 5) gives the following two very useful criteria:
- Convergence criterion that determines whether Nourein’s method is convergent.
- Accuracy criterion that determines whether Nourein’s method has reached a preset accuracy . It can be used as stopping criterion.
Below, we consider the criteria obtained from Theorem 12. As in the previous sections, we define the functions , , and by (4), (80), (81) and (84), respectively.
Convergence criterion. If there exists an integer such that
then f has only simple zeros and Nourein’s iteration (7) starting from is well-defined and converges to a root vector of f with order of convergence four. In each example, we calculate the smallest m that satisfies convergence criterion (88).
Accuracy criterion (stopping criterion). Let . If there exists an integer , such that
then the iterate approximates the vector of zeros of f with accuracy . Moreover, the guaranteed accuracy is . Indeed, according to Theorem 11, we have
where the distance function is defined by (71) and is a root vector of f. In each example, we calculate the smallest k that satisfies accuracy criterion (89) with
In the examples, we apply Nourein’s method to three monic polynomials f of degree taken from [17]. In each example, we choose two types of very crude initial approximations as follows:
First type of initial approximations. For a monic polynomial
of degree , we choose the coordinates of the initial vector by Aberth’s formula [37]:
where is a parameter.
The Aberth’s initial approximations are equidistantly spaced on the circle with radius with center and radius . We take very crude Aberth’s approximations on the circle with radius for Example 1 and for Examples 2 and 3.
Second type of initial approximations. We choose the coordinates of the initial vector randomly in the square
where is the same as in the previous type of initial approximations.
We use CAS Wolfram Mathematica 11 to implement the corresponding algorithms and to present approximations of higher accuracy.
Example 1.
Let us consider Wilkinson’s ill-conditioned polynomial, often a hard nut to crack for most methods:
Our random initial guess for Example 1 is
Example 2.
Consider the following polynomial with clusters
The random initial guess for Example 2 is
Example 3.
Consider the polynomial with ring zeros:
The random initial guess for Example 3 is
Numerical results. In Table 1 are presented the results for the considered examples, we exhibit the values of m, , , k and . We recall that:

Table 1.
Numerical results.
- m is the smallest nonnegative integer that satisfies the convergence criterion (88);
- is defined in (89) and denotes the guaranteed accuracy (by Theorem 12) for the approximation of the zeros of f;
- k is the smallest nonnegative integer that satisfies convergence accuracy criterion (89) with the preset accuracy ;
- is the guaranteed accuracy (Theorem 12) for the approximation of the zeros of f.
It can be seen from the table that, in all six experiments, Theorem 12 guarantees that Nourein’s method (7) is convergent under the given very rough initial approximations. Also it shows on which iteration that the preset accuracy is reached.
For instance, for Example 1, under the first initial approximation, it is seen that the convergence criterion (88) is satisfied for and that the accuracy criterion (89) is satisfied for , which means that the preset accuracy is reached. Moreover, the table shows that, at 33 iterations, Theorem 12 guarantees an accuracy of and at 34 iterations, it guarantees that each of the roots of the polynomial (91) is calculated with a guaranteed accuracy of .
In Figure 1, Figure 2 and Figure 3, we present the trajectories of approximations in the complex plane with different colors. For the random initial guess (second type), all initial approximations are numbered and colored by blue. From these figures, one can observe that all trajectories starting with Aberth’s initial approximations have regular paths. However, it is not necessary that the initial approximations lie in an inclusion disk with a minimum radius to have this nice and regular form. About the second type of initial approximations, one can see that some initial points during iterating are not going to the nearest zero of the polynomial.
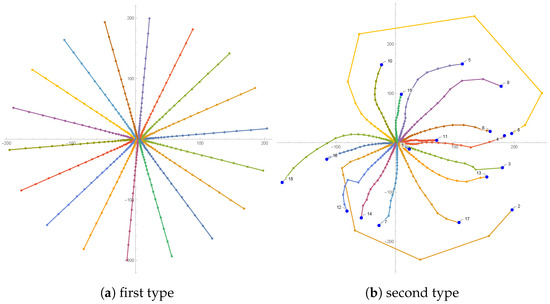
Figure 1.
Trajectories of approximations for Example 1.
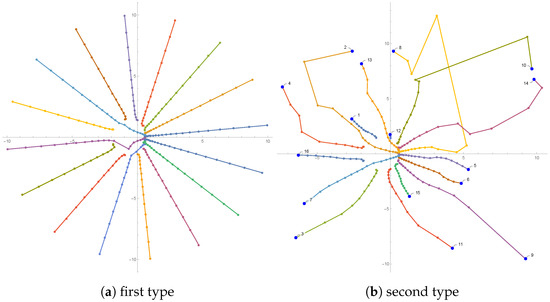
Figure 2.
Trajectories of approximations for Example 2.
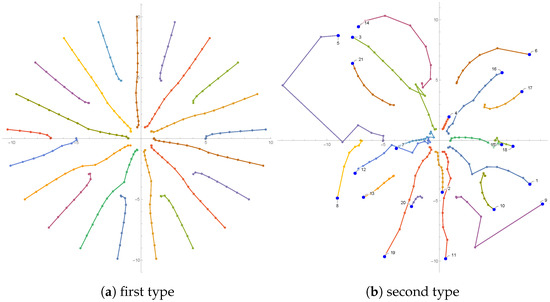
Figure 3.
Trajectories of approximations for Example 3.
9. Conclusions
In this paper, we studied the convergence of two well-known iterative methods for finding all zeros of a polynomial simultaneously. The first one is due to Nourein [1] and it has quartic convergence when all zeros of the polynomial are simple. It is also known as Ehrlich’s method with Newton’s corrections because it is obtained by combining Ehrlich’s method [6] and the classical Newton’s method. The second one is a generalization of Nourein’s method for simultaneously finding all zeros of a polynomial that has at least one multiple zero. To our knowledge, it appears for the first time in the book of Sendov, Andreev and Kjurkchiev [2].
We have proved several new local and semilocal convergence theorems (Theorems 6–8, 11 and 12) for the classical Nourein’s method (7) under different initial conditions. The initial conditions and error bounds of the semilocal convergence results (Theorems 11 and 12) are computationally verifiable, which is of practical importance. Each of our semilocal convergence results improves the previous result due to Petković, Petković and Rančić [19] in several directions. We note that our approach to semilocal convergence analysis is different from those of the previous authors [18,19]. In Section 8, we present several numerical examples that show the applicability of our semilocal convergence results.
We have obtained two new local convergence theorems (Theorems 3 and 5) for the generalized Nourein’s method (11) under different initial conditions. To the best of authors’ knowledge, our local convergence theorems are the first local convergence results in the literature about Nourein’s method (for simple or multiple zeros).
Author Contributions
The authors contributed equally to the writing and approved the final manuscript of this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Science Fund of the Bulgarian Ministry of Education and Science under grant DN 12/12.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nourein, A.W.M. An improvement on two iteration methods for simultaneous determination of the zeros of a polynomial. Intern. J. Comput. Math. 1977, 6, 241–252. [Google Scholar] [CrossRef]
- Sendov, B.; Andreev, A.; Kjurkchiev, N. Numerical Solution of Polynomial Equations. In Handbook of Numerical Analysis; Ciarlet, P., Lions, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1994; Volume III, pp. 625–778. [Google Scholar] [CrossRef]
- Weierstrass, K. Neuer Beweis des Satzes, dass jede ganze rationale Function einer Veränderlichen dargestellt werden kann als ein Product aus linearen Functionen derselben Veränderlichen. Sitzungsber. Königl. Akad. Wiss. Berlin 1891, II, 1085–1101. [Google Scholar] [CrossRef]
- Proinov, P.D.; Petkova, M.D. A new semilocal convergence theorem for the Weierstrass method for finding zeros of a polynomial simultaneously. J. Complex. 2014, 30, 366–380. [Google Scholar] [CrossRef]
- Proinov, P.D. General convergence theorems for iterative processes and applications to the Weierstrass root-finding method. J. Complex. 2016, 33, 118–144. [Google Scholar] [CrossRef]
- Ehrlich, L. A modified Newton method for polynomials. Commun. ACM 1967, 10, 107–108. [Google Scholar] [CrossRef]
- Börsch-Supan, W. Residuenabschätzung für Polynom-Nullstellen mittels Lagrange Interpolation. Numer. Math. 1970, 14, 287–296. [Google Scholar] [CrossRef]
- Werner, W. On the simultaneous determination of polynomial roots. Lect. Notes Math. 1982, 953, 188–202. [Google Scholar]
- Proinov, P.D. On the local convergence of Ehrlich method for numerical computation of polynomial zeros. Calcolo 2016, 53, 413–426. [Google Scholar] [CrossRef]
- Proinov, P.D. A general semilocal convergence theorem for simultaneous methods for polynomial zeros and its applications to Ehrlich’s and Dochev-Byrnev’s methods. Appl. Math. Comput. 2016, 284, 102–114. [Google Scholar] [CrossRef]
- Shemyakov, S.; Chernov, R.; Rumiantsau, D.; Schleicher, D.; Schmitt, S.; Shemyakov, A. Finding polynomial roots by dynamical systems—A case study. Discret. Contin. Dyn. Syst. Ser. A 2020, 40, 6845–6965. [Google Scholar] [CrossRef]
- Proinov, P.D. General local convergence theory for a class of iterative processes and its applications to Newton’s method. J. Complex. 2009, 25, 38–62. [Google Scholar] [CrossRef]
- Proinov, P.D. New general convergence theory for iterative processes and its applications to Newton Kantorovich type theorems. J. Complex. 2010, 26, 3–42. [Google Scholar] [CrossRef]
- Proinov, P.D. Relationships between different types of initial conditions for simultaneous root finding methods. Appl. Math. Lett. 2016, 52, 102–111. [Google Scholar] [CrossRef]
- Nourein, A.W. An improvement on Noureins method for the simultaneous determination of the zeros of a polynomial (an algorithm). J. Comput. Appl. Math. 1977, 3, 109–110. [Google Scholar] [CrossRef][Green Version]
- Milovanović, G.; Petković, M. On computational efficiency of the iterative methods for simultaneous approximation of polynomial zeros. ACM Trans. Math. Softw. 1986, 12, 295–306. [Google Scholar] [CrossRef]
- Petković, I.; Herceg, Đ. Computer methodologies for comparison of computational efficiency of simultaneous methods for finding polynomial zeros. J. Comput. Appl. Math. 2020, 368, 112513. [Google Scholar] [CrossRef]
- Petković, M.; Herceg, Đ.; Ilić, S. Point estimation and some applications to iterative methods. BIT Numer. Math. 1998, 38, 112–126. [Google Scholar] [CrossRef]
- Petković, M.S.; Petković, L.D.; Rančić, L.Z. Point estimation of simultaneous methods for solving polynomial equations: A survey (II). J. Comput. Appl. Math. 2007, 205, 32–52. [Google Scholar] [CrossRef]
- Petkovic, M. Point Estimation of Root Finding Methods; Lecture Notes in Mathematics; Springer: Berlin, Germany, 2008; Volume 1933. [Google Scholar] [CrossRef]
- Schröder, E. Über unendlich viele Algorithmen zur Autlösung der Glleichungen. Math. Anal. 1870, 2, 317–365. [Google Scholar] [CrossRef]
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint Methods for Solving Nonlinear Equations; Elsevier/Academic Press: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Proinov, P.D.; Cholakov, S.I. Convergence of Chebyshev-like method for simultaneous approximation of multiple polynomial zeros. Compt. Rend. Acad. Bulg. Sci. 2014, 67, 907–918. [Google Scholar]
- Proinov, P.D. On the local convergence of Gargantini-Farmer-Loizou method for simultaneous approximation of multiple polynomial zeros. J. Nonlinear Sci. Appl. 2018, 11, 1045–1055. [Google Scholar] [CrossRef]
- Proinov, P.D.; Vasileva, M.T. On the convergence of high-order Gargantini-Farmer-Loizou type iterative methods for simultaneous approximation of polynomial zeros. Appl. Math. Comput. 2019, 361, 202–214. [Google Scholar] [CrossRef]
- Proinov, P.D. Unified convergence analysis for Picard iteration in n-dimensional vector spaces. Calcolo 2018, 55, 6. [Google Scholar] [CrossRef]
- Proinov, P.D.; Vasileva, M.T. On the convergence of high-order Ehrlich-type iterative methods for approximating all zeros of a polynomial simultaneously. J. Inequal. Appl. 2015, 2015, 336. [Google Scholar] [CrossRef]
- Dochev, K. A variant of Newton’s method for the simultaneous approximation of all roots of an algebraic equation. Phys. Math. J. Bulg. Acad. Sci. 1962, 5, 136–139. [Google Scholar]
- Cholakov, S.I. Local convergence of Chebyshev-like method for simultaneous finding polynomial zeros. Comp. Rend. Acad. Bulg. Sci. 2013, 66, 1081–1090. [Google Scholar]
- Cholakov, S.I.; Petkova, M.D. On the convergence of a fourth-order method for simultaneous finding polynomial zeros. Indian J. Appl. Res. 2015, 5, 397–402. [Google Scholar]
- Cholakov, S.I. Local and semilocal convergence of Wang-Zheng’s method for simultaneous finding polynomial zeros. Symmetry 2019, 11, 736. [Google Scholar] [CrossRef]
- Proinov, P.D.; Ivanov, S.I. Convergence analysis of Sakurai-Torii-Sugiura iterative method for simultaneous approximation of polynomial zeros. J. Comput. Appl. Math. 2019, 357, 56–70. [Google Scholar] [CrossRef]
- Proinov, P.D.; Petkova, M.D. Local and semilocal convergence of a family of multi-point Weierstrass-type root-finding methods. Mediterr. J. Math. 2020, 17, 107. [Google Scholar] [CrossRef]
- Wang, D.R.; Zhao, F.G. Complexity analysis of a process for simultaneously obtaining all zeros of polynomials. Computing 1989, 43, 187–197. [Google Scholar] [CrossRef]
- Cholakov, S.I.; Vasileva, M.T. A convergence analysis of a fourth-order method for computing all zeros of a polynomial simultaneously. J. Comput. Appl. Math. 2017, 321, 270–283. [Google Scholar] [CrossRef]
- Ivanov, S.I. A unified semilocal convergence analysis of a family of iterative algorithms for computing all zeros of a polynomial simultaneously. Numer. Algorithms 2017, 75, 1193–1204. [Google Scholar] [CrossRef]
- Aberth, O. Iteration methods for finding all zeros of a polynomial simultaneously. Math. Comput. 1973, 27, 339–344. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).