1. Introduction
The rapid development of inter-networking technology can gather data from many sources, such as, the Internet of Things, social networks, websites, health-related systems, and mobile devices, to name a few. The increment of the usage requirements and types of the device causes the number of attributes to rise. The increase in data volume is usually due to storage in real-time. The historical data will be used to assist in decision-making processes [
1,
2], in which a popular tool is machine learning (ML). However, the increased data attributes may lead to redundancy and irrelevance, resulting in the efficiency of an algorithm [
3].
Generally, the feature extraction/representation modules and the classification are two main processing steps of ML [
3]. Since the first step may produce high redundant or irrelevant data, selecting the data with essential features and deleting irrelevant features before feeding them to the classification step can increase efficiency and accuracy [
2]. The decrease in the number of high-dimensional data features makes it challenging to design an efficient algorithm because the computational complexity is very high [
2]. However, this challenge is worthy. A metaheuristic algorithm is usually an exploration-oriented population-based algorithm and development-oriented search algorithm [
4]. For the past decade, metaheuristic algorithms, which are superior to precise search and random search, have been widely used for feature selection. Though it might not be the best solution to the problem, the algorithm allows the user to produce an acceptable solution within a limited time [
5]. Many search options have been applied to feature selection. Several articles reviewed metaheuristic algorithms for feature selection, such as References [
2,
3,
6].
Particle swarm optimization (PSO) is a highly cited and generally widely used metaheuristic algorithm [
6]. PSO is in the group of swarm algorithms. Recently, competitive swarm optimization (CSO), which is a significant variant of PSO, was proposed by Chen and Jin [
7]. Based on the numerical benchmarks function in Reference [
7], CSO performs well at large-scale numerical optimization problems. The critical steps of CSO are competition and update steps. The competition divides the population into winners and losers: the winners continue in further iterations, while the losers are updated. CSO has a lower computational cost than PSO because only half of its population is evaluated and updated. CSO has been improved to increase its efficiency [
8,
9,
10]. Furthermore, CSO has been used to solve other problems, such as feature selection [
11,
12], to increase the efficiency of extreme learning machines [
13], and for applications in cyber-physical systems [
14]. These are shreds of evidence showing the excellent ability of the CSO algorithm in the literature. Based on PSO and CSO’s comparison, conducted on six datasets, in the feature selection of high-dimensional classification [
12], PSO decreased efficiency when the data dimension is high, while the CSO did not.
A nonlinear phenomenon called chaos has been used to enhance several metaheuristic algorithms. For instance, the CPSO algorithm is PSO with embedded chaos [
15]. It outperformed the original PSO. Chaotic sequences help PSO efficiently balance the exploration and exploitation abilities [
15], and the search capability of the algorithm increases when optimizing complex high-dimensional functions [
16]. Furthermore, chaos can improve other swarm algorithms [
17,
18,
19,
20,
21].
The hybridization of metaheuristic algorithms could also improve their performance compared to the canonical algorithms [
22]. An exciting algorithm for hybridizing with a metaheuristic algorithm is the simulated annealing (SA) algorithm. SA enables local search and dramatically enhances local optimal hybrid algorithms [
4].
In this study, we suppose that a dataset has
n attributes; in other words, the dataset has a length of
n. The critical point of feature selection is identifying the solution in
. The complexity of this problem is very high [
2]. However, a metaheuristic optimization algorithm can optimize for an acceptable solution. The optimization algorithms work on real values. Therefore, each particle’s value must be mapped to the range of (0, 1) to produce a binary solution. A “0” means the feature is not selected, and a “1” means the corresponding attribute is chosen. For example, an explanation of a dataset of length 6 with a value of “001101” is that attributes 3, 4, and 6 are selected, and the rest are discarded. For any two different solutions producing the same accuracy, fewer 1 s, aka a more compact solution, is preferable. Therefore, we propose a new asymmetric chaotic map to use for generating new particles in CSO. This chaotic map distribution is asymmetric and right-skewed, producing zero value with a higher probability than one value.
Other than applying the original CSO algorithm to solve binary optimization problems with high dimensions, the main contributions of this paper are as follows:
We propose a novel feature selection method based on an embedding of the proposed asymmetric chaotic map in CSO. The proposed method can deal with high-dimensional problems effectively. This paper is the first work combining asymmetric chaotic CSO.
The proposed method is compared with wrapper feature selection methods based on other swarm optimization algorithms in terms of classification accuracy and the selected feature subset’s compactness.
A graphical competitive magic quadrant is used to depict the ability of the proposed method.
This paper is organized as follows.
Section 1 introduces the overall background of the study and presents other related studies. The materials and methods used in this study are described in
Section 2. The proposed method is elaborated in
Section 3.
Section 4 presents and discusses the experiments and results. Finally,
Section 5 presents the conclusions.
3. The Proposed Asymmetric Chaotic Competitive Swarm Optimization
This section describes the development of the proposed asymmetric chaotic map. The proposed chaotic map is used to develop an asymmetric chaotic CSO (ACCSO) algorithm and an ACCSO followed by SA algorithm (ACCSO-SA).
3.1. The Proposed Asymmetric (Right-Skewed) Chaotic Map
Existing PSO variants attempt to modify the global best solution, resulting in only limited performance [
7]. CSO has also been done on developing PSO. However, CSO has shown performance for the high-dimensional data. In CSO, the new particles are usually updated from the loser’s velocity vectors using three uniform random vectors:
. This paper proposes an asymmetric chaotic map based on a combination of Kent map and the neuron map for producing those three vectors. The existing Kent map, which is computed by Equation (3) and produces values in (0, 1), has been used in many applications [
24]. Similarly, neuron map chaos, which is computed by Equation (4) and generates values in (−1.5, 0.5), has achieved excellent performance on several vital benchmarks [
23]. The proposed chaotic map generates chaotic sequences in (0, 1), and a new map is formed as Equation (5). Switching between the Kent map and the neuron map is controlled by the parameter
, defined as 0.72 in this paper.
Kent map, Equation (3), generates sequences in (0, 1) if 0 <
< 1.
Neuron map, Equation (4), generates sequences in (−1.5, 0.5) if
η = 0.5,
γ = 5, where
η and
γ denote the attenuation factor and proportionality factor, respectively.
The proposed asymmetric chaotic map, Equation (5), generates sequences in (0, 1) if 0 < < 1.
Figure 1a shows a histogram of the Kent map, and
Figure 1b shows a histogram of the neuron map. The histogram and examples of chaotic sequences produced by the proposed chaotic map are shown in
Figure 2a,b, respectively.
The incorporation of the two chaotic maps results in a new hybrid chaotic map that is different from the neuron map and Kent map. The Kent map histogram illustrates a nearly uniform structure ranging from 0 to 1. The neuron map histogram structure roughly shows three clusters ranging from −1.5 to 1. The histogram of the proposed chaotic map shown in
Figure 2a depicts an asymmetric chaos histogram structure and is in a step shape.
Figure 2b suggests that the proposed chaotic map sequences range from 0 to 1. Though the asymmetric chaos map generates values in the range of (0, 1), it has the highest possibility of generating values in the range of (0.3, 0.4), whereas values in the range of (0, 0.077) are scarce.
Feature selection is a binary and high-dimensional problem. The values generated from each chaotic function are mapped to the range of (0, 1). Let be the set of generated values greater than or equal to 0.5, and be the set of generated values that are less than 0.5. A value of will be interpreted as a 0 or not selected, whereas a value of will be interpreted as a 1 or selected. From our experiments, the ratios of produced from the asymmetric chaos map, neuron map, and Kent map are 0.7496, 0.8223, and 0.9977, respectively. These results mean that the asymmetric chaos map has more asymmetry than the neuron map and Kent map do. CSO can use a chaotic map to produce its particle. Therefore, an algorithm that uses the proposed asymmetric chaotic function will prefer “0” (not selected) to “1” (selected). Thus, the solution produced by the proposed method should be more compact than those produced from different algorithms.
3.2. The Process Approach
A multiobjective optimization with two different objectives can regard feature selection. The first objective is to obtain the least number of selected features, and the second objective is to produce the highest accuracy. A solution can be regarded as a better solution when it involves fewer selected features with higher accuracy. Two goals are combined as one fitness function and shown in Equation (6). The dataset with the selected features is classified by the K-nearest neighbor (KNN) classifier, as in Reference [
4]. The search algorithms use Equation (6) as their fitness function.
where
defines the given classification error rate,
is the cardinality of the selected subset,
is the total number of features in the dataset, and
and
are parameters corresponding to the importance of the classification of the number of selected features.
and
, and
in current experiments [
27].
3.3. An Asymmetric Chaotic CSO
This study proposes a way to increase CSO’s effectiveness by using an asymmetric chaos map instead of a uniform random generator. Therefore, we name the new method as an asymmetric chaotic CSO (ACCSO). For m = 0.72, the chaotic sequences in the interval (0, 1) can be obtained. The pseudocode of ACCSO is shown in Algorithm 3.
| Algorithm 3: An asymmetric chaotic competitive swarm optimization (ACCSO) |
| 1: | The pseudocode of Algorithm 3 is as same as Algorithm 2. |
| 2: | There are three modifications in Algorithm 2. |
| 3: | The first modification is at line number 2: a population of N particles is initialized using the proposed asymmetric chaos map. |
| 4: | The second change is at line number 14: the three vectors are randomly generated vectors within using the proposed asymmetric chaos function. |
| 5. | Line numbers 20 and 21 of Algorithm 2 will be removed.
The rest remains the same. |
3.4. An Asymmetric Chaos CSO Followed by SA (ACCSO-SA)
If the SA algorithm is used to hybrid with ACCSO, then the method is called an ACCSO-SA. The pseudocode is shown in Algorithm 4.
| Algorithm 4: An asymmetric chaotic competitive swarm optimization followed by SA (ACCSO-SA) |
| 1: | The pseudocode of Algorithm 4 is as the same as Algorithm 3, but line numbers 20 and 21 are uncommented. |
| 2: | The rest remains the same. |
5. Conclusions
In this study, CSO using an asymmetric chaos map was proposed to solve the problem of feature selection and was validated using 12 datasets taken from UCI and ASU. The fitness function depends on the number of selected features and the classification error rate. The proposed asymmetric chaos map makes CSO prefer a “0” than a “1”.
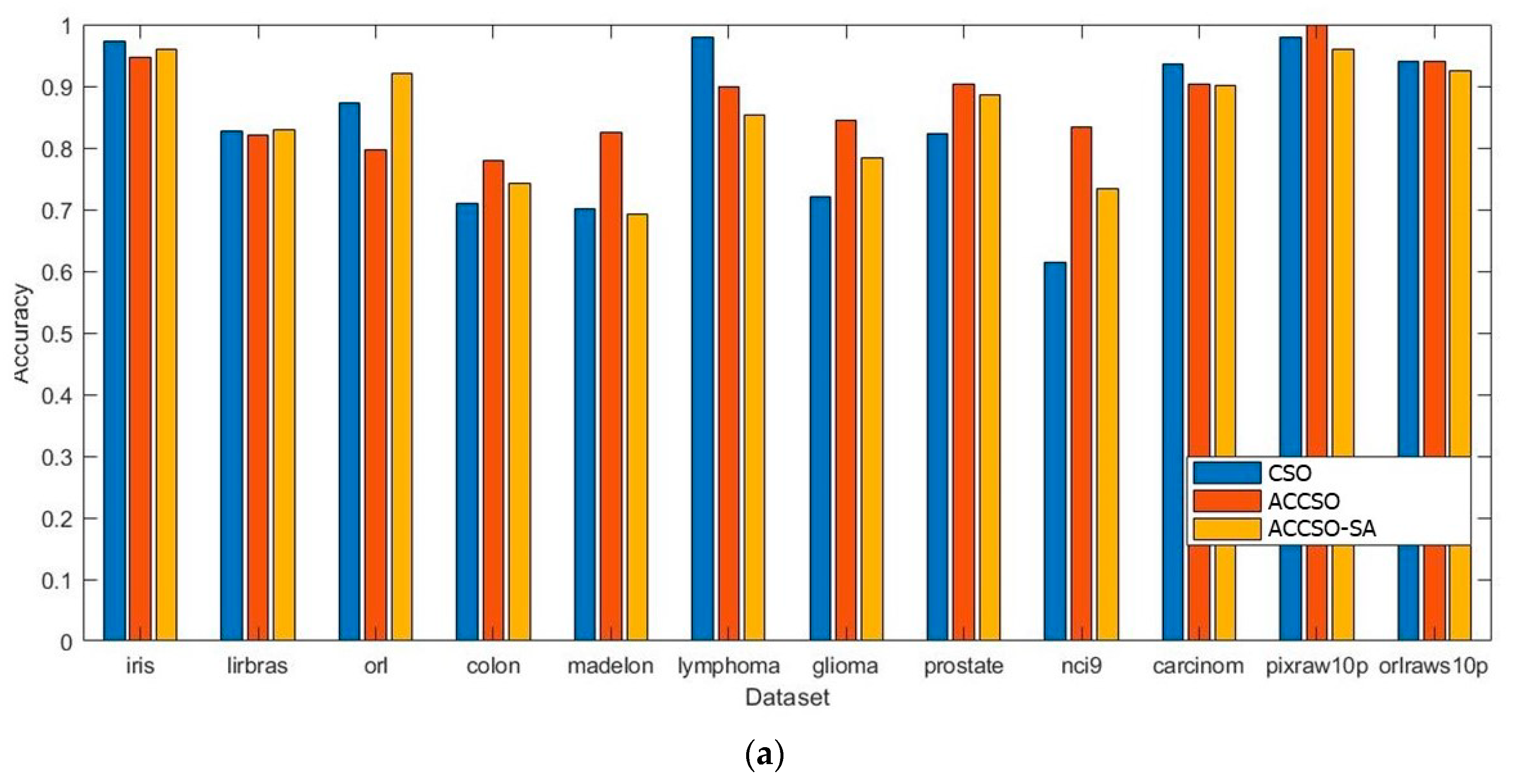
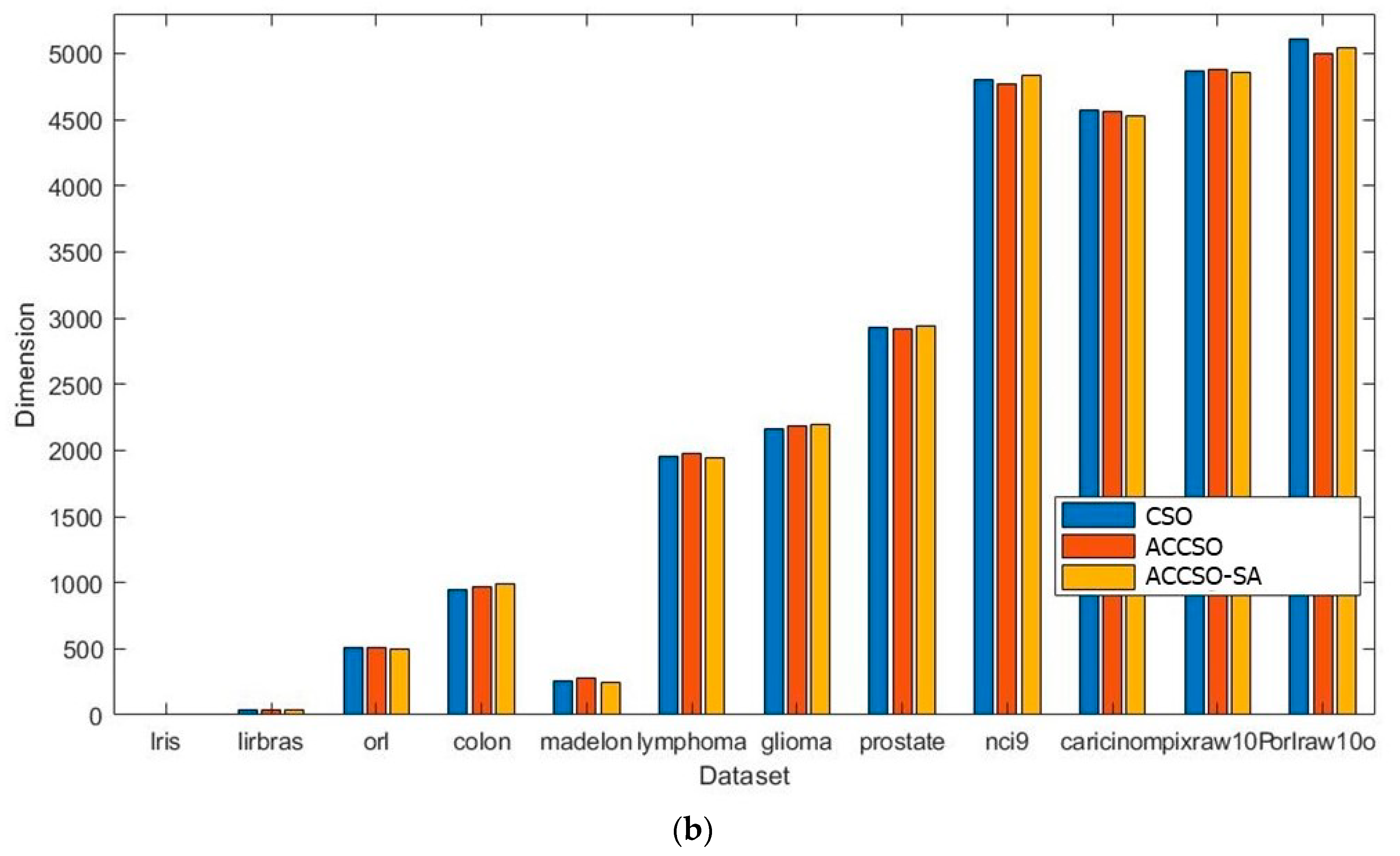
By comparing three algorithms, CSO, ACCSO, and ACCSO-SA, on the 12 datasets, we found that ACCSO-SA is best on more datasets than the other algorithms, 6 out of 12, based on the number of selected features, and ACCSO is best on more datasets than the other algorithms, 9 out of 12, based on the classification accuracy. If the summation of the numbers of selected features is computed from all datasets, then ACCSO has the lowest number of chosen features among the three algorithms. This evidence shows that SA should not follow ACCSO because the algorithm will produce an overfitting solution.
Therefore, the proposed asymmetric chaotic map combined with CSO can boost the algorithm search capability to achieve higher accuracy and more compact selected features than the Kent map and neuron map.
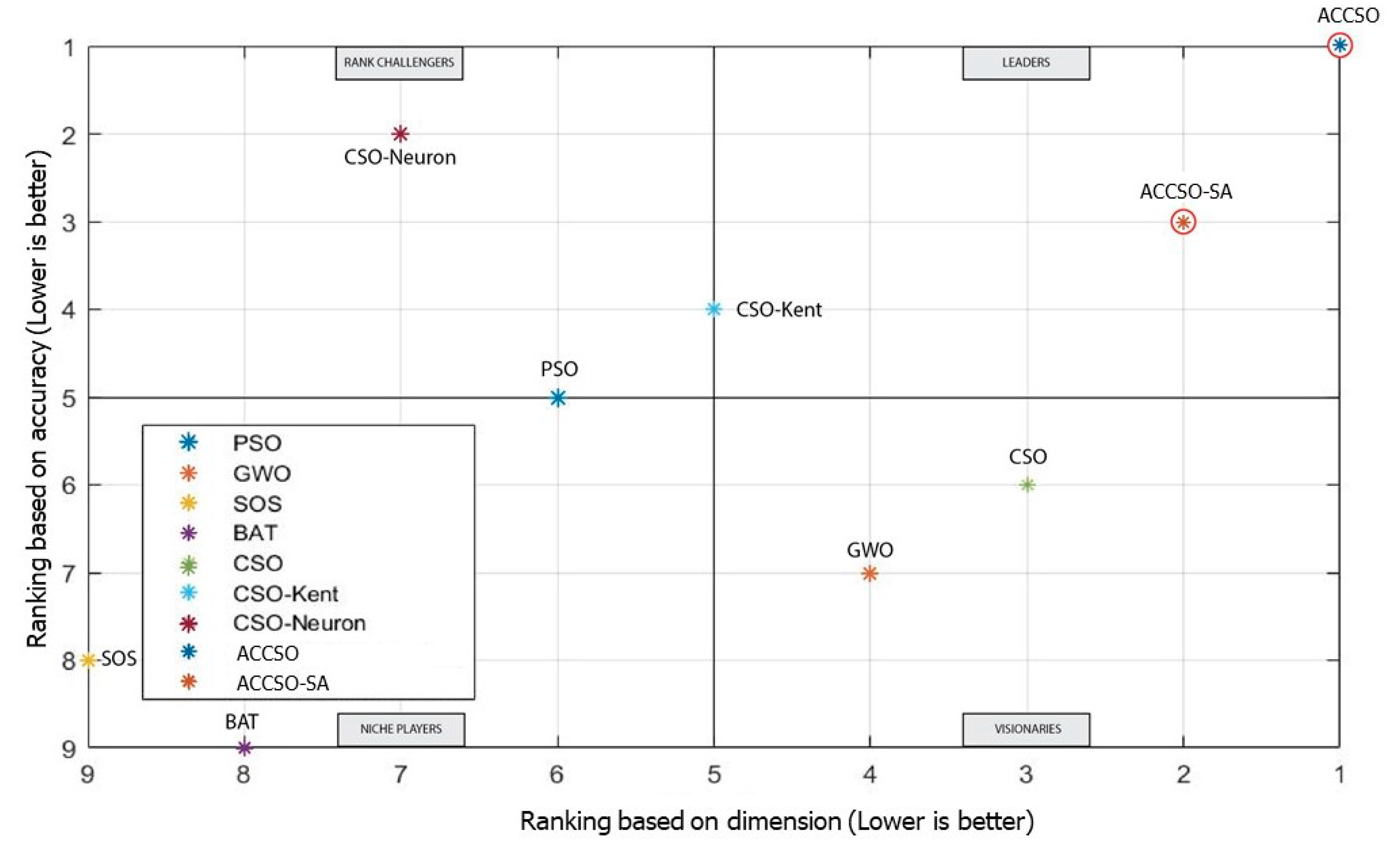
The ACCSO outperformed the other algorithms, ACCSO-SA, PSO, GWO, SOS, BAT, and CSO, for feature selection in high-dimensional data. All the algorithms were then ranked and presented via a magic quadrant. The magic quadrant revealed that the improved CSO outperformed the original CSO algorithm, PSO, GWO, SOS, and BAT in solving the problem of feature selection for high dimensions.
There are still many aspects to be developed for further research, such as increasing ACCSO’s effectiveness by hybridizing it with other state-of-the-art metaheuristic algorithms to solve engineering problems or other challenging issues. Furthermore, the proposed asymmetric chaotic map might be effectively used in different metaheuristic algorithms.