Nonlocal Conservation Laws of PDEs Possessing Differential Coverings ^†

Abstract

In his 1892 paper, L. Bianchi noticed, among other things, that quite simple transformations of the formulas that describe the Bäcklund transformation of the sine-Gordon equation lead to what is called a nonlocal conservation law in modern language. Using the techniques of differential coverings, we show that this observation is of a quite general nature. We describe the procedures to construct such conservation laws and present a number of illustrative examples.

1. Introduction

In [1], L. Bianchi, dealing with the celebrated Bäcklund auto-transformation (I changed the original notation slightly)

$${\displaystyle \frac{\partial (u-w)}{\partial x}}=sin(u+w),{\displaystyle \frac{\partial (u+w)}{\partial y}}=sin(u-w)$$

(1)

for the sine-Gordon equation

$$\frac{{\partial }^2\left(2u\right)}{\partial x\partial y}=sin\left(2u\right)$$

(2)

in the course of intermediate computations (see ([1], p. 10)) notices that the function

$$\psi =ln\frac{\partial u}{\partial C},$$

where C is an arbitrary constant on which the solution u may depend, enjoys the relations

$$\frac{\partial \psi }{\partial x}=cos(u+w),\frac{\partial \psi }{\partial y}=cos(u-w).$$

Reformulated in modern language, this means that the 1-form

$$\omega =cos(u+w)dx+cos(u-w)dy$$

is a nonlocal conservation law for Equation (1).

It became clear much later, some 100 years after the publication of [1], that nonlocal conservation laws are important invariants of PDEs and are used in numerous applications, e.g.,: numerical methods [2,3], sociological models [4,5], integrable systems [6], electrodynamics [7,8], mechanics [9,10,11], etc.

Actually, Bianchi’s observation is of a very general nature and this is shown below.

In Section 2, I shortly introduce the basic constructions in nonlocal geometry of PDEs, i.e., the theory of differential coverings, [12]. Section 3 contains an interpretation of the result by L. Bianchi in the most general setting. In Section 4, a number of examples is discussed.

Everywhere below we use the notation $\mathcal{F}(·)$ for the $\mathbb{R}$-algebra of smooth functions, $D(·)$ for the Lie algebra of vector fields, and ${\Lambda }^{*}(·)={\oplus }_{k\ge 0}{\Lambda }^k(·)$ for the exterior algebra of differential forms.

2. Preliminaries

Following [13], we deal with infinite prolongations $\mathcal{E}\subset J^{\infty }\left(\pi \right)$ of smooth submanifolds in $J^k\left(\pi \right)$, where $\pi :E\to M$ is a smooth locally trivial vector bundle over a smooth manifold M, $dimM=n$, $rank\pi =m$. These $\mathcal{E}$ are differential equations for us. Solutions of $\mathcal{E}$ are graphs of infinite jets that lie in $\mathcal{E}$. In particular, $\mathcal{E}=J^{\infty }\left(\pi \right)$ is the tautological equation $0=0$.

The bundle ${\pi }_{\infty }:\mathcal{E}\to M$ is endowed with a natural flat connection $\mathcal{C}:D\left(M\right)\to D\left(\mathcal{E}\right)$ called the Cartan connection. Flatness of $\mathcal{C}$ means that ${\mathcal{C}}_{[X,Y]}=[{\mathcal{C}}_X,{\mathcal{C}}_Y]$ for all X, $Y\in D\left(M\right)$. The distribution on $\mathcal{E}$ spanned by the fields of the form ${\mathcal{C}}_X$ (the Cartan distribution) is Frobenius integrable. We denote it by $\mathcal{C}\subset D\left(\mathcal{E}\right)$ as well.

A (higher infinitesimal) symmetry of $\mathcal{E}$ is a ${\pi }_{\infty }$-vertical vector field $S\in D\left(\mathcal{E}\right)$ such that $[X,\mathcal{C}]\subset \mathcal{C}$.

Consider the submodule ${\Lambda }_h^k\left(\mathcal{E}\right)$ generated by the forms ${\pi }_{\infty }^{*}\left(\theta \right)$, $\theta \in {\Lambda }^k\left(M\right)$. Elements $\omega \in {\Lambda }_h^k\left(\mathcal{E}\right)$ are called horizontal k-forms. Generalizing slightly the action of the Cartan connection, one can apply it to the de Rham differential $d:{\Lambda }^k\left(M\right)\to {\Lambda }^{k+1}\left(M\right)$ and obtain the horizontal de Rham complex

$$0⟶\mathcal{F}\left(\mathcal{E}\right)⟶\cdots ⟶{\Lambda }_h^k\left(\mathcal{E}\right)\stackrel{d_h}{⟶}{\Lambda }_h^{k+1}\left(\mathcal{E}\right)⟶\cdots ⟶{\Lambda }_h^n\left(\mathcal{E}\right)⟶0$$

on $\mathcal{E}$. Elements of its $(n-1)$st cohomology group $H_h^{n-1}\left(\mathcal{E}\right)$ are called conservation laws of $\mathcal{E}$. We always assume $\mathcal{E}$ to be differentially connected which means that $H_h^0\left(\mathcal{E}\right)=\mathbb{R}$.

Remark 1.

The concept of a differentially connected equation reflects Vinogradov’s correspondence principle [14], (p. 195): when ‘secondary dimension’ (dimension of the Cartan distribution) $\mathrm{Dim}\to 0$, the objects of PDE geometry degenerate to their counterparts in geometry of finite-dimensional manifolds. Following this principle, we informally have

$$\underset{\mathrm{Dim}\to 0}{lim}{H}_h^i\left(\mathcal{E}\right)=H_{\mathrm{dR}}^i\left(M\right).$$

Since $H_{\mathrm{dR}}^0\left(M\right)$ is responsible for topological connectedness of M, the group $H_h^0\left(\mathcal{E}\right)$ stands for differential one.

Coordinates. Consider a trivialization of $\pi$ with local coordinates $x^1,\cdots ,x^n$ in $\mathcal{U}\subset M$ and $u^1,\cdots ,u^m$ in the fibers of ${\left.\pi \right|}_{\mathcal{U}}$. Then in ${\pi }_{\infty }^{-1}\left(\mathcal{U}\right)\subset J^{\infty }\left(\pi \right)$ the adapted coordinates $u_{\sigma }^i$ arise and the Cartan connection is determined by the total derivatives

$$\mathcal{C}:\frac{\partial }{\partial x^i}\mapsto D_i=\frac{\partial }{\partial x^i}+\sum _{j,\sigma }{u}_{\sigma i}^j\frac{\partial }{\partial u_{\sigma }^j}.$$

Let $F=(F^1,\cdots ,F^r)$, where $F^j$ are smooth functions on $J^k\left(\pi \right)$. The the infinite prolongation of the locus

$$\{z\in J^k\left(\pi \right)\mid F^1\left(z\right)=\cdots =F^r\left(z\right)=0\}\subset J^k\left(\pi \right)$$

is defined by the system

$$\mathcal{E}={\mathcal{E}}_F=\{z\in J^{\infty }\left(\pi \right)\mid D_{\sigma }\left(F^j\right)\left(z\right)=0,j=1,\cdots ,r,\left|\sigma \right|\ge 0\},$$

where $D_{\sigma }$ denotes the composition of the total derivatives corresponding to the multi-index $\sigma$. The total derivatives, as well as all differential operators in total derivatives, can be restricted to infinite prolongations and we preserve the same notation for these restrictions. Given an $\mathcal{E}$, we always choose internal local coordinates in it for subsequent computations. To restrict an operator to $\mathcal{E}$ is to express this operator in terms of internal coordinates.

Any symmetry of $\mathcal{E}$ is an evolutionary vector field

$${\mathbf{E}}_{\phi }=\sum D_{\sigma }\left({\phi }^j\right)\frac{\partial }{\partial u_{\sigma }^j}$$

(summation on internal coordinates), where the functions ${\phi }^1,\cdots ,{\phi }^m\in \mathcal{F}\left(\mathcal{E}\right)$ satisfy the system

$$\sum _{\sigma ,\alpha }\frac{\partial F^j}{\partial u_{\sigma }^{\alpha }}{D}_{\sigma }\left({\phi }^{\alpha }\right)=0,j=1,\cdots ,r.$$

A horizontal $(n-1)$-form

$$\omega =\sum _i{a}_{i}d{x}^1\wedge \cdots \wedge d{x}^{i-1}\wedge d{x}^{i+1}\wedge \cdots \wedge d{x}^n$$

defines a conservation law of $\mathcal{E}$ if

$$\sum _i{(-1)}^{i+1}{D}_i\left(a_i\right)=0.$$

We are interested in nontrivial conservation laws, i.e., such that $\omega$ is not exact.

Finally, $\mathcal{E}$ is differentially connected if the only solutions of the system

$$D_1\left(f\right)=\cdots =D_n\left(f\right)=0,f\in \mathcal{F}\left(\mathcal{E}\right),$$

are constants.

Consider now a locally trivial bundle $\tau :\tilde{\mathcal{E}}\to \mathcal{E}$ such that there exists a flat connection $\tilde{\mathcal{C}}$ in ${\pi }_{\infty }\circ \tau :\tilde{\mathcal{E}}\to M$. Following [12], we say that $\tau$ is a (differential) covering over $\mathcal{E}$ if one has

$${\tau }_{*}\left({\tilde{\mathcal{C}}}_X\right)={\mathcal{C}}_X$$

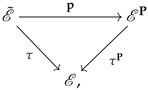
for any vector field $X\in D\left(M\right)$. Objects existing on $\tilde{\mathcal{E}}$ are nonlocal for $\mathcal{E}$: e.g., symmetries of $\tilde{\mathcal{E}}$ are nonlocal symmetries of $\mathcal{E}$, conservation laws of $\tilde{\mathcal{E}}$ are nonlocal conservation laws of $\mathcal{E}$, etc. A derivation $S:\mathcal{F}\left(\mathcal{E}\right)\to \mathcal{F}\left(\tilde{\mathcal{E}}\right)$ is called a nonlocal shadow if the diagram

is commutative for any $X\in D\left(M\right)$. In particular, any symmetry of the equation $\mathcal{E}$, as well as restrictions ${\left.\tilde{S}\right|}_{\mathcal{F}\left(\mathcal{E}\right)}$ of nonlocal symmetries may be considered as shadows. A nonlocal symmetry is said to be invisible if its shadow ${\left.\tilde{S}\right|}_{\mathcal{F}\left(\mathcal{E}\right)}$ vanishes.

A covering $\tau$ is said to be irreducible if $\tilde{\mathcal{E}}$ is differentially connected. Two coverings are equivalent if there exists a diffeomorphism $g:{\tilde{\mathcal{E}}}_1\to {\tilde{\mathcal{E}}}_2$ such that the diagrams

are commutative. Note also that for any two coverings their Whitney product is naturally defined. A covering is called linear if $\tau$ is a vector bundle and the action of vector fields ${\tilde{\mathcal{C}}}_X$ preserves the subspace of fiber-wise linear functions in $\mathcal{F}\left(\tilde{\mathcal{E}}\right)$.

In the case of 2D equations, there exists a fundamental relation between special type of coverings over $\mathcal{E}$ and conservation laws of the latter. Let $\tau$ be a covering of rank $l<\infty$. We say that $\tau$ is an Abelian covering if there exist l independent conservation laws $\left[{\omega }_i\right]\in H_h^1\left(\mathcal{E}\right)$, $i=1,\cdots ,l$, such that the forms ${\tau }^{*}\left({\omega }_i\right)$ are exact. Then equivalence classes of such coverings are in one-to-one correspondence with l-dimensional $\mathbb{R}$-subspaces in $H_h^1\left(\mathcal{E}\right)$.

Coordinates. Choose a trivialization of the covering $\tau$ and let $w^1,\cdots ,w^l,\cdots$ be coordinates in fibers (the are called nonlocal variables). Then the covering structure is given by the extended total derivatives

$${\tilde{D}}_i=D_i+X_i,i=1,\cdots ,n,$$

where

$$X_i=\sum _{\alpha }{X}_i^{\alpha }\frac{\partial }{\partial w^{\alpha }}$$

are $\tau$-vertical vector fields (nonlocal tails) enjoying the condition

$$D_i\left(X_j\right)-D_j\left(X_i\right)+[X_i,X_j]=0,i<j.$$

(3)

Here $D_i\left(X_j\right)$ denotes the action of $D_i$ on coefficients of $X_j$. Relations (3) (flatness of $\tilde{\mathcal{C}}$) amount to the fact that the manifold $\tilde{\mathcal{E}}$ endowed with the distribution $\tilde{\mathcal{C}}$ coincides with the infinite prolongation of the overdetermined system

$$\frac{\partial w^{\alpha }}{\partial x^i}=X_i^{\alpha },$$

which is compatible modulo $\mathcal{E}$.

Irreducible coverings are those for which the system of vector fields ${\tilde{D}}_1,\cdots ,{\tilde{D}}_n$ has no nontrivial integrals. If $\overline{\tau }$ is another covering with the nonlocal tails ${\overline{X}}_i=\sum {\overline{X}}_i^{\beta }\partial /\partial {\overline{w}}^{\beta }$, then the Whitney product $\tau \oplus \overline{\tau }$ of $\tau$ and $\overline{\tau }$ is given by

$${\tilde{D}}_i=D_i+\sum _{\alpha }{X}_i^{\alpha }\frac{\partial }{\partial w^{\alpha }}+\sum _{\beta }{\overline{X}}_i^{\beta }\frac{\partial }{\partial {\overline{w}}^{\beta }}.$$

A covering is Abelian if the coefficients $X_i^{\alpha }$ are independent of nonlocal variables $w^j$. If $n=2$ and ${\omega }_{\alpha }=X_1^{\alpha }d{x}^1+X_2^{\alpha }d{x}^2$, $\alpha =1,\cdots ,l$, are conservation laws of $\mathcal{E}$ then the corresponding Abelian covering is given by the system

$$\frac{\partial w^{\alpha }}{\partial x^i}=X_i^{\alpha },i=1,2,\alpha =1,\cdots ,l,$$

or

$${\tilde{D}}_i=D_i+\sum _{\alpha }{X}_i^{\alpha }\frac{\partial }{\partial w^{\alpha }}.$$

Vice versa, if such a covering is given, then one can construct the corresponding conservation law.

The horizontal de Rham differential on $\tilde{\mathcal{E}}$ is ${\tilde{d}}_h={\sum }_{i}d{x}^i\wedge {\tilde{D}}_i$. A covering is linear if

$$X_i^{\alpha }=\sum _{\beta }{X}_{i,\beta }^{\alpha }{w}^{\beta },$$

(4)

where $X_{i,\beta }^{\alpha }\in \mathcal{F}\left(\mathcal{E}\right)$.

Remark 2.

Denote by ${\mathbf{X}}_i$ the $\mathcal{F}\left(\mathcal{E}\right)$-valued matrix $\left(X_{i,\beta }^{\alpha }\right)$ that appears in (4). Then Equation (3) may be rewritten as

$$D_i\left({\mathbf{X}}_{\mathbf{j}}\right)-D_j\left({\mathbf{X}}_{\mathbf{i}}\right)+[{\mathbf{X}}_{\mathbf{i}},{\mathbf{X}}_{\mathbf{j}}]=0.$$

for linear coverings. Thus, a linear covering defines a zero-curvature representation for $\mathcal{E}$ and vice versa.

A nonlocal symmetry in $\tau$ is a vector field

$$S_{\phi ,\psi }=\sum {\tilde{D}}_{\sigma }\left({\phi }^j\right)\frac{\partial }{\partial u_{\sigma }^j}+\sum {\psi }^{\alpha }\frac{\partial }{\partial w^{\alpha }},$$

where the vector functions $\phi =({\phi }^1,\cdots ,{\phi }^m)$ and $\psi =({\psi }^1,\cdots ,{\psi }^{\alpha },\cdots )$ on $\tilde{\mathcal{E}}$ satisfy the system of equations

$$\begin{array}{cc}\hfill & \sum \frac{\partial F^j}{\partial u_{\sigma }^j}{\tilde{D}}_{\sigma }\left({\phi }^j\right)=0,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & {\tilde{D}}_i\left({\psi }^{\alpha }\right)=\sum \frac{\partial X_i^{\alpha }}{\partial u_{\sigma }^j}{\tilde{D}}_{\sigma }\left({\phi }^j\right)+\sum \frac{\partial X_i^{\alpha }}{\partial w^{\beta }}{\psi }^{\beta }.\hfill \end{array}$$

(6)

Nonlocal shadows are the derivations

$${\tilde{\mathbf{E}}}_{\phi }=\sum {\tilde{D}}_{\sigma }\left({\phi }^j\right)\frac{\partial }{\partial u_{\sigma }^j},$$

where $\phi$ satisfies Equation (5), invisible symmetries are

$$S_{0,\psi }=\sum {\psi }^{\alpha }\frac{\partial }{\partial w^{\alpha }},$$

where $\psi$ satisfies

$${\tilde{D}}_i\left({\psi }^{\alpha }\right)=\sum \frac{\partial X_i^{\alpha }}{\partial w^{\beta }}{\psi }^{\beta }.$$

(7)

In what follows, we use the notation ${\tau }^{\mathbf{I}}:{\tilde{\mathcal{E}}}^{\mathbf{I}}\to \tilde{\mathcal{E}}$ for the covering defined by Equation (7).

Remark 3.

Equation (7) defines a linear covering over $\tilde{\mathcal{E}}$. Due to Remark 2, we see that for any non-Abelian covering we obtain in such a way a nonlocal zero-curvature representation with the matrices ${\mathbf{X}}_i=(\partial X_i^{\alpha }/\partial w^{\beta })$.

Remark 4.

The covering ${\tau }^{\mathbf{I}}:{\tilde{\mathcal{E}}}^{\mathbf{I}}\to \tilde{\mathcal{E}}$ is the vertical part of the tangent covering$\mathbf{t}:\mathcal{T}\tilde{\mathcal{E}}\to \tilde{\mathcal{E}}$, see the definition in [15].

3. The Main Result

From now on we consider two-dimensional scalar equations with the independent variables x and y. We shall show that any such an equation that admits an irreducible covering possesses a (nonlocal) conservation law.

Example 1.

Let us revisit the Bianchi example discussed in the beginning of the paper. Equation (1) define a one-dimensional non-Abelian covering $\tau :\tilde{\mathcal{E}}=\mathcal{E}\times \mathbb{R}\to \mathcal{E}$ over the sine-Gordon Equation (2) with the nonlocal variable w. Then the defining Equation (7) for invisible symmetries in this covering are

$$\frac{\partial \psi }{\partial x}=-cos(u+w)\psi ,\frac{\partial \psi }{\partial y}=-cos(u-w)\psi .$$

This is a one-dimensional linear covering over $\tilde{\mathcal{E}}$ which is equivalent to the Abelian covering

$$\frac{\partial \overline{\psi }}{\partial x}=-cos(u+w),\frac{\partial \overline{\psi }}{\partial y}=-cos(u-w),$$

where $\overline{\psi }=ln\psi$. Thus, we obtain the nonlocal conservation law

$$\omega =-cos(u+w)dx-cos(u-w)dy$$

of the sine-Gordon equation.

The next result shows that Bianchi’s observation is of a quite general nature.

Proposition 1.

Let $\tau :\tilde{\mathcal{E}}\to \mathcal{E}$ be a one-dimensional non-Abelian covering over $\mathcal{E}$. Then, if τ is irreducible, ${\tau }^{\mathbf{I}}:{\tilde{\mathcal{E}}}^{\mathbf{I}}\to \tilde{\mathcal{E}}$ defines a nontrivial conservation law of the equation $\tilde{\mathcal{E}}$ (and, consequently, of $\mathcal{E}$ too).

Proof. 

Consider the total derivatives

$$\begin{array}{cc}\hfill D_x^{\mathbf{I}}& ={\tilde{D}}_x+\frac{\partial X}{\partial w}\psi \frac{\partial }{\partial \psi }=D_x+X\frac{\partial }{\partial w}+\frac{\partial X}{\partial w}\psi \frac{\partial }{\partial \psi }\hfill \\ \hfill D_y^{\mathbf{I}}& ={\tilde{D}}_y+\frac{\partial Y}{\partial w}\psi \frac{\partial }{\partial \psi }=D_y+Y\frac{\partial }{\partial w}+\frac{\partial Y}{\partial w}\psi \frac{\partial }{\partial \psi }\hfill \end{array}$$

on ${\mathcal{E}}^{\mathbf{I}}$ and assume that $a\in \mathcal{F}\left(\tilde{\mathcal{E}}\right)$ is a common nontrivial integral of these fields:

$$D_x^{\mathbf{I}}\left(a\right)=D_y^{\mathbf{I}}\left(a\right)=0,a\ne const.$$

(8)

Choose a point in ${\mathcal{E}}^{\mathbf{I}}$ and assume that the formal series

$$a_0+a_1\psi +\cdots +a_j{\psi }^j+\cdots ,a_j\in \mathcal{F}\left(\tilde{\mathcal{E}}\right),$$

(9)

converges to a in a neighborhood of this point. Substituting relations (9) to (8) and equating coefficients at the same powers of $\psi$, we get

$${\tilde{D}}_x\left(a_j\right)+j\frac{\partial X}{\partial w}{a}_j=0,{\tilde{D}}_y\left(a_j\right)+j\frac{\partial Y}{\partial w}{a}_j=0,j=0,1,\cdots ,$$

and, since $\tau$ is irreducible, this implies that $a_0=k_0=const$ and

$$\frac{{\tilde{D}}_x\left(a_j\right)}{a_j}=j\frac{{\tilde{D}}_x\left(a_1\right)}{a_1},\frac{{\tilde{D}}_y\left(a_j\right)}{a_j}=j\frac{{\tilde{D}}_y\left(a_1\right)}{a_1}.$$

Hence, $a_j=k_j{\left(a_1\right)}^j$, $j>0$. Substituting these relations to (9), we see that $a=a\left(\theta \right)$, where $\theta =a_1\psi$, $a_1\in \mathcal{F}\left(\mathcal{E}\right)$. Then Equation (8) take the form

$$\dot{a}\psi \left({\tilde{D}}_x\left(a_1\right)+\frac{\partial X}{\partial w}\right)=0,\dot{a}\psi \left({\tilde{D}}_y\left(a_1\right)+\frac{\partial Y}{\partial w}\right)=0,\dot{a}=\frac{da}{d\theta }.$$

Thus

$$\frac{\partial X}{\partial w}=-{\tilde{D}}_x\left(a_1\right),\frac{\partial Y}{\partial w}=-{\tilde{D}}_y\left(a_1\right)$$

and the function $w+a_1$ is a nontrivial integral of ${\tilde{D}}_x$ and ${\tilde{D}}_y$. Contradiction.

Finally, repeating the scheme of Example 1, we pass to the equivalent covering by setting $\overline{\psi }=ln\psi$ and obtain the nontrivial conservation law

$$\omega =\frac{\partial X}{\partial w}dx+\frac{\partial Y}{\partial w}dy$$

on ${\mathcal{E}}^{\mathbf{I}}$. □

Indeed, Bianchi’s result has a further generalization. To formulate the latter, let us say that a covering $\tau :\tilde{\mathcal{E}}\to \mathcal{E}$ is strongly non-Abelian if for any nontrivial conservation law $\omega$ of the equation $\mathcal{E}$ its lift ${\tau }^{*}\left(\omega \right)$ to the manifold $\tilde{\mathcal{E}}$ is nontrivial as well. Now, a straightforward generalization of Proposition 1 is

Proposition 2.

Let $\tau :\tilde{\mathcal{E}}\to \mathcal{E}$ be an irreducible covering over a differentially connected equation. Then τ is a strongly non-Abelian covering if and only if the covering ${\tau }^{\mathbf{I}}$ is irreducible.

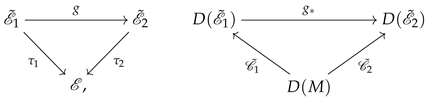
We shall now need the following construction. Let $\tau :\tilde{\mathcal{E}}\to \mathcal{E}$ be a linear covering. Consider the fiber-wise projectivization ${\tau }^{\mathbf{P}}:{\tilde{\mathcal{E}}}^{\mathbf{P}}\to \mathcal{E}$ of the vector bundle $\tau$. Denote by $\mathbf{p}:\tilde{\mathcal{E}}\to {\mathcal{E}}^{\mathbf{P}}$ the natural projection. Then, obviously, the projection ${\mathbf{p}}_{*}\left(\tilde{\mathcal{C}}\right)$ is well defined and is an n-dimensional integrable distribution on ${\mathcal{E}}^{\mathbf{P}}$. Thus, we obtain the following commutative diagram of coverings

where $rank\left(\mathbf{p}\right)=1$ and $rank\left({\tau }^{\mathbf{P}}\right)=rank\left(\tau \right)-1$.

Proposition 3.

Let $\tau :\tilde{\mathcal{E}}\to \mathcal{E}$ be an irredicible covering. Then the covering ${\tau }^{\mathbf{P}}$ is irreducible as well.

Coordinates. Let $rank\left(\tau \right)=l>1$ and

$$w_{x^i}^{\alpha }=\sum _{\beta =1}^l{X}_{i,\beta }^{\alpha }{w}^{\beta },i=1,\cdots ,n,\alpha =1,\cdots ,l,$$

(10)

be the defining equations of the covering $\tau$, see Equation (4). Choose an affine chart in the fibers of ${\tau }^{\mathbf{P}}$. To this end, assume for example that $w^l\ne 0$ and set

$${\overline{w}}^{\alpha }=\frac{w^{\alpha }}{w^l},l=1,\cdots ,l-1,$$

in the domain under consideration. Then from Equation (10) it follows that the system

$${\overline{w}}_{x^i}^{\alpha }=X_{i,l}^{\alpha }-X_{i,l}^l{\overline{w}}^{\alpha }+\sum _{\beta =1}^{l-1}{X}_{i,\beta }^{\alpha }{\overline{w}}^{\beta }-{\overline{w}}^{\alpha }\sum _{\beta =1}^{l-1}{X}_{i,\beta }^l{\overline{w}}^{\beta },i=1,\cdots ,n,\alpha =1,\cdots ,l-1.$$

locally provides the defining equation for the covering ${\tau }^{\mathbf{P}}$.

We are now ready to state and prove the main result.

Theorem 1.

Assume that a differentially connected two-dimensional equation $\mathcal{E}$ admits a nontrivial covering $\tau :\tilde{\mathcal{E}}\to \mathcal{E}$ of finite rank. Then it possesses at least one nontrivial(nonlocal)conservation law.

Proof. 

Actually, the proof is a description of a procedure that allows one to construct the desired conservation law.

Note first that we may assume the covering $\tau$ to be irreducible. Indeed, otherwise the space $\tilde{\mathcal{E}}$ is foliated by maximal integral manifolds of the distribution $\tilde{\mathcal{C}}$. Let $l_0$ denote the codimension of the generic leaf and $l=rank\left(\tau \right)$. Then

• $l>l_0$, because $\tau$ is a nontrivial covering;
• the integral leaves project to $\mathcal{E}$ surjectively, because $\mathcal{E}$ is a differentially connected equation.

This means that in vicinity of a generic point we can consider $\tau$ as an $l_0$-parametric family of irreducible coverings whose rank is $r=l-l_0>0$. Let us choose one of them and denote it by ${\tau }_0:{\mathcal{E}}_0\to \mathcal{E}$.

If ${\tau }_0$ is not strongly non-Abelian, then this would mean that $\mathcal{E}$ possesses at least one nontrivial conservation law and we have nothing to prove further. Assume now that the covering ${\tau }_0$ is strongly non-Abelian. Then due to Proposition 2 the linear covering ${\tau }_0^{\mathbf{I}}$ is irreducible and by Proposition 3 its projectivization ${\tau }_1={\left({\tau }_0^{\mathbf{I}}\right)}^{\mathbf{P}}$ possesses the same property and $rank\left({\tau }_1\right)=r-1$. Repeating the construction, we arrive to the diagram

where $rank\left({\tau }_i\right)=l-i$. Thus, in $r-1$ steps at most we shall arrive to a one-dimensional irreducible covering and find ourselves in the situation of Proposition 1 and this finishes the proof. □

4. Examples

Let us discuss several illustrative examples.

Example 2.

Consider the Korteweg-de Vries equation in the form

$$u_t=u{u}_x+u_{xxx}$$

(11)

and the well known Miura transformation [16]

$$u=w_x-\frac{1}{6}{w}^2.$$

The last formula is a part of the defining equations for the non-Abelian covering

$$\begin{array}{ccc}\hfill w_x& =& u+{\displaystyle \frac{1}{6}}{w}^2,\hfill \\ \hfill w_t& =& u_{xx}+{\displaystyle \frac{1}{3}}w{u}_x+{\displaystyle \frac{1}{3}}{u}^2+{\displaystyle \frac{1}{18}}{w}^{2}u,\hfill \end{array}$$

the covering equation being

$$w_t=w_{xxx}-\frac{1}{6}{w}^2{w}_x,$$

i.e., the modified KdV equation. Then the corresponding covering ${\tau }^{\mathbf{I}}$ is defined by the system

$$\begin{array}{ccc}\hfill {\psi }_x& =& {\displaystyle \frac{1}{3}}w\psi ,\hfill \\ \hfill {\psi }_t& =& {\displaystyle \frac{1}{3}}\left(u_x+{\displaystyle \frac{1}{3}}wu\right)\psi \hfill \end{array}$$

that, after relabeling $\psi \mapsto 3ln\psi$ gives us the nonlocal conservation law

$$\omega =wdx+\left(u_x+{\displaystyle \frac{1}{3}}wu\right)dt$$

of the KdV equation.

Example 3.

The well known Lax pair, see [17], for the KdV equation may be rewritten in terms of zero-curvature representation

$$D_x\left(\mathbf{T}\right)-D_t\left(\mathbf{X}\right)+[\mathbf{X},\mathbf{T}]=0.$$

The $(2\times 2)$ matrices $\mathbf{X}$ and $\mathbf{T}$ become much simpler if we present the equation in the form

$$u_t=6u{u}_x-u_{xxx}.$$

In this case, they are

$$\mathbf{X}=\left(\begin{array}{cc}0& 1\\ u-\lambda & 0\end{array}\right),\mathbf{T}=\left(\begin{array}{cc}-u_x& 2(u+2\lambda )\\ 2u^2-u_{xx}+2\lambda u-4{\lambda }^2& u_x\end{array}\right),$$

$\lambda \in \mathbb{R}$ being a real parameter. As it follows from Remark 2, this amounts to existence of the two-dimensional linear covering τ given by the system

$$\begin{array}{cc}\hfill w_{1,x}& =w_2,\hfill \\ \hfill w_{1,t}& =-u_x{w}_1+2(u+2\lambda )w_2,\hfill \\ \hfill w_{2,x}& =(u-\lambda )w_1,\hfill \\ \hfill w_{2,t}& =(2u^2-u_{xx}+2\lambda u-4{\lambda }^2)w_1+u_x{w}_2.\hfill \end{array}$$

Let us choose for the affine chart the domain $w_2\ne 0$ and set $\psi =w_1/w_2$. Then the covering ${\tau }^{\mathbf{P}}$ is described by the system

$$\begin{array}{cc}\hfill {\psi }_x& =1-(u-\lambda )\psi ,\hfill \\ \hfill {\psi }_t& =2(u+2\lambda )-2u_x\psi -(2u^2-u_{xx}+2\lambda u-4{\lambda }^2){\psi }^2,\hfill \end{array}$$

while ${\tau }_1={\left({\tau }^{\mathbf{P}}\right)}^{\mathbf{I}}$ is given by

$$\begin{array}{cc}\hfill {\tilde{\psi }}_x& =(\lambda -u)\tilde{\psi },\hfill \\ \hfill {\tilde{\psi }}_t& =-2\left(u_x+(2u^2-u_{xx}+2\lambda u-4{\lambda }^2)\psi \right)\tilde{\psi }.\hfill \end{array}$$

Thus, we obtain the conservation law

$$\omega =(\lambda -u)dx-2\left(u_x+(2u^2-u_{xx}+2\lambda u-4{\lambda }^2)\psi \right)dt$$

that depends on the nonlocal variable ψ.

Example 4.

Consider the potential KdV equation in the form

$$u_t=3u_x^2+u_{xxx}$$

Its Bäcklund auto-transformation is associated to the covering τ

$$\begin{array}{cc}\hfill w_x& =\lambda -u_x-\frac{1}{2}{(w-u)}^2,\hfill \\ \hfill w_t& =2{\lambda }^2-2\lambda u_x-u_x^2-u_{xxx}+2u_{xx}(w-u)-(\lambda +u_x){(w-u)}^2,\hfill \end{array}$$

where $\lambda \in \mathbb{R}$, see [18]. Then the covering ${\tau }^{\mathbf{I}}$ is

$$\begin{array}{cc}\hfill {\psi }_x& =-(w-u)\psi ,\hfill \\ \hfill {\psi }_t& =2\left(u_{xx}\psi -(\lambda +u_x)(w-u)\right)\psi ,\hfill \end{array}$$

which leads to the nonlocal conservation law

$$\omega =-(w-u)dx+2\left(u_{xx}\psi -(\lambda +u_x)(w-u)\right)dt$$

of the potential KdV equation.

Example 5.

The Gauss-Mainardi-Codazzi equations read

$$u_{xy}=\frac{g-fh}{sinu},f_y=g_x+\frac{h-gcosu}{sinu}{u}_x,g_y=h_x-\frac{f-gcosu}{sinu}{u}_y,$$

(12)

see [19]. This is an under-determined system, and imposing additional conditions on the unknown functions u, f, g, and h one obtains equations that describe various types of surfaces in ${\mathbb{R}}^2$, cf. [20]. System (12) always admits the following $\mathbb{C}$-valued zero-curvature representation

$$D_x\left(\mathbf{Y}\right)-D_y\left(\mathbf{X}\right)+[\mathbf{X},\mathbf{Y}]=0$$

with the matrices

$$\mathbf{X}=\frac{\mathrm{i}}{2}\left(\begin{array}{cc}{u}_x& {\displaystyle \frac{{\mathrm{e}}^{\mathrm{i}u}f-g}{sinu}}\\ {\displaystyle \frac{{\mathrm{e}}^{-\mathrm{i}u}f-g}{sinu}}& -u_x\end{array}\right),\mathbf{Y}=\frac{\mathrm{i}}{2}\left(\begin{array}{cc}0& {\displaystyle \frac{{\mathrm{e}}^{iu}g-h}{sinu}}\\ {\displaystyle \frac{{\mathrm{e}}^{-\mathrm{i}u}g-h}{sinu}}& 0\end{array}\right)$$

The corresponding two-dimensional linear covering τ is defined by the system

$$\begin{array}{ccc}\hfill w_x^1& =& u_x{w}^1+{\displaystyle \frac{{\mathrm{e}}^{\mathrm{i}u}f-g}{sinu}}{w}^2,\hfill \\ \hfill w_y^1& =& {\displaystyle \frac{{\mathrm{e}}^{iu}g-h}{sinu}}{w}^2,\hfill \end{array}\begin{array}{ccc}\hfill w_x^2& =& {\displaystyle \frac{{\mathrm{e}}^{-\mathrm{i}u}f-g}{sinu}}{w}^1-u_x{w}^2,\hfill \\ \hfill w_y^2& =& {\displaystyle \frac{{\mathrm{e}}^{-\mathrm{i}u}g-h}{sinu}}{w}^1.\hfill \end{array}$$

Hence, the covering ${\tau }^{\mathbf{P}}$ in the domain $w^2\ne 0$ is

$${\psi }_x=\frac{{\mathrm{e}}^{\mathrm{i}u}f-g}{sinu}+2u_x\psi -\frac{{\mathrm{e}}^{-\mathrm{i}u}f-g}{sinu}{\psi }^2,{\psi }_y=\frac{{\mathrm{e}}^{\mathrm{i}u}g-h}{sinu}-\frac{{\mathrm{e}}^{-\mathrm{i}u}g-h}{sinu}{\psi }^2.$$

Thus, the covering ${\left({\tau }^{\mathbf{P}}\right)}^{\mathbf{I}}$, given by

$${\tilde{\psi }}_x=2\left(u_x-\frac{{\mathrm{e}}^{-\mathrm{i}u}f-g}{sinu}\psi \right)\tilde{\psi },{\tilde{\psi }}_y=-2\frac{{\mathrm{e}}^{-\mathrm{i}u}g-h}{sinu}\psi \tilde{\psi },$$

defines the nonlocal conservation law

$$\omega =\left(u_x-\frac{{\mathrm{e}}^{-\mathrm{i}u}f-g}{sinu}\psi \right)dx-\frac{{\mathrm{e}}^{-\mathrm{i}u}g-h}{sinu}\psi dy$$

of the Gauss-Mainardi-Codazzi equations.

Example 6.

The last example shows that the above described techniques fail for infinite-dimensional coverings (such coverings are typical for equations of dimension greater than two).

Consider the equation

$$u_{yy}=u_{tx}+u_y{u}_{xx}-u_x{u}_{xy}$$

that arises in the theory of integrable hydrodynamical chains, see [21]. This equation admits the covering τ with the nonlocal variables $w^i$, $i=0,1,\cdots$, that enjoy the defining relations

$$\begin{array}{cc}\hfill & w_t^0+u_y{w}_x^1=0,w_y^0+u_x{w}_x^1=0,\hfill \\ \hfill & w_x^i=w^{i+1},i\ge 0,\hfill \\ \hfill & w_t^i+D_x^i\left(u_y{w}_x^1\right)=0,w_y^i+D_x^i\left(u_x{w}_x^1\right)=0,i\ge 1.\hfill \end{array}$$

see [22]. This is a linear covering, but its projectivization does not lead to construction of conservation laws.

5. Discussion

We described a procedure that allows one to associate, in an algorithmic way, with any nontrivial finite-dimensional covering over a differentially connected equation a nonlocal conservation law. Nevertheless, this method fails in the case of infinite-dimensional coverings. It is unclear, at the moment at least, whether this is an immanent property of such coverings or a disadvantage of the method. I hope to clarify this in future research.