D-Stability of the Initial Value Problem for Symmetric Nonlinear Functional Differential Equations

Abstract

This paper presents a method of establishing the D-stability terms of the symmetric solution of scalar symmetric linear and nonlinear functional differential equations. We determine the general conditions of the unique solvability of the initial value problem for symmetric functional differential equations. Here, we show the conditions of the symmetric property of the unique solution of symmetric functional differential equations. Furthermore, in this paper, an illustration of a particular symmetric equation is presented. In this example, all theoretical investigations referred to earlier are demonstrated. In addition, we graphically demonstrate two possible linear functions with the required symmetry properties.

1. Introduction

Time-reversal symmetry is one of the fundamental symmetries discussed in natural science. Consequently, it arises in many physically motivated dynamical systems, in particular, in classical and quantum mechanics [1]. There are various approaches which have attracted our interest that utilize the modeling of reversible dynamical systems, such as the study of time-reversal symmetry in nonequilibrium statistical mechanics [2], the time reversibility investigation in nonequilibrium thermodynamics [3], and the evaluation of certain properties of the Liapunov spectrum for the driven Lorentz gas [4].

The investigation of the impact of symmetries in functional differential equations is a topical problem. It is known that the well-posed problem or stability of solutions is one of the most important properties of functional differential equations. There are many publications that study this problem (herein, we only cite some of them: see, for example, [5,6,7,8,9,10] and the references therein). Using the results from [5,6,11,12,13,14], we investigate the D-stability of the symmetric solutions for functional differential equations. Here, the general symmetry of the solution (see (3)) is studied, which is a generalization of the periodicity of solutions. A similar problem is studied, for example, in [11,15,16,17].

The main focus of our research was to obtain the conditions of D-stability of functional differential equations. A similar topic was studied by Azbelev et al. in [5,6]. However, much more research is devoted to differential equations with delays (see, for example, [7,8,9,18,19] and the references therein). Moreover, the big amount of the theorems in this field is based on Schauder’s theorem or Banach’s theorem of contractive mapping for the unique solvability or the Bohl–Perron theorem to prove the exponential stability, which imposes serious restrictions. In the present paper, an alternative research method that can be applied to a wide range of differential equations is described. It allows one to obtain not only unique solvability conditions but also a representation of the unique solution in the form of a functional series. Then, the symmetry conditions of the unique solution can be easily obtained. The principles of the obtained results for linear functional differential equations, the conditions of D-stability, and the symmetry of nonlinear equations were established. Thanks to the symmetry conditions, the examination of the equations is now possible on the full $\mathbb{R}$ axis, using the theory of boundary value problems. We see the limitations of this method only in its application to positive operators.

The present paper was mainly motivated by several papers that deal with the conditions of stability and solvability of differential equations with delay. For example, the solution estimate for a differential equation with delay $x^{\prime }\left(t\right)+{\sum }_{k=1}^m{b}_k\left(t\right)x\left(h_k\left(t\right)\right)=0,t\ge t_0,x\left(t\right)=\varphi \left(t\right),t\le 0,k=1,\dots ,m$ was obtained in [7]. New explicit conditions of exponential stability for the nonautonomous linear equation $x^{\prime }\left(t\right)+{\sum }_{k=1}^m{a}_k\left(t\right)x\left(h_k\left(t\right)\right)=0$ were studied in [8]. In [9], they deal with the influence of “mistakes” in coefficients and delays on a solutions’ behavior in the delay differential neutral system $x_i^{\prime }\left(t\right)-q_i\left(t\right)x_i^{\prime }(t-{\theta }_i\left(t\right))+{\sum }_{j=1}^n(p_{ij}\left(t\right)-\Delta p_{ij}\left(t\right))x_j(t-{\tau }_{ij}\left(t\right)-\Delta {\tau }_{ij}\left(t\right))=f_i\left(t\right),i=1,\dots ,n$, $t\in [0,\infty )$.

Our investigation of functional differential equations with symmetric properties starts in [11,12]. They present the applicability of the theory of boundary value problems in the investigation of functional differential equations with symmetric properties on $\mathbb{R}$. Then, the unique solvability conditions of linear functional differential equations were established in [13,14,20], which represent the unique solution in view of the functional series.

2. Problem Formulation

A class of symmetric solutions of the scalar nonlinear functional differential equations is considered here

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x^{\prime }\left(t\right)+\sum _{i=1}^m{g}_i\left(t\right)x\left({\nu }_i\left(t\right)\right)-\sum _{i=1}^m{p}_i\left(t\right)x& ({\mu }_i\left(t\right))-\hfill \\ & -f(x\left({\tau }_1\left(t\right)\right),x\left({\tau }_2\left(t\right)\right),\dots ,x\left({\tau }_m\left(t\right)\right),x\left(t\right),t)=q\left(t\right),t\in \mathbb{R},\hfill \end{array}\end{array}$$

(1)

where $t\in \mathbb{R}$, $f:{\mathbb{R}}^{m+2}\to \mathbb{R}$ is continuous, $m\ge 1$, ${\mu }_i,{\nu }_i,{\tau }_i:\mathbb{R}\to \mathbb{R}$ are measurable functions, and $p_i,g_i,q\in L(\mathbb{R},\mathbb{R})$, $i=1,2,\dots ,m$.

Definition 1

([5]). By the solution of the Equation (1), we understand an absolutely continuous function $x:\mathbb{R}\to \mathbb{R}$ on every compact interval which satisfies (1) almost everywhere.

The main focus of this paper was to obtain the D-stability conditions (see Definition 4) for the unique solution for Equation (1), with initial value condition

$$x\left(t_0\right)=\alpha ,$$

(2)

and with the symmetric property

$$x\left(t\right)=x\left(\psi \right(t\left)\right),t\in (-\infty ,+\infty ),$$

(3)

where $\psi$ is a monotonously increasing $C^1$-function. The value of alpha in Formula (2) is selected by Condition (8). A typical example is a periodicity with $\psi \left(t\right)=t+p$. Because in reality there is no periodic symmetry, since there are always small noises, we demonstrate our theory in an example with a perturbation of periodic symmetry in Section 8. Of course, we develop our results for the more general $\psi \left(t\right)$ introduced above.

The paper is structured as follows: the main result of this investigation is presented in Section 7, in which we establish the D-stability conditions for the trivial solution of the nonlinear scalar initial value Problems (1) and (2) with the symmetric property (3). Notation and definitions can be found in Section 3 and Section 5, respectively. In Section 4, we summarize the conditions from [11,12] under which the symmetric functional differential Equation (1) setting on $\mathbb{R}$ can be studied using boundary value theory. In Section 6.1, we establish the conditions for a unique solution for the initial value linear symmetric scalar problem, where we also find conditions under which the unique solution is symmetrical (see Section 6.2).

3. Notation

• $\mathbb{R}$ is the space of real numbers with norm $|·|$;
• $I_{\psi }=[t_0,\psi \left(t_0\right)]$;
• L is the Banach space of Lebesgue integrable functions $p:[t_0,\psi \left(t_0\right)]\to \mathbb{R}$, with norm ${\parallel p\parallel }_L={\int }_{t_0}^{\psi \left(t_0\right)}\left|p\left(s\right)\right|ds$;
• D is the Banach space of absolutely continuous functions $x:[t_0,\psi \left(t_0\right)]\to \mathbb{R}$, with norm ${\parallel x\parallel }_D={\int }_{t_0}^{\psi \left(t_0\right)}\parallel x^{\prime }\left(\xi \right)\parallel d\xi +\parallel x\left(t_0\right)\parallel$;
• $g_i,{\nu }_i,p_i,{\mu }_i,{\tau }_i$, $i=1,\dots ,m$, q are Lebesgue measurable functions, $g_i,p_i$, $i=1,\dots ,m$, are essentially bounded functions on $\mathbb{R}$;
• The function ${\mu }_i\circ \psi$ defined by ${\mu }_i\left(\psi \left(t\right)\right)$ is called the composite function (or superposition) of ${\mu }_i$, $\psi$ and ${\mu }_i\circ \psi ={\psi }^j\circ {\mu }_i,i,j=1,2,\dots ,m,$ means that ${\mu }_i\left(\psi \left(t\right)\right)=\psi (\underset{j}{\underbrace{\psi (\dots }}\psi \left({\mu }_i\left(t\right)\right)\underset{j}{\underbrace{\dots \left)\right)}}$.

4. Symmetric Properties

Let us consider the special case in which deviations of the arguments ${\mu }_i$, ${\nu }_i$, ${\tau }_i$, $i=1,2,\dots ,$ m, and function $f:{\mathbb{R}}^{m+2}\to \mathbb{R}$ in Equation (1), as described in the next lemma.

Lemma 1

(Lemma 3.1 [12]). If there exist such integers $j_i,r_i,k_i$, $i=1,2,\dots ,m$, $m\in \mathbb{N}$, that deviations of the argument ${\mu }_i,{\nu }_i$ and ${\tau }_i$, $i=1,2,\dots ,m$ have the following properties:

$$\begin{array}{c}\hfill {\mu }_i\circ \psi ={\psi }^{j_i}\circ {\mu }_i,i=1,2,\dots ,m,\end{array}$$

(4)

$$\begin{array}{c}\hfill {\nu }_i\circ \psi ={\psi }^{r_i}\circ {\nu }_i,i=1,2,\dots ,m,\end{array}$$

(5)

$$\begin{array}{c}\hfill {\tau }_i\circ \psi ={\psi }^{k_i}\circ {\tau }_i,i=1,2,\dots ,m,\end{array}$$

(6)

then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\psi }^{\prime }\left(t\right)\left[\sum _{i=1}^m\right(p_i\left(\psi \left(t\right)\right)x\left({\mu }_i\left(\psi \left(t\right)\right)\right)-g_i\left(\psi \left(t\right)\right)& x\left({\nu }_i\left(\psi \left(t\right)\right)\right))+\hfill \\ \hfill +f(x\left({\tau }_1\left(\psi \left(t\right)\right)\right),x({\tau }_2& \psi \left(t\right)\left)\right),\dots ,x({\tau }_m\left(\psi \left(t\right)\right),x\left(\psi \left(t\right)\right),\psi \left(t\right)\left)\right]=\hfill \\ \hfill =\sum _{i=1}^m(p_i\left(t\right)& x\left(\psi \left({\mu }_i\left(t\right)\right)\right)-g_i\left(t\right)x\left(\psi \left({\nu }_i\left(t\right)\right)\right))+\hfill \\ & +f(x\left(\psi \left({\tau }_1\left(t\right)\right)\right),x\left(\psi \left({\tau }_2\left(t\right)\right)\right),\dots ,x\left(\psi \left({\tau }_m\left(t\right)\right)\right),x\left(\psi \left(t\right)\right),t)\hfill \end{array}\end{array}$$

(7)

for all $x:\mathbb{R}\to \mathbb{R}$, $i=1,\dots ,m$, with Property (3) and every $t\in \mathbb{R}$.

From the problem formulation, it is clear that a restriction $y=x{|}_{I_{\psi }}$ of every solution x on the interval $I_{\psi }:=[t_0,\psi \left(t_0\right)]$ satisfies a two-point boundary value condition

$$y\left(t_0\right)=y\left(\psi \left(t_0\right)\right)=\alpha .$$

(8)

Introducing the following notation and assumptions are necessary for further investigation:

• The increasing function $\psi$ generates an increasing numerical sequence

  $$\dots <{\psi }^{-2}\left(t_0\right)<{\psi }^{-1}\left(t_0\right)<t_0<\psi \left(t_0\right)<{\psi }^2\left(t_0\right)<\dots ;$$

  (9)
• Every point from Sequence (9) from (1) divides $\mathbb{R}$ on a specified quantity of intervals

  $$[{\psi }^j\left(t_0\right),{\psi }^{j+1}\left(t_0\right)],j\in \mathbb{Z};$$

  (10)
• Assume that the number j is a number of the interval (10).

Definition 2

([12]). For every $t\in \mathbb{R}$, we define the number $l\left(t\right)$ by a number of the interval (10) that contains the point t.

Taking into account the definition of the function $l:\mathbb{R}\to \mathbb{Z}$, then the next lemma is true.

Lemma 2

(Lemma 3.4 [12]). If function $y:I_{\psi }\to \mathbb{R}$ satisfies the two-point boundary value condition (8), then the function

$$x\left(t\right):=y\left({\psi }^{-l\left(t\right)}\left(t\right)\right),t\in \mathbb{R}$$

(11)

has Property (3).

Let us consider operators $\{{\xi }_i,{\kappa }_i,{\sigma }_i\}:C(I_{\psi },\mathbb{R})\to L_1(I_{\psi },\mathbb{R})$ for $i=1,2,\dots ,m$,

$$\left({\xi }_{i}x\right)\left(t\right):=\left\{\begin{array}{cc}x\left({\mu }_i\left(t\right)\right),\hfill & \mathrm{if}{\mu }_i\left(t\right)\in I_{\psi },\hfill \\ x\left({\psi }^{-l\left({\mu }_i\left(t\right)\right)}\left({\mu }_i\left(t\right)\right)\right),\hfill & \mathrm{if}{\mu }_i\left(t\right)\notin I_{\psi },\hfill \end{array}\right.$$

(12)

$$\left({\kappa }_{i}x\right)\left(t\right):=\left\{\begin{array}{cc}x\left({\nu }_i\left(t\right)\right),\hfill & \mathrm{if}{\nu }_i\left(t\right)\in I_{\psi },\hfill \\ x\left({\psi }^{-l\left({\nu }_i\left(t\right)\right)}\left({\nu }_i\left(t\right)\right)\right),\hfill & \mathrm{if}{\nu }_i\left(t\right)\notin I_{\psi },\hfill \end{array}\right.$$

(13)

$$\left({\sigma }_{i}x\right)\left(t\right):=\left\{\begin{array}{cc}x\left({\tau }_i\left(t\right)\right),\hfill & \mathrm{if}{\tau }_i\left(t\right)\in I_{\psi },\hfill \\ x\left({\psi }^{-l\left({\tau }_i\left(t\right)\right)}\left({\tau }_i\left(t\right)\right)\right),\hfill & \mathrm{if}{\tau }_i\left(t\right)\notin I_{\psi },\hfill \end{array}\right.$$

(14)

where $l\left(t\right)$ is the number of the intervals that contain a point $t\in \mathbb{R}$ (see Definition 2).

Lemma 3

(Lemma 3.5 [12]). Assume that function $y:I_{\psi }\to \mathbb{R}$ is a solution of the equation

$$y^{\prime }\left(t\right)=\sum _{i=1}^m\left(p_i\left(t\right)\left({\xi }_{i}y\right)\left(t\right)-g_i\left(t\right)\left({\kappa }_{i}y\right)\left(t\right)\right)+f\left(\left({\sigma }_{1}y\right)\left(t\right),\left({\sigma }_{2}y\right)\left(t\right),\dots ,\left({\sigma }_{m}y\right)\left(t\right),t\right),t\in I_{\psi },$$

(15)

and has Property (8).

Then, the function $x:\mathbb{R}\to \mathbb{R}$ defined by (11) is a solution to the problem ((1) and (3)).

5. Definitions of the $\mathit{D}$-Stability

Taking into account (12)–(14), and Lemma 3, let us apply Equation (1) for $t\in I_{\psi }$

$$\left(\mathcal{L}y\right)\left(t\right):=y^{\prime }\left(t\right)+\sum _{i=1}^m\left(g_i\left(t\right)\left({\xi }_{i}y\right)\left(t\right)-p_i\left(t\right)\left({\kappa }_{i}y\right)\left(t\right)\right),$$

(16)

$$\left(\mathcal{F}y\right)\left(t\right):=f\left(\left({\sigma }_{1}y\right)\left(t\right),\left({\sigma }_{2}y\right)\left(t\right),\dots ,\left({\sigma }_{m}y\right)\left(t\right),y\left(t\right),t\right).$$

(17)

Definition 3

([5]). The linear Equation

$$\mathcal{L}y=q,$$

(18)

is $\mathit{D}$-stable if Problem (18), (8) have a unique solution $\mathit{y}\in \mathit{D}$ for arbitrary $\mathit{q}\in \mathit{L}$, $\mathbf{\alpha }\in \mathbb{R}$ and this solution continuously depends on $\{\mathit{q},\mathbf{\alpha }\}$; this mean that for arbitrary $\mathbf{\epsilon }>\mathbf{0}$, there exists $\mathbf{\delta }>\mathbf{0}$ such that $\parallel {\mathit{y}}_{\mathbf{1}}-\mathit{y}\parallel <\mathbf{\epsilon }$ if $\parallel {\mathit{q}}_{\mathbf{1}}{-\mathit{q}\parallel }_{\mathit{L}}<\mathbf{\delta }$, $|{\mathbf{\alpha }}_{\mathbf{1}}-\mathbf{\alpha }|<\mathbf{\delta }$, where ${\mathit{y}}_{\mathbf{1}}$ is the solution of the Problem (18), (8) with $\mathit{q}={\mathit{q}}_{\mathbf{1}}$, $\mathbf{\alpha }={\mathbf{\alpha }}_{\mathbf{1}}$.

Let us consider the nonlinear functional differential Equation

$$\mathcal{N}y=q,y\left(t_0\right)=\alpha$$

(19)

where operator $\mathcal{N}:D\to L$ and $\mathcal{N}\left(0\right)=0$.

Definition 4

([5]). The nonlinear equation $\mathcal{N}y=0$ has a $\mathit{D}$-stable property in the vicinity of the trivial solution $\mathit{y}\equiv \mathbf{0}$ if there exist such ${\mathbf{\delta }}_{\mathbf{0}}>\mathbf{0}$ that for every pair $\{\mathit{q},\mathbf{\alpha }\}\in \mathit{L}\times \mathbb{R}$, satisfying conditions ${\parallel \mathit{q}\parallel }_{\mathit{L}}<{\mathbf{\delta }}_{\mathbf{0}}$, $\left|\mathbf{\alpha }\right|<{\mathbf{\delta }}_{\mathbf{0}}$, the problem (19) has a unique solution $\mathit{x}\in \mathit{D}$ and for arbitrary $\mathbf{\epsilon }>\mathbf{0}$ there exists such $\mathbf{\delta }=\mathbf{\delta }(\mathit{x},\mathbf{\epsilon })>\mathbf{0}$ that $\parallel {\mathit{y}}_{\mathbf{1}}{-\mathit{y}\parallel }_{\mathit{D}}<\mathbf{\epsilon }$ if $\parallel {\mathit{q}}_{\mathbf{1}}{-\mathit{q}\parallel }_{\mathit{L}}<\mathbf{\delta }$, $|{\mathbf{\alpha }}_{\mathbf{1}}-\mathbf{\alpha }|<\mathbf{\delta }$, where ${\mathit{y}}_{\mathbf{1}}$ is the solution of the problem (19) with $\mathit{q}={\mathit{q}}_{\mathbf{1}}$, $\mathbf{\alpha }={\mathbf{\alpha }}_{\mathbf{1}}$ and $\parallel {\mathit{q}}_{\mathbf{1}}{\parallel }_{\mathit{L}}<{\mathbf{\delta }}_{\mathbf{0}}$, $|{\mathbf{\alpha }}_{\mathbf{1}}|<{\mathbf{\delta }}_{\mathbf{0}}$.

6. A Unique and Symmetric Solution for the Initial Value Problem for Linear Scalar Functional Differential Equations

Remark 1.

Taking into account Lemmas 2 and 3, we study the initial-value problem (2) for nonlinear Equation (1) with the symmetric property (3) as a Problem (15), (8) in which operators ${\xi }_i$, ${\kappa }_i$, ${\sigma }_i$ and functions ${\mu }_i$, ${\nu }_i$, ${\tau }_i$ have properties (12)–(14) and (4)–(7) on interval $I_{\psi }$, respectively.

6.1. Unique Solvability

Here, we consider symmetric linear functional differential Equation (16) as a homogenous initial value problem

$$\begin{array}{cc}\hfill & y^{\prime }\left(t\right)=\sum _{i=1}^m{p}_i\left(t\right)\left({\xi }_{i}y\right)\left(t\right)-\sum _{i=1}^m{g}_i\left(t\right)\left({\kappa }_{i}y\right)\left(t\right),t\in I_{\psi },\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & y\left(t_0\right)=0\hfill \end{array}$$

(21)

and a nonhomogenous initial value problem

$$\begin{array}{cc}\hfill & y^{\prime }\left(t\right)=\sum _{i=1}^m{p}_i\left(t\right)\left({\xi }_{i}y\right)\left(t\right)-\sum _{i=1}^m{g}_i\left(t\right)\left({\kappa }_{i}y\right)\left(t\right)+q\left(t\right),t\in I_{\psi },\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & y\left(t_0\right)=\alpha ,\hfill \end{array}$$

(23)

where operators ${\xi }_i$ and ${\kappa }_i$, $i=1,2,\dots ,m$ are defined by (12) and (13) with properties (4) and (5) and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\psi }^{\prime }\left(t\right)\left[\sum _{i=1}^m\left(p_i\left(\psi \left(t\right)\right)y\left({\mu }_i\left(\psi \left(t\right)\right)\right)-g_i\left(\psi \left(t\right)\right)y\left({\nu }_i\left(\psi \left(t\right)\right)\right)\right)\right]=\hfill \\ & =\sum _{i=1}^m\left(p_i\left(t\right)y\left(\psi \left({\mu }_i\left(t\right)\right)\right)-g_i\left(t\right)y\left(\psi \left({\nu }_i\left(t\right)\right)\right)\right).\hfill \end{array}\end{array}$$

(24)

For the following investigation, we use the well-known result from the general theory of boundary value problems for the functional differential equation.

Lemma 4.

The nonhomogeneous Problem (23) for linear Equation (22) is uniquely solvable if the corresponding homogeneous Problem (21) for linear Equation (20) only has a trivial solution.

In Section 6.1, theorems are established regarding the conditions of the existence of a trivial solution for the homogenous Problem (21) for linear Equation (20) and regarding a unique solution for the corresponding nonhomogeneous Problem (23) for linear Equation (22). Furthermore, in Section 6.2, we find conditions in $\alpha$ from (2) sufficient for the symmetric property of the unique solution from Section 6.1.

If we take (12) and (13) into account, then the next obvious Lemma is true.

Lemma 5.

If measurable functions

$$\{{\nu }_i,{\mu }_i\},i=1,2,\dots ,m:I_{\psi }\to I_{\psi }$$

(25)

have the properties (4), (5), and (24), and operators ${\xi }_i$, ${\kappa }_i$ are defined by (12) and (13), then the nonhomogeneous Equation (22) is equivalent to the following equation:

$$y^{\prime }\left(t\right)+\sum _{i=1}^m\left(g_i\left(t\right)y\left({\nu }_i\left(t\right)\right)-p_i\left(t\right)y\left({\mu }_i\left(t\right)\right)\right)=q\left(t\right),t\in I_{\psi },$$

(26)

and the homogeneous Equation (20) is equivalent to the following equation:

$$y^{\prime }\left(t\right)+\sum _{i=1}^m\left(g_i\left(t\right)y\left({\nu }_i\left(t\right)\right)-p_i\left(t\right)y\left({\mu }_i\left(t\right)\right)\right)=0,t\in I_{\psi }.$$

(27)

Let us specify an arbitrary absolutely continuous $u_0\in C(I_{\psi },\mathbb{R})$ and construct a sequence of functions $u_k,k=0,1,\dots$ defined by the recurrence relation

$$u_k\left(t\right):=\sum _{i=1}^r{b}_i{\int }_{t_0}^t\sum _{i=1}^m(p_i\left(s\right)u_{k-i}\left({\mu }_i\left(s\right)\right)-g_i\left(s\right)u_{k-i}\left({\nu }_i\left(s\right)\right))ds,t\in I_{\psi },$$

(28)

where functions $\{{\nu }_i,{\mu }_i\},i=1,2,$ have the properties (25) and functions

$$u_k\left(t\right)\ge 0,t\in I_{\psi },\mathrm{and}{u}_k\left(t_0\right)=0.$$

(29)

In the case where $r=1$ and $b_1=1$, Equality (28) can be rewritten as

$$u_k\left(t\right):={\int }_{t_0}^t\sum _{i=1}^m(p_i\left(s\right)u_{k-1}\left({\mu }_i\left(s\right)\right)-g_i\left(s\right)u_{k-1}\left({\nu }_i\left(s\right)\right))ds,t\in I_{\psi },k=1,2,\dots ,$$

(30)

where functions $\{{\nu }_i,{\mu }_i\},i=1,2,$ have properties (25). Obviously, Formula (30) defines the standard iteration sequence used in studies of the uniqueness of the trivial solution of the integral functional equation

$$y\left(t\right)={\int }_{t_0}^t\sum _{i=1}^m(p_i\left(s\right)y\left({\mu }_i\left(s\right)\right)-g_i\left(s\right)y\left({\nu }_i\left(s\right)\right)ds,t\in I_{\psi },$$

which, obviously, is equivalent to the homogeneous problem ((27) and (21)).

Definition 5.

Consider the following equation:

$$y^{\prime }\left(t\right)=\left(ly\right)\left(t\right)+q\left(t\right),t\in I_{\psi }.$$

(31)

An operator l is said to be positive if for all $t\in I_{\psi }$, the relation $y\left(t\right)\ge 0$ implies that $\left(ly\right)\left(t\right)\ge 0$ for almost every $t\in I_{\psi }$.

Lemma 6.

If measurable functions $\{{\nu }_i,{\mu }_i\},i=1,2,$ have the properties (25) and

$$p_i\left(t\right)\ge 0,g_i\left(t\right)\le 0\mathit{for}\mathit{all}t\in I_{\psi }\mathit{and}i\in \mathbb{N}$$

(32)

are fulfilled, then the operator

$$\left(ly\right)(·):=\sum _{i=1}^m\left(p_i(·)y\left({\mu }_i(·)\right)-g_i(·)y\left({\nu }_i(·)\right)\right)$$

(33)

is positive.

Proof. 

Taking into account Definition 5 and (32), one can conclude that operator (33) is positive. □

In Theorems 1, 3, and Corollaries 1–3, the conditions regarding the existence of trivial solution of the linear Cauchy problem (21) for the Equation (20) are established, and correspondingly, on a unique solution for the linear Cauchy problem (23) for the Equation (22) with a variable deviation (not only a delay deviation).

Theorem 1.

Suppose that (32) is true and functions ${\mu }_i$ and ${\nu }_i$, $i=1,2,\dots ,m$, have the properties (24) and (25). Assume also that one can specify some integers r and m, $m\ge r\ge 1$, a real number $\rho \in (1,+\infty )$, some constants ${\left\{{\beta }_k\right\}}_{k=1}^m\subset [0,+\infty )$ and ${\left\{b_i\right\}}_{i=1}^r\subset [0,+\infty )$, and certain absolutely continuous vector-functions $u_0,u_1,\dots ,u_{r-1}$ satisfying Conditions (28) and (29), and the relation

$$\sum _{k=0}^r{\beta }_k{u}_k\left(t\right)>0\mathit{for}\mathit{all}t\in (t_0,\psi \left(t_0\right)]$$

(34)

such that the functional differential inequality

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sum _{k=0}^r{\beta }_k{u}_k^{\prime }\left(t\right)+\sum _{k=0}^r\left(\sum _{j\in T_{r,m}\left(k\right)}{\beta }_{j+k}{b}_j-\rho {\beta }_k\right)\sum _{i=1}^m(& p_i\left(t\right)u_k\left({\mu }_i\left(t\right)\right)g_i\left(t\right)u_k\left({\nu }_i\left(t\right)\right))-\hfill \\ & -\rho {\beta }_m\sum _{i=1}^m\left(p_i\left(t\right)u_m\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)u_m\left({\nu }_i\left(t\right)\right)\right)\ge 0\hfill \end{array}\end{array}$$

(35)

is satisfied for almost every t from $I_{\psi }$, where, by definition

$$T_{r,m}\left(k\right):=\{j\in \mathbb{N}|j\le r\le j+k\le m\}$$

(36)

for $r\in \mathbb{N}$, $m\ge r$, and $k=0,1,\dots ,m-1$.

Then, the homogenous linear initial value problem (21) for the Equation (27) only has a trivial solution and the nonhomogeneous linear Cauchy problem (23) for the Equation (26) is uniquely solvable for an arbitrary $\alpha \in \mathbb{R}$ and an arbitrary function $q\in L(I_{\psi },\mathbb{R})$. The unique solution of the problem (23) for the Equation (26) is representable in the form of a functional series

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill y\left(t\right)=\tilde{q}\left(t\right)& +{\int }_{t_0}^t\sum _{i=1}^m{p}_i\left(r\right)\tilde{q}\left(r\right)dr-{\int }_{t_0}^t\sum _{i=1}^m{g}_i\left(r\right)\tilde{q}\left(r\right)dr+\hfill \\ & +{\int }_{t_0}^t\sum _{i=1}^m{p}_i\left(r\right){\int }_{t_0}^{{\mu }_i\left(r\right)}\sum _{i=1}^m{p}_i\left(\xi \right)\tilde{q}\left(\xi \right)d\xi dr-{\int }_{t_0}^t\sum _{i=1}^m{p}_i\left(r\right){\int }_{t_0}^{{\mu }_i\left(r\right)}\sum _{i=1}^m{g}_i\left(\xi \right)\tilde{q}\left(\xi \right)d\xi dr-\hfill \\ & -{\int }_{t_0}^t\sum _{i=1}^m{g}_i\left(r\right){\int }_{t_0}^{{\nu }_i\left(r\right)}\sum _{i=1}^m{p}_i\left(\xi \right)\tilde{q}\left(\xi \right)d\xi dr+{\int }_{t_0}^t\sum _{i=1}^m{g}_i\left(r\right){\int }_{t_0}^{{\nu }_i\left(r\right)}\sum _{i=1}^m{g}_i\left(\xi \right)\tilde{q}\left(\xi \right)d\xi dr+\dots ,\hfill \end{array}\end{array}$$

(37)

where

$$\tilde{q}\left(t\right):=\alpha +{\int }_{t_0}^{t}q\left(s\right)ds$$

(38)

is uniformly convergent on $I_{\psi }$.

Moreover, if α and the function q are such that for all t from $I_{\psi }$, one has

$${\int }_{t_0}^{t}q\left(s\right)ds\ge -\alpha ,$$

(39)

then, at every point t of the interval $I_{\psi }$, the unique solution (37) of a problem (23) for the Equation (26) is non-negative.

Proof. 

For further investigation, we need Theorem 2.2 from [13]. □

Theorem 2

(Theorem 2.2 [13]). Suppose that the operator $l:C[I_{\psi },\mathbb{R}]\to L[I_{\psi },\mathbb{R}]$ in the linear functional differential Equation (31) is positive. Assume also that one can specify some integers r and m, $m\ge r\ge 1$, a real number $\rho \in (1,+\infty )$, some constants ${\left\{{\beta }_k\right\}}_{k=1}^m\subset [0,+\infty )$ and ${\left\{b_i\right\}}_{i=1}^r\subset [0,+\infty )$, and certain absolutely continuous vector-functions $u_0,u_1,\dots ,u_{r-1}$ constructed by the recurrence relation

$$u_k\left(t\right)=\sum _{i=1}^r{b}_i{\int }_{t_0}^t\left(l{u}_{k-i}\right)\left(s\right)ds,t\in I_{\psi },k\ge r,$$

satisfying Condition (29), and relation (34) such that the functional differential inequality

$$\sum _{k=0}^r{\beta }_k{u}_k^{\prime }\left(t\right)+\sum _{k=0}^{m-1}\left(\sum _{j\in T_{r,m}\left(k\right)}{\beta }_{j+k}{b}_j-\rho {\beta }_k\right)\left(l{u}_k\right)\left(t\right)-\rho {\beta }_m\left(l{u}_m\right)\left(t\right)\ge 0$$

(40)

is satisfied for almost every t from $I_{\psi }$, where, by definition $T_{r,m}\left(k\right)$ is defined by (36) for $r\in \mathbb{N}$, $m\ge r$, and $k=0,1,\dots ,m-1$.

Then, the homogeneous linear Cauchy problem (21) for the Equation (31) (with $q=0$) only has a trivial solution and the inhomogeneous linear Cauchy problem (23) for the Equation (31) is uniquely solvable for an arbitrary $\alpha \in \mathbb{R}$ and an arbitrary function $q\in L(I_{\psi },\mathbb{R})$. The unique solution of the problem (23) for the Equation (31) is representable in the form of a functional series uniformly convergent on $I_{\psi }$, namely,

$$y\left(t\right)=\tilde{q}\left(t\right)+{\int }_{t_0}^t\left(l\tilde{q}\right)\left(s\right)ds+{\int }_{t_0}^{t}l\left({\int }_{t_0}^{·}\left(l\tilde{q}\right)\left(\xi \right)d\xi \right)ds+\dots ,t\in I_{\psi },$$

(41)

where $\tilde{q}\left(t\right)$ is defined by (38).

Moreover, if α and the function q are such that for all t from $I_{\psi }$, one has (39), then, at every point t of the interval $I_{\psi }$, the unique solution (41) of a problem (23) for the Equation (31) is non-negative.

Now, let us put operator l by (33). Obviously, operator l in (33) is positive. Using Formula (33), it is easy to verify that, in this case, (35) coincides with Inequality (40). Applying Theorem 2, we obtain Theorem 1.

Remark 2.

For an arbitrary integer k such that $0\le k\le m-1$, a number j belongs to the set $T_{2,m}\left(k\right)$ if and only if either $j=1$ or $j=2$, i.e., ${\cup }_{k=0}^{m-1}{T}_{2,m}\left(k\right)\subset \{1,2\}$. Therefore, with these values of the parameters, the differential inequality (35) has the form

$$\begin{array}{c}{\beta }_0{u}_0^{\prime }\left(t\right)+{\beta }_1{u}_1^{\prime }\left(t\right)+(b_2{\beta }_2-\rho {\beta }_0)\sum _{i=1}^m\left(p_i\left(t\right)u_0\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)u_0\left({\nu }_i\left(t\right)\right)\right)+\hfill \\ +\sum _{k=1}^{m-2}(b_1{\beta }_{k+1}+b_2{\beta }_{k+2}-\rho {\beta }_k)\sum _{i=1}^m\left(p_i\left(t\right)u_k\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)u_k\left({\nu }_i\left(t\right)\right)\right)+\\ +(b_1{\beta }_m-\rho {\beta }_{m-1})\sum _{i=1}^m\left(p_i\left(t\right)u_{m-1}\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)u_{m-1}\left({\nu }_i\left(t\right)\right)\right)-\\ \hfill -\rho {\beta }_m\sum _{i=1}^m\left(p_i\left(t\right)u_m\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)u_m\left({\nu }_i\left(t\right)\right)\right)\ge 0.\end{array}$$

Let us assume that

$$b_1{\beta }_{k+1}+b_2{\beta }_{k+2}=\rho {\beta }_k.$$

(42)

Then, the following Corollary is true.

Corollary 1.

Suppose that (32) is true and functions ${\mu }_i$ and ${\nu }_i$, $i=1,2,\dots ,m$, have the properties (24) and (25). Furthermore, there exist some $\rho \in (1,\infty )$, $\gamma \in (0,\rho )$, and certain absolutely continuous vector-functions $z_0,z_1:I_{\psi }\to \mathbb{R}$ satisfying conditions $z_k\left(t\right)>0$ and $z_k\left(t_0\right)=0$ for all $t\in (t_0,\psi \left(t_0\right)]$, $k=0,1$, and for almost every t from $I_{\psi }$, the inequality

$$\begin{array}{c}\hfill z_0^{\prime }\left(t\right)+z_1^{\prime }\left(t\right)-(\rho -\gamma )\sum _{i=1}^m\left(p_i\left(t\right)z_0\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)z_0\left({\nu }_i\left(t\right)\right)\right)-\gamma \sum _{i=1}^m\left(p_i\left(t\right)z_1\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)z_1\left({\nu }_i\left(t\right)\right)\right)-\\ \hfill -\rho \sum _{i=1}^m\left(p_i\left(t\right)z_2\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)z_2\left({\nu }_i\left(t\right)\right)\right)\ge 0,\end{array}$$

(43)

where

$$z_2\left(t\right):=(\rho -\gamma ){\int }_{t_0}^t\sum _{i=1}^m\left(p_i\left(t\right)z_1\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)z_1\left({\nu }_i\left(t\right)\right)\right)ds+\gamma {\int }_{t_0}^t\sum _{i=1}^m\left(p_i\left(t\right)z_0\left({\mu }_i\left(t\right)\right)-g_i\left(t\right)z_0\left({\nu }_i\left(t\right)\right)\right)ds,$$

then the assertion of Theorem 1 is true.

Proof. 

To prove Corollary 1, we need Theorem 1. First of all, note that Sequence (43) is a particular case of (35) with a suitable choice of coefficients. More precisely, $u_0=z_0$, $u_1=z_1$, $r=2$, $m=2$ and

$$b_2=b,b_1=b.$$

(44)

We can apply Theorem 1. Indeed, let us set ${\beta }_k=\beta$, $k=0,1,2$ where $\beta$ is a certain positive constant. Since, by (44), $b_1+b_2=\rho$, it is obvious that the relations (42) are satisfied. Inequality (35) in our case has the form (43). □

Theorem 3.

Suppose that (32) is true and functions ${\mu }_i$ and ${\nu }_i$, $i=1,2,\dots ,m$, have properties (24) and (25), and, moreover, there exist an absolutely continuous function $u_0:I_{\psi }\to \mathbb{R}$ with properties

$$u_0\left(t_0\right)=0\mathit{and}{u}_0\left(t\right)>0\mathit{for}t\in (t_0,\psi \left(t_0\right)],$$

(45)

a natural number m, non-negative integers k and $r\ge 1$, and real numbers ρ, $\rho >1$, $c\in (0,1)$ such that, for almost every t from the interval $I_{\psi }$, the following inequality is satisfied:

$$u_0^{\prime }\left(t\right)-\frac{{\rho }^{k+1}}{1-c}\sum _{i=1}^m\left(p_i\left(t\right)\left({\rho }^r{u}_{k+r}\left({\mu }_i\left(t\right)\right)-c{u}_k\left({\mu }_i\left(t\right)\right)\right)-g_i\left(t\right)\left({\rho }^r{u}_{k+r}\left({\nu }_i\left(t\right)\right)-c{u}_k\left({\nu }_i\left(t\right)\right)\right)\right)\ge 0,$$

(46)

where $u_k$ is constructed by (30).

Then, the assertion of Theorem 1 is true.

Proof. 

To prove Theorem 3, we need Theorem 2 from [14]. □

Theorem 4

(Theorem 2 [14]). Suppose that in the linear functional differential equation (31) with initial condition (23), operator $l:C[I_{\psi },\mathbb{R}]\to L[I_{\psi },\mathbb{R}]$ is positive and, moreover, there exists an absolutely continuous function $u_0:I_{\psi }\to \mathbb{R}$ with property (45), a natural number m, non-negative integers k and $r\ge 1$, and real numbers ρ, $\rho >1$, $c\in (0,1)$ such that, for almost every t from the interval $I_{\psi }$, the following inequality is satisfied:

$$u_0^{\prime }\left(t\right)-\frac{{\rho }^{k+1}}{1-c}l\left({\rho }^r{u}_{k+r}-c{u}_k\right)\left(t\right)\ge 0t\in I_{\psi }.$$

(47)

Then, the assertion of Theorem 2 is true.

It is easy to see that (46) is Inequality (47) with operator l defined by (33). Condition (32) ensures the positivity of the operator from Equations (20) and (22). Applying Theorem 4, we adhere to the conditions of Theorem 3.

Corollary 2.

Suppose that (32) is true and functions ${\mu }_i$ and ${\nu }_i$, $i=1,2,\dots ,m$, have the properties (24) and (25). Moreover, let there exist real numbers $c\in (0,1)$ and $\rho \in (1,+\infty )$, non-negative integers k and $r\ge 1$ such that, for almost every t from the interval $I_{\psi }$, the following inequalities are satisfied:

$$\begin{array}{cc}\hfill d|t-t_0{|}^{d-1}\ge \frac{\rho }{1-c}\sum _{i=1}^m{p}_i\left(t\right){\int }_{t_0}^{{\mu }_i\left(t\right)}\sum _{i=1}^m(p_i\left(s\right)|{\mu }_i& \left(s\right)-t_0{|}^d-g_i\left(s\right){|{\nu }_i\left(s\right)-t_0|}^d)ds-\hfill \\ \hfill -\frac{\rho }{1-c}\sum _{i=1}^m{g}_i\left(t\right){\int }_{t_0}^{{\nu }_i\left(t\right)}\sum _{i=1}^m(p_i\left(s\right)& |{\mu }_i\left(s\right)-t_0{|}^d-g_i\left(s\right){|{\nu }_i\left(s\right)-t_0|}^d)ds-\hfill \\ & -\sum _{i=1}^m{p}_i\left(t\right)c|{\mu }_i\left(t\right)-t_0{|}^d+\sum _{i=1}^m{g}_i\left(t\right)c{|{\nu }_i\left(t\right)-t_0|}^d.\hfill \end{array}$$

(48)

Then, the assertion of Theorem 1 is true.

Proof. 

To prove Theorem 2, we need Theorem 3. Here, we have function $u_0$ defined by

$$u_0\left(t\right):={|t-t_0|}^d,t\in I_{\psi },d\in \mathbb{N}.$$

(49)

In this case, according to (49),

$$u_0^{\prime }\left(t\right)=d{|t-t_0|}^{d-1},t\in I_{\psi },d\in \mathbb{N}.$$

(50)

Taking into account the recurrent sequence (30), we obtain (48) from (46). Applying Theorem 3 with $k=0$ and $r=1$, we obtain Corollary 2. □

Corollary 3.

Suppose that (32) is true, functions ${\mu }_i$ and ${\nu }_i$, $i=1,2,\dots ,m$, have the properties (24) and (25), and inequality

$${\int }_{t_0}^t\sum _{i=1}^m\left(p_i\left(s\right)|{\mu }_i\left(s\right)-t_0{|}^d-g_i\left(s\right){|{\nu }_i\left(s\right)-t_0|}^d\right)ds\le \gamma {|t-t_0|}^d,t\in I_{\psi }$$

(51)

is fulfilled, where $\gamma \in (0,1)$ is a certain constant.

Then, the assertion of Theorem 1 is true.

Proof. 

For $\gamma \in (0,1)$ and $r\in N$, we choose number c and $\rho$ such that

$$0<c<1,\rho >1,\gamma =\frac{c}{{\rho }^r}.$$

This can obviously be done. In view of (32) for ${\mu }_i$ and ${\nu }_i$, $i=1,2,\dots ,m$, with properties (24) and (25) for such c and $\rho$, the relation (51) yields

$$\begin{array}{cc}\hfill & \gamma |t-t_0{|}^d-{\int }_{t_0}^t\sum _{i=1}^m\left(p_i\left(s\right)|{\mu }_i\left(s\right)-t_0{|}^d-g_i\left(s\right){|{\nu }_i\left(s\right)-t_0|}^d\right)ds\ge 0\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\int }_{t_0}^t\sum _{i=1}^m\left(p_i\left(s\right)|{\mu }_i\left(s\right)-t_0{|}^d-g_i\left(s\right){|{\nu }_i\left(s\right)-t_0|}^d\right)ds-\gamma {|t-t_0|}^d\le 0.\hfill \end{array}$$

Let us define $u_0$ by (49). In view of (50), $(u_0^{\prime }\left(t\right)\ge 0)$ implies that the condition (46) is satisfied for the values of c and $\rho$ specified above and the positivity of the operator (33) (in view of Lemma 6). It is easy to verify that Inequality (51) is a particular case of (46) for $k=0$, $r=1$, and, in this case, according to (30), we have

$$u_1\left(t\right)={\int }_{t_0}^t\sum _{i=1}^m\left(p_i\left(s\right)|{\mu }_i\left(s\right)-t_0{|}^d-g_i\left(s\right){|{\nu }_i\left(s\right)-t_0|}^d\right)ds.$$

Applying Theorem 3, we obtain Corollary 3. □

There are many more other conditions on the unique solvability of the initial value problem for functional differential equations, for example, in [13,14,20,21,22,23] and the references therein.

6.2. Symmetric Solution

The objective of our investigation was to find not only a unique solution for the linear problem (23) for the Equation (22) but also a symmetric solution (solution with Property (3)).

It is a well-known representation of the solution (37) of the problem (23) for the Equation (26) from

$$y\left(t\right)=\alpha y_0\left(t\right)+Q\left(t\right),$$

(52)

where

$$\begin{array}{cc}\hfill y_0\left(t\right)=1+{\int }_{t_0}^t\sum _{i=1}^m(p_i\left(r\right)-g_i\left(r\right))dr+{\int }_{t_0}^t\sum _{i=1}^m& (p_i\left(r\right){\int }_{t_0}^{{\mu }_i\left(r\right)}\sum _{i=1}^m(p_i\left(s\right)-g_i\left(s\right))dsdr-\hfill \\ \hfill & -{\int }_{t_0}^t\sum _{i=1}^m{g}_i\left(r\right){\int }_{t_0}^{{\nu }_i\left(r\right)}\sum _{i=1}^m(p_i\left(s\right)-g_i\left(s\right))dsdr+\dots ,\hfill \end{array}$$

(53)

is the solution (37) of Equation (26) with $q\left(t\right)=0$ and $\alpha =1$; and

$$\begin{array}{cc}\hfill Q\left(t\right)={\int }_{t_0}^{t}q\left(s\right)ds+{\int }_{t_0}^t\sum _{i=1}^m(p_i\left(s\right)& -g_i\left(s\right)){\int }_{t_0}^{s}q\left(v\right)dv)ds+\hfill \\ \hfill +{\int }_{t_0}^t\sum _{i=1}^m{p}_i\left(r\right)& {\int }_{t_0}^{{\mu }_i\left(r\right)}\left(\sum _{i=1}^m(p_i\left(\xi \right)-g_i\left(\xi \right)){\int }_{t_0}^{\xi }q\left(v\right)dv\right)d\xi dr-\hfill \\ & -{\int }_{t_0}^t\sum _{i=1}^m{g}_i\left(r\right){\int }_{t_0}^{{\nu }_i\left(r\right)}\sum _{i=1}^m(p_i\left(\xi \right)-g_i\left(\xi \right)){\int }_{t_0}^{\xi }q\left(v\right)dv)d\xi dr+\dots ,\hfill \end{array}$$

(54)

is the solution (37) of Equation (26) with $\alpha =0$ and arbitrary $q\left(t\right)\in L$. Assume that $y_0\left(\psi \left(t_0\right)\right)\ne 1$ (which means that this is not case of resonance), then from (8) and (52), we have

$$\alpha =\alpha y_0\left(\psi \left(t_0\right)\right)+Q\left(\psi \left(t_0\right)\right),$$

where $y_0$ and $Q\left(t\right)$ are defined by (53) and (54), respectively.

If we have the resonance case $y_0\left(\psi \left(t_0\right)\right)=1$, then this is Fredholm’s alternative, and a solution exists only for $q\left(t\right)$ such that $Q\left(\psi \left(t_0\right)\right)=0$, which is not unique and the kernel is 1-dimensional.

Now, we are ready to establish the next Theorem.

Theorem 5.

If α in (2) has the representation

$$\alpha =\frac{Q\left(\psi \left(t_0\right)\right)}{1-y_0\left(\psi \left(t_0\right)\right)}$$

(55)

and

$$\begin{array}{c}{\int }_{t_0}^{\psi \left(t_0\right)}\sum _{i=1}^m(p_i\left(r\right)-g_i\left(r\right))dr+{\int }_{t_0}^{\psi \left(t_0\right)}\sum _{i=1}^m(p_i\left(r\right){\int }_{t_0}^{{\mu }_i\left(r\right)}\sum _{i=1}^m(p_i\left(s\right)-g_i\left(s\right))dsdr-\hfill \\ \hfill -{\int }_{t_0}^{\psi \left(t_0\right)}\sum _{i=1}^m{g}_i\left(r\right){\int }_{t_0}^{{\nu }_i\left(r\right)}\sum _{i=1}^m(p_i\left(s\right)-g_i\left(s\right))dsdr,+\cdots \ne 0,\end{array}$$

where

$$\begin{array}{cc}\hfill y_0\left(\psi \left(t_0\right)\right)=1+{\int }_{t_0}^{\psi \left(t_0\right)}\sum _{i=1}^m(p_i\left(r\right)-g_i\left(r\right))dr& +{\int }_{t_0}^{\psi \left(t_0\right)}\sum _{i=1}^m(p_i\left(r\right){\int }_{t_0}^{{\mu }_i\left(r\right)}\sum _{i=1}^m(p_i\left(s\right)-g_i\left(s\right))dsdr-\hfill \\ \hfill & -{\int }_{t_0}^{\psi \left(t_0\right)}\sum _{i=1}^m{g}_i\left(r\right){\int }_{t_0}^{{\nu }_i\left(r\right)}\sum _{i=1}^m(p_i\left(s\right)-g_i\left(s\right))dsdr+\dots ,\hfill \end{array}$$

(56)

and

$$\begin{array}{cc}\hfill Q\left(\psi \left(t_0\right)\right)={\int }_{t_0}^{\psi \left(t_0\right)}q\left(s\right)ds+& {\int }_{t_0}^{\psi \left(t_0\right)}\sum _{i=1}^m\left(p_i\left(s\right)-g_i\left(s\right)\right){\int }_{t_0}^{s}q\left(v\right)dv)ds+\hfill \\ \hfill +{\int }_{t_0}^{\psi \left(t_0\right)}& \sum _{i=1}^m{p}_i\left(r\right){\int }_{t_0}^{{\mu }_i\left(r\right)}\left(\sum _{i=1}^m(p_i\left(\xi \right)-g_i\left(\xi \right)){\int }_{t_0}^{\xi }q\left(v\right)dv\right)d\xi dr-\hfill \\ & -{\int }_{t_0}^{\psi \left(t_0\right)}\sum _{i=1}^m{g}_i\left(r\right){\int }_{t_0}^{{\nu }_i\left(r\right)}\sum _{i=1}^m(p_i\left(\xi \right)-g_i\left(\xi \right)){\int }_{t_0}^{\xi }q\left(v\right)dv)d\xi dr+\dots ,\hfill \end{array}$$

(57)

then, the problem (23) for the Equation (26) has a unique symmetric solution represented by (52) with (53)–(55).

7. $\mathit{D}$-Stability of Nonlinear Functional Differential Equations

In this section, we assume that operator $\mathcal{N}$ from (19) has the representation

$$\mathcal{N}x\equiv \mathcal{L}x-\mathcal{F}x-q,$$

(58)

where $\mathcal{L}:D\to L$ is a linear bounded operator from (16) and $\mathcal{F}:D\to L$ is a nonlinear operator from (17) and has the property $\mathcal{F}\left(0\right)=0$ and $q\in L$.

In further investigations, we only study the D-stability of the trivial solution of Equation (1), as more general cases come down to this one.

Theorem 6.

Assume there exist $K>0$, $M>0$ and $\delta >0$ such that, for all $\parallel y_i{\parallel }_D\le \delta$, $i=1,2$, the inequalities

$${∥\sum _{i=1}^m(p_i\left(t\right)\left({\xi }_i{y}_1\right)\left(t\right)-g_i\left(t\right)\left({\kappa }_i{y}_1\right)\left(t\right))-\sum _{i=1}^m(p_i\left(t\right)\left({\xi }_i{y}_2\right)\left(t\right)-g_i\left(t\right)\left({\kappa }_i{y}_2\right)\left(t\right))∥}_L\le K{\parallel y_1-y_2\parallel }_D$$

(59)

and

$$\parallel f\left(\left({\sigma }_1{y}_1\right),\left({\sigma }_2{y}_1\right),\dots ,\left({\sigma }_m{y}_1\right),y_1,t\right)-f\left(\left({\sigma }_1{y}_2\right),\left({\sigma }_2{y}_2\right),\dots ,\left({\sigma }_m{y}_2\right),y_2,t\right){\parallel }_L\le M{\parallel y_1-y_2\parallel }_D$$

(60)

are true and

$$(\psi \left(t_0\right)-t_0)(K+M)<1.$$

(61)

If

$$f(0,0,\dots ,0,t)=0,$$

(62)

then the problem ((1) and (2)) is D-stable in the vicinity of the trivial solution.

Proof. 

In view of Lemmas 1 and 3, the initial value problem ((1) and (2)) is equivalent to the following equation:

$$\begin{array}{cc}\hfill y\left(t\right)={\int }_{t_0}^t(\sum _{i=1}^m{p}_i\left(s\right)y\left({\mu }_i\left(s\right)\right)& -\sum _{i=1}^m{g}_i\left(s\right)y\left({\nu }_i\left(s\right)\right)+\hfill \\ \hfill & +f(\left({\sigma }_{1}y\right)\left(s\right),\left({\sigma }_{2}y\right)\left(s\right),\dots ,\left({\sigma }_{m}y\right)\left(s\right),y\left(s\right),s)+q\left(s\right))ds+\alpha t\in I_{\psi }.\hfill \end{array}$$

(63)

From the conditions of our theorem, we have that for some positive $(K+M)<\frac{1}{\psi \left(t_0\right)-t_0}$ there exists such $\delta >0$ that for arbitrary $y_i\in D$, $\parallel y_i{\parallel }_D\le \delta$, $i=1,2$, the inequalities (59)–(61) are fulfilled. Taking into account (59)–(61) and the local Banach theorem regarding contractive mapping in a sphere $\{\parallel y{\parallel }_D\le \delta \}$ with ${\parallel r\parallel }_D<\delta (1-(\psi \left(t_0\right)-t_0)(K+M))$, where

$$r\left(t\right):={\int }_{t_0}^{t}q\left(s\right)ds+\alpha ,$$

(64)

there exists a unique solution $y\in D$ for Equation (63) and, in view of Lemmas 1 and 3, correspondingly, there exists a unique solution to the problem ((1) and (2)). Furthermore, for the solutions $y_i$, $i=1,2$, of this problem with the condition

$$\parallel q_i{\parallel }_L<{\delta }_0,\left|{\alpha }_i\right|<{\delta }_0,i=1,2,$$

(65)

where

$${\delta }_0=\frac{\delta (1-(\psi \left(t_0\right)-t_0)(K+M))}{1+(\psi \left(t_0\right)-t_0)},$$

(66)

we have that

$$\parallel y_1-y_2{\parallel }_D\le \frac{\parallel r_1-r_2{\parallel }_D}{1-(\psi \left(t_0\right)-t_0)(K+M)}\le \frac{(\psi \left(t_0\right)-t_0)\parallel q_1-q_2{\parallel }_L+|{\alpha }_1-{\alpha }_2\left|\right)}{1-(\psi \left(t_0\right)-t_0)(K+M)}.$$

(67)

It follows the continuous dependence of the solution y of Equation (63) on a norm of the space D from r with ${\parallel r\parallel }_D<\delta (1-(\psi \left(t_0\right)-t_0)(K+M))$ and, consequently, for the problem (1) from q and $\alpha$ with ${\parallel q\parallel }_L<\delta$, $\left|\alpha \right|<\delta$. Thus, the theorem is proved. □

Taking into account Theorem 6, the next obvious Corollary, i.e., 4, and Theorem 7 from Theorem 1, Theorem 3, Corollary 1, Corollary 2, or Corollary 3, are true.

Corollary 4.

Assume that the conditions from Theorem 1, Theorem 3, Corollary 1, Corollary 2, or Corollary 3 are true. Then, the linear problem ((22) and (23)) is D-stable (see Definition 3).

If the measurable functions ${\nu }_i,{\mu }_i$, $i=1,2,\dots ,m$ have the properties (24) and (25) then the next Theorem is true.

Theorem 7.

Assume that the conditions from Theorem 1, Theorem 3, Corollary 1, Corollary 2, or Corollary 3 are true, and for any $M>0$, there is a $\delta >0$ such that inequality (60) holds for all $\parallel y_1{\parallel }_D\le \delta$, $\parallel y_2{\parallel }_D\le \delta$, and (62) is also satisfied. Then, the problem ((1) and (2)) is D-stable in the vicinity of the trivial solution (see Definition 4). If the assumptions of Theorem 5 are true, then the symmetric problem ((1) and (3)) is D-stable in the vicinity of the trivial solution.

8. Application

Here, we investigate the more interesting case of Equation (1):

$$x^{\prime }\left(t\right)=\sum _{i=1}^m{p}_i\left(t\right)x(t+\frac{1}{2}sint)+\frac{c\left(t\right){\left(x\left({\tau }_1\left(t\right)\right)\right)}^{2\nu +1}}{a\left(t\right)+{\left(x\left({\tau }_2\left(t\right)\right)\right)}^{2\nu }}+q\left(t\right),$$

(68)

with symmetric property (3), in view of

$$x\left(t\right)=x(t+\frac{1}{2}sint+2\pi ),t\in (-\infty ,\infty ),$$

(69)

and the initial value condition (2), where $t\in \mathbb{R}$, $m\ge 1$, ${\tau }_i:\mathbb{R}\to \mathbb{R}$, $i=1,2,\dots ,m$, are measurable functions, $p_i,q\in L(\mathbb{R},\mathbb{R})$, $i=1,2,\dots ,m$, and a, $p_i$, c are functions integrable on every bounded interval, such that

$$\begin{array}{cc}\hfill \sum _{i=1}^m{p}_i\left(t\right)\ge 0,\sum _{i=1}^m{p}_i\left(t\right)=(1+\frac{1}{2}cost)& \sum _{i=1}^m{p}_i(t+\frac{1}{2}sint+2\pi );\hfill \\ \hfill a\left(t\right)=a(t+\frac{1}{2}sint+& 2\pi );c\left(t\right)=(1+\frac{1}{2}cost)c(t+\frac{1}{2}sint+2\pi );\hfill \\ \hfill & {\tau }_j(t+\frac{1}{2}sint+2\pi )={\tau }_j\left(t\right)+\frac{1}{2}sin\left({\tau }_j\left(t\right)\right)+2\pi ,j=1,2\hfill \end{array}$$

(70)

for all $t\in (-\infty ,\infty )$. Property (70) has, for example, functions ${\tau }_j\left(t\right)=t+2n_j\pi ,j=1,2,n_j\in \mathbb{N},t\in \mathbb{R}$; ${\tau }_j\left(t\right)=t+\frac{1}{2}sint,j=1,2,t\in \mathbb{R}$.

It is easy to see that the problem ((68) and (69)) is a particular case of the general problem from (1) and (3) with $\psi \left(t\right)=t+\frac{1}{2}sint+2\pi$ on $\mathbb{R}$, $g\left(t\right)\equiv 0$, $\mu \left(t\right)=t+\frac{1}{2}sint$, $f\left(t\right)=\frac{c\left(t\right){\left(x\left({\tau }_1\left(t\right)\right)\right)}^{2\nu +1}}{a\left(t\right)+{\left(x\left({\tau }_2\left(t\right)\right)\right)}^{2\nu }}$.

It is easy to see that in Term (70), Equation (68) has the properties (4)–(7)

$$\begin{array}{cc}\hfill & (1+\frac{1}{2}cost)(\sum _{i=1}^m{p}_i(t+\frac{1}{2}sint+2\pi )x\left(t+\frac{1}{2}sint+2\pi +\frac{1}{2}sin(t+\frac{1}{2}sint)\right)+\hfill \\ \hfill +& \frac{c(t+\frac{1}{2}sint+2\pi ){\left(x\left({\tau }_1(t+\frac{1}{2}sint+2\pi )\right)\right)}^{2\nu +1}}{a(t+\frac{1}{2}sint+2\pi )+{\left(x\left({\tau }_2(t+\frac{1}{2}sint+2\pi )\right)\right)}^{2\nu }})=\hfill \\ \hfill =& \sum _{i=1}^m{p}_i\left(t\right)x\left(t+\frac{1}{2}sint+\frac{1}{2}sin(t+\frac{1}{2}sint)+2\pi \right)+\frac{c\left(t\right){\left(x({\tau }_1\left(t\right)+\frac{1}{2}sin\left({\tau }_1\left(t\right)\right)+2\pi )\right)}^{2\nu +1}}{a\left(t\right)+{\left(u({\tau }_2\left(t\right)+\frac{1}{2}sin\left({\tau }_2\left(t\right)\right)+2\pi )\right)}^{2\nu }}\hfill \end{array}$$

for any t with the given $\psi \left(t\right)=t+\frac{1}{2}sint+2\pi$ and $k_1=1$, $k_2=1$.

Consequently, taking into account Lemmas 1, 3, and 5, the problem of finding solutions $x:\mathbb{R}\to \mathbb{R}$ of (68) possessing property (69) can be replaced by the corresponding two-point problem

$$\begin{array}{cc}\hfill u^{\prime }\left(t\right)& =\sum _{i=1}^m{p}_i\left(t\right)u(t+\frac{1}{2}sint)+\frac{c\left(t\right){\left(u\left({\tau }_1\left(t\right)\right)\right)}^{2\nu +1}}{a\left(t\right)+{\left(u\left({\tau }_2\left(t\right)\right)\right)}^{2\nu }}+q\left(t\right),\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill u\left(0\right)& =u\left(2\pi \right),\hfill \end{array}$$

(72)

on a bounded interval $[0,2\pi ]$.

Function $p\left(t\right)$ in the general case can be represented, for example, by the graph in Figure 1.

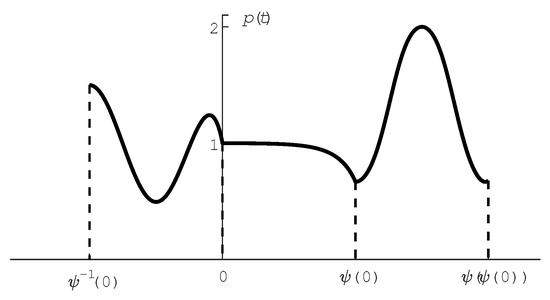
Figure 1. Function $p\left(t\right)$ on the interval $[{\psi }^{-1}\left(0\right),0]\cup [0,\psi \left(0\right)]\cup [\psi \left(0\right),\psi \left(\psi \left(0\right)\right)].$

Here,

$$\begin{array}{cc}\hfill p\left(t\right)=& 8\sqrt{1-\frac{1}{970}exp(t+\frac{1}{2}sint+2\pi )}\left(1+\frac{cost}{2}\right)\mathrm{on}[{\psi }^{-1}\left(0\right),0],\hfill \\ \hfill p\left(t\right)=& 8\sqrt{1-\frac{1}{970}exp\left(t\right)}\mathrm{on}[0,\psi \left(0\right)],\hfill \\ \hfill p\left(t\right)=& \frac{16\sqrt{1-\frac{1}{970}exp\left(\gamma \left(t\right)\right)}}{2+cos\left(\gamma \right(t\left)\right)}\mathrm{on}[\psi \left(0\right),\psi \left(\psi \left(0\right)\right)],\hfill \end{array}$$

(73)

where

$$\begin{array}{cc}\hfill \gamma \left(t\right):={\psi }^{-1}\left(t\right)=-2\pi +\frac{3(t-2\pi )}{2}-\frac{{(t-2\pi )}^3}{12}& +\frac{{(t-2\pi )}^5}{240}-\hfill \\ \hfill -\frac{{(t-2\pi )}^7}{\mathrm{10,080}}+\frac{{(t-2\pi )}^9}{\mathrm{725,760}}-\frac{{(t-2\pi )}^{11}}{\mathrm{79,833,600}}& +\frac{{(t-2\pi )}^{13}}{\mathrm{12,454,041,600}}+\frac{{(t-2\pi )}^{15}}{\mathrm{2,615,348,736,000}}+\hfill \\ & +\frac{{(t-2\pi )}^{17}}{\mathrm{711,374,856,192,000}}+O({(t-2\pi )}^{19})\hfill \end{array}$$

(74)

is the inverse Taylor series for function $\psi \left(t\right)=t+\frac{1}{2}sint+2\pi$. Note, that in a general case, if $t\in [0,\psi (0\left)\right]$, then $p\left({\psi }^n\left(t\right)\right)=\frac{p\left(t\right)}{{\psi }^{\prime }\left(t\right){\psi }^{\prime }\left(\psi \left(t\right)\right)\dots ,{\psi }^{\prime }\left({\psi }^{n-1}\left(t\right)\right)}$ for $\psi \left(t\right)\in [{\psi }^n\left(0\right),{\psi }^{n+1}\left(0\right)]$.

Analogically, function $a\left(t\right)$ in the general case can be represented, for example, by the graph in Figure 2.

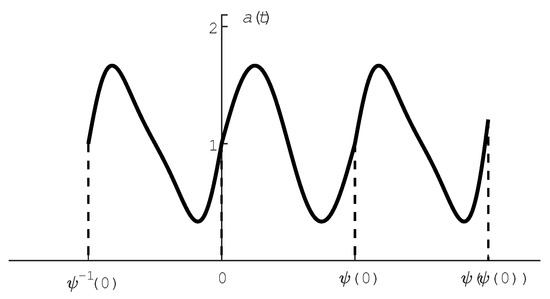
Figure 2. Function $a\left(t\right)$ on the interval $[{\psi }^{-1}\left(0\right),0]\cup [0,\psi \left(0\right)]\cup [\psi \left(0\right),\psi \left(\psi \left(0\right)\right)].$

Here,

$$\begin{array}{cc}\hfill a\left(t\right)=& 1+\frac{2}{3}sin(t+\frac{1}{2}sint+2\pi )\mathrm{on}[{\psi }^{-1}\left(0\right),0],\hfill \\ \hfill a\left(t\right)=& 1+\frac{2}{3}sint\mathrm{on}[0,\psi \left(0\right)],\hfill \\ \hfill a\left(t\right)=& 1+\frac{2}{3}sin\left(\gamma \left(t\right)\right)\mathrm{on}[\psi \left(0\right),\psi \left(\psi \left(0\right)\right)],\hfill \end{array}$$

where $\gamma$ is defined by (74) and, in the general case, if $t\in [0,\psi (0\left)\right]$, then $a\left({\psi }^n\left(t\right)\right)=\frac{a\left(t\right)}{{\psi }^{\prime }\left(t\right){\psi }^{\prime }\left(\psi \left(t\right)\right)\dots ,{\psi }^{\prime }\left({\psi }^{n-1}\left(t\right)\right)}$ for $\psi \left(t\right)\in [{\psi }^n\left(0\right),{\psi }^{n+1}\left(0\right)]$.

8.1. Unique Solvability of the Initial Value Problem for Linear Scalar Functional Differential Equations

Here, we establish conditions sufficient for the unique solvability of the initial value problem for the following linear scalar functional differential equation:

$$\begin{array}{cc}\hfill u^{\prime }\left(t\right)& =\sum _{i=1}^m{p}_i\left(t\right)u(t+\frac{1}{2}sint)+q\left(t\right),t\in [0,2\pi ],q\in L([0,2\pi ],\mathbb{R}),\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill u\left(0\right)& =\alpha \hfill \end{array}$$

(76)

The next Theorem is true.

Theorem 8.

Suppose that (70) is true, and for a certain constant $\gamma \in (0,1)$ and d satisfying condition $d>0$, the following inequality holds almost everywhere on $[0,2\pi ]$:

$${\int }_0^t\sum _{i=1}^m{p}_i\left(s\right)|s+\frac{1}{2}{sins|}^{d}ds\le \gamma {\left|t\right|}^d,t\in I_{\psi }.$$

(77)

Then, the linear initial value problem ((75) and (76)) is uniquely solvable for an arbitrary $\alpha \in \mathbb{R}$ and an arbitrary function $q\in L\left(\right[0,2\pi ],\mathbb{R})$. The unique solution of the problem ((75) and (76)) is representable in the form of a functional series

$$u\left(t\right)=\tilde{q}\left(t\right)+{\int }_0^t\sum _{i=1}^m{p}_i\left(s\right)\tilde{q}\left(s\right)dr+{\int }_0^t\sum _{i=1}^m{p}_i\left(s\right){\int }_0^{s+\frac{1}{2}sins}\sum _{i=1}^m{p}_i\left(\xi \right)\tilde{q}\left(\xi \right)d\xi ds+\dots ,$$

(78)

where $\tilde{q}\left(t\right):=\alpha +{\int }_0^{t}q\left(v\right)dv$ is uniformly convergent on $[0,2\pi ]$.

Moreover, if α and function q is such that, for all t from $[0,2\pi ]$, one has ${\int }_0^{t}q\left(v\right)dv\ge -\alpha$, then, at every point t of the interval $[0,2\pi ]$, the unique solution (78) of the problem ((75) and (76)) is non-negative.

Proof. 

Taking into account Corollary 3, where $\mu \left(t\right)=t+\frac{1}{2}sint$: $[0,2\pi ]\to [0,2\pi ]$, $y_0\left(t\right)=\theta {|t-t_0|}^k$ and ${\sum }_{i=1}^m{p}_i\left(t\right)\ge 0$, we obtain the assertion of Theorem 8. □

Remark 3.

Obviously, (77) is fulfilled for $p\left(t\right)$ defined by (73) on $[0,\psi (0\left)\right]$.

Remark 4.

Note that function p(t) cannot be a constant function because p(t) = constant does not fulfil the symmetric property (7).

8.2. Symmetric Property of the Unique Solution of the Initial Value Problem for Linear Scalar Functional Differential Equations

Here, we investigate a unique solution (78) with symmetric property (72). Assuming that $u_0\left(2\pi \right)\ne 1$ (which means that this is not a resonance case), then $u_0\left(2\pi \right)$ is defined by (53):

$$u_0\left(2\pi \right)=1+{\int }_0^{2\pi }\sum _{i=1}^m{p}_i\left(r\right)dr+{\int }_0^{2\pi }\sum _{i=1}^m{p}_i\left(s\right){\int }_0^{s+\frac{1}{2}sins}\sum _{i=1}^m{p}_i\left(\xi \right)d\xi ds+\dots ,$$

(79)

then the next Theorem is true.

Theorem 9.

If α in (76) has the representation

$$\alpha =\frac{Q\left(2\pi \right)}{1-u_0\left(2\pi \right)}$$

(80)

and

$${\int }_0^{2\pi }\sum _{i=1}^m{p}_i\left(s\right)ds+{\int }_0^{2\pi }\sum _{i=1}^m{p}_i\left(s\right){\int }_0^{s+\frac{1}{2}sins}\sum _{i=1}^m{p}_i\left(\xi \right)d\xi ds+\cdots \ne 0,$$

where $u_0\left(2\pi \right)$ is defined by (79) and

$$Q\left(2\pi \right)={\int }_0^{2\pi }q\left(s\right)ds+{\int }_0^{2\pi }{\sum }_{i=1}^m{p}_i\left(s\right){\int }_0^{s}q\left(v\right)dvds+{\int }_0^{2\pi }{\sum }_{i=1}^m{p}_i\left(s\right){\int }_0^{s+\frac{1}{2}sins}{\sum }_{i=1}^m{p}_i\left(\xi \right)\left({\int }_0^{\xi }q\left(v\right)dv\right)d\xi ds+\dots .,$$

then the problem ((75) and (76)) has a unique symmetric solution represented by (78).

Proof. 

It is easy to see that Theorem 9 is a particular case of Theorem 5. □

8.3. D-Stability of Nonlinear Functional Differential Equations

Remark 5.

In further investigations, we only study the D-stability of the trivial solution of Equation (1), as more general cases come down to this one.

Taking into account Definition 4, the next obvious Corollary 5, from Corollary 4 and Theorem 8, is true.

Corollary 5.

Assume that the conditions from Theorem 8 are true. Then, the linear problem ((75) and (76)) is D-stable (see Definition 4).

Theorem 10.

Assume that the conditions of Theorem 8 are fulfilled and for arbitrary $M>0$ there exists $\delta >0$, such that

$$\parallel \frac{c\left(t\right){\left(u_1\left({\tau }_1\left(t\right)\right)\right)}^{2\nu +1}}{a\left(t\right)+{\left(u_1\left({\tau }_2\left(t\right)\right)\right)}^{2\nu }}-\frac{c\left(t\right){\left(u_2\left({\tau }_1\left(t\right)\right)\right)}^{2\nu +1}}{a\left(t\right)+{\left(u_2\left({\tau }_2\left(t\right)\right)\right)}^{2\nu }}\parallel \le M{\parallel u_1-u_2\parallel }_D$$

(81)

for all $\parallel u_1{\parallel }_D\le \delta$, $\parallel u_2{\parallel }_D\le \delta$.

Then, the nonhomogeneous problem (2) for the Equation (68) is D-stable in the vicinity of the trivial solution. If the assumptions of Theorem 5 are true, then the symmetric problem (69) for the Equation (68) is D-stable in the vicinity of the trivial solution.

Proof. 

It is easy to see that Theorem 10 is a particular case of the Theorem 7. □

9. Conclusions

The aim of the present manuscript was to establish conditions on the D-stability of the initial value problem for a class of nonlinear symmetric functional differential equations. Furthermore, we construct conditions on the unique solvability of the initial value problem for a class of linear symmetric functional differential equations. In view of the symmetric properties and our previous results, we study the aforementioned problem on $\mathbb{R}$ using the theory of boundary value problems. The unique solution is represented in the form of a functional series. The conditions of the symmetric property of the unique solution of the symmetric functional differential equations are also given. In addition, we present the application of the obtained results in an example.

The question of the D-stability of functional differential equations with symmetries in ${\mathbb{R}}^n$ remains open, i.e., considering the D-stability of symmetric solutions of higher dimensional functional differential equations satisfying $Ax\left(t\right)=x\left(\psi \right(t\left)\right)$ for a matrix A.