Genetic Algorithm Based on Natural Selection Theory for Optimization Problems
Abstract
1. Introduction
2. Materials and Methods
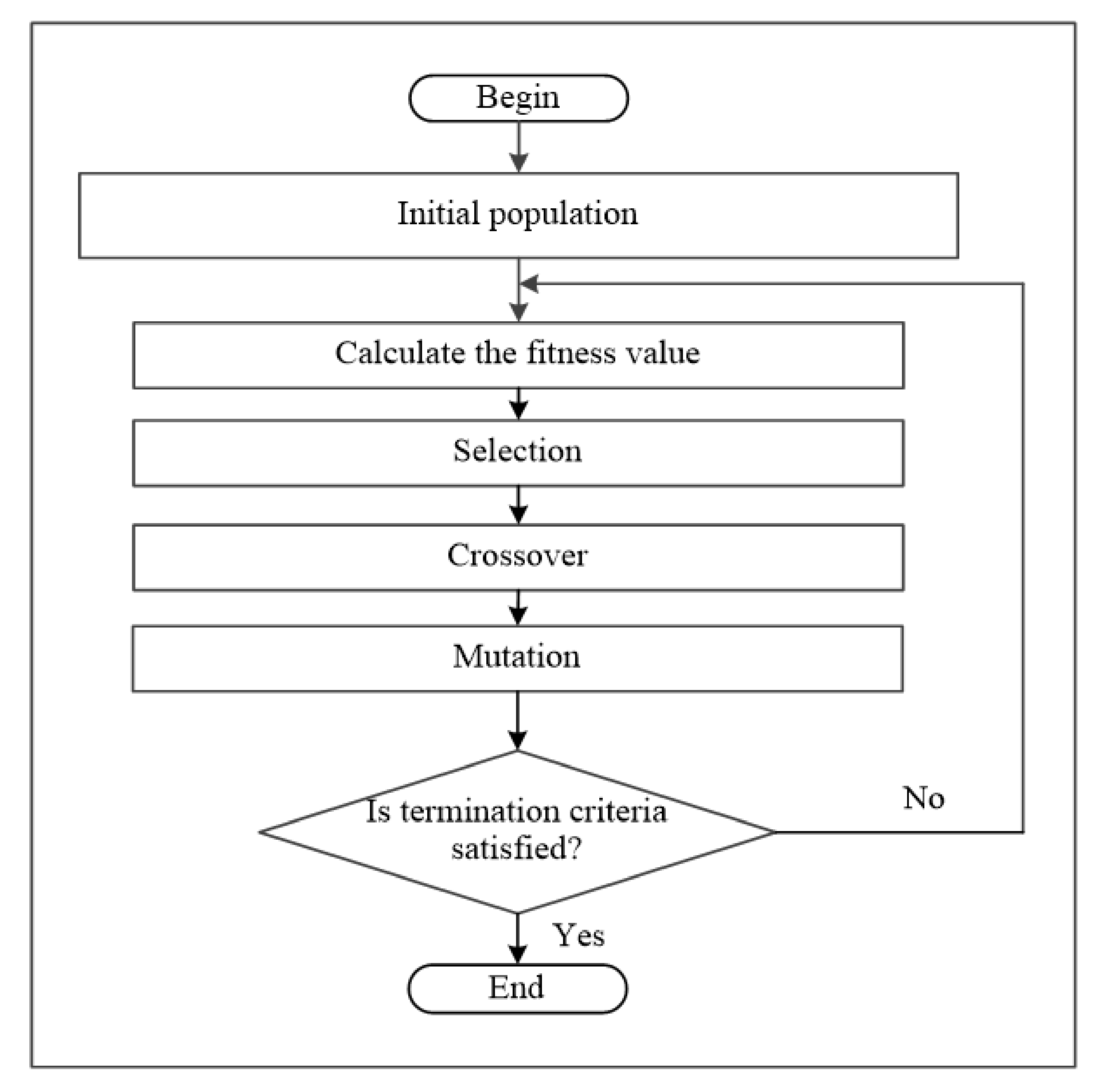
2.1. Genetic Algorithm
2.2. Genetic Algorithm Based on Natural Selection Theory (GABONST)
- Beginning of the algorithm.
- Set number of population n and number of iteration NumIter.
- Generate the population (chromosomes (S)) randomly; where S = {s1, s2, …, sn}.
- Calculate the fitness value of each chromosome in the population g(S).
- Calculate the mean of the fitness values using Equation (1).
- 6.
- Compare the fitness value of each chromosome g(si) with the mean:
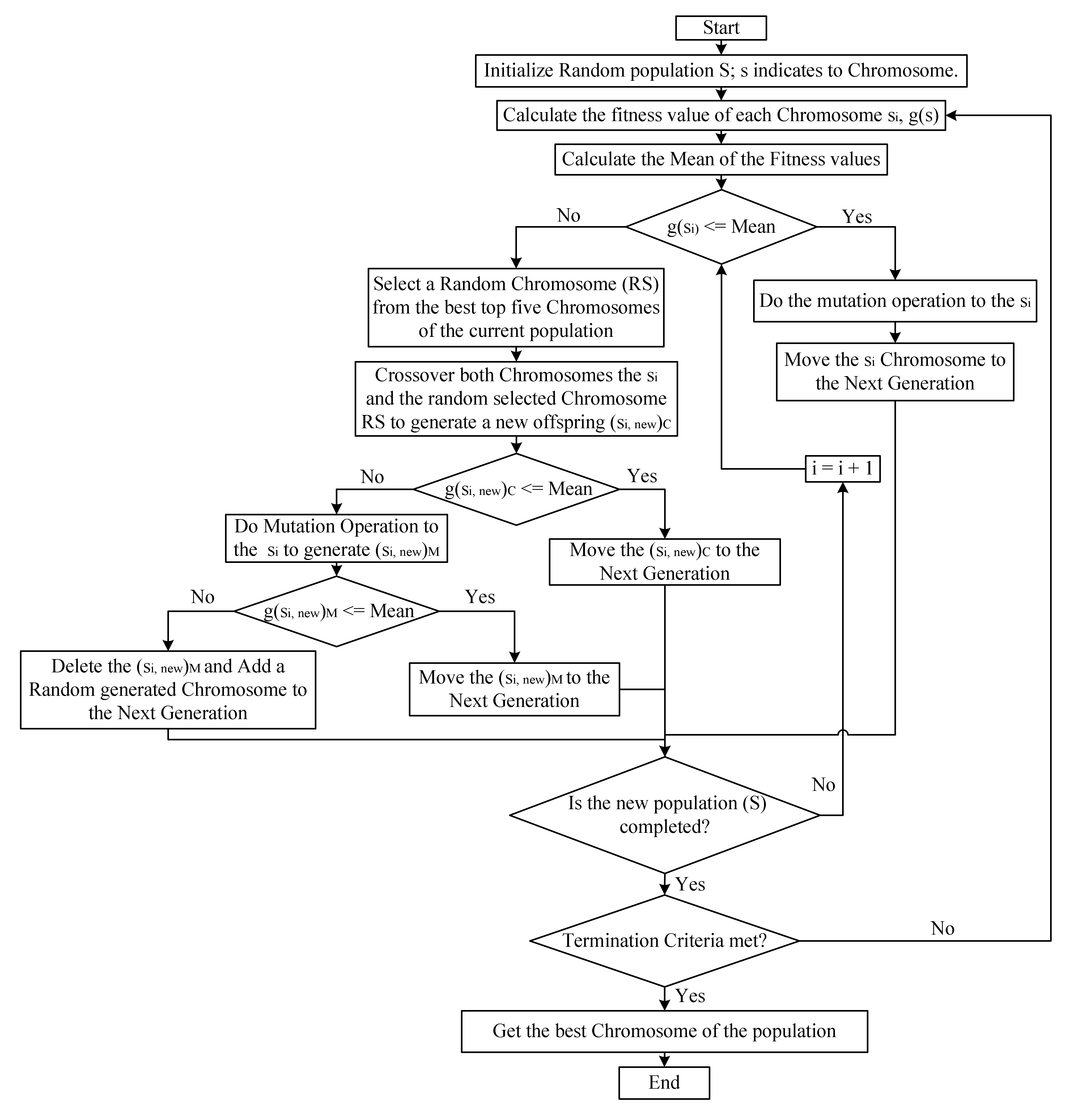
- If g(si) is less or equal to the mean then implement the mutation operation on the si and move to the next generation. This represents the right side of the GABONST flowchart (see Figure 2), where the right side simulates the well-qualified organisms (chromosomes) to survive the current environment.
- Otherwise, the chromosome si will get two chances to be improved, this represents the left side of the GABONST flowchart (see Figure 2), where the left side simulates the idea of giving the unqualified organisms (chromosomes) two chances to adjust their genes and be qualified to survive the current environment:
- i.
- The first chance is through getting married to a well-qualified organism (crossover the weak chromosome (si) with a well-qualified chromosome (RS)). If the new chromosome (si, new)C, which is obtained by crossover si and RS, qualifies to survive the current environment (g(si, new)C less or equal to the mean) then the (si, new)C move to the next generation. Otherwise, go to the second chance, step (ii).
- ii.
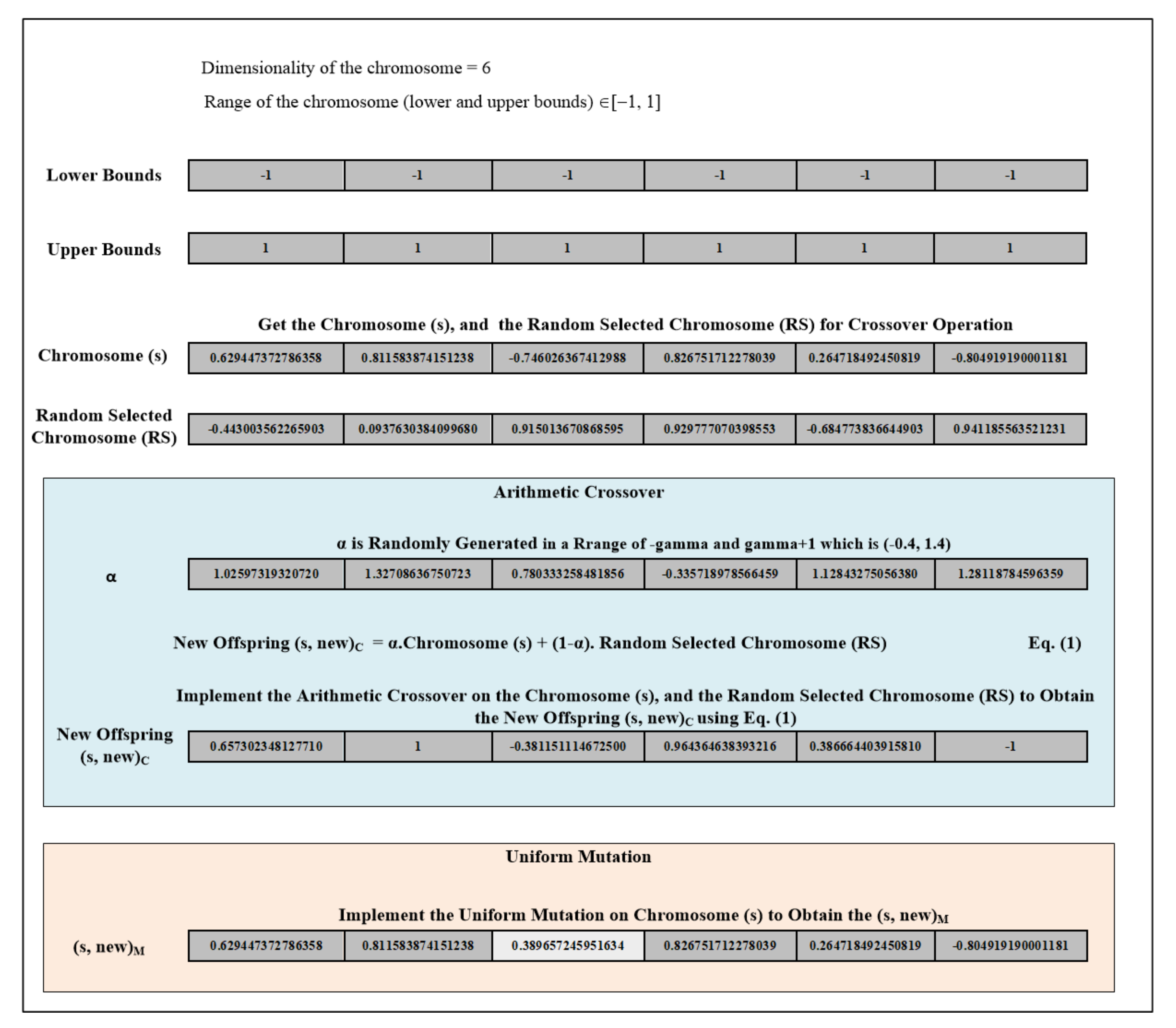
- The second chance is through the genetic mutation (implement the mutation operation to the weak chromosome (si)). If the new chromosome (si, new)M, which is obtained by applying the mutation operation on si, qualifies to survive the current environment (g(si, new)M less or equal to the mean) then the (si, new)M move to the next generation. Otherwise, in the case that the organism (chromosome (si)) has missed both of the chances to be qualified to survive in the current environment then that organism will die (that chromosome (si) will be deleted) and a new one comes to life (add a random generated chromosome to the next generation). Figure 3 provides an example of the arithmetic crossover and uniform mutation operations that have been applied in GABONST.
| Algorithm 1 GABONST |
|
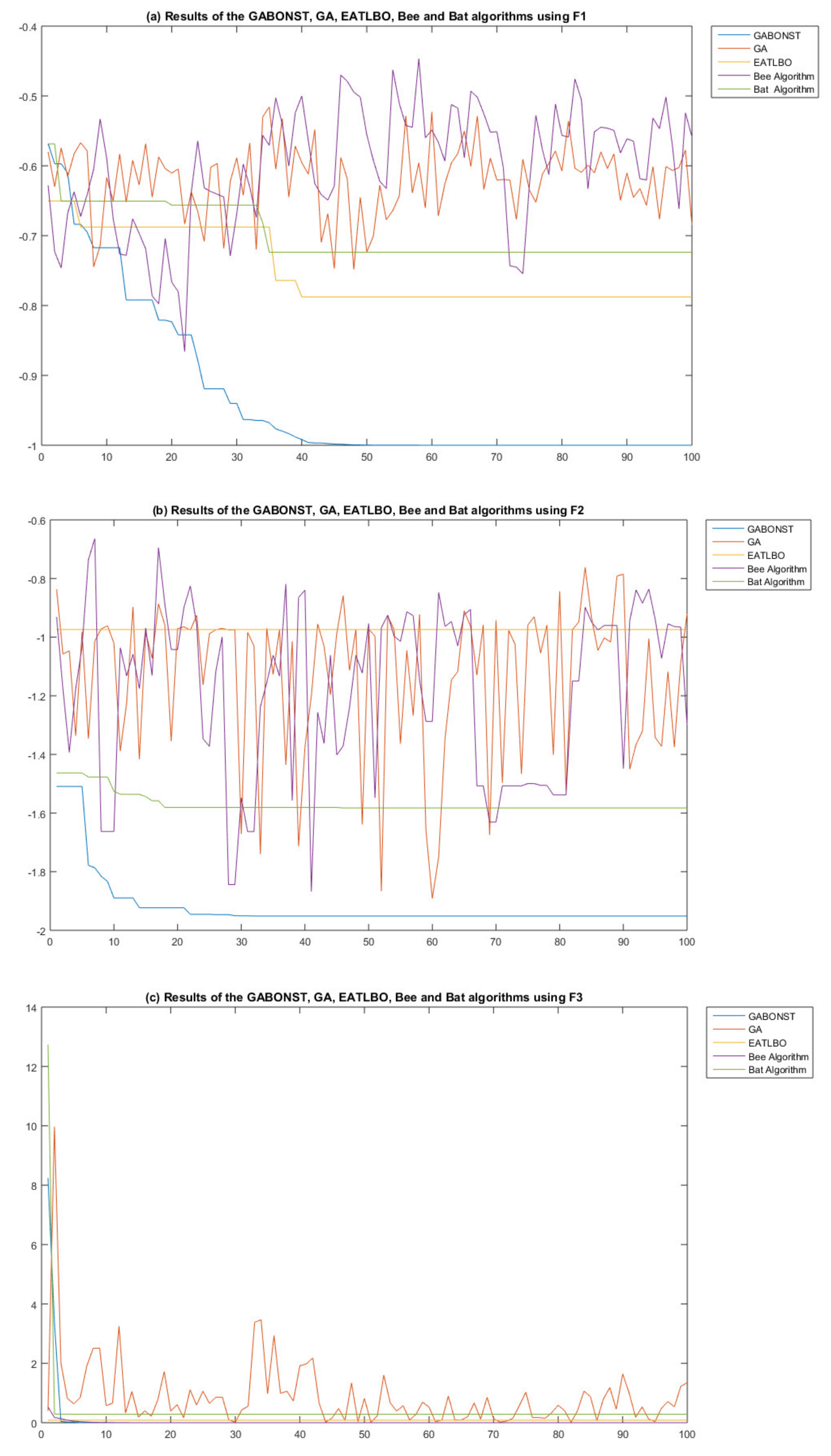
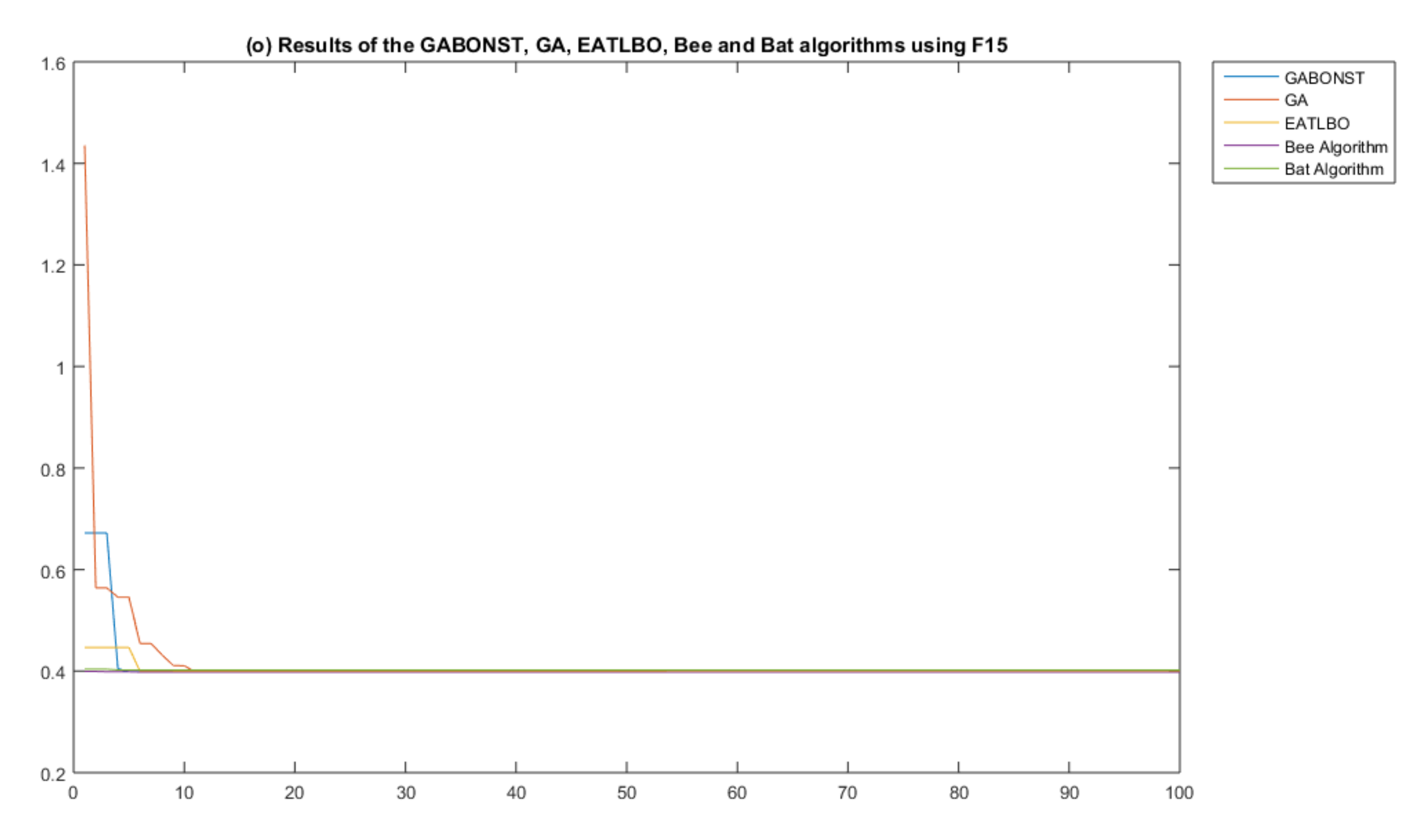
3. Results
3.1. Experimental Test One
3.2. Experimental Test Two
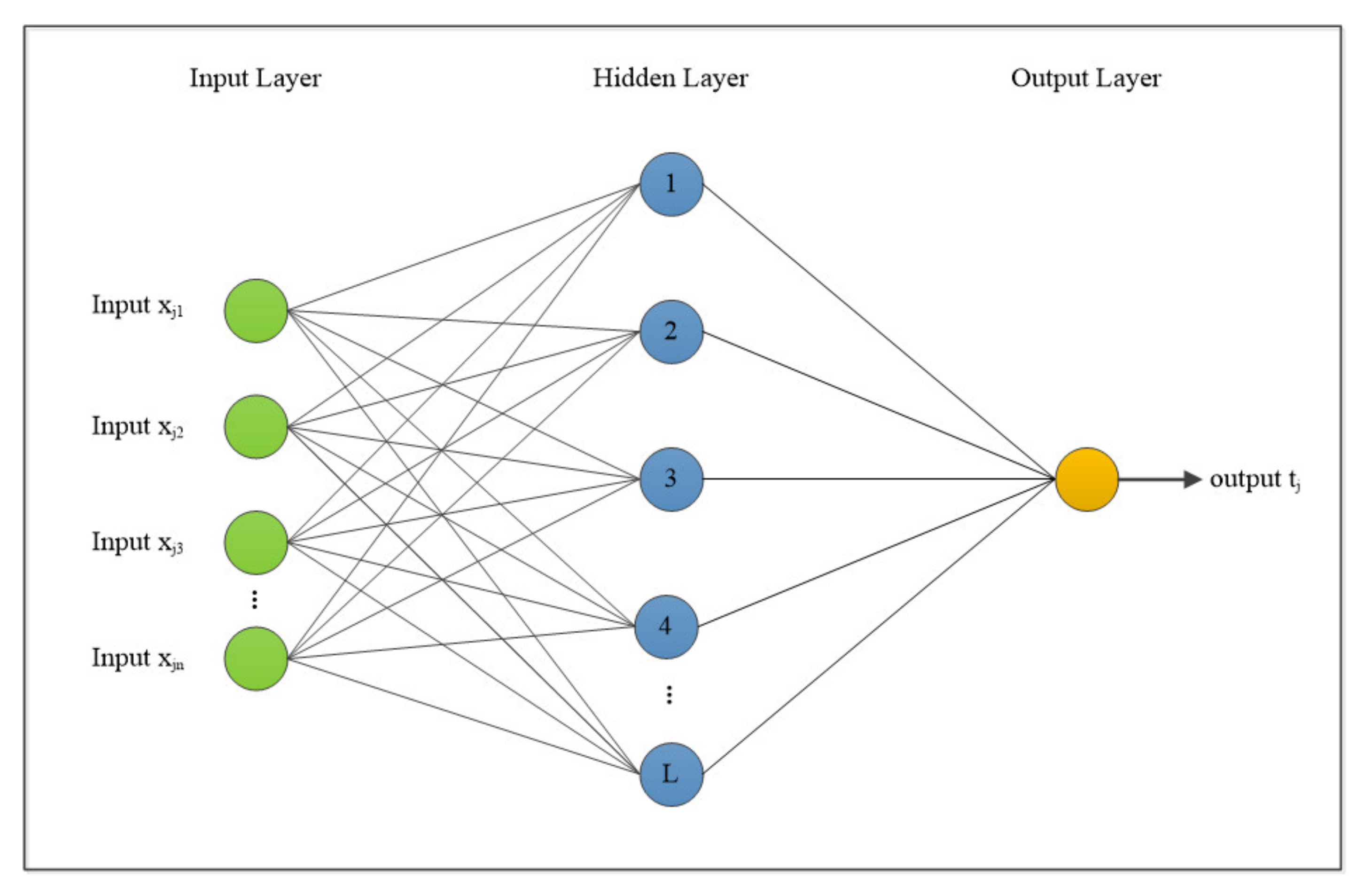
3.2.1. Basic ELM
3.2.2. GABONST–ELM
- wij [−1, 1], is the input weight value that connect ith hidden node and jth input node
- bi [0, 1] = ith hidden node bias
- n = input node numbers
- m = hidden node numbers
- m × (n + 1) represents the chromosome’s dimension, hence requiring parameter optimizations. Therefore, the fitness function in the GABONST–ELM set is calculated utilizing Equation (6).
- : output weight matrix
- yj: true value
- N: number of training samples
- A.
- The arithmetical crossover operation is used for exchanging information between that chromosome and a randomly selected chromosome from the top five chromosomes of the current population. The new offspring will be compared to the mean:If it is equal to or less than the mean then move the new offspring into the new generation.If it is greater than the mean then implement step B.
- B.
- The uniform mutation operation is applied to change the genes of that chromosome and generate a new chromosome. The new chromosome will be compared to the mean: if it is equal to or less than the mean then move it into the new generation. If it is greater than the mean then delete that chromosome and add a randomly generated chromosome.
3.2.3. LID Dataset
- The sampling rate is 44,100 Hz, based on the Nyquist frequency the highest frequency was 22,050 Hz. The length of 30 s utterance was approximately 1,323,000 (44,100 * 30) samples.
- Quantization: represents real-valued numbers as integers of a 16-bit range (values from −32,768 to 32,767). The following is a depiction of the utilized dataset:
3.2.4. Evaluation of the Different Learning Model Parameters
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alzaqebah, M.; Abdullah, S. An adaptive artificial bee colony and late-acceptance hill-climbing algorithm for examination timetabling. J. Sched. 2013, 17, 249–262. [Google Scholar] [CrossRef]
- Alzaqebah, M.; Abdullah, S. Hybrid bee colony optimization for examination timetabling problems. Comput. Oper. Res. 2015, 54, 142–154. [Google Scholar] [CrossRef]
- Aziz, R.A.; Ayob, M.; Othman, Z.; Ahmad, Z.; Sabar, N.R. An adaptive guided variable neighborhood search based on honey-bee mating optimization algorithm for the course timetabling problem. Soft Comput. 2016, 21, 6755–6765. [Google Scholar] [CrossRef]
- Sabar, N.R.; Ayob, M.; Kendall, G.; Qu, R. A honey-bee mating optimization algorithm for educational timetabling problems. Eur. J. Oper. Res. 2012, 216, 533–543. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Abdullah, S.; Hamdan, A.R. Multi-population cooperative bat algorithm-based optimization of artificial neural network model. Inf. Sci. 2015, 294, 628–644. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Abdullah, S.; Hamdan, A.R. A solution representation of genetic algorithm for neural network weights and structure. Inf. Process. Lett. 2016, 116, 22–25. [Google Scholar] [CrossRef]
- Serapião, A.B.; Corrêa, G.S.; Gonçalves, F.B.; Carvalho, V.O. Combining K-Means and K-Harmonic with Fish School Search Algorithm for data clustering task on graphics processing units. Appl. Soft Comput. 2016, 41, 290–304. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Moftah, H.M.; Azar, A.T.; Shoman, M. MRI breast cancer diagnosis hybrid approach using adaptive ant-based segmentation and multilayer perceptron neural networks classifier. Appl. Soft Comput. 2014, 14, 62–71. [Google Scholar] [CrossRef]
- Krishna, P.V. Honey bee behavior inspired load balancing of tasks in cloud computing environments. Appl. Soft Comput. 2013, 13, 2292–2303. [Google Scholar]
- Albadr, M.A.A.; Tiun, S. Spoken Language Identification Based on Particle Swarm Optimisation–Extreme Learning Machine Approach. Circuits Syst. Signal. Process. 2020, 1–27. [Google Scholar] [CrossRef]
- Albadr, M.A.A.; Tiun, S.; Ayob, M.; Al-Dhief, F.T. Spoken language identification based on optimised genetic algorithm–extreme learning machine approach. Int. J. Speech Technol. 2019, 22, 711–727. [Google Scholar] [CrossRef]
- Yassen, E.T.; Ayob, M.; Nazri, M.Z.A.; Sabar, N.R. A Hybrid Meta-Heuristic Algorithm for Vehicle Routing Problem with Time Windows. Int. J. Artif. Intell. Tools 2015, 24, 1550021. [Google Scholar] [CrossRef]
- Yassen, E.T.; Ayob, M.; Nazri, A.; Zakree, M. The Effect of Hybridizing Local Search Algorithms with Harmony Search for the Vehicle Routing Problem with Time Windows. J. Theor. Appl. Inf. Technol. 2015, 73, 43–58. [Google Scholar]
- Yassen, E.T.; Ayob, M.; Nazri, M.Z.A.; Sabar, N.R. Meta-harmony search algorithm for the vehicle routing problem with time windows. Inf. Sci. 2015, 325, 140–158. [Google Scholar] [CrossRef]
- Agarwal, P.; Mehta, S. Nature-Inspired Algorithms: State-of-Art, Problems and Prospects. Int. J. Comput. Appl. 2014, 100, 14–21. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Abdullah, S. Optimization of neural network using kidney-inspired algorithm with control of filtration rate and chaotic map for real-world rainfall forecasting. Eng. Appl. Artif. Intell. 2018, 67, 246–259. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT press: Cambridge, MA, USA, 1992. [Google Scholar]
- Yang, X.-S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Alvankarian, J.; Abdullah, S. Kidney-inspired algorithm for optimization problems. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 358–369. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 2012, 7, 1482. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: New York, NY, USA, 2019; pp. 43–55. [Google Scholar] [CrossRef]
- Contreras-Bolton, C.; Parada, V. Automatic Combination of Operators in a Genetic Algorithm to Solve the Traveling Salesman Problem. PLoS ONE 2015, 10, e0137724. [Google Scholar] [CrossRef] [PubMed]
- Anam, S. Parameters Estimation of Enzymatic Reaction Model for Biodiesel Synthesis by Using Real Coded Genetic Algorithm with Some Crossover Operations; IOP Publishing: Bristol, UK, 2019; Volume 546, p. 052006. [Google Scholar]
- Malik, A. A Study of Genetic Algorithm and Crossover Techniques. Int. J. Comput. Sci. Mob. Comput. 2019, 8, 335–344. [Google Scholar]
- Mankad, K.B. A Genetic Fuzzy Approach to Measure Multiple Intelligence; Sardar Patel University: Gujarat, India, 2013. [Google Scholar]
- Albadr, M.A.A.; Tiun, S.; Al-Dhief, F.T.; Sammour, M.A.M. Spoken language identification based on the enhanced self-adjusting extreme learning machine approach. PLoS ONE 2018, 13, e0194770. [Google Scholar] [CrossRef]
- Holland, J.H. Adaption in Natural and Artificial Systems. An Introductory Analysis with Application to Biology, Control and Artificial Intelligence, 1st ed.; The University of Michigan: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Bi, C. Deterministic local alignment methods improved by a simple genetic algorithm. Neurocomputing 2010, 73, 2394–2406. [Google Scholar] [CrossRef]
- Mohamed, M.H. Rules extraction from constructively trained neural networks based on genetic algorithms. Neurocomputing 2011, 74, 3180–3192. [Google Scholar] [CrossRef]
- Höschel, K.; Lakshminarayanan, V. Genetic algorithms for lens design: A review. J. Opt. 2018, 48, 134–144. [Google Scholar] [CrossRef]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs. Math. Intell. 1996, 18, 71. [Google Scholar] [CrossRef]
- Yu, F.; Fu, X.; Li, H.; Dong, G. Improved Roulette Wheel Selection-Based Genetic Algorithm for TSP. In Proceedings of the 2016 International Conference on Network and Information Systems for Computers (ICNISC), Wuhan, China, 15–17 April 2016; pp. 151–154. [Google Scholar]
- Zhi, H.; Liu, S. Face recognition based on genetic algorithm. J. Vis. Commun. Image Represent. 2019, 58, 495–502. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Ge, J.; Zhang, Z.; Zong, B. A hybrid adaptively genetic algorithm for task scheduling problem in the phased array radar. Eur. J. Oper. Res. 2019, 272, 868–878. [Google Scholar] [CrossRef]
- Wong, K.-W.; Yap, W.-S.; Wong, D.C.-K.; Phan, R.C.-W.; Goi, B.-M. Cryptanalysis of genetic algorithm-based encryption scheme. Multimedia Tools Appl. 2020, 79, 25259–25276. [Google Scholar] [CrossRef]
- Ahmed, R.; Zayed, T.; Nasiri, F. A Hybrid Genetic Algorithm-Based Fuzzy Markovian Model for the Deterioration Modeling of Healthcare Facilities. Algorithms 2020, 13, 210. [Google Scholar] [CrossRef]
- Kar, S.; Kabir, M.M.J. Comparative Analysis of Mining Fuzzy Association Rule using Genetic Algorithm. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–5. [Google Scholar]
- Tan, X.; Wu, J.; Mao, T.; Tan, Y. Multi-attribute intelligent decision-making method based on triangular fuzzy number hesitant intuitionistic fuzzy sets. Syst. Eng. Electron. 2017, 39, 829–836. [Google Scholar]
- Li, X.; Wang, Z.; Sun, Y.; Zhou, S.; Xu, Y.; Tan, G. Genetic algorithm-based content distribution strategy for F- RAN architectures. ETRI J. 2019, 41, 348–357. [Google Scholar] [CrossRef]
- Serbanescu, M.-S. Genetic algorithm/extreme learning machine paradigm for cancer detection. Ann. Univ. Craiova Math. Comput. Sci. Ser. 2019, 46, 372–380. [Google Scholar]
- Choudhary, A.; Kumar, M.; Gupta, M.K.; Unune, D.K.; Mia, M. Mathematical modeling and intelligent optimization of submerged arc welding process parameters using hybrid PSO-GA evolutionary algorithms. Neural Comput. Appl. 2019, 1–14. [Google Scholar] [CrossRef]
- Jamali, B.; Rasekh, M.; Jamadi, F.; Gandomkar, R.; Makiabadi, F. Using PSO-GA algorithm for training artificial neural network to forecast solar space heating system parameters. Appl. Therm. Eng. 2019, 147, 647–660. [Google Scholar] [CrossRef]
- Lipare, A.; Edla, D.R.; Cheruku, R.; Tripathi, D. GWO-GA Based Load Balanced and Energy Efficient Clustering Approach for WSN. In Smart Trends in Computing and Communications; Springer: Singapore, 2020; pp. 287–295. [Google Scholar] [CrossRef]
- Beg, A.H.; Islam, Z. Novel crossover and mutation operation in genetic algorithm for clustering. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 2114–2121. [Google Scholar] [CrossRef]
- Kora, P.; Yadlapalli, P. Crossover Operators in Genetic Algorithms: A Review. Int. J. Comput. Appl. 2017, 162, 34–36. [Google Scholar] [CrossRef]
- Darwin, C.; Wallace, A.R. Evolution by Natural Selection; Cambridge University Press: Cambridge, UK, 1958. [Google Scholar]
- Livezey, R.L.; Darwin, C. On the Origin of Species by Means of Natural Selection. Am. Midl. Nat. 1953, 49, 937. [Google Scholar] [CrossRef][Green Version]
- Jamil, M.; Yang, X.S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Alexander, V.; Annamalai, P. An Elitist Genetic Algorithm Based Extreme Learning Machine. Softw. Eng. Intell. Syst. 2015, 301–309. [Google Scholar] [CrossRef]
- Nayak, P.K.; Mishra, S.; Dash, P.K.; Bisoi, R. Comparison of modified teaching–learning-based optimization and extreme learning machine for classification of multiple power signal disturbances. Neural Comput. Appl. 2015, 27, 2107–2122. [Google Scholar] [CrossRef]
- Niu, P.; Ma, Y.; Li, M.; Yan, S.; Li, G. A Kind of Parameters Self-adjusting Extreme Learning Machine. Neural Process. Lett. 2016, 44, 813–830. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, T.; Zhang, D. A novel algorithm with differential evolution and coral reef optimization for extreme learning machine training. Cogn. Neurodyn. 2015, 10, 73–83. [Google Scholar] [CrossRef]
- Albadra, M.A.A.; Tiuna, S. Extreme learning machine: A review. Int. J. Appl. Eng. Res. 2017, 12, 4610–4623. [Google Scholar]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond Accuracy, F-Score and ROC: A Family of Discriminant Measures for Performance Evaluation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1015–1021. [Google Scholar]
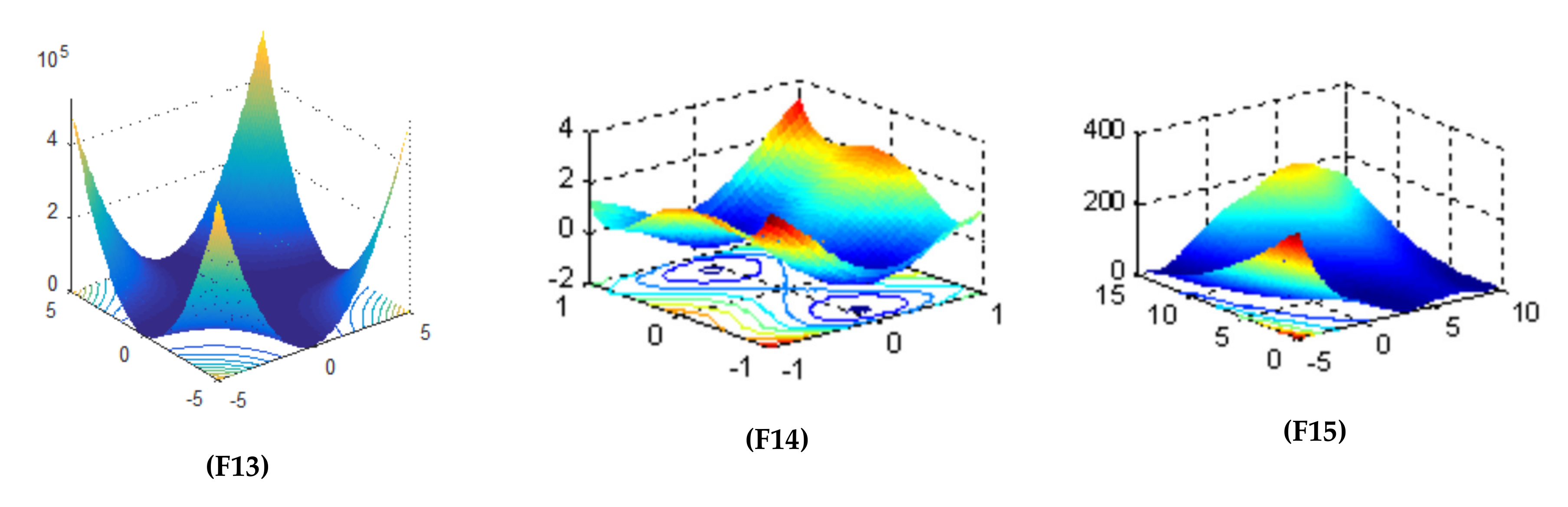






| Objective Function | Dim | Range | Optimal Solution |
|---|---|---|---|
| 10 | [−1, 1] | −1 | |
| 2 | [0, π] | −1.8013 | |
| 2 | [−10, 10] | 0 | |
| 10 | [−5, 5] | −391.6599 | |
| 2 | [0, 10] | −6.1295 | |
| 256 | [−5.12, 5.12] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−1.28, 1.28] | 0 | |
| 30 | [−5.12, 5.12] | 0 | |
| 128 | [−32.768, 32.768] | 0 | |
| 30 | [−600, 600] | 0 | |
| 2 | [−2, 2] | 3 | |
| 4 | [−5, 5] | 0.00030 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−5, 5] | 0.398 |
| F1 | F2 | F3 | F4 | F5 | |
| GA–RMSE | 0.408266 | 0.66005 | 0.457172 | 69.84426 | 2.734866 |
| GABONST–RMSE | 0.008912 | 0.1498 | 0 | 15.50201 | 0 |
| EATLBO–RMSE | 0.241362 | 0.803974 | 0.379706 | 148.6135 | 0.715572 |
| Bat-RMSE | 0.3820 | 0.4033 | 5.7316 | 153.3258 | 0.2902 |
| Bee-RMSE | 1.0000 | 0.5693 | 9.2615 × 10−10 | 186.7217 | 0.2444 |
| GA–Mean | −0.60383 | −1.20717 | 18.4889 | −326.997 | −3.7482 |
| GABONST–Mean | −0.99688 | −1.9511 | 0 | −380.897 | −6.1295 |
| EATLBO–Mean | −0.77554 | −0.99733 | 0.27178 | −245.971 | −5.67757 |
| Bat-Mean | −0.6215 | −1.5889 | 3.3044 | −240.5929 | −5.9602 |
| Bee-Mean | −9.4481 × 10−11 | −1.3024 | 6.1739 × 10−10 | −207.6444 | −6.0014 |
| GA–STD | 0.099654 | 0.290461 | 0.271562 | 26.66188 | 1.358616 |
| GABONST–STD | 0.008434 | 2.24299 × 10−15 | 0 | 11.26751 | 4.48598 × 10−15 |
| EATLBO–STD | 0.089637 | 0.00257 | 0.267856 | 29.62479 | 0.56043 |
| Bat-STD | 0.0526 | 0.3463 | 4.7307 | 26.4876 | 0.2381 |
| Bee-STD | 3.1940 × 10−11 | 0.2769 | 6.9736 × 10−10 | 31.9960 | 0.2103 |
| F6 | F7 | F8 | F9 | F10 | |
| GA–RMSE | 115.0308 | 8.1381 × 103 | 0.1612 | 42.7116 | 10.9405 |
| GABONST–RMSE | 0 | 0 | 2.2336 × 10−4 | 0 | 0 |
| EATLBO–RMSE | 4.4872 × 10−56 | 28.9495 | 2.7609 × 10−4 | 205.0804 | 2.8037 |
| Bat-RMSE | 1.2039 × 103 | 9.0087 × 107 | 74.3799 | 364.5571 | 20.1364 |
| Bee-RMSE | 1.7538 × 103 | 2.3143 × 107 | 14.6593 | 141.4336 | 19.6219 |
| GA–Mean | 113.9390 | 6.7387 × 103 | 0.1464 | 41.6742 | 10.9243 |
| GABONST–Mean | 0 | 0 | 1.5895 × 10−4 | 0 | 0 |
| EATLBO–Mean | 3.3624 × 10−56 | 28.9495 | 2.0063 × 10−4 | 202.5195 | 2.6162 |
| Bat-Mean | 1.1761 × 103 | 8.1520 × 107 | 67.4795 | 362.3866 | 20.1321 |
| Bee-Mean | 1.7533 × 103 | 2.1898 × 107 | 14.3940 | 140.4960 | 19.6218 |
| GA–STD | 15.9710 | 4.6090 × 103 | 0.0682 | 9.4516 | 39.3751 |
| GABONST–STD | 0 | 0 | 1.5852 × 10−4 | 0 | 0 |
| EATLBO–STD | 3.0016 × 10−56 | 0.0175 | 1.9160 × 10−4 | 32.6362 | 1.0182 |
| Bat-STD | 259.8600 | 3.8731 × 107 | 31.6047 | 40.1246 | 0.4206 |
| Bee-STD | 39.3751 | 7.5653 × 106 | 2.8049 | 16.4241 | 0.0496 |
| F11 | F12 | F13 | F14 | F15 | |
| GA–RMSE | 2.2342 | 6.4588 × 10−6 | 0.0018 | 2.8284 × 10−5 | 1.1264 × 10−4 |
| GABONST–RMSE | 0 | 7.6591 × 10−14 | 1.4195 × 10−4 | 2.8453 × 10−5 | 1.1264 × 10−4 |
| EATLBO–RMSE | 0 | 9.9516 | 0.0067 | 0.0372 | 0.1170 |
| Bat-RMSE | 348.4865 | 21.6007 | 0.0645 | 0.8243 | 0.5704 |
| Bee-RMSE | 221.4966 | 2.5635 × 10−9 | 2.7909 × 10−4 | 2.8453 × 10−5 | 1.1264 × 10−4 |
| GA–Mean | 2.1932 | 3.000000925712561 | 0.0017 | −1.031628252987515 | 0.3978873583048 |
| GABONST–Mean | 0 | 2.999999999999923 | 4.0025 × 10−4 | −1.031628453489878 | 0.3978873577297 |
| EATLBO–Mean | 0 | 9.9257 | 0.0042 | −1.0078 | 0.4496 |
| Bat-Mean | 338.7847 | 18.6428 | 0.0464 | −0.4807 | 0.7070 |
| Bee-Mean | 219.4071 | 3.000000001676081 | 5.1854 × 10−4 | −1.031628453353341 | 0.3979 |
| GA–STD | 0.4302 | 6.4570 × 10−6 | 0.0011 | 1.3312 × 10−6 | 2.3933 × 10−9 |
| GABONST–STD | 0 | 1.8266 × 10−15 | 1.0152 × 10−4 | 5.4942 × 10−16 | 3.3645 × 10−16 |
| EATLBO–STD | 0 | 7.2188 | 0.0055 | 0.0288 | 0.1061 |
| Bat-STD | 82.4855 | 15.0473 | 0.0455 | 0.6194 | 0.4843 |
| Bee-STD | 30.6602 | 1.9593 × 10−9 | 1.7534 × 10−4 | 2.0841 × 10−10 | 1.0905 × 10−10 |
| Notations | Implications |
|---|---|
| N | distinct samples set (Xi, ti), where: Xi = [xi1, xi2, …, xin]T Rn ti = [ti1, ti2, …, tim]T Rm |
| L | hidden neurons number |
| g(x) | activation function, described in Equation (2) [53]. |
| Wi = [Wi1, Wi2, …, Win]T | input weights that connect the ith input neurons and the hidden neurons |
| = [T | output weight that connect the ith output neurons and the hidden neurons |
| bi | threshold of the ith hidden neurons |
| ELM | GABONST | ||
|---|---|---|---|
| Parameters | Values | Parameters | Values |
| C | Bias and input weight assemble | Iteration numbers | 100 |
| Output weight matrix | Population size (PS) | 50 | |
| Input–weights | −1 to 1 | Crossover operation | Arithmetical crossover |
| Bias values | 0–1 | Mutation operation | Uniform mutation |
| Number of input nodes | Input attributes | Selection operation | Select a random solution from the top five solutions of the current population |
| Number of hidden nodes | 650–900, with increment or step of 25 | Mean | |
| Output neurones | Class values | Gamma | 0.4 |
| Activation function | Sigmoid | ||
| No | Chanel | Language |
|---|---|---|
| 1 | Syrian TV | Arabic |
| 2 | British Broadcasting Corporation | English |
| 3 | TV9, TV3, and TV2 | Malay |
| 4 | TF1 HD | French |
| 5 | La1, La2, and Real Madrid TV HD | Spanish |
| 6 | Zweites Deutsches Fernsehen | German |
| 7 | Islamic Republic of Iran News Network | Persian |
| 8 | GEO Kahani | Urdu |
| Hidden Neuron Numbers | Accuracy | Precision | Recall | F-Measure | G-Mean |
|---|---|---|---|---|---|
| 650 | 94.37 | 77.50 | 77.50 | 77.50 | 62.76 |
| 675 | 94.37 | 77.50 | 77.50 | 77.50 | 62.50 |
| 700 | 93.75 | 75.00 | 75.00 | 75.00 | 59.38 |
| 725 | 94.37 | 77.50 | 77.50 | 77.50 | 62.81 |
| 750 | 95.63 | 82.50 | 82.50 | 82.50 | 69.64 |
| 775 | 95.00 | 80.00 | 80.00 | 80.00 | 66.11 |
| 800 | 95.63 | 82.50 | 82.50 | 82.50 | 69.64 |
| 825 | 95.00 | 80.00 | 80.00 | 80.00 | 66.16 |
| 850 | 95.00 | 80.00 | 80.00 | 80.00 | 66.16 |
| 875 | 96.25 | 85.00 | 85.00 | 85.00 | 73.41 |
| 900 | 95.00 | 80.00 | 80.00 | 80.00 | 66.20 |
| Hidden Neuron Numbers | Accuracy | Precision | Recall | F-Measure | G-Mean |
|---|---|---|---|---|---|
| 650 | 92.50 | 70.00 | 70.00 | 70.00 | 53.40 |
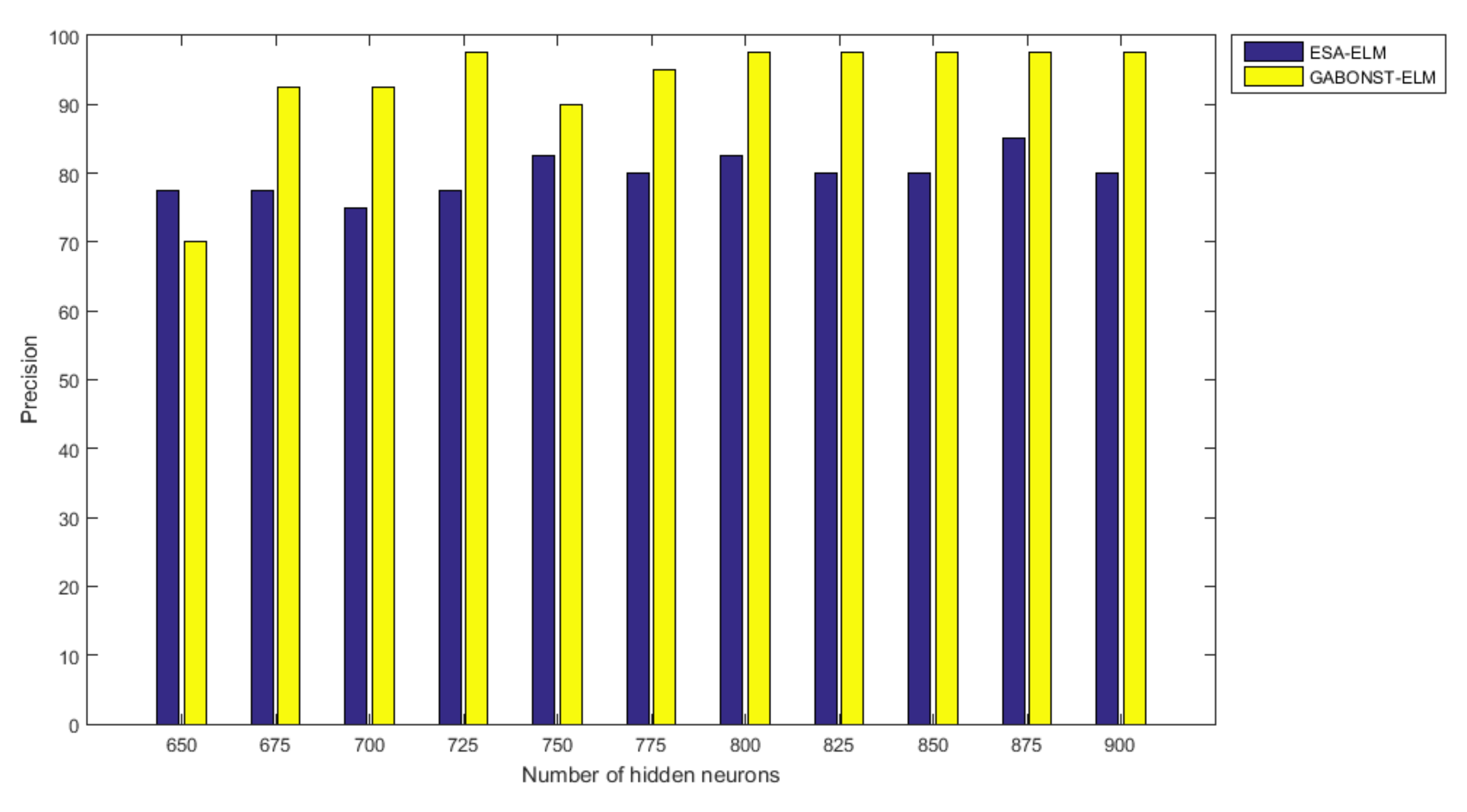
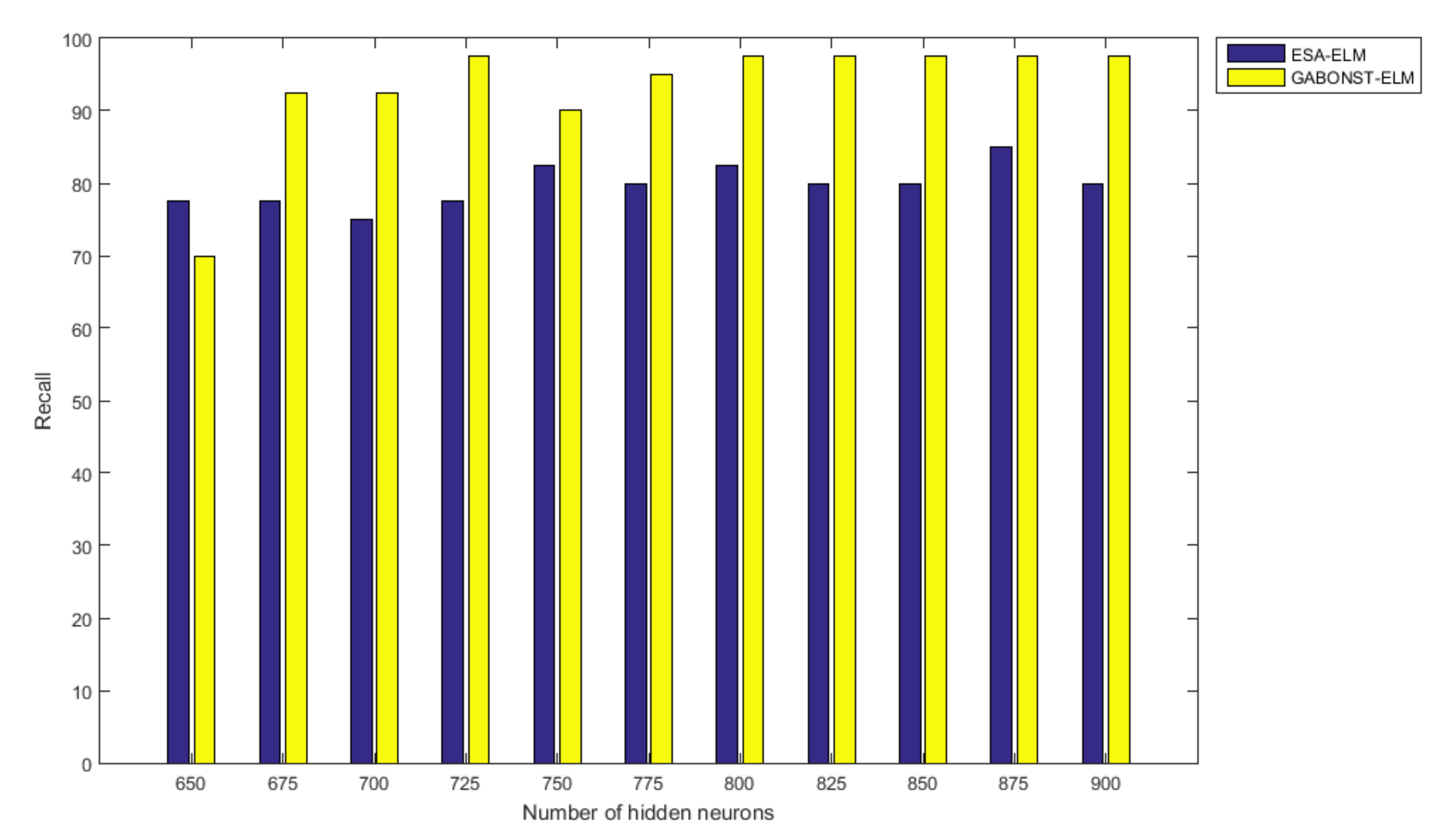
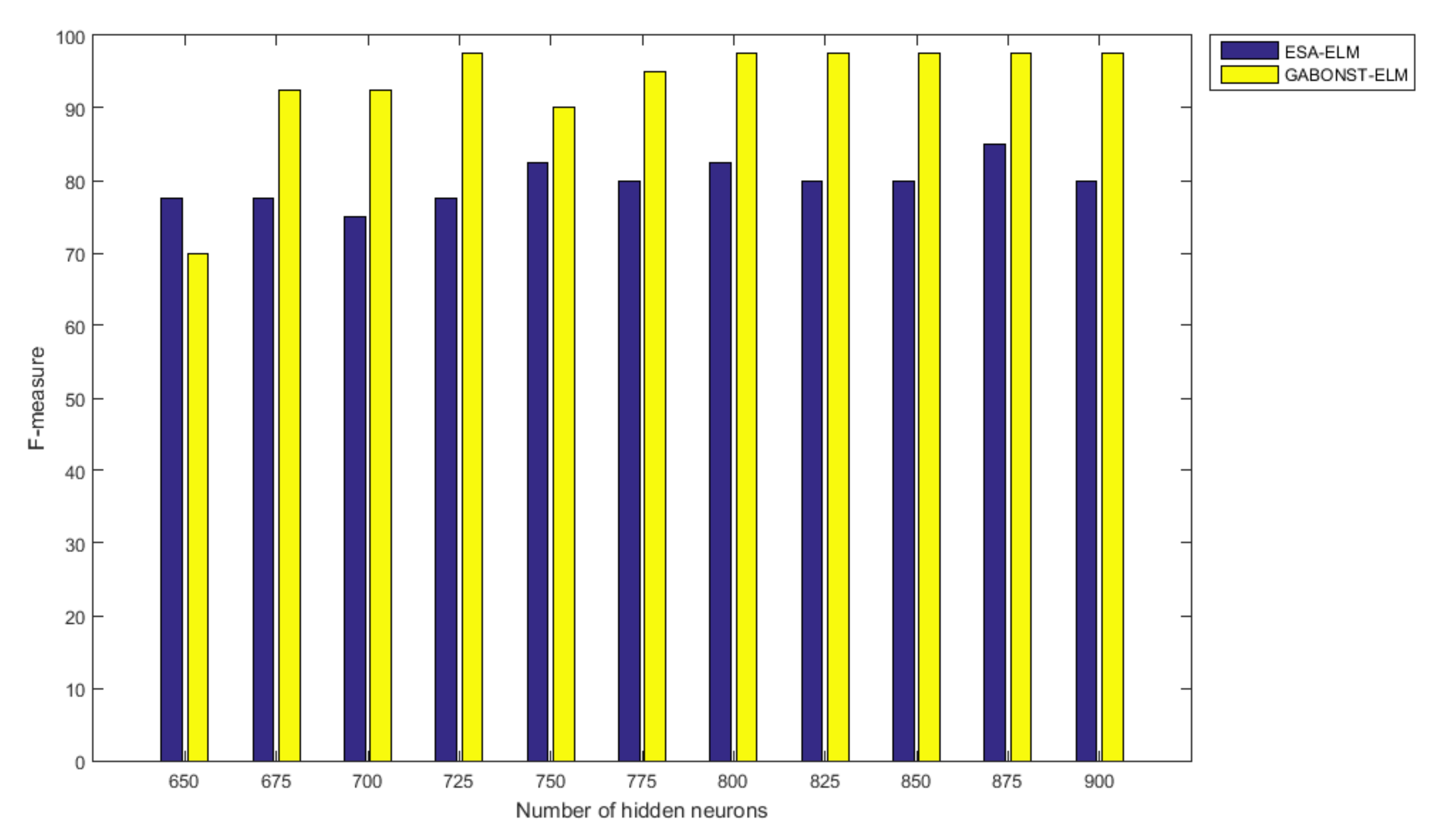
| 675 | 98.12 | 92.50 | 92.50 | 92.50 | 85.85 |
| 700 | 98.12 | 92.50 | 92.50 | 92.50 | 85.85 |
| 725 | 99.38 | 97.50 | 97.50 | 97.50 | 95.06 |
| 750 | 97.50 | 90.00 | 90.00 | 90.00 | 81.56 |
| 775 | 98.75 | 95.00 | 95.00 | 95.00 | 90.25 |
| 800 | 99.38 | 97.50 | 97.50 | 97.50 | 95.06 |
| 825 | 99.38 | 97.50 | 97.50 | 97.50 | 95.06 |
| 850 | 99.38 | 97.50 | 97.50 | 97.50 | 95.06 |
| 875 | 99.38 | 97.50 | 97.50 | 97.50 | 95.06 |
| 900 | 98.12 | 92.50 | 92.50 | 92.50 | 85.85 |
| Hidden Neuron Numbers | Accuracy | Precision | Recall | F-Measure | G-Mean |
|---|---|---|---|---|---|
| 650 | 89.44 | 55.00 | 55.00 | 55.00 | 31.49 |
| 675 | 90.02 | 57.50 | 57.50 | 57.50 | 39.85 |
| 700 | 90.55 | 52.50 | 52.50 | 52.50 | 27.67 |
| 725 | 88.88 | 47.50 | 47.50 | 47.50 | 27.00 |
| 750 | 89.44 | 42.50 | 42.50 | 42.50 | 20.34 |
| 775 | 89.16 | 45.00 | 45.00 | 45.00 | 22.80 |
| 800 | 90.00 | 55.00 | 55.00 | 55.00 | 36.13 |
| 825 | 89.72 | 55.00 | 55.00 | 55.00 | 30.03 |
| 850 | 88.88 | 50.00 | 50.00 | 50.00 | 25.95 |
| 875 | 90.55 | 55.00 | 55.00 | 55.00 | 30.36 |
| 900 | 90.55 | 52.50 | 52.50 | 52.50 | 29.51 |
| Hidden Neuron Numbers | Accuracy | Precision | Recall | F-Measure | G-Mean |
|---|---|---|---|---|---|
| 650 | 84.38 | 37.50 | 37.50 | 37.50 | 25.36 |
| 675 | 87.50 | 50.00 | 50.00 | 50.00 | 34.19 |
| 700 | 85.00 | 40.00 | 40.00 | 40.00 | 27.13 |
| 725 | 87.50 | 50.00 | 50.00 | 50.00 | 33.69 |
| 750 | 86.88 | 47.50 | 47.50 | 47.50 | 32.21 |
| 775 | 88.75 | 55.00 | 55.00 | 55.00 | 38.43 |
| 800 | 86.25 | 45.00 | 45.00 | 45.00 | 30.34 |
| 825 | 88.75 | 55.00 | 55.00 | 55.00 | 38.34 |
| 850 | 86.88 | 47.50 | 47.50 | 47.50 | 31.86 |
| 875 | 89.38 | 57.50 | 57.50 | 57.50 | 40.53 |
| 900 | 86.88 | 47.50 | 47.50 | 47.50 | 31.86 |
| Hidden Neuron Numbers | Accuracy | Precision | Recall | F-Measure | G-Mean |
|---|---|---|---|---|---|
| 650 | 88.12 | 52.50 | 52.50 | 52.50 | 36.00 |
| 675 | 89.38 | 57.50 | 57.50 | 57.50 | 40.63 |
| 700 | 88.75 | 55.00 | 55.00 | 55.00 | 38.40 |
| 725 | 92.50 | 70.00 | 70.00 | 70.00 | 53.44 |
| 750 | 90.00 | 60.00 | 60.00 | 60.00 | 42.88 |
| 775 | 88.75 | 55.00 | 55.00 | 55.00 | 38.16 |
| 800 | 90.63 | 62.50 | 62.50 | 62.50 | 45.26 |
| 825 | 89.38 | 57.50 | 57.50 | 57.50 | 40.49 |
| 850 | 88.75 | 55.00 | 55.00 | 55.00 | 38.09 |
| 875 | 88.12 | 52.50 | 52.50 | 52.50 | 36.24 |
| 900 | 90.00 | 60.00 | 60.00 | 60.00 | 42.65 |
| Number of Hidden Neurons | Accuracy | Precision | Recall | F-Measure | G-Mean |
|---|---|---|---|---|---|
| 650 | 96.88 | 87.50 | 87.50 | 87.50 | 77.43 |
| 675 | 96.25 | 85.00 | 85.00 | 85.00 | 73.19 |
| 700 | 95.00 | 80.00 | 80.00 | 80.00 | 66.16 |
| 725 | 97.50 | 90.00 | 90.00 | 90.00 | 81.61 |
| 750 | 93.75 | 75.00 | 75.00 | 75.00 | 59.11 |
| 775 | 97.50 | 90.00 | 90.00 | 90.00 | 81.56 |
| 800 | 96.88 | 87.50 | 87.50 | 87.50 | 77.43 |
| 825 | 92.50 | 70.00 | 70.00 | 70.00 | 53.40 |
| 850 | 95.63 | 82.50 | 82.50 | 82.50 | 69.74 |
| 875 | 96.88 | 87.50 | 87.50 | 87.50 | 77.27 |
| 900 | 95.00 | 80.00 | 80.00 | 80.00 | 66.16 |
| Number of Hidden Neurons | Accuracy | Precision | Recall | F-Measure | G-Mean |
|---|---|---|---|---|---|
| 650 | 93.13 | 72.50 | 72.50 | 72.50 | 56.20 |
| 675 | 94.37 | 77.50 | 77.50 | 77.50 | 62.58 |
| 700 | 93.13 | 72.50 | 72.50 | 72.50 | 56.16 |
| 725 | 93.75 | 75.00 | 75.00 | 75.00 | 59.46 |
| 750 | 91.87 | 67.50 | 67.50 | 67.50 | 50.44 |
| 775 | 92.50 | 70.00 | 70.00 | 70.00 | 53.12 |
| 800 | 93.13 | 72.50 | 72.50 | 72.50 | 56.37 |
| 825 | 93.75 | 75.00 | 75.00 | 75.00 | 59.38 |
| 850 | 93.13 | 72.50 | 72.50 | 72.50 | 56.20 |
| 875 | 93.75 | 75.00 | 75.00 | 75.00 | 59.33 |
| 900 | 92.50 | 70.00 | 70.00 | 70.00 | 53.09 |
| Number of Hidden Neurons | Accuracy | Precision | Recall | F-Measure | G-Mean |
|---|---|---|---|---|---|
| 650 | 93.75 | 75.00 | 75.00 | 75.00 | 59.54 |
| 675 | 93.13 | 72.50 | 72.50 | 72.50 | 56.37 |
| 700 | 92.50 | 70.00 | 70.00 | 70.00 | 53.56 |
| 725 | 93.75 | 75.00 | 75.00 | 75.00 | 59.32 |
| 750 | 91.87 | 67.50 | 67.50 | 67.50 | 50.24 |
| 775 | 93.75 | 75.00 | 75.00 | 75.00 | 59.50 |
| 800 | 93.13 | 72.50 | 72.50 | 72.50 | 56.16 |
| 825 | 93.75 | 75.00 | 75.00 | 75.00 | 59.37 |
| 850 | 93.13 | 72.50 | 72.50 | 72.50 | 56.21 |
| 875 | 95.00 | 80.00 | 80.00 | 80.00 | 66.25 |
| 900 | 92.50 | 70.00 | 70.00 | 70.00 | 53.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albadr, M.A.; Tiun, S.; Ayob, M.; AL-Dhief, F. Genetic Algorithm Based on Natural Selection Theory for Optimization Problems. Symmetry 2020, 12, 1758. https://doi.org/10.3390/sym12111758
Albadr MA, Tiun S, Ayob M, AL-Dhief F. Genetic Algorithm Based on Natural Selection Theory for Optimization Problems. Symmetry. 2020; 12(11):1758. https://doi.org/10.3390/sym12111758
Chicago/Turabian StyleAlbadr, Musatafa Abbas, Sabrina Tiun, Masri Ayob, and Fahad AL-Dhief. 2020. "Genetic Algorithm Based on Natural Selection Theory for Optimization Problems" Symmetry 12, no. 11: 1758. https://doi.org/10.3390/sym12111758
APA StyleAlbadr, M. A., Tiun, S., Ayob, M., & AL-Dhief, F. (2020). Genetic Algorithm Based on Natural Selection Theory for Optimization Problems. Symmetry, 12(11), 1758. https://doi.org/10.3390/sym12111758






