Vibrational Circular Dichroism Detects Symmetry Breaking due to Conformational Mobility in C2-Symmetry Chiral Molecules and Provides Further Insight into Inter-Chromophoric Interactions
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
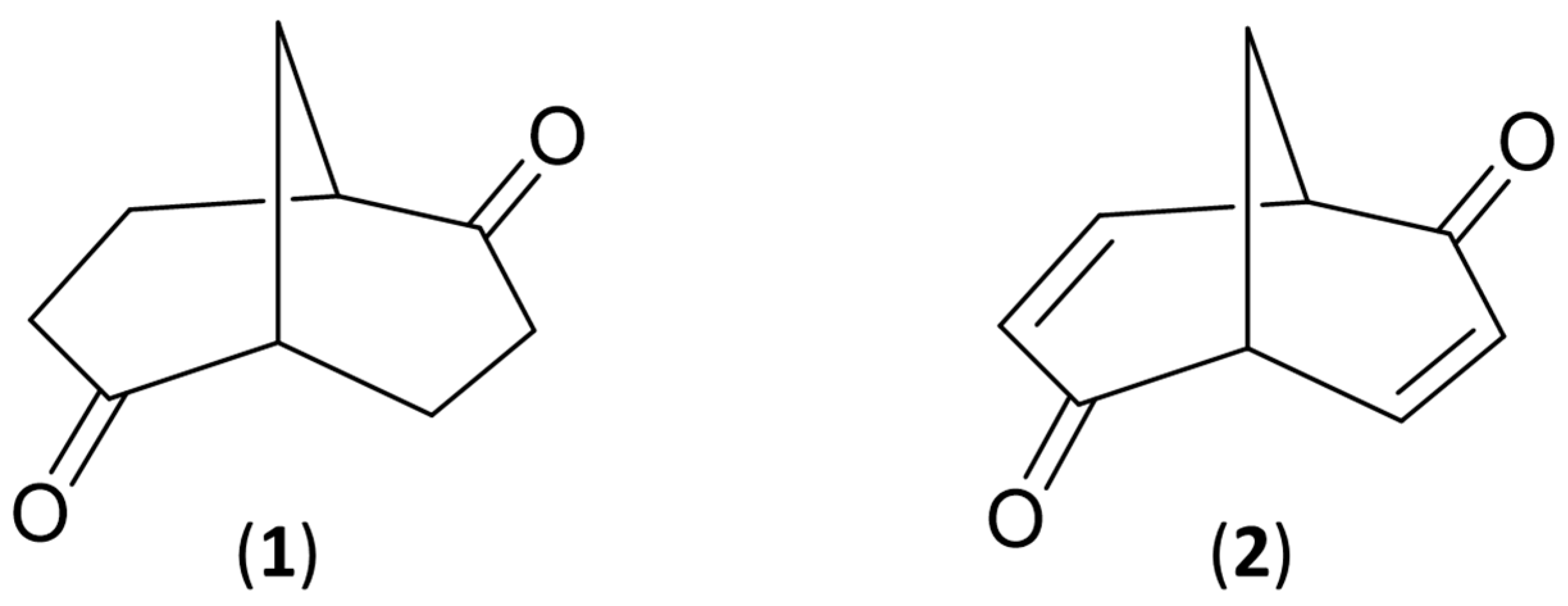
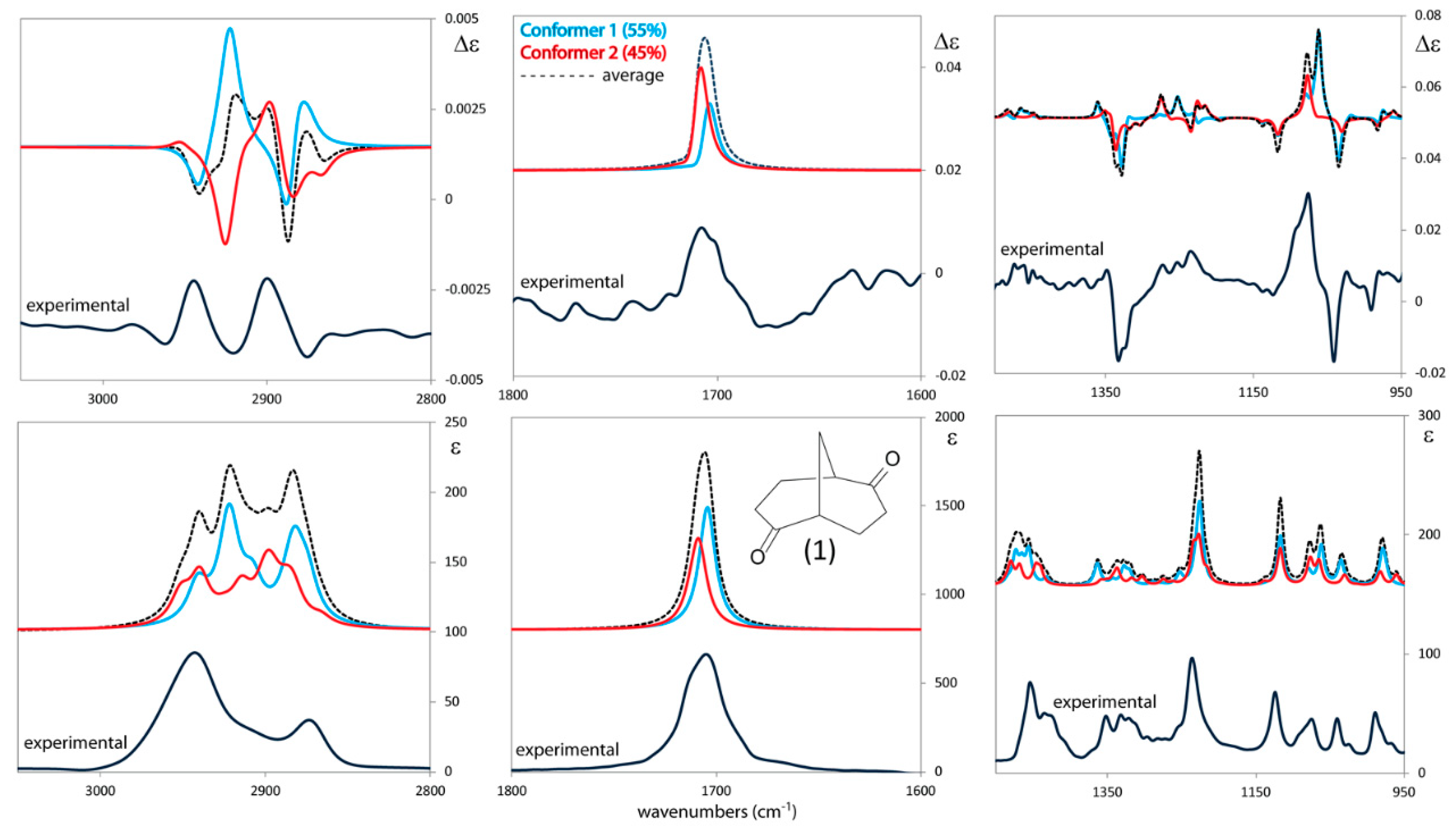
3.1. IR and VCD Spectra of 1
3.2. Symmetry Breaking from Chair-Chair→ to Chair-Boat in Compound 1
3.3. IR and VCD Spectra of 2
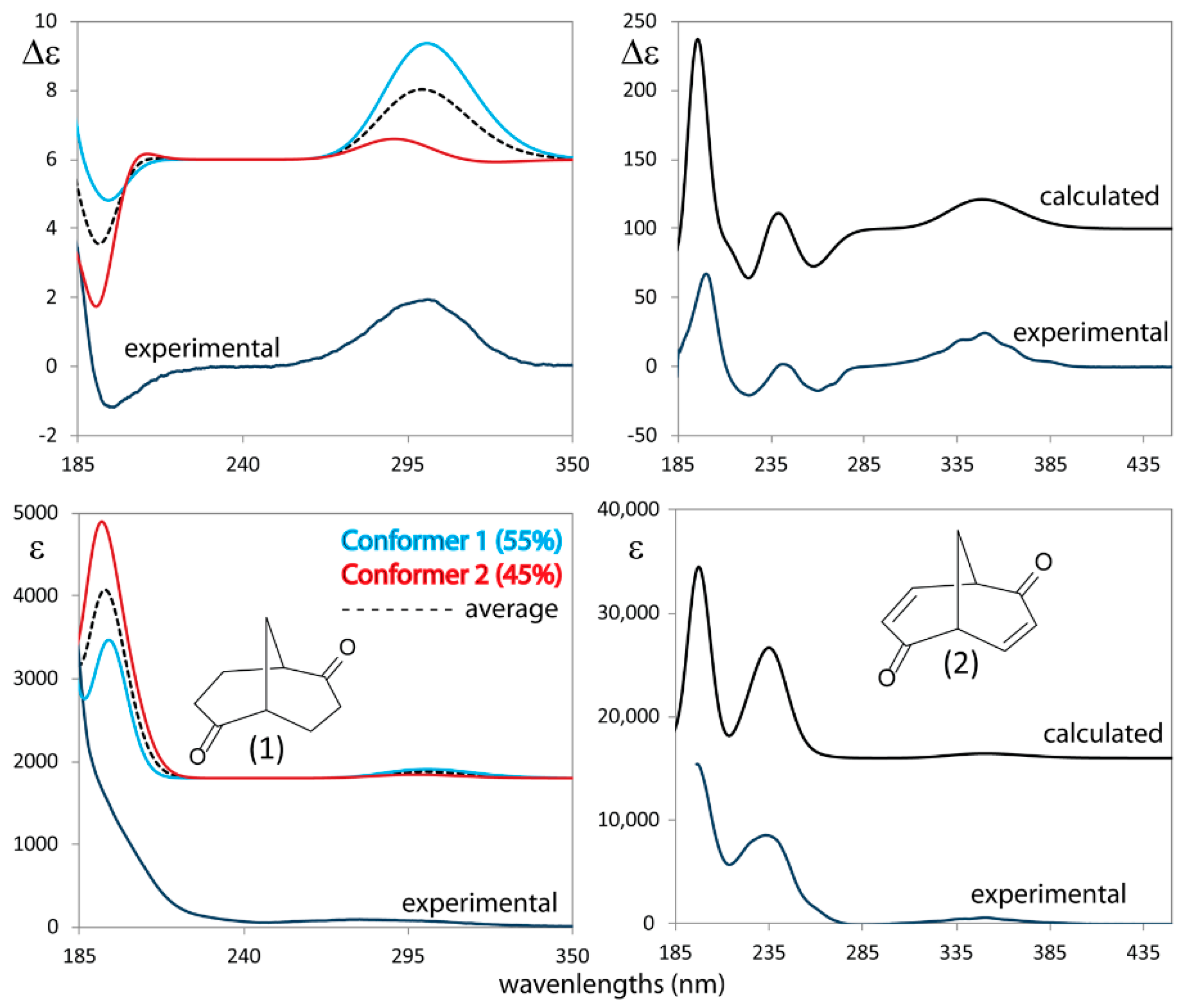
3.4. UV and ECD Spectra of 1 and 2
3.5. Interaction of the Ketone Carbonyls in Diketone 1
3.6. The Role of the C=C Double Bonds in the ECD and VCD (Carbonyl Stretching Region)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doerner, T.; Gleiter, R.; Robbins, T.A.; Chayangkoon, P.; Lightner, D.A. Homoconjugation and Transannular Orbital Interactions Detected by Photoelectron and 13C-NMR Spectroscopy. Bicyclo[3.3.1]nonane-2,6-dione and bicyclo[3.3.1]nona-3,7-diene-2,6-dione. J. Am. Chem. Soc. 1992, 114, 3235–3241. [Google Scholar] [CrossRef]
- Lightner, D.A.; Gurst, J.E. Stereochemstry from Circular Dichroism Spectroscopy; Wiley-VCH: New York, NY, USA, 2000. [Google Scholar]
- Gerlach, H. Racematspaltung und Bestimmung der absoluten Konfiguration von 2,6-disubstituierten Bicyclo [3.3.1]nonanen. Helv. Chim. Acta 1978, 61, 2773–2776. [Google Scholar] [CrossRef]
- Berg, U.; Butkus, E. Enantiomer separation and circular dichroism spectra of bicyclo[3.3.1]nonanediones. J. Chem. Res. 1993, 3, 116–117. [Google Scholar]
- Berg, U.; Butkus, E. An analysis of the circular dichroism spectra of bicyclo[3.3.1]nonanediones. J. Chem. Res. 1994, 9, 356–357. [Google Scholar]
- Buktus, E.; Stoncius, S.; Zilinskas, A. Determination of the Absolute Configuration of Bicyclo[3.3.1]nonane-2,7-dione by Circular Dichroism Spectroscopy and Chemical Correlation. Chirality 2001, 13, 694–698. [Google Scholar]
- Hoffman, R.; Inamura, A.; Hehre, W.J. Benzynes, dehydroconjugated molecules, and the interaction of orbitals separated by a number of intervening sigma bonds. J. Am. Chem. Soc. 1968, 99, 1499–1509. [Google Scholar] [CrossRef]
- Hansen, A.E. On the Optical Activity of Compounds Containing Coupled Chromophores. Ph.D. Thesis, H.C. Ørsted Institute, Copenhagen, Denmark, 1964. [Google Scholar]
- Moscowitz, A.; Hansen, A.E.; Forster, L.S.; Rosenheck, K. Prototypic Systems for Optically Active Helical Polypeptides. Biopolym. Symp. 1964, 1, 75–89. [Google Scholar]
- Moscowitz, A. Some Comments on the Relevance of Charge Transfer for the 300 nm Transition in β, γ Unsaturated Ketones. Proc. R. Soc. Lond. 1967, 297, 40–42. [Google Scholar]
- Nafie, L.A. Vibrational Optical Activity. Principles and Applications; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Stephens, P.J.; Devlin, F.J.; Cheeseman, J.R. VCD Spectroscopy for Organic Chemists; CRC Press: New York, NY, USA, 2012. [Google Scholar]
- Taniguchi, T.; Monde, K. Exciton Chirality Method in Vibrational Circular Dichroism. J. Am. Chem. Soc. 2012, 134, 3695–3698. [Google Scholar] [CrossRef]
- Abbate, S.; Mazzeo, G.; Meneghini, S.; Longhi, G.; Boiadjiev, S.E.; Lightner, D.A. Bicamphor: A prototypic molecular system to investigate vibrational excitons. J. Phys. Chem. A 2015, 119, 4261–4267. [Google Scholar] [CrossRef]
- Covington, C.L.; Nicu, V.P.; Polavarapu, P.L. Determination of the Absolute Configurations Using Exciton Chirality Method for Vibrational Circular Dichroism: Right Answers for the Wrong Reasons? J. Phys. Chem. A 2015, 119, 10589–10602. [Google Scholar] [CrossRef] [PubMed]
- Nicu, V.P. Revisiting an old concept: The coupled oscillator model for VCD. Part 2: Implications of the generalised coupled oscillator mechanism for the VCD robustness concept. Phys. Chem. Chem. Phys. 2016, 18, 21213–21225. [Google Scholar] [CrossRef] [PubMed]
- Abbate, S.; Bruhn, T.; Pescitelli, G.; Longhi, G. Vibrational Optical Activity of BODIPY Dimers: The Role of Magnetic−Electric Coupling in Vibrational Excitons. J. Phys. Chem A 2017, 121, 394–400. [Google Scholar] [CrossRef]
- Mazzeo, G.; Santoro, E.; Abbate, S.; Fabris, F.; Zonta, C.; Longhi, G. Testing the Vibrational Exciton and the Local Mode Models on the Instructive Cases of Dicarvone, Dipinocarvone, and Dimenthol Vibrational Circular Dichroism Spectra. Chirality 2020, 32, 907–921. [Google Scholar] [CrossRef]
- Abbate, S.; Lebon, F.; Longhi, G.; Boiadjiev, S.E.; Lightner, D.A. Vibrational and Electronic Circular Dichroism of Dimethyl Mesobilirubins-XIIIalpha. J. Phys. Chem. B 2012, 116, 5628–5636. [Google Scholar] [CrossRef]
- Passarello, M.; Abbate, S.; Longhi, G.; Lepri, S.; Ruzziconi, R.; Nicu, V.P. Importance of C*−H Based Modes and Large Amplitude Motion: Effects in Vibrational Circular Dichroism Spectra: The Case of the Chiral Adduct of Dimethyl Fumarate and Anthracene. J. Phys. Chem A 2014, 118, 4339–4350. [Google Scholar] [CrossRef]
- Mazzeo, G.; Abbate, S.; Longhi, G.; Castiglioni, E.; Boiadjiev, S.E.; Lightner, D.A. pH Dependent Chiroptical Properties of (1R,2R)- and (1S,2S)-trans-Cyclohexane Diesters and Diamides from VCD, ECD, and CPL Spectroscopy. J. Phys. Chem. B 2016, 120, 2380–2387. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Stephens, P.J.; McCann, D.M.; Butkus, E.; Stoncius, S.; Cheeseman, J.R.; Frisch, M.J. Determination of Absolute Configuration Using Concerted ab Initio DFT Calculations of Electronic Circular Dichroism and Optical Rotation: Bicyclo[3.3.1]nonane Diones. J. Org. Chem. 2004, 69, 1948–1958. [Google Scholar] [CrossRef]
- Paoloni, L.; Mazzeo, G.; Longhi, G.; Abbate, S.; Fusé, M.; Bloino, J.; Barone, V. Toward Fully Unsupervised Anharmonic Computations Complementing Experiment for Robust and Reliable Assignment and Interpretation of IR and VCD Spectra from Mid-IR to NIR: The Case of 2,3-Butanediol and trans-1,2-Cyclohexanediol. J. Phys. Chem. A 2020, 124, 1011–1024. [Google Scholar] [CrossRef]
- Abbate, S.; Wunder, S.L.; Zerbi, G. Conformational dependence of Fermi Resonance in n-Alkanes Raman Spectra of 1,1,1,4,4,4,-Hexadeuteriobutane. J. Phys. Chem. 1984, 88, 593–600. [Google Scholar] [CrossRef]
- Abbate, S.; Castiglioni, E.; Gangemi, F.; Gangemi, R.; Longhi, G.; Ruzziconi, R.; Spizzichino, S. Harmonic and Anharmonic Features of IR and NIR Absorption and VCD Spectra of Chiral 4-X-[2.2]Paracyclophanes. J. Phys. Chem. A 2007, 111, 7031–7040. [Google Scholar] [CrossRef] [PubMed]
- Longhi, G.; Abbate, S.; Scafato, P.; Rosini, C. A Vibrational Circular Dichroism Approach to the Determination of the Absolute Configuration of Flexible and Transparent Molecules: Fluorenone Ketals of 1,n-Diols. Phys. Chem. Chem. Phys. 2010, 12, 4703–4712. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Longhi, G.; Tommasini, M.; Abbate, S.; Polavarapu, P.L. The Connection Between Robustness Angles and Dissymmetry Factors in Vibrational Circular Dichroism Spectra. Chem. Phys. Lett. 2015, 623, 320–325. [Google Scholar] [CrossRef]
- Paddon-Row, M.N. On the Origin of Transannular Interactions in Diketones and Methylene-Ketones, as Detected by 13C N.M.R. Spectroscopy: An Ab Initio MO Study. Tetrahedron 1994, 50, 10813–10828. [Google Scholar] [CrossRef]
- Moore, B., II; Srebro, M.; Autschbach, J. Analysis of Optical Activity in Terms of Bonds and Lone-Pairs: The Exceptionally Large Optical Rotation of Norbornenone. J. Chem. Theory Comput. 2012, 8, 4336–4346. [Google Scholar] [CrossRef]
- Caricato, M.; Vaccaro, P.H.; Crawford, T.D.; Wiberg, K.W.; Lahiri, P. Insights on the Origin of the Unusually Large Specific Rotation of (1S,4S)-Norbornenone. J. Phys. Chem. A 2014, 118, 4863–4871. [Google Scholar] [CrossRef]
- Wiberg, K. Chirality Induced by the Interaction of C=C and C=X Bonds (X=CH2, NH, NH2+, O, and S) Separated by a Methylene Group. J. Phys. Chem. A 2016, 120, 7771–7777. [Google Scholar] [CrossRef]
- Gawroński, J.K. Chapter 3, Conformations, Chiroptical and Related Spectral Properties of Enones. In The Chemistry of Enones. Part I; Patai, S., Rapport, Z., Eds.; Wiley & Sons: Hoboken, NJ, USA, 1989; pp. 55–103. [Google Scholar] [CrossRef]
- Jaffe, H.H.; Orchin, M. Theory and Applications of Ultraviolet Spectroscopy; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Scott, A.I. Interpretation of the Ultraviolet Spectra of Natural Products; The Macmillan Company: New York, NY, USA, 1964. [Google Scholar]
- Longhi, G.; Castiglioni, E.; Abbate, S.; Lebon, F.; Lightner, D.A. Experimental and Calculated CPL spectra and related spectroscopic data of camphor and other simple chiral bicyclic ketones. Chirality 2013, 25, 589–599. [Google Scholar] [CrossRef]
- Polavarapu, P.L.; Santoro, E.; Covington, C.L.; Raghavan, V. Enhancement of the chiroptical response of α-amino acids via N-substitution for molecular structure determination using vibrational circular dichroism. Chirality 2020, 32, 564–578. [Google Scholar] [CrossRef]
- Gleiter, R.; Lange, H.; Borzyk, O. Photoelectron Spectra, Ab Initio SCF MO, and Natural Bond Orbital Studies on Stellenes. Long Range π/σ Interactions. J. Am. Chem. Soc. 1996, 118, 4889–4895. [Google Scholar] [CrossRef]
- Paoloni, L.; Fusè, M.; Baiardi, A.; Barone, V. Interplay of Stereoelectronic and Vibrational Modulation Effects in Tuning the UPS Spectra of Unsaturated Hydrocarbon Cage Compounds. J. Chem. Theory Comput. 2020, 16, 5218–5226. [Google Scholar] [CrossRef] [PubMed]


| cpd | Wavenumber (cm−1) | IR Band Area (103 cm2/mol) | CD Band Area (103 cm2/mol) | g (×105) |
|---|---|---|---|---|
| 1 | 1704 | 14150 | 0.40 | 2.83 |
| 2 | 1679 | 18630 | 1.80 | 9.66 |
| Compound 1 | ||
| εmax (nm) | ∆εmax (nm) | Transition |
| 50.1 (287.0) | +1.9 (301.6) | n-π* |
| 1329.3 (196.9) | −1.2 (196.9) | π-π* |
| Compound 2 | ||
| εmax (nm) | ∆εmax (nm) | Transition |
| 741.8 (350.3) | +24.5 (350.3) | n-π* |
| 1544.3 (259.5) | −17.5 (259.5) | π-π* (E.T.) |
| 8543.9 (233.1) | −20.8 (222.8) | π-π* (E.T.) |
| 15,423.3 (196.6) | +67.5 (199.7) | π-π* |
| A | 1-cc | nm | eV | |μ| | |m| | E-M | R | D |
| 1 | 293 | 4.23 | 0.058 | 1.636 | 63 | 10.08 | 249 | |
| 2 | 292 | 4.25 | 0.008 | 0.144 | 180 | −0.31 | 4 | |
| 3 | 193 | 6.41 | 0.245 | 0.502 | 180 | −29.81 | 3868 | |
| 4 | 193 | 6.43 | 0.226 | 0.389 | 0 | 21.32 | 3281 | |
| 5 | 186 | 6.65 | 0.236 | 0.345 | 78 | 3.86 | 3609 | |
| B | 1-cb | nm | eV | |μ| | |m| | E-M | R | D |
| 1 | 293 | 4.24 | 0.016 | 1.240 | 113 | −1.84 | 16 | |
| 2 | 289 | 4.29 | 0.042 | 1.094 | 50 | 7.04 | 123 | |
| 3 | 199 | 6.24 | 0.181 | 0.352 | 106 | −4.11 | 2112 | |
| 4 | 193 | 6.41 | 0.306 | 0.656 | 85 | 4.20 | 6049 | |
| 5 | 186 | 6.67 | 0.296 | 0.620 | 94 | −2.88 | 5695 | |
| C | 1-mono-conf1 | nm | eV | |μ| | |m| | E-M | R | D |
| 1 | 292 | 4.25 | 0.041 | 1.164 | 66 | 4.57 | 124 | |
| 2 | 196 | 6.31 | 0.205 | 0.537 | 90 | −0.09 | 2714 | |
| 3 | 183 | 6.78 | 0.348 | 0.225 | 115 | −7.73 | 7815 |
| A | 2 | nm | eV | |μ| | |m| | E-M | R | D |
 | 1 | 348 | 3.56 | 0.106 | 0.533 | 180 | −12.88 | 741 |
| 2 | 336 | 3.69 | 0.308 | 1.228 | 20 | 82.35 | 6143 | |
| 3 | 242 | 5.12 | 0.163 | 1.623 | 180 | −62.39 | 1699 | |
| 4 | 224 | 5.55 | 1.174 | 0.328 | 51 | 55.5 | 88,731 | |
| 5 | 215 | 5.77 | 0.023 | 0.07 | 180 | −0.08 | 46 | |
| 6 | 210 | 5.89 | 0.735 | 0.703 | 139 | −90.63 | 34,914 | |
| 7 | 192 | 6.46 | 0.084 | 0.698 | 180 | −11.52 | 449 | |
| B | α,β | nm | eV | |μ| | |m| | E-M | R | D |
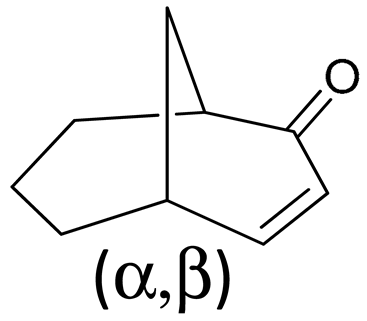 | 1 | 332 | 3.73 | 0.067 | 0.845 | 60 | 6.58 | 282 |
| 2 | 215 | 5.77 | 1.238 | 1.694 | 91 | −8.05 | 99,039 | |
| 3 | 193 | 6.43 | 0.084 | 0.578 | 30 | 9.9 | 451 | |
| 4 | 191 | 6.5 | 0.137 | 0.379 | 115 | −5.49 | 1216 | |
| C | β,γ | nm | eV | |μ| | |m| | E-M | R | D |
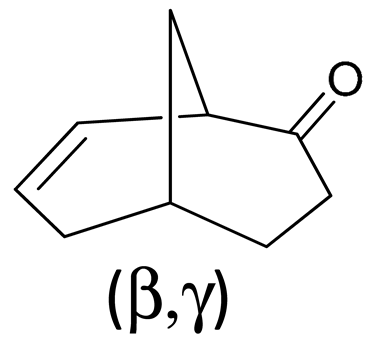 | 1 | 294 | 4.22 | 0.191 | 1.239 | 28 | 48.59 | 2377 |
| 2 | 206 | 6.02 | 0.126 | 0.431 | 88 | 0.44 | 1008 | |
| 3 | 195 | 6.36 | 0.796 | 0.969 | 90 | −0.87 | 40,956 | |
| 4 | 190 | 6.52 | 0.421 | 0.78 | 97 | −9.84 | 11,480 |
| Compound 1 (cc Conformer) | ||||||
| Atom | APT(xz) | APT(yz) | APT(zz) | AAT(xz) | AAT(yz) | AAT(zz) |
| C | −0.105 | −0.006 | 1.313 | −0.154 | 0.118 | 0.041 |
| O | 0.040 | 0.021 | −1.224 | 0.173 | −0.150 | −0.061 |
| Compound 2 | ||||||
| Atom | APT(xz) | APT(yz) | APT(zz) | AAT(xz) | AAT(yz) | AAT(zz) |
| C | −0.195 | −0.053 | 1.542 | −0.309 | 0.260 | 0.318 |
| O | 0.128 | 0.056 | −1.358 | 0.305 | −0.311 | −0.225 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazzeo, G.; Abbate, S.; Boiadjiev, S.E.; Lightner, D.A.; Longhi, G. Vibrational Circular Dichroism Detects Symmetry Breaking due to Conformational Mobility in C2-Symmetry Chiral Molecules and Provides Further Insight into Inter-Chromophoric Interactions. Symmetry 2020, 12, 1752. https://doi.org/10.3390/sym12111752
Mazzeo G, Abbate S, Boiadjiev SE, Lightner DA, Longhi G. Vibrational Circular Dichroism Detects Symmetry Breaking due to Conformational Mobility in C2-Symmetry Chiral Molecules and Provides Further Insight into Inter-Chromophoric Interactions. Symmetry. 2020; 12(11):1752. https://doi.org/10.3390/sym12111752
Chicago/Turabian StyleMazzeo, Giuseppe, Sergio Abbate, Stefan E. Boiadjiev, David A. Lightner, and Giovanna Longhi. 2020. "Vibrational Circular Dichroism Detects Symmetry Breaking due to Conformational Mobility in C2-Symmetry Chiral Molecules and Provides Further Insight into Inter-Chromophoric Interactions" Symmetry 12, no. 11: 1752. https://doi.org/10.3390/sym12111752
APA StyleMazzeo, G., Abbate, S., Boiadjiev, S. E., Lightner, D. A., & Longhi, G. (2020). Vibrational Circular Dichroism Detects Symmetry Breaking due to Conformational Mobility in C2-Symmetry Chiral Molecules and Provides Further Insight into Inter-Chromophoric Interactions. Symmetry, 12(11), 1752. https://doi.org/10.3390/sym12111752







