Gyro Motor State Evaluation and Prediction Using the Extended Hidden Markov Model
Abstract
1. Introduction
2. Literature Review
3. The Model
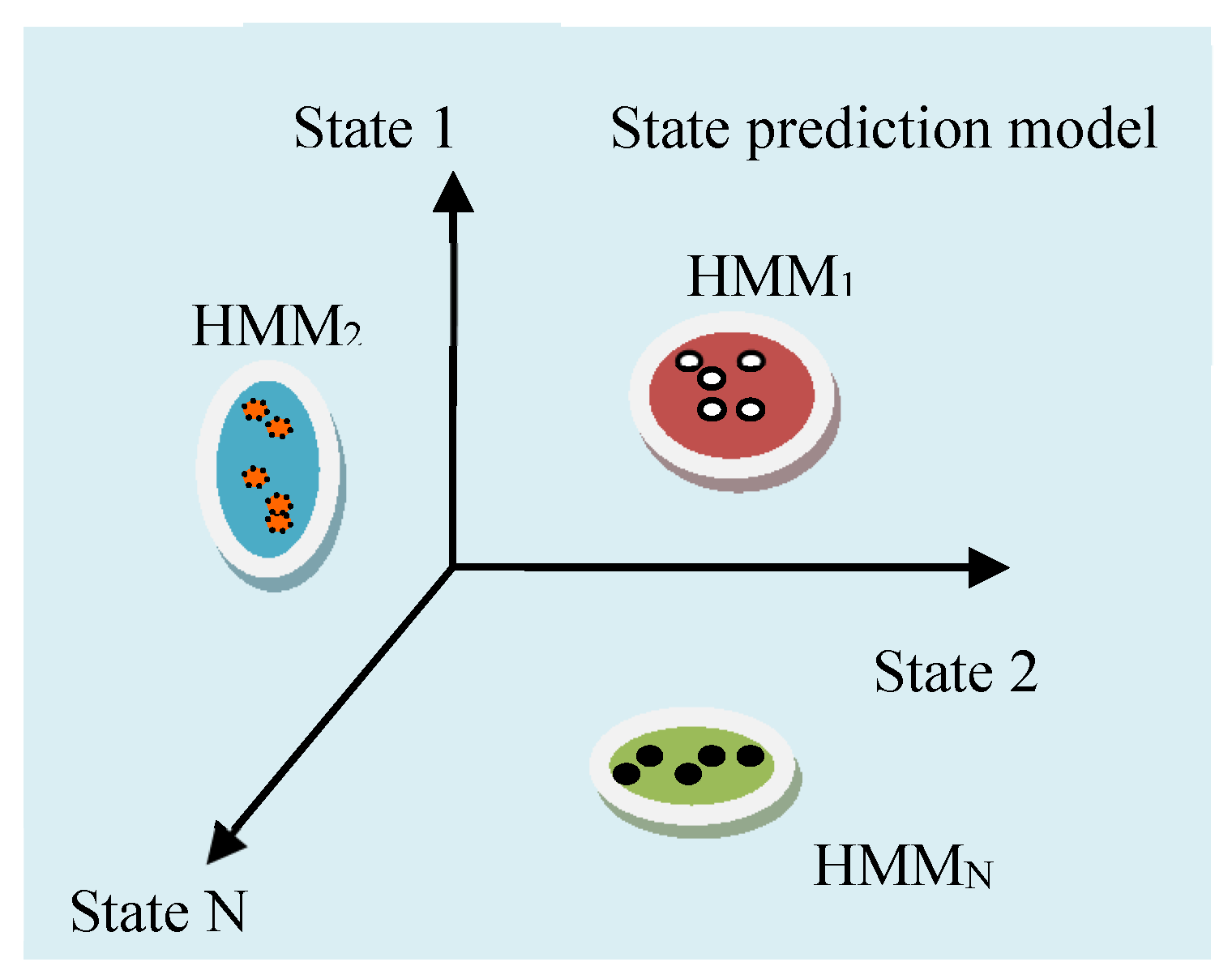
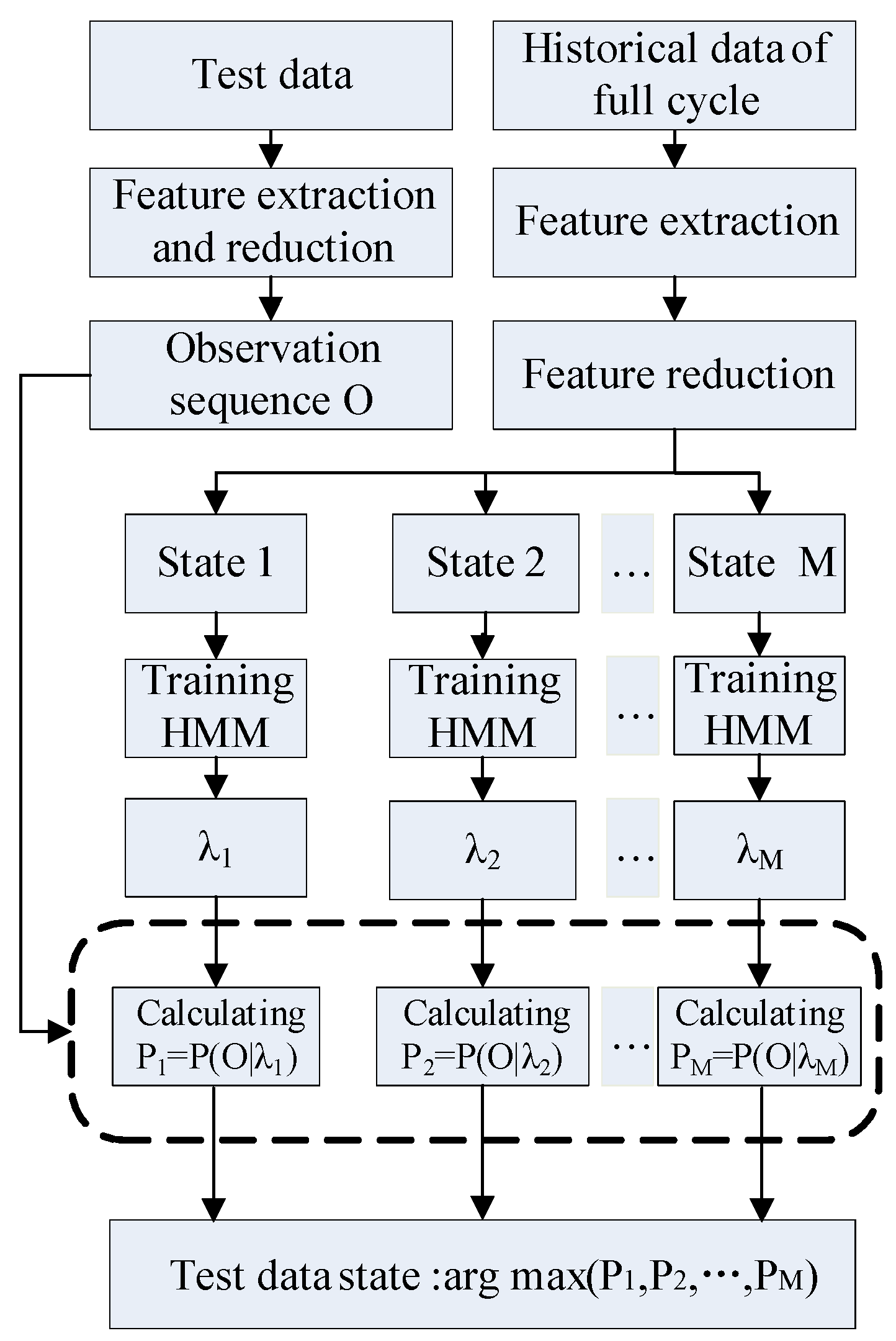
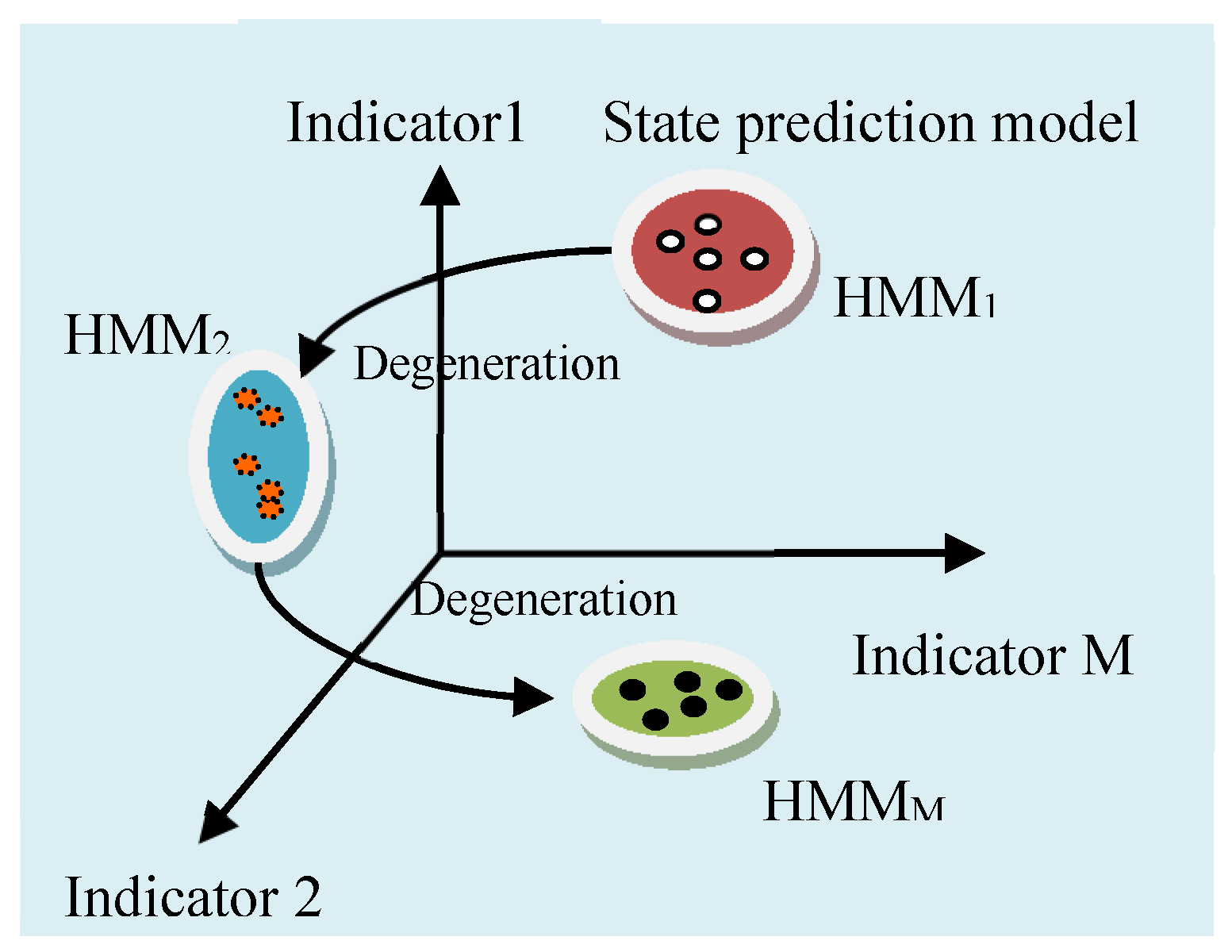
3.1. Principle and Structure of the Prediction Model
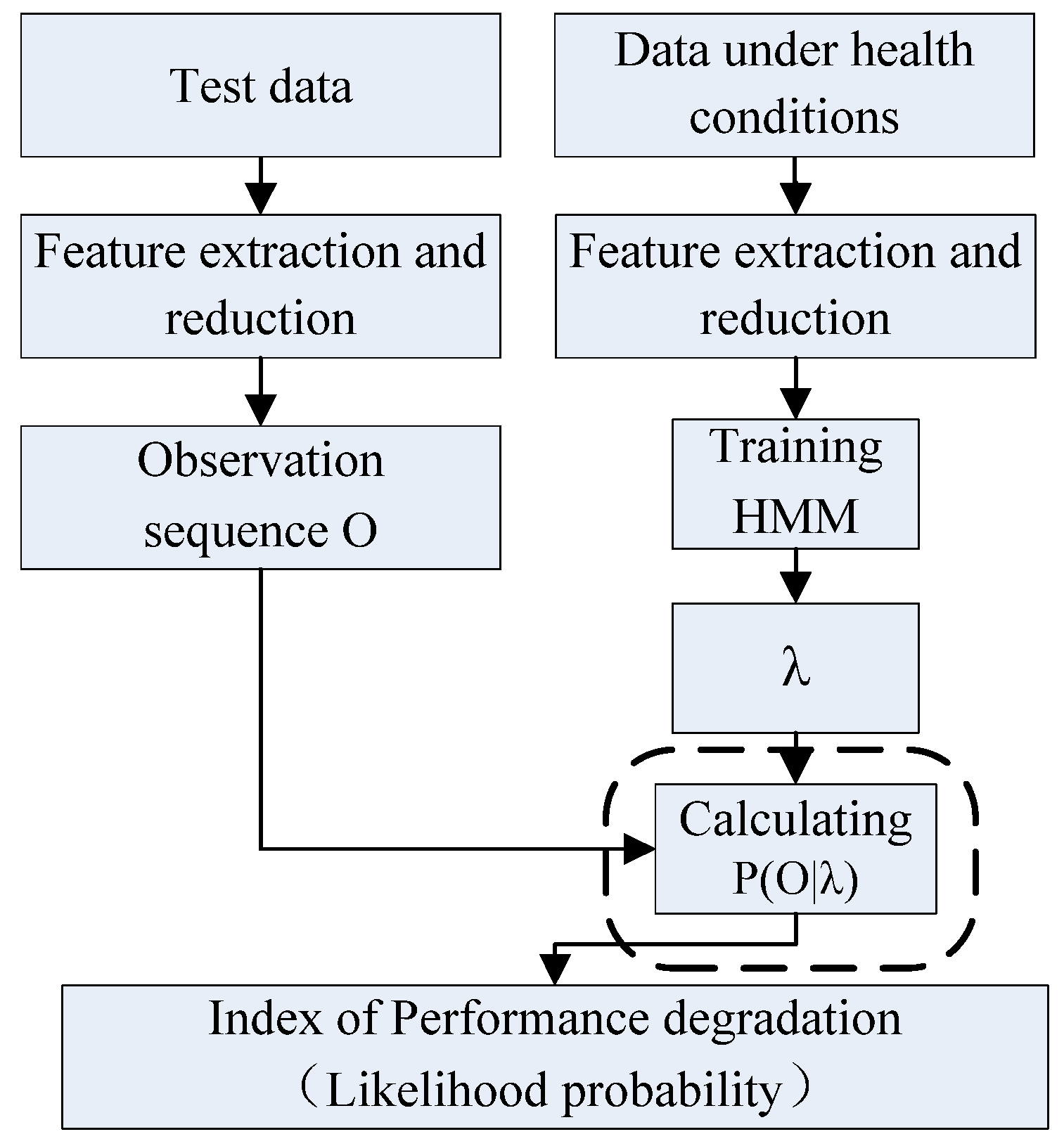
3.2. Modeling and Learning with Complete Data
4. Diagnosis and Prediction Results
4.1. Experimental Devices and Schemes
- (1)
- Place the cleaned bearing into the gyro motor to prevent interference from being introduced. Align the motor to a proper state and put the motor into a special test fixture.
- (2)
- Start the motor on a 24-h non-stop running mode with 24 h as a time unit.
- (3)
- Carry out one data acquisition in a fixed length way every 24 h of running. Acquire 10,000 points for each data set. Conduct the acquisition during the stable operation of the motor. If the motor needs to be restarted due to a power outage, then do not begin the data acquisition until the motor has run for five minutes.
- (4)
- Check the operational conditions of the gyro motor after every 24 h of operation, identify the state the gyro motor is in according to the changes in the gyro motor current and motor voice, see if the fault occurs, and keep records.
- (5)
- Restart the experiment by repeating steps (2) to (4) until the gyro motor loses efficacy when the test stops.
4.2. Time Domain Statistical Feature Analysis
4.3. Experimental Results
5. Comparing Analysis
5.1. Multi-HMM State Prediction Method
5.2. Health Condition HMM Prediction Method
5.3. Test Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Darong, H.; Lanyan, K.; Chu, X.; Zhao, L.; Mi, B. Fault diagnosis for the motor drive system of urban transit based on improved Hidden Markov Model. Microelectron. Reliab. 2018, 82, 179–189. [Google Scholar] [CrossRef]
- Tobon-Mejia, D.A.; Medjaher, K.; Zerhouni, N.; Tripot, G. A data-driven failure prognostics method based on mixture of Gaussians hidden Markov models. IEEE Trans. Reliab. 2012, 61, 491–503. [Google Scholar] [CrossRef]
- Zhu, J.; Ge, Z.; Song, Z. HMM-driven robust probabilistic principal component analyzer for dynamic process fault classification. IEEE Trans. Ind. Electron. 2015, 62, 3814–3821. [Google Scholar] [CrossRef]
- Zhang, S.-q.; Lin, K.-P. Short-term traffic flow forecasting based on data-driven model. Mathematics 2020, 8, 152. [Google Scholar] [CrossRef]
- Dash, S.; Venkatasubramanian, V. Challenges in the industrial applications of fault diagnostic systems. Comput. Chem. Eng. 2000, 24, 785–791. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Kavuri, S.N.; Yin, K. A review of process fault detection and diagnosis: Part III: Process history based methods. Comput. Chem. Eng. 2003, 27, 327–346. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Zhong, Y.; Zhou, Y. Convolutional neural network-based hidden Markov models for rolling element bearing fault identification. Knowl. Based Syst. 2018, 144, 65–76. [Google Scholar] [CrossRef]
- Baruah, P.; Chinnam, R.B. HMMs for diagnostics and prognostics in machining processes. Int. J. Prod. Res. 2005, 43, 1275–1293. [Google Scholar] [CrossRef]
- Ilhem, B.; Amar, B.; Lebaroud, A. Classification method for faults diagnosis in reluctance motors using Hidden Markov Models. In Proceedings of the Industrial Electronics (ISIE), 2014 IEEE 23rd International Symposium on IEEE, Istanbul, Turkey, 1–4 June 2014; pp. 984–991. [Google Scholar]
- Le, D.; Provost, E.M. Emotion recognition from spontaneous speech using hidden Markov models with deep belief networks. In Proceedings of the 2013 IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU), Olomouc, Czech Republic, 8–12 December 2013; pp. 216–221. [Google Scholar]
- Cai, Y.; Shi, X.; Shao, H.; Wang, R.; Liao, S. Energy efficiency state identification in milling processes based on information reasoning and Hidden Markov Model. J. Clean. Prod. 2018, 193, 397–413. [Google Scholar] [CrossRef]
- Putland, R.L.; Ranjard, L.; Constantine, R.; Radford, C.A. A hidden Markov model approach to indicate Bryde’s whale acoustics. Ecol. Indic. 2018, 84, 479–487. [Google Scholar] [CrossRef]
- Roman-Galvez, R.; Roman-Roldana, R.; Martınez-Arozab, J.; Gomez-Loper, J.F. Semi-hidden Markov models for generation and analysis of sequences. Math. Comput. Simul. 2015, 118, 320–328. [Google Scholar] [CrossRef]
- Ali, S.M.; Bhatti, U.I.; Munawwar, K.; Alsaggaf, U.M.; Mansoor, S.; Ali, J. Gyroscopic Drift Compensation by Using Low Cost Sensors for Improved Attitude Determination. Measurement 2018, 116, 199–206. [Google Scholar] [CrossRef]
- Jang, H.S.; Bae, K.Y.; Park, H.S.; Sung, D.K. Solar power prediction based on satellite images and support vector machine. IEEE Trans. Sustain. Energy 2016, 7, 1255–1263. [Google Scholar] [CrossRef]
- Wang, S.; Chen, M.; Song, M. Energy constraints, green technological progress, and business profit ratios: Evidence from big data of Chinese enterprises. Int. J. Prod. Res. 2018, 56. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, K.; Zhang, W.; Zhang, Y.; Gu, J. Deep Neural Networks for wireless localization in indoor and outdoor environments. Neurocomputing 2016, 194, 279–287. [Google Scholar] [CrossRef]
- Ren, Y.; Li, H.; Lin, H.C. Optimization of Feedforward Neural Networks Using an Improved Flower Pollination Algorithm for Short-Term Wind Speed Prediction. Energies 2019, 12, 4126. [Google Scholar] [CrossRef]
- Paya, B.A.; Esat, I.I.; Badi, M.N.M. Artificial neural network based fault diagnostics of rotating machinery using wavelet transforms as a preprocessor. Mech. Syst. Signal Process. 1997, 11, 751–765. [Google Scholar] [CrossRef]
- Li, B.; Chow, M.Y.; Tipsuwan, Y.; Hung, J.C. Neural-network-based motor rolling bearing fault diagnosis. IEEE Trans. Ind. Electron. 2000, 47, 1060–1069. [Google Scholar] [CrossRef]
- Gan, S.; Liang, S.; Li, K.; Deng, J.; Cheng, T. Trajectory length prediction for intelligent traffic signaling: A data-driven approach. IEEE Trans. Intell. Transp. Syst. 2018, 19, 426–435. [Google Scholar] [CrossRef]
- Nagulan, S.; Selvaraj, J.; Arunachalam, A.; Sivanandam, K. Performance of artificial neural network in prediction of heave displacement for non-buoyant type wave energy converter. IET Renew. Power Gener. 2016, 11, 81–84. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, G.; Liu, H.; Zou, H.; Guo, W. Applying improved multi-scale entropy and support vector machines for bearing health condition identification. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 1315–1325. [Google Scholar] [CrossRef]
- Widodo, A.; Kim, E.Y.; Son, J.D.; Yang, B.S.; Tan, A.C.; Gu, D.S.; Choi, B.-K.; Mathew, J. Fault diagnosis of low speed bearing based on relevance vector machine and support vector machine. Expert Syst. Appl. 2009, 36, 7252–7261. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S.; Han, T. Combination of independent component analysis and support vector machines for intelligent faults diagnosis of induction motors. Expert Syst. Appl. 2007, 32, 299–312. [Google Scholar] [CrossRef]
- Rojas, A.; Nandi, A.K. Practical scheme for fast detection and classification of rolling-element bearing faults using support vector machines. Mech. Syst. Signal Process. 2006, 20, 1523–1536. [Google Scholar] [CrossRef]
- Li, L.; Lv, C.M.; Tseng, M.L.; Song, M. Renewable energy utilization method: A novel Insulated Gate Bipolar Transistor switching losses prediction model. J. Clean. Prod. 2018, 176, 852–863. [Google Scholar] [CrossRef]
- Li, L.; Lin, G.Q.; Tseng, M.L.; Tan, K.; Lim, M.K. A Maximum Power Point Tracking Method for PV System with Improved Gravitational Search Algorithm. Appl. Soft Comput. 2018, 65, 333–348. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Z.; Zhang, P.; Wang, S. UD-HMM: An unsupervised method for shilling attack detection based on hidden Markov model and hierarchical clustering. Knowl. Based Syst. 2018, 148, 146–166. [Google Scholar] [CrossRef]
- Liang, J.; Ma, M.; Sadiq, M.; Yeung, K.H. A filter model for intrusion detection system in Vehicle Ad Hoc Networks: A hidden Markov methodology. Knowl. Based Syst. 2019, 163, 611–623. [Google Scholar] [CrossRef]
- Fu, R.; Wang, H.; Zhao, W. Dynamic driver fatigue detection using hidden Markov model in real driving condition. Expert Syst. Appl. 2016, 63, 397–411. [Google Scholar] [CrossRef]
- Khan, S.S.; Karg, M.; Kuli, D.; Hoey, J. Detecting falls with X-Factor Hidden Markov Models. Appl. Soft Comput. 2017, 55, 168–177. [Google Scholar] [CrossRef]
- Yuwono, M.; Guo, Y.; Wall, J.; Li, J.; West, S.; Platt, G.; Su, S.W. Unsupervised feature selection using swarm intelligence and consensus clustering for automatic fault detection and diagnosis in Heating Ventilation and Air Conditioning systems. Appl. Soft Comput. 2015, 34, 402–425. [Google Scholar] [CrossRef]
- Song, M.; Wang, J.; Zhao, J.; Baležentis, T.; Shen, Z. Production and safety efficiency evaluation in Chinese coal mines: Accident deaths as undesirable output. Ann. Oper. Res. 2018, 291, 827–845. [Google Scholar] [CrossRef]
- Song, M.; Du, Q. Analysis and exploration of damage-reduction measures for flood disasters in China. Ann. Oper. Res. 2019, 283, 795–810. [Google Scholar] [CrossRef]
- Song, M.; Wang, S. The impact of knowledge trade on sustainable development and environment-biased technical progress. Technol. Forecast. Soc. Chang. 2019, 144, 512–523. [Google Scholar] [CrossRef]
- Xiong, X.; Chen, L.; Liang, J. A new framework of vehicle collision prediction by combining SVM and HMM. IEEE Trans. Intell. Transp. Syst. 2018, 19, 699–710. [Google Scholar] [CrossRef]
- Soualhi, A.; Clerc, G.; Razik, H.; Guillet, F. Hidden Markov models for the prediction of impending faults. IEEE Trans. Ind. Electron. 2016, 63, 3271–3281. [Google Scholar] [CrossRef]
- Tobon-Mejia, D.A.; Medjaher, K.; Zerhouni, N.; Tripot, G. Hidden Markov models for failure diagnostic and prognostic. In Proceedings of the Prognostics and System Health Management Conference (PHM-Shenzhen), Shenzhen, China, 24–25 May 2011; pp. 1–8. [Google Scholar]
- Dong, L.; Li, W.M.; Wang, C.H.; Lin, K.P. Gyro motor fault classification model based on a coupled hidden Markov model with a minimum intra-class distance algorithm. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 234. [Google Scholar] [CrossRef]
- Soualhi, A.; Razik, H.; Clerc, G.; Doan, D.D. Prognosis of bearing failures using hidden Markov models and the adaptive neuro-fuzzy inference system. IEEE Trans. Ind. Electron. 2014, 61, 2864–2874. [Google Scholar] [CrossRef]
- Campos-Delgado, D.U.; Pecina-Sánchez, J.A.; Espinoza-Trejo, D.R.; Arce-Santana, E.R. Diagnosis of open-switch faults in variable speed drives by stator current analysis and pattern recognition. IET Electr. Power Appl. 2013, 7, 509–522. [Google Scholar] [CrossRef]



| State | Change Tendency | Classification Effect | Degeneration State Indication before Failure | |
|---|---|---|---|---|
| Name | ||||
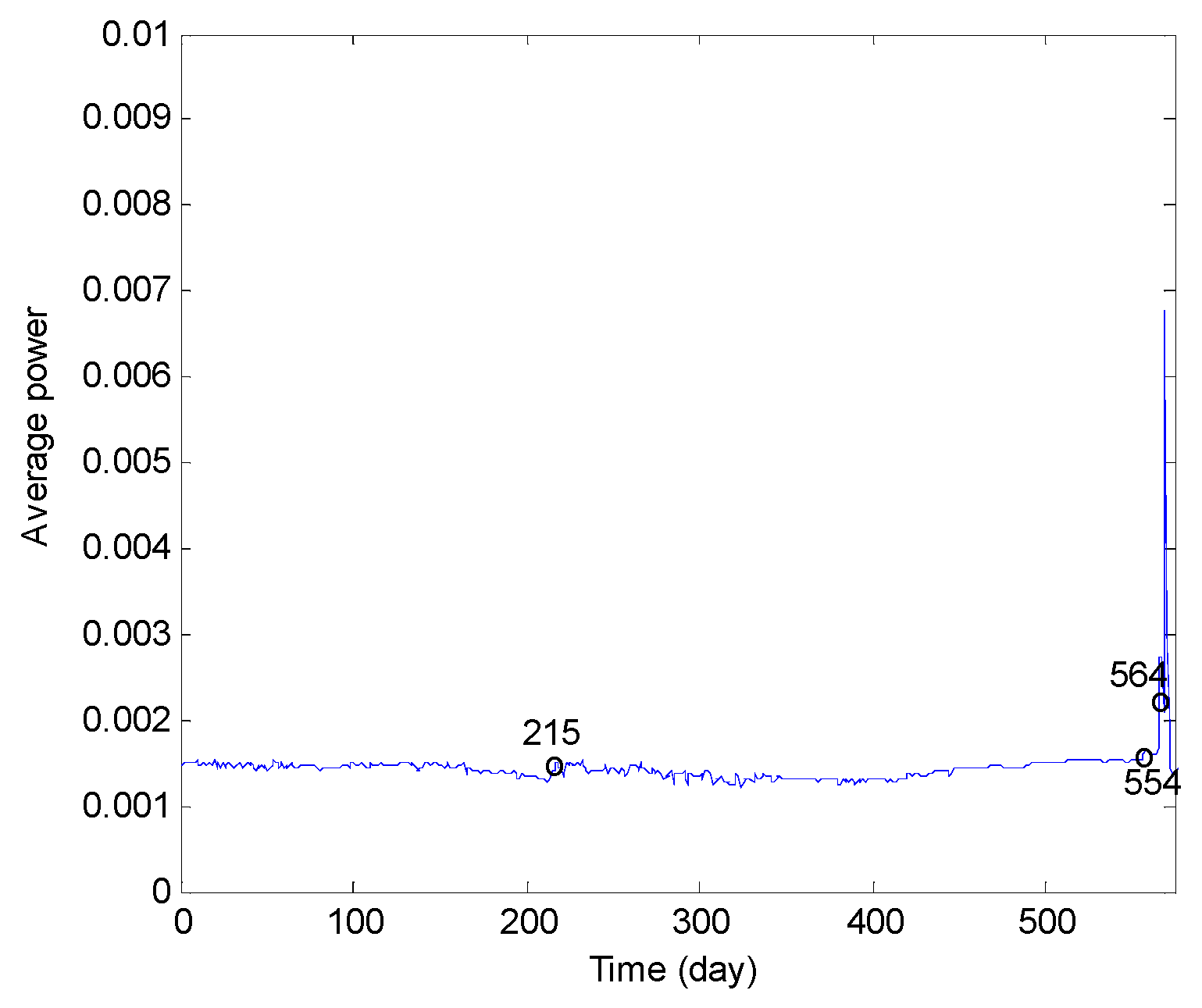
| Mean value | average | obvious | ||
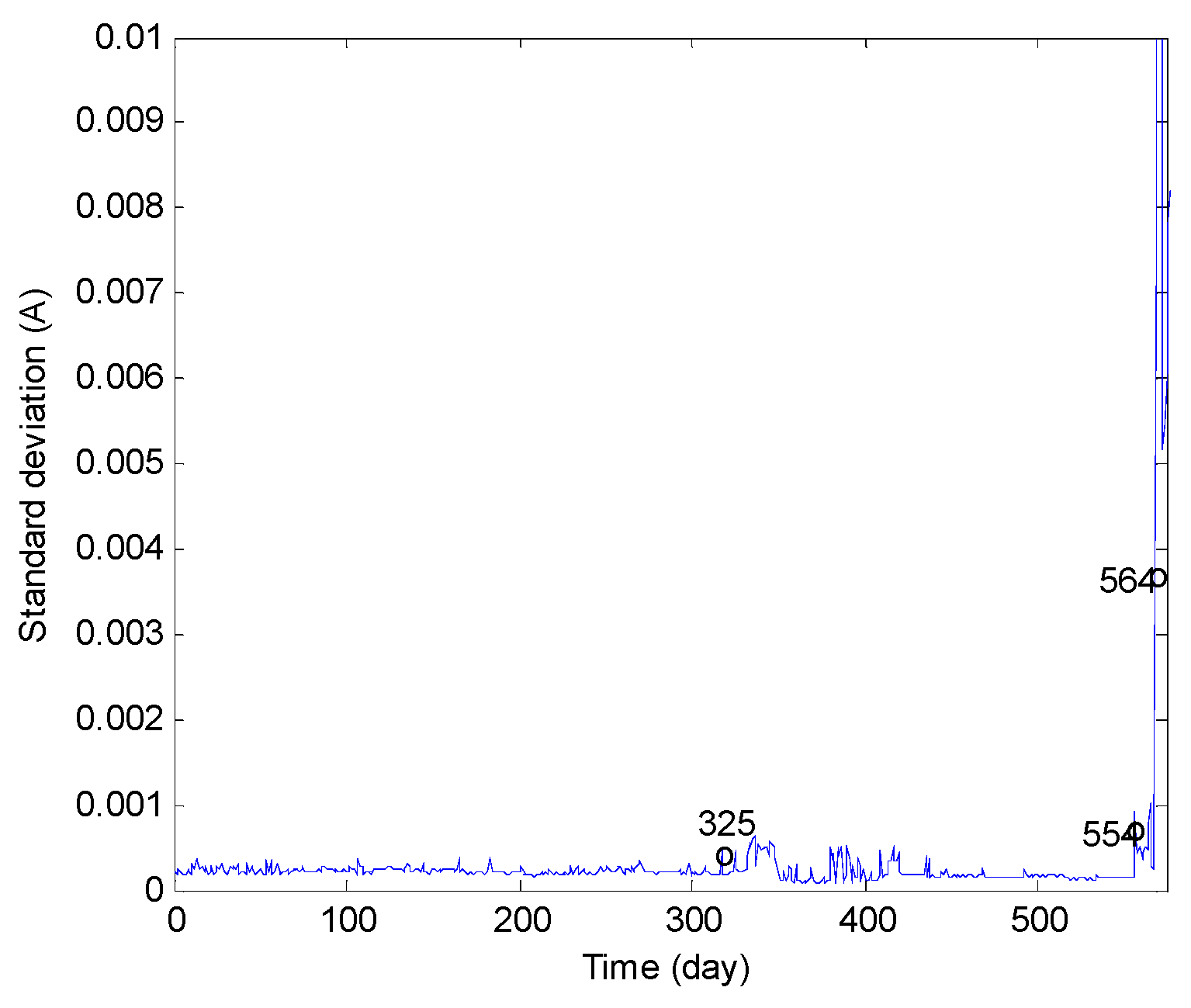
| Standard deviation | average | obvious | ||
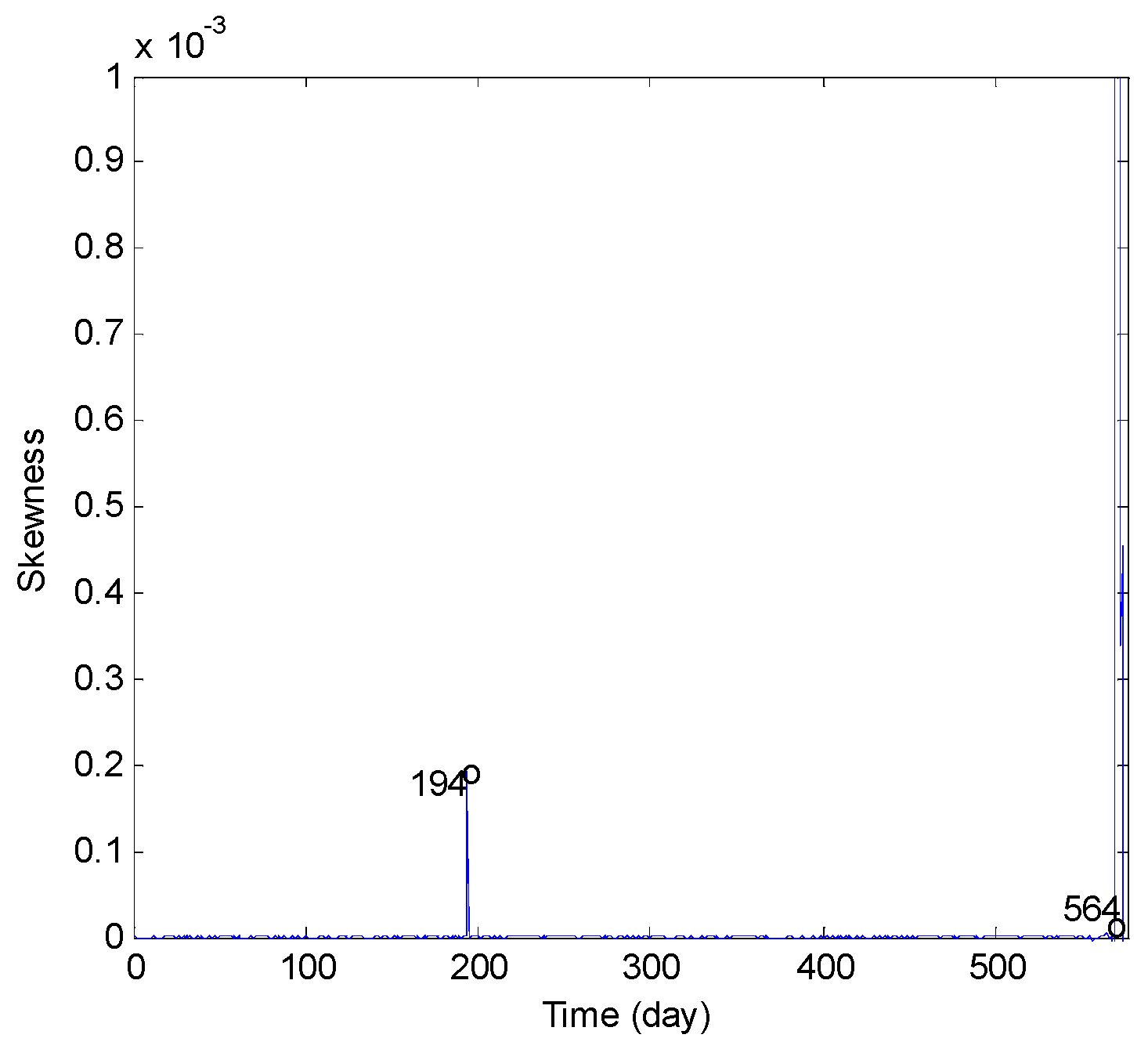
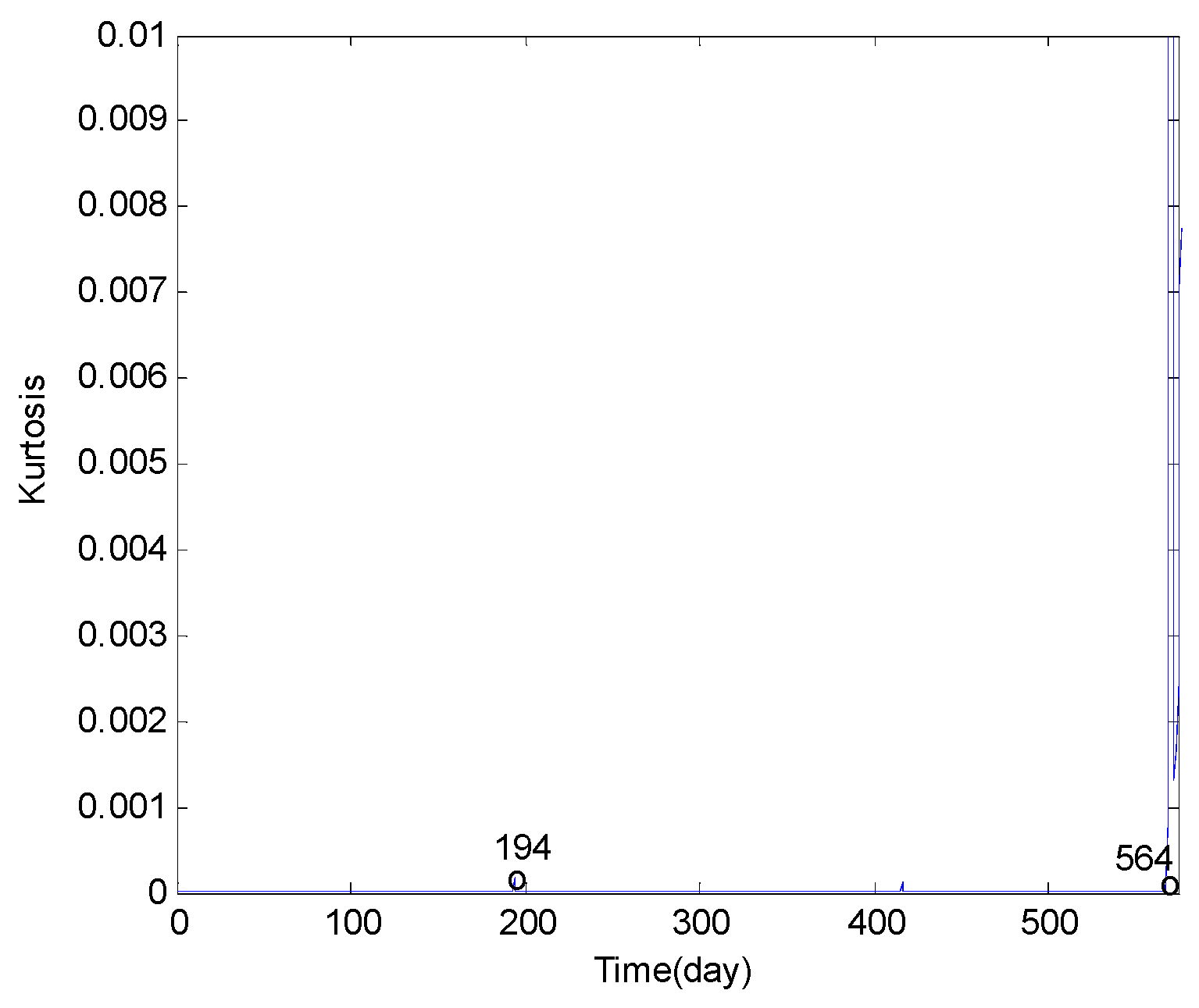
| Kurtosis | fairly bad | not obvious | ||
| Skewness | fairly bad | not obvious | ||
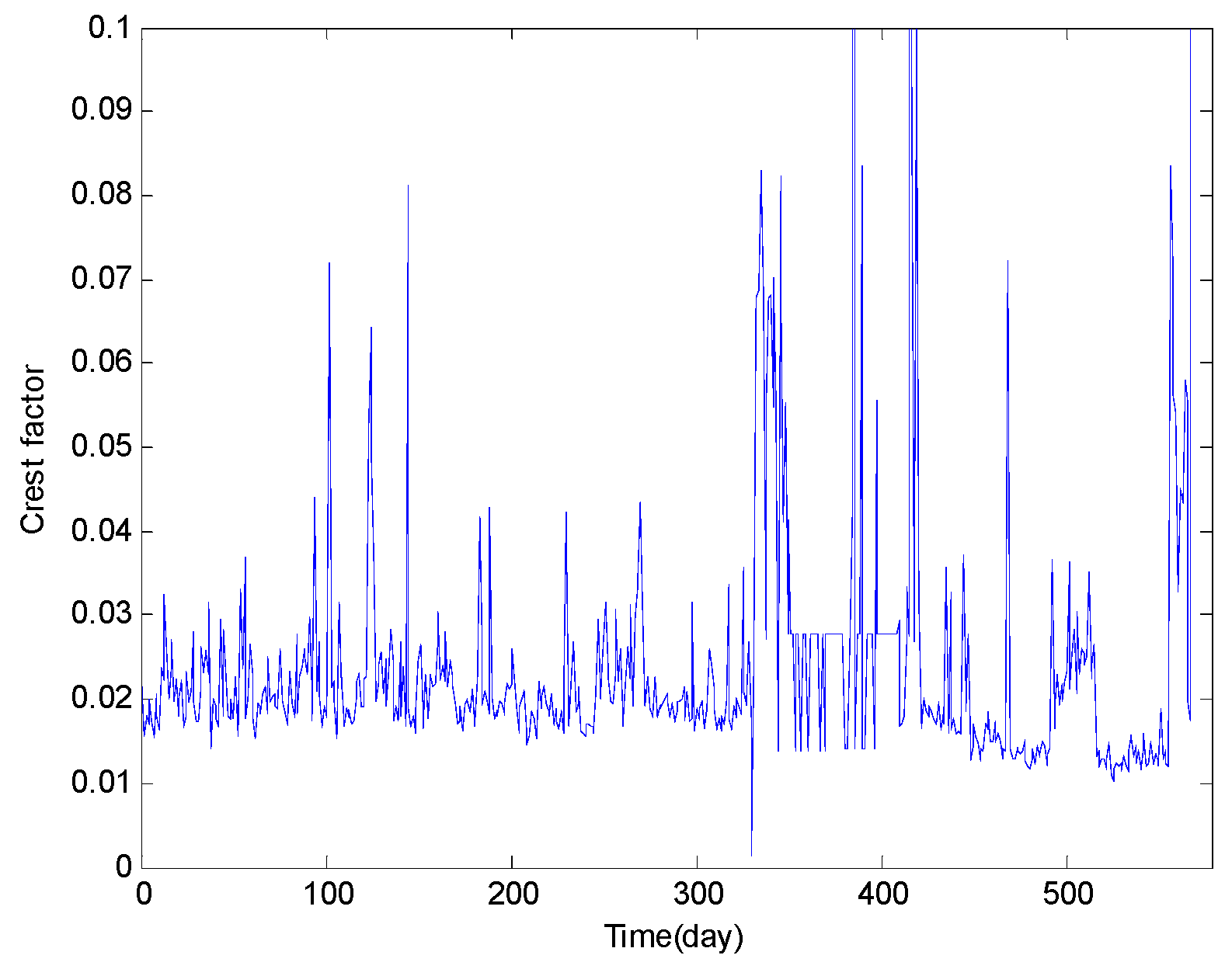
| Crest factor | Repeated oscillation | very bad | not obvious | |
| Power factor | average | obvious | ||
| State | Running-In Period | Run-In Period | Normal State | Preliminary Degeneration State | Degeneration State before Failure | Failure State | |
|---|---|---|---|---|---|---|---|
| Content | |||||||
| Working days (day) | 60 | 154 | 414 | 119 | 10 | 12 | |
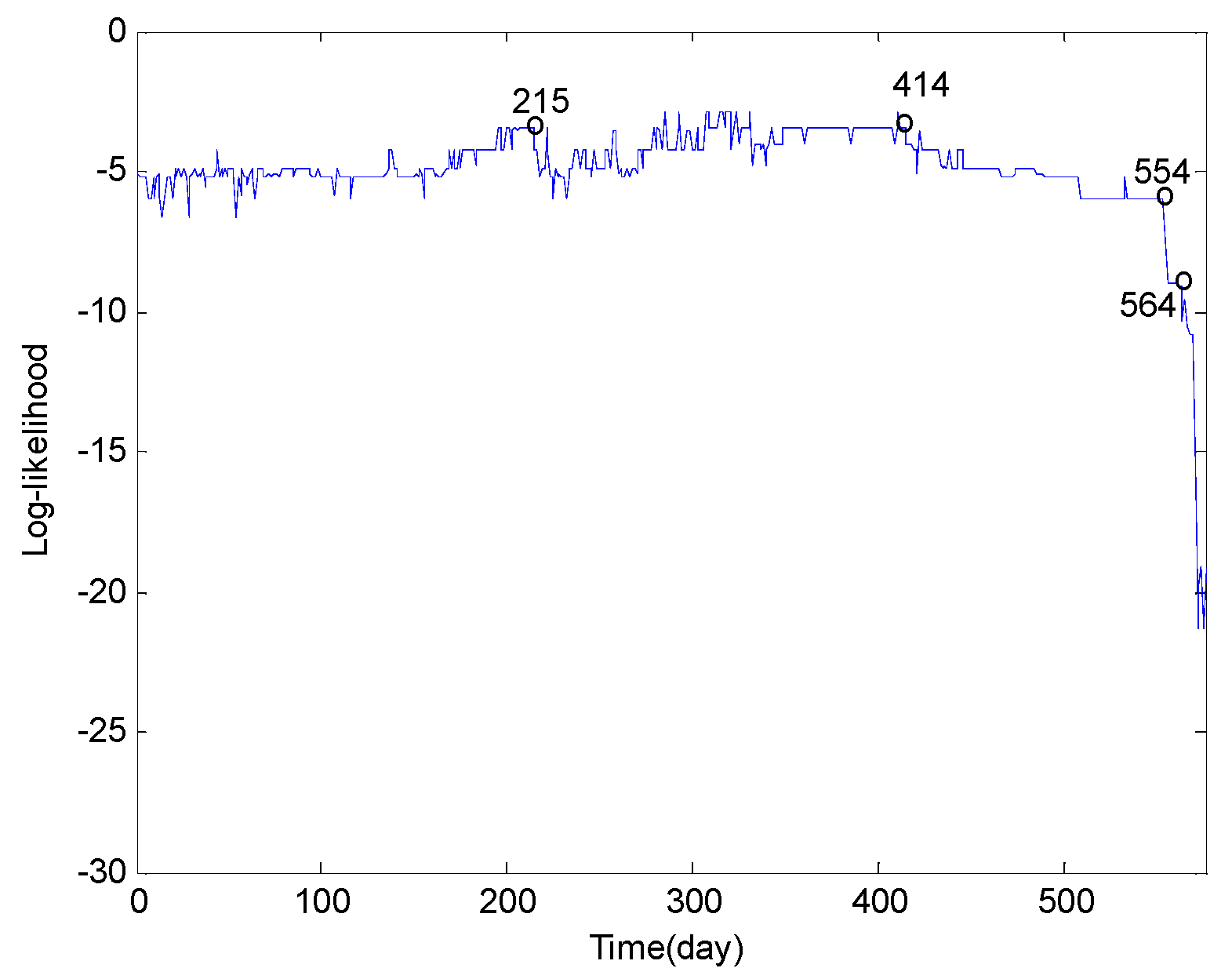
| Log likelihood probability range | −4.9~−6.6 | −3.4~−6.0 | −5.1~−3.4 | −4.2~−6.0 | −8.9~−9.0 | <−9.0 | |
| Select Samples | Actual State | Probability | State Estimation | Actual Remaining Life (day) | Remaining Life Prediction (day) |
|---|---|---|---|---|---|
| Day 72 | ① | −5.1 | ①, ② or ③ | 491 | >63 |
| Day 79 | ① | −4.9 | ①, ② or ③ | 484 | >68 |
| Day 171 | ① | −4.1 | ①, ② or ③ | 392 | >140 |
| Day 208 | ② | −3.4 | ② | 355 | 149~368 |
| Day 314 | ② | −2.8 | ② | 249 | 233~256 |
| Day 385 | ② | −4.1 | ①, ② or ③ | 178 | >140 |
| Day 443 | ③ | −4.2 | ①, ② or ③ | 120 | >140 |
| Day 468 | ③ | −5.2 | ①, ② or ③ | 95 | >55 |
| Day 516 | ③ | −6.0 | ① or ③ | 47 | 10~54 |
| Day 555 | ④ | −8.9 | ④ | 8 | 2~9 |
| Day 557 | ④ | −8.9 | ④ | 6 | 2~9 |
| Day 562 | ④ | −9.0 | ④ | 1 | 2~9 |
| Day 564 | ⑤ | −15.5 | ⑤ | 0 | 0 |
| Day 568 | ⑤ | −21.3 | ⑤ | 0 | 0 |
| Day 570 | ⑤ | −10.3 | ⑤ | 0 | 0 |
| State | Multi-HMM Prediction Method | Single HMM Prediction Method | Time-Probability Curve Model | |
|---|---|---|---|---|
| Content | ||||
| Data needed to be trained | Full life cycle data | Data under health conditions | Full life cycle data | |
| Utilization ratio of training data | High | Low | High | |
| Evaluation method | State identification by means of output probability | State identification by means of alarm door | State identification by means of time-probability curve | |
| Life span prediction capability | Estimation stage | Estimation stage | Fairly accurate | |
| Classification of degeneration state | Needed | Not needed | Not needed | |
| Select Samples | Actual State | Residual Life | Multi-HMM State Prediction Method | Health Condition HMM Prediction Method | ||
|---|---|---|---|---|---|---|
| Classification Results | Remaining Life Prediction (day) | Log Likelihood Probability | Remaining Life Prediction (day) | |||
| Day 72 | ① | 491 | Error | >10 | −5.0 | Unattainable |
| Day 79 | ① | 484 | Right | >349 | −4.9 | |
| Day 171 | ① | 392 | Error | >149 | −4.2 | |
| Day 208 | ② | 355 | Right | >149 | −3.4 | |
| Day 314 | ② | 249 | Right | >149 | −2.8 | |
| Day 385 | ② | 178 | Right | >149 | −4.0 | |
| Day 443 | ③ | 120 | Error | >149 | −4.2 | |
| Day 468 | ③ | 95 | Error | >10 | −5.2 | |
| Day 516 | ③ | 47 | Right | >10 | −6.0 | |
| Day 555 | ④ | 8 | Right | 0~9 | −9.1 | |
| Day 557 | ④ | 6 | Right | 0~9 | −9.1 | |
| Day 562 | ④ | 1 | Right | 0~9 | −9.2 | |
| Day 564 | ⑤ | 0 | Right | 0 | -Inf(overflow) | |
| Day 568 | ⑤ | 0 | -Inf(overflow) | 0 | -Inf(overflow) | |
| Day 570 | ⑤ | 0 | -Inf(overflow) | 0 | -Inf(overflow) | |
| Comparative Content | Multi-HMM State Prediction Method | Health Condition HMM Prediction Method | Time-Probability Curve Model |
|---|---|---|---|
| Assessment results | Output classification results | Output log likelihood probability | Judging the state by time-probability curve |
| Residual life estimation | Larger error | Inestimable | High accuracy |
| Dependence on partitioned States | Needed | Not needed | Not needed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Wang, J.; Tseng, M.-L.; Yang, Z.; Ma, B.; Li, L.-L. Gyro Motor State Evaluation and Prediction Using the Extended Hidden Markov Model. Symmetry 2020, 12, 1750. https://doi.org/10.3390/sym12111750
Dong L, Wang J, Tseng M-L, Yang Z, Ma B, Li L-L. Gyro Motor State Evaluation and Prediction Using the Extended Hidden Markov Model. Symmetry. 2020; 12(11):1750. https://doi.org/10.3390/sym12111750
Chicago/Turabian StyleDong, Lei, Jianfei Wang, Ming-Lang Tseng, Zhiyong Yang, Benfu Ma, and Ling-Ling Li. 2020. "Gyro Motor State Evaluation and Prediction Using the Extended Hidden Markov Model" Symmetry 12, no. 11: 1750. https://doi.org/10.3390/sym12111750
APA StyleDong, L., Wang, J., Tseng, M.-L., Yang, Z., Ma, B., & Li, L.-L. (2020). Gyro Motor State Evaluation and Prediction Using the Extended Hidden Markov Model. Symmetry, 12(11), 1750. https://doi.org/10.3390/sym12111750







