Numerical Investigations on Magnetohydrodynamic Pump Based Microchannel Cooling System for Heat Dissipating Element
Abstract
1. Introduction
2. Method
2.1. Numerical Modeling
2.2. Governing Equations and Boundary Conditions
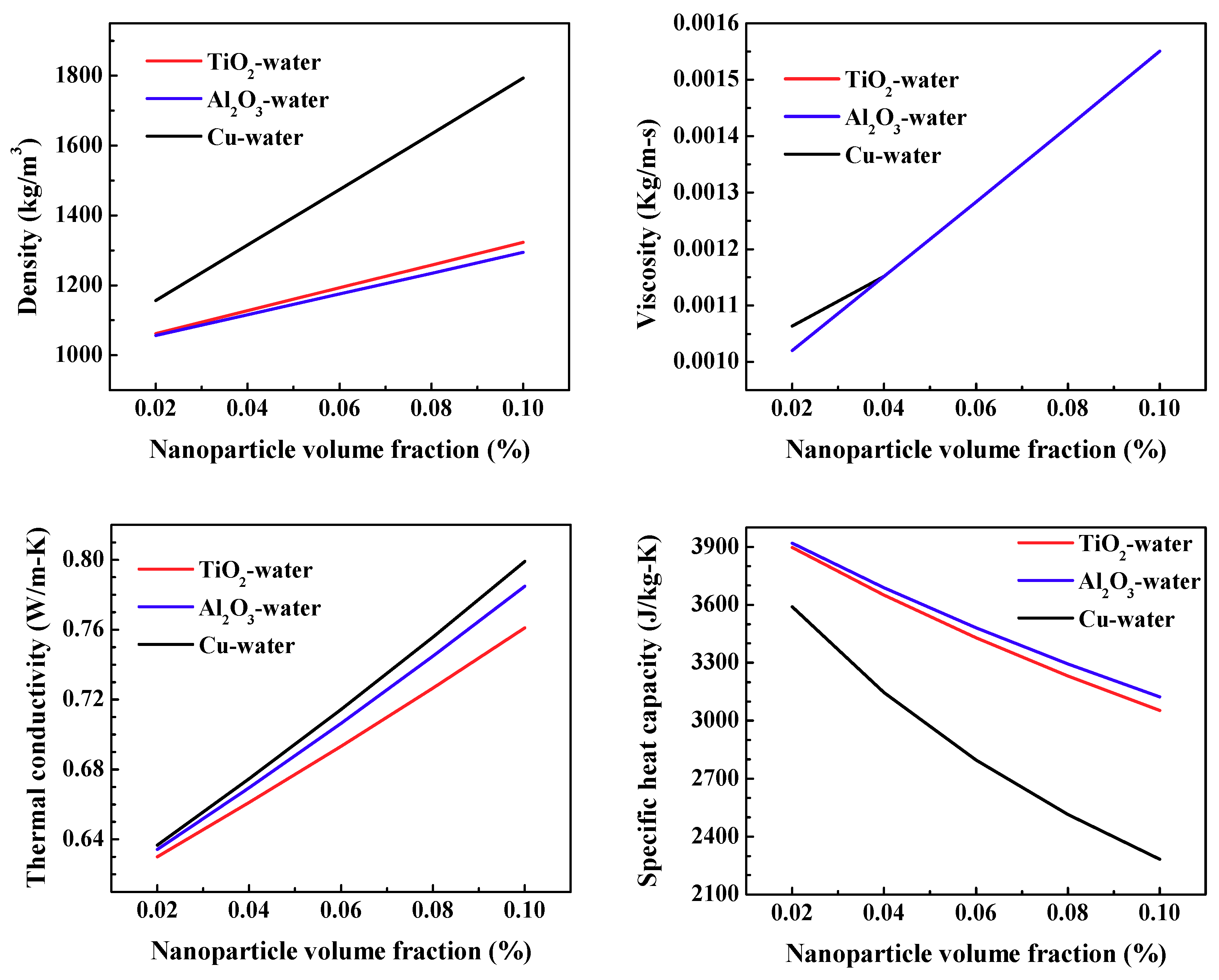
2.3. Nanofluid Relations
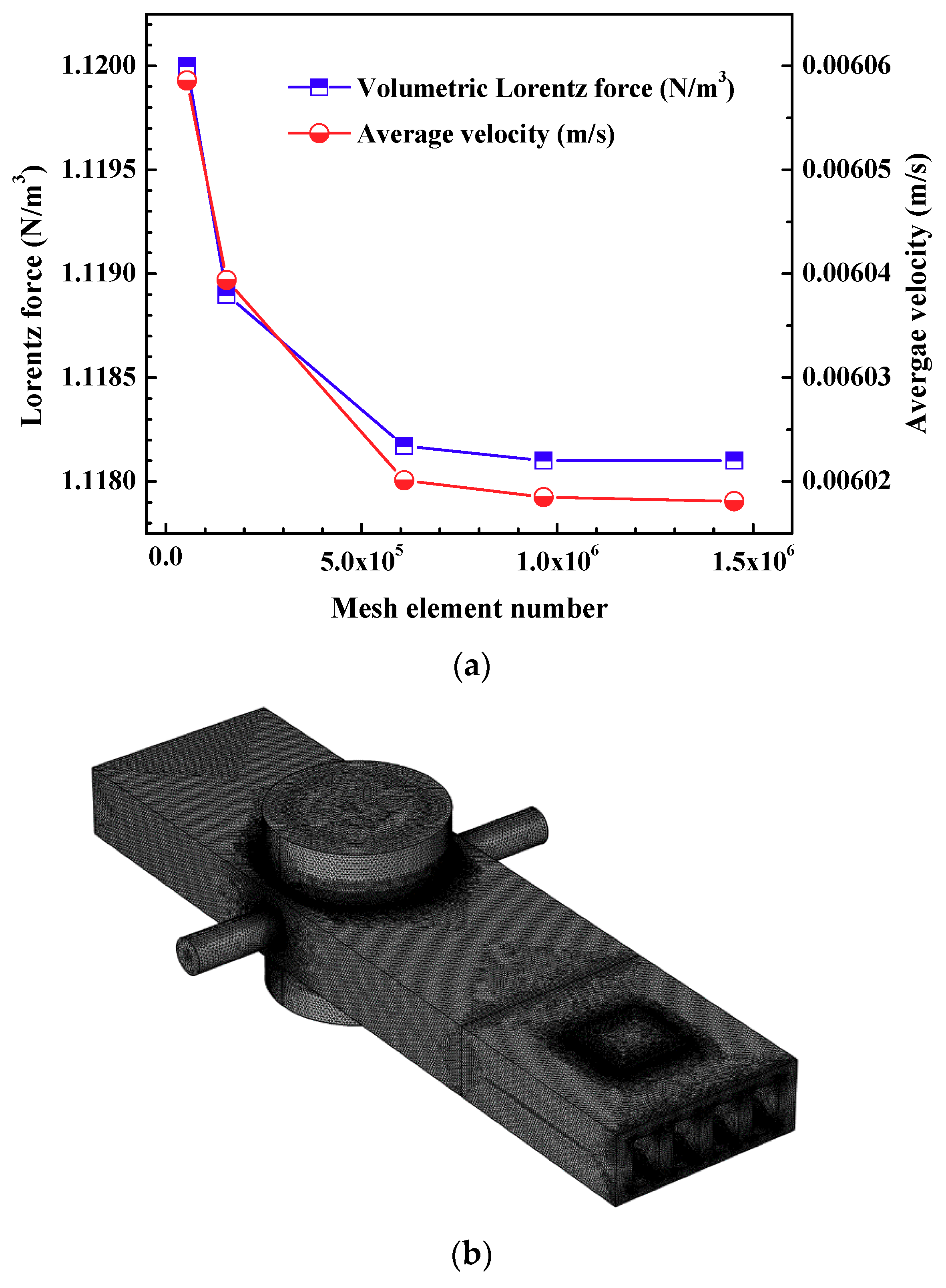
2.4. Mesh Independency
2.5. Data Reduction
3. Results and Discussion
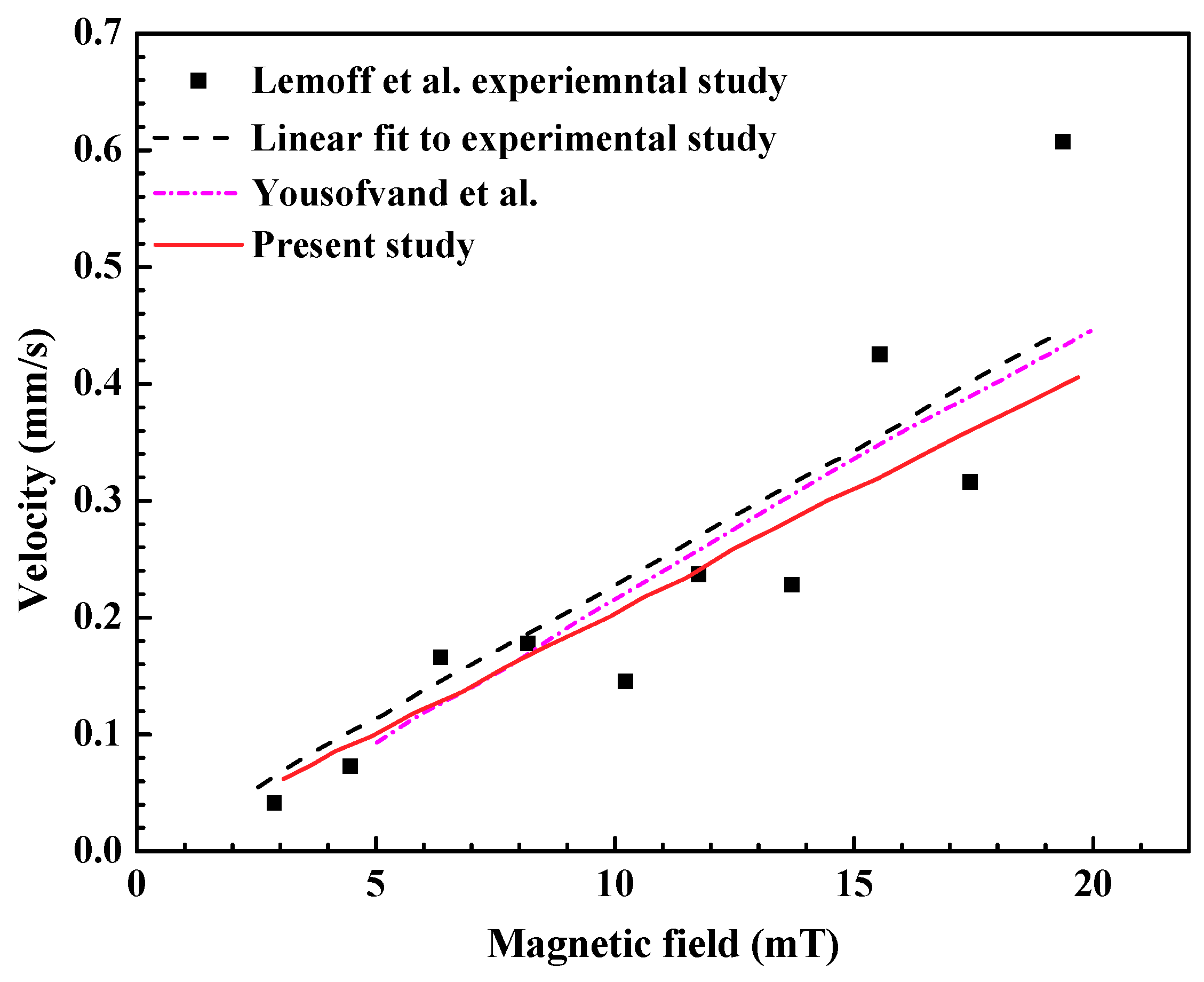
3.1. Validation
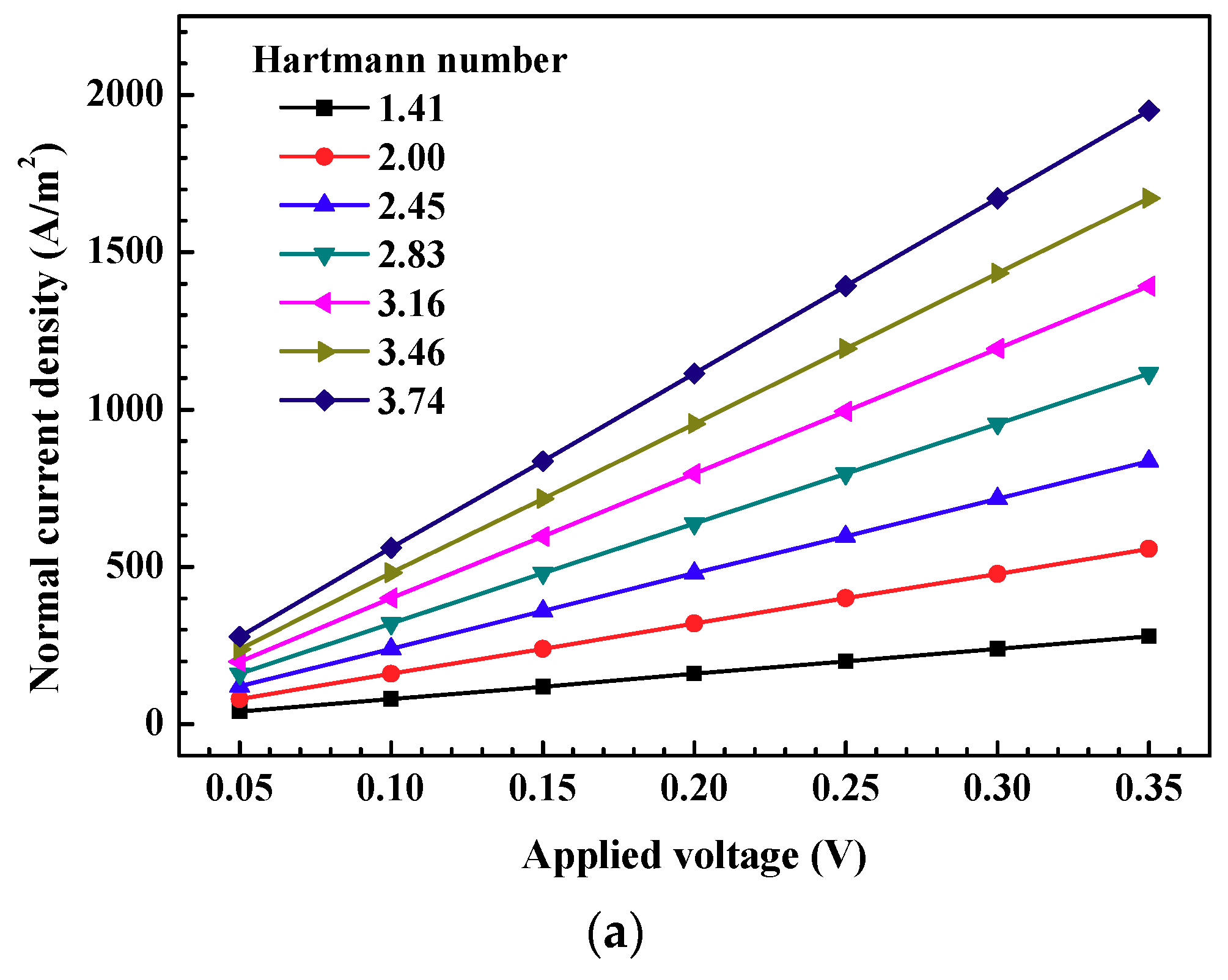
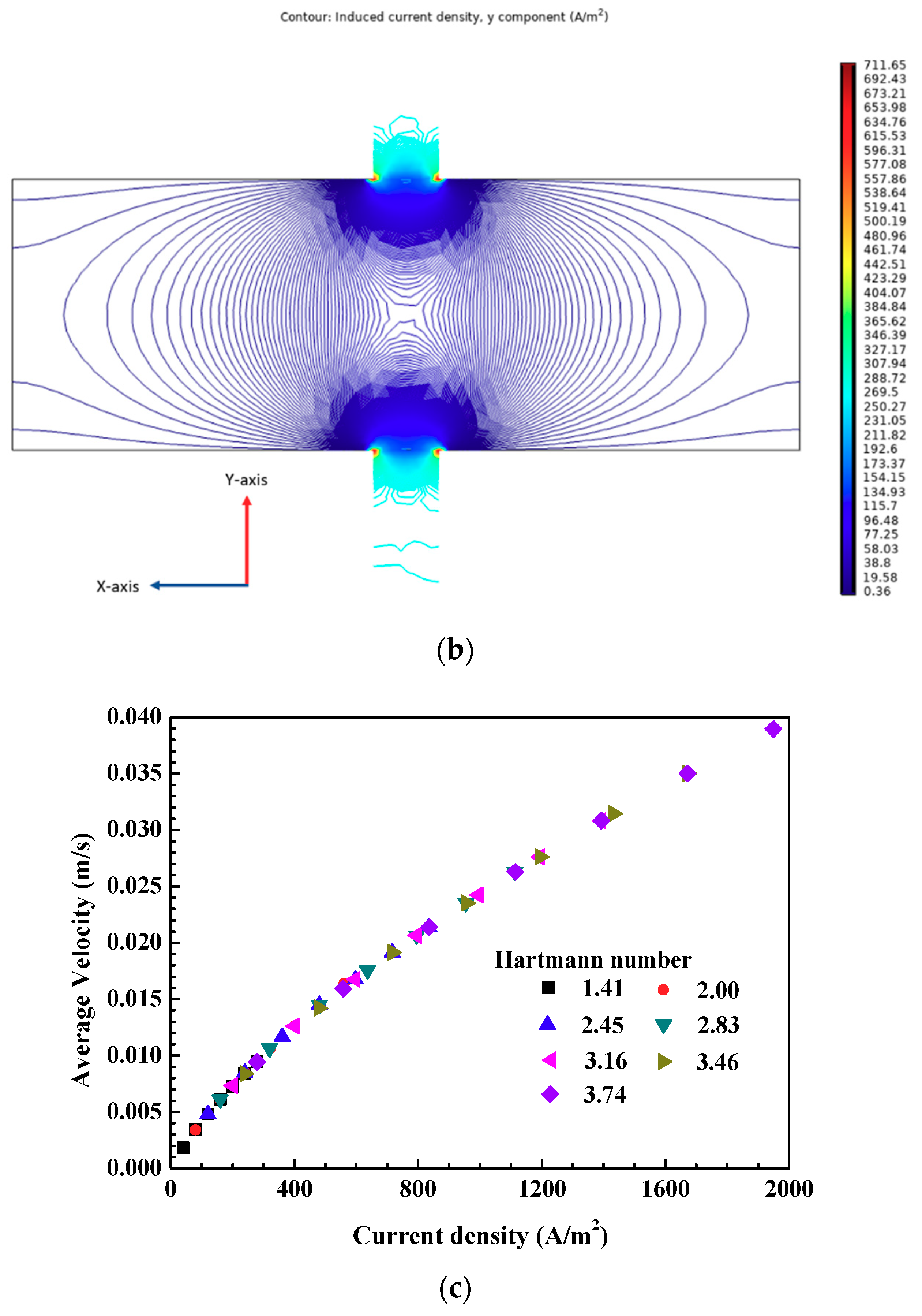
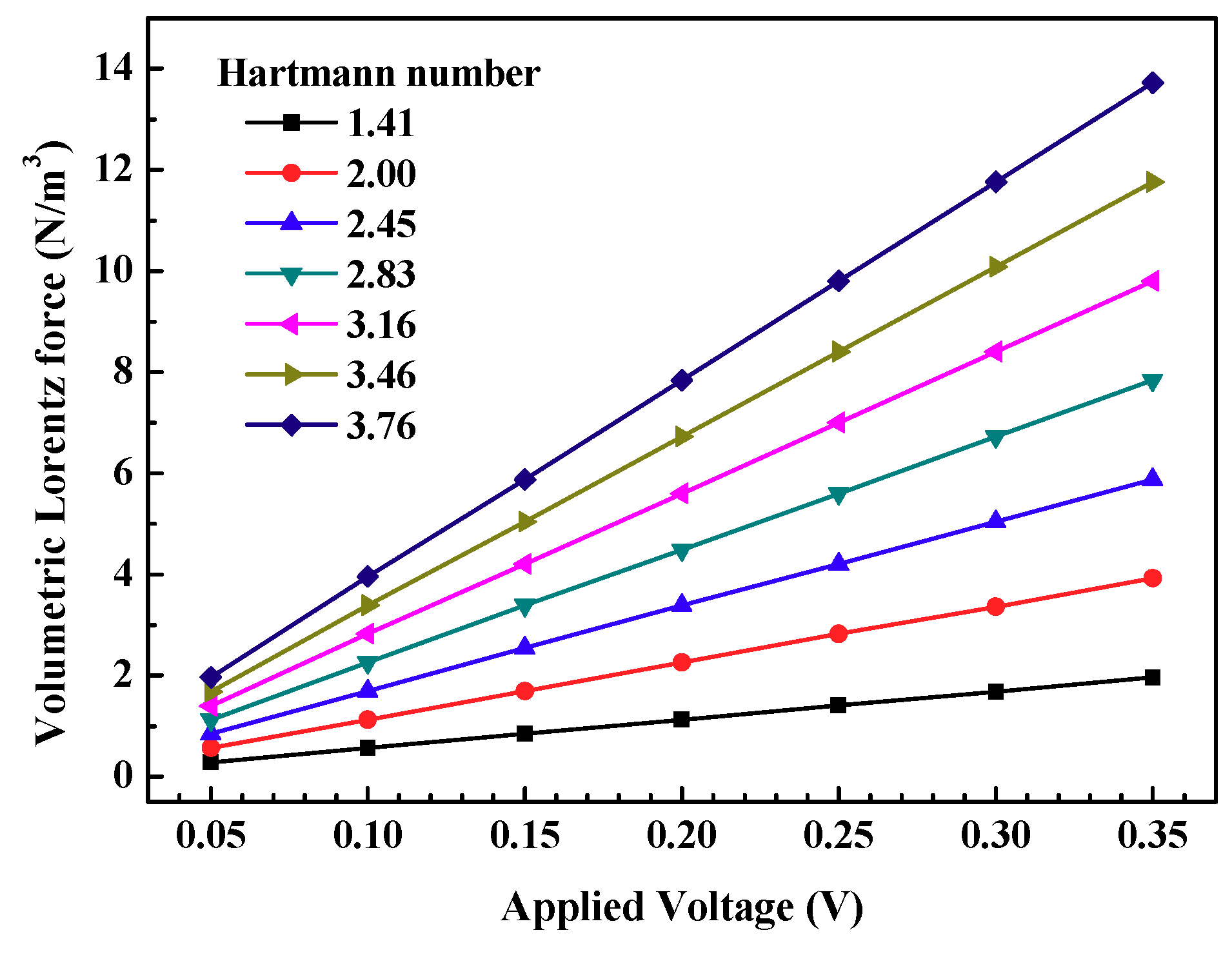
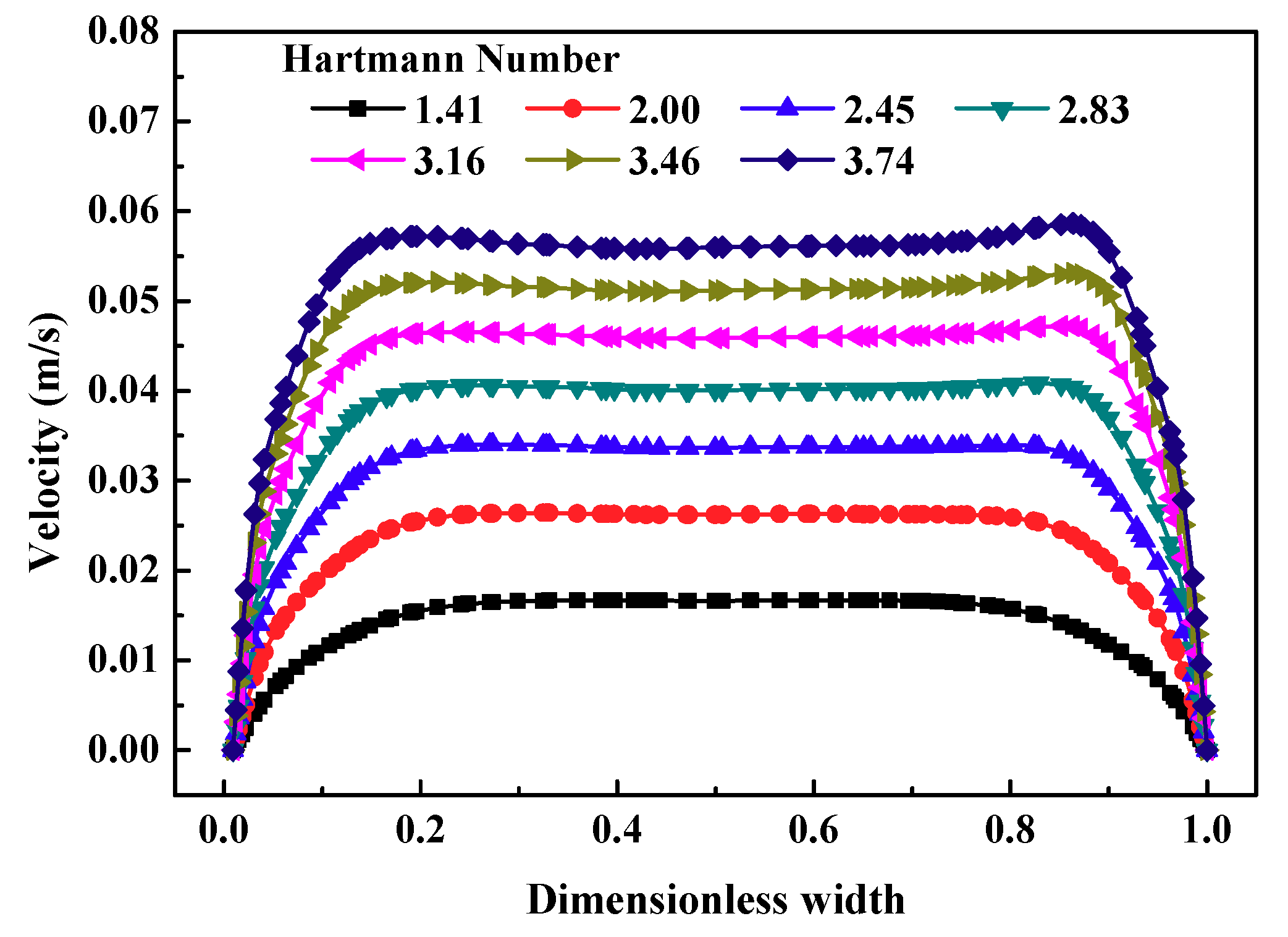
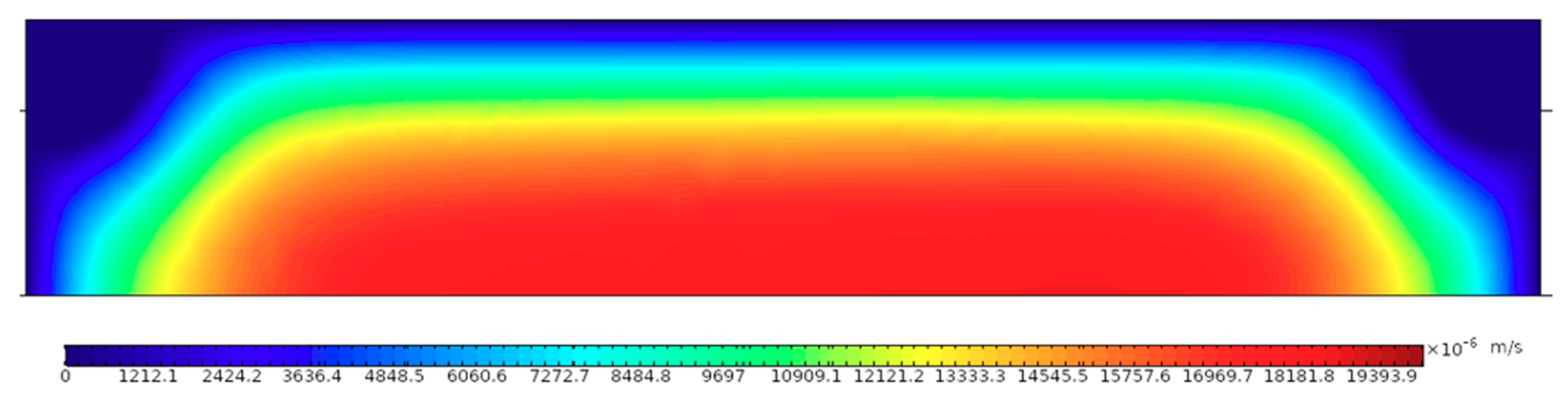
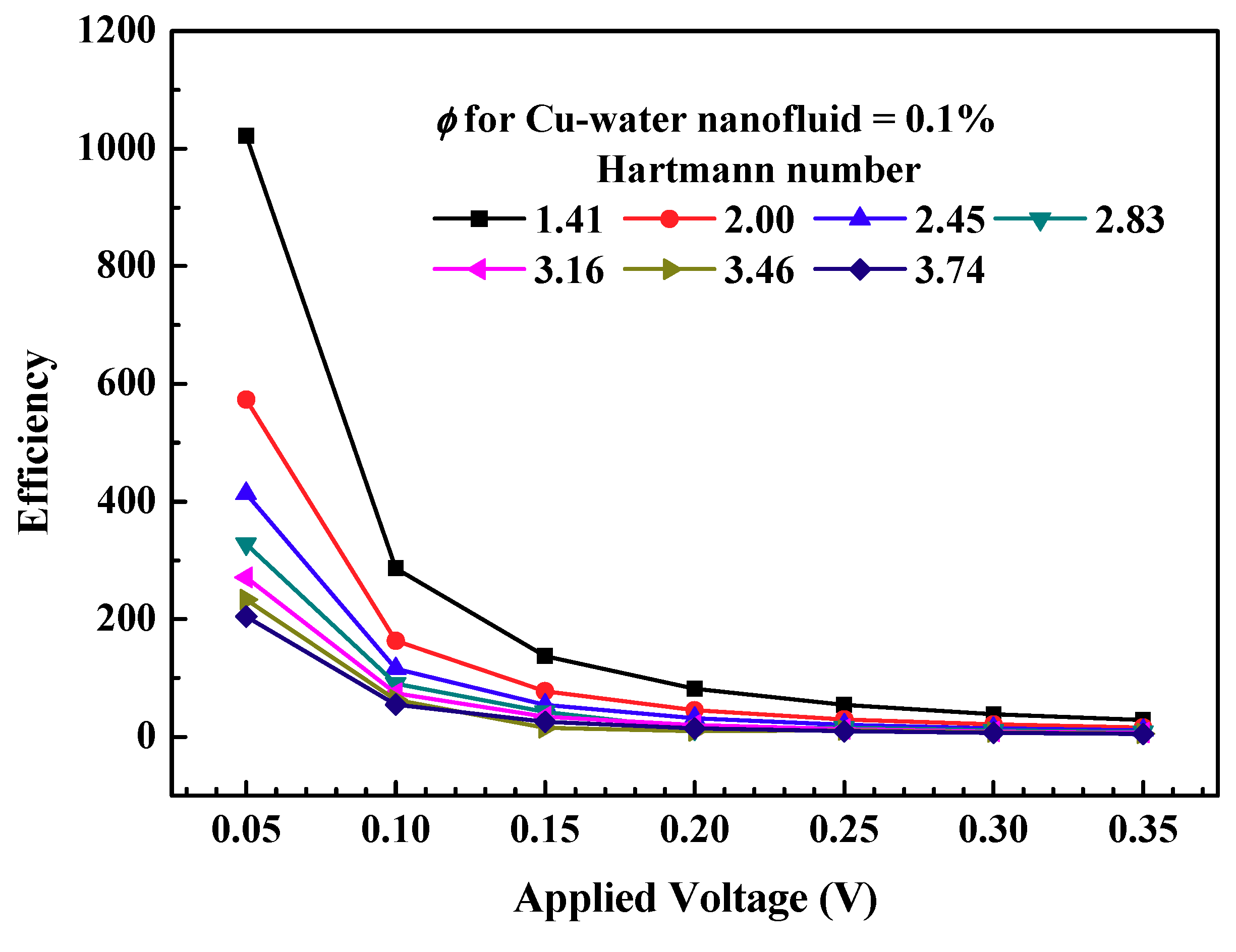
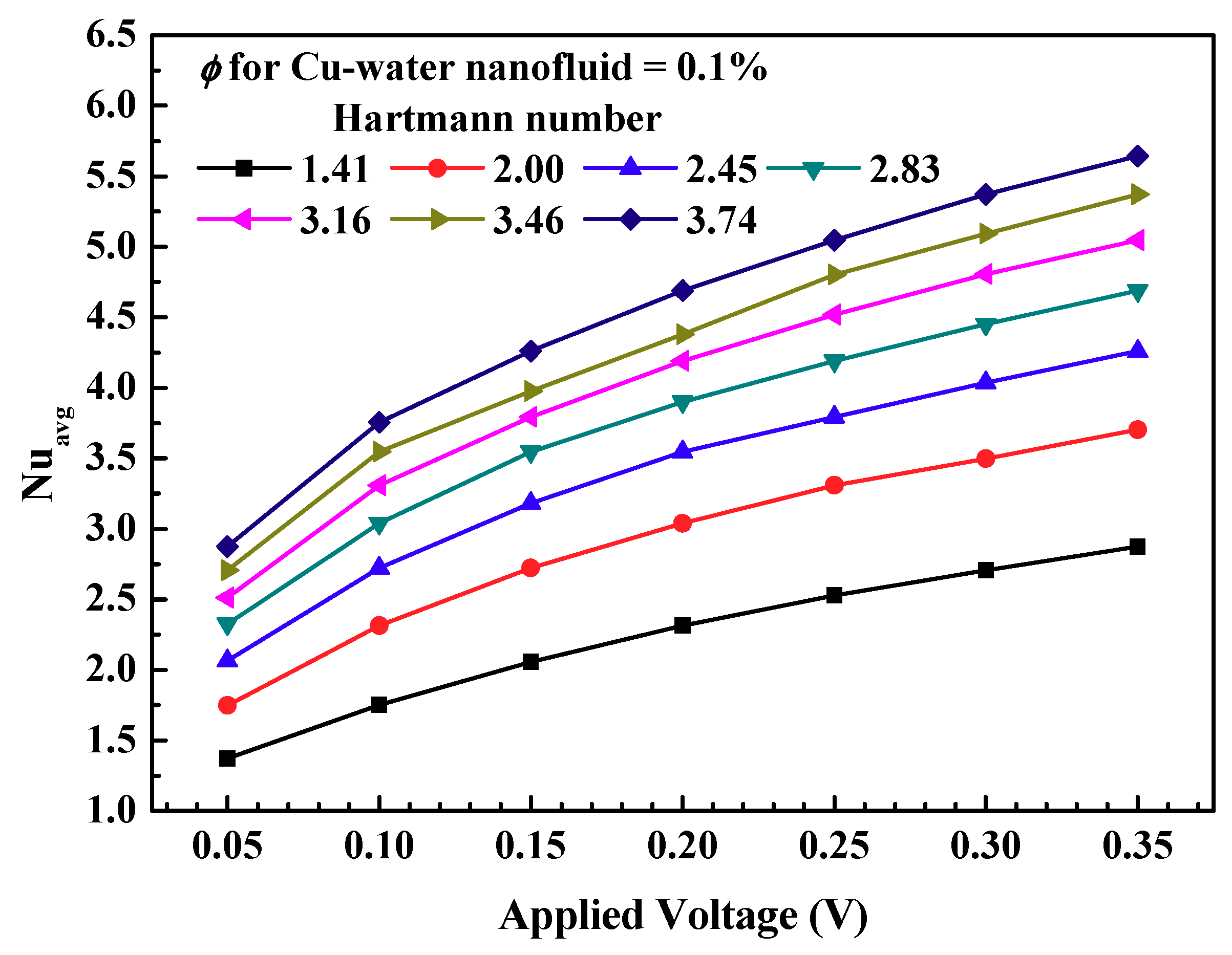
3.2. Magnetohydrodynamic Pump (MHD) Performance
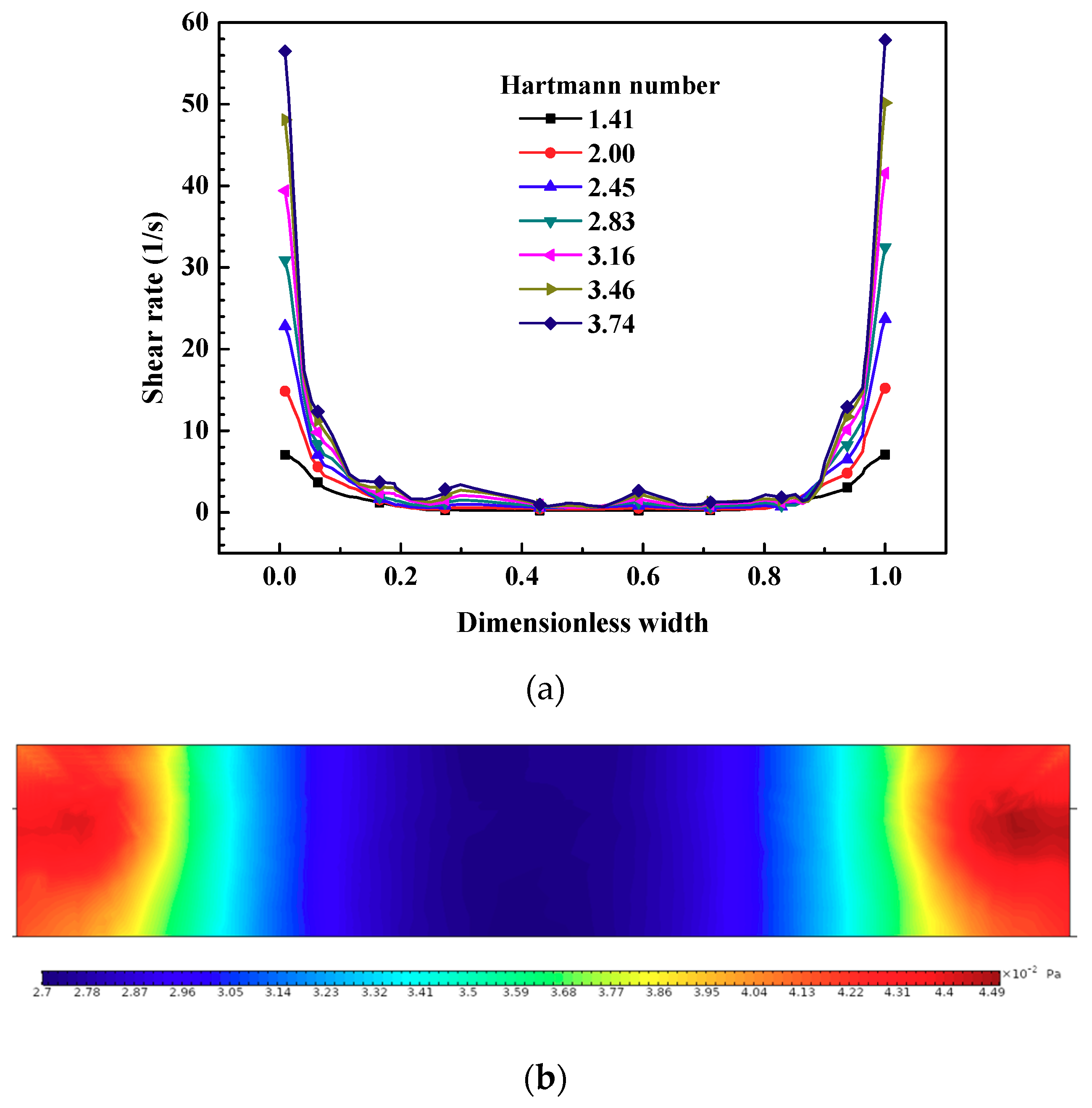
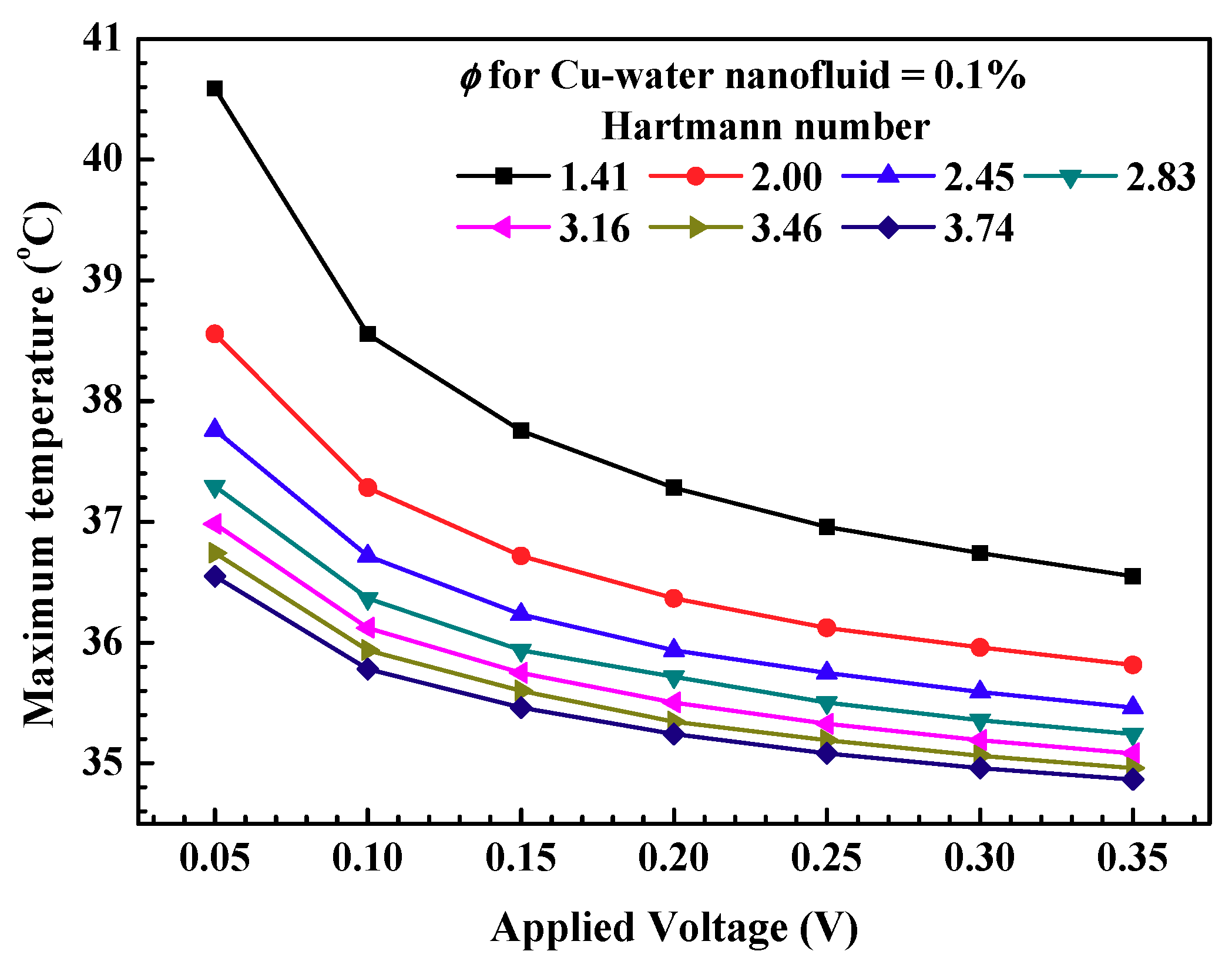
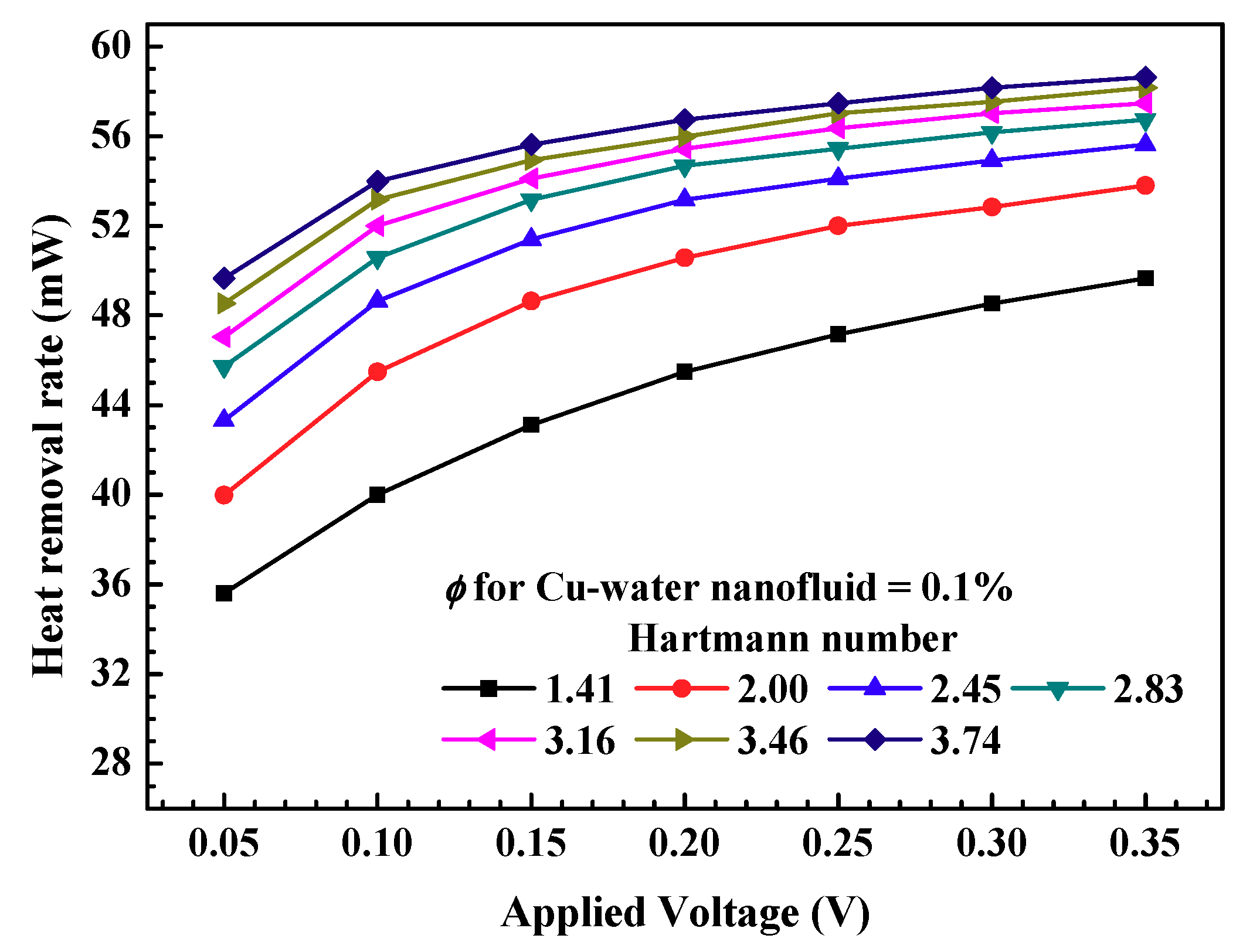
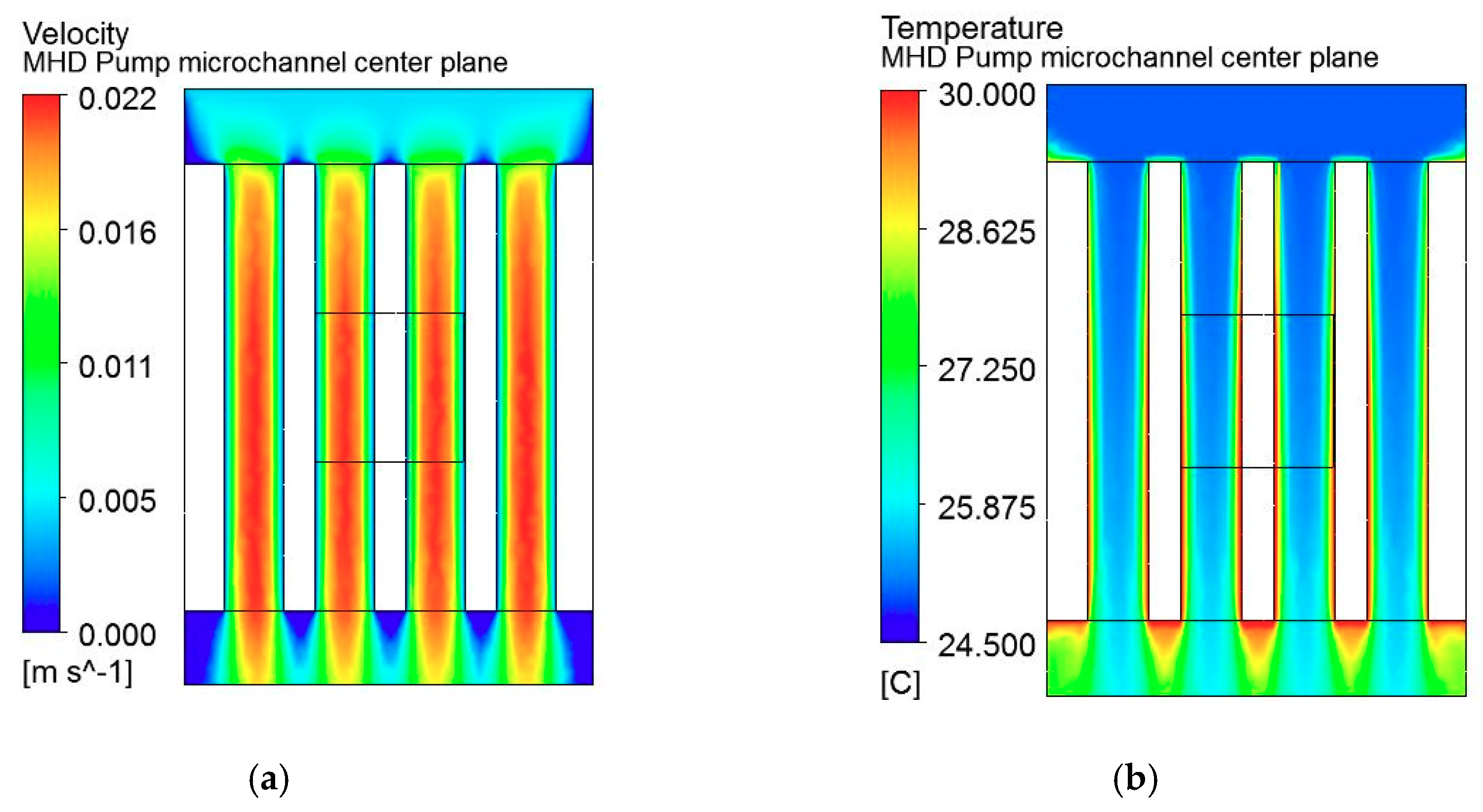
3.3. MHD-Based Microchannel Cooling System
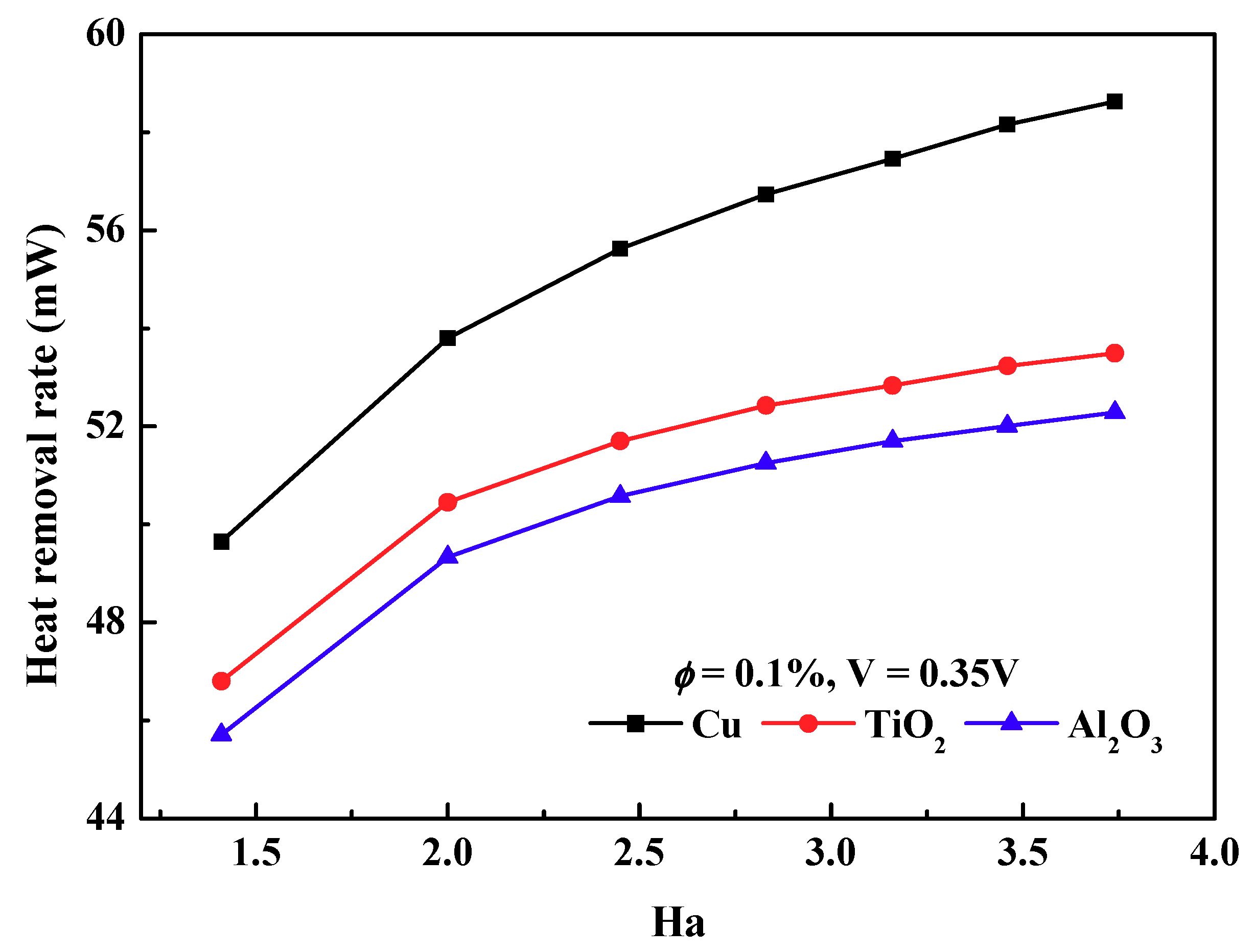
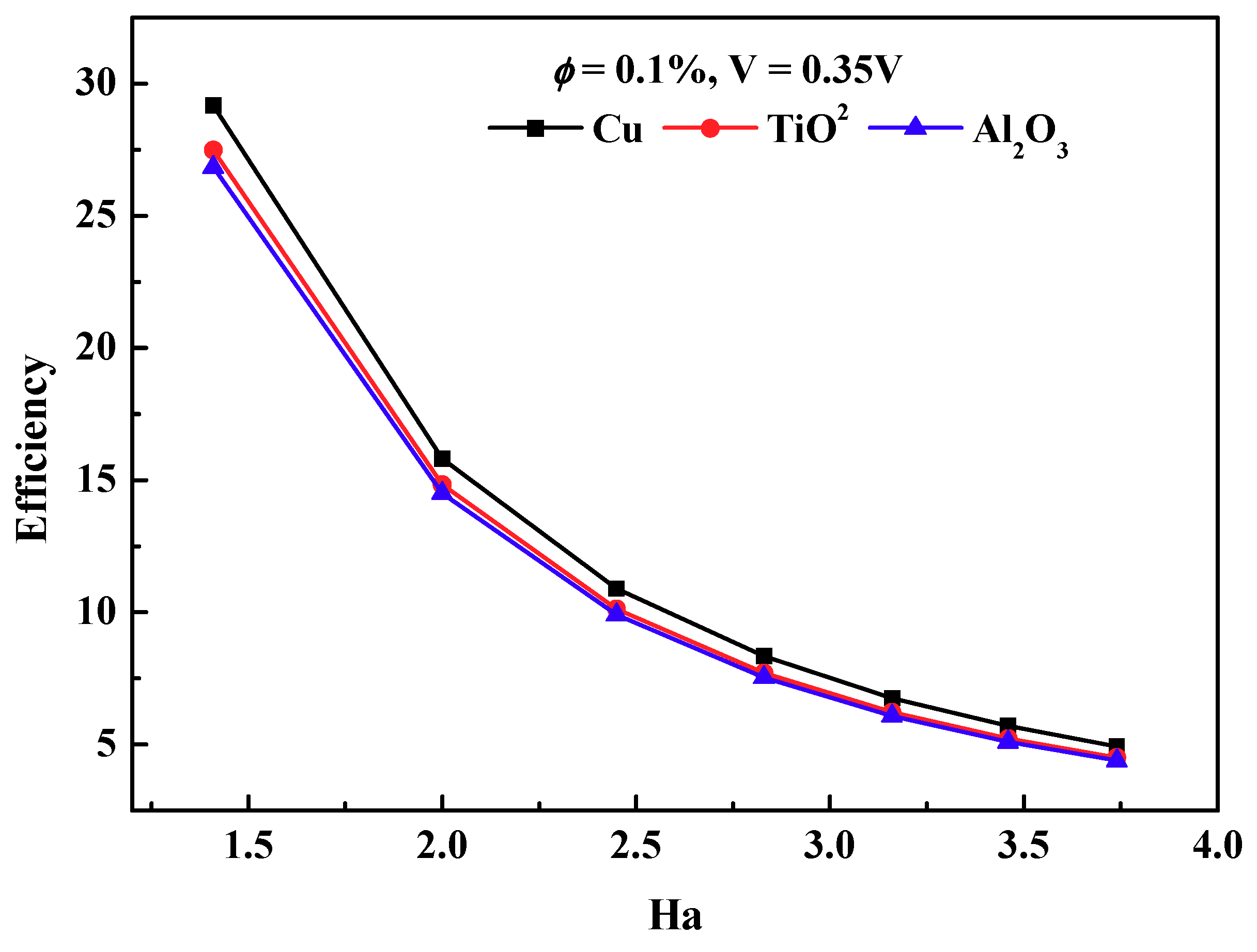
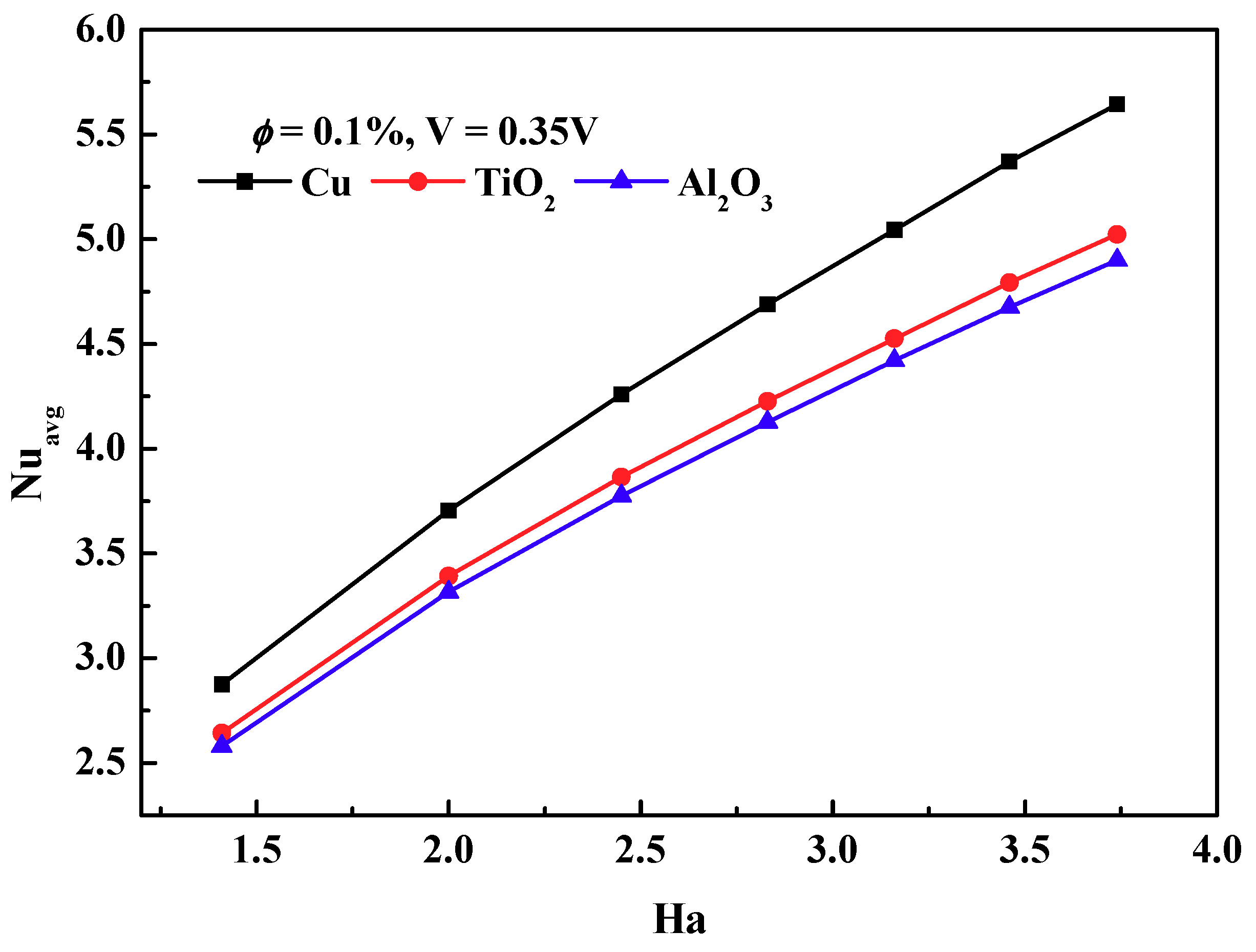
3.4. Influence of Various Nanofluids
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | cross-sectional area (m2) |
| magnetic field vector (T) | |
| B | magnitude of the magnetic field (T) |
| Cp | specific heat at constant pressure (J/kg-K) |
| Dh | hydraulic diameter (m) |
| electric field vector (V/m) | |
| electromagnetic force (N) | |
| havg | average heat transfer coefficient (W/m2-K) |
| Ha | Hartmann number |
| current density (A/m2) | |
| L | characteristic length (mm) |
| MHD | magnetohydrodynamic |
| average Nusselt number | |
| P | pressure (Pa) |
| Q | heat transfer rate (W) |
| T | temperature (°C/K) |
| t | time (s) |
| velocity (m/s) | |
| Greek symbols | |
| gradient operator | |
| α | thermal diffusivity (m2/s) |
| σ | electrical conductivity (S/m) |
| ρ | density (kg/m3) |
| ν | kinematic fluid viscosity (m2/s) |
| μ | dynamic viscosity (Pa-s) |
| k | thermal conductivity (W/m-K) |
| volume fraction (%) | |
| Subscripts | |
| avg | average |
| bulk | bulk property |
| conv | convective heat transfer |
| f | fluid |
| in | inlet |
| LMTD | logarithmic mean temperature difference |
| n | nanoparticle |
| nf | nanofluid |
| out | outlet |
| wall | wall |
References
- Al-Habahbeh, O.M.; Al-Saqqa, M.; Safi, M.; Abo Khater, T. Review of magnetohydrodynamic pump applications. Alexandria Eng. J. 2016, 55, 1347–1358. [Google Scholar] [CrossRef]
- Derakhshan, S.; Rezaee, M.; Sarrafha, H. A Molecular Dynamics Study of Description Models for Shear Viscosity in Nanochannels: Mixtures and Effect of Temperature. Nanoscale Microscale Thermophys. Eng. 2015, 19, 206–220. [Google Scholar] [CrossRef]
- Derakhshan, S.; Adibi, I.; Sarrafha, H. Numerical study of electroosmotic micropump using Lattice Boltzmann method. Comput. Fluids 2015, 114, 232–241. [Google Scholar] [CrossRef]
- Tay, F.E.H. Literature Review for Micropumps; Springer: Boston, MA, USA, 2002; pp. 3–24. [Google Scholar]
- Zhang, X.; Jaluria, Y. Optimization of microchannel-based cooling systems. Numer. Heat Transf. Part A Appl. 2018, 74, 1053–1067. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.H.; Panchal, S.; Jee, S.W.; Lee, M.Y. Investigation on thermal performance of water-cooled Li-ion pouch cell and pack at high discharge rate with U-turn type microchannel cold plate. Int. J. Heat Mass Transf. 2020, 155, 119728. [Google Scholar] [CrossRef]
- Lemoff, A.V.; Lee, A.P. AC magnetohydrodynamic micropump. Sens. Actuators B Chem. 2000, 63, 178–185. [Google Scholar] [CrossRef]
- Rivero, M.; Cuevas, S. Analysis of the slip condition in magnetohydrodynamic (MHD) micropumps. Sens. Actuators B Chem. 2012, 166–167, 884–892. [Google Scholar] [CrossRef]
- Zhao, G.; Jian, Y.; Chang, L.; Buren, M. Magnetohydrodynamic flow of generalized Maxwell fluids in a rectangular micropump under an AC electric field. J. Magn. Magn. Mater. 2015, 387, 111–117. [Google Scholar] [CrossRef]
- Yousofvand, R.; Derakhshan, S.; Ghasemi, K.; Siavashi, M. MHD transverse mixed convection and entropy generation study of electromagnetic pump including a nanofluid using 3D LBM simulation. Int. J. Mech. Sci. 2017, 133, 73–90. [Google Scholar] [CrossRef]
- Moghaddam, S. Analytical solution of MHD micropump with circular channel. Int. J. Appl. Electromagn. Mech. 2012. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A.; Oztop, H.F.; Al-Salem, K. MHD natural convection in a partially open trapezoidal cavity filled with a nanofluid. Int. J. Mech. Sci. 2016, 119, 294–302. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of double diffusive MHD (magnetohydrodynamic) natural convection and entropy generation in an open cavity filled with power-law fluids in the presence of Soret and Dufour effects (Part I: Study of fluid flow, heat and mass transfer). Energy 2016, 107, 889–916. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of double diffusive MHD (magnetohydrodynamic) natural convection and entropy generation in an open cavity filled with power-law fluids in the presence of Soret and Dufour effects (part II: Entropy generation). Energy 2016, 107, 917–959. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Öztop, H.F.; Al-Salem, K. Mixed magnetohydrodynamic convection in a Cu-water-nanofluid-filled ventilated square cavity using the Taguchi method: A numerical investigation and optimization. Eur. Phys. J. Plus 2017, 132, 204. [Google Scholar] [CrossRef]
- Kiyasatfar, M.; Pourmahmoud, N.; Golzan, M.; Mirzaee, I. Investigation of thermal behavior and fluid motion in direct current magnetohydrodynamic pumps. Therm. Sci. 2014. [Google Scholar] [CrossRef]
- Larimi, M.M.; Ghanaat, A.; Ramiar, A.; Ranjbar, A.A. Forced convection heat transfer in a channel under the influence of various non-uniform transverse magnetic field arrangements. Int. J. Mech. Sci. 2016, 118, 101–112. [Google Scholar] [CrossRef]
- Kolsi, L.; Alrashed, A.A.A.A.; Al-Salem, K.; Oztop, H.F.; Borjini, M.N. Control of natural convection via inclined plate of CNT-water nanofluid in an open sided cubical enclosure under magnetic field. Int. J. Heat Mass Transf. 2017, 111, 1007–1018. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. FDLBM simulation of magnetic field effect on natural convection of non-Newtonian power-law fluids in a linearly heated cavity. Powder Technol. 2014, 256, 87–99. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of magnetic field effect on non-Newtonian blood flow between two-square concentric duct annuli using FDLBM. J. Taiwan Inst. Chem. Eng. 2014, 45, 1184–1196. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Simulation of vertical and horizontal magnetic fields effects on non-Newtonian power-law fluids in an internal flow using FDLBM. Comput. Fluids 2015, 114, 12–25. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Ferrohydrodynamic and magnetohydrodynamic effects on ferrofluid flow and convective heat transfer. Energy 2014, 75, 400–410. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D. Numerical investigation of MHD effects on Al2O3-water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM. Energy 2013, 60, 501–510. [Google Scholar] [CrossRef]
- Patil, M.S.; Bang, Y.M.; Seo, J.H.; Kim, D.W.; Cho, B.D.; Lee, M.Y. Experimental investigation of heat transfer characteristics of battery management system and electronic control unit of neighborhood electric vehicle. In Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2017; Volume 415, pp. 205–211. ISBN 9783319509037. [Google Scholar]
- Patil, M.S.; Seo, J.; Panchal, S.; Lee, M. Numerical study on sensitivity analysis of factors influencing liquid cooling with double cold-plate for lithium-ion pouch cell. Int. J. Energy Res. 2020, 1–27. [Google Scholar] [CrossRef]
- Joye, D.D.; Bushinsky, J.P.; Saylor, P.E. Mixed Convection Heat Transfer at High Grashof Number in a Vertical Tube. Ind. Eng. Chem. Res. 1989, 28, 1899–1903. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.H.; Bang, Y.M.; Lee, M.Y. Analysis of factors influencing on heat transfer characteristics of automobile LED headlamp. Int. J. Control Autom. 2016, 9, 263–272. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.-H.; Bang, Y.-M.; Lee, M.-Y. Experimental Study on the Performance Characteristics of an Air-Cooled LED Cooling System for Headlamp of a Passenger Vehicle. Adv. Sci. Technol. Lett. 2016, 120, 120–128. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.H.; Kim, C.M.; Lee, J.Y.; Lee, M.Y. Numerical study on magneto-acoustic thermal characteristics of micro-speaker for mobile phones. Int. J. Heat Mass Transf. 2021, 164, 120479. [Google Scholar] [CrossRef]
- Khan, A.A.; Kim, K.Y. Evaluation of Various Channel Shapes of a Microchannel Heat Sink. Int. J. Air-Cond. Refrig. 2016, 24, 1650018. [Google Scholar] [CrossRef]
- Saqib, M.; Shafie, S.; Khan, I.; Chu, Y.M.; Nisar, K.S. Symmetric MHD channel flow of nonlocal fractional model of BTF containing hybrid nanoparticles. Symmetry 2020, 12, 663. [Google Scholar] [CrossRef]
- Permanasari, A.A.; Kuncara, S.; Puspitasari, P.; Sukarni, S.; Ginta, T.L.; Irdianto, W. Convective heat transfer characteristics of TiO2-EG nanofluid as coolant fluid in heat exchanger. AIP Conf. Proc. 2019, 2120, 50014. [Google Scholar] [CrossRef]
- Abu-Nada, E. Effects of variable viscosity and thermal conductivity of Al2O3-water nanofluid on heat transfer enhancement in natural convection. Int. J. Heat Fluid Flow 2009, 30, 679–690. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. 1998. [Google Scholar] [CrossRef]
- Zhong, D.; Zhong, H.; Wen, T. Investigation on the thermal properties, heat transfer and flow performance of a highly self-dispersion TiO2 nanofluid in a multiport mini channel. Int. Commun. Heat Mass Transf. 2020. [Google Scholar] [CrossRef]
- Batchelor, G.K. The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977. [Google Scholar] [CrossRef]
- Vand, V. Theory of viscosity of concentrated suspensions. Nature 1945, 155, 364–365. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Choi, S.U.S. Thermal conductivity of nanoparticle-fluid mixture. J. Thermophys. Heat Transf. 1999. [Google Scholar] [CrossRef]
- Duangthongsuk, W.; Wongwises, S. Measurement of temperature-dependent thermal conductivity and viscosity of TiO2-water nanofluids. Exp. Therm. Fluid Sci. 2009. [Google Scholar] [CrossRef]
- Bobbo, S.; Fedele, L.; Benetti, A.; Colla, L.; Fabrizio, M.; Pagura, C.; Barison, S. Viscosity of water based SWCNH and TiO2 nanofluids. Exp. Therm. Fluid Sci. 2012. [Google Scholar] [CrossRef]
- Timofeeva, E.V.; Gavrilov, A.N.; McCloskey, J.M.; Tolmachev, Y.V.; Sprunt, S.; Lopatina, L.M.; Selinger, J.V. Thermal conductivity and particle agglomeration in alumina nanofluids: Experiment and theory. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000. [Google Scholar] [CrossRef]
- Hwang, S.; Jeong, J.H. Performance Comparison of Modified Offset Strip Fins Using a CFD Analysis. Int. J. Air-Conditioning Refrig. 2016, 24, 1650015. [Google Scholar] [CrossRef]
- Aoki, L.P.; Schulz, H.E.; Maunsell, M.G. An MHD Study of the Behavior of an Electrolyte Solution using3D Numerical Simulation and Experimental results. In Proceedings of the COMSOL Conference, Boston, MA, USA, 14 October 2013. [Google Scholar]
- Kandev, N.; Kagan, V.; Daoud, A. Electromagnetic DC pump of liquid aluminium: Computer simulation and experimental study. Fluid Dyn. Mater. Process. 2010. [Google Scholar] [CrossRef]
- Zakeri, R.; Sabouri, M.; Maleki, A.; Abdelmalek, Z. Investigation of Magneto Hydro-Dynamics Effects on a Polymer Chain Transfer in Micro-Channel Using Dissipative Particle Dynamics Method. Symmetry 2020, 12, 397. [Google Scholar] [CrossRef]
- Daoud, A.; Kandev, N. Magneto-hydrodynamic numerical study of DC electromagnetic pump for liquid metal. In Proceedings of the COMSOL Conference, Hannover, Germany, 5 November 2008. [Google Scholar]
- Ekanayake, G.; Patil, M.S.; Seo, J.-H.; Lee, M.-Y. Numerical study of fin geometry on the heat transfer characteristics of 72 V ECU heatsink for an electric three-wheeler. J. Mech. Sci. Technol. 2019, 33, 1451–1462. [Google Scholar] [CrossRef]
- Seo, J.H.; Patil, M.S.; Cho, C.P.; Lee, M.Y. Heat transfer characteristics of the integrated heating system for cabin and battery of an electric vehicle under cold weather conditions. Int. J. Heat Mass Transf. 2018. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Analysis of MHD mixed convection in a flexible walled and nanofluids filled lid-driven cavity with volumetric heat generation. Int. J. Mech. Sci. 2016, 118, 113–124. [Google Scholar] [CrossRef]
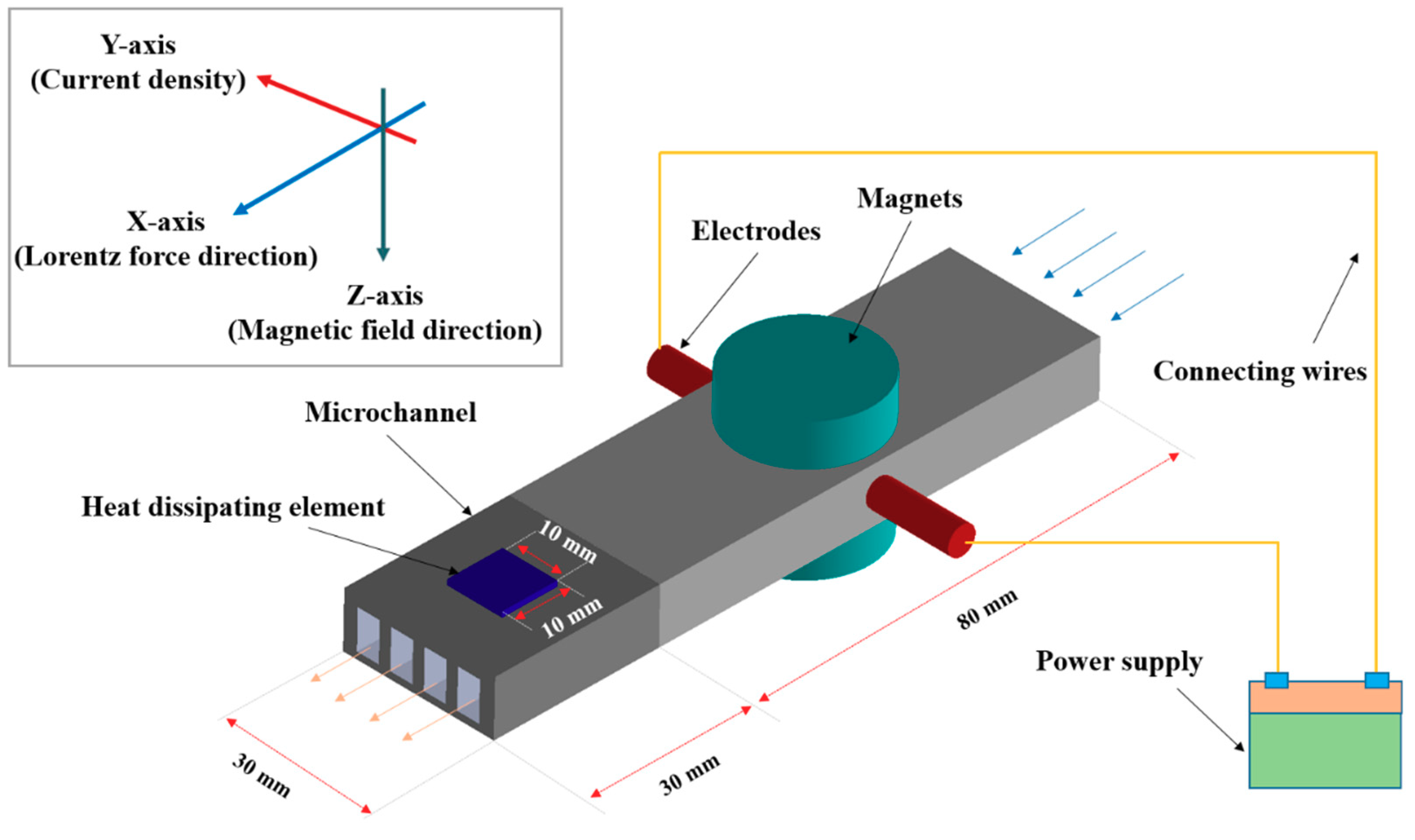

| Item | Parameter | Values |
|---|---|---|
| MHD pump | Length × Height (mm) | 80 × 10 |
| Microchannel | Length × Width × Height (mm) | 30 × 30 × 10 |
| Number of channel slots (ea) | 4 | |
| Single channel | Width × Height (mm) | 4 × 7 |
| Magnet radius | Radius × Height (mm) | 15 × 7.5 |
| Heat dissipating element | Length × Width × Height (mm) | 10 × 10 × 1 |
| Specifications | Values | |||
|---|---|---|---|---|
| Boundary conditions | ||||
| Inlet coolant temperature (°C) | 25 | |||
| Applied Voltage (V) | 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35 | |||
| Volumetric heat generation rate (W/m3) | 1.0 × 108 | |||
| Coolant inlet | Opening at atmospheric pressure | |||
| Coolant outlet | Opening at atmospheric pressure | |||
| Thermophysical properties | ||||
| Water | Cu | TiO2 [32] | Al2O3 [33] | |
| Density (kg/m3) | 997 | 8954 | 4260 | 3970 |
| Thermal conductivity (W/m-K) | 0.6069 | 400 | 8.9 | 25 |
| Specific heat (J/kg-K) | 4181.7 | 383 | 686.2 | 765 |
| Mesh Type | Number of Elements |
|---|---|
| Type 1 | 5.43 × 104 |
| Type 2 | 1.56 × 105 |
| Type 3 | 6.09 × 105 |
| Type 4 | 9.65 × 105 |
| Type 5 | 1.45 × 106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, J.-H.; Patil, M.S.; Panchal, S.; Lee, M.-Y. Numerical Investigations on Magnetohydrodynamic Pump Based Microchannel Cooling System for Heat Dissipating Element. Symmetry 2020, 12, 1713. https://doi.org/10.3390/sym12101713
Seo J-H, Patil MS, Panchal S, Lee M-Y. Numerical Investigations on Magnetohydrodynamic Pump Based Microchannel Cooling System for Heat Dissipating Element. Symmetry. 2020; 12(10):1713. https://doi.org/10.3390/sym12101713
Chicago/Turabian StyleSeo, Jae-Hyeong, Mahesh Suresh Patil, Satyam Panchal, and Moo-Yeon Lee. 2020. "Numerical Investigations on Magnetohydrodynamic Pump Based Microchannel Cooling System for Heat Dissipating Element" Symmetry 12, no. 10: 1713. https://doi.org/10.3390/sym12101713
APA StyleSeo, J.-H., Patil, M. S., Panchal, S., & Lee, M.-Y. (2020). Numerical Investigations on Magnetohydrodynamic Pump Based Microchannel Cooling System for Heat Dissipating Element. Symmetry, 12(10), 1713. https://doi.org/10.3390/sym12101713







