Abstract
This paper presents a modeling and simulation approach in order to perform a generative analysis of folktales aimed at validating Claude Lévi-Strauss’ theory and method. To this aim, a discrete-event simulation is proposed. The simulation is based on the development of a set of discrete-event models dedicated to generating a set of folktales from an initial one, according to Claude Lévi-Strauss’ structural analysis based on symmetry and double twist transformations. This paper describes in detail how these discrete-event models have been implemented in the framework of the DEVSimPy software environment by using myths of Native American mythology and folktales of Corsican oral literature. The validation involved the following steps: (i) definition of a reference folktale (according to Claude Lévi-Strauss’ methodology) (ii) generation of a set of folktales by performing their own transformations (iii) generation of a graph allowing to analyze the links that have been created after performing a set of folktales transformations. Finally, the computational validation of Lévi-Strauss’s method is intended to ground a new research that may reformulate structural analysis and elaborate a neo-structural model of canonical formalization based on transformational morphodynamics. The aim is to conceptualize and measure recursively the structural dynamics and the recurrent patterns of current identity transformations in liberal democracies, especially in US and EU contexts where ethnic/racial divisions and migration challenges are becoming more acute than ever.
1. Introduction
This paper presents a modeling and simulation (M+S) approach allowing to perform myth transformations and myth analysis according to Claude Lévi-Strauss’ theory and method of structural analysis based on Symmetry and Double Twist transformations [1]. This approach is based on the DEVS (Discrete Event system Specification) formalism [2,3,4,5]. It concerns: (i) the modeling of a reference narrative extracted from a set of myths of a given geographical area (ii) the simulation of transformations described by Claude Lévi-Strauss in his structural analysis of myths and (iii) the generation of a graph allowing to analyze the links that have been created after performing a set of myths transformations. To perform simulations allowing to generate a set of narratives from an initial myth, a DEVS simulation is proposed. The simulation is based on the development of a DEVS model library dedicated to myth transformation and myth analysis.
This paper describes how this DEVS model library has been implemented. Previous works have already presented the ideas of a M+S DEVS scheme for performing Claude Lévi-Strauss’ structural analysis [6] and how such a discrete-event simulation scheme can be merged with the structural anthropology concepts of Claude Lévi-Strauss in order perform myths analysis [7]. Two new features of the proposed approach are pointed out: (i) the development of a set of DEVS models to efficiently perform the transformations of myths (ii) the development of a set of DEVS models to perform the analysis of a given myth based on the visualization of a transformations graph. After having described how the DEVS models have been defined and implemented, this paper points out how to use this DEVS models library in order to generate a set of myths belonging to a given geographical zone and to perform a visualization of the associated transformations.
The two following steps are described in detail: (i) automatic generative process of folktales; thanks to DEVS simulation, we accomplished this in a typically structural way by focusing on the underlying structure of relationships between the elements of the story rather than on the content of the story itself; (ii) analysis of a given myth; thanks to DEVS simulation we allow a user to automatically obtain the visualization of a transformations graph associated with a given initial myth according to the materialization of myths (as described by Claude Lévi-Strauss in [8,9,10,11]); the result of the simulation is visualized under the form of a graph which displays all the transformations.
The next section is devoted to the presentation of Claude Lévi-Strauss theory concerning mythical transformations. Section 2 describes the specification of functionalities we have to implement in order to automate the structural analysis of myths as described by Claude Lévi-Strauss. Section 3 summarizes the basic notions of DEVS formalism and introduces the DEVSimPy environment [12], which is the DEVS software framework that we have chosen in order to implement the DEVS models allowing both the generation of myths and the analysis of transformations using visualization. We described in Section 4 how we implement the DEVS models using the DEVSimPy environment in two main steps: the myth generation process and the visualization of the transformations graph. The validation of the proposed approach is given is in Section 5 by using the previously introduced models in order to deal with Native American myths already analyzed by Claude Lévi-Strauss [8,9,10,11].
We complete the validation of the proposed DEVS models by generating a set of myths and other narratives belonging to a completely different culture. While we also intend to apply the proposed approach to Greek mythology, we deal at this time with folktales from the Corsican oral literature (Corsica is a small island of the Mediterranean sea depicted in Figure 1). We have to point out that elements of folktales belonging to the Corsican oral literature very often refer to megaliths [13] which are signs of an old mythology. A discussion allows one to point out the interest of DEVS simulation in the myths transformation process for experimentally validating Lévi-Strauss’ theory and method of structural analysis by means of symmetry and double twist transformations. Finally, Section 7 is devoted to the presentation of future applications and opens the possibility of the extension of structural methodology to other domains, while the last section provides concluding remarks.
Figure 1.
Corsica (in black) is a small island in the middle of the Mediterranean sea.
2. Transformational Analysis of Myths Following Structural Methodology
2.1. Introduction to Structural Analysis
For a period, Claude Lévi-Strauss’ structural analysis had a powerful influence on both British and American anthropologists, offering a way out of functionalism and empiricism [14,15]. Although his reception in the Anglo-American world was always mixed [16,17], there was also support and admiration for Lévi-Strauss even late in life [18]. More importantly, he had remained a source of fascination and inspiration for a younger generation of knowledge-based anthropologists. Over the years, the coming back of structural methodology as “the only way out of the postmodernist perplexing difficulties” is also heard from younger colleagues in international anthropological meetings. (According to Pierre Maranda in an essay discussing the impact of structural analysis presented at the University of British Columbia, quoted in [19]).
Much understanding of the structural method emanated from Lévi-Strauss’ early manifesto-like pronouncements and the reinterpretations or misinterpretations offered by poststructuralists, notoriously Derrida and his imposturous critique of Lévi-Strauss on the place of writing [20,21]. Recently, several scholars have argued that structuralism, as it is popularly imagined, is a retrospective invention by poststructuralists, which has come to be substituted for the real thing [18,22,23]. Such caricatured reconceptualizations of structure and structuralism cannot and should not obscure Lévi-Strauss’ more decisive notions of differential imbalance and transformation. Actually, some of Lévi-Strauss’ achievements could lay strong claim to having mapped within anthropology and the philosophical parameters of an increasing preoccupation with issues of contextualization and reflexivity in the face of the declining coherence of meta-narrative and grand theory, as well as with issues of political concern and engagement in the post-colonial era [24]. We may be correct in asserting that Lévi-Strauss used structural arguments coherently and correctly to analyze the cultural order and its transient character by means of entropy and irreversibility, as well as, unsurprisingly, to examine deconstruction, or rather “dissolution” (in his own words), and self-reflexivity.
Lévi-Strauss’ contribution is also far-reaching and represents the most compelling challenge to the future of anthropology in the twenty-first century [22,25]. While establishing the theoretical and methodological foundations of a scientific revolution in anthropology, his ambition was to provide a new epistemology, involving a set of novel assumptions and procedures for the acquisition of knowledge, a new approach to methodology, and a new global awareness. For Lévi-Strauss, since human brains are themselves natural objects, and since they are substantially the same throughout the species homo sapiens, we must suppose that when cultural products are generated the process must impart to them certain universal (natural) characteristics of the brain itself [17]. Thus, in investigating the elementary structures of cultural products and social institutions like myth or kinship, we are also making discoveries about the nature of humankind. Verbal categories found in myths and other narratives provide the mechanism through which universal structural characteristics of human brains are transformed into universal structural characteristics of human culture. In this way, category formation in human beings follows universal natural paths. It is not that it must always happen the same way everywhere, but that the human brain is constructed in such a way that it is predisposed to develop categories of a particular kind in a particular way.
The primary modes of thought in human mentality and the foundations of human social life conceal in themselves an infinite intellectual virtuosity by means of natural classifications that show logical possibilities unknown by classical logic. Herein lies the real source of that “science of the concrete”, which creates abstract classifications by means of contrasting similiarities and oppositions, not only to think and modify the concrete things, but also to construct mental structures that facilitate and aim at understanding the world. This speculative interest forms a total well-articulated system that remains independent of scientific logical systems, a concrete way of thinking that suggests that it is not our thinking that shapes the world, but that the world around us contains in itself a power to format our thinking.
Totemic beliefs and practices do not reflect the “primitive” ignorance of indigenous people or an important commodity for functionalist survival, but the concrete embodiment of the abstract means by which these people expressed fundamental ideas about their relations to each other and to their environment. As Lévi-Strauss stated, “the animals in totemism cease to be solely or principally creatures which are feared, admired or envied: their perceptible reality permits the embodiment of ideas and relations conceived by speculative thought on the basis of empirical observations” [26]. We can understand, then, that natural species are chosen not because they are “good to eat”, as the functionalists held following Malinowski and Radcliffe-Brown who believed that the social lives of indigenous peoples were determined by basic needs like sex and hunger, but because they are “good to think” [26]. This concrete way of thinking is a universal mode of thought, which Lévi-Strauss qualified as a “savage thought”. It is savage and undomesticated, just like the wild pansy that he put on the cover of The Savage Mind [27], which established that human thinking and social life are not emotional, instinctive or mystical. In their unprecedented symbolic drive and their capacity for infinite extension, they are inherently intellectual, rational and logical. Lévi-Strauss witnessed these concrete ways of thinking and this intellectual quest for order in everything among indigenous people, from their face-painting to the layout of their camps, and mostly in their myths, which they pieced together with borrowed scraps of older ones, in the same way that a computer programmer might patch together different codes. He found out that indigenous people are every bit as scientifically minded as the ethnographers who investigate them. The only major difference, Lévi-Strauss claimed, is the “totalitarian ambition of the savage mind”, which operates on the assumption that if you could not explain everything, you had not explained anything. Arguably, this kind of totalitarian ambition of the savage mind becomes the ethnographer’s own ambition for the objective conditions of scientific validity in anthropology.
In Lévi-Strauss’ work, the properties of the structuration “frames” of myths open onto a second level of structuration of the transformations of myths, which implied the “mythical thought in a savage state” where the procedures of information processing of the brain had not yet been reformatted by the intellectual technologies of writing, computing, or scientific experimentation. Lévi-Strauss used these cognitive structures in his analyses of the convertibility and mediation of codes and axes, or in his analysis of the combinatorial permutations by inversion or symmetrization of mythical structures (armatures). His famous statement about the myths that “think each other (se pensent) in people’s minds without their being aware of the fact” [8], is quoted at length by his critics and is often interpreted obtusely as being literal. For some, “Lévi-Strauss’ formulas are superb and provocative, but they, literally, make no sense. Myths are thought expressed in different languages, but they are not thinking subjects. They can neither operate (penser) through men nor reflect (penser) upon themselves. A physicist may as well say that the waves and particles that make up light are operating (pensent) in his/her mind and reflecting (se pensent) upon themselves there.” [28].
Acute and subtle thinkers among Lévi-Strauss’ critics must know that the algorithmic formality of myths demonstrated by Lévi-Strauss is actually something existing independently of individual human minds. In addition, a simple algorithm can produce complex autonomous systems that can reproduce human conditions, and one can read Lévi-Strauss’ Mythologiques as a sort of Turing test of the corpus of Amerindian mythology [29]. Critics might also be aware that in quantum mechanics, waves and particles operate with a “spooky action at a distance”, as contemporary physicists put it (after Einstein [30]), and they parallel mythical structures in Lévi-Strauss’ sense, by actually reflecting upon each other, not in the anthropologist’s or physicist’s mind, but like myths, in their own quantum entanglement [31,32]. Far from a pseudo-mathematical mystification, as many Anglo-American anthropologists learnt it [33,34,35], Lévi-Strauss’ structural method originated in mathematics and in applied group theory, dealing primarily with the algebraic models of kinship structures [36,37,38,39]. Afterwards, it has gone on to be well received by modern scholars seeking to study culture and society by formal means [40,41,42,43,44]. The majority of commentators, either admirers or critics, have retained from the structural analysis of myth only its capacity to disclose stable, common, and probably universal frameworks. Fundamentally, however, Lévi-Strauss preferred to look for rules that would ideally make it possible to generate, starting from an unspecified myth of reference, the finite or infinite whole of all other real or possible myths. In the structural study of myths, Lévi-Strauss demonstrated the transformational morphodynamics of mythical networks. One of the more powerful of Lévi-Strauss’ ideas is his description of the generative engine of myths on the basis of the set of their own transformations.
In [1], Claude Lévi-Strauss stated: “As a myth is spread and retold in different contexts, new variations occur”.
While the basic mythical structures (armatures) remain unchanged, characters may change, roles may be inverted based on symmetry, elements of the myth may be lost or inserted, oppositions may become weaker, etc. In short, a number of what Lévi-Strauss calls transformations of the myth will occur. Since they are all related to one another, they form a group of transformations, where each variant is a symmetric transformation of the others and none of them has any preeminence in logic, analysis, or history over the others.
The description of these transformations relies on the concepts of terms and functions. When analyzing myths, Lévi-Strauss often talks of terms that are qualified with different functions. Terms can be persons (in the forms of humans, animals, divinities etc.), or things which have the ability to take up roles. Functions are the different roles carried by these terms. In myths, we encounter a number of characters (terms), all of which have a great number of possible roles (functions).
A myth, understood as a group of transformations occurring from one to another of its variants, is further decomposed into a set of basic elements called mythems, which are also characterized by the notions of terms and functions. Lévi-Strauss distinguished a set of basic operations of homology, inversion, opposition and symmetrization, between a number of characters or terms of myths and their large number of possible roles or functions. In mythical thought, these basic operations account for the convertibility, the mediation and the combinatorial permutations of codes and axes between terms and functions. They can be controlled by means of a special relationship that Lévi-Strauss formulated in a canonical way through various mathematical expressions, which demonstrate how the transformations of the myths can be captured and how new myths are generated from any specified myth of reference. Lévi-Strauss’ concept of canonical formulation that articulates the transformational dynamics of mythical networks transcends a simple analogical relation to a quadratic, as shown in Equation (1),
This equation articulates a dynamic homology between meaningful elements and their propositional functions. This formulation made it possible for Lévi-Strauss to detect a sort of genuine logical machine generative of open-ended meaning within specified mythical networks. In a quadratic equation of this kind, the generative virtues of the so-called “double twist” of the canonical transformation in the structural study of myth imply two conditions internal to canonical formalization. According to Lévi-Strauss, a formulation of this type reflects a group of transformations in which it is assumed that a relation of equivalence exists between two situations defined respectively by an inversion of terms and relations, provided that (i) one of the terms is replaced by its opposite and that (ii) a correlative inversion is made between the function value and the term value of two elements [1]. We may remark that Claude Lévi-Strauss used three or more mathematical expressions of the same quadratic Equation (1) [8,9,10,11,45,46].
After the method for the structural study of myth was introduced in 1955, the generative virtues of the so-called “double twist” of canonical transformation have remained not understood for a long time. Lévi-Strauss almost never mentioned explicitly his formulation of transformational dynamics, even though this was implicit in the massive work of his Mythologiques series published between 1964 and 1971 [8,9,10,11]. The morphodynamic principles of canonical transformations were explicitly operationalized only in his more recent inquiries published between 1985 and 1991 [45,46]. This does not mean, however, that Lévi-Strauss did not understand from the start his own theories and that only advanced mathematicians are up to that task. Instead, we might wonder where that might bring anthropologists, were we to realize that we had to wait, starting from 1972 [47,48], for the knowledge progress in qualitative mathematics become sufficiently advanced for us to understand Lévi-Strauss’ theories. Indeed, they were made comprehensible afterwards as a complex variety of analogies, a torus, a Moebius strip, a Klein group, or aptly as an anticipated formalization of catastrophe models in new mathematics and morphodynamics [49,50,51,52,53,54,55,56,57,58]. What is more important, for a catastrophist operation of this kind to take place, is that the very idea of canonical relation requires a third operating condition as a boundary condition external to canonical formalization. In all cases, boundary condition refers to the empirical evidence from outside the realm of the myths being analyzed, which Lévi-Strauss carefully identified in each case as the necessity of the crossing of a spatiotemporal boundary, defined in territorial, ecological, linguistic, cultural, social, or whatever other terms. Boundary condition is also a formal mathematical concept, required to be satisfied at the boundary of a topological domain in which a set of differential equations is to be solved. A boundary condition of this kind is claimed by Lévi-Strauss to be important in determining the mathematical solutions to various mythical problems. In his further canonical formalisation, boundary condition is used to account for the morphogenetic and morphodynamic transformation of myths across the boundaries existing between one people and another. Namely, a series of variations inherent in the myths of a given people cannot be fully understood without going through myths belonging to another people, which are in a relation of inverse transformation with the formers.
2.2. Understanding Claude Lévi-Strauss Method of Myth Analysis
Following Claude Lévi-Strauss’ methodology, we specify a representation for a myth in terms of the basic elements of the narrative, the mythems involving a term and a function. We can give an example corresponding to an excerpt of a basic folktale of Corsican oral literature. The beginning of the story can be described through the following mythems:
- The ogre (named Orcu) knows the secret of the fabrication of Corsican cheese using milk.
- The shepherds are jealous of the Orcu because of this secret.
- The ogre is captured because of an ingenious trap.
- The shepherds ask for the secret of the fabrication of the cheese.
We give below for each mythem the value of the variables a and x:
- 1st mythem: ;
- 2nd mythem: ;
- 3rd mythem: ;
- 4th mythem: ;
The structural analysis defined by Claude Lévi-Strauss involved in structural analysis consists in showing how a set of mythical transformations are generated from an initial reference myth. We can list several types of transformation of a given myth that are encountered in his books: (i) four basic kinds of transformations (homology, inversion, opposition, symmetry) (ii) the canonical formula; (iii) two additional transformations described as addition and suppression of a mythem. Each type of these transformations can be understood as follows:
- A homology between two terms a and b. The result of a homology between a and b consists in replacing term a by term b in each mythem in order to obtain a new generated mythical transformation. For example, considering the four mythems previously introduced, we are able to generate mythems of a new myth using a homology between the ogre and the Sybille. The result consists in replacing the term ogre by the term Sybille in all the mythems containing the ogre term: first and third mythems.
- Inversion. The result of an inversion of a term a consists in replacing the term a by term in each mythem of the given myth in order to obtain a new generated mythical transformation. For example, in the Corsican culture, the devil is often considered as having an inverse character to the ogre. So, we are able to generate a mythem of a new myth using an inversion of the terms ogre and devil. The result consists of replacing the term ogre by the term devil in all the mythems containing the ogre term: first and third mythems.
- Opposition. The result of an opposition of a term a consists in replacing term a by term in each mythem of the given myth in order to obtain a new generated mythical transformation. For example, we can point to usual oppositions introduced by Claude Lévi-Strauss in the Mythologiques Series: fire = , Jaguar = , vegetable = .
- Symmetry. The result of a symmetry of a term consists in replacing term a by term in each mythem in order to obtain a new generated mythical transformation. For example, in some myths studied by Claude Lévi-Strauss, a menstruating woman is sterile. She becomes a non-woman (symmetry operation), but without being a man (opposition operation).
- The canonical formula transformation (also double twist transformation) leans on the algebraic expression given in Equation (1).
Equation (1) can be understood as follows: a / b is a qualitative opposition of terms, x / y a qualitative opposition of functions, where means that the term t has the function f and where means: (i) that there has been an inversion of the value of term a into an inverse value and (ii) that there has been an exchange between a term value and a function value. These two kinds of exchanges have been called the double twist.
In order for the reader to better grasp the meaning of such a formula, we can take an example from The Jealous Potter [45]. In the canonical formula, if one replaces term a by term n (nightjar) and term b by term w (woman), x by j (jealousy) and y by p (potter), then this gives: . This means: the function of the is to the function of the woman, what the function of the woman is to the inverted function of the potter. This last relationship (the inverted function of the potter) is equivalent to the function of the potter (because = ). Claude Lévi-Strauss highlights that the ovenbird is a specialist in terms of pottery. This relationship introduces a new mythem: “the potter is good as an ovenbird for pottery”. Finally, Claude Lévi-Strauss points out that this new mythem belongs to a set of other myths of South America, so that he demonstrates that new myths can be obtained using the canonical formula. The generative engine of myths is perfectly illustrated through this example.
- Adding a mythem: this is a very simple transformation which consists in adding a mythem to a given myth. The new mythem is built with a term a and a function x.
- Removing a mythem: once again a very simple transformation which consists in removing a given mythem from a given myth.
2.3. Applying Claude Lévi-Strauss Method of Myth Analysis
The transformational analysis of myths according to the Claude Lévi-Strauss’ structural method is complex enough to be a nightmare when being performed by an anthropologist. Anthropologists are confused because they cannot understand it without the help of mathematics and computer science. For that reason, they are unable or reluctant to apply it to other domains, even though the validity of Lévi-Strauss’ theory and method is beyond discussion, as it is by now confirmed by mathematical validation [49,50,51,52,53,54,55,56,57,58]. This sub-section presents the specifications of the tasks that have to be realized using a software approach in order to provide an additional experimental validation of Lévi-Strauss’ theory and method by using an M+S approach based on discrete-event system specification dedicated to show how a set of folk narratives are generated based on symmetry and double twist transformations.
Existing works have already explored the links between computer science and structural anthropology, focused on the structural study of narratives [59,60], or on myth transformation modeling [61,62,63], including attempts to formalize the analysis of myths and folktales developed by Claude Lévi-Strauss [1] and Vladimir Propp [59]. Another logical-mathematical methodology, based on Lévi-Strauss’ claim of an algebraic structure to human mind and cognition derived from his structural analysis of myths, is used to map sub-literal meanings of narrative and discourse analysis. The new method is validated by findings of research on a set of systemic numeric references found in oral narratives and forming mathematically constructive algebraic groups, such as the specifically commutative Abelian semi-group with identity [64,65,66,67]. Some approaches are also based on computer sciences in order to perform a systematic narrative transformations software [68,69]. Despite their good results in terms of narrative generation software, even these interesting attempts have not succeeded in this task, as they do not include myths analysis. In order to help an anthropologist to perform structural analysis, we propose a software approach which may guide them in the different steps of the research method: (i) selection of a “reference” myth (ii) definition of the transformations in order to generate a set of myth (iii) generation of the set of new myths according to the previously defined transformations (iv) overview of the different transformations based on a graph visualization. The software approach should be able to realize the following tasks:
- To allow a user to define an initial myth of reference, defined the Myth M1 by Claude Lévi-Strauss.
- To allow the modeling of a given myth through a set of mythems. The software will allow a user to define a myth as an interconnection of mythems which is represented using two variables: a term usually noted a and a function usually noted x.
- To allow a user to generate a new myth from a given myth by performing a transformation selected through the following set of basic operations which have been presented and detailed previously (homology, inversion, symmetry, opposition, addition of a mythem, removal of a mythem) as well as the Canonical formula.
- To allow a user to visualize the set of transformations already performed using a graph representation. The graph should present the transformation relations between the myths. The nodes of the graph will represent the set of myths labeled by their associated number.
In order to implement these tasks, we propose to develop a set of models based on the formalism of discrete event systems specification (DEVS), introduced by Zeigler [2] in the late 1970s. It provides a way to specify any system as a mathematical object, which enables the modeling and computer simulation of complex discrete event systems by means of a formal method mathematically demonstrated [2]. It is based on a formal representation of discrete-event systems and allows an explicit separation from the M+S part. This means that one can define a model of the behavior of a given system without having to take into account the simulation phase. This explicit separation between the modeling phase and the simulation phase [4] allows DEVS formalism to be one of the best ways to perform efficient simulations of complex systems. Highly pertinent to our concerns at this time is the fact that we have recently extended DEVS formalism in its PythonDEVS kernel to be used within a DEVSimPy environment [12] and software mechanism, which could now be used for the analysis of myths following the morphodynamics of Lévi-Strauss’ structural analysis of mythical thought. In practical terms, the software mechanism is based on the modeling of myths as discrete-event systems by means of a DEVS simulation that allows the generation of myths from an original myth based on structural analysis as defined by Lévi-Strauss [6]. Such a recent elaboration of computer M+S concepts [70] is further used to deal with dynamic variable structures applied in several approaches from social sciences and the humanities to object-oriented models for the analysis of narrative transformations [7,71].
The next section will present the DEVS formalism and the simulation software framework (the Python Based DEVSimPy Framework) that has been used in order to implement the DEVS models to perform the generation of a set of myths from a reference myth based on mainly symmetry and double twist transformations.
3. DEVS Formalism Based Software Framework
In this section, we first present the basic concepts involved in the DEVS formalism. This section also describes the M+S software framework that has been used in order to implement the DEVS models required to perform myth transformation and myth analysis.
3.1. Basic Concepts of the DEVS Formalism
A DEVS model has a time base, inputs, states, outputs, and functions for computing next states and outputs given current states and inputs. The DEVS formalism is a way to characterize how discrete-event simulation languages may specify discrete-event system parameters. It provides a formal representation of discrete-event systems, allowing mathematical manipulation just as differential equations serve this role. In the DEVS formalism, we have to specify: (i) basic models and (ii) how these models are connected together in a hierarchical fashion. DEVS defines two kinds of models: atomic models and coupled models.
An atomic model is a basic model which specifies the dynamics of the model in a timed state transition level. A DEVS atomic model contains a set of states and transition functions that are executed by the simulator. More specifically, an atomic model is defined as follows:
where:
- : the set of input ports and values.
- :the set of output ports and values.
- S is the set of states.
- : the internal transition function that allows the system to go into the next state after the time returned by the time advance function.
- : the external transition function that allows to schedule the states changes according to an external input event.
- : the output function that allows to generate external events on the outputs before the internal transition will be executed.
- : the time advance function, that gives the life time of the current state.
The dynamic interpretation can be described as follows:
- is the total state set,
- is the elapsed time since last transition, and the partial set of states for the duration of if no external event occur.
- the model being in a at , it will move into , , if no external events occurs before .
- when an external event occurs, the model being in the state since the elapsed time moves in , The next state depends on the elapsed time in the present state. At every state change, is reset to 0.
- the output function is executed before an internal transition and before emitting an output event, the model remains in a transient state.
- A state with an infinite life time is a passive state otherwise it is an active state (transient state). If the is passive, the model can evolve only when an input event occurs.
Connections between atomic models can be performed by a coupled model (CM) [2,3,4,5]). Coupled models describe how to couple several component models together to form a new model. This kind of model can be used as a component in a larger coupled model, thus allowing the construction of complex models in a hierarchical fashion. The DEVS coupled model is a structure:
where:
- X: the set of input ports for the reception of external events.
- Y: the set of output ports for the emission of external events.
- : the set of components (coupled or basic models).
- : the DEVS model for each .
- : the set of input links, that connects the inputs of the coupled model to inputs of the components that it contains.
- : the set of output links, that connects the outputs of contained components to the output of the coupled model.
- : the set of internal links, that connects the output ports of components to the input ports of components in the coupled models.
In a coupled model, an output port from a model can be connected to the input of another , but cannot be connected directly to itself.
A simulator is associated with DEVS models in order to exercise a coupled model’s instructions to actually generate its behavior. The DEVS simulation architecture is derived from the abstract simulator concepts [4] associated with the DEVS formalism.
3.2. The DEVSimPy Framework
We implemented the previous functionalities using a software environment called DEVSimPy (DEVS Simulator in Python) [12]. This environment provides a user-friendly interface in order to create DEVS models. The simulation is performed by running the Python-DEVS simulator [72]. The Python-DEVS M+S package [72] provides an implementation of the classic DEVS formalism described in Section 3.2. The package consists of two files, DEVS.py and simulator.py. The first one offers class architecture that allows DEVS models to be defined by subclassing the and classes. The simulator kernel (SK) is implemented in the second file. Based on the principles of simulation defined by B.P. Zeigler [2,3,4,5] and described previously, it allows one to perform a discrete-event simulation. We have been able to perform the simulation algorithm of PythonDEVS by calling the methods extransition (), intransition (), etc., just by subclassing both the atomic model class and the coupled model class inherent to the PythonDEVS package.
Figure 2 gives an example of the general interface of DEVSimPy.
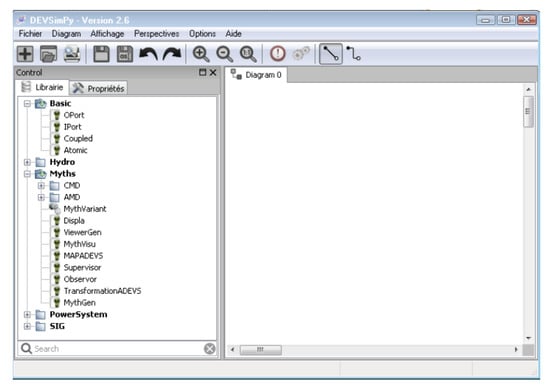
Figure 2.
The DEVSimPy general interface with the Myths library on the left panel.
Figure 2 points out that the window is split into two parts: The left part allows one to visualize the classes which can be instantiated. Two kinds of classes appear: (i) basic classes (basic components of DEVS formalism) and already defined using the classical PythonDEVS software [72]; (ii) classes which have been defined for performing myth transformations which may be found under the Myths and Atomic Models (AM) folder. The right part allows the design of coupled models with a simple drag and drop of classes, and is in the left part of the window. The created coupled model is saved under a format allowing it to be easily reused. We describe in the next section how we have been able to implement the specifications listed in Section 2.2 using the software framework introduced in this section.
4. Implementation of DEVS M+S of Claude Lévi-Strauss Myth Analysis
In order to model the transformation of myths based on Lévi-Strauss’ method, we have to develop a M+S approach, allowing one to implement the four basic functionalities listed in Section 2:
- Modeling of a given myth through a set of mythems. The software will allow a user to define a myth as an interconnection of mythems.
- Definition of an initial myth as descried by Claude Lévi-Strauss.
- Generation of a new myth from a given myth by performing a set of transformations belonging to several types of basic transformation (Section 2.2).
- Visualization of the set of transformations already performed using a graph representation.
We have defined the following DEVS atomic models to implement the previous functionalities: , , , , and .
4.1. Myth Modeling Based on the Notion of Mythems
To represent a narrative belonging to a set of variants of a given myth, we model the architecture of the narrative using a coupled model of the DEVS formalism. This coupled model contains a set of atomic models corresponding to the different parts of the narrative. At the leaf level, we use atomic models of the DEVS formalism to model the narrative structures. Each atomic model corresponds to a mythem as basic element of Claude Lévi-Strauss theory. A mythem involves two variables: a~and x. A narrative is therefore split into mythems and stored in a text file (see in Figure 3 an example of narrative split into a set of mythems).
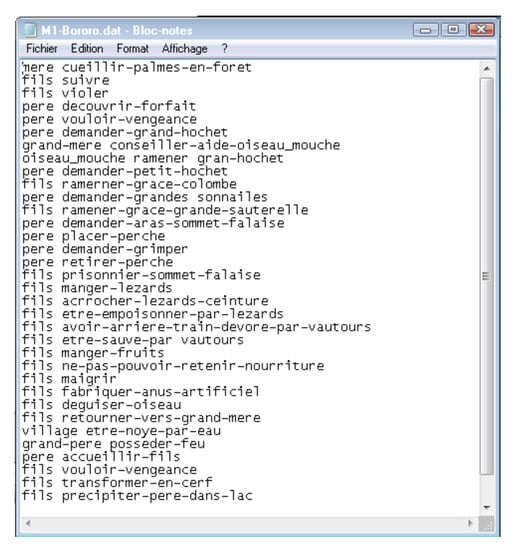
Figure 3.
Example of mythems involved in the myth called M1-Bororo.
4.2. Definition of an Initial Myth
The initial myth is defined by instantiating the Class. In the example of Figure 4, the first myth is called M1-Bororo; it corresponds to the name of the reference myth given by Claude Lévi-Strauss [8]. The window entitled M1-BORORO in Figure 4 presents the attributes of the instance of the Class. One of the main attributes is the filename attribute which is used to store the complete path name of the file linked to the myth. The corresponding myth is given in the window entitled M1-BORORO-dat in Figure 4. The Class is used in order to generate events which should be sent towards the input ports of an instance of the Class. The events are computed by the output function of atomic model and consist in a list of tuple containing a term and a function both of them extracted from each mythem of the myth.
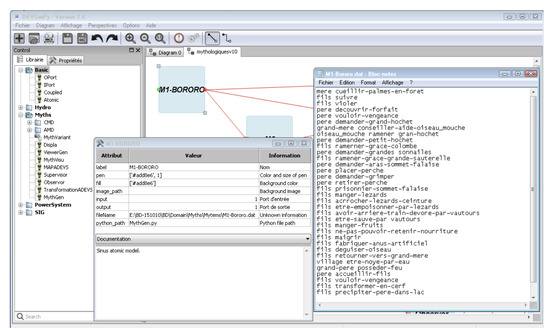
Figure 4.
Creation of the first myth: M1-Bororo.
4.3. Generation of a New Myth from a Given Myth
The generation of a new myth leans on the model class called . An attribute of this class contains the operations which have to be performed in order to generate a new myth. The transformation operations are described in the attribute (as may be seen in Figure 5 in the window entitled ). In the same way, the second part of transformation operations is described in the attribute of the M2-BORORO instance (see window M2-BORORO in Figure 5). An example of the format of the transformation list of operations is given in the window List Editor of the Figure 5. The reader may notice the information set up in the attribute: first the name of the new myth which is going to be generated, and then the list of transformations modelled as follows: each element of the list is composed of a tuple containing the type of transformation (h for homology, d for deleting a mythem etc.) and then the parameters of the transformation. Figure 5 presents how a new myth (M2-BORORO) is generated from myth M1-BORORO. When the generation process is complex (a lot of basic transformations), the new generated myth may be obtained using several instances. For example, in Figure 5, two instances are used: the atomic model instance M1-BORORO is connected with an instance of the class (called ), which is itself interconnected with the instance of the (called M2-BORORO). In both cases, the new myth is generated during the simulation by performing the operations stored in the attribute of each instance of the atomic model ( and M2-Bororo in the example on Figure 5).
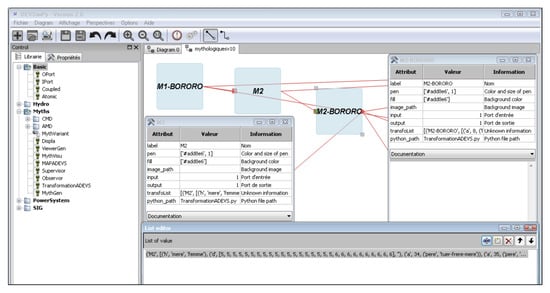
Figure 5.
The generation of a new myth.
4.4. Visualization of the Set of Transformations Already Performed
The goal is to facilitate the visualization of the set of transformations concerning the myths already generated. We choose to use a graph representation. Graph visualization leans on the representation of the relations between myths as diagrams where nodes are labelled with the different myths. Furthermore, oriented arcs between two nodes represents the generation process. The successor node of a given arc corresponds to a myth which has been obtained from the myth involved by the predecessor node of the same arc.
We use the Python library [73] in order to perform automatic graph visualization. The visualization is obtained using the atomic model class called Collector. By clicking on an instance of the Collector Class, the graph of the interconnection of myths linked by a transformation operation is automatically generated. Figure 6 described how all the instances of the Class are connected to the Collector instance. Moreover, the result of the automatic generation of the corresponding graph is given in Figure 7. The next section presents how the DEVS models library has been validated.
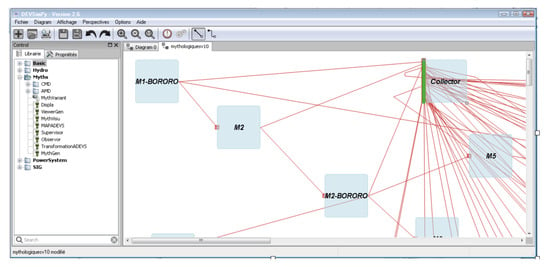
Figure 6.
The Collector model which collects all of the events.
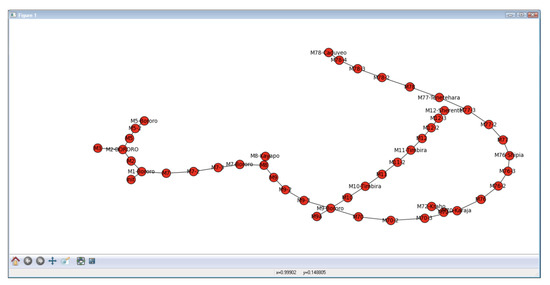
Figure 7.
The resulting graph after myths generation and double clicking on the Collector model.
5. Validation
In this section, we described how the main steps of our approach have been validated. The myth generation has been validated on both Native American myths and Corsican folktales.
A first set of experiments has been defined following the analysis of Native American myths described in the Claude Lévi-Strauss Mythologiques cycle. We have completed the experiments by considering a set of folktales of Corsican oral literature. Corsica is a Mediterranean island, where more than 6500 years ago, megaliths emerged. These megaliths [13] are stones that define a sacred space linked to very old mythology. Some Corsican myths can be found in [7]. We have validated the developed software by performing a set of transformations from a list of 70 myths issued from the Mythologiques series [8,9,10,11] and from a list of 28 folktales belonging to Corsican oral literature.
In both of the two cases, starting from a reference myth, we generated the set of variations. Two sets of experiments have been defined considering: (i) myths issued from the Mythologiques cycle and (ii) folktales issued from the Corsican oral literature. Then we checked the correctness of the transformations of some myths belonging to Lévi-Strauss Mythologiques series [8,9,10,11]. Then, we checked the correctness of the transformations involved in the second set of experiments based on the knowledge of specialists of Corsican oral literature [74].
Figure 8 represents part of the DEVS experiment test which has been conducted for the validation of the myths belonging to the Mythologiques cycle. This experiment of Figure 8 has been simulated and the obtained result (the graph of all generated myths) has been compared with the generation performed manually by Claude Lévi-Strauss.
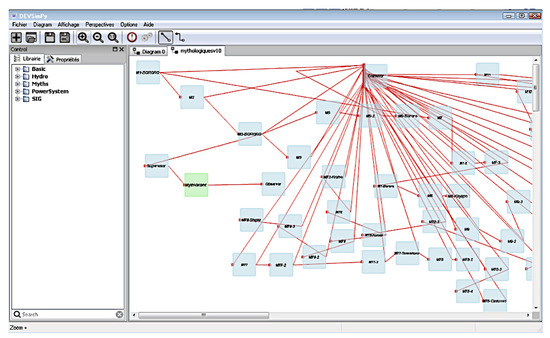
Figure 8.
DEVS experiment corresponding to the generation of myths belonging to the Mythologiques.
We have been able to generate all the considered 70 myths. Figure 9 presents the experiment conducted to validate our approach by means of Corsican folktales. The generated myths have been acknowledged by specialists of Corsican oral literature [74].
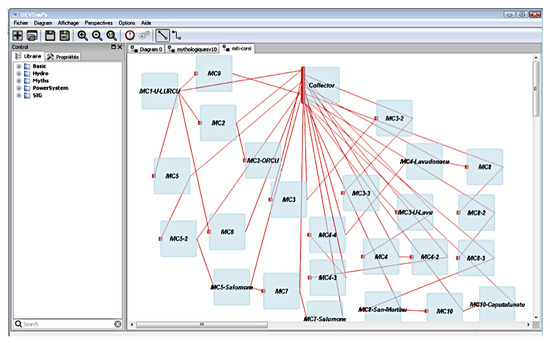
Figure 9.
DEVS experiment in order to generate myths belonging to the Corsican Culture.
Both experiments can be replicated from the DEVSimPy in version 2.9 (https://github.com/capocchi/DEVSimPy/tree/version-2.9) and by visiting https://mycore.core-cloud.net/index.php/s/IjFmwlxEAf3nvdC, which contains:
- Lib_to_copy_to_Domain_dir which gives the directory containing all the python code dedicated to myths transformation. It must be extracted in the DEVSimPy Domain directory and added to the variable in the
- M1-Bororo.dat which is the file containing the initial myth of the South America myths transformations. It must be used to initialized the attribute of the M1-Bororo DEVS model
- MC1-U-Lurcu.dat which is the file containing the initial myth for the Corsica myths transformations. It must by used as the M1-Bororo model
- MythCLSv7.dsp which is the file to be selected in order to perform the South America myths transformations
- MythsCorsi2020.dsp which is the file to be selected to perform the Corsican myths transformations
- MythsCorsi2020.mp4 which gives a video retracing how to perform myths transformation.
6. Discussion
We discuss in this part the interest of the DEVS formalism, in order to study the transformation of myths. The results presented in the previous sections are also examined.
The DEVS formalism is used: (i) to model the structure of a given myth and (ii) to perform the transformation of this structure into a new one, resulting in a new variant of the given myth. We also investigated the temporal aspects. We have to point out what kinds of events are going to be simulated and what results of the simulations can be expected. The temporal aspects concern the evolution of a myth according to transformations (basic operations or using the canonical formula) selected by the user. The time occurrence of an event (representing the execution of a transformation) means that a transformation has to be performed after or before another one. The time basis is not associated with the historical time; it is only a mean to order the selected transformations which are going to generate myths according to Claude Lévi-Strauss’ theory; when we transform a myth we use information form, which is not obtained from the software system. For example, we have stated in Section 2 that, in the Corsican oral literature, the devil is often considered as having an inverse character compared with the ogre. This kind of information should be known in order to build the model which will allow to perform the associated transformation. Without this information, it is impossible to define the transformation in the DEVS model.
The DEVS M+S approach based on structural analysis developed in this paper has been validated through its application on both a set of narratives belonging to Corsican oral literature and to Native American mythology. We detailed the obtained results in the previous section. We have been able to validate the developed software by performing a set of transformations on a list of 70 myths issued from the Mythologiques series [8,9,10,11] and on a list of 28 myths belonging to Corsican oral literature. By selecting each time a set of transformations to be applied on a given myth, we have been able to generate all possible narrative structures belonging to the 70 myths issued from the Claude Lévi-Strauss Mythologiques series and to the 28 Corsican folktales. The transformations as well as the resulting myths have been validated in each case: (i) by specialists of Corsican oral literature [74] for the 28 Corsican folktales and (ii) with Claude Lévi-Strauss’ variations described in his books [8,9,10,11] for the 70 Native American myths.
7. Future Applications
One of the most powerful of Lévi-Strauss’ ideas is the differential imbalance that indicates a tension between cultures. Rather than the identification of and a praise for bounded cultural difference, this is a belief that transformations prevail over identity, structure, or the cultural system, all of which are based on morphodynamic and morphogenetic transformations. His magnum opus on the Mythologiques [8,9,10,11] was massively open-ended and could never be completed, even after his small Mythologiques [45,46], since the possible permutation and transformation of mythical structures (armatures) are virtually never-ending agentive algorithms in a sort of Turing test of Amerindian mythology [29]. This is a point demonstrated by the Quadratura Americana suites [75,76,77], essentially taking up where the Mythologiques left off.
Lévi-Strauss’ notions of differential imbalance and transformation make it possible to show that structural anthropology may innovatively account, both for the dynamic process of praxis by which social relations and social systems are enacted and transformed and for the competitive and strategic practices of social behavior. It may well be that returning to Lévi-Strauss will give us the courage to attempt once again a new syncretism, encompassing structural methodology, mathematics, computer science, information theory, cybernetics, cognition, and reasoning. Thanks to Lévi-Strauss’ notion of transformation, the conception of structure decisively moved away from the binary logic of the linguistic model of differential elements, to which it is too often and obstinately reduced, in order to become a combinatorial analysis of morphogenetic dynamics. In his conceptualization of the generative engine of myths based on their own transformations, he staked the strongest claim to structural analysis as a scientific method that could be applied objectively, and which could reveal a level of reality encoded in the myths themselves. In a broad sense, while the key categories that Lévi-Strauss developed are embodied in the anthropological objects he studied (myths and mythical networks), they have the potential to be productively and critically applied to other domains if radically tweaked. In particular, if structural thinking is enlarged to include hidden ideology and instrumental politics, a convincing argument can be offered to reveal the continued relevance and usefulness of Lévi-Strauss’ work for contemporary social scientists and theorists.
Many studies show that the structural analysis initiated by Lévi-Strauss may innovatively account for the ways in which social relations are ever more mediated by and implicated in broader political processes [78,79,80]. Lévi-Strauss may still be a source of inspiration even for highbrow ideas of our days, sometimes even without proper acknowledgment. These may include the creation of a ritual and symbolic atmosphere to address climate change as part of the Paris COP21 negotiations [81], the Holocene resurgence of a multi-species model countering the proliferation of polluted forms of life in the Anthropocene “plantation” [82], or the accelerated change of global modernity in terms of “overheating” [83]. They all parallel his insights, which are often thought in these authors’ minds, at best, as Lévi-Strauss would have put it, without them being aware of the fact.
More importantly, it could be argued that some aspects of Lévi-Strauss’ theory could be advanced as a workable methodology to help us build innovative anthropological approaches to agency and politics, by contextualizing them within history, culture, and society. In particular, the requirement of an operating condition that in the study of myth is expressed as a boundary condition in mathematical sense can be thought to anticipate the discursive activation of a particular cultural ideology acting as a hidden agency of instrumental politics. The idea is to develop a neo-structural model of canonical formalization based on discourse analysis and transformational morphodynamics, which may take lead from the abstract mathematical operations and the evolution rules of canonical transformations suggested by Lévi-Strauss for the structural study of myth, and which make it necessary to isolate an analytical device as a boundary condition for mathematical validation.
Based on this epistemological insight, it can be argued that we may establish a more sophisticated approach following structural procedures of transformational analysis and formalization. While it may not hitherto have been expressed so directly, this means that we may be correct in asserting that from an empirical situation of social change, including social conflict, identity construction and ethnic identification, transcribed in a canonical way, we can in theory deduce the possibly hidden reality of an external boundary, borderland existence, or border-crossing movement. As argued elsewhere, the concept of boundary condition could be expanded to account for the social morphodynamics of this reality, which would reveal itself in the form of a particular cultural ideology that might be discursively activated and amplified to act as a hidden agency of instrumental politics in actual sociocultural situations [84]. Namely, a comparative analysis of transformations resulting from intercultural dynamics [85], especially in processes of identity construction and identity politics [86,87], could make it possible to construe such a conceptual extension. In particular, morphodynamic analyses of the empirical evidence about actual instances of women’s agency, about family structures and fertility rates, about mass rapes in ethnic conflicts, or about identity transformations in the European context, provide some illustrative examples of an instrumental agency of hidden politics, revealing the workings of the ideologies of gender, familism, honor and blood, and identity building, respectively [88,89,90]. This is what is called “cultural activism”, which is defined as a driving force external to a sociocultural situation and which may be thought, aptly in the case of family structures and fertility rates, as a kind of “sociocultural viagra” to change or perpetuate the system [89].
The hidden reality so revealed is necessarily organized around a specific category of social hierarchy associated with the value of one identity element, human agency and social action, but having inverse propositional characteristics to that element, course of action and agency. To put it the other way around, the morphodynamic formalization of cultural activism may allow us to identify instrumental ideologies and to anticipate new social change and identity construction as a result of the mediating logical operation of a boundary condition within the same sociocultural system or institutional frameworks, and we are able to set off in their search and their appreciation.
Potentially, we foresee a new research undertaking to reformulate Lévi-Strauss’ structural analysis in order to elaborate a neo-structural model of canonical formalization based on transformational morphodynamics. The aim is to conceptualize and measure recursively the structural dynamics and the recurrent patterns of current identity transformations in liberal democracies, especially in US and EU contexts, where ethnic/racial divisions and migration challenges are becoming more acute than ever. The new approach is based on a complex research strategy, including the use of Bayesian inference for the construction of object-oriented sets of systemic numeric references to identity discursive practices and the use of DEVS formalism for their specification as discrete event systems that form constructive and commutative groups with identity. The outcome of this research will be to allow for a critical understanding of core values and identity transformations, which eventually may anticipate policy insights and provide a powerful decision-making instrument to be used by scholars and policy practitioners for identifying and following up the structural dynamics and the recurring patterns of identity transformations in the contemporary world.
If we are correct in these assumptions, we should consider that Lévi-Strauss’ structural legacy provides us a new anthropologically informed movement in social theory that could account for the structural dynamics of change and conflict, while revealing the hidden aspects of ideological agencies and political projects in the contemporary world. In particular, these conceptual aspects suggest a novel approach that requires one to not rely only on surface observations of data and ethnography. Rather, critical analyses of empirical evidence and intersections of ethnography with both experiential understanding and structural formalization can yield new insights in the space between idiographic and nomothetic understandings of culture, politics, and ideology.
8. Conclusions
We have presented, in this paper, a set of DEVS models in order to perform Claude Lévi-Strauss Structural Anthropology method. A brief overview of Claude Lévi-Strauss transformations and analysis of myths has been given before we presented the specifications of the software approach for performing myth transformations and analysis according to Claude Lévi-Strauss’ theory. Finally, we described how we implemented DEVS models using the DEVSimPy environment in order to generate a set of myths and to perform myth analysis using transformations graph visualization. The validation process has been realized on a set of Native American myths taken from Claude Lévi-Strauss’ Mythologiques series and using a set of folktales issued from Corsican oral literature.
The short-term future work is the modelling of the 813 myths defined by Claude Lévi-Strauss in his Mythologiques Series and the defining of a model of a set of more than 200 folktales coming from the Corsican oral literature. The final task of the simulation of a given myth is to dynamically visualize the unfolding of narratives on a map. We also envision to examine and develop some aspects of the potential challenges of structural methodology for future applications to other social and cultural domains. The idea is to elaborate a neo-structural model of canonical formalization based on transformational morphodynamics which could account for current identity transformations in the contempory world.
Author Contributions
Development of concepts, software implementation and writing of the paper with emphasis on the computer science features, J.-F.S. and L.C.; Development of concepts and writing of the paper with emphasis on the structural anthropology features, A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lévi-Strauss, C. The Structural Study of Myth. J. Am. Folk. 1955, 68, 428–444. [Google Scholar] [CrossRef]
- Zeigler, B.P. Theory of Modeling and Simulation; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Zeigler, B.P.; Praehofer, H.; Kim, T.G. Theory of Modeling and Simulation, 2nd ed.; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Zeigler, B.P. Object-Oriented Simulation with Hierarchical, Modular Models; Academic Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Zeigler, B.; Muzy, A.; Kofman, E. Theory of Modeling and Simulation: Discrete Event & Iterative System Computational Foundations; Elsevier Science: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Santucci, J.F.; de Gentili, E. Dynamic Variable Structure Modelling and Simulation of the Claude Lévi-Strauss’ Mythical Thought Morphodynamics. In Proceedings of the 2009 Spring Simulation Multiconference, San Diego, CA, USA, 22–27 March 2009. [Google Scholar]
- Santucci, J.F.; de Gentili, E.; Thury-Bouvet, G. Discrete Event Modeling and Simulation of the Mythical Thought Morphodynamics Involved in Claude Lévi-Strauss Structural Analysis. In Handbook of Research on Culturally-Aware Information Technology: Perspectives and Models; Blanchard, E., Allard, D., Eds.; IGI Global: Hershey, PA, USA, 2010; Chapter 8. [Google Scholar]
- Lévi-Strauss, C. The Raw and the Cooked: Introduction to a Science of Mythology; Harper & Row: New York, NY, USA, 1970; Volume 1. [Google Scholar]
- Lévi-Strauss, C. From Honey to Ashes; Harper & Row: New York, NY, USA, 1973. [Google Scholar]
- Lévi-Strauss, C. The Origin of Table Manners; Harper & Row: New York, NY, USA, 1978. [Google Scholar]
- Lévi-Strauss, C. The Naked Man; Harper & Row: New York, NY, USA, 1981. [Google Scholar]
- Capocchi, L.; Santucci, J.F.; Poggi, B.; Nicolai, C. DEVSimPy: A Collaborative Python Software for Modeling and Simulation of DEVS Systems. In Proceedings of the 20th IEEE International Workshops on Enabling Technologies: Infrastructures for Collaborative Enterprises, Paris, France, 27–29 June 2011; pp. 170–175. [Google Scholar] [CrossRef]
- Thury-Bouvet, G.; Santucci, J.F.; Khoumeri, E.H.; Ottavi, A. Orientations of Corsican Dolmens. J. Hist. Astron. 2006, 37, 299–306. [Google Scholar] [CrossRef]
- Doja, A. The Advent of Heroic Anthropology in the History of Ideas. J. Hist. Ideas 2005, 66, 633–650. [Google Scholar] [CrossRef]
- Doja, A. The Shoulders of our Giants: Claude Lévi-Strauss and his Legacy in Current Anthropology. Soc. Sci. Inf. 2006, 45, 79–107. [Google Scholar] [CrossRef]
- Geertz, C. The Cerebral Sauvage: On the Work of Claude Lévi-Strauss. In The Intrepretation of Cultures; Basic Books: New York, NY, USA, 1973; pp. 345–359. [Google Scholar]
- Leach, E. Lévi-Strauss; Fontana/Collins: London, UK, 1970. [Google Scholar]
- Wiseman, B. The Cambridge Companion to Lévi-Strauss; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Mauzé, M.; Harkin, M.; Kan, S. (Eds.) Coming to Shore: Northwest Coast Ethnology, Traditions, and Visions; University of Nebraska Press: Lincoln, NE, USA, 2004; p. 90. [Google Scholar]
- Doja, A. The Kind of Writing: Anthropology and the Rhetorical Reproduction of Postmodernism. Crit. Anthropol. 2006, 26, 157–180. [Google Scholar] [CrossRef]
- Doja, A. Creative Misreading and Bricolage Writing: A Structural Appraisal of a Poststructuralist Debate. Port. Rev. Hist. Book 2007, 11, 89–104. [Google Scholar]
- Doja, A. Claude Lévi-Strauss at his Centennial: Toward a Future Anthropology. Theory Cult. Soc. 2008, 25, 321–340. [Google Scholar] [CrossRef]
- Henaff, M. Adieu à la structure? Esprit 2011, 8–9, 114–119. [Google Scholar] [CrossRef]
- Doja, A. The Predicament of Heroic Anthropology. Anthropol. Today 2006, 22, 18–22. [Google Scholar] [CrossRef]
- Doja, A. Claude Lévi-Strauss (1908–2009): The Apotheosis of Heroic Anthropology. Anthropol. Today 2010, 26, 18–23. [Google Scholar] [CrossRef]
- Levi-Strauss, C. Le totémisme aujourd’hui; Presses Universitaires de France: Paris, France, 1962. [Google Scholar]
- Levi-Strauss, C. The Savage Mind; University of Chicago Press: Chicago, IL, USA, 1966. [Google Scholar]
- Godelier, M. Claude Lévi-Strauss: A Critical Study of His Thought; Verso: London, UK, 2018. [Google Scholar]
- Harkin, M.E. Lévi-Strauss: Two lives. Rev. Anthropol. 2019, 48, 88–102. [Google Scholar] [CrossRef]
- Einstein, A.; Born, M.; Born, H. The Born-Einstein Letters: Friendship, Politics, and Physics In Uncertain Times: Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955 with Commentaries by Max Born; Macmillan: New York, NY, USA, 2005. [Google Scholar]
- Doja, A. Lévi-Strauss’ Heroic Anthropology Facing Contemporary Problems of the Modern World. Rev. Anthropol. 2020, 1–35. [Google Scholar] [CrossRef]
- Doja, A. Celebrations of Lévi-Strauss’s Heroic Legacy. J. R. Anthropol. Inst. 2020, 26, 1–8. [Google Scholar] [CrossRef]
- Diamond, S. The Inauthenticity of Anthropology: The Myth of Structuralism. In Search of the Primitive; a Critique of Civilization; Transaction Books: New Brunswick, NJ, USA, 2018; Chapter 10; pp. 292–331. [Google Scholar]
- Turner, T. On Structure and Entropy: Theoretical Pastiche and the Contradictions of “Structuralism”. Curr. Anthropol. 1990, 31, 563–568. [Google Scholar] [CrossRef]
- Launay, R. Is Lévi-Strauss Still Good to Think? Rev. Anthropol. 2013, 42, 38–49. [Google Scholar] [CrossRef]
- Cargal, J. The Problem with Algebraic Models of Marriage and Kinship Structure. UMAP J. 1996, 22, 345–353. [Google Scholar]
- Le Roux, R. Lévi-Strauss, une réception paradoxale de la cybernétique. L’Homme 2009, 189, 165–190. [Google Scholar] [CrossRef]
- Rauff, J.V. The Algebra of Marriage: An Episode in Applied Group Theory. BSHM Bull. J. Br. Soc. Hist. Math. 2016, 31, 230–244. [Google Scholar] [CrossRef]
- Harrod, J. A Post-Structuralist Revised Weil–Lévi-Strauss Transformation Formula for Conceptual Value-Fields. Sign Syst. Stud. 2018, 46, 255. [Google Scholar] [CrossRef]
- Barbosa-de Almeida, M. Symmetry and Entropy: Mathematical Metaphors in the Work of Lévi-Strauss. Curr. Anthropol. 1990, 31, 367–385. [Google Scholar] [CrossRef]
- Marcus, G.F. The Algebraic Mind: Integrating Connectionism and Cognitive Science; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Morava, J. From Lévi-Strauss to Chaos and Complexity. In On the Order of Chaos: Social Anthropology and the Science of Chaos; Berghahn Books: New York, NY, USA, 2005; pp. 47–63. [Google Scholar]
- Lafontaine, C. The Cybernetic Matrix of ‘French Theory’. Theory Cult. Soc. 2007, 24, 27–46. [Google Scholar] [CrossRef]
- Geoghegan, B.D. From Information Theory to French Theory: Jakobson, Lévi-Strauss, and the Cybernetic Apparatus. Crit. Inq. 2011, 38, 96–126. [Google Scholar] [CrossRef]
- Lévi-Strauss, C. The Jealous Potter; University of Chicago Press: Chicago, IL, USA, 1988. [Google Scholar]
- Lévi-Strauss, C. The Story of Lynx; University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Thom, R. Stabilité structurelle et morphogénèse: Essai d’une théorie générale des modèles; Interéditions: Paris, France, 1972. [Google Scholar]
- Thom, R. Modèles mathématiques de la morphogenèse; Christian Bourgeois Edition: Paris, France, 1981. [Google Scholar]
- Petitot, J. Approche morphodynamique de la formule canonique du mythe. L’Homme 1988, 28, 106–107. [Google Scholar] [CrossRef]
- Petitot, J. Note complémentaire sur l’approche morphodynamique de la formule canonique du mythe. L’Homme 1995, 35, 17–23. [Google Scholar] [CrossRef]
- Mosko, M.S. The Canonic Formula of Myth and Nonmyth. Am. Ethnol. 1991, 18, 126–151. [Google Scholar] [CrossRef]
- Côté, A. Qu’est-ce que la formule canonique? L’Homme 1995, 35, 35–41. [Google Scholar] [CrossRef][Green Version]
- Désveaux, E. Groupe de Klein et formule canonique. L’Homme 1995, 35, 43–49. [Google Scholar] [CrossRef]
- Scubla, L. À propos de la formule canonique, du mythe, et du rite. L’Homme 1995, 35, 51–63. [Google Scholar] [CrossRef]
- Scubla, L. Lire Lévi-Strauss: Le déploiement d’une intuition; Odile Jacob.: Paris, France, 1998. [Google Scholar]
- Marcus, S. The Togical and Semiotic Status of the Canonic Formula of Myth. Semiotica 1997, 116, 115–188. [Google Scholar] [CrossRef]
- Maranda, P. The Double Twist: From Ethnography to Morphodynamics; University of Toronto Press: Toronto, ON, Canada, 2001. [Google Scholar]
- Morava, J. Une interprétation mathématique de la formule canonique de Claude Lévi-Strauss. Cahier de L’Herne 2004, 88, 216–218. [Google Scholar]
- Propp, V.I. Morphology of the Folktale; University of Texas Press: Austin, TX, USA, 1968. [Google Scholar]
- Greimas, A. Sémantique Structurale: Recherche de Méthode; Larousse: Paris, France, 1966. [Google Scholar]
- Petitot, J. Cognitive Morphodynamics—Dynamical Morphological Models of Constituency in Perception and Syntax; Lang: Bern, Switzerland, 2011. [Google Scholar]
- Jason, H.; Segal, D. Patterns in Oral Literature; Mouton: The Hague, The Netherlands, 1977. [Google Scholar]
- Richard, P.; Jaulin, R. Anthropologie et calcul; 10/18; Union Générale: Lyon, France, 1971. [Google Scholar]
- Haskell, R.; Badalamenti, A. Algebraic Structure of Verbal Narratives with Dual Meanings. Math. Comput. Model. 2003, 37, 383–393. [Google Scholar] [CrossRef]
- Haskell, R. A Logico-mathematic, Structural Methodology: Part II, Experimental Design and Epistemological Issues. J. Mind Behav. 2003, 24, 401–421. [Google Scholar]
- Haskell, R. A Logico-mathematic, Structural Methodology: Part III, Theoretical, Evidential, and Corroborative Bases of a New Cognitive Unconscious for Sub-literal (SubLit) Cognition and Language. J. Mind Behav. 2004, 25, 287–321. [Google Scholar]
- Haskell, R. Claude Lévi-Strauss Reconsidered: Cognitive science, epistemology, and the (not so savage) algebraic mind. Cogn. Semiot. 2008, 2008, 65–90. [Google Scholar] [CrossRef]
- Hobbs, R.L.; Potts, C. Hyperscenarios: A Framework for Active Narrative. In Proceedings of the 38th Annual Southeast Regional Conference, Clemson, CA, USA, 7–8 April 2000; pp. 201–210. [Google Scholar] [CrossRef]
- Kato, T.; Miyazaki, K.; Nakatsu, R. Analysis of Japanese folktales for the purpose of story generation. In Proceedings of the 3rd International Conference on Digital Interactive Media in Entertainment and Arts, ACM International Conference Proceeding Series, Athens, Greece, 10–12 September 2008; Volume 349, pp. 415–419. [Google Scholar]
- Santucci, J.F.; Capocchi, L.; Zeigler, B.P. System Entity Structure Extension to Integrate Abstraction Hierarchies and Time Granularity into DEVS Modeling and Simulation. Simulation 2016, 92, 747–769. [Google Scholar] [CrossRef]
- Santucci, J.F.; Capocchi, L. Visualization of Folktales on a Map by Coupling Dynamic DEVS Simulation within Google Earth. In Simultech; SciTePress: Setubal, Portugal, 2011; pp. 128–133. [Google Scholar]
- Bolduc, J.S.; Vangheluwe, H. The Modelling and Simulation Package PythonDEVS for Classical Hierarchical DEVS; MSDL Technical Report MSDL-TR-2001–01; McGill University: Montreal, QC, Canada, 2001. [Google Scholar]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Giannesini, G.; Luccioni, P. Religiosité,croyances et rituels populaires; Albiana éditions: Ajaccio, France, 2010. [Google Scholar]
- Desveaux, E. Spectres de l’anthropologie. Suite nord-américaine; Lieux-d’être: Montreuil, France, 2007. [Google Scholar]
- Desveaux, E. La parole et la substance: Anthropologie comparée de l’Amérique et de l’Europe; Indes-Savantes: Paris, France, 2017. [Google Scholar]
- Désveaux, E. Quadratura americana, Essai d’anthropologie lévi-straussienne; Georg: Geneve, Switzerland, 2001. [Google Scholar]
- Asch, M. Levi-Strauss and the Political: The Elementary Structures of Kinship and the Resolution of Relations Between Indigenous People and Settler States. J. R. Anthropol. Inst. 2005, 11, 425–444. [Google Scholar] [CrossRef]
- Marchart, O. Ungesellschaftliche Gesellschaftlichkeit: Exklusion und Antagonismus bei Lévi-Strauss, unter Berücksichtigung von Lacan, Laclau und Luhmann. Soz. Syst. 2008, 14, 370–396. [Google Scholar] [CrossRef]
- Constable, N. The Commodification of Intimacy: Marriage, Sex, and Reproductive Labor. Annu. Rev. Anthropol. 2009, 38, 49–64. [Google Scholar] [CrossRef]
- Latour, B. Face a Gaia. Huit conférences sur le nouveau regime climatique; La Decouverte: Paris, France, 2015. [Google Scholar]
- Tsing, A.L. The Mushroom at the End of the World: On the Possibility of Life in Capitalist Ruins; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Eriksen, T.H. Overheating: An Anthropology of Accelerated Change; London: Pluto, UK, 2016. [Google Scholar]
- Doja, A. Social Morphodynamics: Mapping Identity Transformations, Cultural Encounters, and the Evolution of Core Values. Soc. Epistemol. Rev. Reply Collect. 2018, 7, 14–25. [Google Scholar]
- Doja, A. Invitation au Terrain: Mémoire personnel de la construction du projet socio-anthropologique; Peter Lang: Bruxelles, Belgium, 2013. [Google Scholar] [CrossRef]
- Doja, A. Naître et grandir chez les Albanais: La Construction Culturelle de la Personne; L’Harmattan: Paris, France, 2000; p. 324. [Google Scholar]
- Doja, A. Socializing Enchantment: A socio-anthropological approach to infant-directed singing, music education and cultural socialization. Int. Rev. Aesthet. Sociol. Music 2014, 45, 115–147. [Google Scholar]
- Doja, A. Instrumental borders of gender and religious conversions in the Balkans. Relig. State Soc. 2008, 36, 55–63. [Google Scholar] [CrossRef]
- Doja, A. Fertility Trends, Marriage Patterns and Savant Typologies in Albanian Context. J. Fam. Hist. 2010, 35, 346–367. [Google Scholar] [CrossRef] [PubMed]
- Doja, A. Politics of Mass Rapes in Ethnic Conflict: A Morphodynamics of raw Madness and Cooked Evil. Crime Law Soc. Chang. 2019, 71, 541–580. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).