A Discrete-Event Simulation of Claude Lévi-Strauss’ Structural Analysis of Myths Based on Symmetry and Double Twist Transformations
Abstract
1. Introduction
2. Transformational Analysis of Myths Following Structural Methodology
2.1. Introduction to Structural Analysis
2.2. Understanding Claude Lévi-Strauss Method of Myth Analysis
- The ogre (named Orcu) knows the secret of the fabrication of Corsican cheese using milk.
- The shepherds are jealous of the Orcu because of this secret.
- The ogre is captured because of an ingenious trap.
- The shepherds ask for the secret of the fabrication of the cheese.
- 1st mythem: ;
- 2nd mythem: ;
- 3rd mythem: ;
- 4th mythem: ;
- A homology between two terms a and b. The result of a homology between a and b consists in replacing term a by term b in each mythem in order to obtain a new generated mythical transformation. For example, considering the four mythems previously introduced, we are able to generate mythems of a new myth using a homology between the ogre and the Sybille. The result consists in replacing the term ogre by the term Sybille in all the mythems containing the ogre term: first and third mythems.
- Inversion. The result of an inversion of a term a consists in replacing the term a by term in each mythem of the given myth in order to obtain a new generated mythical transformation. For example, in the Corsican culture, the devil is often considered as having an inverse character to the ogre. So, we are able to generate a mythem of a new myth using an inversion of the terms ogre and devil. The result consists of replacing the term ogre by the term devil in all the mythems containing the ogre term: first and third mythems.
- Opposition. The result of an opposition of a term a consists in replacing term a by term in each mythem of the given myth in order to obtain a new generated mythical transformation. For example, we can point to usual oppositions introduced by Claude Lévi-Strauss in the Mythologiques Series: fire = , Jaguar = , vegetable = .
- Symmetry. The result of a symmetry of a term consists in replacing term a by term in each mythem in order to obtain a new generated mythical transformation. For example, in some myths studied by Claude Lévi-Strauss, a menstruating woman is sterile. She becomes a non-woman (symmetry operation), but without being a man (opposition operation).
- The canonical formula transformation (also double twist transformation) leans on the algebraic expression given in Equation (1).
- Adding a mythem: this is a very simple transformation which consists in adding a mythem to a given myth. The new mythem is built with a term a and a function x.
- Removing a mythem: once again a very simple transformation which consists in removing a given mythem from a given myth.
2.3. Applying Claude Lévi-Strauss Method of Myth Analysis
- To allow a user to define an initial myth of reference, defined the Myth M1 by Claude Lévi-Strauss.
- To allow the modeling of a given myth through a set of mythems. The software will allow a user to define a myth as an interconnection of mythems which is represented using two variables: a term usually noted a and a function usually noted x.
- To allow a user to generate a new myth from a given myth by performing a transformation selected through the following set of basic operations which have been presented and detailed previously (homology, inversion, symmetry, opposition, addition of a mythem, removal of a mythem) as well as the Canonical formula.
- To allow a user to visualize the set of transformations already performed using a graph representation. The graph should present the transformation relations between the myths. The nodes of the graph will represent the set of myths labeled by their associated number.
3. DEVS Formalism Based Software Framework
3.1. Basic Concepts of the DEVS Formalism
- : the set of input ports and values.
- :the set of output ports and values.
- S is the set of states.
- : the internal transition function that allows the system to go into the next state after the time returned by the time advance function.
- : the external transition function that allows to schedule the states changes according to an external input event.
- : the output function that allows to generate external events on the outputs before the internal transition will be executed.
- : the time advance function, that gives the life time of the current state.
- is the total state set,
- is the elapsed time since last transition, and the partial set of states for the duration of if no external event occur.
- the model being in a at , it will move into , , if no external events occurs before .
- when an external event occurs, the model being in the state since the elapsed time moves in , The next state depends on the elapsed time in the present state. At every state change, is reset to 0.
- the output function is executed before an internal transition and before emitting an output event, the model remains in a transient state.
- A state with an infinite life time is a passive state otherwise it is an active state (transient state). If the is passive, the model can evolve only when an input event occurs.
- X: the set of input ports for the reception of external events.
- Y: the set of output ports for the emission of external events.
- : the set of components (coupled or basic models).
- : the DEVS model for each .
- : the set of input links, that connects the inputs of the coupled model to inputs of the components that it contains.
- : the set of output links, that connects the outputs of contained components to the output of the coupled model.
- : the set of internal links, that connects the output ports of components to the input ports of components in the coupled models.
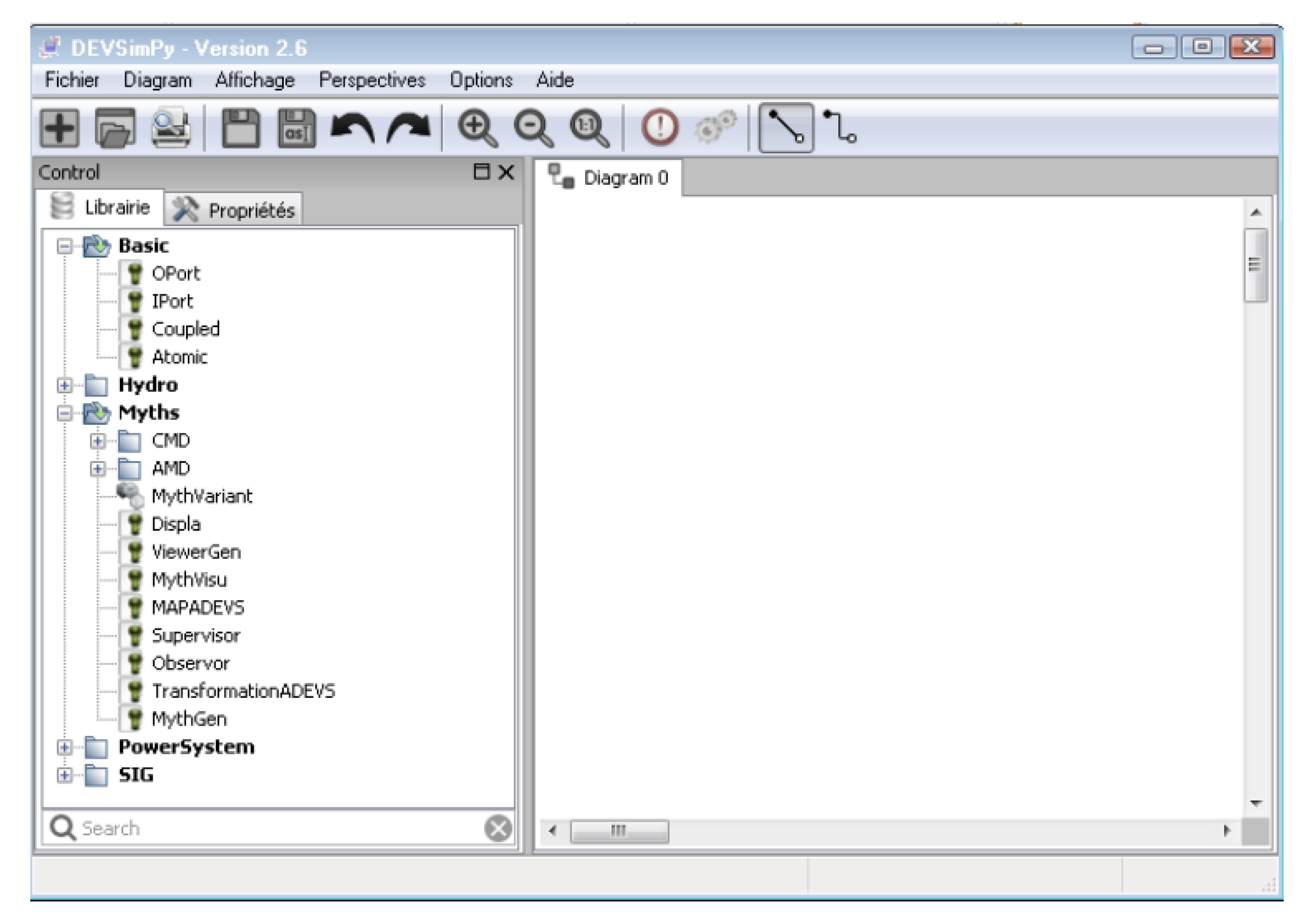
3.2. The DEVSimPy Framework
4. Implementation of DEVS M+S of Claude Lévi-Strauss Myth Analysis
- Modeling of a given myth through a set of mythems. The software will allow a user to define a myth as an interconnection of mythems.
- Definition of an initial myth as descried by Claude Lévi-Strauss.
- Generation of a new myth from a given myth by performing a set of transformations belonging to several types of basic transformation (Section 2.2).
- Visualization of the set of transformations already performed using a graph representation.
4.1. Myth Modeling Based on the Notion of Mythems
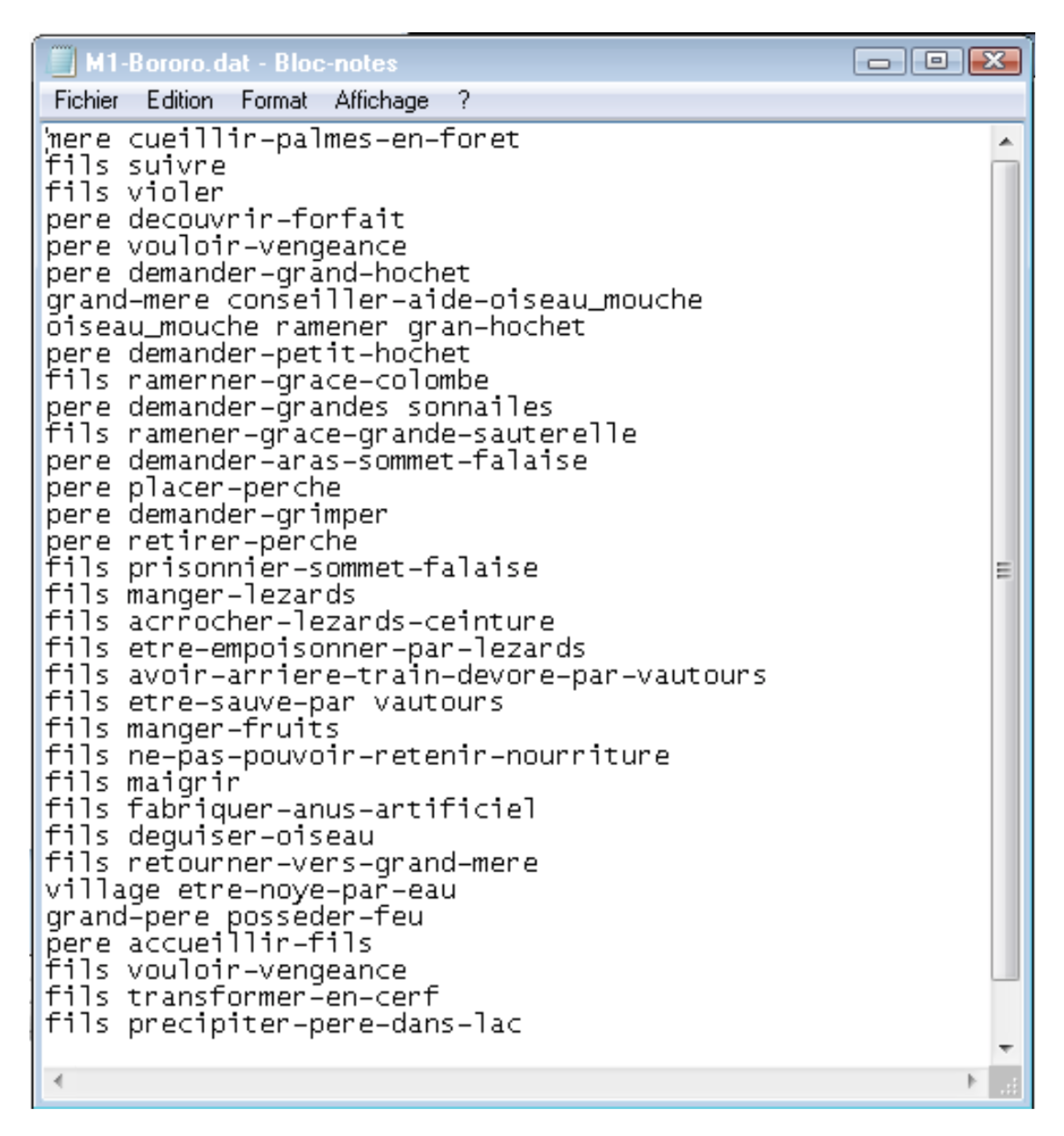
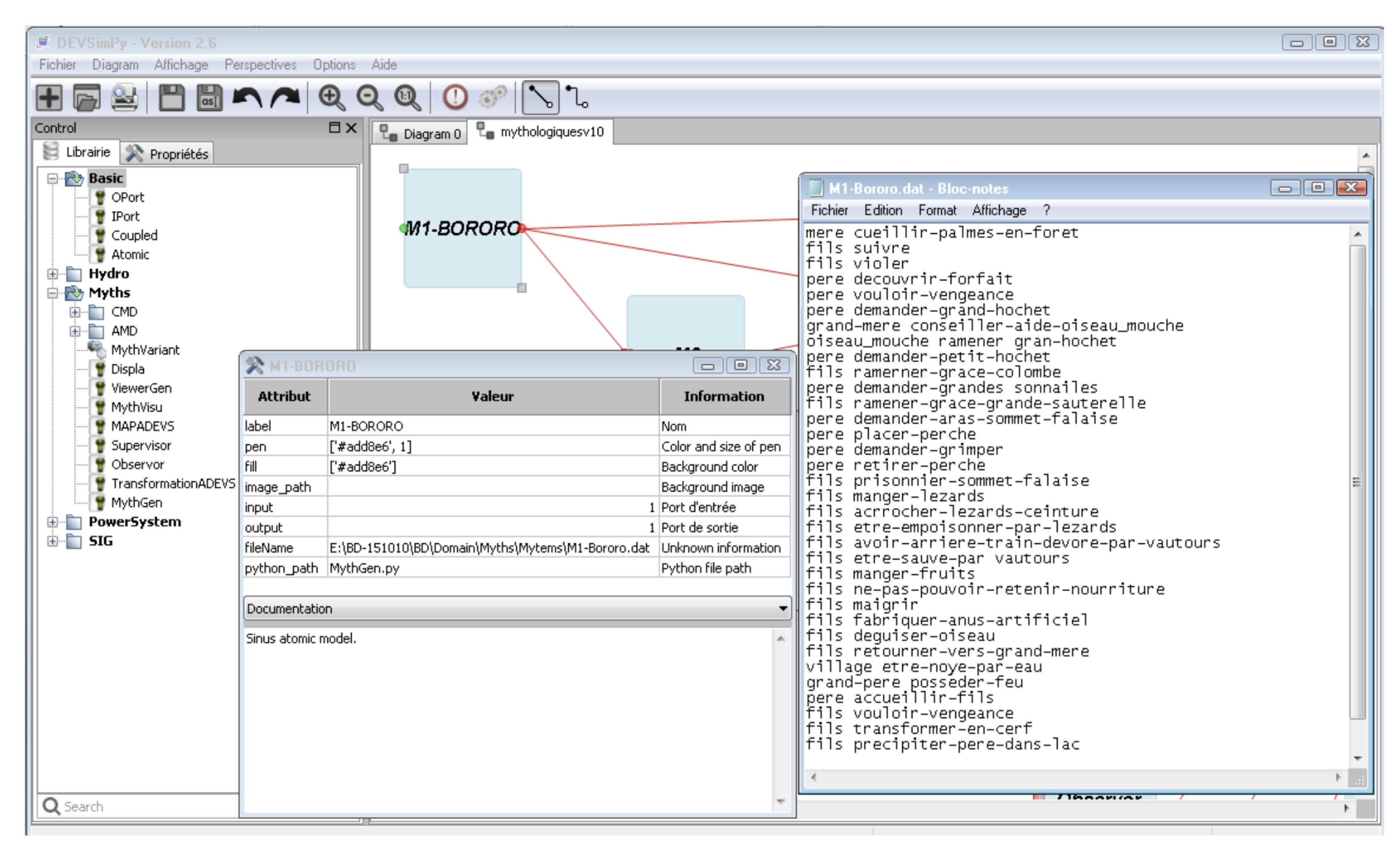
4.2. Definition of an Initial Myth
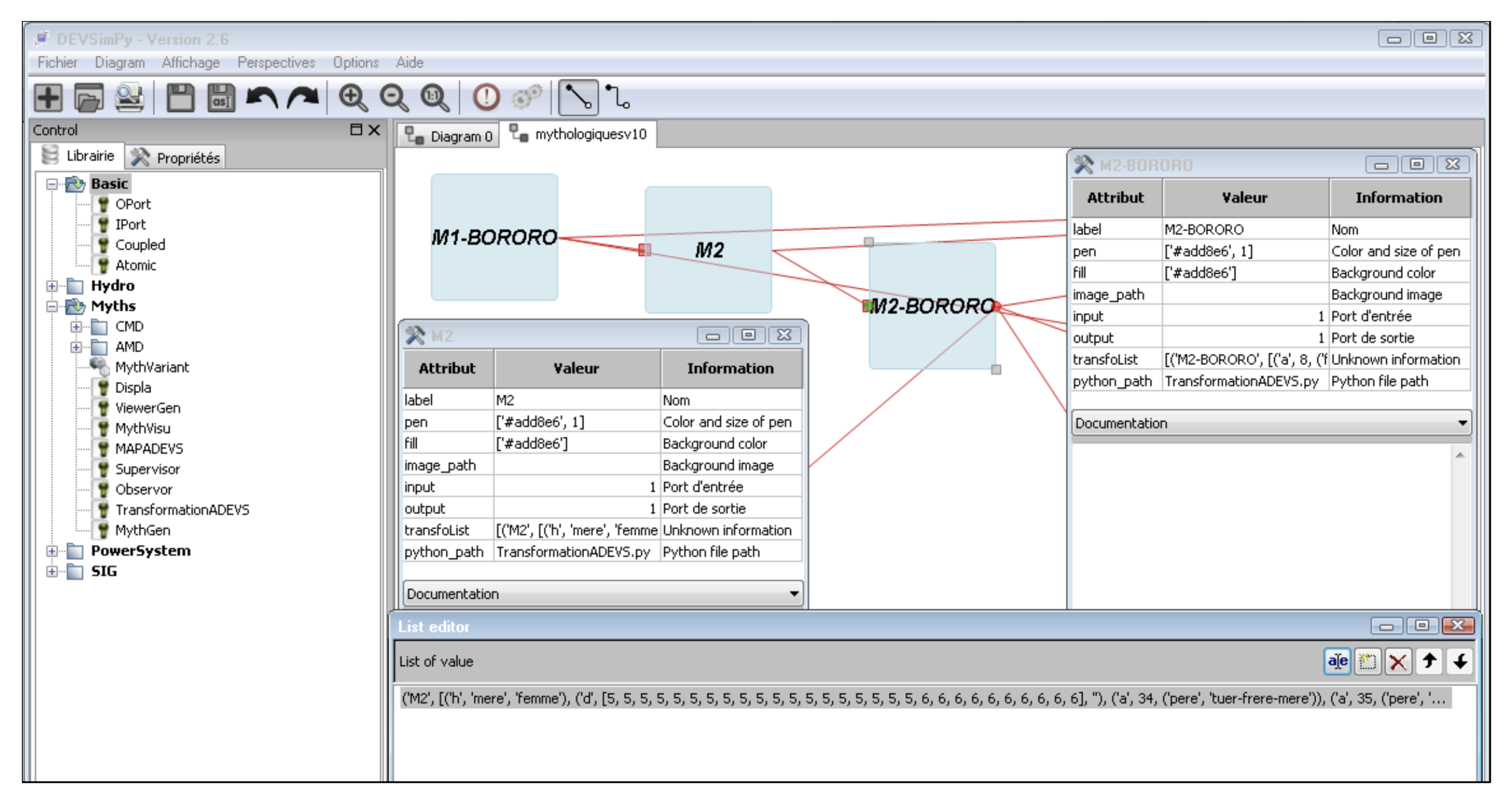
4.3. Generation of a New Myth from a Given Myth
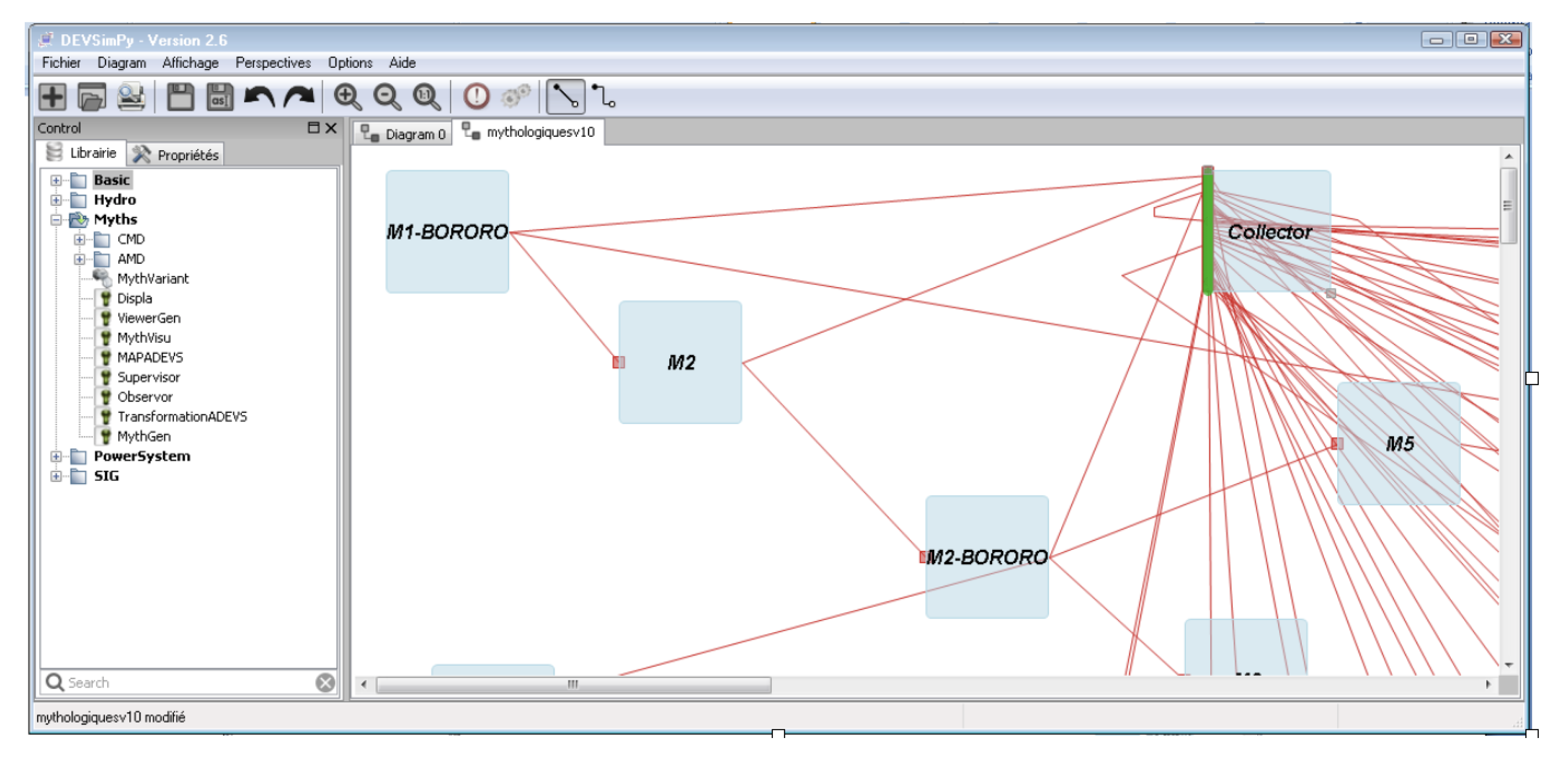
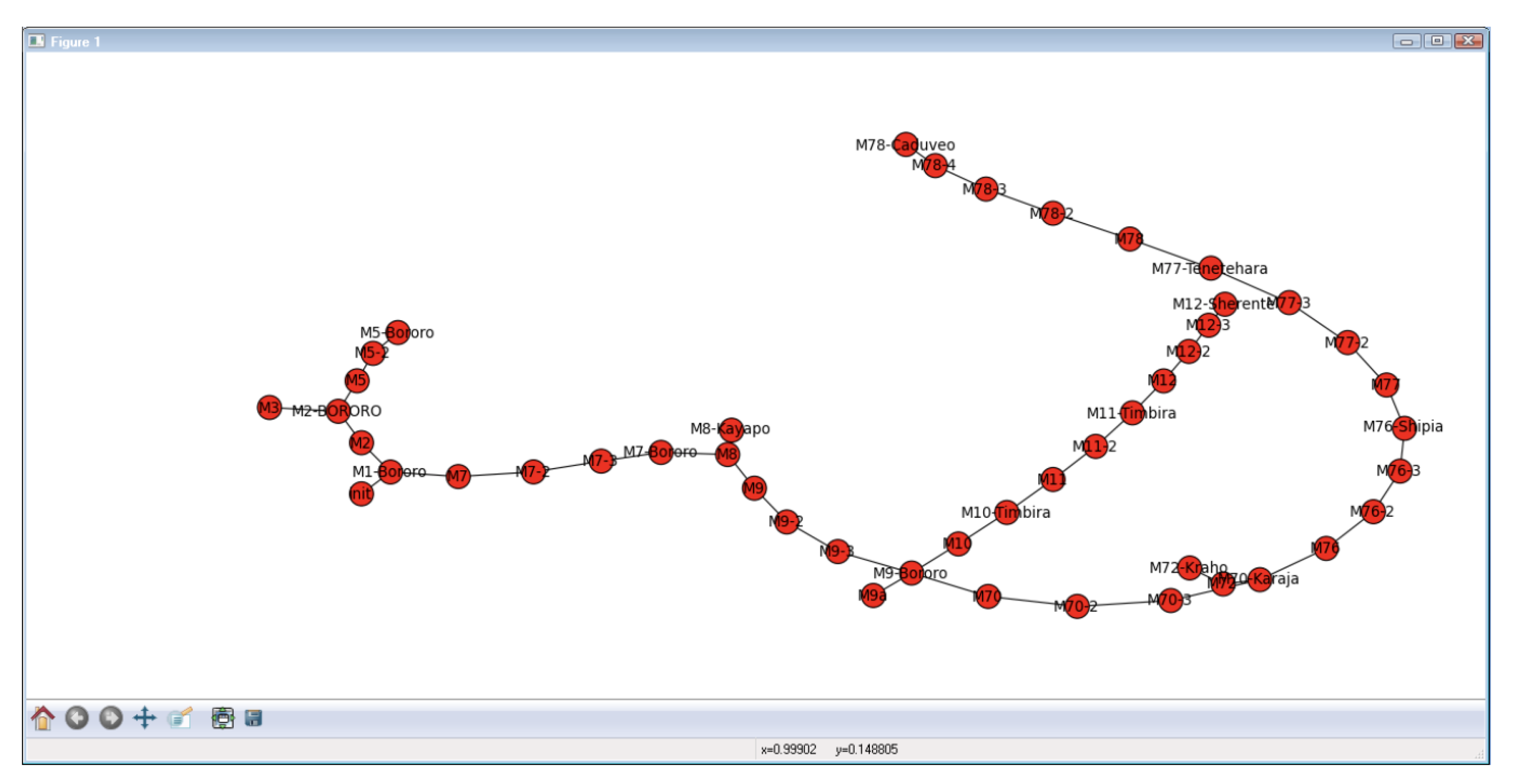
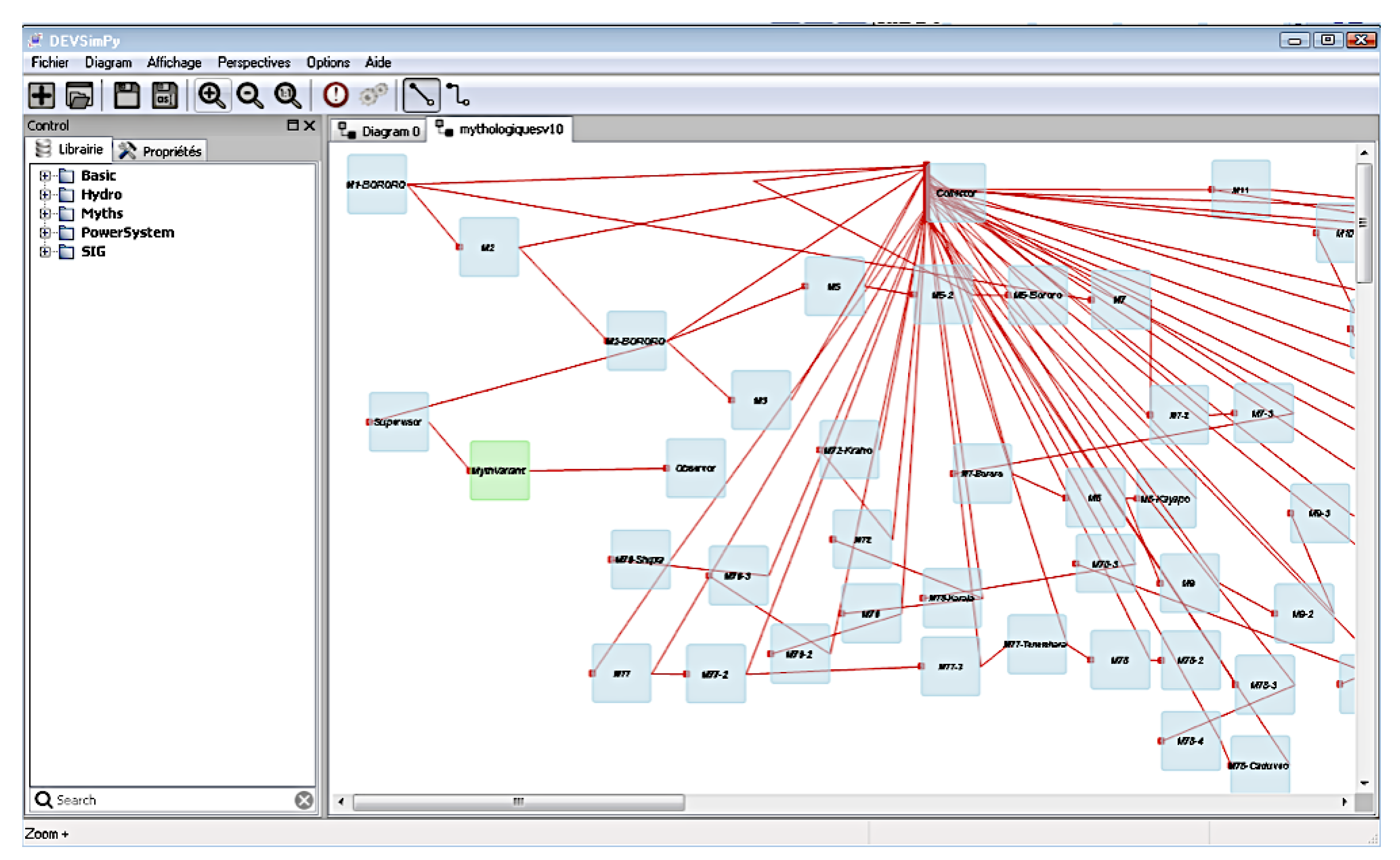
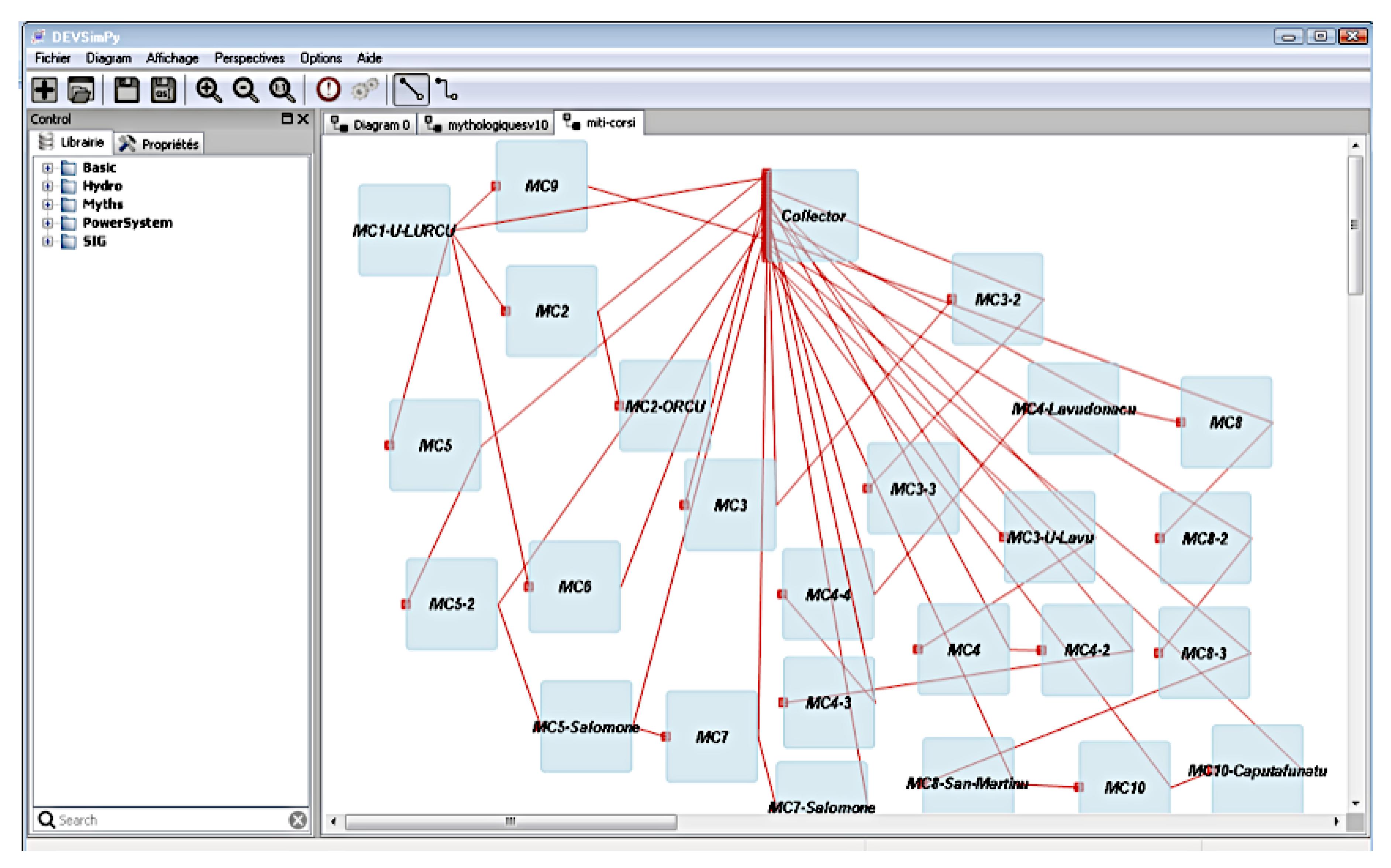
4.4. Visualization of the Set of Transformations Already Performed
5. Validation
- Lib_to_copy_to_Domain_dir which gives the directory containing all the python code dedicated to myths transformation. It must be extracted in the DEVSimPy Domain directory and added to the variable in the
- M1-Bororo.dat which is the file containing the initial myth of the South America myths transformations. It must be used to initialized the attribute of the M1-Bororo DEVS model
- MC1-U-Lurcu.dat which is the file containing the initial myth for the Corsica myths transformations. It must by used as the M1-Bororo model
- MythCLSv7.dsp which is the file to be selected in order to perform the South America myths transformations
- MythsCorsi2020.dsp which is the file to be selected to perform the Corsican myths transformations
- MythsCorsi2020.mp4 which gives a video retracing how to perform myths transformation.
6. Discussion
7. Future Applications
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lévi-Strauss, C. The Structural Study of Myth. J. Am. Folk. 1955, 68, 428–444. [Google Scholar] [CrossRef]
- Zeigler, B.P. Theory of Modeling and Simulation; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Zeigler, B.P.; Praehofer, H.; Kim, T.G. Theory of Modeling and Simulation, 2nd ed.; Academic Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Zeigler, B.P. Object-Oriented Simulation with Hierarchical, Modular Models; Academic Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Zeigler, B.; Muzy, A.; Kofman, E. Theory of Modeling and Simulation: Discrete Event & Iterative System Computational Foundations; Elsevier Science: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Santucci, J.F.; de Gentili, E. Dynamic Variable Structure Modelling and Simulation of the Claude Lévi-Strauss’ Mythical Thought Morphodynamics. In Proceedings of the 2009 Spring Simulation Multiconference, San Diego, CA, USA, 22–27 March 2009. [Google Scholar]
- Santucci, J.F.; de Gentili, E.; Thury-Bouvet, G. Discrete Event Modeling and Simulation of the Mythical Thought Morphodynamics Involved in Claude Lévi-Strauss Structural Analysis. In Handbook of Research on Culturally-Aware Information Technology: Perspectives and Models; Blanchard, E., Allard, D., Eds.; IGI Global: Hershey, PA, USA, 2010; Chapter 8. [Google Scholar]
- Lévi-Strauss, C. The Raw and the Cooked: Introduction to a Science of Mythology; Harper & Row: New York, NY, USA, 1970; Volume 1. [Google Scholar]
- Lévi-Strauss, C. From Honey to Ashes; Harper & Row: New York, NY, USA, 1973. [Google Scholar]
- Lévi-Strauss, C. The Origin of Table Manners; Harper & Row: New York, NY, USA, 1978. [Google Scholar]
- Lévi-Strauss, C. The Naked Man; Harper & Row: New York, NY, USA, 1981. [Google Scholar]
- Capocchi, L.; Santucci, J.F.; Poggi, B.; Nicolai, C. DEVSimPy: A Collaborative Python Software for Modeling and Simulation of DEVS Systems. In Proceedings of the 20th IEEE International Workshops on Enabling Technologies: Infrastructures for Collaborative Enterprises, Paris, France, 27–29 June 2011; pp. 170–175. [Google Scholar] [CrossRef]
- Thury-Bouvet, G.; Santucci, J.F.; Khoumeri, E.H.; Ottavi, A. Orientations of Corsican Dolmens. J. Hist. Astron. 2006, 37, 299–306. [Google Scholar] [CrossRef]
- Doja, A. The Advent of Heroic Anthropology in the History of Ideas. J. Hist. Ideas 2005, 66, 633–650. [Google Scholar] [CrossRef]
- Doja, A. The Shoulders of our Giants: Claude Lévi-Strauss and his Legacy in Current Anthropology. Soc. Sci. Inf. 2006, 45, 79–107. [Google Scholar] [CrossRef]
- Geertz, C. The Cerebral Sauvage: On the Work of Claude Lévi-Strauss. In The Intrepretation of Cultures; Basic Books: New York, NY, USA, 1973; pp. 345–359. [Google Scholar]
- Leach, E. Lévi-Strauss; Fontana/Collins: London, UK, 1970. [Google Scholar]
- Wiseman, B. The Cambridge Companion to Lévi-Strauss; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Mauzé, M.; Harkin, M.; Kan, S. (Eds.) Coming to Shore: Northwest Coast Ethnology, Traditions, and Visions; University of Nebraska Press: Lincoln, NE, USA, 2004; p. 90. [Google Scholar]
- Doja, A. The Kind of Writing: Anthropology and the Rhetorical Reproduction of Postmodernism. Crit. Anthropol. 2006, 26, 157–180. [Google Scholar] [CrossRef]
- Doja, A. Creative Misreading and Bricolage Writing: A Structural Appraisal of a Poststructuralist Debate. Port. Rev. Hist. Book 2007, 11, 89–104. [Google Scholar]
- Doja, A. Claude Lévi-Strauss at his Centennial: Toward a Future Anthropology. Theory Cult. Soc. 2008, 25, 321–340. [Google Scholar] [CrossRef]
- Henaff, M. Adieu à la structure? Esprit 2011, 8–9, 114–119. [Google Scholar] [CrossRef]
- Doja, A. The Predicament of Heroic Anthropology. Anthropol. Today 2006, 22, 18–22. [Google Scholar] [CrossRef]
- Doja, A. Claude Lévi-Strauss (1908–2009): The Apotheosis of Heroic Anthropology. Anthropol. Today 2010, 26, 18–23. [Google Scholar] [CrossRef]
- Levi-Strauss, C. Le totémisme aujourd’hui; Presses Universitaires de France: Paris, France, 1962. [Google Scholar]
- Levi-Strauss, C. The Savage Mind; University of Chicago Press: Chicago, IL, USA, 1966. [Google Scholar]
- Godelier, M. Claude Lévi-Strauss: A Critical Study of His Thought; Verso: London, UK, 2018. [Google Scholar]
- Harkin, M.E. Lévi-Strauss: Two lives. Rev. Anthropol. 2019, 48, 88–102. [Google Scholar] [CrossRef]
- Einstein, A.; Born, M.; Born, H. The Born-Einstein Letters: Friendship, Politics, and Physics In Uncertain Times: Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955 with Commentaries by Max Born; Macmillan: New York, NY, USA, 2005. [Google Scholar]
- Doja, A. Lévi-Strauss’ Heroic Anthropology Facing Contemporary Problems of the Modern World. Rev. Anthropol. 2020, 1–35. [Google Scholar] [CrossRef]
- Doja, A. Celebrations of Lévi-Strauss’s Heroic Legacy. J. R. Anthropol. Inst. 2020, 26, 1–8. [Google Scholar] [CrossRef]
- Diamond, S. The Inauthenticity of Anthropology: The Myth of Structuralism. In Search of the Primitive; a Critique of Civilization; Transaction Books: New Brunswick, NJ, USA, 2018; Chapter 10; pp. 292–331. [Google Scholar]
- Turner, T. On Structure and Entropy: Theoretical Pastiche and the Contradictions of “Structuralism”. Curr. Anthropol. 1990, 31, 563–568. [Google Scholar] [CrossRef]
- Launay, R. Is Lévi-Strauss Still Good to Think? Rev. Anthropol. 2013, 42, 38–49. [Google Scholar] [CrossRef]
- Cargal, J. The Problem with Algebraic Models of Marriage and Kinship Structure. UMAP J. 1996, 22, 345–353. [Google Scholar]
- Le Roux, R. Lévi-Strauss, une réception paradoxale de la cybernétique. L’Homme 2009, 189, 165–190. [Google Scholar] [CrossRef]
- Rauff, J.V. The Algebra of Marriage: An Episode in Applied Group Theory. BSHM Bull. J. Br. Soc. Hist. Math. 2016, 31, 230–244. [Google Scholar] [CrossRef]
- Harrod, J. A Post-Structuralist Revised Weil–Lévi-Strauss Transformation Formula for Conceptual Value-Fields. Sign Syst. Stud. 2018, 46, 255. [Google Scholar] [CrossRef]
- Barbosa-de Almeida, M. Symmetry and Entropy: Mathematical Metaphors in the Work of Lévi-Strauss. Curr. Anthropol. 1990, 31, 367–385. [Google Scholar] [CrossRef]
- Marcus, G.F. The Algebraic Mind: Integrating Connectionism and Cognitive Science; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Morava, J. From Lévi-Strauss to Chaos and Complexity. In On the Order of Chaos: Social Anthropology and the Science of Chaos; Berghahn Books: New York, NY, USA, 2005; pp. 47–63. [Google Scholar]
- Lafontaine, C. The Cybernetic Matrix of ‘French Theory’. Theory Cult. Soc. 2007, 24, 27–46. [Google Scholar] [CrossRef]
- Geoghegan, B.D. From Information Theory to French Theory: Jakobson, Lévi-Strauss, and the Cybernetic Apparatus. Crit. Inq. 2011, 38, 96–126. [Google Scholar] [CrossRef]
- Lévi-Strauss, C. The Jealous Potter; University of Chicago Press: Chicago, IL, USA, 1988. [Google Scholar]
- Lévi-Strauss, C. The Story of Lynx; University of Chicago Press: Chicago, IL, USA, 1996. [Google Scholar]
- Thom, R. Stabilité structurelle et morphogénèse: Essai d’une théorie générale des modèles; Interéditions: Paris, France, 1972. [Google Scholar]
- Thom, R. Modèles mathématiques de la morphogenèse; Christian Bourgeois Edition: Paris, France, 1981. [Google Scholar]
- Petitot, J. Approche morphodynamique de la formule canonique du mythe. L’Homme 1988, 28, 106–107. [Google Scholar] [CrossRef]
- Petitot, J. Note complémentaire sur l’approche morphodynamique de la formule canonique du mythe. L’Homme 1995, 35, 17–23. [Google Scholar] [CrossRef]
- Mosko, M.S. The Canonic Formula of Myth and Nonmyth. Am. Ethnol. 1991, 18, 126–151. [Google Scholar] [CrossRef]
- Côté, A. Qu’est-ce que la formule canonique? L’Homme 1995, 35, 35–41. [Google Scholar] [CrossRef][Green Version]
- Désveaux, E. Groupe de Klein et formule canonique. L’Homme 1995, 35, 43–49. [Google Scholar] [CrossRef]
- Scubla, L. À propos de la formule canonique, du mythe, et du rite. L’Homme 1995, 35, 51–63. [Google Scholar] [CrossRef]
- Scubla, L. Lire Lévi-Strauss: Le déploiement d’une intuition; Odile Jacob.: Paris, France, 1998. [Google Scholar]
- Marcus, S. The Togical and Semiotic Status of the Canonic Formula of Myth. Semiotica 1997, 116, 115–188. [Google Scholar] [CrossRef]
- Maranda, P. The Double Twist: From Ethnography to Morphodynamics; University of Toronto Press: Toronto, ON, Canada, 2001. [Google Scholar]
- Morava, J. Une interprétation mathématique de la formule canonique de Claude Lévi-Strauss. Cahier de L’Herne 2004, 88, 216–218. [Google Scholar]
- Propp, V.I. Morphology of the Folktale; University of Texas Press: Austin, TX, USA, 1968. [Google Scholar]
- Greimas, A. Sémantique Structurale: Recherche de Méthode; Larousse: Paris, France, 1966. [Google Scholar]
- Petitot, J. Cognitive Morphodynamics—Dynamical Morphological Models of Constituency in Perception and Syntax; Lang: Bern, Switzerland, 2011. [Google Scholar]
- Jason, H.; Segal, D. Patterns in Oral Literature; Mouton: The Hague, The Netherlands, 1977. [Google Scholar]
- Richard, P.; Jaulin, R. Anthropologie et calcul; 10/18; Union Générale: Lyon, France, 1971. [Google Scholar]
- Haskell, R.; Badalamenti, A. Algebraic Structure of Verbal Narratives with Dual Meanings. Math. Comput. Model. 2003, 37, 383–393. [Google Scholar] [CrossRef]
- Haskell, R. A Logico-mathematic, Structural Methodology: Part II, Experimental Design and Epistemological Issues. J. Mind Behav. 2003, 24, 401–421. [Google Scholar]
- Haskell, R. A Logico-mathematic, Structural Methodology: Part III, Theoretical, Evidential, and Corroborative Bases of a New Cognitive Unconscious for Sub-literal (SubLit) Cognition and Language. J. Mind Behav. 2004, 25, 287–321. [Google Scholar]
- Haskell, R. Claude Lévi-Strauss Reconsidered: Cognitive science, epistemology, and the (not so savage) algebraic mind. Cogn. Semiot. 2008, 2008, 65–90. [Google Scholar] [CrossRef]
- Hobbs, R.L.; Potts, C. Hyperscenarios: A Framework for Active Narrative. In Proceedings of the 38th Annual Southeast Regional Conference, Clemson, CA, USA, 7–8 April 2000; pp. 201–210. [Google Scholar] [CrossRef]
- Kato, T.; Miyazaki, K.; Nakatsu, R. Analysis of Japanese folktales for the purpose of story generation. In Proceedings of the 3rd International Conference on Digital Interactive Media in Entertainment and Arts, ACM International Conference Proceeding Series, Athens, Greece, 10–12 September 2008; Volume 349, pp. 415–419. [Google Scholar]
- Santucci, J.F.; Capocchi, L.; Zeigler, B.P. System Entity Structure Extension to Integrate Abstraction Hierarchies and Time Granularity into DEVS Modeling and Simulation. Simulation 2016, 92, 747–769. [Google Scholar] [CrossRef]
- Santucci, J.F.; Capocchi, L. Visualization of Folktales on a Map by Coupling Dynamic DEVS Simulation within Google Earth. In Simultech; SciTePress: Setubal, Portugal, 2011; pp. 128–133. [Google Scholar]
- Bolduc, J.S.; Vangheluwe, H. The Modelling and Simulation Package PythonDEVS for Classical Hierarchical DEVS; MSDL Technical Report MSDL-TR-2001–01; McGill University: Montreal, QC, Canada, 2001. [Google Scholar]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Giannesini, G.; Luccioni, P. Religiosité,croyances et rituels populaires; Albiana éditions: Ajaccio, France, 2010. [Google Scholar]
- Desveaux, E. Spectres de l’anthropologie. Suite nord-américaine; Lieux-d’être: Montreuil, France, 2007. [Google Scholar]
- Desveaux, E. La parole et la substance: Anthropologie comparée de l’Amérique et de l’Europe; Indes-Savantes: Paris, France, 2017. [Google Scholar]
- Désveaux, E. Quadratura americana, Essai d’anthropologie lévi-straussienne; Georg: Geneve, Switzerland, 2001. [Google Scholar]
- Asch, M. Levi-Strauss and the Political: The Elementary Structures of Kinship and the Resolution of Relations Between Indigenous People and Settler States. J. R. Anthropol. Inst. 2005, 11, 425–444. [Google Scholar] [CrossRef]
- Marchart, O. Ungesellschaftliche Gesellschaftlichkeit: Exklusion und Antagonismus bei Lévi-Strauss, unter Berücksichtigung von Lacan, Laclau und Luhmann. Soz. Syst. 2008, 14, 370–396. [Google Scholar] [CrossRef]
- Constable, N. The Commodification of Intimacy: Marriage, Sex, and Reproductive Labor. Annu. Rev. Anthropol. 2009, 38, 49–64. [Google Scholar] [CrossRef]
- Latour, B. Face a Gaia. Huit conférences sur le nouveau regime climatique; La Decouverte: Paris, France, 2015. [Google Scholar]
- Tsing, A.L. The Mushroom at the End of the World: On the Possibility of Life in Capitalist Ruins; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Eriksen, T.H. Overheating: An Anthropology of Accelerated Change; London: Pluto, UK, 2016. [Google Scholar]
- Doja, A. Social Morphodynamics: Mapping Identity Transformations, Cultural Encounters, and the Evolution of Core Values. Soc. Epistemol. Rev. Reply Collect. 2018, 7, 14–25. [Google Scholar]
- Doja, A. Invitation au Terrain: Mémoire personnel de la construction du projet socio-anthropologique; Peter Lang: Bruxelles, Belgium, 2013. [Google Scholar] [CrossRef]
- Doja, A. Naître et grandir chez les Albanais: La Construction Culturelle de la Personne; L’Harmattan: Paris, France, 2000; p. 324. [Google Scholar]
- Doja, A. Socializing Enchantment: A socio-anthropological approach to infant-directed singing, music education and cultural socialization. Int. Rev. Aesthet. Sociol. Music 2014, 45, 115–147. [Google Scholar]
- Doja, A. Instrumental borders of gender and religious conversions in the Balkans. Relig. State Soc. 2008, 36, 55–63. [Google Scholar] [CrossRef]
- Doja, A. Fertility Trends, Marriage Patterns and Savant Typologies in Albanian Context. J. Fam. Hist. 2010, 35, 346–367. [Google Scholar] [CrossRef] [PubMed]
- Doja, A. Politics of Mass Rapes in Ethnic Conflict: A Morphodynamics of raw Madness and Cooked Evil. Crime Law Soc. Chang. 2019, 71, 541–580. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santucci, J.-F.; Doja, A.; Capocchi, L. A Discrete-Event Simulation of Claude Lévi-Strauss’ Structural Analysis of Myths Based on Symmetry and Double Twist Transformations. Symmetry 2020, 12, 1706. https://doi.org/10.3390/sym12101706
Santucci J-F, Doja A, Capocchi L. A Discrete-Event Simulation of Claude Lévi-Strauss’ Structural Analysis of Myths Based on Symmetry and Double Twist Transformations. Symmetry. 2020; 12(10):1706. https://doi.org/10.3390/sym12101706
Chicago/Turabian StyleSantucci, Jean-Francois, Albert Doja, and Laurent Capocchi. 2020. "A Discrete-Event Simulation of Claude Lévi-Strauss’ Structural Analysis of Myths Based on Symmetry and Double Twist Transformations" Symmetry 12, no. 10: 1706. https://doi.org/10.3390/sym12101706
APA StyleSantucci, J.-F., Doja, A., & Capocchi, L. (2020). A Discrete-Event Simulation of Claude Lévi-Strauss’ Structural Analysis of Myths Based on Symmetry and Double Twist Transformations. Symmetry, 12(10), 1706. https://doi.org/10.3390/sym12101706





