An Improved Local Search Genetic Algorithm with a New Mapped Adaptive Operator Applied to Pseudo-Coloring Problem †
Abstract
1. Introduction
2. Related Works
3. Mathematical Formulation of Pseudo-Coloring Problem
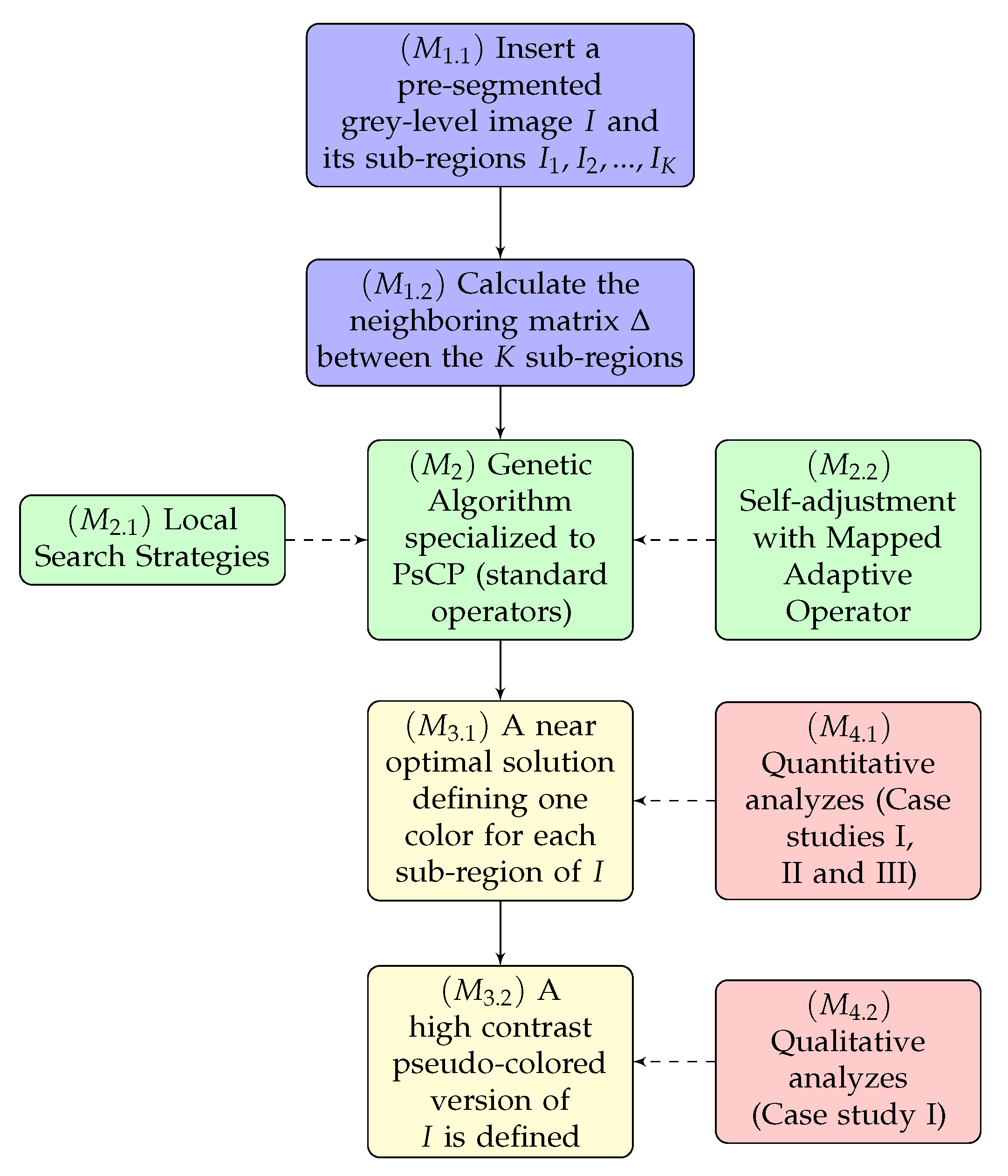
4. Methodology
- Domain definition: This phase consists of defining the image in grey-levels that must be pseudo-colored by our technique.
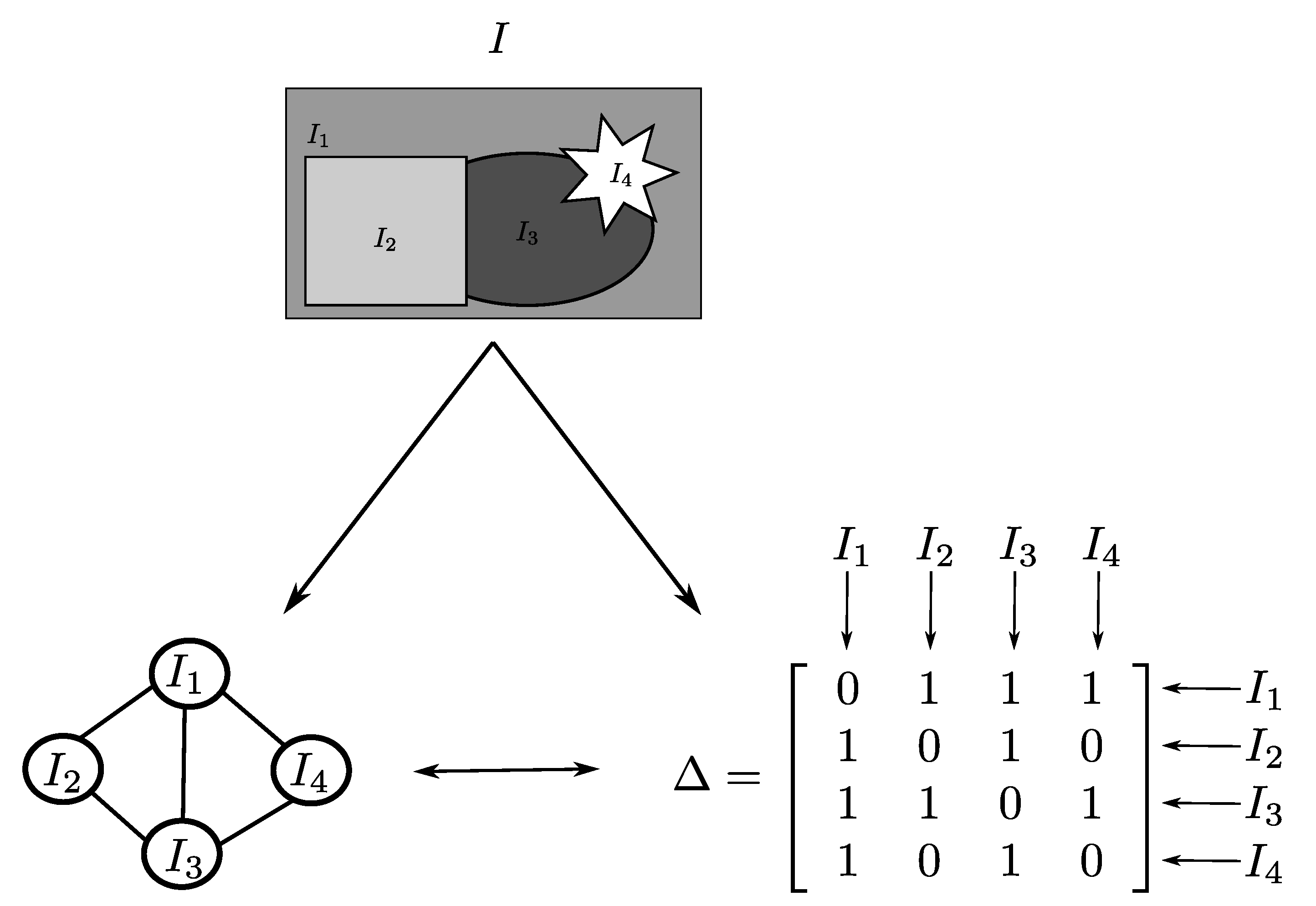
- However, all results can be easily extended to consider classes of images that have not passed any segmentation process, given the advances achieved in recent years in the area of image segmentation [42,43,44]. This type of consideration is outside the scope of the paper, so we will assume in this work that the method must work on an image in grey levels I pre-segmented into K sub-regions.
- Once we have the pre-segmented image I, we need to define the neighborhood matrix of this image so that the algorithm can perform the optimization having the information of which subregions of I are neighbors to each other and, consequently, they are assigned different colors.
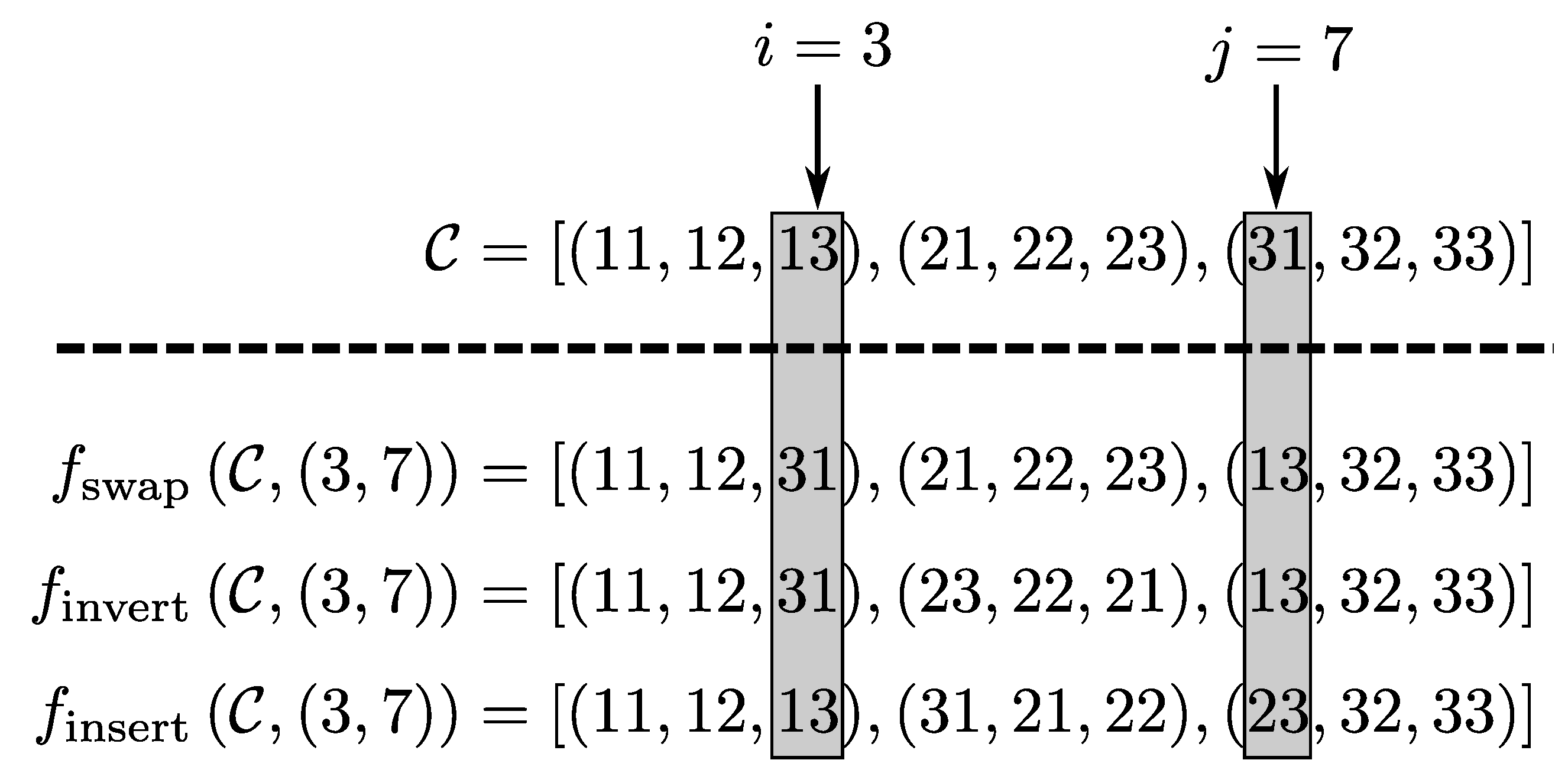
- Proposed optimization method: In this step of the methodology, we use the proposed meta-heuristic, which consists of a genetic algorithm that was specifically designed to search in a color space for an optimal solution for PsCP. Our main contributions to the method are given in the form of two operators:
- Local search strategies: As in our preliminary work [21], we will also use local search strategies in our GA in two operators: the mutation operator and an exclusive operator dedicated to conducting a local search with massive behavior.
- Adaptive rules: In this text, we generalize the use of the rules for self-adaptation of parameters proposed in our preliminary work [21] having as inspiration ideas that have been successfully used in other classes of combinatorial optimization problems [20]. In this case, we make use of mapping functions to automate the way that mutation and crossing rates are updated in the course of GA iterations.
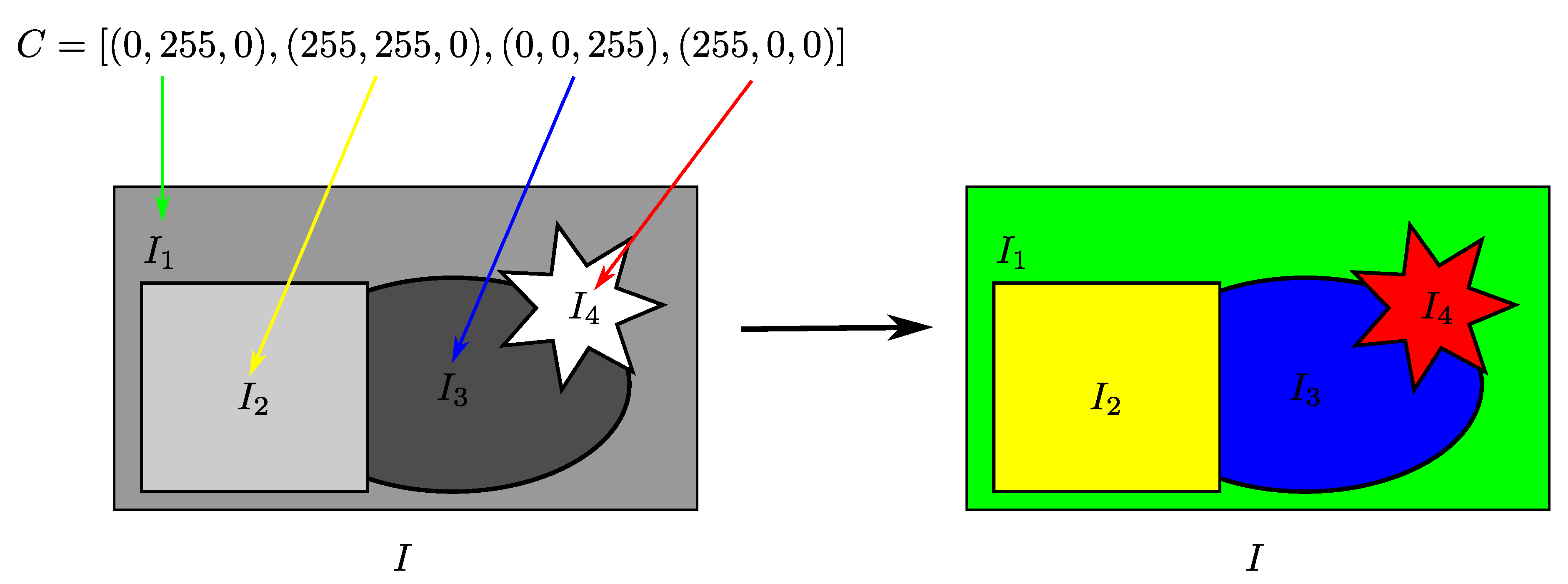
- Algorithm responses: After the optimization process carried out by our technique, we obtain two types of responses: a numerical and vector solution in the K-dimensional color space () and the pseudo-colored image (). In the first case, we have numerical and quantitative information on how different are the colors attributed to I, calculated from the measures of Radlak and Smolka [14]. In the second case, the method must establish the pseudo-colored version of I from the obtained vector solution.
- Validation scenarios: In our methodology, we will validate the solutions found by our meta-heuristics in a quantitative () and in a qualitative () ways through three different case studies (CS):
- -
- CS I: In the first CS, we will compare the quantitative and qualitative results obtained by our method that represent information on how distant the colors attributed to the I regions are in the CIELAB space and compare the results with the most recent color-coding techniques available in the specialized literature.
- -
- CS II: In the second CS, we will compare the quantitative results obtained by our method in 24 synthetic and abstract unreal images in comparison to the other existing techniques in this field of study.
- -
- CS III: In the third CS, we we will compare the quantitative results obtained by our method considering the Munsell atlas color space in comparison to the other existing techniques in the specialized literature.
5. Mapped Local Search Adaptive Genetic Algorithm for PsCP
- A new self-parameter adjustment operator [17] to avoid well-known problems in GA such as premature convergence and getting stuck in local optima. In addition, we present the generalization of our preliminary adaptive strategy from [21] using mapping functions, which proved to be favorable in studies related to other types of combinatorial optimization [19,20].
- The advancement of experimental results in benchmarks that define the state-of-the-art.
5.1. Chromosome Decoding
5.2. Fitness Function
- Both and are defined taking into account the neighborhood matrix . That is, both functions are defined from the image structure that we intend to color.
- The main difference between and is that the first one takes into account the order of the coordinates in the chromosome C, while the second one acts on a set . Didactically, it is simpler to reproduce and, therefore, we define the fitness function in this way.
- The meta-heuristic that finds the greatest values assumed by will find possible solutions to the problem presented in Equation (4), since these two situations consist of determining K colors with the greatest possible visual dissimilarity. In this way, the feasibility and the equivalence of the problem are maintained.
5.3. Selection Process
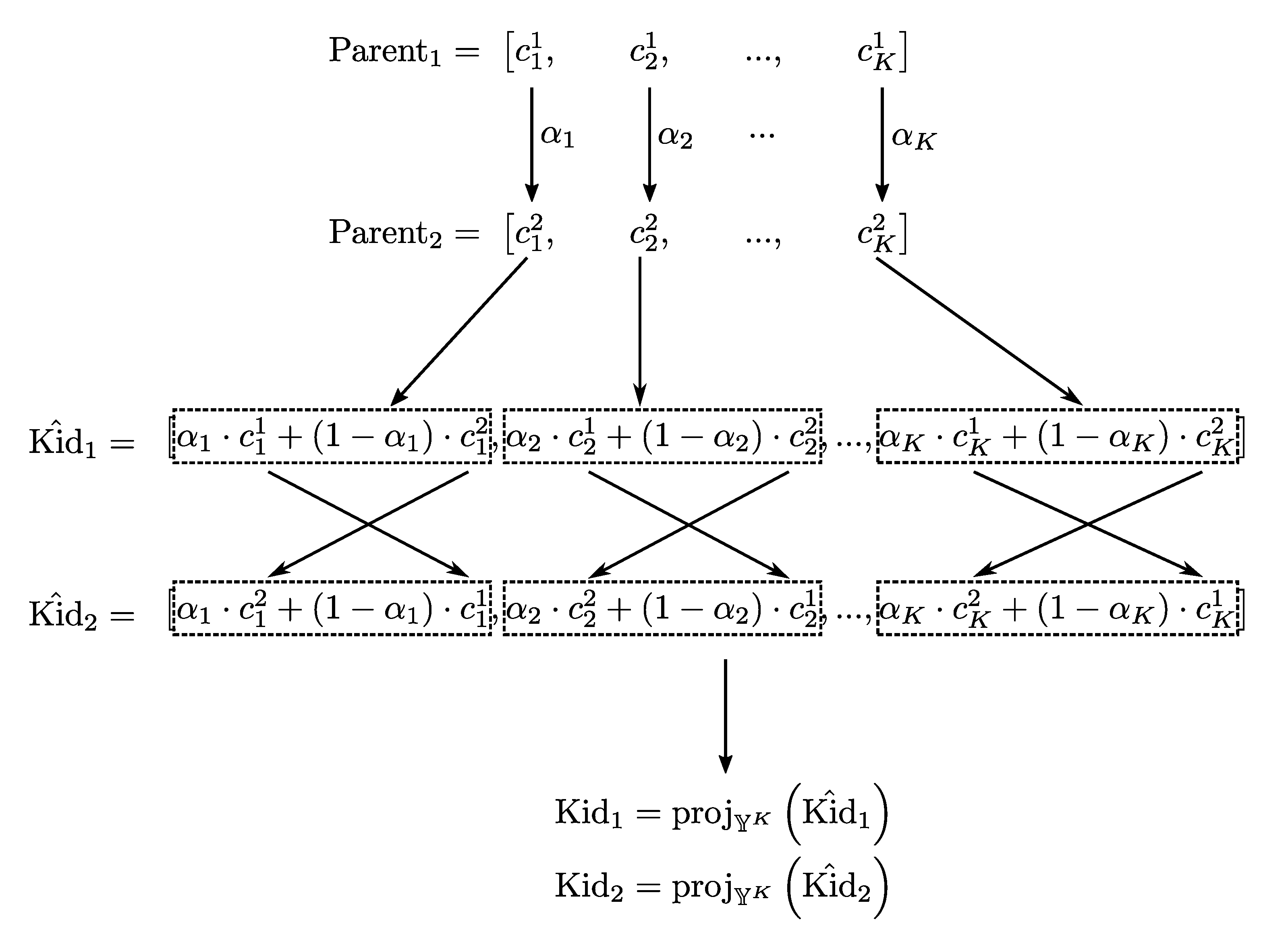
5.4. Crossover Operator
5.5. Mutation Operator
- : In this routine, a mutation function is randomly taken into a set of mutation functions, and, using this function, perturbations are performed on the chromosome, so that the good perturbations are maintained and the bad ones are ignored.
- : In this routine, a simple Gaussian mutation is applied to the chromosome.
| Algorithm 1 Proposed mutation operator. | ||
| Input: | Offsprings generated in crossover | |
| Fitness function | ||
| Probability of mutation | ||
| Probability of | ||
| Number of mutation function applications for | ||
|
1: ▹ The function randomly returns an element from a set. 2: 3:for do 4: if then ▹ Apply mutation in percent of kids. 5: break 6: else if then ▹ Apply in percent of cases. 7: 8: for to do ▹ Apply times. 9: 10: 11: 12: 13: if then ▹ If the perturbation is beneficial, then it must be maintained. 14: 15: 16: end if 17: end for 18: else ▹ () Apply only once. 19: 20: end if 21: 22:end for | ||
| Output: | Population of mutated individuals | |
5.6. Massive Local Search Operator
- Step 1: The color receives a random increase, making it lighter.
- Step 2: The perturbation is maintained only if it is beneficial, increasing the fitness value of .
- Step 3: If was not modified in the previous step, then a random decrease in is applied, making it darker.
- Step 4: The perturbation should be maintained if it is beneficial.
| Algorithm 2 Proposed massive search operator. | ||
| Input: | Best chromosome in the population | |
| Fitness function | ||
| 1: for to K do 2: ▹ Initially, is equal to . 3: 4: ▹ (Step 1) Random increase. 5: 6: if then ▹ (Step 2) If the perturbation is beneficial, then update to . 7: 8: else ▹ If the increase wasn’t beneficial, then try apply a decrease on . 9: ▹ (Step 3) Random decrease. 10: 11: if then ▹ (Step 4) If the perturbation is beneficial, then update to . 12: 13: end if 14: end if 15: end for 16: ▹ The new chromosome is updated considering only the perturbations that were beneficial and contributed to improving the fitness value of | ||
| Output: | Best individual in the neighborhood of | |
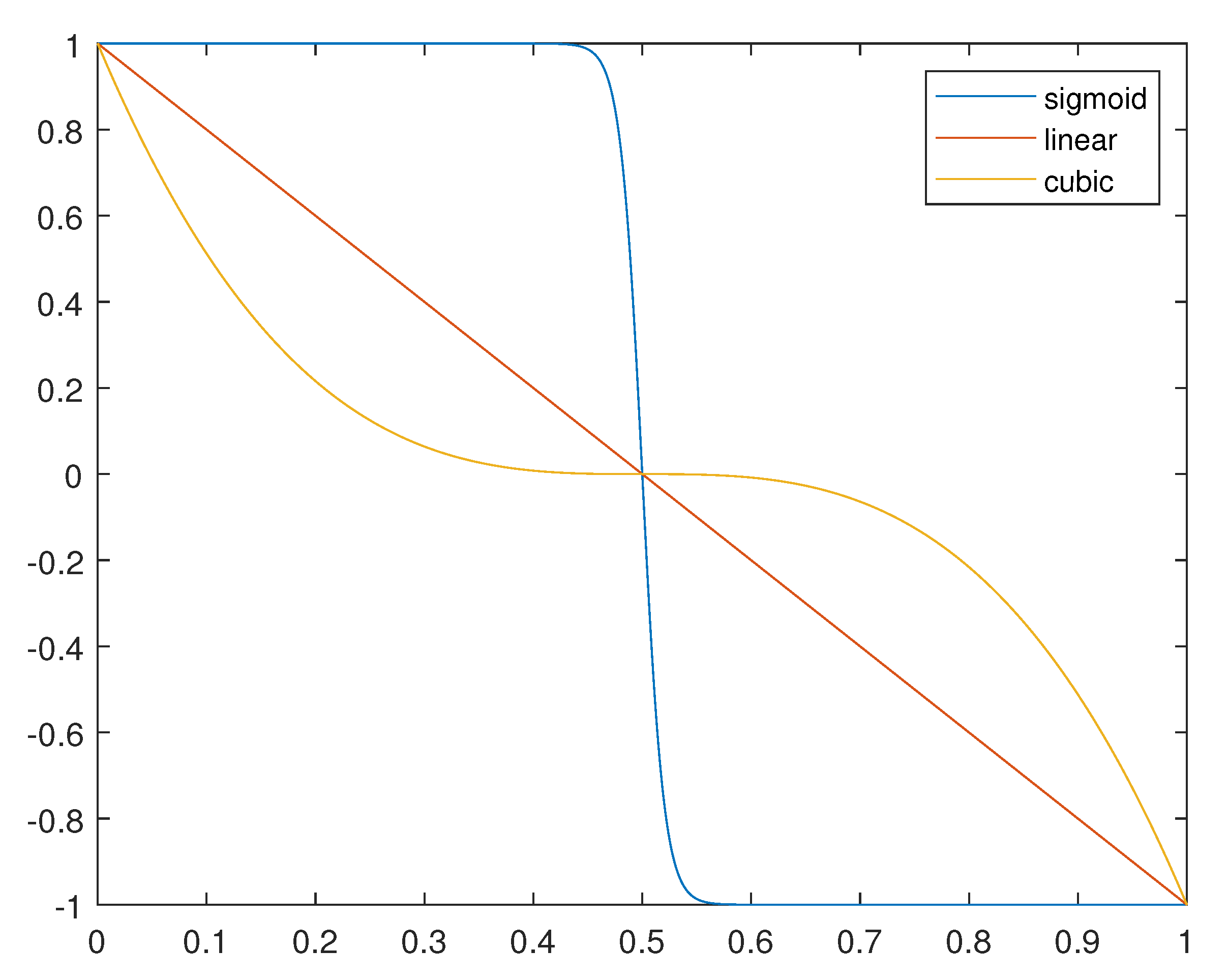
5.7. Mapped Adaptive Rules
- Fact 1: The statistical measures used are calculated using the vectors and . Since the coordinates of these vectors are contained in the interval due to the normalization caused by the multiplication of the factor , then all the statistical measures are contained in the interval . In this way, each one of the four addends of can account for a maximum of and, therefore, the values assumed by the function are contained in the range .
- Fact 2: If there are no changes between two consecutive generations, then there will be no differences between and . Thus, and, therefore, .
- Fact 3: From the two previous facts, we can easily deduce that the greater the differences between the fitness of two consecutive generations, the closer to 1 will be the value of associated with these values of fitness. At the same time, the more similar the fitness values of two consecutive generations, the closer to zero will be the respective value of . This means that the function defined in Equation (12) is able to establish a good numerical correspondence between changes in fitness values between two consecutive populations and can be used as an indicator of population stagnation.
- Situation 1: There are signs of stagnation in relation to the populations and : In this case, we will have and, to reverse this situation we are going to increase the mutation rate and decrease the crossover rate.
- Situation 2: There is a significant improvement in the population compared to the population . In this case, we will have and, therefore, we can start to return the mutation and crossover rates to their initially defined values. For that, we must decrease the mutation rate and increase the crossover rate.
5.8. Proposed Algorithm
- Step 1
- A population of chromosomes must be generated, each of which must be defined by K colors taken randomly in space ;
- Step 2
- Select individuals taking into account their fitness values for the crossover operator;
- Step 3
- Evaluate these individuals;
- Step 4
- Randomly select individuals to undergo mutation;
- Step 5
- Select the best individual among all those considered so far;
- Step 6
- Massively search its neighborhood for individuals with a better fitness value;
- Step 7
- Adjust the method parameters with the adaptation operator;
- Step 8
- Create a new population and evaluate it;
- Step 9
- If the maximum number of iterations has not been reached, then you need to go back to step 2.
6. Experiments and Results
6.1. Setup and Implementation
6.2. Case Study I: Qualitative and Quantitative Analysis Considering Real World Images and
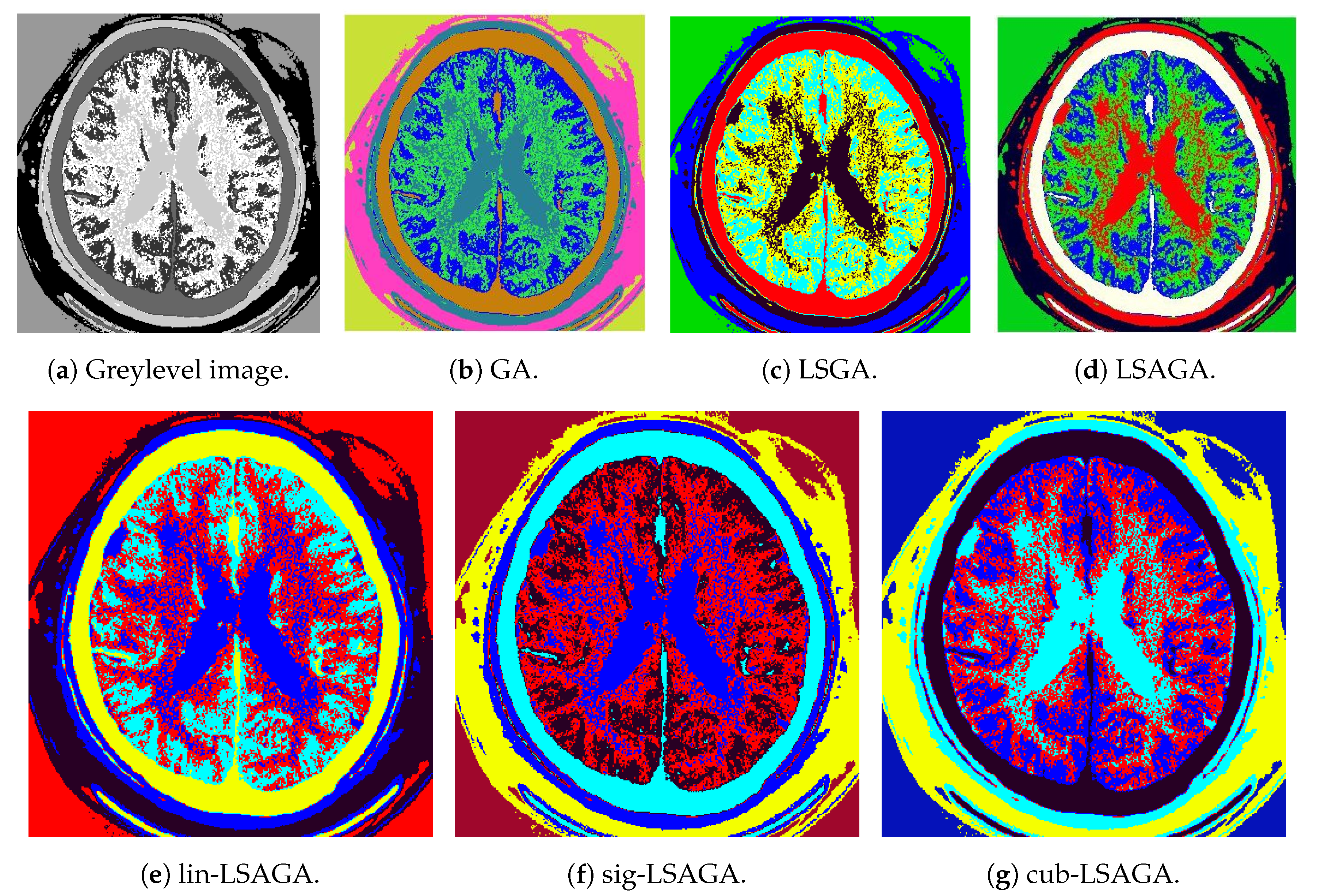
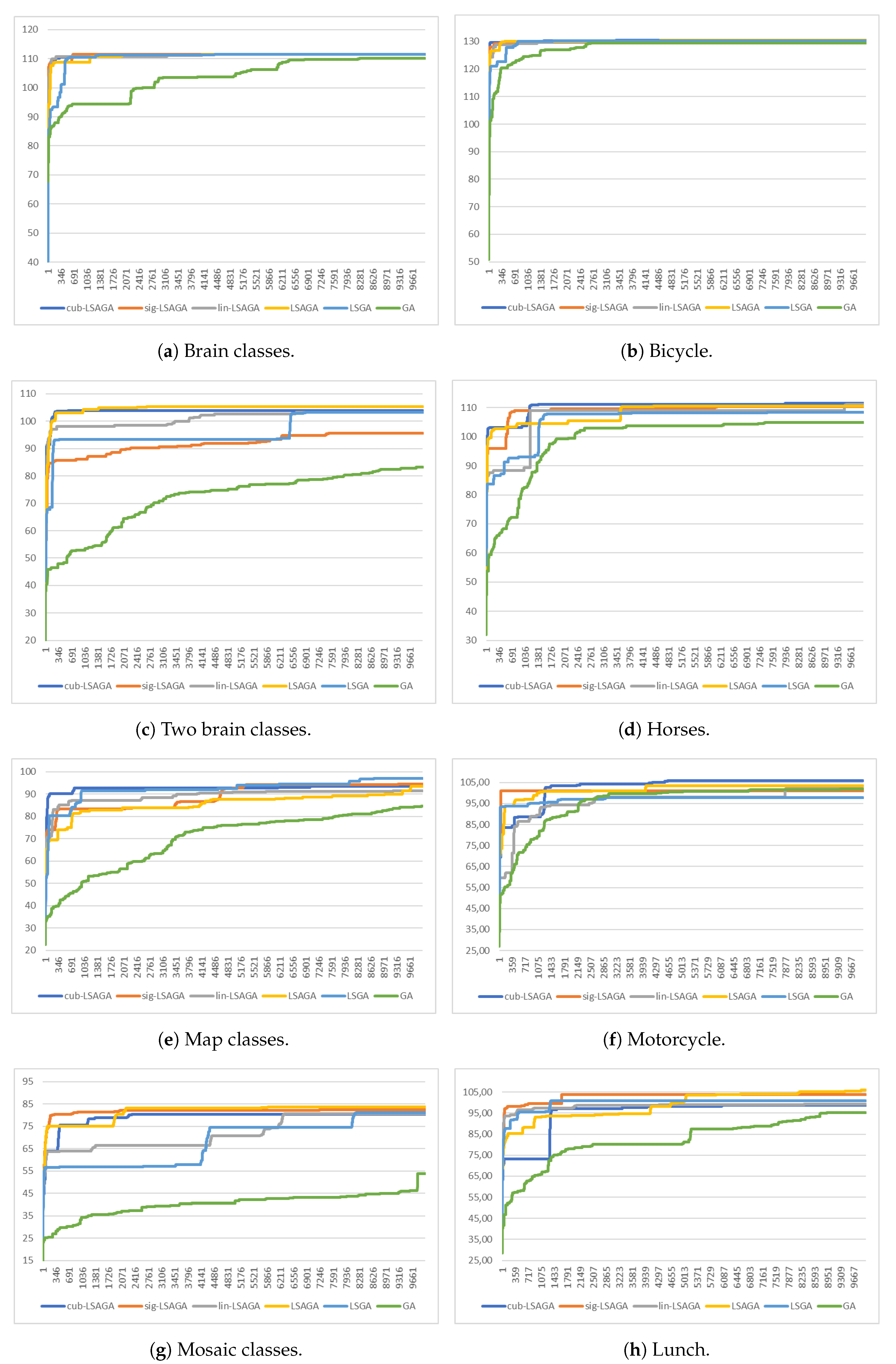
- Brains: This image is not very complex, as it has only six sub-regions. However, we can see that, in the case of the pseudo-colorization obtained by GA (Figure 9b), the colors used in the central part of the brain are two different shades of green, which can cause some visual confusion. This does not occur with the pseudo-colorizations obtained by the other methods.
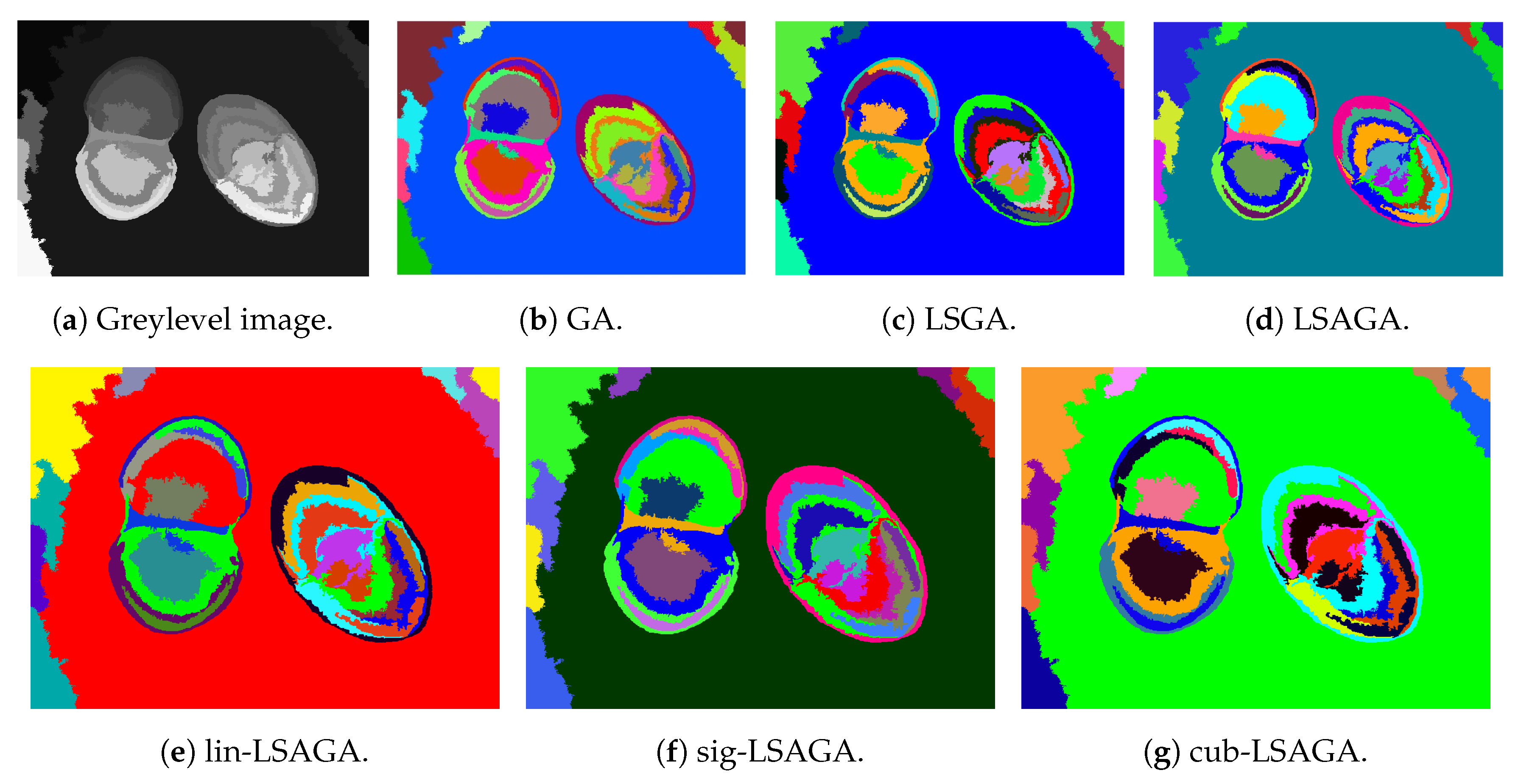
- Two Brains: Concerning the images of the Two Brains, we can see that basic GA (Figure 10b) obtains a reasonably good visual separation between the sub-regions, presenting some confusion only with the colored regions in shades of red and pink in the central-left region of the image. In the pseudo-colorized image calculated by the LSGA method, there is also a confusion problem as well as in the basic GA. When analyzing Figure 10c, the central right region has a dark blue color very close to a region that was colored with black. These problems do not occur in the pseudo-colorization performed by the proposed technique with the addition of adaptive rules.
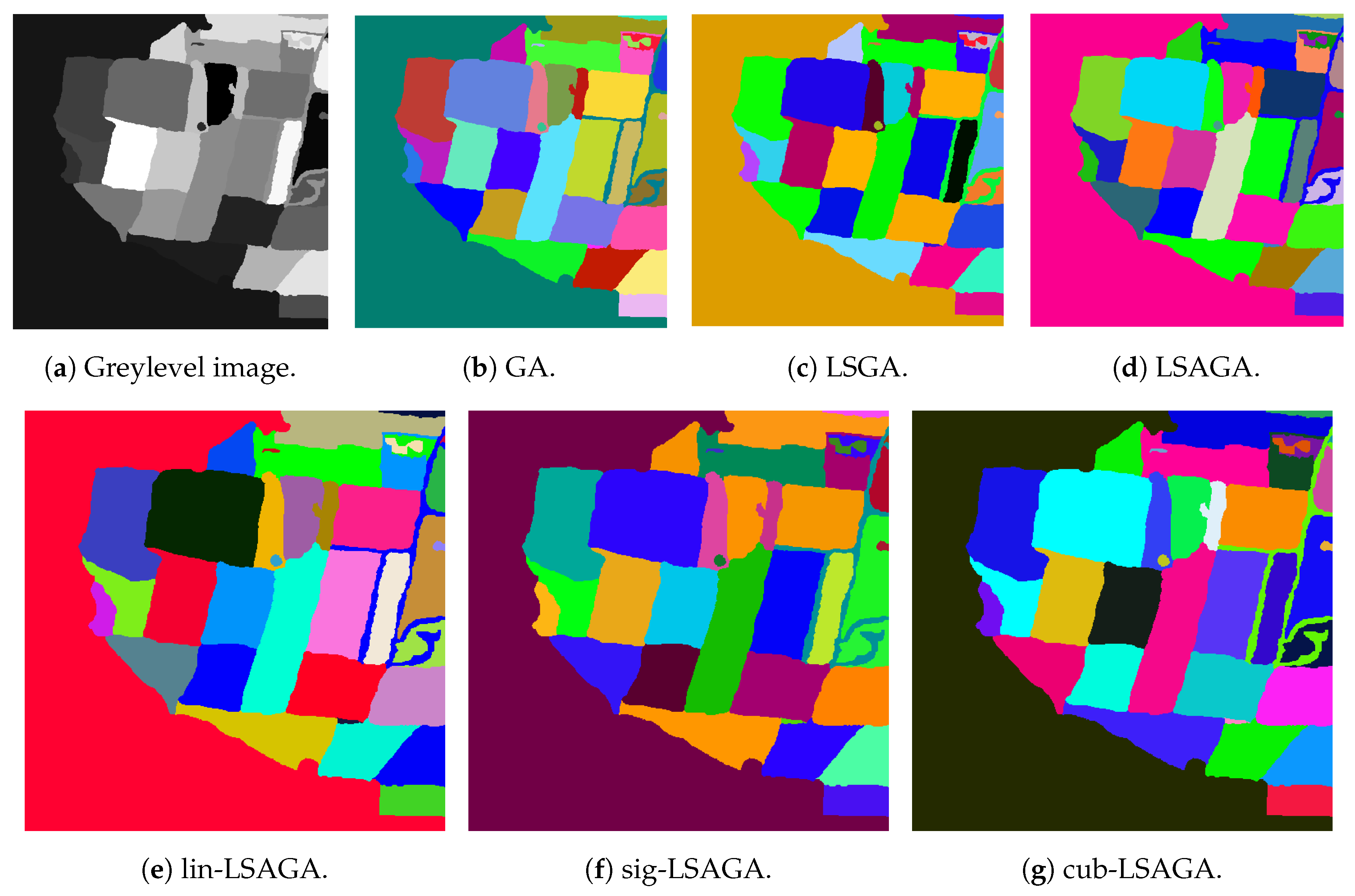
- Maps: All methods used many shades of blue to pseudo-color this image, which can cause some visual confusion. For example, in the top-right section of the pseudo-colored image using the LSAGA technique (Figure 11d), we can see three colored regions with similar shades of blue. In addition, the pseudo-colored image with GA (Figure 11b) presents more serious issues. In detail, note that there is a small circular subregion in the right section of all pseudo-colored images, however, this subregion is almost visually imperceptible in the pseudo-colored image with GA.
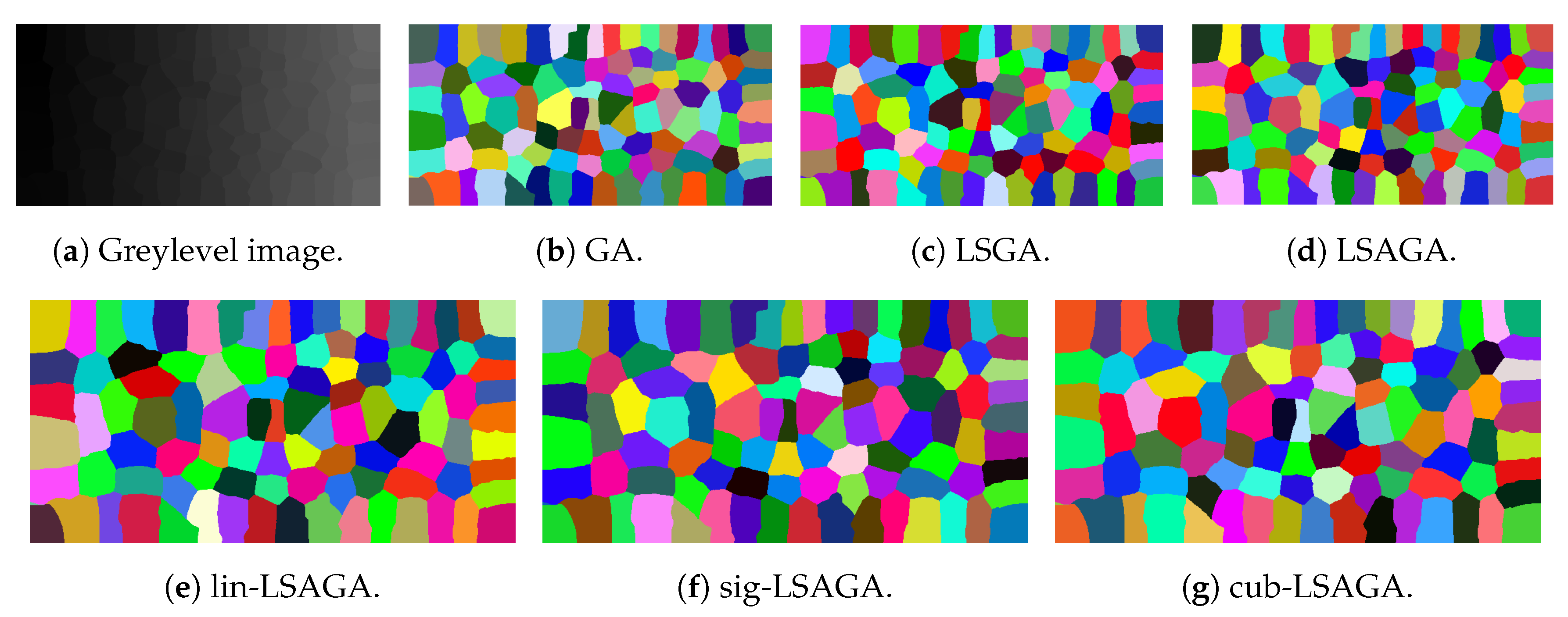
- Mosaic: That is an image in which the methods have great difficulty for pseudo-coloring due to their high number of sub-regions. However, even though all pseudo-colored images have a high degree of visual separability between their regions, it is possible to see that the pseudo-colorized version by GA (Figure 12b) has in its top-left part several shades of yellow in neighboring areas and has in its bottom-right section neighboring regions colored with similar shades of red and pink. Something similar also occurs with the pseudo-colorized image with the LSGA (Figure 12c).
- Bicycle: The image has sub-regions and a small number of connections are defined by the neighborhood matrix. Therefore, all techniques have good visual results. However, all images show shades of blue in some pair of neighboring sub-regions, but this does not compromise the visual distinction of each sub-region, since the shades of blue used are very dissimilar.
- Horses: Analyzing the image, we can see that all methods present good pseudo-coloring results, with dissimilar color assignments in neighboring areas. However, this fact does not happen, for example, in the GA pseudo-colored image (Figure 14c), in which the blue horse in the central part of the image is pseudo-colored with a color visually similar to the background color.
- Motorcycle: This image has a reasonably large number of sub-regions (), yet all the techniques were able to associate a good pseudo-coloring for each sub-region, we highlight some negative points, such as in the case of the pseudo-colorized image by LSAGA (Figure 15e), which contains two people in the top-left part of the background that represent adjacent areas and that have been colored with shades visually similar in blue.
- Lunch: That image is also highly complex, due to the number of sub-regions () that define a connection in the neighborhood matrix. Thus, not all techniques perform well. For example, in the pseudo-colorized image by our LSGA (Figure 16d), the table in the top-right part of the image receives a color similar to the background color. Something similar occurs with the color of the chair in the top-left section. Another example is presented by the pseudo-coloring obtained by our LSAGA (Figure 16e), which contains shades of blue in very close areas, such as the person in blue, in the central part of the image, sitting in a blue chair, in the case of the pseudo-colorized image by mapped methods this does not occur.
6.3. Case Study II: Quantitative Analysis Considering a Synthetic Benchmark of Images and
6.4. Case Study III: Quantitative Analysis Considering Real World Images and as Munsell Atlas Color Set
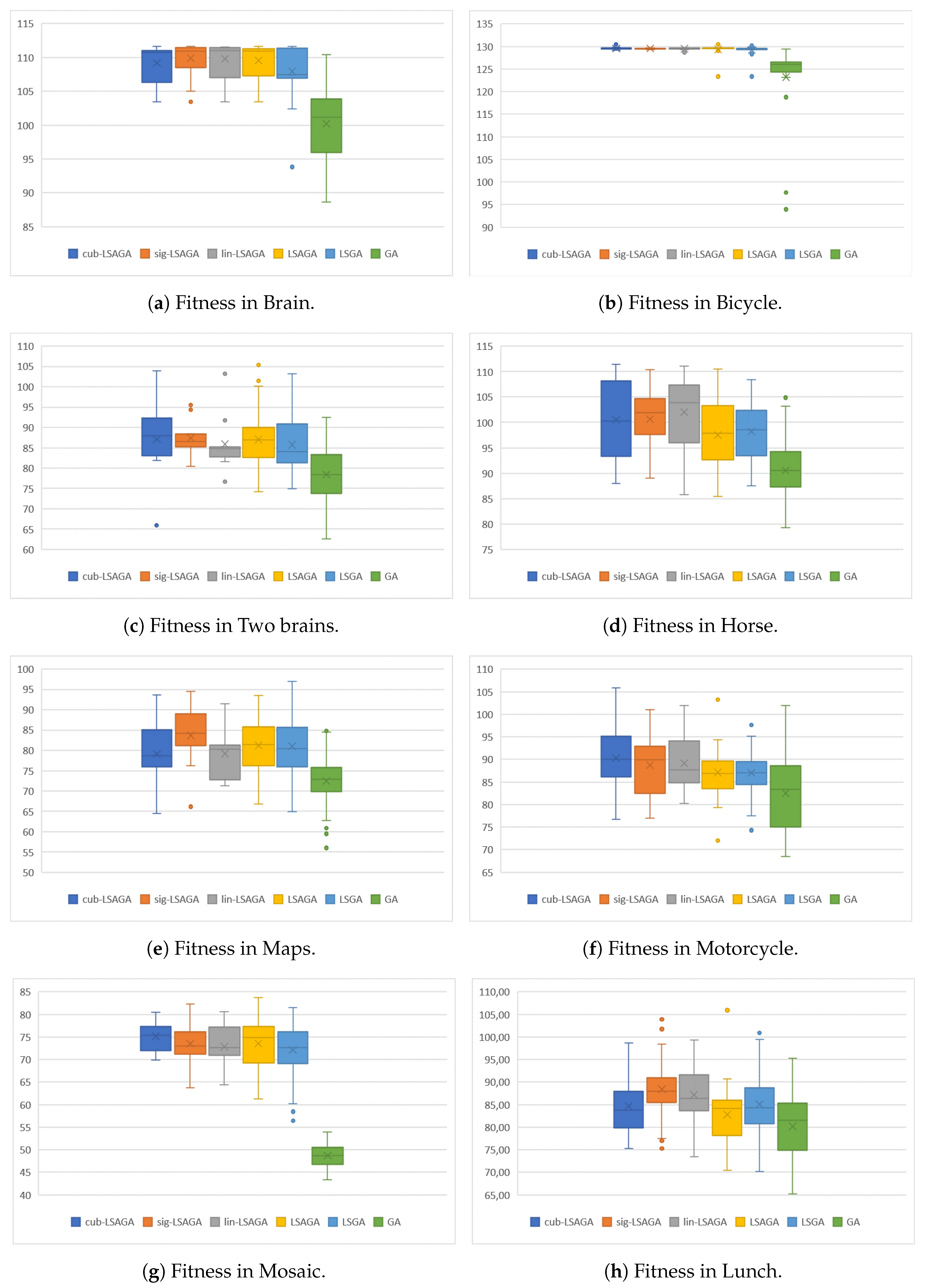
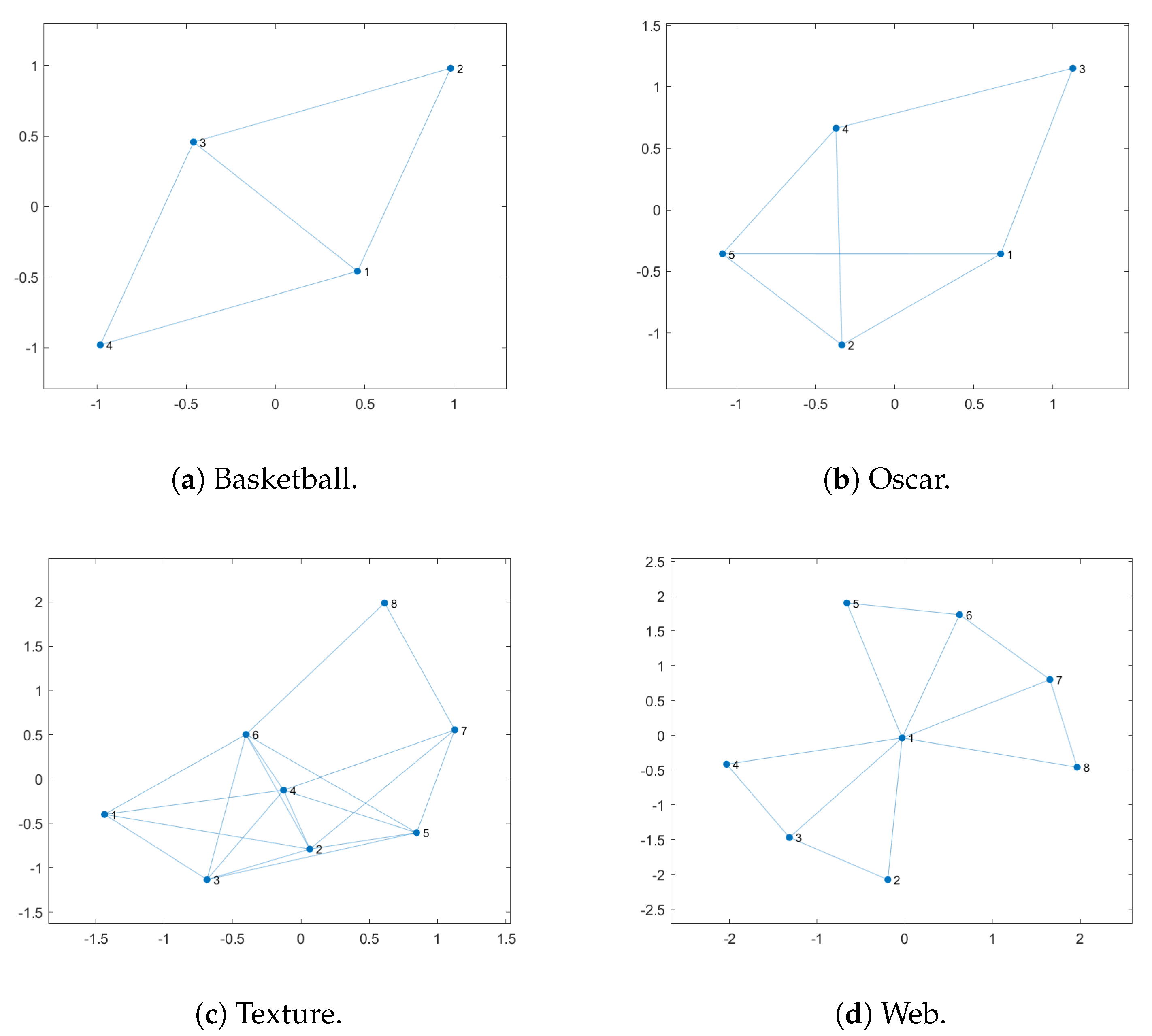
- Basketball: All the proposed methods have the same best value (Max) considering the 50 iterations. However, our cub-LSAGA method presents superior results considering the other statistical measures: worst value (Min), mean and standard deviation (STD). The LS method is deterministic and, therefore, presents the same solution in every evaluation. However, all of our methods have the worst values (Min), results higher than the result obtained by LS.
- Texture: In this case, LS presents competitive results to our techniques. However, except for our cub-LSAGA, all the techniques proposed in this text have the best fitness value greater than the value obtained by LS. In addition, all techniques that make use of adaptation strategies presented a value of fitness as the worst value (Min), better than the best value presented by the Random technique. Likewise, our lin-LSAGA had the worst value greater than the best value presented by GA. This technique also presented the best average among all the compared techniques.
- Oscar: In this case, except for cub-LSAGA, all of our techniques showed the highest best value. In addition, except for computational time, our sig-LSAGA presents the best statistical measures. It is worth mentioning that, all of the proposed techniques obtain a worse value for fitness than a better result than the other techniques with more than 10 units of difference.
- Webpage: For this image, our sig-LSAGA presents the best fitness and average value. Meanwhile, our cub-LSAGA stands out considering the worst fitness value and the standard deviation. However, all the proposed techniques have higher average values than the best values presented by the other techniques.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anitha, U.; Malarkkan, S.; Premalatha, J.; Manonmani, V. Comparison of standard edge detection techniques along with morphological processing and pseudo coloring in sonar image. In Proceedings of the 2016 International Conference on Emerging Trends in Engineering, Technology and Science (ICETETS), Pudukkottai, India, 24–26 February 2016; pp. 1–4. [Google Scholar]
- Dmitruk, K.; Denkowski, M.; Mazur, M.; Mikołajczak, P. Sharpening filter for false color imaging of dual-energy X-ray scans. Signal Image Video Process. 2017, 11, 613–620. [Google Scholar] [CrossRef]
- Etehadtavakol, M.; Ng, E.Y. Color segmentation of breast thermograms: A comparative study. In Application of Infrared to Biomedical Sciences; Springer: Singapore, 2017; pp. 69–77. [Google Scholar]
- Semary, N.A. A proposed Hsv-Based Pseudo-Coloring Scheme For Enhancing Medical Images. Comput. Sci. Inf. Technol. 2018. [Google Scholar] [CrossRef]
- Pipatnoraseth, T.; Phognsuphap, S.; Wiratkapun, C.; Tanawongsuwan, R.; Sajjacholapunt, P.; Shimizu, I. Breast Microcalcification Visualization Using Pseudo-Color Image Processing. In Proceedings of the 2019 12th Biomedical Engineering International Conference (BMEiCON), Ubon Ratchathani, Thailand, 19–22 November 2019; pp. 1–5. [Google Scholar]
- Zeng, X.; Tong, S.; Lu, Y.; Xu, L.; Huang, Z. Adaptive Medical Image Deep Color Perception Algorithm. IEEE Access 2020, 8, 56559–56571. [Google Scholar] [CrossRef]
- Pablo, R.; Verstraelen, P.; Simona, T.; Muthukumar, G.; Marzia, P.; Isabel, P.; Nathalie, C.; De Miguel-Pérez, D.; Riccardo, A.; Bals, S.; et al. Improving extracellular vesicles visualization: From static to motion. Sci. Rep. 2020, 10, 1–9. [Google Scholar]
- Wu, M.; Jin, X.; Jiang, Q.; Lee, S.; Guo, L.; Di, Y.; Huang, S.; Huang, J. Remote Sensing Image Colorization Based on Multiscale SEnet GAN. In Proceedings of the 2019 12th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Huaqiao, China, 19–21 October 2019; pp. 1–6. [Google Scholar]
- Beauchemin, M. Unsupervised colour coding for visualization of categorical maps. Remot. Sens. Lett. 2019, 10, 77–85. [Google Scholar] [CrossRef]
- Zheng, P.; Zhang, J. Quantitative nondestructive testing of wire rope based on pseudo-color image enhancement technology. Nondestruct. Test. Eval. 2019, 34, 221–242. [Google Scholar] [CrossRef]
- Burger, P.; Gillies, D. Interactive Computer Graphics: Functional, Procedural and Device-Level Methods; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Moodley, K.; Murrell, H. A colour-map plugin for the open source, Java based, image processing package, ImageJ. Comput. Geosci. 2004, 30, 609–618. [Google Scholar] [CrossRef]
- Carter, R.C.; Carter, E.C. High-contrast sets of colors. Appl. Opt. 1982, 21, 2936–2939. [Google Scholar] [CrossRef]
- Radlak, K.; Smolka, B. Visualization enhancement of segmented images using genetic algorithm. In Proceedings of the 2014 International Conference on Multimedia Computing and Systems (ICMCS), Marrakech, Morocco, 14–16 April 2014; pp. 391–396. [Google Scholar]
- Zang, W.; Ren, L.; Zhang, W.; Liu, X. A cloud model based DNA genetic algorithm for numerical optimization problems. Future Gener. Comput. Syst. 2018, 81, 465–477. [Google Scholar] [CrossRef]
- Asadzadeh, L. A local search genetic algorithm for the job shop scheduling problem with intelligent agents. Comput. Ind. Eng. 2015, 85, 376–383. [Google Scholar] [CrossRef]
- Lin, C. An adaptive genetic algorithm based on population diversity strategy. In Proceedings of the 2009 Third International Conference on Genetic and Evolutionary Computing, Guilin, China, 14–17 October 2009; pp. 93–96. [Google Scholar]
- Shojaedini, E.; Majd, M.; Safabakhsh, R. Novel adaptive genetic algorithm sample consensus. Appl. Soft Comput. 2019, 77, 635–642. [Google Scholar] [CrossRef]
- Zhu, K.Q. A diversity-controlling adaptive genetic algorithm for the vehicle routing problem with time windows. In Proceedings of the 15th IEEE International Conference on Tools with Artificial Intelligence, Sacramento, CA, USA, 3–5 November 2003; pp. 176–183. [Google Scholar]
- Xing, Y.; Chen, Z.; Sun, J.; Hu, L. An improved adaptive genetic algorithm for job-shop scheduling problem. In Proceedings of the Third International Conference on Natural Computation (ICNC 2007), Haikou, China, 24–27 August 2007; pp. 287–291. [Google Scholar]
- Contreras, R.C.; Morandin Junior, O.; Viana, M.S. A New Local Search Adaptive Genetic Algorithm for the Pseudo-Coloring Problem. In Advances in Swarm Intelligence; Tan, Y., Shi, Y., Tuba, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 349–361. [Google Scholar]
- Appel, K.I.; Haken, W. Every Planar Map is Four Colorable; American Mathematical Soc.: Providence, RI, USA, 1989; Volume 98. [Google Scholar]
- Jensen, T.R.; Toft, B. Graph Coloring Problems; John Wiley & Sons: New York, NY, USA, 2011; Volume 39. [Google Scholar]
- Christensen, J.; Shieber, S.M.; Marks, J. Placing Text Labels on Maps and Diagrams; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Welsh, T.; Ashikhmin, M.; Mueller, K. Transferring Color to Greyscale Images. In Proceedings of the 29th Annual Conference on Computer Graphics and Interactive Techniques, San Antonio, TX, USA, 23–26 July 2002. [Google Scholar]
- Zare, M.; Lari, K.B.; Jampour, M.; Shamsinejad, P. Multi-GANs and its application for Pseudo-Coloring. In Proceedings of the 2019 4th International Conference on Pattern Recognition and Image Analysis (IPRIA), Tehran, Iran, 6–7 March 2019; pp. 1–6. [Google Scholar]
- Fang, F.; Wang, T.; Zeng, T.; Zhang, G. A Superpixel-based Variational Model for Image Colorization. IEEE Trans. Vis. Comput. Graph. 2019, 26, 2931–2943. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Xia, Y.; Qi, L.; Yang, Y.; Atiquzzaman, M. Automated Colorization of a Grayscale Image With Seed Points Propagation. IEEE Trans. Multimed. 2020, 22, 1756–1768. [Google Scholar] [CrossRef]
- Li, B.; Lai, Y.K.; Rosin, P.L. A review of image colourisation. In Handbook Of Pattern Recognition And Computer Vision; World Scientific: Singapore, 2020; p. 139. [Google Scholar]
- Dai, J.; Zhou, S. Computer-aided pseudocolor coding of gray images: Complementary color-coding technique. In Electronic Imaging and Multimedia Systems; Li, C.S., Stevenson, R.L., Zhou, L., Eds.; International Society for Optics and Photonics (SPIE): Beijing, China, 1996; Volume 2898, pp. 186–191. [Google Scholar]
- Campadelli, P.; Mora, P.; Schettini, R. Color set selection for nominal coding by Hopfield networks. Vis. Comput. 1995, 11, 150–155. [Google Scholar] [CrossRef]
- Green-Armytage, P. A colour alphabet and the limits of colour coding. JAIC J. Int. Colour Assoc. 2010, 5, 1–23. [Google Scholar]
- Campadelli, P.; Posenato, R.; Schettini, R. An algorithm for the selection of high-contrast color sets. Color Res. Appl. 1999, 24, 132–138. [Google Scholar] [CrossRef]
- Brill, M.H.; Robertson, A.R.; Schanda, J. Open problems on the validity of Grassmann’s laws. Color. Underst. Cie Syst. 2007, 245–259. [Google Scholar]
- Glasbey, C.; van der Heijden, G.; Toh, V.F.; Gray, A. Colour displays for categorical images. Color Res. Appl. 2007, 32, 304–309. [Google Scholar] [CrossRef]
- Bianco, S.; Citrolo, A.G. High Contrast Color Sets under Multiple Illuminants. In Computational Color Imaging; Tominaga, S., Schettini, R., Trémeau, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 133–142. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Bianco, S.; Schettini, R. Unsupervised color coding for visualizing image classification results. Inf. Vis. 2018, 17, 161–177. [Google Scholar] [CrossRef]
- Connolly, C.; Fleiss, T. A study of efficiency and accuracy in the transformation from RGB to CIELAB color space. IEEE Trans. Image Process. 1997, 6, 1046–1048. [Google Scholar] [CrossRef]
- Mahyar, F.; Cheung, V.; Westland, S.; Henry, P. Investigation of complementary colour harmony in CIELAB colour space. In Proceedings of the AIC Midterm Meeting, Hangzhou, China, 12–14 July 2007. [Google Scholar]
- Hoeser, T.; Kuenzer, C. Object Detection and Image Segmentation with Deep Learning on Earth Observation Data: A Review-Part I: Evolution and Recent Trends. Remot. Sens. 2020, 12, 1667. [Google Scholar] [CrossRef]
- Pare, S.; Kumar, A.; Singh, G.; Bajaj, V. Image segmentation using multilevel thresholding: A research review. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1–29. [Google Scholar] [CrossRef]
- Taghanaki, S.A.; Abhishek, K.; Cohen, J.P.; Cohen-Adad, J.; Hamarneh, G. Deep semantic segmentation of natural and medical images: A review. Artif. Intell. Rev. 2020, 14, 1–42. [Google Scholar] [CrossRef]
- Viana, M.S.; Morandin Junior, O.; Contreras, R.C. A Modified Genetic Algorithm With Local Search Strategies And Multi-Crossover Operator For Job Shop Scheduling Problem. Sensors 2020, 20, 5440. [Google Scholar] [CrossRef]
- Zames, G.; Ajlouni, N.; Holland, J.; Hills, W.; Goldberg, D. Genetic algorithms in search, optimization and machine learning. Inf. Technol. J. 1981, 3, 301–302. [Google Scholar]
- Goldberg, D.E. Genetic algorithms in search. Optim. Mach. 1989, 1. [Google Scholar]
- Dioşan, L.; Oltean, M. Evolving crossover operators for function optimization. In European Conference on Genetic Programming; Springer: Berlin/Heidelberg, Germany, 2006; pp. 97–108. [Google Scholar]
- Ombuki, B.M.; Ventresca, M. Local search genetic algorithms for the job shop scheduling problem. Appl. Intell. 2004, 21, 99–109. [Google Scholar] [CrossRef]
- Amjad, M.K.; Butt, S.I.; Kousar, R.; Ahmad, R.; Agha, M.H.; Faping, Z.; Anjum, N.; Asgher, U. Recent research trends in genetic algorithm based flexible job shop scheduling problems. Math. Probl. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Bäck, T.; Schwefel, H.P. An overview of evolutionary algorithms for parameter optimization. Evol. Comput. 1993, 1, 1–23. [Google Scholar] [CrossRef]
- Hinterding, R. Gaussian mutation and self-adaption for numeric genetic algorithms. In Proceedings of the 1995 IEEE International Conference on Evolutionary Computation, Perth, Australia, 29 November–1 December 1995; p. 384. [Google Scholar]
- Bulmer, M.G. Principles of Statistics; Courier Corporation: New York, NY, USA, 1979. [Google Scholar]
- Kelly, K.L. Twenty-two colors of maximum contrast. Color Eng. 1965, 3, 26–27. [Google Scholar]
- Everingham, M.; Winn, J. The pascal visual object classes challenge 2012 (voc2012) development kit. Pattern Anal. Stat. Model. Comput. Learn. Tech. Rep. 2011, 8, 1–32. [Google Scholar]
- Everingham, M.; Eslami, S.A.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes challenge: A retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Newhall, S.M.; Nickerson, D.; Judd, D.B. Final report of the OSA subcommittee on the spacing of the Munsell colors. JOSA 1943, 33, 385–418. [Google Scholar] [CrossRef]
- Munsell, A.H. Munsell Book of Color: Matte Finish Collection; Munsell Color: Baltimore, MD, USA, 1992. [Google Scholar]
- Campadelli, P.; Schettini, R.; Zuffi, S. A system for the automatic selection of conspicuous color sets for qualitative data display. IEEE Trans. Geosci. Remot. Sens. 2001, 39, 2283–2286. [Google Scholar] [CrossRef][Green Version]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Xue, Z.; Blum, R.S. Concealed weapon detection using color image fusion. In Proceedings of the 6th International Conference on Information Fusion, Cairns, Queensland, Australia, 8–11 July 2003; pp. 622–627. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |

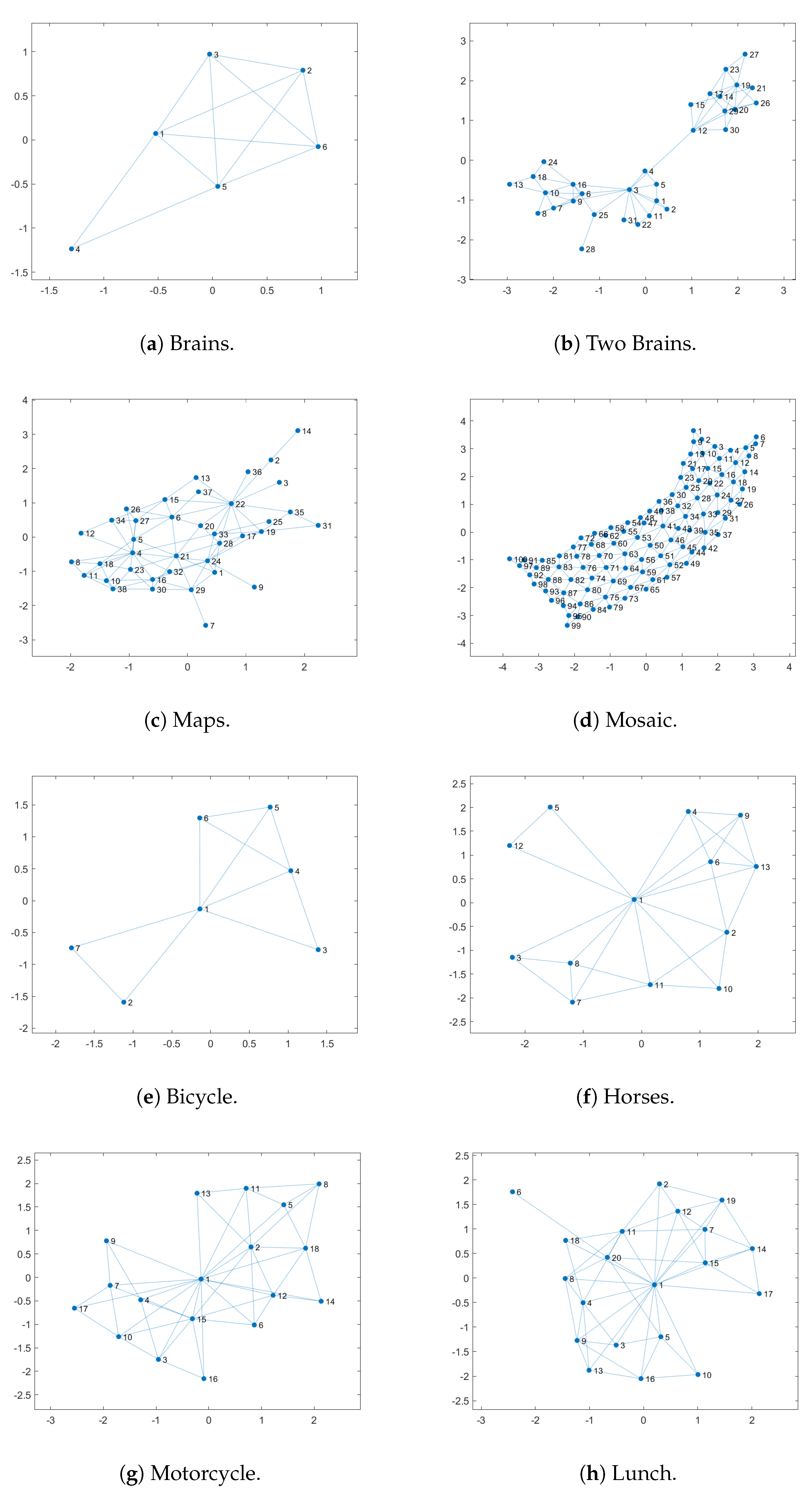




| Image | Number of Subregions (K) | Nonzero Values in | Number of Connections in the Graph |
|---|---|---|---|
| Brains | 6 | 24 | 12 |
| Two Brains | 31 | 132 | 66 |
| Maps | 38 | 174 | 87 |
| Mosaic | 100 | 502 | 251 |
| Bicycle | 7 | 22 | 11 |
| Horses | 13 | 58 | 29 |
| Motorcycle | 18 | 96 | 48 |
| Lunch | 20 | 110 | 55 |
| Method | Local Search | Simple Adaptive Rules | Mapped Adaptive Rules | Mapping Function |
|---|---|---|---|---|
| GA | No | No | No | - |
| LSGA | Yes | No | No | - |
| LSAGA | Yes | Yes | No | - |
| lin-LSAGA | Yes | No | Yes | Yes (Equation (16a)) |
| sig-LSAGA | Yes | No | Yes | Yes (Equation (16b)) |
| cub-LSAGA | Yes | No | Yes | Yes (Equation (16c)) |
| Cub-LSAGA | Sig-LSAGA | Lin-LSAGA | LSAGA | LSGA | GA | |
|---|---|---|---|---|---|---|
| Image | Brain | |||||
| Max | 111.5897 | 111.5897 | 111.5685 | 111.5897 | 111.5897 | 110.4434 |
| Min | 103.4240 | 103.4240 | 103.4240 | 103.4240 | 93.8159 | 88.6637 |
| Mean | 109.2113 | 109.9077 | 109.7841 | 109.5214 | 107.9427 | 100.2385 |
| STD | 2.9257 | 2.3071 | 2.4198 | 2.3563 | 3.9305 | 5.2523 |
| AT (s) | 39.9599 | 46.4401 | 45.1142 | 44.4965 | 33.9584 | 66.9531 |
| Image | Two Brains | |||||
| Max | 103.8950 | 95.5579 | 103.2217 | 105.3690 | 103.2437 | 92.4752 |
| Min | 65.8645 | 80.4354 | 76.6066 | 74.1934 | 74.9277 | 62.6070 |
| Mean | 87.0920 | 87.4156 | 85.8846 | 87.0389 | 85.7157 | 78.3665 |
| STD | 9.4722 | 4.3749 | 6.8571 | 6.2291 | 6.9172 | 6.9151 |
| AT (s) | 160.4555 | 157.1275 | 163.7412 | 158.64375 | 144.0959 | 97.7062 |
| Image | Maps | |||||
| Max | 93.7054 | 94.5564 | 91.4757 | 93.5399 | 97.0676 | 85.1661 |
| Min | 64.4656 | 66.1475 | 71.2507 | 66.8662 | 64.9360 | 55.9863 |
| Mean | 79.1163 | 83.6823 | 79.2163 | 81.2258 | 80.9922 | 72.4412 |
| STD | 8.0998 | 7.6433 | 6.1562 | 6.6415 | 6.4602 | 6.2322 |
| AT (s) | 222.9510 | 226.4532 | 226.4238 | 224.1458 | 203.8438 | 130.4597 |
| Image | Mosaic | |||||
| Max | 80.4838 | 82.2895 | 80.6392 | 83.7880 | 81.5133 | 53.8912 |
| Min | 69.8773 | 63.7500 | 64.4427 | 61.2706 | 56.4168 | 43.3865 |
| Mean | 75.1833 | 73.5342 | 72.8356 | 73.5591 | 72.1155 | 48.7392 |
| STD | 3.4294 | 4.9239 | 5.1849 | 6.2869 | 5.7767 | 2.4751 |
| AT (s) | 990.0295 | 992.4713 | 991.2589 | 989.3925 | 936.8443 | 331.4825 |
| Image | Bicycle | |||||
| Max | 130.4377 | 129.6426 | 129.6426 | 130.5154 | 130.2436 | 129.3809 |
| Min | 129.1017 | 129.3329 | 128.6836 | 123.3457 | 123.3457 | 93.9292 |
| Mean | 129.5630 | 129.5257 | 129.4862 | 129.3585 | 129.2352 | 123.2097 |
| STD | 0.2439 | 0.1219 | 0.2094 | 1.2629 | 1.2606 | 8.5688 |
| AT (s) | 40.3541 | 42.4896 | 48.4984 | 45.5781 | 34.0573 | 68.9844 |
| Image | Horse | |||||
| Max | 111.4548 | 110.3349 | 111.0386 | 110.5609 | 108.4003 | 104.8786 |
| Min | 87.9770 | 89.0085 | 85.7987 | 85.3845 | 87.4883 | 79.3059 |
| Mean | 100.5157 | 100.6137 | 102.0270 | 97.4747 | 98.1981 | 90.5370 |
| STD | 7.6174 | 5.6810 | 6.5707 | 7.2756 | 5.8545 | 6.0897 |
| AT (s) | 72.5547 | 73.9412 | 75.2496 | 69.1302 | 53.5729 | 74.4583 |
| Image | Motorcycle | |||||
| Max | 105.8383 | 101.0411 | 101.9775 | 103.5309 | 97.8846 | 101.8992 |
| Min | 76.7733 | 77.0004 | 80.2057 | 72.0469 | 74.3101 | 68.4586 |
| Mean | 90.3223 | 88.7403 | 89.1553 | 87.0939 | 87.0660 | 82.5259 |
| STD | 7.1476 | 6.4653 | 6.1515 | 6.6437 | 6.0711 | 8.9604 |
| AT (s) | 89.7412 | 85.9214 | 86.6647 | 89.6563 | 73.5052 | 85.3021 |
| Image | Lunch | |||||
| Max | 98.6577 | 103.8848 | 99.3338 | 105.9357 | 100.8967 | 95.3289 |
| Min | 75.2950 | 75.2677 | 73.4639 | 70.43786 | 70.1481 | 65.2178 |
| Mean | 84.7076 | 88.4268 | 87.1569 | 82.81681 | 85.0893 | 80.1618 |
| STD | 6.0211 | 7.3464 | 6.1305 | 7.3561 | 7.2866 | 7.7565 |
| AT (s) | 103.2497 | 99.1463 | 98.8976 | 100.8177 | 82.4479 | 87.6302 |
| Regions (K) | Cub-LSAGA | Sig-LSAGA | Lin-LSAGA | LSAGA | LSGA | GA [14] | Greedy [14] |
|---|---|---|---|---|---|---|---|
| 2 | 249.2 | 249.2 | 249.2 | 249.2 | 249.2 | 249.2 | 233.85 |
| 3 | 166.11 | 166.11 | 166.11 | 166.11 | 166.11 | 166.11 | 164.64 |
| 4 | 130.64 | 130.64 | 130.64 | 130.64 | 129.64 | 130.21 | 129.64 |
| 5 | 111.59 | 111.59 | 111.59 | 111.59 | 111.59 | 111.43 | 108.81 |
| 6 | 102.58 | 102.58 | 102.58 | 102.58 | 102.58 | 102.48 | 93.78 |
| 7 | 94.7 | 94.7 | 94.7 | 94.7 | 93.75 | 93.04 | 86.95 |
| 8 | 86.15 | 86.15 | 86.15 | 86.15 | 86.13 | 84.78 | 80.03 |
| 9 | 81.49 | 81.49 | 81.49 | 81.49 | 80.43 | 78.68 | 74.45 |
| 10 | 77.8 | 77.8 | 77.8 | 77.8 | 74.9 | 74.65 | 71.92 |
| 11 | 68.1 | 69.43 | 69.43 | 69.43 | 68.1 | 66.71 | 65.77 |
| 12 | 65.61 | 65.61 | 65.61 | 65.61 | 64.65 | 64.84 | 61.86 |
| 13 | 64.26 | 64.26 | 64.26 | 64.26 | 62.5 | 63.13 | 57.79 |
| 14 | 60.89 | 60.89 | 60.89 | 60.89 | 59.1 | 58.8 | 57.32 |
| 15 | 57.16 | 57.16 | 57.16 | 57.16 | 56.7 | 53.52 | 55.27 |
| 16 | 51.53 | 55.82 | 55.82 | 55.82 | 51.53 | 51.01 | 53.4 |
| 17 | 53.56 | 53.56 | 53.56 | 53.56 | 52.55 | 49.67 | 51.32 |
| 18 | 50.56 | 50.56 | 50.56 | 50.56 | 50.47 | 48.17 | 49.42 |
| 19 | 45.08 | 50.5 | 47.9 | 50.5 | 48.24 | 45.08 | 47.9 |
| 20 | 44.67 | 49.26 | 49.26 | 49.26 | 45.83 | 44.67 | 47.57 |
| 21 | 46.54 | 45.68 | 45.68 | 45.68 | 44.78 | 42.66 | 46.54 |
| 22 | 46.36 | 46.36 | 44.23 | 46.36 | 44.87 | 41.63 | 44.23 |
| 23 | 44.74 | 44.74 | 44.74 | 43.62 | 43.28 | 41.3 | 44.74 |
| 24 | 39.77 | 43.86 | 39.77 | 43.86 | 42.22 | 39.77 | 43.61 |
| 25 | 38.55 | 43.09 | 38.55 | 43.09 | 41.82 | 38.55 | 41.98 |
| Image | Number of Subregions (K) | Nonzero Values in | Number of Connections in the Graph |
|---|---|---|---|
| Basketball | 4 | 10 | 5 |
| Texture | 8 | 38 | 19 |
| Oscar | 5 | 14 | 7 |
| Webpage | 8 | 24 | 12 |
| Cub-LSAGA | Sig-LSAGA | Lin-LSAGA | LSAGA | LSGA | GA [14,39] | Random [39] | LS [39] | |
|---|---|---|---|---|---|---|---|---|
| Image | Basketball | |||||||
| Max | 83.8193 | 83.8193 | 83.8193 | 83.8193 | 83.8193 | 70.1 | 60.95 | 70.1 |
| Min | 80.9203 | 80.2733 | 80.9203 | 78.1239 | 74.6126 | - | - | - |
| Mean | 82.5140 | 82.2057 | 82.2179 | 82.0358 | 81.8048 | 61.68 | 17.76 | - |
| STD | 0.7331 | 0.8182 | 0.7500 | 1.2027 | 1.4551 | - | - | - |
| AT (s) | 38.3354 | 40.4001 | 38.7352 | 39.6563 | 32.3594 | 15.08 | 0.0013 | 3.03 |
| Image | Texture | |||||||
| Max | 58.7465 | 63.5075 | 63.0651 | 66.3612 | 63.0651 | 47.45 | 45.15 | 60.63 |
| Min | 46.7823 | 46.0836 | 47.7114 | 45.8120 | 36.5557 | - | - | - |
| Mean | 53.0731 | 54.4095 | 55.4383 | 54.6570 | 52.4303 | 43.75 | 17.78 | - |
| STD | 3.3279 | 4.0777 | 3.4021 | 4.6342 | 5.7014 | - | - | - |
| AT (s) | 58.1205 | 59.9801 | 59.2552 | 50.5365 | 35.8229 | 29.48 | 0.0021 | 18.87 |
| Image | Oscar | |||||||
| Max | 82.4165 | 83.8193 | 83.8193 | 83.8193 | 83.8193 | 59.76 | 56.44 | 63.5 |
| Min | 78.1239 | 79.5652 | 78.1239 | 77.3148 | 76.4953 | - | - | - |
| Mean | 81.8081 | 82.0605 | 81.9420 | 81.7832 | 81.2568 | 54.74 | 18.74 | - |
| STD | 1.3161 | 0.9360 | 1.0757 | 1.4110 | 1.6553 | - | - | - |
| AT (s) | 39.8854 | 42.1464 | 40.7552 | 39.0000 | 28.5573 | 17.93 | 0.0015 | 5.56 |
| Image | Webpage | |||||||
| Max | 80.9203 | 82.3743 | 82.2811 | 82.1702 | 80.9203 | 50.13 | 42.93 | 62.33 |
| Min | 67.2430 | 62.8774 | 64.4095 | 62.8774 | 62.2342 | - | - | - |
| Mean | 75.7342 | 76.9152 | 76.1263 | 76.0651 | 73.6511 | 44.15 | 14.89 | - |
| STD | 4.0863 | 4.7845 | 4.6217 | 4.6063 | 5.5967 | - | - | - |
| AT (s) | 50.1254 | 47.8946 | 47.7740 | 48.6667 | 37.0156 | 30.36 | 0.002 | 18.99 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viana, M.S.; Morandin Junior, O.; Contreras, R.C. An Improved Local Search Genetic Algorithm with a New Mapped Adaptive Operator Applied to Pseudo-Coloring Problem. Symmetry 2020, 12, 1684. https://doi.org/10.3390/sym12101684
Viana MS, Morandin Junior O, Contreras RC. An Improved Local Search Genetic Algorithm with a New Mapped Adaptive Operator Applied to Pseudo-Coloring Problem. Symmetry. 2020; 12(10):1684. https://doi.org/10.3390/sym12101684
Chicago/Turabian StyleViana, Monique Simplicio, Orides Morandin Junior, and Rodrigo Colnago Contreras. 2020. "An Improved Local Search Genetic Algorithm with a New Mapped Adaptive Operator Applied to Pseudo-Coloring Problem" Symmetry 12, no. 10: 1684. https://doi.org/10.3390/sym12101684
APA StyleViana, M. S., Morandin Junior, O., & Contreras, R. C. (2020). An Improved Local Search Genetic Algorithm with a New Mapped Adaptive Operator Applied to Pseudo-Coloring Problem. Symmetry, 12(10), 1684. https://doi.org/10.3390/sym12101684







