On Schwarzschild’s Interior Solution and Perfect Fluid Star Model
Abstract
1. A Boundary Value Problem
2. Pressure Field
3. Volume Calculations
4. Conclusions and Open Problems
Author Contributions
Funding
Conflicts of Interest
Appendix A. An Abelian Integral
| Cases | Real Root | Free Term | ||
|---|---|---|---|---|
| (I) | ||||
| , | ||||
| (II) |
- (i
- ,
- (i
- ,
- (ii)
- ,
- (iii
- ,
- (iii
- .
- (iv)
- .
References
- Schwarzschild, K. Über das Gravitationsfeld einer Kugel aus Inkompressibler Flüssigkeit nach der Einsteinschen Theorie; Sitzber. Preuss. Akad. Wiss.: Berlin, Germany, 1916; pp. 424–434. [Google Scholar]
- Clarke, C.J.S. The Analysis of Space-Time Singularities; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Florides, P.S. A new interior Schwarzschild solution. Proc. Royal Soc. London Ser. A 1974, 337, 529–535. [Google Scholar]
- Mehra, A.L. An interior solution for a charge sphere in general relativity. Phys. Lett. A 1983, 88, 159–161. [Google Scholar] [CrossRef]
- Kofinti, N.K. On a new interior Schwarzschild solution. Gen. Relativ. Grav. 1985, 17, 245–249. [Google Scholar] [CrossRef]
- Gron, O. A charged generalization of Florides’ interior Schwarzschild solution. Gen. Relativ. Grav. 1986, 18, 591–596. [Google Scholar] [CrossRef]
- Ségransan, D.; Kervella, P.; Forveille, T.; Queloz, D. First radius measurements of very low mass stars with the VLTI. Astron. Astrophys. 2003, 397, L5–L8. [Google Scholar] [CrossRef]
- Carroll, W.B.; Ostlie, A.D. An Introduction to Modern Astrophysics; Cambridge University Press, University Printing House: Cambridge, UK, 2017; p. 409. [Google Scholar]
- Ribas, I. Solar and Stellar Variability: Impact on Earth and Planets; Kosovichev, A.G., Andrei, A.H., Roelot, J.P., Eds.; International Astronomical Union Symposium, Volume 264; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Adler, R.; Bazin, M.; Schiffer, M. Introduction to General Relativity; McGraw-Hill Book Co.: New York, NY, USA, 1965. [Google Scholar]
- Vartanyan, Y.L.; Grigoryan, A.K.; Khachatryan, G.A. On the mass defect of strange stars. Astrophysics 1995, 38, 152–156. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Quantum geometry and the Schwarzschild singularity. arXiv 2005, arXiv:gr-qc/0509075v1. [Google Scholar] [CrossRef]
- Husain, V.; Winkler, O. On singularity resolution in quantum gravity. Phys. Rev. D 2003, 69, 084016. [Google Scholar] [CrossRef]
- Husain, V.; Winkler, O. Quantum resolution of black hole singularities. Class. Quantum Gravity 2005, 22, L127. [Google Scholar] [CrossRef]
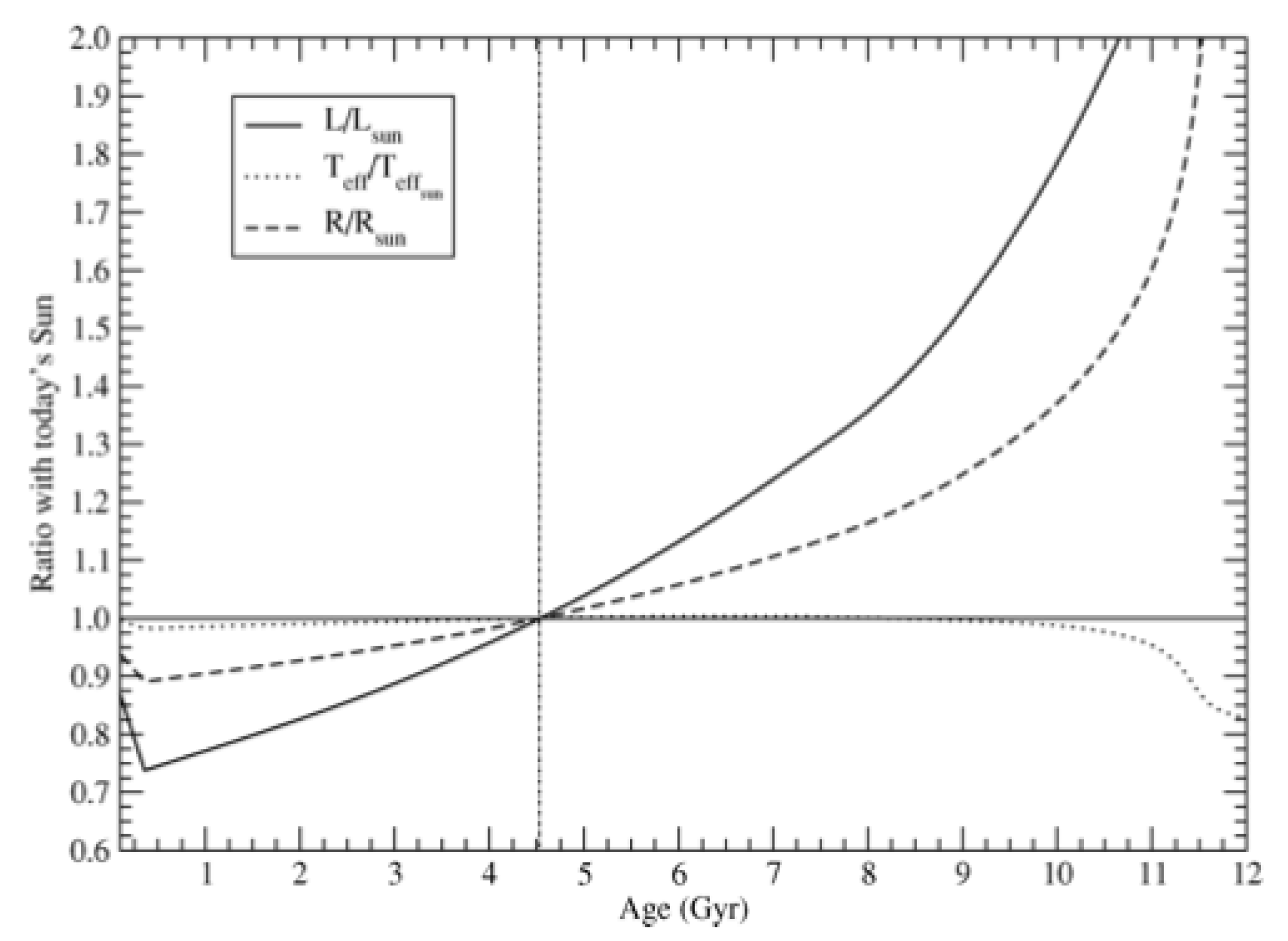
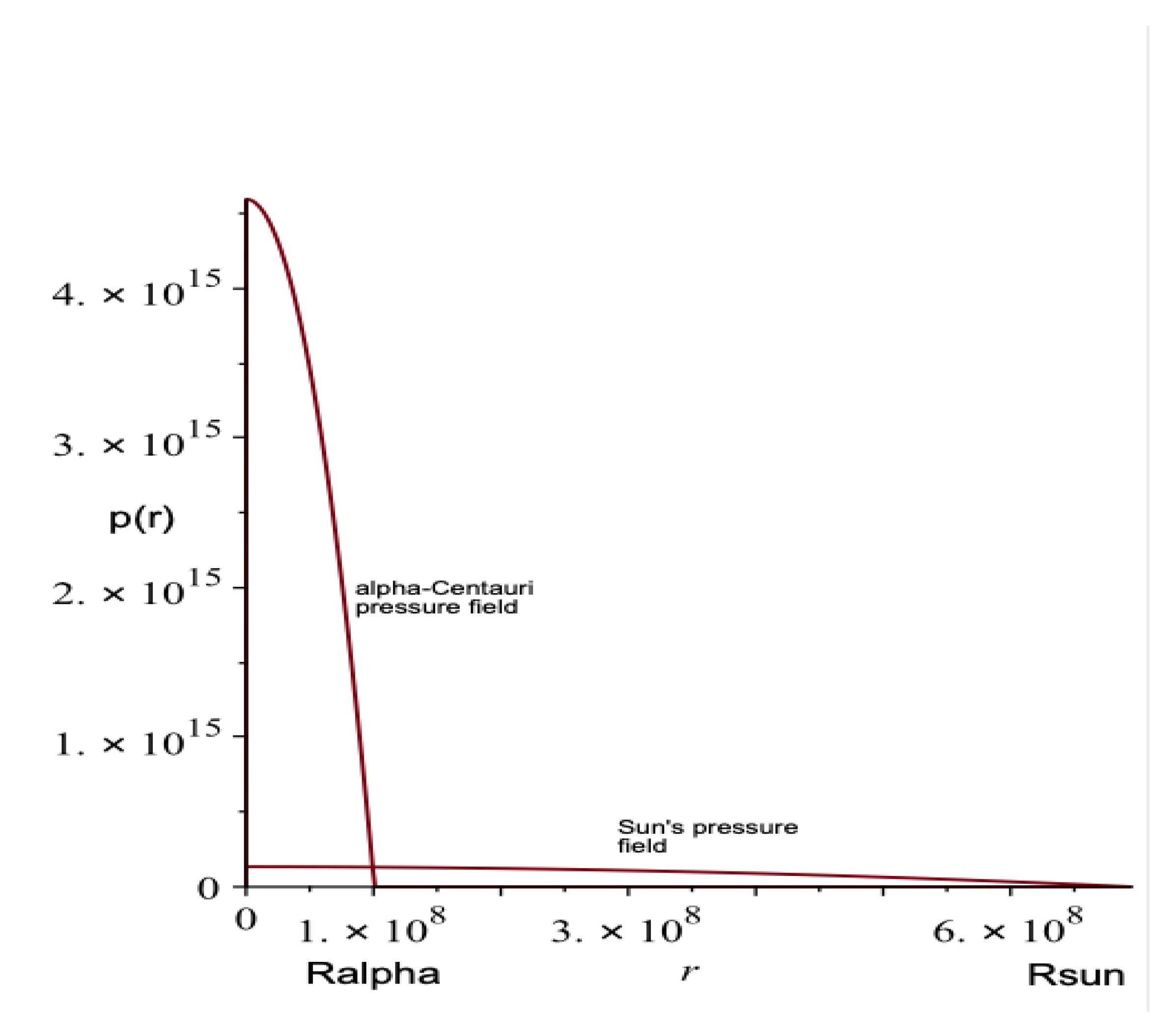
| Star | M | |||
|---|---|---|---|---|
| -Centauri | 0.001896996991 | |||
| Sun | age | |||
| 0.002059672106 | ||||
| 0.00202464319 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barletta, E.; Dragomir, S.; Esposito, F. On Schwarzschild’s Interior Solution and Perfect Fluid Star Model. Symmetry 2020, 12, 1669. https://doi.org/10.3390/sym12101669
Barletta E, Dragomir S, Esposito F. On Schwarzschild’s Interior Solution and Perfect Fluid Star Model. Symmetry. 2020; 12(10):1669. https://doi.org/10.3390/sym12101669
Chicago/Turabian StyleBarletta, Elisabetta, Sorin Dragomir, and Francesco Esposito. 2020. "On Schwarzschild’s Interior Solution and Perfect Fluid Star Model" Symmetry 12, no. 10: 1669. https://doi.org/10.3390/sym12101669
APA StyleBarletta, E., Dragomir, S., & Esposito, F. (2020). On Schwarzschild’s Interior Solution and Perfect Fluid Star Model. Symmetry, 12(10), 1669. https://doi.org/10.3390/sym12101669






