A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics
Abstract
1. Introduction
- The solution of the mathematical expression for the nonlinear SITR model for novel COVID-19 dynamics is calculated viably by using the novel application of the intelligent neuro-evolution-based integrated computing paradigm, i.e., FF-ANN-GASQP.
- Closely matching of the results of the proposed FF-ANN-GASQP solver with the solutions of the reference state of the art numerical procedure of Adams methods for variants of the nonlinear SITR-based mathematical model established the value and worth.
- Authentication and verification of the performance through statistical assessments studies is proven on multiple implementations of FF-ANN-GASQP in terms of Theil’s inequality coefficient (TIC) as well as root mean square error (RMSE)-based indices.
- In addition to the precise and accurate solutions for the SITR-based mathematical model of the COVID-19 pandemic, other valuable perks are that it is easy to understand the concepts, and it also has smooth operation, exhaustive applicability, consistency, and extendibility.
2. Proposed Methodology
- To exploit the FF-ANN models, an error-based objective function is introduced.
- Optimize the objective function for system (1) using the hybrid GA-SQ programming approach.
2.1. ANN Modeling
2.2. Optimization Technique: Hybrid of GA with SQP
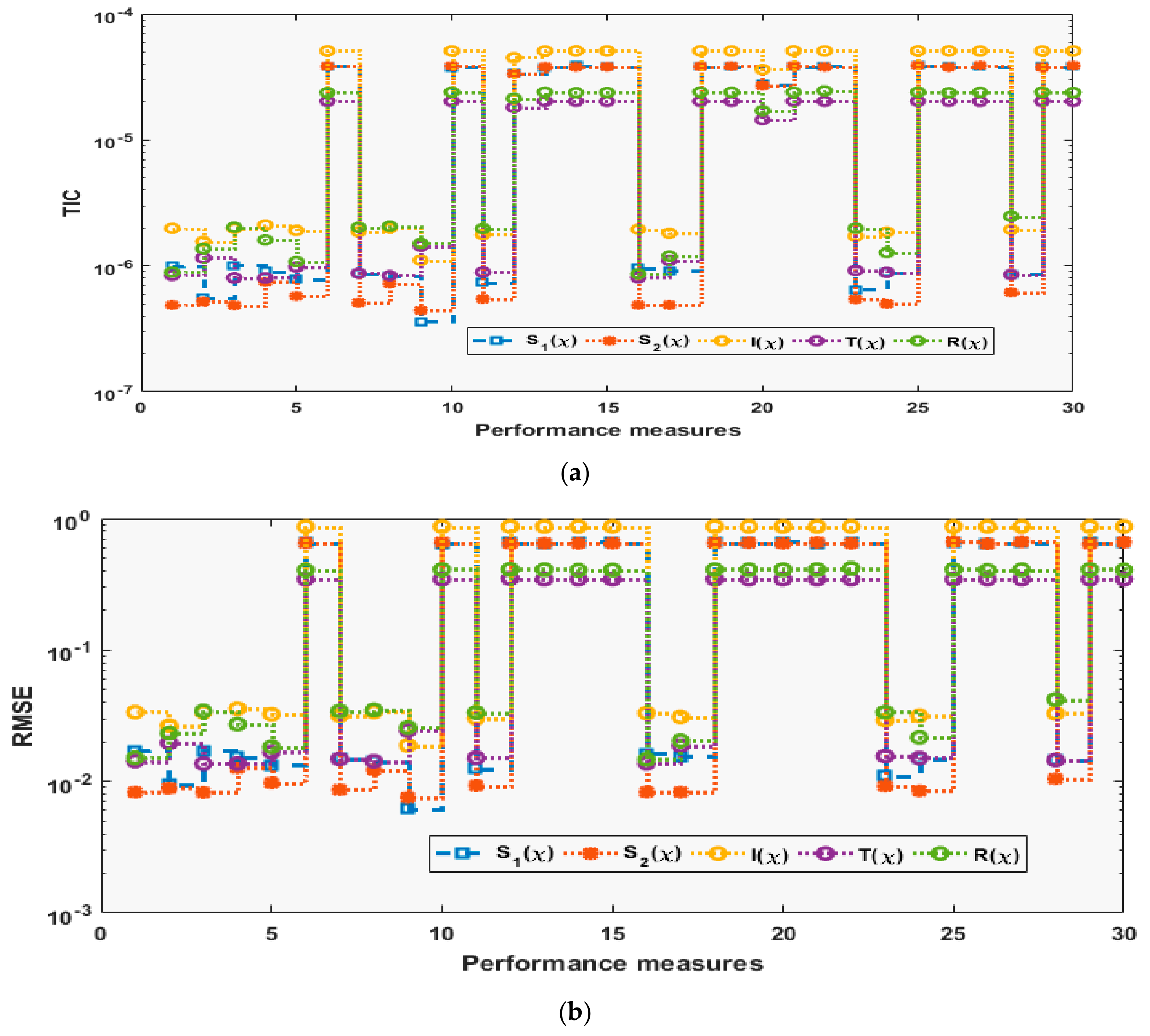
3. Performance Measures
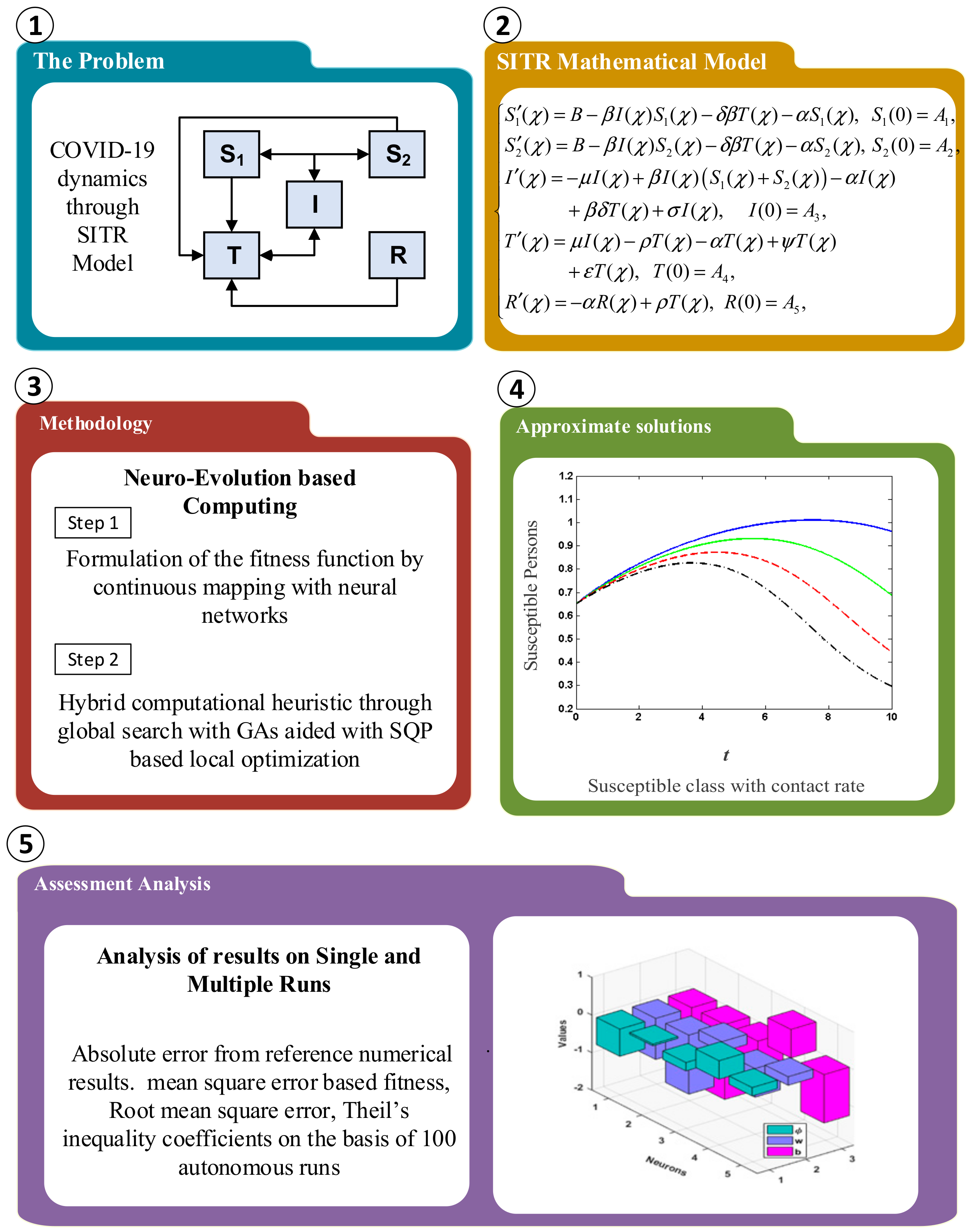
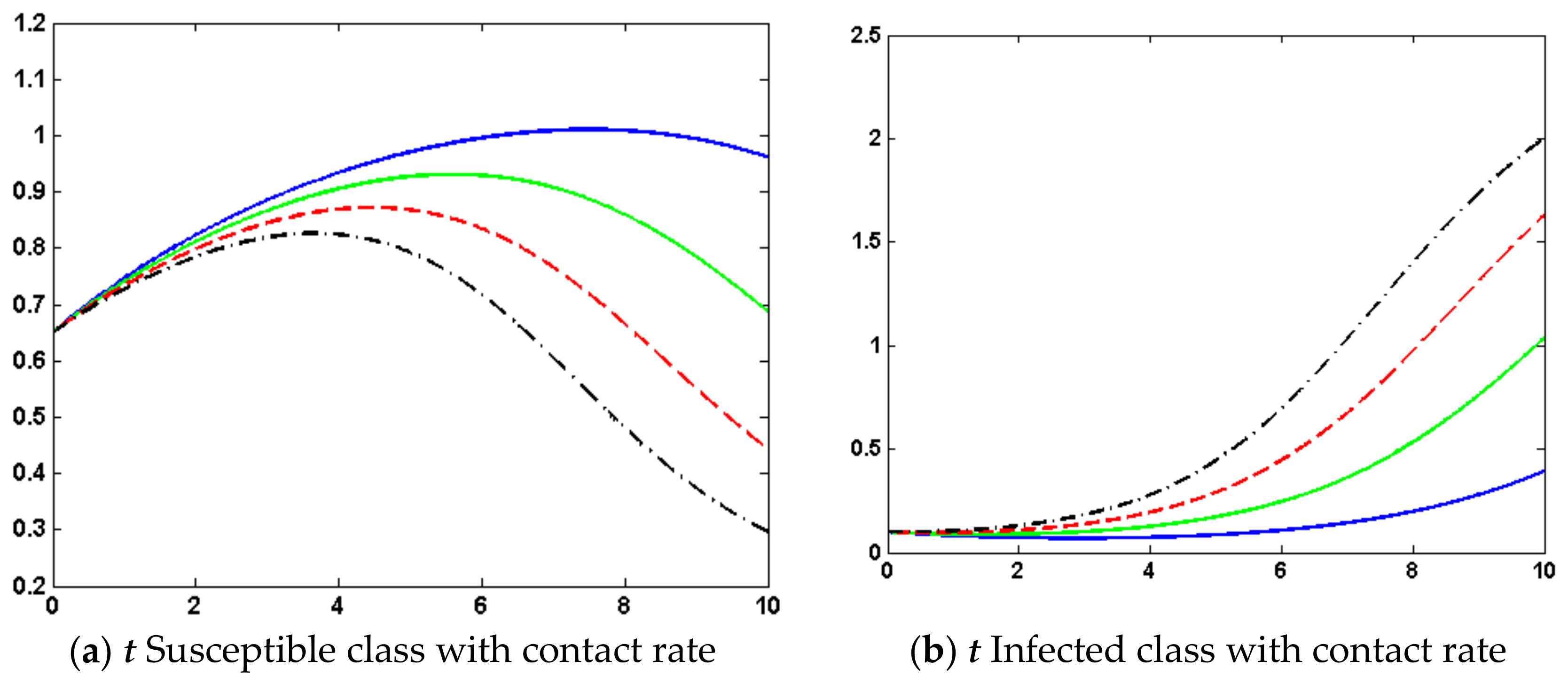
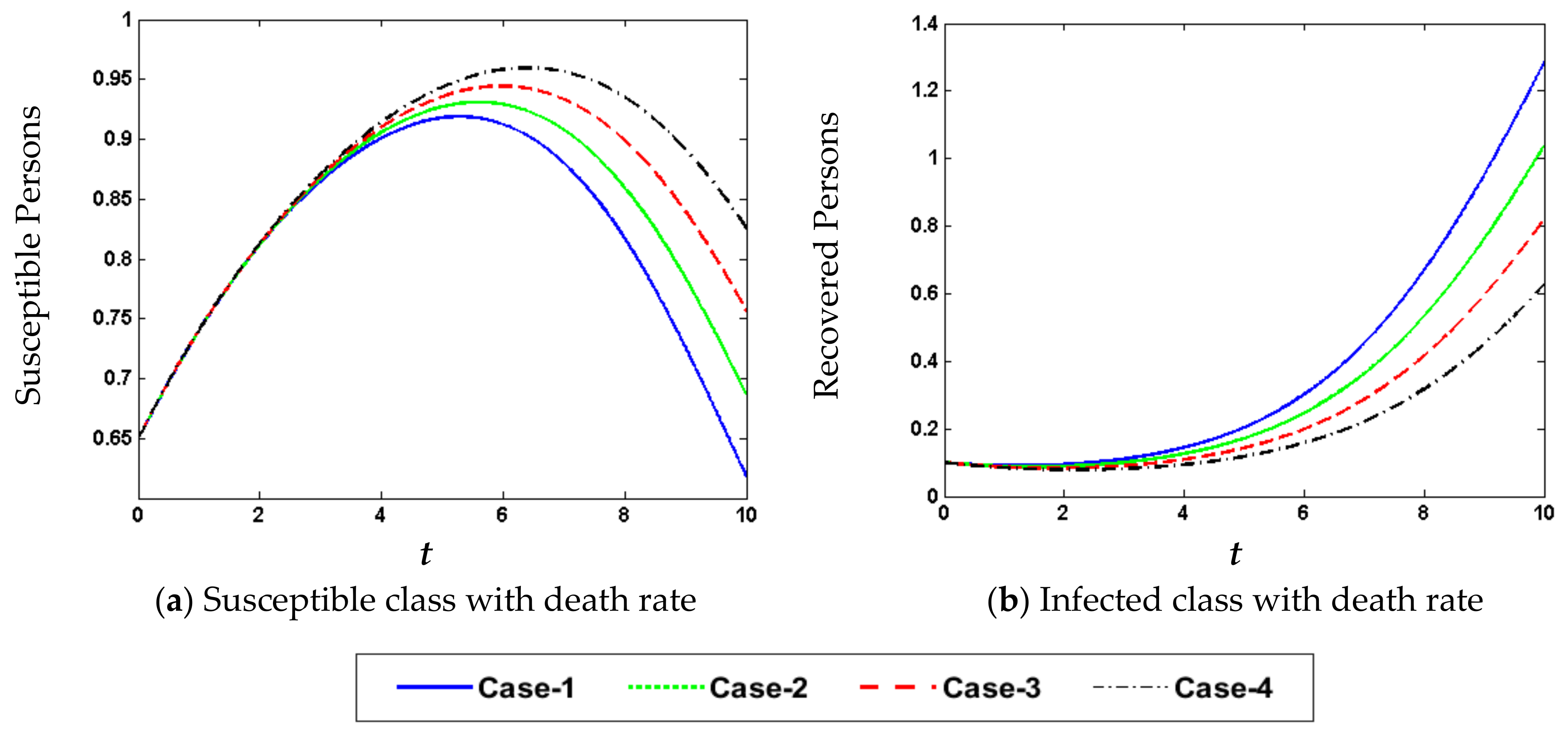
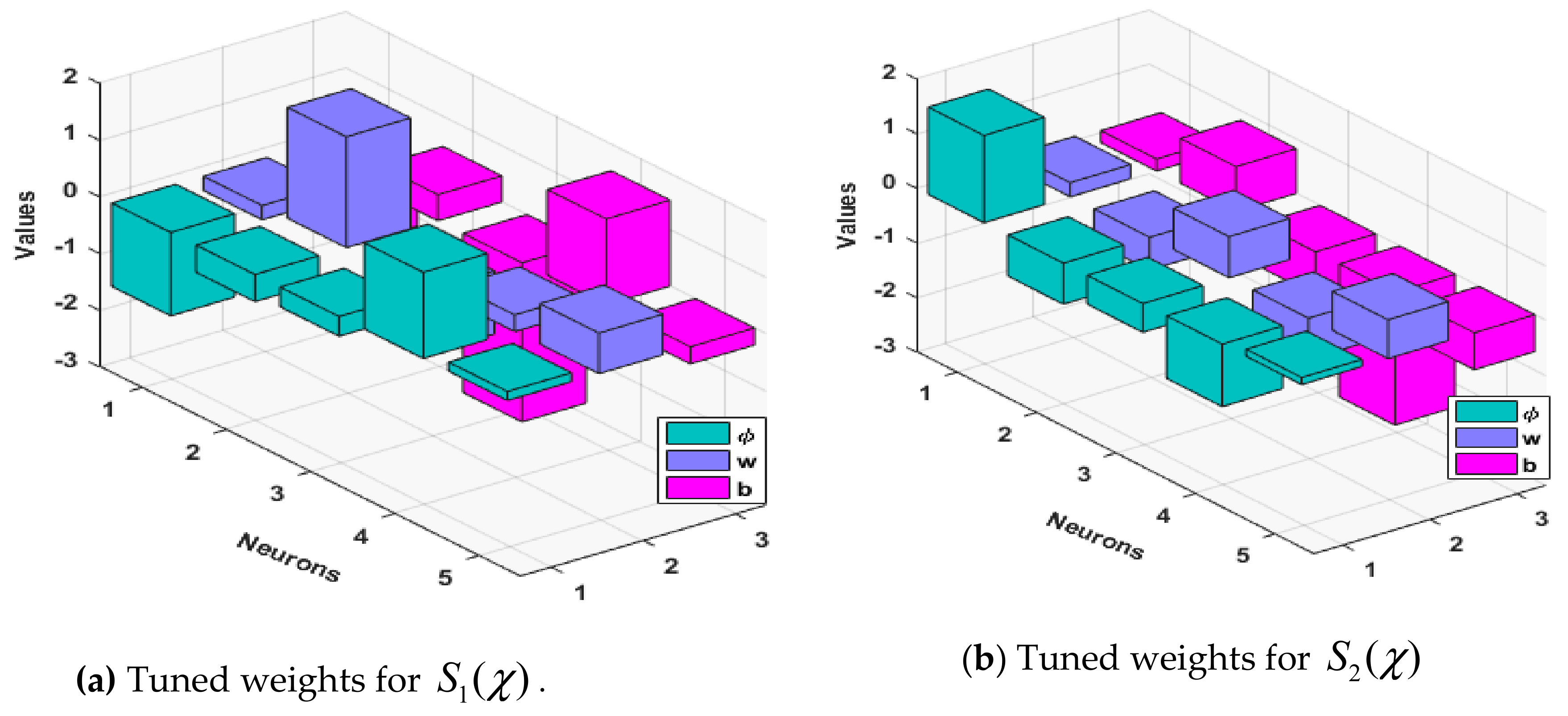
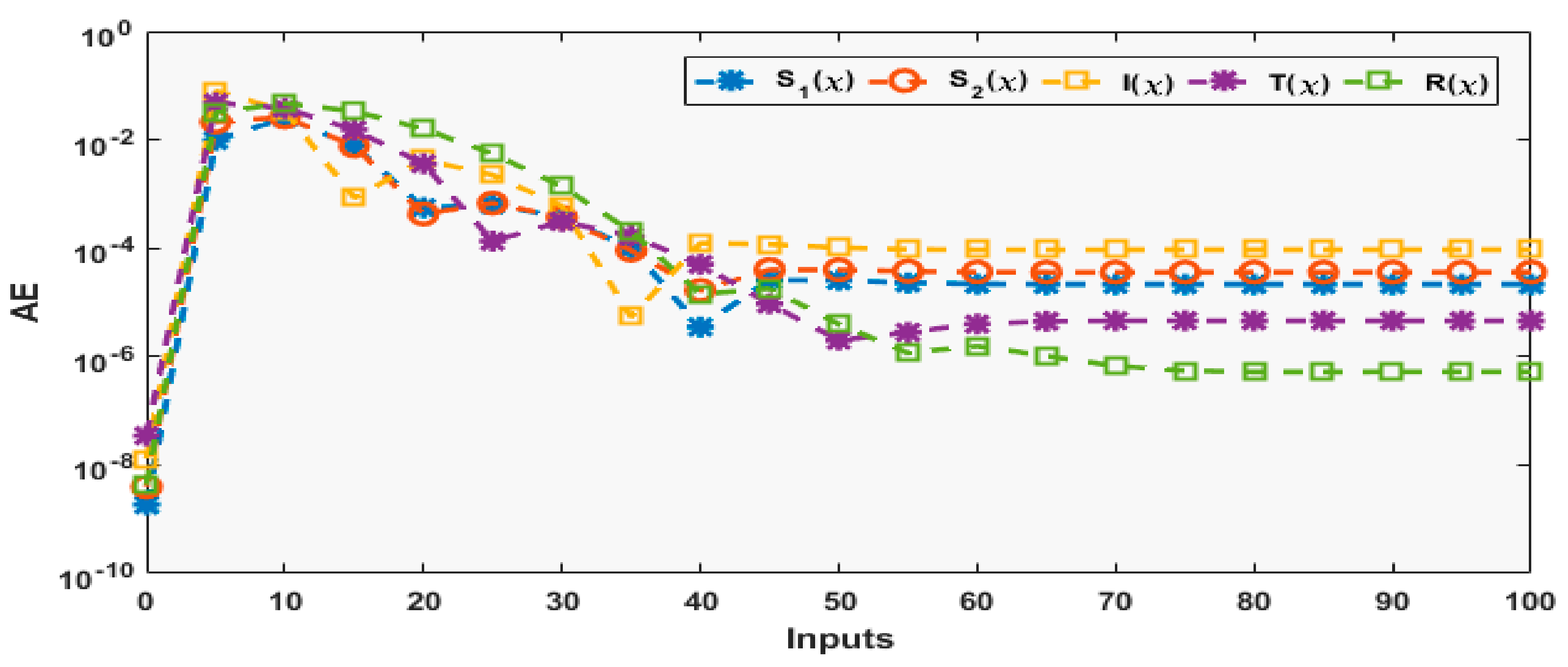
4. Results and Discussion
Nonlinear SITR Model Based on COVID-19
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- China Virus Death Toll Rises to 41, more than 1300 Infected Worldwide. CNBC, 24 January 2020. Available online: https://www.cnbc.com/2020/01/24/chinas-hubei-province-confirms-15-more-deaths-due-to-coronavirus.html (accessed on 10 June 2020).
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Sabir, Z.; Umar, M.; Guirao, J.L.; Shoaib, M.; Raja, M.A.Z. Integrated intelligent computing paradigm for nonlinear multi-singular third-order Emden–Fowler equation. Neural Comput. Appl. 2020, 1–20. [Google Scholar] [CrossRef]
- Zúñiga-Aguilar, C.; Ugalde, H.M.R.; Gómez-Aguilar, J.F.; Escobar-Jiménez, R.F.; Valtierra-Rodríguez, M. Solving fractional differential equations of variable-order involving operators with Mittag-Leffler kernel using artificial neural networks. Chaos Solitons Fractals 2017, 103, 382–403. [Google Scholar] [CrossRef]
- Sabir, Z.; Saoud, S.; Raja, M.A.Z.; Wahab, H.A.; Arbi, A. Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation. Math. Comput. Simul. 2020, 178, 534–548. [Google Scholar] [CrossRef]
- Sabir, Z.; Wahab, H.A.; Umar, M.; Sakar, M.G.; Raja, M.A.Z. Novel design of Morlet wavelet neural network for solving second order Lane–Emden equation. Math. Comput. Simul. 2020, 172, 1–14. [Google Scholar] [CrossRef]
- Zuñiga-Aguilar, C.J.; Coronel-Escamilla, A.; Gómez-Aguilar, J.F.; Alvarado-Martínez, V.M.; Ugalde, H.M.R. New numerical approximation for solving fractional delay differential equations of variable order using artificial neural networks. Eur. Phys. J. Plus 2018, 133, 75. [Google Scholar] [CrossRef]
- Sabir, Z.; Baleanu, D.; Shoaib, M.; Raja, M.A.Z. Design of stochastic numerical solver for the solution of singular three-point second-order boundary value problems. Neural Comput. Appl. 2020, 1–17. [Google Scholar] [CrossRef]
- Bukhari, A.H.; Raja, M.A.Z.; Sulaiman, M.; Islam, S.; Shoaib, M.; Kumam, P. Fractional Neuro-Sequential ARFIMA-LSTM for Financial Market Forecasting. IEEE Access 2020, 8, 71326–71338. [Google Scholar] [CrossRef]
- Sabir, Z.; Manzar, M.A.; Raja, M.A.Z.; Sheraz, M.; Wazwaz, A.-M. Neuro-heuristics for nonlinear singular Thomas-Fermi systems. Appl. Soft Comput. 2018, 65, 152–169. [Google Scholar] [CrossRef]
- Bukhari, A.H.; Sulaiman, M.; Islam, S.; Shoaib, M.; Kumam, P.; Raja, M.A.Z. Neuro-fuzzy modeling and prediction of summer precipitation with application to different meteorological stations. Alex. Eng. J. 2020, 59, 101–116. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z. Intelligent computing for numerical treatment of nonlinear prey–predator models. Appl. Soft Comput. 2019, 80, 506–524. [Google Scholar] [CrossRef]
- Hassan, A.; Ahmad, S.-U.-I.; Kamran, M.; Illahi, A.; Zahoor, R.M.A. Design of cascade artificial neural networks optimized with the memetic computing paradigm for solving the nonlinear Bratu system. Eur. Phys. J. Plus 2019, 134, 122. [Google Scholar] [CrossRef]
- Majeed, K.; Masood, Z.; Samar, R.; Raja, M.A.Z. A genetic algorithm optimized Morlet wavelet artificial neural network to study the dynamics of nonlinear Troesch’s system. Appl. Soft Comput. 2017, 56, 420–435. [Google Scholar] [CrossRef]
- Mehmood, A.; Zameer, A.; Ling, S.H.; Raja, M.A.Z. Design of neuro-computing paradigms for nonlinear nanofluidic systems of MHD Jeffery–Hamel flow. J. Taiwan Inst. Chem. Eng. 2018, 91, 57–85. [Google Scholar] [CrossRef]
- Sabir, Z.; Wahab, H.A.; Umar, M.; Erdogan, F. Stochastic numerical approach for solving second order nonlinear singular functional differential equation. Appl. Math. Comput. 2019, 363, 124605. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M. Neuro-swarm intelligent computing to solve the second-order singular functional differential model. Eur. Phys. J. Plus. 2020, 135, 474. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Shah, F.H.; Alaidarous, E.S.; Syam, M.I. Design of bio-inspired heuristic technique integrated with interior-point algorithm to analyze the dynamics of heartbeat model. Appl. Soft Comput. 2017, 52, 605–629. [Google Scholar] [CrossRef]
- Mehmood, A.; Zameer, A.; Raja, M.A.Z. Intelligent computing to analyze the dynamics of Magnetohydrodynamic flow over stretchable rotating disk model. Appl. Soft Comput. 2018, 67, 8–28. [Google Scholar] [CrossRef]
- Umar, M.; Amin, F.; Wahab, H.A.; Baleanu, D. Unsupervised constrained neural network modeling of boundary value corneal model for eye surgery. Appl. Soft Comput. 2019, 85, 105826. [Google Scholar] [CrossRef]
- Mehmood, A.; Zameer, A.; Ling, S.H.; Rehman, A.U.; Raja, M.A.Z. Integrated computational intelligent paradigm for nonlinear electric circuit models using neural networks, genetic algorithms and sequential quadratic programming. Neural Comput. Appl. 2019, 1–21. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Mehmood, J.; Sabir, Z.; Nasab, A.K.; Manzar, M.A. Numerical solution of doubly singular nonlinear systems using neural networks-based integrated intelligent computing. Neural Comput. Appl. 2017, 31, 793–812. [Google Scholar] [CrossRef]
- Ahmad, I.; Ilyas, H.; Urooj, A.; Aslam, M.S.; Shoaib, M.; Raja, M.A.Z. Novel applications of intelligent computing paradigms for the analysis of nonlinear reactive transport model of the fluid in soft tissues and microvessels. Neural Comput. Appl. 2019, 31, 9041–9059. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Guirao, J.L.G.; Shoaib, M. A Neuro-Swarming Intelligence-Based Computing for Second Order Singular Periodic Non-linear Boundary Value Problems. Front. Phys. 2020, 8. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Umar, M.; Sabir, Z.; Khan, J.A.; Baleanu, D. A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head. Eur. Phys. J. Plus 2018, 133, 364. [Google Scholar] [CrossRef]
- Ahmad, S.U.I.; Faisal, F.; Shoaib, M.; Raja, M.A.Z. A new heuristic computational solver for nonlinear singular Thomas–Fermi system using evolutionary optimized cubic splines. Eur. Phys. J. Plus 2020, 135, 55. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Manzar, M.A.; Samar, R. An efficient computational intelligence approach for solving fractional order Riccati equations using ANN and SQP. Appl. Math. Model. 2015, 39, 3075–3093. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Umar, M.; Shoaib, M. Design of neuro-swarming-based heuristics to solve the third-order nonlinear multi-singular Emden–Fowler equation. Eur. Phys. J. Plus 2020, 135, 410. [Google Scholar] [CrossRef]
- Lodhi, S.; Manzar, M.A.; Raja, M.A.Z. Fractional neural network models for nonlinear Riccati systems. Neural Comput. Appl. 2017, 31, 359–378. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Khan, J.A.; Bilal, M. A new stochastic approach for solution of Riccati differential equation of fractional order. Ann. Math. Artif. Intell. 2010, 60, 229–250. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Samar, R.; Manzar, M.A.; Shah, S.M. Design of unsupervised fractional neural network model optimized with interior point algorithm for solving Bagley–Torvik equation. Math. Comput. Simul. 2017, 132, 139–158. [Google Scholar] [CrossRef]
- Khan, N.; Hameed, T.; Khan, N.; Raja, M.A.Z. A heuristic optimization method of fractional convection reaction: An application to diffusion process. Therm. Sci. 2018, 22, 243–252. [Google Scholar] [CrossRef]
- Ara, A.; Alam Khan, N.; Razzaq, O.A.; Hameed, T.; Raja, M.A.Z. Wavelets optimization method for evaluation of fractional partial differential equations: An application to financial modelling. Adv. Differ. Equ. 2018, 2018, 8. [Google Scholar] [CrossRef]
- Sanchez, Y.G.; Sabir, Z.; Guirao, J.L.G. Design of a Nonlinear Sitr Fractal Model Based on the Dynamics of a Novel Coronavirus (COVID-19). Fractals 2020. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muilti-objective optimization using no dominated sorting in genetic algorithms. Evolut. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Zameer, A.; Majeed, M.; Mirza, S.M.; Raja, M.A.Z.; Khan, A.; Mirza, N.M. Bio-inspired heuristics for layer thickness optimization in multilayer piezoelectric transducer for broadband structures. Soft Comput. 2018, 23, 3449–3463. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Shah, A.A.; Mehmood, A.; Chaudhary, N.I.; Aslam, M.S. Bio-inspired computational heuristics for parameter estimation of nonlinear Hammerstein controlled autoregressive system. Neural Comput. Appl. 2016, 29, 1455–1474. [Google Scholar] [CrossRef]
- Tan, J.; Kerr, W.L. Determination of glass transitions in boiled candies by capacitance based thermal analysis (CTA) and genetic algorithm (GA). J. Food Eng. 2017, 193, 68–75. [Google Scholar] [CrossRef]
- Jamal, R.; Men, B.; Khan, N.H.; Raja, M.A.Z.; Men, K.R. Hybrid Bio-Inspired Computational Heuristic Paradigm for Integrated Load Dispatch Problems involving Stochastic Wind. Energies 2019, 12, 2568. [Google Scholar] [CrossRef]
- Khan, W.U.; Ye, Z.; Altaf, F.; Chaudhary, N.I.; Raja, M.A.Z. A novel application of fireworks heuristic paradigms for reliable treatment of nonlinear active noise control. Appl. Acoust. 2019, 146, 246–260. [Google Scholar] [CrossRef]
- Mehmood, A.; Chaudhary, N.I.; Zameer, A.; Raja, M.A.Z. Novel computing paradigms for parameter estimation in power signal models. Neural Comput. Appl. 2019, 32, 6253–6282. [Google Scholar] [CrossRef]
- Raja, M.A.Z. Solution of the one-dimensional Bratu equation arising in the fuel ignition model using ANN optimised with PSO and SQP. Connect. Sci. 2014, 26, 195–214. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Manzar, M.A.; Shah, S.M.; Chen, Y. Integrated Intelligence of Fractional Neural Networks and Sequential Quadratic Programming for Bagley–Torvik Systems Arising in Fluid Mechanics. J. Comput. Nonlinear Dyn. 2020, 15. [Google Scholar] [CrossRef]
- Khan, W.U.; Ye, Z.; Chaudhary, N.I.; Raja, M.A.Z. Backtracking search integrated with sequential quadratic programming for nonlinear active noise control systems. Appl. Soft Comput. 2018, 73, 666–683. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Imran, A.; Wahab, A.H.; Shoaib, M.; Raja, M.A.Z. The 3-D flow of Casson nanofluid over a stretched sheet with chemical reactions, velocity slip, thermal radiation and Brownian motion. Therm. Sci. 2020, 24, 2929–2939. [Google Scholar] [CrossRef]
- Sabir, Z.; Imran, A.; Umar, M.; Zeb, M.; Shoaib, M.; Raja, M.A.Z. A numerical approach for two-dimensional Sutterby fluid flow bounded at a stagnation point with an inclined magnetic field and thermal radiation impacts. Therm. Sci. 2020, 186. [Google Scholar] [CrossRef]
- Sabir, Z.; Akhtar, R.; Zhiyu, Z.; Umar, M.; Imran, A.; Wahab, H.A.; Shoaib, M.; Raja, M.A.Z. A Computational Analysis of Two-Phase Casson Nanofluid Passing a Stretching Sheet Using Chemical Reactions and Gyrotactic Microorganisms. Math. Probl. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Sabir, Z.; Ayub, A.; Guirao, J.L.; Bhatti, S.; Shah, S.Z.H. The Effects of Activation Energy and Thermophoretic Diffusion of Nanoparticles on Steady Micropolar Fluid along with Brownian Motion. Adv. Mater. Sci. Eng. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Umar, M.; Akhtar, R.; Sabir, Z.; Wahab, H.A.; Zhiyu, Z.; Imran, A.; Shoaib, M.; Raja, M.A.Z. Numerical Treatment for the Three-Dimensional Eyring-Powell Fluid Flow over a Stretching Sheet with Velocity Slip and Activation Energy. Adv. Math. Phys. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Chaudhary, N.I.; Zubair, S.; Aslam, M.S.; Raja, M.A.Z.; Machado, J.A.T. Design of momentum fractional LMS for Hammerstein nonlinear system identification with application to electrically stimulated muscle model. Eur. Phys. J. Plus 2019, 134, 407. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Akhtar, R.; Chaudhary, N.I.; Zhiyu, Z.; Khan, Q.; Rehman, A.U.; Zaman, F. A new computing paradigm for the optimization of parameters in adaptive beamforming using fractional processing. Eur. Phys. J. Plus 2019, 134, 1–13. [Google Scholar] [CrossRef]
- Masood, Z.; Samar, R.; Raja, M.A.Z. Design of fractional order epidemic model for future generation tiny hardware implants. Futur. Gener. Comput. Syst. 2020, 106, 43–54. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, R.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y. Design of Fractional Swarm Intelligent Computing With Entropy Evolution for Optimal Power Flow Problems. IEEE Access 2020, 8, 111401–111419. [Google Scholar] [CrossRef]
- Sabir, Z.; Günerhan, H.; Guirao, J.L. On a New Model Based on Third-Order Nonlinear Multisingular Functional Differential Equations. Math. Probl. Eng. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Akbar, S.; Zaman, F.; Asif, M.; Rehman, A.U.; Raja, M.A.Z. Novel application of FO-DPSO for 2-D parameter estimation of electromagnetic plane waves. Neural Comput. Appl. 2018, 31, 3681–3690. [Google Scholar] [CrossRef]
- Zaman, F.; Hassan, A.; Akbar, S.; Rehman, A.U.; Raja, M.A.Z. Novel Computational Heuristics for Wireless Parameters Estimation in Bistatic Radar systems. Wirel. Pers. Commun. 2019, 111, 909–927. [Google Scholar] [CrossRef]
- Sabir, Z.; Guirao, J.L.; Saeed, T.; Erdoğan, F. Design of a Novel Second-Order Prediction Differential Model Solved by Using Adams and Explicit Runge–Kutta Numerical Methods. Math. Probl. Eng. 2020, 2020, 9704968. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Amin, F.; Guirao, J.L.; Raja, M.A.Z. Stochastic numerical technique for solving HIV infection model of CD4+ T cells. Eur. Phys. J. Plus 2020, 135, 1–19. [Google Scholar] [CrossRef]
- Umar, M.; Raja, M.A.Z.; Sabir, Z.; Alwabli, A.S.; Shoaib, M. A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment. Eur. Phys. J. Plus 2020, 135, 1–23. [Google Scholar] [CrossRef]
- Guerrero-Sánchez, Y.; Sabir, Z.; Günerhan, H.; Baskonus, H.M. Analytical and Approximate Solutions of a Novel Nervous Stomach Mathematical Model. Discret. Dyn. Nat. Soc. 2020, 2020, 5063271. [Google Scholar] [CrossRef]

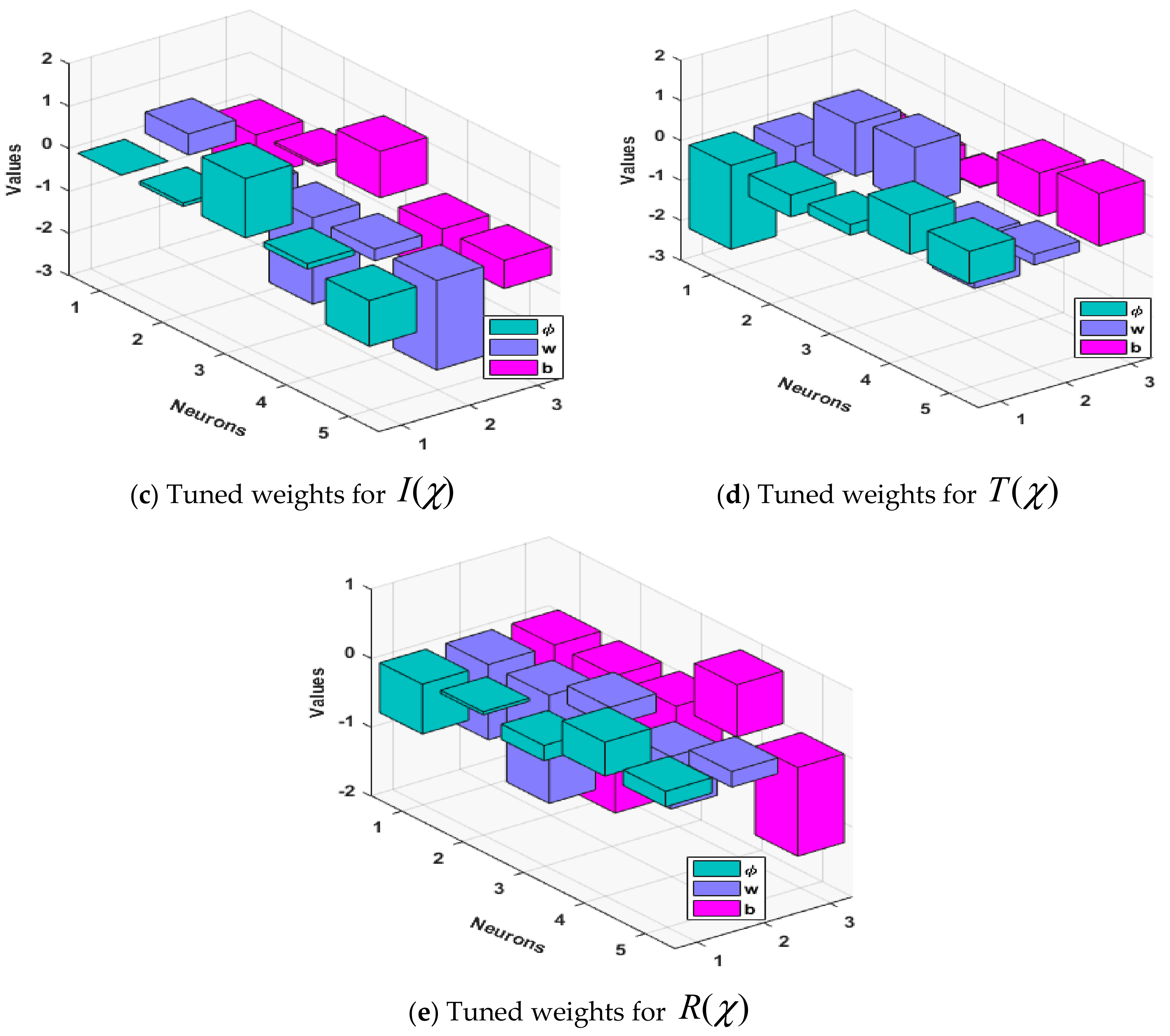
| Variable | Description |
|---|---|
| Non-infected individuals | |
| Non-infected older or major diseased people | |
| Rate of infected from COVID-19 | |
| Recovery rate from COVID-19 | |
| Treatment |
| Parameter | Description |
|---|---|
| Contact rate | |
| Rate of natural birth | |
| Reduce infection from treatment | |
| Fever, tiredness and dry cough rate | |
| Recovery rate | |
| Death rate | |
| Rate of infection from treatment | |
| Healthy food rate | |
| Sleep rate | |
| Initial conditions |
| Start the GA process |
| Inputs: The individuals with genes equally representing the decision values of FF-ANN as: |
| , where , , |
| , and as per the details provided |
| in the system (3). |
| Population: Number of chromosomes in a set define a population as: |
| , for ith component |
| with |
| , , , |
| , and |
| Output: The best global decision variables/trained weights of the ANN-GASQ programming scheme denoted as WGA-Best |
| Initialization: Generate chromosome W and P with pseudo random numbers. |
| Initialization is performed for {GA} and {gaoptimset} routines with |
| suitable declarations and settings. |
| Fitness evaluated: Calculate the fitness and its parts shown in Equations (5)–(10) for each {W} in P. |
| Termination: Terminate the procedure, when any requirements meets |
| • {Achieved Fitness = 10−20},{Generations = 60} |
| • {Tolerances: {TolFun= 10−20 and TolCon =10−21}, |
| • {StallGenLimit=100},{Population size = 300} |
| • Others values: default. |
| When the above conditions meet, go to storage |
| Ranking: Rank is proficient for every ‘W’ of ‘P’ indicates the attained |
| fitness. |
| Reproduction: |
| • {Selection: selectionuniform} |
| • {Mutations: mutationadaptfeasible}. |
| • {Crossover: crossoverheuristic}. |
| • {Elitism: Transmit 5% individuals in P} |
| Go to fitness assessment step. |
| Storage: Store the WGA-Best, i.e., the weight vector, fitness assessment, |
| generations, time and count of functions for the present run of |
| GAs. |
| End of GA |
| SQP Process Start |
| Inputs: Start point is WGA-Best |
| Output: GASQP best weights are denoted as WGASQ |
| Initialize: Set the limited constraints, iterations and other values of |
| optimset. |
| Terminate: The SQ programming process terminates when one the criteria |
| meets |
| {Generations = 900}, {Fitness = 10−18}, |
| (TolFun = TolCon = TolX = 10−22) and {MaxFunEvals = 285000}. |
| While (Terminate) |
| Fitness Evaluate: Compute fitness value of every W of P by using |
| system (4) to (10). |
| Adjustments: Fine-tune {fmincon} with SQ programming scheme to tune |
| W and adjust again the fitness value by using systems (4) to (10). |
| Accumulate Store fitness, time, WGASQ, function counts and generations for multiple trials of SQ programming. |
| End of the SQ programming scheme |
| Data Generations |
| Repeat the procedure 30 times based on the GASQ programming to get a |
| massive dataset of the optimization variables of ANNs for numerical |
| solutions of the SITR model based on COVID-19 |
| Symbol | Parameter Description | Assigned Value |
|---|---|---|
| Contact rate | 0.3 | |
| Natural birth rate | 0.3 | |
| Reduce infection from the treatment | 0.3 | |
| Fever, tiredness, and dry cough rate | 0.005 | |
| Recovery rate | 0.1 | |
| Death rate | 0.25 | |
| Rate of infection from the treatment | 0.3 | |
| Healthy food rate | 0.2 | |
| Sleep rate | 0.1 |
| Scenarios | Variable Parameter | Case I | Case II | Case III | Case IV |
|---|---|---|---|---|---|
| 1 | Contact Rate | = 0.25 | = 0.30 | = 0.35 | = 0.40 |
| 2 | Recovery Rate | = 0.08 | = 0.10 | = 0.12 | = 0.14 |
| 3 | Death Rate | = 0.20 | = 0.25 | = 0.30 | = 0.35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umar, M.; Sabir, Z.; Raja, M.A.Z.; Shoaib, M.; Gupta, M.; Sánchez, Y.G. A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics. Symmetry 2020, 12, 1628. https://doi.org/10.3390/sym12101628
Umar M, Sabir Z, Raja MAZ, Shoaib M, Gupta M, Sánchez YG. A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics. Symmetry. 2020; 12(10):1628. https://doi.org/10.3390/sym12101628
Chicago/Turabian StyleUmar, Muhammad, Zulqurnain Sabir, Muhammad Asif Zahoor Raja, Muhammad Shoaib, Manoj Gupta, and Yolanda Guerrero Sánchez. 2020. "A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics" Symmetry 12, no. 10: 1628. https://doi.org/10.3390/sym12101628
APA StyleUmar, M., Sabir, Z., Raja, M. A. Z., Shoaib, M., Gupta, M., & Sánchez, Y. G. (2020). A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics. Symmetry, 12(10), 1628. https://doi.org/10.3390/sym12101628







