Abstract
It is the intention of the current study to suggest a trajectory for the advancement of prospective mathematics teachers’ use of meta-cognitive skills in solving mathematics-based programming problems with Scratch. Scratch is a code-based program that can be utilized in teaching various disciplines, especially geometry and its rich range of subjects such as the topic of symmetry. The present study suggests that advancing prospective teachers’ meta-cognitive skills in the Scratch environment could be done through problem solving and negotiations. The present paper analyzed the implementation of the trajectory by two pedagogic supervisors who attempted, in the frame of one-year preparation (2018–2019), to educate 18 prospective teachers to use meta-cognitive skills in mathematics-based programming activities, where this attempt was based on problem solving and negotiation processes. Data were collected through videoing and recording the learning sessions of the prospective teachers and was analyzed using deductive and inductive constant comparison methods. The deductive analysis utilized theoretical models of meta-cognitive processes and negotiation processes. The research results indicated that the negotiation processes supported the development of the prospective teachers’ meta-cognitive processes in solving mathematics-based programming problems with Scratch.
1. Introduction
Tools and strategies are suggested as means that empower students in their mathematics problem solving activity. Two such tools and strategies are technology (e.g., [1,2]), especially programming (e.g., [3]), and meta-cognition (e.g., [4,5,6]). For tools and strategies to be effective in processes of teaching and learning, an expert teacher is needed, which indicates the need for prospective teachers’ preparation in the utilization of tools and strategies in the classroom processes. This is especially true for a programming environment that is considered a fruitful environment for students’ learning [3]. The previous argument is supported by researchers’ call for new approaches in integrating technology in education during the teacher education programs, which would result in digitally competent teachers [7].
Scratch utilization in mathematics has been considered a factor that assists students’ and prospective teachers’ learning of mathematical concepts and relations, specifically on the topic of symmetry (e.g., [8]). This is especially important as symmetry is one of the main concepts in mathematics. Yanofsky and Zelcer [9] argue that considering mathematics on the basis of symmetry can help in answering important questions as to what mathematics is, why we are certain of mathematics, and why we see the semantics of mathematics in line with the semantics of scientific discourse (p. 495).
In light of the above, Scratch is a functional tool in mathematics, especially for the learning of symmetry concepts and relations, as symmetry concepts and coding enrich each other [10]. Here, we are interested in other transformation concepts such as rotation. Scratch helps mathematical concepts emerge as meaningful concepts, where meta-cognition supports this emergence as it entails monitoring and regulating processes that are done through evaluating questions [11]. In the social environment of the mathematic class, negotiations and problem solving are two important aspects of mathematics, wherein they monitor the work of students in a technological environment [12], in this case a programming one. The current research verifies how problem solving and negotiation processes, during practical training, support prospective teachers in developing their knowledge of meta-cognitive skills in solving mathematics-based programming problems.
2. Literature Review
Education systems show interest in introducing programming to schools in many countries around the world, both through the school curriculum and through after-school activities [13]. This programming is suggested as part of the technology curriculum in schools or as an environment for teaching other subjects such as mathematics. Programming provides an environment to write clear, accurate, executable, and verifiable forms for solving problems. Therefore, learning how to program has the potential for enhancing higher order thinking skills [14] and logical reasoning [15]. This programming is not new, especially in mathematics education, as programming, such as Logo, was suggested for the learning of mathematical ideas since the emergence of computers (e.g., [16,17]). Mathematics education researchers (e.g., [3]) emphasized that the Logo environment facilitates children’s manipulation of objects that represent mathematical ideas, which helps the connection between concrete Logo experiences and the associated mathematical ideas. Programming in Logo also has a positive effect on problem-solving, spatial reasoning ability [18], divergent thinking, and meta-cognition [19]. Scratch, which is related to Logo language [20], is at least expected to be similar to Logo in making the connection between the visual and symbolic objects in Scratch and the mathematical ideas.
2.1. Scratch in Problem Solving
Researchers define Scratch as a block-based visual programming language that users program by using code blocks that they sequence to create a program. This block-based programming requires an efficient pedagogy to make it an effective tool for the consideration of mathematics in Scratch programming activities [21,22].
Taylor et al. [12] found that Scratch could encourage students to study cooperatively and to use problem-solving processes such as goal setting and generating and testing of ideas when learning mathematics. Rodríguez-Martínez et al. [23] found that Scratch can be used to develop both sixth-grade students’ mathematical ideas and computational thinking. Calder [24] examined how mathematical thinking emerges among children who work with Scratch. The research results indicated that Scratch positively affected the children’s affective aspects of learning. These aspects included their engagement in mathematical learning and their motivation to explore mathematical concepts.
Little research has been done on meta-cognition in the Scratch environment. One attempt to do so was by Cho et al. [25], who reported that using a game developing programming with Scratch significantly improved the meta-cognition of middle school students in a programming class. Here, we attempt to verify how prospective teachers would develop their meta-cognitive processes in mathematics-based programming problems in the Scratch environment.
2.2. Meta-Cognition in Problem Solving
Meta-cognition is considered as a cognition about cognition or knowledge about knowledge. The study in [26] used the term “metacognition” to refer to the individual’s awareness, consideration, and control of her/his own cognitive processes/strategies. Since then, a variety of definitions has been given to “metacognition”. The authors in [27] argues that the given definitions of meta-cognitive processes emphasize the monitoring and regulation of cognitive processes. Moreover, the study in [5] argued that meta-cognitive processes promote effective understanding through fine-tuning the cognitive processes used in the activity. Furthermore, the authors in [28] stated that meta-cognitive processes affect cognitive processes through coordinating them, which affects students’ academic success. Schoenfeld [29] emphasizes the dynamic interaction between the mathematical concepts and processes, such as the meta-cognitive ones that are utilized to solve mathematical problems. Saying that, he argues that the meta-cognitive processes develop simultaneously with the mathematical insight related to the mathematical concepts. Thus, meta-cognition could be related to sense-making in mathematical learning, as it develops students’ mathematical insight. Thus, using meta-cognition in the mathematics classroom meets the emphasis of educational institutions about the need to teach mathematics using methods that emphasize sense-making (e.g., [30]).
Researchers argued that meta-cognition is composed of two different components connected to each other: meta-cognitive knowledge and meta-cognitive skills [31]. A different categorization of meta-cognition is that of the author of [32], who defined meta-cognition as related to person, the task, and the strategy. At the same time, meta-cognitive skills involve planning, monitoring, evaluating, and regulating the processes leading to attaining objective. The authors of [33] described a theoretical framework that includes the following meta-cognitive skills: encoding, representation, decomposition, planning, selecting strategy, monitoring, evaluating, and suggesting other strategies. In the present study, we focused primarily on meta-cognitive skills, utilizing the previous framework to introduce meta-cognition to prospective mathematics teachers. To do so, we utilized problem solving and negotiations as tools for developing the intended learning and teaching strategies among the participating prospective teachers.
Utilizing the previous framework, we operationalized the previous processes in the following way: encoding (writing the main words in the problem and appropriate symbols for them); representation of the givens (representing the givens algebraically or visually as using a graph); problem decomposition (writing equations for each given); planning (writing a sequence of steps for the solution); selecting and implementing strategies to reach the goal (considering all the strategies that could solve the problem or a sequence of strategies); monitoring of the plan (assessing the advancement of the solution process in terms of reaching the goal); evaluating the solutions (evaluating the correctness of each step); searching for other solutions (assessing whether other solutions exist); evaluating the strategies used (assessing whether the chosen strategies helped in arriving at goals); and searching for other strategies (looking for other strategies that could improve and make the solution process more effective).
2.3. Problem Solving and Negotiations as Tools for Educating Learners and Teachers
Problem solving is suggested as a learning and teaching method in programming and mathematics classrooms. Researchers connected between programming and problem solving (e.g., [34,35]), while others found that programming does not significantly enhance students’ problem solving (e.g., [35,36]).
Lambdin [37] says that problem solving assists the student in understanding mathematical ideas and relations. Stein et al. [38] argued that problem solving assists the teacher in supporting students in their learning of mathematics. In addition, they state that conversations among teachers who are working to implement problem solving approaches provide the teachers with opportunities to advance their implementation. Negotiations through conversations are also vital when teachers, prospective teachers in our case, intend to develop their implementation of meta-cognitive processes in the solving of mathematics-based programming problems.
Problem solving and negotiations are also suggested for teacher education. Blanco [39] suggests problem solving as reference for teacher education, especially for prospective teachers, in order to create learning environments, referred to as “learning to teach mathematics” (p. 31). One study [4] describes the use of problem solving as a tool to educate prospective teachers in using meta-cognitive processes to solve mathematical problems with mobile tools. In addition, researchers point at negotiations as part of the learning in the community of inquiry. Jaworski [40] describes negotiations between teachers as part of an inquiry community. Here, the emphasis is on using problem solving and negotiations to assist the development of prospective teachers’ meta-cognitive processes in carrying out mathematics-based programming activities.
Models were suggested for negotiation and problem solving. One model of negotiation was developed by Baker [41], who considers negotiation as having learning and interaction goals, problems to be solved, answers to them, topics to be addressed, and explanations, etc. The negotiation, according to Baker [41], has the following components: initial state, negotiation process, final state. The initial state contains the common goal of interacting with the expectation that some learning will take place. The final state includes an agreement with respect of part or all of the initial state. The negotiation processes include examinations of the initial state where different points of views interact.
Montague and Applegate [42] suggested that the framework of problem solving should include the following processes: reading, paraphrasing, visualizing, hypothesizing, estimating, computing, and checking. Montague et al. [43] gave the following descriptions: reading (reading the entire or part of the problems and using key words as clues), paraphrasing (restating the problem), visualizing (referring to drawing, a picture, or a diagram, or making a mental image), hypothesizing (conjecturing a solution for a problem), estimating (predicting an answer or making an “educated” guess), computing (verbalizing computations as they are performed), and checking (checking answers).
3. Research Rationale, Goals, and Questions
3.1. Research Rationale and Goals
Researchers point out that the introduction of programming, such as the Scratch environment, into the school needs to be studied in order to shed light on the several aspects of the introduction such as the cognitive aspects. Specifically, Benton [44] states that research is needed to investigate programming’s effect on learning other subjects such as mathematics. The previous note points out that researchers consider programming a candidate for enriching the curriculum, which points at the need to take care of this tool in teachers’ preparation.
In addition to the above, Benton [44] argues that primary teacherslack the appropriate skills to teach programming, as they are typically generalists. They conclude that this situation points to the need for professional development to support primary teachers in gaining the necessary experience, skills, and confidence in order to teach programming curriculum successfully. We argue that there is also a need for computer and mathematics prospective teachers to participate in training that focuses on mathematics-based programming problems. This need is especially functional as the prospective teachers develop their meta-cognitive skills in solving mathematics-based programming problems. In previous research, we studied the development of prospective teachers’ skills in using meta-cognition, such as in the case of learners and teachers of mathematics in the technological environment (e.g., [4,45]). In the current research, we focus on the development of prospective teachers’ meta-cognitive skills in solving mathematics-based programming problems. This study is especially needed, as little research has been done on the development of meta-cognitive skills in relation to solving programming problems that utilize mathematical thinking.
3.2. Research Question
How would prospective teachers develop their meta-cognitive skills in solving mathematics-based Scratch programming problems as a result of engaging in problem solving and negotiations?
4. Materials and Methods
4.1. Research Context and Participants
The professional development (PD) program was held for a full academic year (2018–2019). Eighteen prospective teachers aged 20–30, with mean age = 22.07 and SD = 2.37, participated in the PD program. A total of 16 of the participants were female, while 2 were male. They were in their third academic year majoring in teaching mathematics and computer science in middle school. Two of the authors were the pedagogical supervisors (PSs) of the participating prospective teachers (PTs). They accompanied the prospective teachers in their practical training in 2 middle schools. The education of the pre-service teachers in meta-cognitive skills was based on the work of Davidson and Sternberg, [33] (see above), with special emphasis on using the Scratch environment for programming as a means for drawing geometric shapes or developing knowledge of other mathematics fields such as algebra. In addition, special attention was given to using meta-cognitive skills in the Scratch programming processes.
The PD program sessions related to utilizing meta-cognitive processes in solving mathematics-based programming problems are described in Table 1. Sessions that are not mentioned did not relate to the research topic.

Table 1.
The professional development (PD) program sessions.
4.2. Data Collection and Analysis
4.2.1. Data Collection Tools
The data were collected through 2 forms of tools: video recording of some preparation workshops held each day after the actual practical training in the schools, and the prospective teachers’ texts for the solutions of the problems that the PSs requested them to solve in the Scratch environment using meta-cognitive skills individually or in small groups. Below, we elaborate on each collection tool.
Video Recording
While the prospective teachers solved the mathematics-based programming problems with Scratch, we video-recorded them and their computer screens. The video recording was done with a computer program that captured the footage in two different windows, one for the computer screen and one for the student. The video recording included negotiations between the PSs and the whole class, as well as negotiations among the prospective teachers when they worked in small groups.
The Prospective Teachers’ Solution Texts
While the prospective teachers solved the mathematics-based programming problems with Scratch, they described their solution processes in terms of use of the meta-cognitive processes, in terms of problem-solving processes, and in terms of programming processes. We requested the students to deliver to us their solution texts, and all of them agreed to do so.
4.2.2. Data Analysis Tools
To analyze the data, we used inductive qualitative content analysis. Inductive qualitative content analysis is a process designed to condense raw data into categories or themes on the basis of valid inference and interpretation that use inductive reasoning. Deductive reasoning can also be used with the goal of generating concepts, categories, themes, or variables from theory [46]. Using deductive reasoning, we looked for themes related to meta-cognitive processes such as in Davidson and Sternberg [33]. In addition, for negotiation processes, we looked at processes as described in Baker [41], where these processes included initial situation, contribution from the participants in the dialogue regarding this initial state, and refinement of the initial state of affairs.
Using the inductive reasoning, we tried to find out if additional themes related to meta-cognitive skills, problem solving and negotiations, and those not given in the literature were present in the data. In the inductive reasoning, we followed our previous utilization of these methods (e.g., [47,48]). To elaborate more, the inductive reasoning consisted of looking for sentences that symbolize a phase of development regarding the use of meta-cognitive processes or the knowledge of Scratch programming. For example, sentences that included “At the beginning I thought how to arrive at the lengths of the sides” indicated a phase in which the prospective teacher uses the “planning” meta-cognitive skill.
To elaborate on the deductive analysis, when we came upon a sentence that includes an interaction between the instructor and a prospective teacher or two prospective teachers, where this interaction included one of the processes mentioned by Baker [41], we considered the sentence as indicating negotiation. To consider a sentence as indicating meta-cognitive process, we looked for occurrences of one of the following processes: encoding, representation, decomposition, planning, selecting strategy, monitoring, evaluating, and suggesting other strategies. To consider a sentence as indicating a problem-solving process, we looked for occurrences of one of the processes mentioned by Montague et al. [42,43]: reading, paraphrasing, visualizing, hypothesizing, estimating, computing, and checking.
Table 2 describes the words used when deciding upon a sentence as including a theme related to the meta-cognitive process, negotiation process, or problem-solving process. In addition, examples of a sentence are given for the occurrence of these words.

Table 2.
Occurrences of themes related to the research variables.
4.2.3. Validity and Reliability of the Analysis
The validity of the research analyzing processes is a consequence of the analysis method that ensured the theoretical saturation. This theoretical saturation is a result of the existence of themes and categories, which ensures that no new category type will emerge. Describing the categories also ensures that they are well developed in terms of their properties and dimensions’ variation ([49], p. 212). Lincoln and Guba [50] state that no validity ensures reliability, and thus satisfying validity also ensures reliability. This means that theoretical saturation keeps not only the validity of the research procedure but its reliability as well. Further, two experienced coders (two of the authors) coded the resulting themes and categories, searching for occurrences of development phases in using meta-cognitive processes for solving mathematics-based programming problems in the Scratch environment. The agreement between the coders (Cohen’s Kappa coefficient), when satisfied, ensures the reliability of the qualitative coding. The computation of Cohen’s Kappa coefficient resulted in 0.87 to 0.93 for the various categories related to the development phases and their characteristics. These values are accepted for the agreement between coders.
5. Results
The present research intended to examine the processes of prospective mathematics and computer teachers in developing their meta-cognitive processes in solving mathematics-based Scratch programming problems as a result of engaging in problem solving and negotiations. The research results indicated that the following trajectory of development processes assisted the prospective teachers’ development in using meta-cognitive skills in their solving of mathematics-based programming problems: (1) negotiating the skills needed for solving the programming problems: programming skills and meta-cognitive skills; (2) problem solving for developing the prospective teachers’ knowledge of Scratch programming; (3) negotiating the meta-cognitive processes with Scratch programming when the prospective teachers solve programming problems individually; (4) negotiating, in groups, the meta-cognitive skills with Scratch; and (5) negotiating, independently, the use of meta-cognitive skills in programming with Scratch. Below, we describe each of the trajectory processes, but first we describe the initial awareness of the prospective teachers regarding using meta-cognitive skills in programming.
5.1. Problem Solving for Setting the Educating Stage: Assessing the Meta-Cognitive Skills of the Prospective Teachers in Solving Mathematical-Based Programming Problems Using Scratch
Setting the stage for educating the prospective teachers to use meta-cognitive processes in Scratch programming was performed through assessing the prospective teachers’ meta-cognitive processes for solving programming problems. This setting of the stage was performed in the context of drawing a geometric figure through programming in Scratch. The participating prospective teachers were requested to draw a canonic-square shape using Scratch programming in addition to writing the steps of this Scratch programming.
Figure 1 shows the text of the problem given to the prospective teachers.
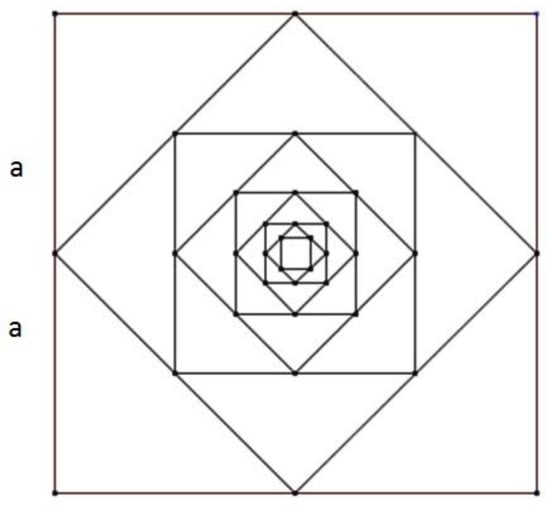
Figure 1.
The first problem given to the prospective teachers.
The following shape includes a canonic-square shape: “You are requested to draw these squares with Scratch. Doing so, you need to write the steps of your drawing, how you planned this drawing, and how you proceeded in this drawing.”
The participants at this stage worked individually, each trying to recognize the potentialities of Scratch that would help draw the sequence of squares imbedded through rotation in each other. The following is part of a prospective teachers’ solution in the frame of this assessment:
“First, we ask about the square side length and set it as a variable, say “side length”. We need a loop of repetition in which, we draw a square of length (side length), then we need to reach the midpoint of the square side. After that, we rotate with 45 degrees to the right and then switch the square length and set it as “((side length)/2) * ”
The previous solution of Salam, a prospective teacher, was suggested at the beginning, intuitively, before the prospective teachers were prepared or exposed to any meta-cognitive skills. At that stage, only Salam succeeded in solving the given problem using her intuitive meta-cognitive skills and mathematics knowledge, while the other prospective teachers used trial and error programming without performing meta-cognitive processes, and they failed to complete the programming of the required shape properly.
5.2. A Trajectory of Problem Solving and Negotiation Processes as Means for Prospective Teachers’ Education
Below, we describe the trajectory of problem solving and negotiation processes in which the prospective teachers were engaged in order to advance their knowledge and experience in utilizing meta-cognitive skills in solving mathematics-based programming problems.
5.2.1. Negotiating the Skills Needed for Solving the Programming Problems: Programming Skills and Meta-Cognitive Skills
Two issues were discussed at the beginning: the potentialities of programming geometric shapes in Scratch and the awareness for using meta-cognitive skills in this programming. Excerpts 1 and 2 are two examples on the discussions between the two PSs and the prospective teachers (PTs) regarding the two issues. In excerpt 1, the discussion is about the potentialities of Scratch for drawing geometric shapes.
- PT:
- I write N but nothing happens in the program.
- PS1:
- You need to go to DATA and drag the variable N, not writing it.
Excerpt 1: Potentialities of Scratch for drawing.
Excerpt 1 shows an initial situation in which the prospective teacher was still struggling technically to program in Scratch. The prospective teacher and the pedagogic supervisor contributed to the conversation, where the initial situation was refined to become a situation in which the prospective teacher was more knowledgeable regarding programming in Scratch.
In Excerpt 2, the discussion is about meta-cognitive processes in solving a programming problem with Scratch.
- PS2:
- Salam, could you describe what you did in order to draw the shape?
- Salam:
- At the beginning, I draw the whole shape on a paper and wrote its mathematical properties on the drawing, so that I can begin to think about drawing it in Scratch.
- PS2:
- How did you program the drawing of the second square?
- Salam:
- Depending on the first.
- PS2:
- O.K. Can you tell us what you thought when you first saw the problem?
- Salam:
- At the beginning I thought how to arrive at the lengths of the sides and the measure of the angles of the second square in order to draw it.
- PS2:
- Have not you done anything before?
- Salam:
- No.
- PS2:
- Have not you written first the lengths of the first square.
- Salam:
- Yes, I did.
- PS2:
- We need to be aware of each step in our solution process.
- Salam:
- You are right. This awareness will help us keep track of our solution process.
Excerpt 2: Cognitive and meta-cognitive processes in solving a programming problem with Scratch.
Excerpt 2 shows an initial situation in which the PT does not describe the meta-cognitive processes she may have used (R50–R53), which makes the PS assume that the PT is not aware of the meta-cognitive activity. This led the PS to attract the attention of the PT to meta-cognitive issues: decompositions (R54) and planning the solution (R56, R60). This dialogue refined the initial situation into a situation in which the PT was aware of the meta-cognitive processes (R61).
5.2.2. Negotiating a Model of Meta-Cognitive Skills:
The negotiation related to meta-cognitive skills in solving programming problems continued between the PSs and the prospective teachers, where the PSs described a model of meta-cognitive skills by [24] that described a theoretical framework that included the following meta-cognitive skills: encoding, representation, decomposition, planning, selecting strategy, monitoring, evaluating, and suggesting other strategies.
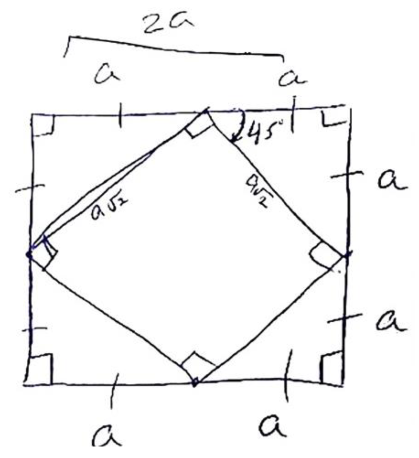
Excerpt 3 shows a discussion between one of the PSs and a PT in front of the whole class, where the PS tried to lead the PT into acknowledging one meta-cognitive skill, namely, the representation skill.
- PS1:
- Huda, could you describe what you did in order to solve the problem?
- Huda:
- Computations.
- PS1:
- Computations! O.K. What were the givens in the problem?
- Huda:
- A square.
- PS1:
- The drawing is part of the givens. We need to consider the unknowns.
- Huda:
- The length of the square.
- PS1:
- [The PS wrote on the board “Unknowns: length of the square = 2a”]. What else?
- Huda:
- The angle of rotation.
- PS1:
- [PS1 wrote on the board in the Unknowns item: “angle of rotation = β”]. What else?
- Huda:
- The number of squares.
- PS1:
- No. This number could be endless. [5] We can say “the side length of the next square” [PS1 adds the new variable to the unknowns item]. We need to take account of these variables. To solve the problem, what did you do Huda? [3]. You drew on paper. Right?
- Huda:
- Right.
- PS1:
- You drew a square, and then drew the next square. [The PS drew the shapes on the board]. Huda, come and tell us the rest.
- Huda:
- [She went to the board] I named this “a” and this “a” [The PT pointed at the appropriate line segments]. What is the problem here? To know the angle of rotation = β, and to know the side length of the next square
- PS:
- [The PS put “?” beside the side of the next square]. We name this the representation of the problem.
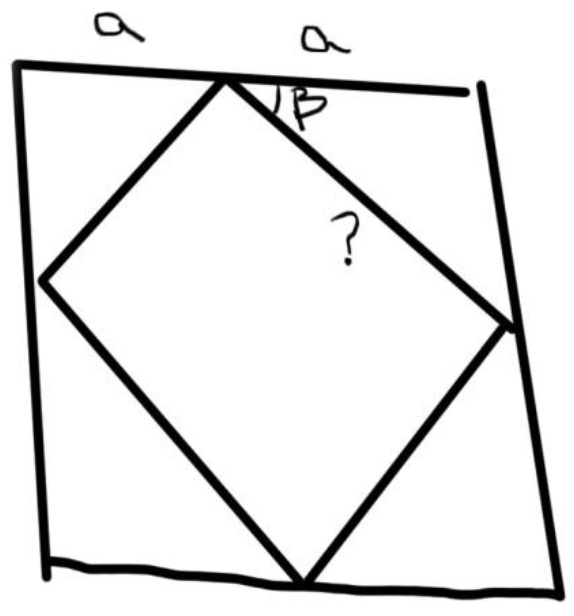
Excerpt 3: Acknowledging one meta-cognitive skill—the representation skill.
Excerpt 3 shows an initial situation in which the PTs were ignorant of meta-cognitive models that could direct the meta-cognitive activity of the learner. This initial situation led the PS to negotiate the meta-cognitive model with the prospective teachers.
This was done by the PS when he led the PT into “considering the unknowns of the problem” (R105), which is the first meta-cognitive skill in the model in [24]. The contribution of the PS and the PT through their interaction (especially R105–R115) refined the initial situation into one in which the PTs became aware of the representation skill in the model of [24].
5.2.3. Problem Solving for Developing the Prospective Teachers’ Knowledge of Scratch Programming
The PSs, besides introducing the meta-cognitive model to the prospective teachers, wanted to make sure that the participants were in control of programming with Scratch. They did this through problem solving related to requesting the prospective teachers to draw geometric shapes in Scratch, and afterwards discussing their programming. Excerpt 4 shows a related discussion between the PSs and the prospective teachers.
- PS1:
- O.K. Let us look at the solution of Salam to assess its accuracy. [The PS started to read every block of the Scratch program and discus its accuracy]. “ask what’s the length? and wait”. This block is to input the length of the square “2a”. O.K. seems good. “Set side length to answer”. The answer means the length of the side of the square. O.K. seems good. Afterwards “Repeat 10”. What is this?
- PTs:
- The number of squares.
- PS1:
- The number of squares. O.K. Afterwards “Repeat 4”. Each loop of the first repeat involves a repeat of 4 times doing some drawing.O.K. “move side length steps” and “turn 90 degrees”. What did we do here?
- PTs:
- This is to draw a square.
- PS1:
- O.K. what did we do after drawing a square?
- PTs:
- These blocks prepare the drawing of the next square starting at the midpoint on the side of the current square, and do rotation of 45 degrees. Then set the side length of the next square as the side length of the current square multiplied by . When performing the next loop in the first repeat, the next square will be drawn.
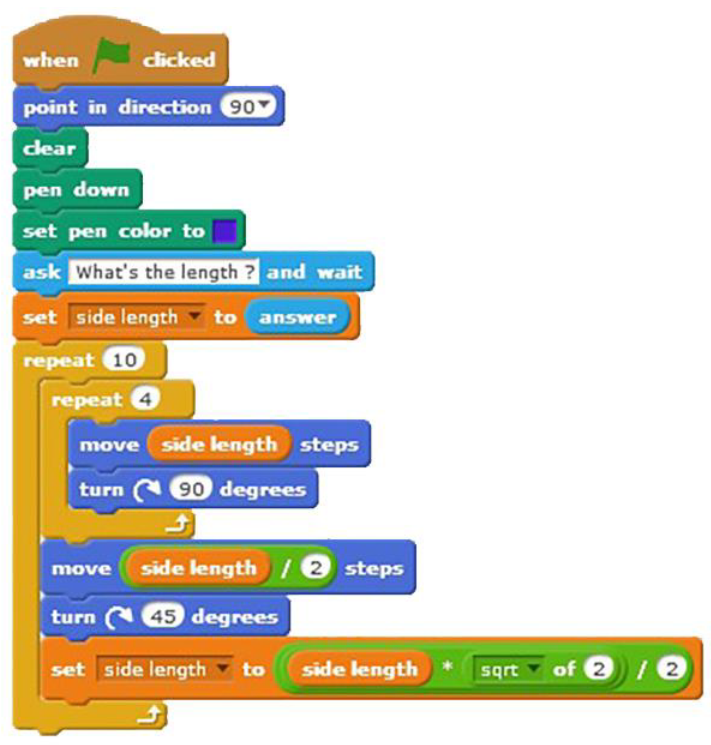
Excerpt 4: Scratch programming.
Excerpt 4 shows an initial situation in which the PTs started to work in the Scratch environment. The PS intended to advance the PTs’ knowledge of mathematics-based programming in the Scratch environment through drawing a geometric shape that was suggested by one of the PTs. Doing so, the PS assessed the prospective teachers’ knowledge of Scratch programming by asking about specific lines in the Scratch program, as, for example, when he asked: “Afterwards ‘Repeat 10’. What is this?” (R150), or when he asked: “O.K. ‘move side length steps’ and ‘turn 90 degrees’. What did we do here?” (R152). Moreover, the PSs emphasized the mathematical concepts and procedures needed to complete the programming problem (as in R154, R155), where this emphasis is related to the need for mathematical thinking and skills in the representation and planning skills in the meta-cognitive processes. The interaction between the PSs and the PTs in the frame of the problem-solving activity refined the PTs’ expertise regarding Scratch programming.
5.2.4. Negotiating the Meta-Cognitive Skills with Scratch Programming when the Prospective Teachers Solved Programming Problems Individually
The PSs’ consideration of the knowledge of the prospective teachers regarding programming with Scratch was a first step towards working for relating programming with Scratch to meta-cognitive skills. Thus, the initial situation did not include this relatedness. To attempt to do this relatedness, the PSs discussed the prospective teachers’ programming when they worked as individuals, as related to the various meta-cognitive processes. Excerpt 5 shows a discussion on this relatedness during the PTs’ attempt to draw a circle with Scratch as a step towards solving the mathematical-based programming problem of drawing two tangents to two given circles from a given point outside the two circles (Figure 2).
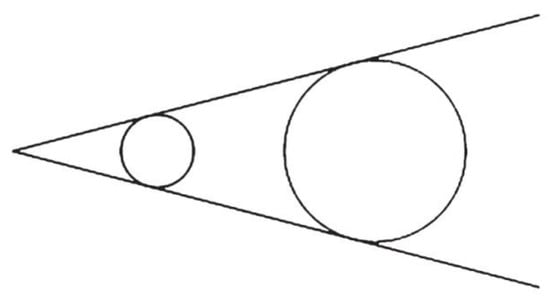
Figure 2.
Two tangents to two given circles from a given point outside the two circles.
- PS1:
- As you say, at the beginning we need to program the shape of a circle. How do you suggest doing this programming?
- Saed:
- My method starts from the center. It depends on using the radius. The goal is to draw the point on the circumference of the circle as the end point of the radius. The radius will not be drawn, for it is used to draw the end point only. We move from the center to the end point and return to the circle center. We turn each time one degree and repeat the procedure until we draw something like 360 points.
- PS1:
- This strategy seems promising. Can you please try to carry out the strategy described by Saed?
- PTs:
- [The prospective teachers got engaged individually with implementing the strategy described by Saed using Scratch].
- PS1:
- Can you write a Scratch description, not necessarily code, of the method described by Saed.
- PTs:
- [The prospective teachers got engaged in writing a more exact Scratch-version of the strategy described by Saed].
- Rola:
- I wrote the following: Go to (x,y) representing the center of the circle. Repeat 360 times the following steps: Move from the center a distance that equals the radius, when the pen is up. Put the pen down to draw a point, then turn 180 degrees, put the pen up and move a distance that equals the radius until you arrive at the center. Turn 180 degrees and then one more degree. Add a counter so that we see the frequency of the repetition during the drawing. This counter starts at one in the block “set a to 1”, and at the end of each loop, the value of “a” changes through “set a to a + 1”.
- PS1:
- Great Rola. Do you think there is another strategy to draw a circle using Scratch?
- Huda:
- I think I got one. It is trigonometry-based. We start from an angle Alpha that measures zero degrees. We repeat 360 times the following steps: define the value of x coordinate for a point on the circumference of the circle: x = the x coordinate of the center + Radius * cos (Alfa). We then define the value of y coordinate for the same point on the circumference of the circle: y = the y coordinate of the center + Radius * sin (Alfa). We put the pen down to draw the point. Then turn one degree and increase Alfa by one degree through “set Alfa to Alfa + 1”. We continue to draw the points one beside the other.
- PS1:
- Fine Huda. [PS1 talks to the whole class] What do we conclude from Saed’s and Huda’s strategies for drawing a circle using Scratch?
- PTs:
- We need to look for more than one strategy to work with Scratch?
- PS1:
- Why do we need to do that?
- PTs:
- One strategy could be easier or more efficient to perform with Scratch than the other.
- PS1:
- What is the difference between the two strategies of Saed and Huda? You can discuss the difference in pairs or groups.
- PTs:
- [The prospective teachers started to discuss the difference between the two strategies]
Excerpt 5: Discussing the use of meta-cognitive strategies in working with Scratch.
Excerpt 5 describes an initial situation in which the PTs possessed neither knowledge nor experiences regarding the use of meta-cognitive processes in programming with Scratch. When the PS described the strategy as promising, it could thus be tried (R203); the PS indicated indirectly that other strategies could be tried, which encouraged the use of the monitoring meta-cognitive process by the PTs. This indication of the existence of other strategies was expressed directly by the PS (R208). Furthermore, the PS emphasized the need to compare between the strategies (R210), as it is part of the meta-cognitive processes. The contributions of the class’s members (especially in R209–R215) refined the PTs’ knowledge and expertise about the relatedness of meta-cognitive processes to programming in Scratch.
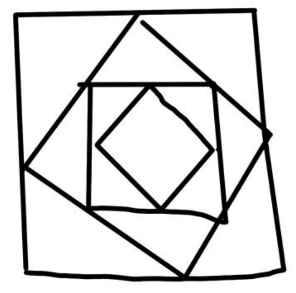
5.2.5. Negotiating, in Groups, the Meta-Cognitive Skills with Scratch
The previous discussion also occurred when the prospective teachers worked on programming geometric shapes with Scratch in groups. The PSs requested the prospective teachers to work in groups in order to program another geometric shape with Scratch. The shape consisted of a sequence of squares, where the vertices of each following square were obtained from the previous square by assigning a point on each side of the previous square. Each point’s distance from the adjacent vertex of the previous square was fixed for the four points (See Figure 3).
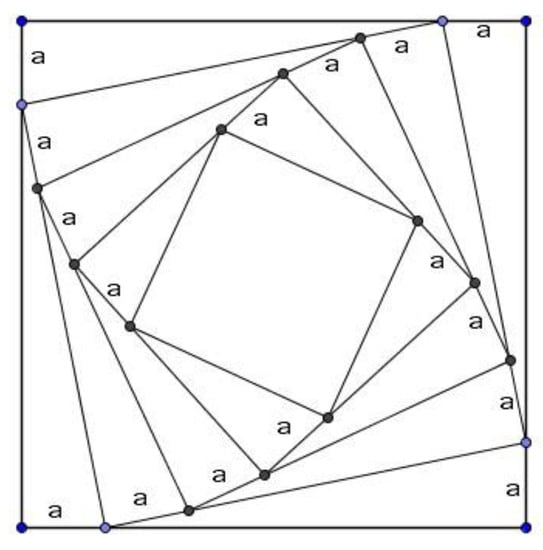
Figure 3.
A geometric shape consisting of a sequence of squares.
The PSs discussed with each group, during the solution process, the negotiations among the group members regarding the meta-cognitive sequence of processes that they were following. After the groups of prospective teachers finished the programming, the PSs had a discussion with them regarding the meta-cognitive skills that they utilized in their programming as well as the mathematical knowledge and thinking that helped them to construct the algorithmic solution of the problem. This discussion was similar to the one in Excerpt 5, where it refined once more the PTs’ knowledge and expertise about the relatedness of meta-cognitive processes to programming in Scratch.
5.2.6. Negotiating, Independently, the Use of Meta-Cognitive Skills in Programming with Scratch
The PSs lessened their intervention in the prospective teachers’ programming. The prospective teachers worked in groups independently to program a new geometric shape consisting of a sequence of triangles (See Figure 4).
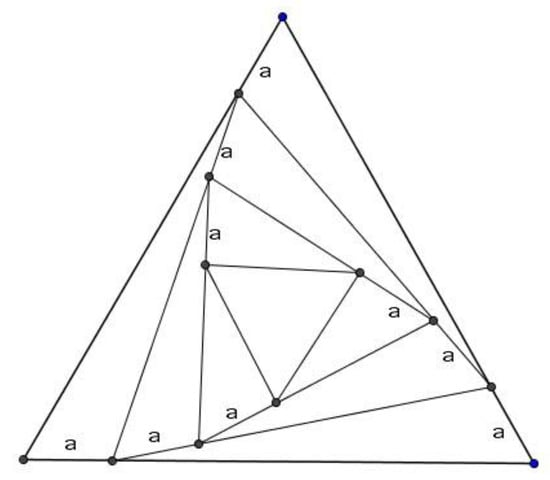
Figure 4.
A geometric shape consisting of a sequence of triangles.
During this programming, the prospective teachers used meta-cognitive skills in their programming, as Excerpt 6 shows.
- Maha:
- It seems there is a problem in the rotation angle, probably in the length of the side too.
- Namarik:
- It could be that the problem is due to the direction of the rotation right/left, or the angle size 120 or −120, or due to a mistake in the algebraic expression of the rotation angle.
- Maisoon:
- Let us go back and check our calculations to be sure of the rotation angle size and the length of the new edge.
- Group:
- [The group members worked again on the calculations]
- Rand:
- We changed the angle size but the mistake is still there. The triangles got turned and moved out. We still have a problem.
- Namarik:
- Maybe we need to change the edge’s length.
- Group:
- [The group members manipulated the geometric shape drawn in Scratch, changing the edge’s length, but without overcoming the mistake.
- Namarik:
- Let us try again to change the angle.
- Group:
- [The group manipulated the angle size and its direction several times].
- Rand:
- [Rand monitored the algebraic expression of the new rotation angle]. Here is the mistake. We missed multiplying by “a”.
- Namarik:
- When the value of “a” becomes negative, the shape gets messed up. We need to add a condition to stop the drawing when “a” turns to be less than zero.
Excerpt 6: Using meta-cognitive processes while solving programming problems in a small group.
Excerpt 6 shows that the prospective teachers as a group used monitoring, regulation, and evaluation in their solving of the programming problem. The use of monitoring occurred, for example, in (R38), observing that there is a problem with the programming. The use of regulation occurred, for example, in (R40) as Maisoon suggested a repeat of the calculations. The use of evaluation occurred, for example, in (R42), where Rand evaluated the programming as problematic. Moreover, in (R44–R48), the group used monitoring and evaluation in Scratch to check their trials and to obtain a better solution.
Table 3 describes the frequencies of the themes related to each phase (category) resulting from the categorization of the data.

Table 3.
Frequencies of the themes related to each phase.
Table 1 shows that, although the prospective teachers were engaged actively in all the phases, they were more engaged when they worked in groups.
6. Discussion
Educating PTs for using new technological tools has attracted the attention of researchers in educational technology, as this education influences teachers’ knowledge and practice as trainees in the schools and as future teachers. The need for educating PTs in the use of technological tools is especially true in the case of programming, as it could be difficult to learn [51]. Szlávi and Zsakó [52] mentioned the problem solving and mathematics contexts as circumstances for teaching programming. In the present research, we followed a trajectory consisting of problem solving and negotiation processes to educate PTs in using meta-cognitive processes in solving mathematics-based programming problems with Scratch. We examined the influence of this trajectory on the advancement of the PTs’ use of such meta-cognitive processes as they come to program geometric shapes with Scratch. The research results indicated that at the beginning of the trajectory, the PTs were not aware of such processes, however, as they advanced in their problem solving, together with the negotiations with the pedagogical supervisors and in the group, they started to use these processes as learners, and gradually this use extended to the programming environment of Scratch. Moreover, the research results indicated that the PTs utilized mathematical thinking and knowledge in the encoding, representation, and decomposition meta-cognitive processes, while they utilized programming thinking with Scratch in the monitoring and evaluating processes. Scratch assistance for advancing the previous specific meta-cognitive processes is due to the visual, dynamic, and friendly interaction properties it provides [11,53]. In the planning and choosing strategy meta-cognitive processes, the research results indicated a combined utilization of mathematical, programming, and algorithmic thinking.
Researchers argue that the education of PTs and in-service teachers contributes to their teaching methods in the classroom [54,55]. Thus, the reported education of PTs in using meta-cognitive skills in solving mathematics-based programming problems will encourage the participating PTs in using meta-cognitive processes as teachers in designing activities and encourage their students to use meta-cognitive processes while solving mathematical-based programming problems.
The research results indicate that meta-cognitive processes for learning and teaching in a programming environment could be learned and developed by teachers, which supports the claim of Ryan and Bagley [56] that “One of the major ways technology-related professional development can be improved is by creating ongoing learning opportunities for teachers” (p. 42). Here, the PTs gained their learning opportunities through multiple forms of problem solving and through negotiations, where these processes enabled them to engage in the practice of meta-cognitive solving of mathematics-based programming problems.
Problem solving and negotiations were contexts for the PTs to try to develop their knowledge and practice in solving mathematics-based programming problems. The activities provided by the PSs had more than one solution strategy based on Scratch programming (such as, for example, programming the circle shape). Negotiating the solutions of the programming problems made the PTs aware of what it means to use different strategies with Scratch programming, which emphasized the importance of considering the meta-cognitive process “choosing a solution strategy” when coming to solve mathematics-based programming problems and mathematical problems in general.
7. Conclusions and Considerations for Practitioners
7.1. Conclusions
To conclude, Sáez-López et al. [57] found that Scratch resulted in significant improvements in innovation, collaboration, active learning, and motivation for prospective teachers. Schmidt-Crawford et al. [58] reported that coding experiences through Scratch and programs similar to it, such as Scratch Junior and Code.org that teach coding, evolves into a commonplace activity for both prospective and in-service teachers. This Scratch and programming experience of coding are needed for prospective and in-service teachers in order to prepare them for teaching programming and mathematics and topics that lie at their intersection such as symmetry.
Prospective and in-service teachers need to engage in programming activities that involve another discipline such as mathematics in order for them to accompany their students in developing skills needed for the 21st century as interdisciplinary skills. Thus, educational institutions need to be concerned about such workshops, not only for prospective teachers, but also for in-service teachers.
The present research suggests that problem solving and negotiations could support PTs, not only in learning coding/programming but also in the development of their meta-cognitive processes for solving mathematics-based programming problems. This education would positively affect their students’ use of meta-cognitive processes [46], especially in an environment of programming such as Scratch, which is pointed out as facilitating mathematics education. Further, by developing their meta-cognitive processes, PTs will positively influence the deeper cognitive processes of the students [5].
7.2. Considerations for Practitioners
We learned that we should not give immediate answers to the learners and allow enough time for them to think and do the work by themselves individually or to negotiate it in groups. Learners’ work needs to be individual at the beginning and then in groups, alongside the assistance of the instructor. Afterwards, the learners should work again individually and then in groups, but instead the work is done independently by the learners. Throughout all the processes, we need to emphasize working in groups and encourage the learners to express their thoughts loudly to each other. In addition, we need to train the learners to listen to the thoughts of others and negotiate these thoughts with tolerance, even when they do not agree with them.
We learned that we need to encourage and even train the learners to follow and monitor their thoughts by expressing them in writing in order to reflect on them. In addition, there is an important place for asking the learners about their thoughts during and after the solution and to negotiate these thoughts together. The learners need to have enough time to solve and negotiate the problems independently.
We learned how to choose the problems given for the learners. The problems need to fit the interaction between the mathematical and the programming contents. The problems need to have different solution strategies, such as the “tangents of two given circles” problem. This would enable the learners to choose one of them and compare between them, which is a meta-cognitive process. The problems need not to be too easy, and thus the learners need to plan their solution, which is another meta-cognitive strategy. It is also important to make sure that the problems are possible to program in Scratch.
Author Contributions
Conceptualization, W.D. and N.B.; methodology, W.D., N.B., O.J., and J.A.S.; formal analysis, W.D., N.B., O.J., and J.A.S.; data analysis: W.D. and N.B.; writing—original draft preparation, W.D.; writing—review and editing, J.A.S. and O.J.; project administration, N.B. and O.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest
References
- Daher, W.; Anabousy, A. Creativity of pre-service teachers in problem posing. Eurasia. J. Math. Sci. Technol. Educ. 2018, 14, 2929–2945. [Google Scholar] [CrossRef]
- Daher, W.; Anabousy, A. Flexibility Processes of Pre-Service Teachers in Problem Solving with Technology. Int. J. Technol. Educ. Sci. 2020, 4, 247–255. [Google Scholar] [CrossRef]
- Clements, D.H.; Sarama, J. Research on Logo: A decade of progress. Comput. Sch. 1997, 14, 9–46. [Google Scholar] [CrossRef]
- Baya’a, N.; Daher, W.; Jaber, O.; Anabousy, A. Educating pre-service teachers in meta-cognitive activities. In Proceedings of the fifth ERME Topic Conference (ETC 5) on Mathematics Education in the Digital Age (MEDA), Copenhagen, Denmark, 5–7 September 2018; Weigand, H.-G., Clark-Wilson, A., Todorova, A.D., Faggiano, E., Grønbæk, N., Trgalova, J., Eds.; University of Copenhagen: Copenhagen, Denmark, 2018; pp. 35–42. [Google Scholar]
- Gavelek, J.R.; Raphael, T.E. Metacognition, instruction, and questioning. In Metacognition, Cognition, and Human Performance; Forrest-Pressley, D.L., MacKinnon, G.E., Waller, T.G., Eds.; Academic Press: Orlando, FL, USA, 1985; Volume II, pp. 103–132. [Google Scholar]
- Daher, W.; Anabousy, A.; Jabarin, R. Metacognition, Positioning and Emotions in Mathematical Activities. Int. J. Res. Educ. Sci. 2018, 4, 292–303. [Google Scholar] [CrossRef]
- Instefjord, E.J.; Munthe, E. Educating digitally competent teachers: A study of integration of professional digital competence in teacher education. Teach. Teach. Educ. 2017, 67, 37–45. [Google Scholar] [CrossRef]
- Dorling, M.; White, D. Scratch: A way to logo and python. In Proceedings of the 46th ACM Technical Symposium on Computer Science Education, Kansas City, MO, USA, 4–7 March 2015; pp. 191–196. [Google Scholar]
- Yanofsky, N.S.; Zelcer, M. The role of symmetry in mathematics. Found. Sci. 2017, 22, 495–515. [Google Scholar] [CrossRef]
- Bolognese, C.A. Writing Code to Assess Geometric Reasoning. Teach. Child. Math. 2016, 3, 236–243. [Google Scholar] [CrossRef]
- Shahbari, J.A.; Daher, W.; Baya’a, N.; Jaber, O. Prospective Teachers’ Development of Meta-Cognitive Functions in Solving Mathematical-Based Programming Problems with Scratch. Symmetry 2020, 12, 1569. [Google Scholar] [CrossRef]
- Taylor, M.; Harlow, A.; Forret, M. Using a computer programming environment and an interactive whiteboard to investigate some mathematical thinking. Procedia-Soc. Behav. Sci. 2010, 8, 561–570. [Google Scholar] [CrossRef]
- Sentance, S.; Csizmadia, A. Computing in the curriculum: Challenges and strategies from a teacher’s perspective. Educ. Inf. Technol. 2017, 22, 469–495. [Google Scholar] [CrossRef]
- Kurland, D.M.; Pea, R.D.; Clement, C.; Mawbry, R. A study of the development of programming ability and thinking skills in high school students. J. Educ. Comput. Res. 1986, 2, 429–455. [Google Scholar] [CrossRef]
- Lai, A.-F.; Chang, W.-C. The learning effect of visualized programming learning on 6th graders’ problem solving and logical reasoning abilities. In Proceedings of the International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2009. [Google Scholar]
- Papert, S. Mindstorms: Children, Computers, and Powerful Ideas; Basic Books: New York, NY, USA, 1980. [Google Scholar]
- Papert, S. The Children’s Machine. Rethinking School in the Age of the Computer; Basic Books: New York, NY, USA, 1993. [Google Scholar]
- Miller, R.B.; Kelly, G.N.; Kelly, J.T. Effects of Logo computer programming experience on problem solving and spatial relations ability. Contemp. Educ. Psychol. 1988, 13, 348–357. [Google Scholar] [CrossRef]
- Clements, D.H.; Gullo, D.F. Effects of computer programming on young children’s cognition. J. Educ. Psychol. 1984, 76, 1051–1058. [Google Scholar] [CrossRef]
- Foerster, K.-T. Integrating programming into the mathematics curriculum: Combining Scratch and geometry in grades 6 and 7. In Proceedings of the 17th Annual Conference on Information Technology Education, Boston, MA, USA, 28 September–1 October 2016. [Google Scholar]
- Grover, S.; Pea, R.; Cooper, S. Designing for deeper learning in a blended computer science course for middle school students. Comput. Sci. Educ. 2015, 25, 199–237. [Google Scholar] [CrossRef]
- Han, B.; Bae, Y.; Park, J. The effect of mathematics achievement variables on Scratch programming activities of elementary school students. Int. J. Software Eng. Its Appl. 2016, 10, 21–30. [Google Scholar] [CrossRef]
- Rodríguez-Martínez, J.A.; González-Calero, J.A.; Sáez-López, J.M. Computational thinking and mathematics using Scratch: An experiment with sixth-grade students. Interact. Learn. Environ. 2020, 28, 316–327. [Google Scholar] [CrossRef]
- Calder, N. Using Scratch: An integrated problem-solving approach to mathematical thinking. Aust. Prim. Math. Classr. 2010, 15, 9–14. [Google Scholar]
- Cho, S.-H.; Song, J.-B.; Kim, S.-S.; Paik, S.-H. The Effect of a Programming Class Using Scratch. J. Korean Assoc. Inf. Educ. 2008, 12, 375–384. [Google Scholar]
- Flavell, J.H. Metacognitive aspects of problem solving. In The Nature of Intelligence Hillsdale; Resnick, L.B., Ed.; Lawrence Erlbaum Associates: Erlbaum, NJ, USA, 1976; pp. 231–236. [Google Scholar]
- Du Toit, S.; Kotze, G. Metacognitive strategies in the teaching and learning of mathematics. Pythagoras 2009, 70, 57–67. [Google Scholar] [CrossRef]
- Panaoura, A.; Philippou, G.; Christou, C. Young pupils’ metacognitive ability in mathematics. In Proceedings of the Third Conference of the European Society for Research in Mathematics Education, Bellaria, Italy, 28 February–3 March 2003. [Google Scholar]
- Schoenfeld, A.H. Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; NCTM: Reston, VA, USA, 1992; pp. 334–370. [Google Scholar]
- National Council of Teachers of Mathematics. A Teacher’s Guide to Reasoning and Sense Making; NCTM: Reston, VA, USA, 2016. [Google Scholar]
- Veenman, M.V.J.; Van Hout-Wolters, B.H.A.M.; Afflerbach, P. Metacognition and Learning: Conceptual and Methodological Considerations. Metacognit. Learn. 2006, 1, 3–14. [Google Scholar] [CrossRef]
- Flavell, J. Cognitive development: Children’s knowledge about the mind. Annu. Rev. Psychol. 1999, 50, 21–45. [Google Scholar] [CrossRef] [PubMed]
- Davidson, J.E.; Sternberg, R.J. Smart problem solving: How metacognition helps. In The Educational Psychology Series. Metacognition in Educational Theory and Practice; Hacker, D.J., Dunlosky, J., Graesser, A.C., Eds.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1998; pp. 47–68. [Google Scholar]
- Chamberlin, S.A. What is problem solving in the mathematics classroom? Philos. Math. Educ. 2008, 23, 1–25. [Google Scholar]
- Kalelioğlu, F.; Gülbahar, Y. The effects of teaching programming via scratch on problem solving skills: A discussion from learners’ perspective. Inform. Educ. 2014, 13, 33–50. [Google Scholar]
- Psycharis, S.; Kallia, M. The effects of computer programming on high school students’ reasoning skills and mathematical self-efficacy and problem solving. Instr. Sci. 2017, 45, 583–602. [Google Scholar] [CrossRef]
- Lambdin, D.V. Benefits of teaching through problem solving. In Teaching Mathematics through Problem Solving: Prekindergarten—Grade 6; Lester, F.K., Ed.; NCTM: Reston, VA, USA, 2003; pp. 3–13. [Google Scholar]
- Stein, M.; Boaler, J.; Silver, E. Teaching mathematics through problem solving: Research perspectives. In Teaching Mathematics through Problem Solving, Grades 6-12; Schoen, H.L., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2003; pp. 245–256. [Google Scholar]
- Blanco, L.J. Problem solving and the initial practical and theoretical education of teachers in Spain. Math. Teach. Educ. Dev. 2004, 6, 31–42. [Google Scholar]
- Jaworski, B. Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. J. Math. Teach. Educ. 2006, 9, 187–211. [Google Scholar] [CrossRef]
- Baker, M. A model for negotiation in teaching-learning dialogues. J. Artif. Intell. Educ. 1994, 5, 199–254. [Google Scholar]
- Montague, M.; Applegate, B. Mathematical problem-solving characteristics of middle school students with learning disabilities. J. Spec. Educ. 1993, 27, 175–201. [Google Scholar] [CrossRef]
- Montague, M.; Warger, C.; Morgan, H. Solve It! Strategy instruction to improve mathematical problem solving. Learn. Disabil. Res. Pract. 2000, 15, 110–116. [Google Scholar] [CrossRef]
- Benton, L.; Hoyles, C.; Kalas, I.; Noss, R. Bridging primary programming and mathematics: Some findings of design research in England. Digit. Exp. Math. Educ. 2017, 3, 115–138. [Google Scholar] [CrossRef]
- Daher, W.; Baya’a, N.; Jaber, O.; Anabousy, A. Developing pre-service mathematics teachers’ meta-cognitive thinking for learning and teaching with mobile technology. Eurasia Proc. Educ. Soc. Sci. 2018, 9, 239–249. [Google Scholar]
- Patton, M.Q. Qualitative Research and Evaluation Methods; Sage: Thousand Oaks, CA, USA, 2002. [Google Scholar]
- Daher, W.; Awawdeh Shahbari, J. Secondary Students’ Identities in the Virtual Classroom. Sustainability 2020, 12, 4407. [Google Scholar] [CrossRef]
- Shahbari, J.A.; Daher, W. Learning Congruent Triangles through Ethnomathematics: The Case of Students with Difficulties in Mathematics. Appl. Sci. 2020, 10, 4950. [Google Scholar] [CrossRef]
- Strauss, A.; Corbin, J. Basics of Qualitative Research: Techniques and Procedures for Developing Grounded Theory; Sage Publications: Thousand Oaks, CA, USA, 1998. [Google Scholar]
- Lincoln, Y.S.; Guba, E.G. Naturalistic Inquiry; Sage Publications: Newbury Park, CA, USA, 1985. [Google Scholar]
- IncRosminah, S.; Md Derus, S.; Mohamad Ali, A.; Ali, M. Difficulties in learning programming: Views of students. In Proceedings of the 1st International Conference on Current Issues in Education (ICCIE2012), Yogyakarta, Indonesia, 16 September 2012; pp. 15–16. [Google Scholar]
- Szlávi, P.; Zsakó, L. Methods of teaching programming. Teach. Math. Comput. Sci. 2003, 1, 247–258. [Google Scholar] [CrossRef]
- Resnick, M.; Maloney, J.; Monroy-Hernández, A.; Rusk, N.; Eastmond, E.; Brennan, K.; Millner, A.; Rosenbaum, E.; Silver, J.; Silverman, B.; et al. Scratch: Programming for All. Commun. ACM 2009, 52, 60–67. [Google Scholar] [CrossRef]
- Sabbah, K.; Kobari, S.; Ahmad, M.A.; Daher, W. The Effect of Education for Future Program on Teachers’ Competencies in a Public School. Univers. J. Educ. Res. 2020, 8, 2890–2897. [Google Scholar] [CrossRef]
- Sahlab, R.; Mukh, Y.A.; Mater, N.; Daher, W. The Influence of Field Training on Pre-service Teachers’ Social Skills for Teaching. Univers. J. Educ. Res. 2020, 8, 4193–4200. [Google Scholar] [CrossRef]
- Ryan, T.; Bagley, G. Nurturing the integration of technology in education. J. Theory Pract. Educ. 2015, 11, 33–50. [Google Scholar]
- Sáez-López, J.M.; del Olmo-Muñoz, J.; González-Calero, J.A.; Cózar-Gutiérrez, R. Exploring the Effect of Training in Visual Block Programming for Preservice Teachers. Multimodal Technol. Interact. 2020, 4, 65. [Google Scholar] [CrossRef]
- Schmidt-Crawford, D.A.; Lindstrom, D.; Thompson, A.D. Coding for teacher education: A recurring theme that requires our attention. J. Digit. Learn. Teach. Educ. 2018, 34, 198–200. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).