Modelling of Material Removal in Abrasive Belt Grinding Process: A Regression Approach

Abstract

This article explores the effects of parameters such as cutting speed, force, polymer wheel hardness, feed, and grit size in the abrasive belt grinding process to model material removal. The process has high uncertainty during the interaction between the abrasives and the underneath surface, therefore the theoretical material removal models developed in belt grinding involve assumptions. A conclusive material removal model can be developed in such a dynamic process involving multiple parameters using statistical regression techniques. Six different regression modelling methodologies, namely multiple linear regression, stepwise regression, artificial neural network (ANN), adaptive neuro-fuzzy inference system (ANFIS), support vector regression (SVR) and random forests (RF) have been applied to the experimental data determined using the Taguchi design of experiments (DoE). The results obtained by the six models have been assessed and compared. All five models, except multiple linear regression, demonstrated a relatively low prediction error. Regarding the influence of the examined belt grinding parameters on the material removal, inference from some statistical models shows that the grit size has the most substantial effect. The proposed regression models can likely be applied for achieving desired material removal by defining process parameter levels without the need to conduct physical belt grinding experiments.

1. Introduction

A compliant belt grinding resembles an elastic grinding in its operating principle, and it offers some potentials like milling, grinding and polishing applications [1]. The abrasive belt grinding process essentially is a two-body abrasive compliant grinding processes wherein the abrasive belt is forced against the components to remove undesired topographies, such as burrs and weld seams, to achieve the required material removal and surface finish [2]. The belt grinding process is widespread in aerospace industries owing to its compliant nature, to machine components of intricate geometry such as fan blades for achieving uniform material removal. Analogous to other abrasive machining processes, many process parameters in the belt grinding impact the material removal performance, which include cutting speed, loading belt tension, the force imparted, infeed rate, workpiece topographies, polymer wheel hardness, wheel geometry and belt topography features, e.g., backing material, grain composition, and grit size [3]. Changing any of these parameters will result in different belt grinding performance. However, the effect will vary from parameter to parameter [4]. Abrasive belt grinding process is highly nonlinear due to the complexity of the underlying compliance mechanism, where some of them remain unknown. The presence of multiple parameters working in different regimes creates a dynamic condition which is not entirely realised well within the workforce. Most belt grinding processes in industry are still primarily based on empirical rules and operator experience. The amount of removed material relies heavily on the distinct local contact conditions, which is completely influenced by the state of the grinding parameters. Material removal in the belt grinding process is determined by force distribution in the contact area between the workpiece and the elastic contact [5]. Zhang et al. [5,6] formed a local grinding model based on support vector regression (SVR) and artificial neural network (ANN) to obtain the force distribution in the contact area between the workpiece and the elastic contact wheel, which offer faster analysis compared to that with the conventional finite element method (FEM). A three-dimensional numerical model to determine the distribution of pressure and real contact and give a better understanding of the material removal mechanism has been presented by Jourani et al. [7]. Ren et al. [3,8] simulated a local process model based to calculate the material removal before machining by calculating the acting force from the information on the local geometry of the workpiece. The result of the simulation offers a methodology to optimise the tool path. Table 1. lists the research outcomes in the literature on abrasive belt grinding to predict material removal and to model the contact conditions.

Table 1. Research efforts so far in modelling of belt grinding process.

Investigators	Contribution
Y. Wang et al. [13]	Developed a controllable material removal strategy to control the acting force and grinding dwell time by modelling the global and local material removal process of belt grinding. A finite element method (FEM) has been adopted to calculate the local force and global grinding model based on the Hertz contact theory.
X. Ren et al. [14]	Established a simulation system using Surfel to visualise the material removal process interactively and to optimise the tool path planning.
S. Wu et al. [15]	Presented a comprehensive platform to simulate the belt grinding system incorporating a kinematic model of the robot for tool path planning, dynamic model of the robot joint, along with the material removal model of the grinding process.
S. Mezgahani et al. [16]	Performed a comparative study of contact pressure and abrasive grit size to material removal keeping parameters such as speed of workpiece, tool hardness, cycle time, coolant, abrasive feed, and tool wear constant. The study showed that a decrease in grain size results in more ploughing action rather than cutting action.
J. Shibata et al. [17]	Offered a metal removal model incorporating the belt wear factor to explain the belt grinding characteristics quantitatively.
A. Khellouki et al. [18]	Theoretically modelled contact conditions between abrasive film and the surface and investigated the effect of average contact pressure, contact duration and the number of active grains in the contact.
V. T. Thien et al. [19] and Y. Sun et al. [20]	Demonstrated that pressure distribution obtained from pressure films can be correlated with a Hertzian model under different loads and hardness of the polymer wheel.
H. Lv et al. [21]	Presented a material removal modelling technique for free-form surface using an echo state network.
W. Wang et al. [22]	Proposed a grinding depth predicting frame working using a local stress model and a local material removal model taking into account the contact wheel deformation.
Y. Sun et al. [11] and V. Pandiyan et al. [23]	Proposed a novel methodology using a dynamic pressure sensor to predict material removal considering belt grinding parameters such as force, workpiece geometry and different types of contact wheel geometry.
Y. J. Wang et al. [24]	Demonstrated that the nonlinear material model performs better than the linear material removal model.

Hamann [9] had proposed a simple linear mathematical model which involves C_A (grinding process constant), K_A (constant of resistance of the workpiece with grinding ability of the belt), k_t (belt wear factor), V_b (grinding rate), V_w (feed-in rate), L_w (machining width), and F_A (normal force). The model states that the overall material removal rate (MRR) r is either proportional or inversely proportional to belt grinding parameters as shown in Equation (1). However, this model does not take into account the interaction between belt grinding parameters.

$$r = C_A.K_A.k_t.\frac{V_b}{V_w.L_w}.F_A$$

(1)

Preston’s fundamental polishing equation as shown in Equation (2) states that MRR, ∂R/∂t, of a belt grinding process has a direct relationship with relative velocity, R_v, and polishing pressure, P [10]. The constant, C, is established to denote other influential parameters and it is determined experimentally for each polishing system.

$$\begin{array}{c}\frac{\partial R}{\partial t} = CP{R}_v\\ \frac{\partial R}{\partial t}\mathrm{is}\mathrm{the}\mathrm{material}\mathrm{removal}\left(\mathrm{R}\right)\mathrm{with}\mathrm{time}\left(\mathrm{t}\right)\end{array}$$

(2)

Archard’s wear based on an equation as shown in Equation (3) predicts wear volume, V_w, to be a function of normal load, Fn, sliding distance, S, and hardness of the softest contacting surface, H, while K is a dimensionless constant [11].

$$V_w=\frac{KFnS}{H}$$

(3)

Though the equations from Preston, Archard, and Hamann give a holistic view on the relationship between MRR and a few process parameters, dimensionless constants in each equation (C_A, K and C) need to be determined after many exhaustive physical experiments. Developing analytical models for such nonlinear processes with a large number of parameters and assumptions may introduce biases and will not be a viable option to model the process. Though the correlation of individual parameters on material removal is understood using ANOVA and statistical techniques, their combined consequence on effective material removal is not well established [12]. The adaptive neuro-fuzzy inference system (ANFIS) model with sigmoidal membership function has been used to determine material removal in a belt grinding process [12].

Most of the developed local material removal models have concentrated on simulating the contact condition of the tool and surface. These local models neglect the granularity parameter of the belt tool and have made assumptions during the development of the material removal model. A more systematic model taking into account the granularity parameter has not been reported yet. Incorporating actual values of parameters will help in developing a conclusive material removal model. A conclusive material removal model with other regression techniques in such a dynamic process has not yet been studied and compared in detail. This paper presents a systematic approach to model material removal using statistical regression techniques. The paper is organised as follows. A brief outline of the abrasive belt grinding process and the problem statement is presented in Section 1, followed by a brief theoretical basis on the belt grinding process and the regression modelling techniques in Section 2. The grinding conditions, belt grinding setup, process parameters and the Taguchi orthogonal array experimental data are listed in Section 3. The results of the six different regression models are discussed in Section 4. Finally, the findings of this paper are reviewed in Section 5.

2. Theoretical Basis

2.1. Abrasive Belt Grinding

An abrasive belt grinding process consists of a coated abrasive belt that is fixed firmly around, at least, two rotating polymer contact wheels (see Figure 1). The polymer wheel enables the grinding process to appropriately manufacture free-form surfaces due to its capability to adjust to the grinding surface [5,18].

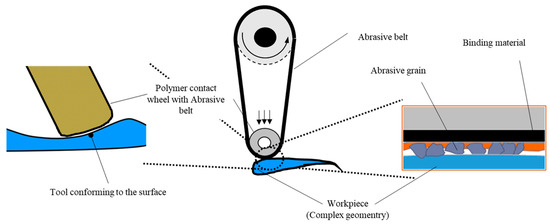
Figure 1. Principle of the belt grinding process.

The significant benefit of the belt grinding process is that there is no requirement of a coolant system as the grinding belts with the typical length of 2 to 5 m can cool down during the return strokes on the process [25]. Similar to traditional grinding processes, many machining parameters, e.g., the grinding belt topography features and belt grinding parameters, have an impact on the grinding result. Although super finishing by belt grinding is a straightforward and inexpensive process, essential aspects of material removal phenomenon are not well grasped. Hence the industry relies heavily on operators’ knowledge.

2.2. Multiple Linear and Stepwise Regression

Multiple linear regression is a promising supervised learning algorithm and the most common form of linear regression analysis. As a predictive analytical tool, multiple linear regression is used to associate one continuous dependent variable to two (or more) independent variables by finding the best suitable fitted line [26]. The best fitted line is a line with total minimum error to all the points. Multiple linear regression analysis helps us to comprehend the rate at which the dependent variable changes when changes are made in the independent variables. Regression models describe the relationship between a dependent variable,$y_i$ also referred to as the response variable and independent variables, $X_{in}$, or predictor variables, by fitting a linear equation as shown in the following equation:

$$y_{i }={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+{\beta }_3{X}_{i3}+\dots +{\beta }_n{X}_{in }+{\mathsf{\epsilon }}_i$$

(4)

where the constant ${\beta }_0$ represents the intercept in the model and ${\beta }_n$ (n ≠ 0) refers to a coefficient. Since the response values for $y_i$ vary about their means, the multiple regression model includes a residual term, ${\mathsf{\epsilon }}_i$, representing the variation. The goal of the multilinear regression is to create a linear model in hyperplane that minimises the sum of the square of the residuals concerning all predictor variables as shown in Figure 2. Multilinear regression identifies the hyperplane, in terms of the slope ${\beta }_n$ and intercept ${\beta }_0,$through the sample data with the minimum sum of the squared errors thereby predicting the regression line.

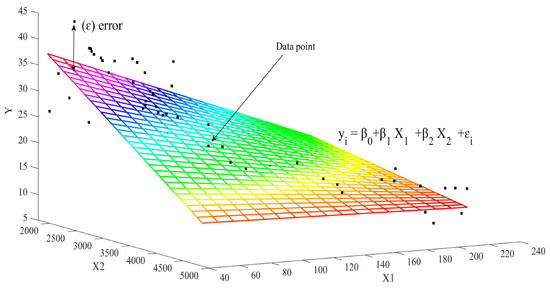
Figure 2. Surface that corresponds to the simplest multiple regression models.

Interaction effects of the predictors through linear regression can be achieved by using the stepwise regression. Stepwise regression essentially does multiple regression a number of times, each time removing the weakest correlated variable based solely on the t-statistics of their estimated coefficients. In the end, the variables that give the best distribution will remain. A linear model containing only the linear terms is used as a starting model whereas a quadratic model containing an intercept, linear terms, interactions, and squared terms are used as a terminating model. Predictor variables are added one at a time as the regression model progresses. At each step, predictor variable or their interaction that increases R² the most are considered significant whereas others are removed.

2.3. Artificial Neural Networks

Artificial neural networks (ANNs) is a method of developing logical systems by imitating the biological architecture of the human brain [27]. Establishing the networks between neuronal nodes determines the structure of the network. Neurons in ANNs are organised in a layered order. Each ANN structure comprises three different neurons namely input, hidden and output neurons. The input values are conveyed to the network through the input neurons, and these nodes pass the information to the next neurons in the hidden layer. Experiments determine the size of hidden layers and the number of neurons that are present according to the problem at hand [28]. The output neurons are where the output values of the network are generated. An ANN processes the information acquired from the input neurons by means of a linear/non-linear activation function and communicates to the subsequent neuron connected to it as illustrated in Figure 3.

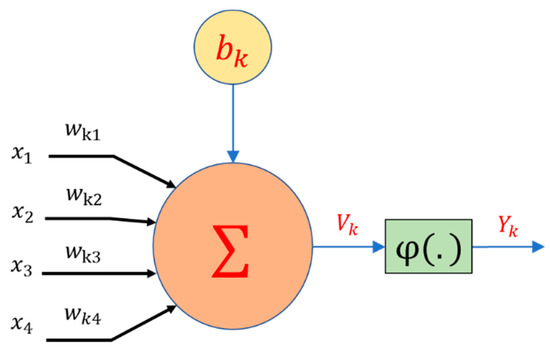
Figure 3. The mathematical model of a neuron.

Each connection between neurons is articulated in terms of a weight value, and these connections are governed based on the training of the network. Expected nodes in the input layer and inputs in every other node are the sum of the weighted outputs of the previous layer. Each node is brought as an active case depending on the input of one node, the activation function and the threshold value of the node. In mathematical terms, a neuron $u_k$ can be described with weights $w_{ji}$ and input $x_i$ by Equation (5)

$$u_k={\displaystyle \sum }_{j=1}^m{w}_{ji}{x}_i$$

(5)

and

$$v_k=u_k+b_k$$

(6)

where $u_k$ is the linear combination output due to input signals and $b_k$ is the bias. The output of the neuron is represented as $y_k$

$$y_k=\phi \left(u_k+b_k\right)=\phi \left(v_k\right)$$

(7)

A neuron in the network produces its output by processing its net input $v_k$ through an activation function otherwise called a transfer function. Every neuron needs a (non-linear) activation function to cater for the non-linear property inside the network. There are several types of activation functions used in ANN, where the three forms of sigmoidal activation function are most the utilised functions Equation (8):

$$f\left(x\right)=\frac{1}{1+e^{-x}}range\left(0,1\right) or \frac{2}{1+e^{-x}}-1range\left(-1,1\right) or \frac{e^x-e^{-x}}{e^x+e^{-x}}range\left(-1,1\right)$$

(8)

The methodology to train connections to achieve anticipated results determines the learning algorithm of the network. There are several learning algorithms out of which the backpropagation learning algorithm is most commonly used. The backpropagation (BP) algorithm is based on the main principle of minimisation of errors in a neural network output and modification of network values according to the minimised values. The error of a neural network is described as the difference between the desired output $D_0$ and the calculated output $C_0$ of the network as shown in Equation (9).

$$E_p=\frac{1}{2}{\displaystyle \sum }_{k=1}^K{\left(D_0-C_0\right)}^2=\frac{1}{2}{\displaystyle \sum }_{k=1}^K{\displaystyle \sum }_{p=1}^p{\left(D_0-C_0\right)}^2$$

(9)

where $p$ indicates the total number of instances and $K$ denotes the number of neurons in the output of the network. By comparing the output value of the network with the desired value, the error of the network is determined which is further minimised by adjusting the weights of the networks.

Backpropagation is an algorithm to minimise the error in the network output based on a gradient descent minimisation method. The process of altering the weights starts at the output neuron and propagates backwards to the hidden layer. The altered weight $w_{ji}^{new}$ is given by the $\eta$ learning parameter

$$w_{ji}^{new}=w_{ji}^{old}\pm \mathsf{\Delta }{w}_{ji}$$

(10)

$$\mathsf{\Delta }{w}_{ji}=\eta \frac{\partial E_p^2}{\partial w_{ji}}$$

(11)

once the weights of all the links of the network are decided, the decision mechanism is then developed.

2.4. Adaptive Neuro-Fuzzy Inference System

Adaptive neuro-fuzzy inference system (ANFIS) overcomes the fundamental problem in fuzzy if-then rules by exploiting the learning competence of ANN for automated optimisation of fuzzy if-then rules during training. This results in an automatic modification of the fuzzy system based on input-output space [29], which lead to optimized membership function of parameters. In other words, ANFIS architecture is a superimposition of FIS on ANN architecture, which will empower FIS to self-tune its rule base based on the output. The ANFIS forms a FIS initially, and the membership function is altered by the backpropagation algorithm and least square method available with ANN [30]. Recent ANFIS application in the manufacturing field to predict the surface finishing quality is presented in Reference [31]. Figure 4 illustrates ANFIS with five layers of neurons with two inputs x and y, which form two fuzzy if-then rules based on a first-order Sugeno fuzzy model [32].

Rule 1: If x is A1 and y is B1, then f1 = p1x + q1y + r1;

Rule 2: If x is A2 and y is B2, then f2 = p2x + q2y + r2;

where p1, p2, q1, q2, r1, and r2 are linear parameters and A1, A2, B1, and B2 are nonlinear parameters. The output of the $i$th node in the membership function layer is denoted as $O_{l,i}$.

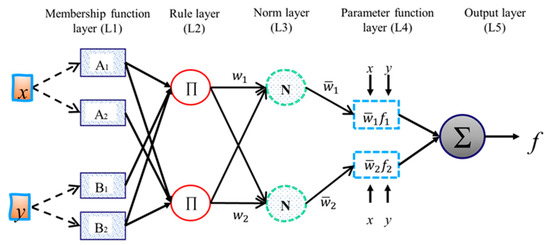
Figure 4. Adaptive neuro-fuzzy inference system structure.

Membership function layer (L₁): Every adaptive node i in the L₁ has a node function.

$$O_{l,i}={\mu }_{A_i}\left(x\right)\mathrm{for}i =1,2\mathrm{or} O_{l,i}={\mu }_{B_{i-2}}\left(y\right)\mathrm{for}i =3,4$$

(12)

where x (or y) is the input to nodes i and A_i (or B_i–2) generating a linguistic label coupled with the node as given by Equation (12). The membership function for A (or B) can be any, such as a sigmoidal membership function given by Equation (13).

$${\mu }_{A_i}\left(x\right)=\frac{1}{1+e^{-a\left(x-c\right)}}$$

(13)

where (c_i, a_i) is the parameter set. These are called premise parameters. As the values of the parameters change, the shape of the membership function varies.

Rule layer (L₂): Every node in L₂ is a fixed node labelled ∏. Each node calculates the firing strength of each rule, which is the output using the simple product operator. The rule premises result is evaluated as the product of all of the incoming signals and given by the Equation (14)

$$O_{2,i}=w_i={\mu }_{A_i}\left(\mathrm{x}\right)\times {\mu }_{B_i}\left(y\right)\mathrm{for}i =1,2$$

(14)

Norm layer (L₃): The ratio of the i^th rule’s firing strength to the sum of all of the rule’s firing strengths is calculated by Equation (15) in L₃. The output of L₃ is called normalised firing strengths.

$$O_{3,i}={\overline{w}}_i=\frac{w_i}{{\sum }_i^2{w}_i}=\frac{w_i}{w_1+w_2}i =1,2$$

(15)

Parameter function layer (L₄): Every node $i$ in L₄ is an adaptive node with a node function. The nodes compute a parameter function on the L₄ output. Parameters in this L₄ are referred to as consequent parameters.

$$O_{4,i}={\overline{w}}_i{f}_i={\overline{w}}_i\left(p_{i}x +q_{i}y +r_i\right)$$

(16)

where w_i is a normalised firing strength from L₃ and (p_i, q_i, r_i) is the parameter set for the node.

Output layer (L₅): L₅ has a single fixed node labelled Σ, which computes the overall output as the summation of all of the incoming signals, as shown in Equation (17). The Σ gives the overall output of the constructed adaptive network, having the same functionality as the Sugeno fuzzy model.

$$O_{5,i}={\displaystyle \sum }_i{\overline{w}}_i{f}_i=\frac{{{\displaystyle \sum }}_i{w}_i{f}_i}{{{\displaystyle \sum }}_i{w}_i}$$

(17)

2.5. Support Vector Regression

A support vector regression (SVR) is a regression version of the support vector machine (SVM) that offers a powerful technique to solve regression problems. The regression problem is solved by introducing an alternative loss function. The SVR is centred on the idea of mapping the data x into a high-dimensional feature space to solve the regression problem [33]. Consider a data set $\left\{\left(x_i,y_i\right) | i = 1,2,\dots l\right\}$where$x_i$ is a D-dimensional input vector, $y_i$ is a scalar output or target, and $l$ is the number of points. In SVR, the goal is to find a function f(x) that has at most ε deviation from the obtained targets $y_i$ for all the training data. The nonlinear relationship between input and output is then described by a regression function f(x) with weight factor $\omega ={{\displaystyle \sum }}_{i=1}^n{\alpha }_i{\mathrm{x}}_{\mathrm{i}}$ and bias $b$. The SVR algorithm can be extended to nonlinear cases by simply preprocessing the training patterns $x_i$, by a map $\varphi :\mathcal{X}\to ℱ$, into some feature space $ℱ$ and then applying the standard SV regression algorithm. In the feature space $ℱ,$ the regression function takes shape using a nonlinear mapping function $\varphi \left(\mathrm{x}\right)$:

$$f\left(\mathrm{x}\right) = {\omega }^{\mathrm{T}}\varphi \left(\mathrm{x}\right) + b = {\displaystyle \sum }_{i=1}^n{\alpha }_i\varphi {\left({\mathrm{x}}_{\mathrm{i}}\right)}^{\mathrm{T}}\varphi \left({\mathrm{x}}_{\mathrm{j}}\right) + b$$

(18)

Nonlinear SVRs are trained by exchanging the inner products with the corresponding kernel $K\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)=\varphi {\left({\mathrm{x}}_{\mathrm{i}}\right)}^{\mathrm{T}}\varphi \left({\mathrm{x}}_{\mathrm{j}}\right)$ and the resulting non-linear SVR is then represented as a kernel function:

$$f\left(\mathrm{x}\right)={\displaystyle \sum }_{i=1}^n{\alpha }_{i}K\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)+b$$

(19)

For the SVR model to have good generalisation performance, $\omega$ needs to be as flat as possible. This means that the norm $(\Vert .\Vert )$ of the $\omega$ vector needs to be minimised for every data $i =1,2,\dots l$

$$minimise \frac{1}{2}{\Vert \omega \Vert }^2$$

(20)

$$\mathrm{subject} \mathrm{to} \{\begin{array}{l}{y}_i - ⟨\omega ,x_i⟩ - b \le \mathsf{\epsilon }\\ ⟨\omega ,x_i⟩ + b - y_i \le \mathsf{\epsilon }\end{array}$$

(21)

Figure 5 shows the regression line, the upper and lower boundary lines and shows the radius of the $\pm \mathsf{\epsilon }$ insensitive loss function. The insensitive zone $(+\mathsf{\epsilon }$ $to -\mathsf{\epsilon }$) controls a number of support vectors. A point is well estimated if the point is within the zone, otherwise, it contributes to the training error loss. If the radius of the insensitive zone increases, numbers in the support vector group reduces, and robustness of the model diminishes.

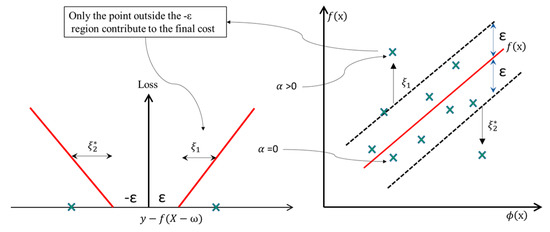
Figure 5. The regression line of support vector regression (SVR) is shown with the loss function and slack variables.

A penalisation is calculated by introducing C for every point that falls outside the insensitive zone $(+\mathsf{\epsilon }$ $to-\mathsf{\epsilon }$) which also defines the flatness and complexity of the model. A higher value of C increases the chance of overfitting, while a smaller value may increase the training errors. An optimum choice of this two-regularisation parameter is necessary for an ideal SVR model. To obtain the optimal hyperplane, the positive slack variable ${\xi }_i$ is introduced to solve the following optimisation problem as illustrated in Figure 5. The constraint problem can be reformulated as shown in Equation (22).

$$\mathrm{minimise} \frac{1}{2}{\Vert \omega \Vert }^2 + C{\displaystyle \sum }_{i=1}^l\left({\xi }_i + {\xi }_i^{*}\right)$$

(22)

$${\left|\xi \right|}_{\mathsf{\epsilon }} = \{\begin{array}{c}0,\hspace{1em}\hspace{1em}if \left|\xi \right|<\mathsf{\epsilon } \\ \left|\xi \right| - \mathsf{\epsilon } \mathrm{otherwise},\hfill \end{array}$$

(23)

$$\mathrm{subject} \mathrm{to} \{\begin{array}{c}{y}_i - ⟨\omega ,x_i⟩ - b \le \left({\xi }_i + {\xi }_i^{*}\right)\\ ⟨\omega ,x_i⟩ + b - y_i \le \left({\xi }_i + {\xi }_i^{*}\right)\\ \left({\xi }_i,{\xi }_i^{*} \ge 0\right)\end{array}$$

(24)

The regression function can be obtained by solving the following optimisation problem using the standard dualization principle utilising the Lagrange multiplier which will give the estimates of $\omega = {{\displaystyle \sum }}_{i=1}^n\left({\alpha }_i^{*} - {\alpha }_i\right)\varphi \left({\mathrm{x}}_{\mathrm{i}}\right)$ and $b$. After solving the dual form, the regression function becomes:

$$f\left(x\right) = {{\displaystyle \sum }_{i=1}^n\left({\alpha }_i^{*} - {\alpha }_i\right)K\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)+b |}_{{\epsilon }_{ 0ptimum}}^{c_{ 0ptimum}}\mathrm{where}{\alpha }_i^{*},{\alpha }_i=\mathrm{Lagrange}\mathrm{multipliers}$$

(25)

Gaussian radial basis function (RBF) with $\gamma$ standard deviation is commonly used due to its better potential to handle higher dimensional input space. For accurate model fitting, three internal parameters of SVM, namely the regularisation parameter (C), the radius of loss of insensitive zone ($\mathsf{\epsilon }$), and standard deviation ($\gamma$) of kernel function are to be correctly set [34]. A Bayesian optimisation approach is used to identify the optimised regularisation parameter.

2.6. Random Forest

One disadvantage of using a single decision tree (DT) is attributed to the risk of overfitting in the training data. A random forest (RF) model is a cumulative model that makes predictions by augmenting decisions from a group of decision trees as base learners [35]. The RF models can be written as:

$$g\left(x\right) = f0\left(x\right) + f1\left(x\right) + f2\left(x\right) + \dots + fN\left(x\right)$$

(26)

where the final model $g$ is the sum of simple base models f_i which basically is a regression decision tree. Unlike linear models, RF can capture the non-linear interaction between the features and the target. One of the most significant advantages of RF over DT is that the algorithm works on bootstrapping [35]. The RF creates a lot of individual DT by re-sampling the data many times with replacement and makes the final prediction at a new point by averaging the predictions from all the individual binary regression trees on this point. Averaging over all the decision trees results in a reduction of variance thereby enhancing the accuracy of the prediction. The accuracy of the RF can be estimated from observations that are not used for individual trees otherwise called “out of the bag data” (OOB) as shown in Equation (27)

$$\mathrm{OOB}\sim \mathrm{MSE} = \frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(y_i - {\overline{\widehat{y}}}_{i OOB}\right)}^2$$

(27)

where ${\overline{\widehat{y}}}_{iOOB}$ denotes the average prediction for the $i^{\mathrm{th}}$ observation from all trees for which this observation has been OOB. The elements not embraced in the bootstrap sample are denoted to as OOB. At each bootstrap iteration, the response value for data not included in the bootstrap sample (OOB data) is predicted and averaged over all trees $t_n$ as shown in Equation (28)

$$OOBMS{E}_t = \frac{1}{n_{OOB, t}}{\displaystyle \sum }_{\begin{array}{c}i=1: \\ i \in OO{B}_t\end{array}}^n{\left(y_i - {\overline{\widehat{y}}}_{i,t }\right)}^2$$

(28)

where ${\overline{\widehat{y}}}_i$, $y_i$, $n_{OOB,t}$ denote average prediction, observed output and the number of OOB observations in tree t respectively. The importance of each predictor is considered by computing the increase in mean squared error (MSE). Then, the variable importance assessments are manipulated to rank the predictors in terms of the strength of their relationship to the response or the process outcome.

3. Experimental Setup

3.1. Methodology

A hand-held electrically powered abrasive belt grinder was customised with a fixture to be used as a belt grinding tool. A contact wheel made of ester polyurethane polymer of different Shore A hardness was used as the grinding end of the custom built setup, as shown in Figure 6. The experiments were conducted by mounting the variable speed electric belt grinder to an ABB 6660-205-193 multi-axis robot as shown in Figure 6. The robot arm was mainly used to deliver designated toolpath trajectories. An ATI Industrial automation force sensor (Omega 160) interfaced the belt sander and the robot arm end effector to ensure that the applied force was maintained constant according to the desired level. Control force was used explicitly to obtain a uniform material removal along the grinding path. In addition, before the experiment, it was also ensured that the surface condition of the machined Aluminium 6061 coupons was uniform for all experimental trials.

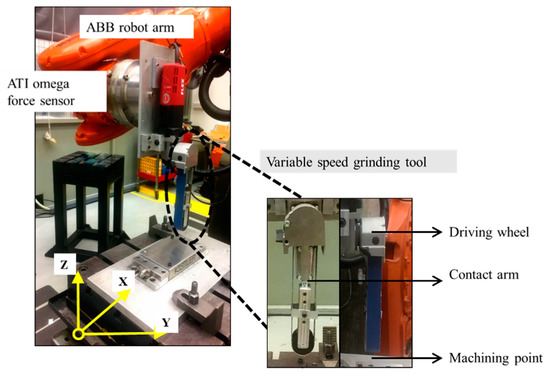
Figure 6. Compliant abrasive belt grinding experimental setup [12].

3.2. Taguchi Design of Experiments (DoE) and Data Collection

The experiments were performed based on Taguchi’s L₂₇ orthogonal array (five-factor, three-level) model. The familiarity of the probable interactions of the belt grinding parameters on material removal was not known therefore the Taguchi-based design of experiments (DoE) methodology was chosen Table 2 shows a list of belt grinding parameters (factors) and their levels used during the belt grinding trials. Material removal was quantified based on the depth of cut, which was measured using a Mitutoyo stylus profilometer with a tip radius of five microns with the accuracy of two decimal places used measure to the depth of cut. The depth of cut was calculated as the distance from the deepest point in the ground path from the unground surface of the workpiece as shown in Figure 7.

Table 2. Belt grinding parameters and their levels.

Parameter	Unit	Levels
		L1	L2	L3
RPM	(m/min)	250	500	700
Feed	(mm/s)	10	20	30
Force	(N)	10	20	30
Rubber hardness	(Shore A)	30	60	90
Grit Size	-	60	120	220

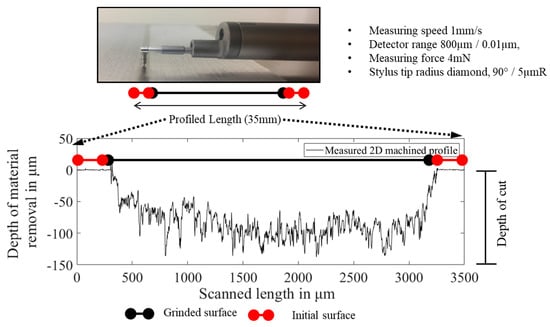
Figure 7. Mitutoyo contact profilometer used to measure the depth of cut across the grinded path.

Based on the parameter combinations from the Taguchi method, 27 combinations were obtained as presented in Table 3. A database of 243 depth of cut readings was created based on 27 Taguchi parametric combinations with nine readings for each combination. The dataset from Table 3. corresponds to only one reading value which was reused from previously published work by the authors [12]. The database with 243 rows of parameter level and depth of cut was used to model the material removal. Six different regression modelling methodologies, namely multiple linear regression, stepwise regression, ANN, ANFIS, SVR and RF were applied, and results obtained by the models are discussed in Section 4.

Table 3. Taguchi design of experiments (DoE) using the L₂₇ orthogonal array and the corresponding depth of cut [12].

Trial No.	Factors					MRR
	RPM	Feed	Force	Hardness	Grit	Depth of Cut
	(m/min)	(mm/s)	(N)	(Shore A)		(μm)
1	250	10	10	30	60	65.60076
2	250	10	10	30	120	25.87109
3	250	10	10	30	220	13.34471
4	250	20	20	60	60	86.10453
5	250	20	20	60	120	44.20156
6	250	20	20	60	220	23.53456
7	250	30	30	90	60	93.8753
8	250	30	30	90	120	54.33391
9	250	30	30	90	220	23.55062
10	500	10	20	90	60	142.9324
11	500	10	20	90	120	86.37583
12	500	10	20	90	220	59.38035
13	500	20	30	30	60	120.6638
14	500	20	30	30	120	57.50747
15	500	20	30	30	220	45.55799
16	500	30	10	60	60	77.47286
17	500	30	10	60	120	26.08495
18	500	30	10	60	220	13.54166
19	700	10	30	60	60	134.8952
20	700	10	30	60	120	76.88529
21	700	10	30	60	220	58.97687
22	700	20	10	90	60	103.8255
23	700	20	10	90	120	56.9663
24	700	20	10	90	220	35.31606
25	700	30	20	30	60	114.009
26	700	30	20	30	120	56.65924
27	700	30	20	30	220	44.31528

4. Regression Modelling for Abrasive Belt Grinding Process

4.1. Multiple Linear Regression Based Modelling

Multilinear regression was performed to determine the relationships between the five grinding parameters Rotation per minute (RPM), force, rubber hardness, grit size, and feed rate to the depth of cut. The schematic model is illustrated in Figure 8.

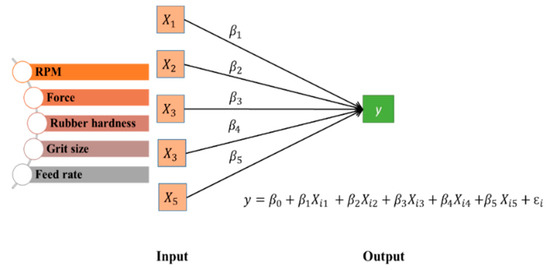
Figure 8. Schematic illustration of the multilinear regression model for prediction of the material removal.

The linear correlation model was developed using MATLAB. The dataset (n = 243) consisting of the five predictors and the response variable was randomly split into 70% training set and 30% testing set. The multilinear model fit the data to a hyperplane upon least square error minimisation. Figure 9 shows the comparison between observed and predicted material removal values on the testing dataset using the developed multilinear regression model. The figure also shows the deviation the predicted values against actual values with multilinear model highlighting a higher root mean squared error (RMSE) of 16.12 which was used as a measure to predict the performance of the model. The developed multilinear model was deficient at predicting the material removal, i.e., depth of cut. The calculated R-squared (R²) gave a value of 0.886, which implied that the fitness of the linear model was inadequate.

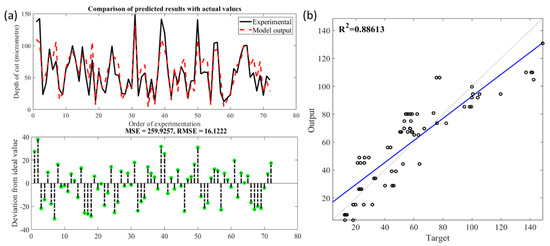
Figure 9. (a). Comparison of the observed and predicted depth of cut using multilinear regression; (b). Statistical analysis fit of the multilinear regression model.

4.2. Stepwise Regression-Based Modelling

The simple multilinear regression based on the least square method as discussed in the previous Section 4.1 indicated its incapability to accurately predict the depth of cut that was attributed to the nonlinear nature of the relationship in grinding process. The deviation from predicted to the original values may occur as the interaction effects between the parameters were ignored which could be analysed using stepwise regression. The training parameters used in the stepwise regression are listed in Table 4. The output of the developed stepwise model containing 13 terms which included five significant interactions and few higher-order polynomials are shown in Table 5.

Table 4. Stepwise multilinear regression training parameters.

Parameter	Value
Training set	70%
Testing set	30%
Method	Forward stepwise regression
Starting model	Linear
Upper limit	Quadratic

Table 5. Estimated coefficients from stepwise regression.

S. No	Predictors	Estimate	Std Error	t-Stat	p-Value
1	(Intercept)	86.755	7.956	10.904	5.392 × 10–21
2	RPM	0.049856	0.0084825	5.8776	2.3937 × 10–8
3	Feed	2.0067	0.51282	3.9131	13.509 × 10–5
4	Force	−2.7861	1.2896	−2.1605	03.2243 × 10–4
5	Rubber hardness	1.7358	0.18569	9.3481	8.2594 × 10–17
6	Grit size	−1.3237	0.062244	−21.266	3.2042 × 10–48
7	RPM: grit size	−0.00014814	4.1438 × 10–5	−3.575	4.6498 × 10–4
8	Feed: force	0.062239	0.011008	5.654	7.1536 × 10–8
9	Feed: rubber hardness	−0.069002	0.0091514	−7.5401	3.4527 × 10–12
10	Force: grit size	−0.0035275	0.00096854	−3.642	3.6624 × 10–4
11	Rubber hardness: grit size	−0.0010501	0.00031645	−3.3184	1.1237 × 10–3
12	Force^2	0.084463	0.029849	2.8297	5.265 × 10–3
13	Grit size^2	0.0039407	0.00018283	21.554	6.5639 × 10–49

Figure 10 shows the comparison between the observed and the predicted material removal values from the 30% testing dataset. In addition, the figure shows the deviation of the predicted values from the actual ones highlighting a reduction in RMSE of 7.77 as compared to least square based multilinear regression. The proposed model was capable but insufficiently robust at predicting material removal. The R-squared (R²) of value 0.975 increased when the regression took in a quadratic form which also took into account the interaction effect between the belt grinding parameters. The order in which predictor variables were removed or added could provide valuable information about the quality of the predictor variables. Referring to the t-stat value of the developed regression model, especially between the predictor interaction from Table 5, it was apparent that grit parameter played a dominant role. The estimated coefficients of the regression model were significant when the interaction happened with the grit size predictor.

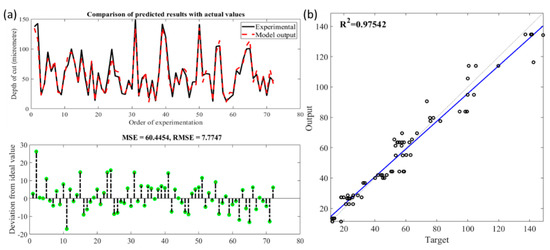
Figure 10. (a). Comparison of observed and predicted depth of cut using stepwise regression; (b) Statistical analysis fit of the stepwise regression model.

Figure 11 depicts the comparison of the residuals from the multilinear model and the stepwise multilinear model. It explicitly indicated that the latter fits the data better. Also, comparing the R² statistical metric values from both approaches, it was clear that the latter performed better than the former as it incorporated a quadratic form, which addressed the influence of the interaction between the grinding parameters and the nonlinear behaviour of the belt grinding process. The proposed methodologies on the multilinear regression and the stepwise multilinear regression provided a useful tool to predict material removal depending on the grinding parameters. The multilinear model may not have been the best choice according to the prediction accuracy and R², but still, we could use it to find the nature of the relationship between the two variables. Interpreting the performance of the model, it was apparent that the data were intrinsically nonlinear and a straight-line relationship should never be assumed in the belt grinding process. The use of a quadratic form in the stepwise regression helped to tune the model to have a better fit.

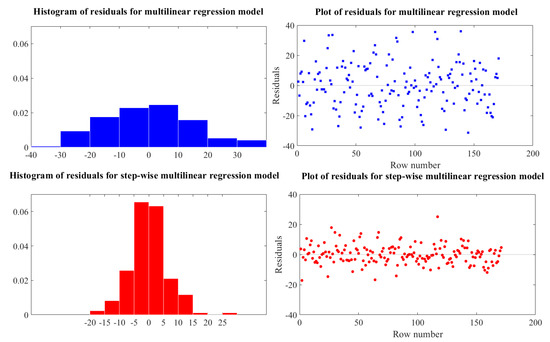
Figure 11. Residual plot observed between the multilinear regression model and stepwise multilinear regression model.

4.3. Artificial Neural Networks Based Modelling

The architecture of the ANN that estimated the material removal in abrasive belt grinding is shown in Figure 12. The accuracy of an ANN model depends on its architecture and on how it is trained. The input layer of the proposed network had five neurons that represented the prediction input, while the output layer had only one neuron to predict the depth of cut. In this study, the backpropagation neural network was used to construct non-linear functions between several inputs and the output. The weights of the networks were adjusted in first place at the output neuron and worked backwards to the hidden layer during the learning, i.e., training procedure until the expected error was achieved. With a hyperbolic tangent sigmoid transfer function, the learning rate of 0.01, and momentum rate of 0.05, the modelling result and the MSE value of material removal were generated by using the ANN toolbox in the MATLAB software.

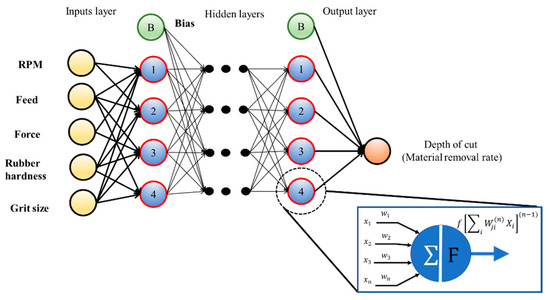
Figure 12. Schematic illustration of an artificial neural network (ANN) model for prediction of the material removal.

The configuration parameters used to determine the best network structure of the ANN prediction model is presented in Table 6. The ANN algorithm used 70% of the input data for model training with the backpropagation method as Bayesian regularisation and used the remainder for model validation. The performance of ANNs depends on the number of hidden layers in the ANN network structure. It is also to be noted that the increase in the number of hidden layers has a direct impact on the cost and the modelling time. The determination of the number of layers and nodes in the hidden layers in the training using the trial-and-error method is based on a minimum number of iterations required to reach the necessary performance goal. Training stops when the error is minimised to the performance goal. Three ANNs with a different number of hidden layer configuration, i.e., 10, 20, and 30 were tested on the same training dataset. The performance of the three configurations was evaluated on minimum epochs required to achieve minimum MSE. From Table 7 it is clear that the epochs rate decreased with the increase of hidden layers. The relationship between the number of iteration and the sum-squared error for an ANN structure with 30 hidden layers is shown in Figure 13.

Table 6. ANN training algorithm configuration parameters.

Parameter	Value
Maximum number of epochs to train	200
Performance goal	0
Backpropagation method	Bayesian regularisation
Initial μ	0.005
Hidden layers	10, 20, 30
Training	70% of the dataset
Testing	30% of the dataset
Weight function	Dot product
Activation function	tansig
Predictors	5
Response	1

Table 7. Comparison of hidden layers against epochs to reach the performance goal.

Hidden Layers	Epochs
10	151
20	62
30	40

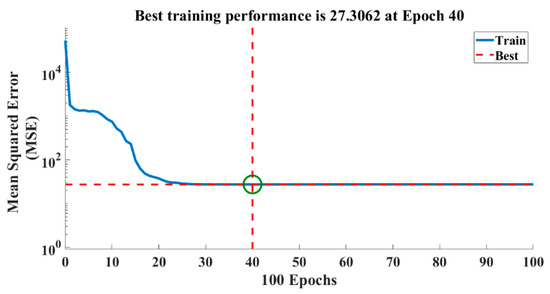
Figure 13. The reduction of the error with an increase in the number of iterations.

It could be noted that the MSE decreased when the iteration numbers using 30 hidden layers is increased. There was a sudden reduction error after 25 iterations, and this reduction went further until it saturated after 40 iterations. Also, while the prediction accuracy increased as the number of hidden layers increased, the performance was not significantly improved by adding more than 30 hidden layers. Upon the completion of the training stage, the network was tested with the validation set. Figure 14 shows the comparison of the actual material removal value with the results of the neural network analysis for all validation data set (71 points). The results indicate the low deviation of the predicted values against actual values with ANNs architecture with 30 hidden layers as represented by an RMSE of 6.64 as shown in Figure 14. The trained ANN model based on backpropagation algorithm was tested with 81 data from the experimental results with the RMSE of 6.649. The predicted values were found to be close to the measured values. The calculated R² of 0.981 suggested a satisfactory fitness model. The results lead to the conclusion that the proposed models could be used to predict the depth of cut in the belt grinding process effectively. Though this network correlates the parameters on its own, as ANN essentially functions as a “black box”, it is trivial to evaluate the association between each independent variable and the dependent variable inside a neural network. Moreover, there is no specific rule for determining the structure of the ANN as the network is configured based on trial and error.

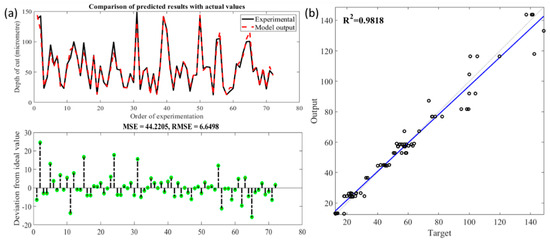
Figure 14. (a). Comparison of observed and predicted depth of cut using neural network regression; (b) Statistical analysis fit of the neural network regression model.

4.4. Adaptive Neuro-Fuzzy Inference System Based Modelling

The ANFIS model developed had multiple inputs, and a single output hence it resembled a multiple inputs–single-output (MISO) system. The architecture of MISO based ANFIS architecture for prediction of material is illustrated in Figure 15. The figure indicates that the input membership functions were non-linear, whereas the output membership functions were linear. For the training set, 70% of the data was chosen stochastically and the remaining 30% used for testing, while the step size for parameter adaptation was 0.1. The ANFIS training parameters for our case are listed in Table 8. The proposed ANFIS contained 243 rules, where each membership function was assigned to each input grinding variable. The MISO model was executed under the MATLAB platform using a Sugeno-type fuzzy inference system with the help of the fuzzy logic toolbox. ANFIS learning used the backpropagation technique for revising membership function shape.

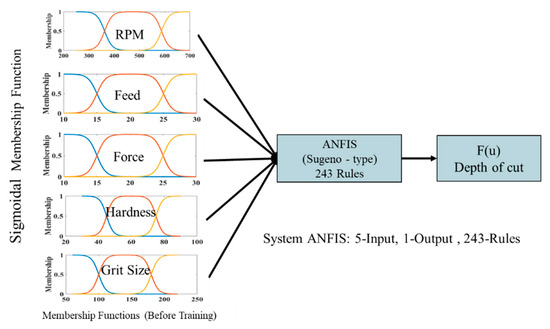
Figure 15. Adaptive Neuro-Fuzzy Inference System (ANFIS) model for belt grinding showing inputs and output [12].

Table 8. The ANFIS training parameters with four different membership functions.

Parameter	Value
andMethod	Prod
orMethod	Max
defuzzMethod	Wtaver (Weighted average)
impMethod	Prod
aggMethod	Max
Membership function	/Sigmoidal/Gaussian bell/Gaussian/Bell-shaped
Learning rules	Gradient descent algorithm

A fuzzy membership function assigns grades of membership between zero and one. The lower the grade, the less significant the membership to the fuzzy set Figure 16 presents the initial and final membership functions of the five belt grinding input parameters derived by using Gaussian membership function training. Comparing the shape of initial and final membership functions of the belt grinding parameters, it could be concluded that the grit size had the most significant impact on the material removal followed by RPM and force. Four types of the membership function, i.e., sigmoidal, Gaussian bell, Gaussian, and bell-shaped, were used and compared to model the belt grind process. Out of all the four types of membership function, we could conclude that sigmoidal membership gave better accuracy, as shown in Table 9.

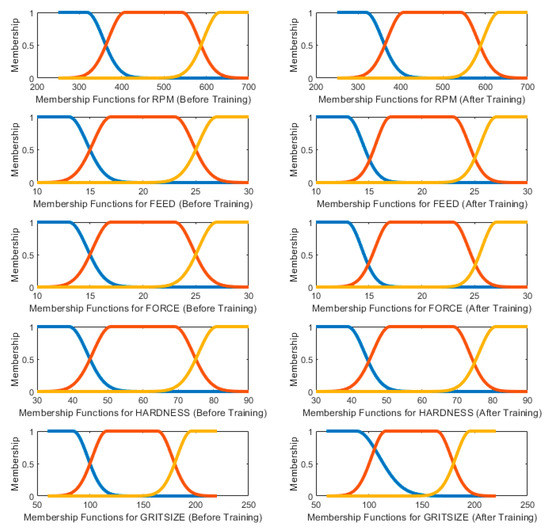
Figure 16. Change in shape of the Gaussian bell membership function for each input before and after training.

Table 9. Comparison of prediction accuracy and membership function.

Membership Function	RMSE
Sigmoidal membership [12]	5.648
Gaussian bell membership	6.7941
Gaussian membership	7.100
Bell-shaped membership	7.0341

Figure 17 gives the comparison of the predicted depth of cut using the established fuzzy model and the data taken from the belt grinding experiments from the validation set. The developed ANFIS system gave an overall RMSE of 6.79 on using Gaussian membership function. The deviation of the outputs generated by the fuzzy model with the experimental data is illustrated in Figure 17. A strong correlation between the simulated results and the experimental results obtained at the same machining conditions is demonstrated in the figure. The R² calculated based on the fitted regression line was 0.980 which also indicated a satisfactory fit of the model. The prediction results showed that by employing a hybrid learning algorithm such as ANFIS, the quality of generated relevant fuzzy if-then rules could be tuned to model the material removal behaviour.

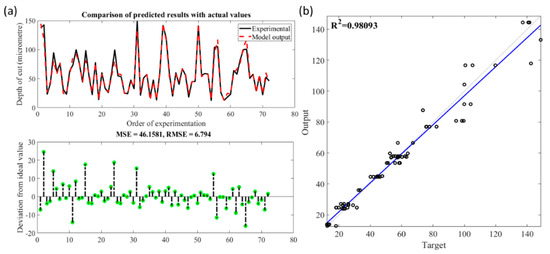
Figure 17. (a). Comparison of observed and predicted depth of cut using ANFIS with Gaussian bell membership function; (b) Statistical analysis fit of the ANFIS model with Gaussian bell membership.

In short, the relationship between the input parameters and the output behaviour of the nonlinear belt grinding process, which was not possible to be modelled using a black-box approach, such as ANN, could be represented satisfactorily using ANFIS. Understanding the input-output correlation from ANFIS architecture helped to characterise the material removal behaviour for which there is no concrete analytical description to date.

4.5. Support Vector Regression Based Modelling

Figure 18 shows the architecture of a regression machine for the belt grinding process. The construction of the material removal model using SVR can be summarised as follows:

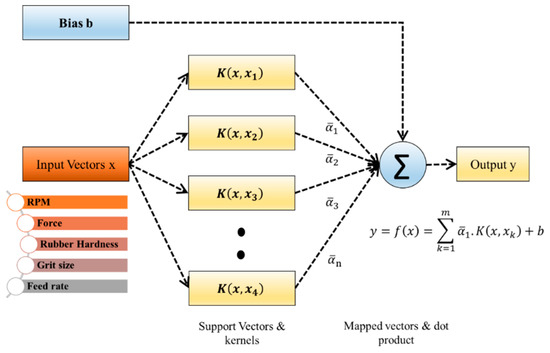
Figure 18. The architecture of a regression machine constructed by the SVR algorithm.

• Define the data, predictors, and response for learning and testing.
• Decide a fitting kernel function (linear, Gaussian, RBF, polynomial, etc.).
• Select an ideal model for training on the input data with predictors and response. The training is done by using a Bayesian optimisation to model material in MATLAB.
• Validation of the testing data set.

Similar to the previous analyses or the development of the model 70% of the recorded data was selected stochastically for training and 30% for testing. The RBF was used as the kernel, where the kernel parameter ($\gamma$) was determined by Bayesian optimisation. The training was performed under the MATLAB platform. From our initial analysis, it was found that regularisation parameter (C = 989.65), the radius of loss insensitive zone ($\mathsf{\epsilon }=0.12457$), and standard deviation ($\gamma = 0.10894$) gave the minimal value of the MSE based on the Bayesian optimisation algorithm as depicted in Figure 19. There was a sudden reduction error after five evaluation and this reduction goes further before it saturates after 15 iterations.

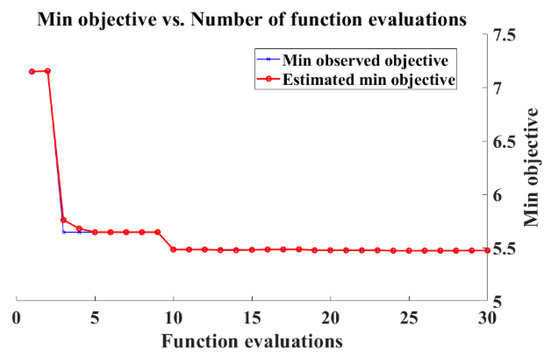
Figure 19. Optimisation of SVR parameters with respect to the number of iterations.

A higher value of C in the feature space signified that the material removal model was highly complex with large random noises which also indicated the nonlinear behaviour of the belt grinding process. The lower values of $\mathsf{\epsilon }$ for material removal indicated that the SVR model could capture the intricacy of the belt grinding process effectively. The tuned parameters used in the SVR model during the learning process is listed in Table 10. Once the model completed the training stage, it was tested with the validation data. The effectiveness of the training could be concluded from its ability to forecast material removal from unseen data. The R² calculated based on the fitted regression line was 0.980 which also showed the good fit of the model.

Table 10. Optimised SVR training parameters.

Parameter	Value
Epsilon ($\mathsf{\epsilon }$)	0.12457
Box Constraint (C)	989.65
Optimisation Method	Bayesian optimisation
Kernel	Gaussian RBF
Kernel scale ($\gamma$)	0.10894

Figure 20 shows the deviation of the predicted values against actual values using the SVR model, highlighting an RMSE of 6.9989. The trained SVR model with optimum parameter settings C, $\mathsf{\epsilon },$ and $\gamma$ obtained using Bayesian optimisation could efficiently predict material removal responses. Though the testing result of developed SVR algorithm favoured the practical use of the model in the chosen range, the main limitation of the support vector approach was attributed to the kernel selection, which was mostly based on trial and error.

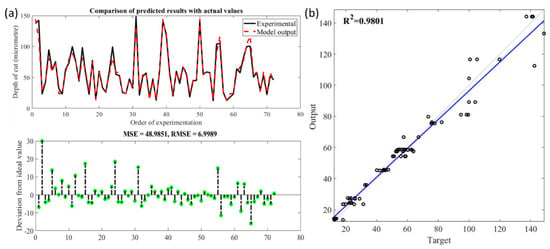
Figure 20. (a) Comparison of observed and predicted depth of cut using SVR; (b) Statistical analysis fit of the SVR model.

4.6. Random Forest Based Modelling

The framework for predicting material removal using a random forest (RF) is illustrated in Figure 21. The algorithm for material removal regression can be summarised as follows:

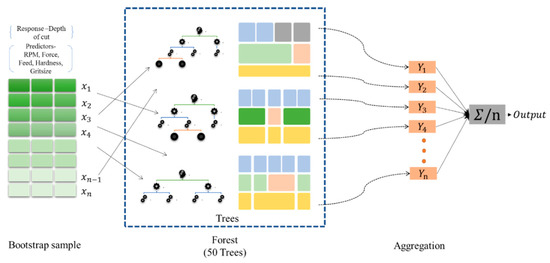
Figure 21. Material removal prediction using a random forest.

• A bootstrap sample $\left(x_1,x_2,x_3,\dots .x_n\right)$ of size, $N$ is to be drawn from the training data consisting of the five predictors and the response variable.
• For each bootstrap sample $x_i$, a regression tree model is constructed by optimising the parameters, such as the number of trees $t_n$ and leaf size based on MSE error.
• Prediction at a new point Z is achieved by aggregating the predictions of the regression tree models.
• The accuracy of the RF model is calculated based on the deviation of the predicted value, x, from the ideal value in the validation data set.

The development of the relationship between the belt grinding parameters and material removal RF model was carried out using MATLAB. Some parameters such as the minimal size of the terminal nodes of the trees, i.e., leaf size and a number of regression trees grown based on a bootstrap sample were optimised in the random forest model upon the minimisation of the MSE. The number of regression trees in a random forest model defines the strength of each tree in the forest and its correlation with other trees. A number of regression trees were optimised based on the MSE by testing with five different tree values (5, 10, 20, 50, and 100) on the training dataset. Figure 22 indicates how the number of regression trees grown in RF affected the prediction error. Inferring from the figure, it is evident that the MSE saturated after 35 trees and did not improve further as the number of trees increased.

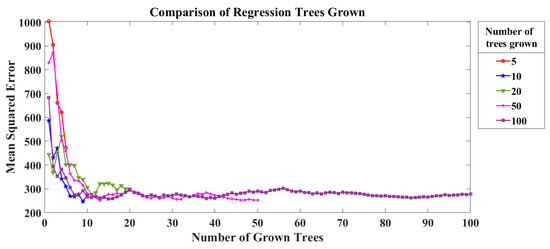
Figure 22. Optimisation of random forest (RF) parameters (number of grown trees) using mean square error (MSE).

The minimum leaf size parameter specifies the smallest number of observations a node can have. Letting the trees split down to leaf nodes with a minimum observation results in the most accurate random forest models. However, it is noted that smaller leaf size results in deeper trees with higher accuracy but also increases the cost of computation time and memory. Figure 23. indicates that the effect of the minimum leaf size and it was quite clear that with minimum leaf size, i.e., deeper trees the prediction ability of the model was higher. The splitting process stopped at the child node if the number of observations in a node was less than five which was used as a stopping criterion in the regression model developed. Based on results from fine-tuning discussed in the section above, an RF was constructed using 50 regression trees. A bootstrap sample of size 40 (0.25% of the training data) was drawn from the training dataset for every iteration. After 50 regression trees were constructed, a prediction at a new point could be made by aggregating the predictions from all the individual binary regression trees on this point. The tuning parameter used for developing the RF regression model is listed in Table 11.

Figure 23. Optimisation of RF parameters (number of leaf size) using MSE.

Table 11. Random forest training parameters.

Parameter	Value
In bag fraction	0.25% of the training dataset
Method used by trees	Regression
Min leaf size	5
Number of trees	50

The RF model can rank the predictors (RPM, hardness, force, grit size and feed rate in our case) based on their importance by estimating out-of-bag (OOB) error. Figure 24 shows the predictors importance measured in terms of the increase in OOB error which states that grit size had a higher correlation with material removal than others. The developed random forest model robustness was evaluated by identifying the deviation of the observed value in the validation dataset and value predicted by the model. The RF model predicted a new point by aggregating the predictions from all the individual 50 regression trees ensembled inside the model.

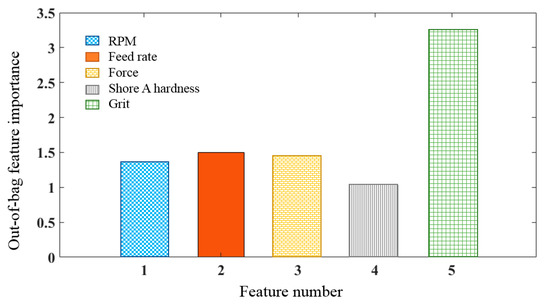
Figure 24. Variables’ importance in predicting material removal using RF.

Figure 25 shows the one to one relationship between observed material removal values as predicted with the test dataset using the RF regression model. It appeared that the proposed model was good at predicting the material removal, i.e., depth of cut. Figure 25 shows the deviation of the predicted values against actual values with RFs highlighting the RMSE of 8.94. The R² calculated based on the fitted regression line was of value 0.975 which also showed that goodness of fit of the RF model was good. Although RF seems more of a “black box” approach compared to regression trees since individual trees cannot be assessed separately, it still provides means for interpretation in giving measures of variable importance.

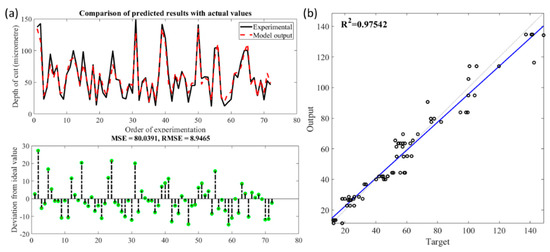
Figure 25. (a). Comparison of observed and predicted depth of cut using RF regression; (b) Statistical analysis fit of the RF regression model.

5. Conclusions

This paper illustrated the application of different statistical regression techniques coupled with the Taguchi design of experiments for the belt grinding process. The outcome demonstrated the practicality of the methodologies in developing a material removal model for the abrasive belt grinding process. Based on the regression models developed the following generalised conclusions were drawn:

• Observing the performance of the multilinear and stepwise regression models, it was seen that belt grinding parameters were intrinsically nonlinear and a straight-line relationship assumption could not satisfy the material removal.
• Although predicted values using ANN networks were close to the measured values, it functioned as a black box model correlating the parameters on its own, and the structure determination was based on trial and error.
• SVR modelling implemented using a Gaussian kernel function showed good accuracy on material removal. However, the drawback of the model was attributed to the selection of the kernel function that was based on trial and error.
• The ANFIS model developed in this research work had acceptable deviations between the predicted and the real results and was viable to predict the depth of cut in the abrasive belt grinding process compared to other regression techniques. The performance of the six algorithms in terms of RMSE is summarised in Figure 26.
  

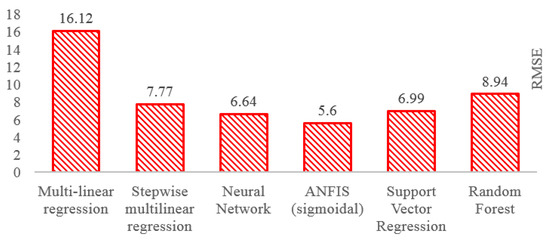  Figure 26. Predictive performance of the regression models.
• In addition, ANFIS could interpret the relationship between the input parameters towards the output behaviour which was not possible using other modelling techniques.
• The random forest model which was based on the frequency table was not able to predict at higher accuracy compared to other complex predictive models even though it performed better than the multilinear regression.
• Analysis of the sigmoidal membership function after training in ANFIS, interpretation on the variable importance results from RF, and the coefficient from stepwise regression techniques indicated that the grit size factor in the belt grinding parameters was the most significant factor on the material removal process.

Overall results from the paper suggest that statistical techniques that have the adaptability to capture nonlinear space performed well and is viable to model the material removal in the abrasive belt grinding process. The proposed regression models can be convenient for defining parameter levels for realising preferred material removal to the operator.