Type II Power Topp-Leone Generated Family of Distributions with Statistical Inference and Applications

Abstract

In this paper, we present and study a new family of continuous distributions, called the type II power Topp-Leone-G family. It provides a natural extension of the so-called type II Topp-Leone-G family, thanks to the use of an additional shape parameter. We determine the main properties of the new family, showing how they depend on the involving parameters. The following points are investigated: shapes and asymptotes of some important functions, quantile function, some mixture representations, moments and derivations, stochastic ordering, reliability and order statistics. Then, a special model of the family based on the inverse exponential distribution is introduced. It is of particular interest because the related probability functions are tractable and possess various kinds of asymmetric shapes. Specially, reverse J, left skewed, near symmetrical and right skewed shapes are observed for the corresponding probability density function. The estimation of the model parameters is performed by the use of three different methods. A complete simulation study is proposed to illustrate their numerical efficiency. The considered model is also applied to analyze two different kinds of data sets. We show that it outperforms other well-known models defined with the same baseline distribution, proving its high level of adaptability in the context of data analysis.

1. Introduction

Among the existing distributions with support over the unit interval, the so-called Topp-Leone distribution, introduced by [1], is one of the most useful. This success is explained by the tractability of the corresponding functions, only depending on a single parameter $\alpha >0$. More precisely, its cumulative distribution function (cdf) and probability density function (pdf) are given by, respectively,

$$F_o(x;\alpha )=x^{\alpha }{(2-x)}^{\alpha },\hspace{1em}x\in (0,1)$$

and

$$f_o(x;\alpha )=2\alpha x^{\alpha -1}(1-x){(2-x)}^{\alpha -1},\hspace{1em}x\in (0,1).$$

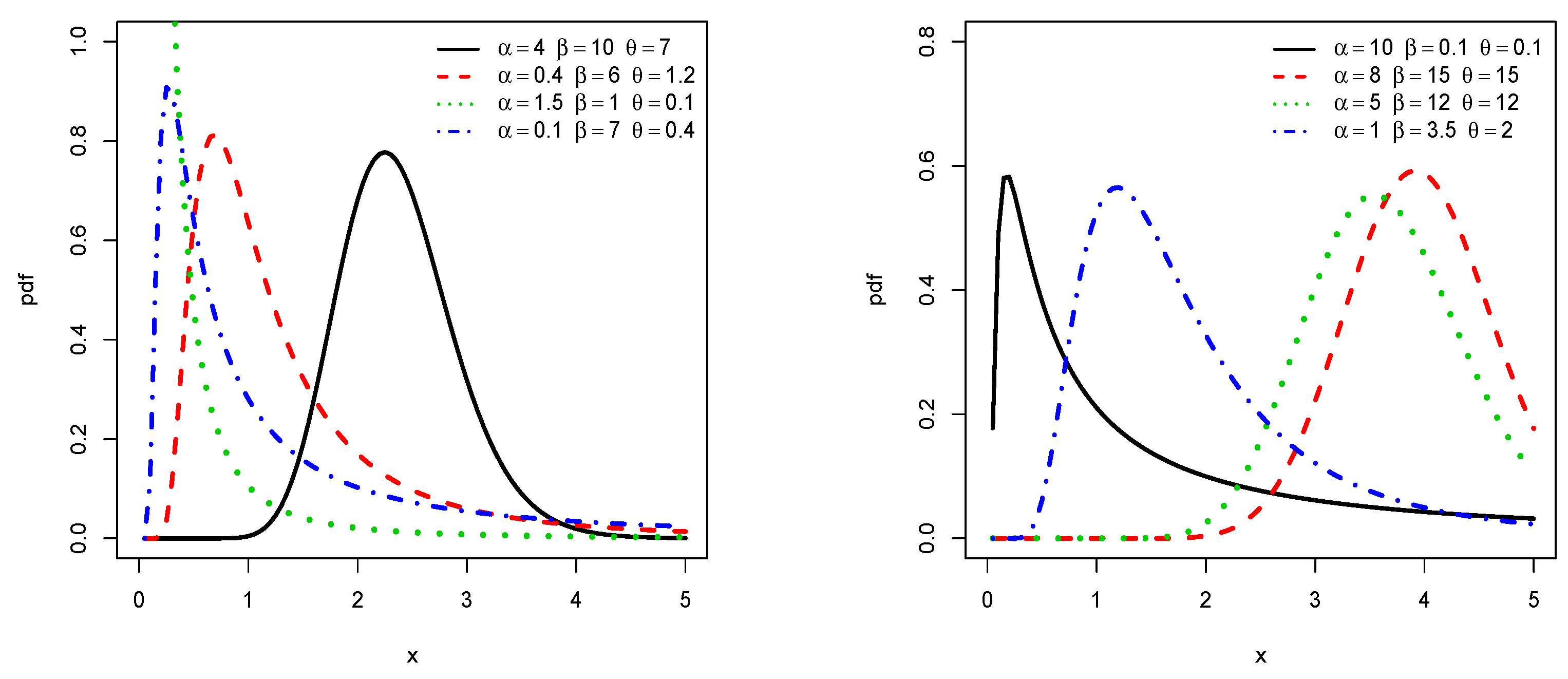
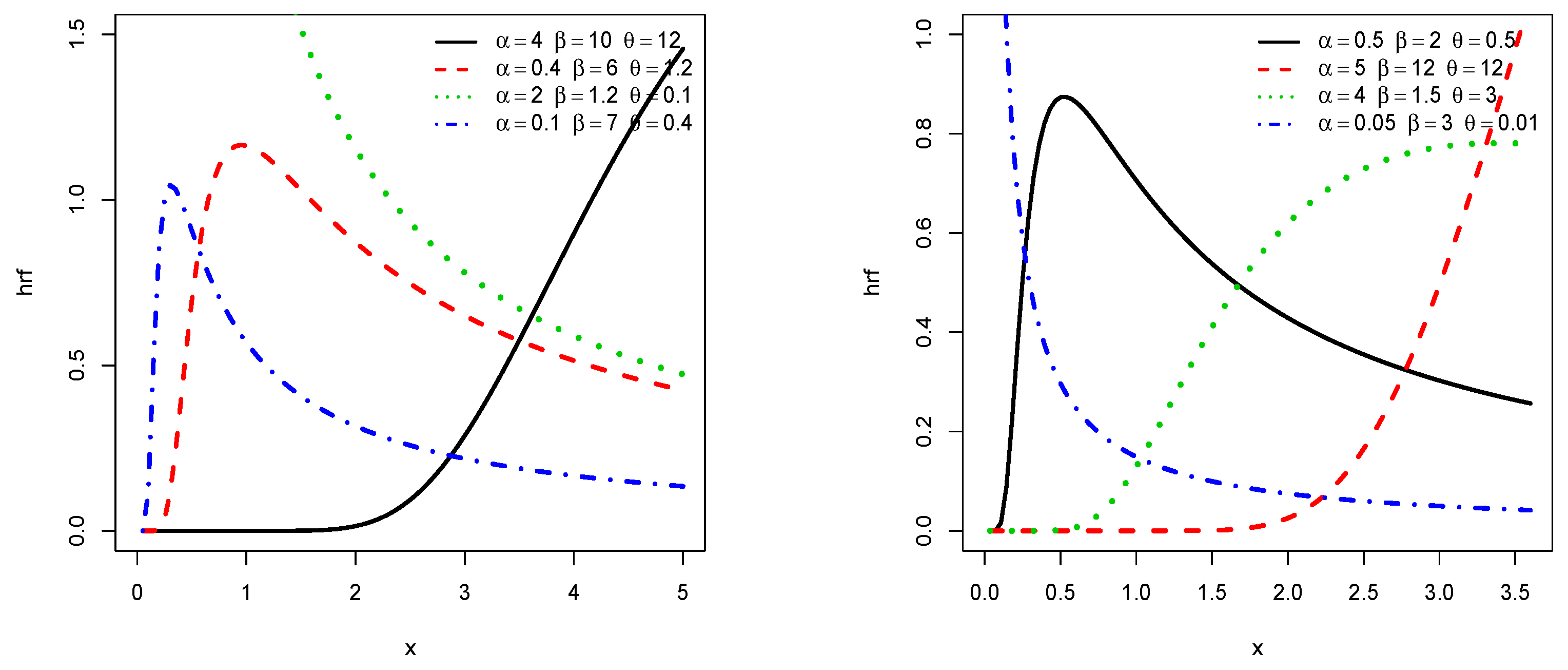
This last function is known to be a perfect example of bounded J-shaped pdf. Also, the corresponding hazard rate function (hrf) is given by

$$h_o(x;\alpha )=\frac{2\alpha x^{\alpha -1}(1-x){(2-x)}^{\alpha -1}}{1-x^{\alpha }{(2-x)}^{\alpha }},\hspace{1em}x\in (0,1).$$

A feature of this hrf is to be of great flexibility; it can have bathtub shape or be non-increasing, depending on the values of $\alpha$. Other nontrivial properties on the Topp-Leone distribution can be found in, e.g., [2,3,4]. For the use of the Topp-Leone distribution in different applied statistical settings, we refer the reader to [5,6,7,8]. Some extensions of the Topp-Leone distribution can be found in [9,10]. On the other side, in the recent years, the Topp-Leone distribution reveals to be particularly efficient to define general families of distributions enjoying nice properties, including a great ability to model different practical data sets. Among these families, there are the Topp-Leone-G family studied via different approaches by [11,12,13,14], the Topp-Leone-G power series family by [15,16], the type II Topp-Leone-G family by [17], the Topp-Leone odd log-logistic family by [18], the type II generalized Topp-Leone-G family by [19], the Fréchet Topp- Leone-G family by [20], the exponentiated generalized Topp-Leone-G family by [21] and the transmuted Topp-Leone-G family by [22]. Now, for the purposes of this paper, let us describe the general family introduced by [23]. It is based on the so-called power Topp-Leone distribution defined with the cdf and pdf given by, respectively,

$$F_{\ast }(x;\alpha ,\beta )=x^{\alpha \beta }{(2-x^{\beta })}^{\alpha },\hspace{1em}x\in (0,1)$$

and

$$f_{\ast }(x;\alpha ,\beta )=2\alpha \beta x^{\alpha \beta -1}(1-x^{\beta }){(2-x^{\beta })}^{\alpha -1},\hspace{1em}x\in (0,1).$$

The power Topp-Leone distribution corresponds to the distribution of the random variable $Y=X^{1/\beta }$, where X is a random variable following the Topp-Leone distribution (with parameter $\alpha$). Obviously, the role of the parameter $\beta$ is to give more flexibility to the former Topp-Leone distribution. In order to take benefit of this new parameter and open new perspectives, ref. [23] developed the power Topp-Leone-G family defined by the following cdf: $F(x;\alpha ,\beta ,\xi )=F_{\ast }\left(G(x;\xi );\alpha ,\beta \right)$, $x\in \mathbb{R}$, where $G(x;\xi )$ denotes the cdf of a continuous distribution depending on a parameter vector $\xi$.

In this paper, we explore a new direction of work by investigating the type II version of the power Topp-Leone-G family. Indeed, we define the type II power Topp-Leone-G (TIIPTL-G) family by the cdf given by

$$F(x;\alpha ,\beta ,\xi )=1-F_{\ast }\left(1-G(x;\xi );\alpha ,\beta \right),\hspace{1em}x\in \mathbb{R},$$

i.e.,

$$F(x;\alpha ,\beta ,\xi )=1-{\left[1-G(x;\xi )\right]}^{\alpha \beta }{\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}^{\alpha },\hspace{1em}x\in \mathbb{R}.$$

To the best of our knowledge, the mathematical foundations of this family has no equivalence in the statistical literature, opening the door of new modelling. Let us just notice that, for $\beta =1$, the corresponding cdf is reduced to $F(x;\alpha ,\beta ,\xi )=1-{\left[1-G{(x;\xi )}^2\right]}^{\alpha }$, which corresponds to the cdf of the type II Topp-Leone-G family developed by [17]. In this sense, the TIIPTL-G family can be viewed as a generalization of the type II Topp-Leone-G family. The overall motivations behind the TIIPTL-G family are to

• create distributions with different shapes for the pdf and hrf,
• transform symmetrical distributions into skewed distributions,
• construct heavy-tailed distributions,
• increase the flexibility of the mode(s), mean, variance, skewness and kurtosis of the baseline distribution,
• provide better fits than other general families (including those based on the Topp-Leone distribution) with the same baseline distribution and possibly more complex (with more parameters).

Most of these points are developed in detail in our study, with the consideration of the inverse exponential distribution as baseline. In order to motivate this choice of baseline, let us recall that the inverse exponential distribution was introduced by [24] as a suitable alternative to the standard exponential distribution. In particular, the inverse exponential model is more appropriated than the exponential one when lifetime data present an inverted bathtub failure rate. We refer to [25] for a complete discussion in this regard. As indicated by its name, if X denotes a random variable following the exponential distribution with parameter $\theta >0$, the inverse of X, i.e., $Y=X^{-1}$, follows the inverse exponential distribution with parameter $\theta$. That is, the corresponding cdf and pdf are given by, respectively,

$$G(x;\theta )=e^{-\theta /x},\hspace{1em}x>0,$$

(1)

and

$$g(x;\theta )=\frac{\theta }{x^2}{e}^{-\theta /x},\hspace{1em}x>0.$$

Thanks to the structure of the TIIPTL-G family, we significantly increase the practical properties of the inverse exponential distribution (more flexible shapes for the corresponding pdf, hrf, mode, skewness, kurtosis, etc.). In particular, we show that the resulting distribution can have better results in fitting data sets than seven adversary distributions, including five also based on the inverse exponential distribution.

The rest of the paper is arranged as follows. Section 2 defines the TIIPTL-G family, with a focus on the special member previously mentioned, i.e., using the inverse exponential distribution as baseline. In Section 3, some of general mathematical properties of the TIIPTL-G family are derived, including the quantile function, mixture representations of the corresponding cdf and pdf, several kinds of moments, stochastic ordering, reliability and order statistics. The Section 4 is devoted to the special TIIPTL-G model using the inverse exponential distribution as baseline, with estimation of the model parameters via three different well-established methods: the maximum likelihood, percentile and right-tail Anderson-Darling methods. The TIIPTL-G models aim to be used in a data analysis setting. In this regard, Section 5 is devoted to the analyzes of two practical data sets, with comprehensible comparison to seven other models having the same baseline distribution. The discussion ends in a conclusion presented in Section 6.

2. Definition of the TIIPTL-G Family

The definition and essential functions of the TIIPTL-G family are set in this section.

2.1. Important Functions

We recall that the TIIPTL-G family is defined with the cdf given by

$$F(x;\alpha ,\beta ,\xi )=1-{\left[1-G(x;\xi )\right]}^{\alpha \beta }{\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}^{\alpha },\hspace{1em}x\in \mathbb{R},$$

(2)

with $\alpha ,\beta >0$ and $G(x;\xi )$ denotes any cdf of a continuous distribution with parameter vector $\xi$.

The corresponding survival function (sf) is given by $S(x;\alpha ,\beta ,\xi )=1-F(x;\alpha ,\beta ,\xi )$, i.e.,

$$S(x;\alpha ,\beta ,\xi )={\left[1-G(x;\xi )\right]}^{\alpha \beta }{\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}^{\alpha },\hspace{1em}x\in \mathbb{R}.$$

(3)

Upon differentiation of $F(x;\alpha ,\beta ,\xi )$, with some algebra, we show that the pdf of the TIIPTL-G family is expressed as

$$f(x;\alpha ,\beta ,\xi )=2\alpha \beta g(x;\xi ){\left[1-G(x;\xi )\right]}^{\alpha \beta -1}{\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}^{\alpha -1}\left\{1-{\left[1-G(x;\xi )\right]}^{\beta }\right\},\hspace{1em}x\in \mathbb{R},$$

(4)

where $g(x;\xi )$ is the pdf corresponding to $G(x;\xi )$.

The cumulative hazard rate function (chrf) of the TIIPTL-G family is given by $H(x;\alpha ,\beta ,\xi )=-\log \left[S\right(x;\alpha ,\beta ,\xi \left)\right]$, i.e.,

$$H(x;\alpha ,\beta ,\xi )=-\alpha \beta \log \left[1-G(x;\xi )\right]-\alpha \log \left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\},\hspace{1em}x\in \mathbb{R}.$$

Upon differentiation of $H(x;\alpha ,\beta ,\xi )$, with some algebra, the corresponding hrf is given by

$$h(x;\alpha ,\beta ,\xi )=\frac{2\alpha \beta g(x;\xi )\left\{1-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}{\left[1-G(x;\xi )\right]\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}},\hspace{1em}x\in \mathbb{R}.$$

(5)

These functions will play a central role in the next, mainly $f(x;\alpha ,\beta ,\xi )$ and $h(x;\alpha ,\beta ,\xi )$, motivating the study of their curvature features in the next section.

2.2. Asymptotes and Shapes

First of all, let us investigate the effects of the parameters $\alpha$, $\beta$ and $\xi$ on the asymptotes of $F(x;\alpha ,\beta ,\xi )$, $f(x;\alpha ,\beta ,\xi )$ and $h(x;\alpha ,\beta ,\xi )$. Using (2), (4) and (5), when $G(x;\xi )\to 0$, we have

$$F(x;\alpha ,\beta ,\xi )\sim \alpha {\beta }^{2}G{(x;\xi )}^2,\hspace{1em}f(x;\alpha ,\beta ,\xi )\sim h(x;\alpha ,\beta ,\xi )\sim 2\alpha {\beta }^{2}g(x;\xi )G(x;\xi ).$$

Also, when $G(x;\xi )\to 1$, we have

$$F(x;\alpha ,\beta ,\xi )\sim 1-2^{\alpha }{[1-G(x;\xi )]}^{\alpha \beta },\hspace{1em}f(x;\alpha ,\beta ,\xi )\sim 2^{\alpha }\alpha \beta g(x;\xi ){[1-G(x;\xi )]}^{\alpha \beta -1}$$

and

$$h(x;\alpha ,\beta ,\xi )\sim \alpha \beta g(x;\xi ){[1-G(x;\xi )]}^{-1}.$$

We see that the asymptotes of $f(x;\alpha ,\beta ,\xi )$ are strongly impacted by $\alpha$, $\beta$ and $\xi$, mainly when $G(x;\xi )\to 1$.

We now present the basics on the critical points for $f(x;\alpha ,\beta ,\xi )$ and $h(x;\alpha ,\beta ,\xi )$. Any critical point $x_{\ast }$ of $f(x;\alpha ,\beta ,\xi )$ is solution of the equation ${\left\{\log \left[f\right(x;\alpha ,\beta ,\xi \left)\right]\right\}}^{\prime }=0$, with

$$\begin{array}{ll}\log \left[f\right(x;\alpha ,\beta ,\xi \left)\right]=& \log \left(2\right)+\log \left(\alpha \right)+\log \left(\beta \right)+\log \left[g(x;\xi )\right]+(\alpha \beta -1)\log \left[1-G(x;\xi )\right]\\ & +(\alpha -1)\log \left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}+\log \left\{1-{\left[1-G(x;\xi )\right]}^{\beta }\right\}\end{array}$$

and

$$\begin{array}{ll}{\left\{\log \left[f\right(x;\alpha ,\beta ,\xi \left)\right]\right\}}^{\prime }=& \frac{g{(x;\xi )}^{\prime }}{g(x;\xi )}-(\alpha \beta -1)\frac{g(x;\xi )}{1-G(x;\xi )}+(\alpha -1)\beta \frac{g(x;\xi ){\left[1-G(x;\xi )\right]}^{\beta -1}}{2-{\left[1-G(x;\xi )\right]}^{\beta }}\\ & +\beta \frac{g(x;\xi ){\left[1-G(x;\xi )\right]}^{\beta -1}}{1-{\left[1-G(x;\xi )\right]}^{\beta }}.\end{array}$$

The nature of $x_{\ast }$ can be determined according to the sign of ${\varphi }_{\ast }={\left\{\log \left[f\right(x;\alpha ,\beta ,\xi \left)\right]\right\}}^{\prime \prime }{\mid }_{x=x_{\ast }}$.

Also, any critical point $x_{\ast \ast }$ of $h(x;\alpha ,\beta ,\xi )$ is solution of the equation ${\left\{\log \left[h\right(x;\alpha ,\beta ,\xi \left)\right]\right\}}^{\prime }=0$, with is equivalent to ${\left\{\log \left[f\right(x;\alpha ,\beta ,\xi \left)\right]\right\}}^{\prime }+h(x;\alpha ,\beta ,\xi )=0$, i.e.,

$$\begin{array}{ll}{\left\{\log \left[h\right(x;\alpha ,\beta ,\xi \left)\right]\right\}}^{\prime }=& \frac{g{(x;\xi )}^{\prime }}{g(x;\xi )}-(\alpha \beta -1)\frac{g(x;\xi )}{1-G(x;\xi )}+(\alpha -1)\beta \frac{g(x;\xi ){\left[1-G(x;\xi )\right]}^{\beta -1}}{2-{\left[1-G(x;\xi )\right]}^{\beta }}\\ & +\beta \frac{g(x;\xi ){\left[1-G(x;\xi )\right]}^{\beta -1}}{1-{\left[1-G(x;\xi )\right]}^{\beta }}+2\alpha \beta \frac{g(x;\xi )\left\{1-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}{\left[1-G(x;\xi )\right]\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}.\end{array}$$

The nature of $x_{\ast \ast }$ can be determined according to the sign of ${\varphi }_{\ast \ast }={\left\{\log \left[h\right(x;\alpha ,\beta ,\xi \left)\right]\right\}}^{\prime \prime }{\mid }_{x=x_{\ast \ast }}$.

Here, $x_{\ast }$ and $x_{\ast \ast }$ are not necessary unique; the presented equations may have several roots, depending on $G(x;\xi )$, $\alpha$ and $\beta$.

2.3. Special Members of the Family

Many special members of the TIIPTL-G family are of potential interest, for tractability of the related functions and flexibility reasons. Some of them are listed in

Table 1. Some special members of the TIIPTL-G family defined with their sfs.

Distribution	Name of $\mathit{G}(\mathit{x};\mathit{\xi })$	$\mathit{\xi }$	Support	$\mathit{S}(\mathit{x};\mathit{\alpha },\mathit{\beta },\mathit{\xi })$
TIIPTLU	Uniform	$\left(\theta \right)$	$(0,\theta )$	${\left[1-\frac{x}{\theta }\right]}^{\alpha \beta }{\left\{2-{\left[1-\frac{x}{\theta }\right]}^{\beta }\right\}}^{\alpha }$
TIIPTLP	Power	$\left(a\right)$	$(0,1)$	${\left[1-x^a\right]}^{\alpha \beta }{\left\{2-{\left[1-x^a\right]}^{\beta }\right\}}^{\alpha }$
TIIPTLIEx	Inverse exponential	$\left(\theta \right)$	$(0,+\infty )$	${\left[1-e^{-\theta /x}\right]}^{\alpha \beta }{\left\{2-{\left[1-e^{-\theta /x}\right]}^{\beta }\right\}}^{\alpha }$
TIIPTLD	Dagum	$(a,b,c)$	$(0,+\infty )$	${\left[1-{\left(1+{\left(\frac{x}{a}\right)}^{-b}\right)}^{-c}\right]}^{\alpha \beta }{\left\{2-{\left[1-{\left(1+{\left(\frac{x}{a}\right)}^{-b}\right)}^{-c}\right]}^{\beta }\right\}}^{\alpha }$
TIIPTLFr	Fréchet	$\left(a\right)$	$(0,+\infty )$	${\left[1-e^{-x^{-a}}\right]}^{\alpha \beta }{\left\{2-{\left[1-e^{-x^{-a}}\right]}^{\beta }\right\}}^{\alpha }$
TIIPTLHC	Half Cauchy	$\left(a\right)$	$(0,+\infty )$	${\left[1-\frac{2}{\pi }\arctan \left(\frac{x}{a}\right)\right]}^{\alpha \beta }{\left\{2-{\left[1-\frac{2}{\pi }\arctan \left(\frac{x}{a}\right)\right]}^{\beta }\right\}}^{\alpha }$
TIIPTLo	Logistic	$(a,b)$	$\mathbb{R}$	${\left[1-\frac{1}{1+e^{-(x-a)/b}}\right]}^{\alpha \beta }{\left\{2-{\left[1-\frac{1}{1+e^{-(x-a)/b}}\right]}^{\beta }\right\}}^{\alpha }$
TIIPTLN	Normal	$(\mu ,\sigma )$	$\mathbb{R}$	${\left[1-\Phi (x;\mu ,\sigma )\right]}^{\alpha \beta }{\left\{2-{\left[1-\Phi (x;\mu ,\sigma )\right]}^{\beta }\right\}}^{\alpha }$

, defined with their sfs for the sake of place.

2.4. The TIIPTLIEx Distribution

Among the presented special members in Table 1, we put emphasis on the TIIPTLIEx distribution, corresponding to the TIIPTL-G defined with the cdf of the inverse exponential distribution with parameter $\theta >0$ as baseline, as defined by (1). That is, the corresponding cdf, sf, pdf, chrf and hrf are, respectively, given by

$$F(x;\alpha ,\beta ,\theta )=1-{\left[1-e^{-\theta /x}\right]}^{\alpha \beta }{\left\{2-{\left[1-e^{-\theta /x}\right]}^{\beta }\right\}}^{\alpha },\hspace{1em}x>0,$$

(6)

$$S(x;\alpha ,\beta ,\theta )={\left[1-e^{-\theta /x}\right]}^{\alpha \beta }{\left\{2-{\left[1-e^{-\theta /x}\right]}^{\beta }\right\}}^{\alpha },\hspace{1em}x>0,$$

$$f(x;\alpha ,\beta ,\theta )=2\alpha \beta \frac{\theta }{x^2}{e}^{-\theta /x}{\left[1-e^{-\theta /x}\right]}^{\alpha \beta -1}{\left\{2-{\left[1-e^{-\theta /x}\right]}^{\beta }\right\}}^{\alpha -1}\left\{1-{\left[1-e^{-\theta /x}\right]}^{\beta }\right\},\hspace{1em}x>0,$$

(7)

$$H(x;\alpha ,\beta ,\theta )=-\alpha \beta \log \left[1-e^{-\theta /x}\right]-\alpha \log \left\{2-{\left[1-e^{-\theta /x}\right]}^{\beta }\right\},\hspace{1em}x>0$$

(8)

and

$$h(x;\alpha ,\beta ,\theta )=\frac{2\alpha \beta \theta e^{-\theta /x}\left\{1-{\left[1-e^{-\theta /x}\right]}^{\beta }\right\}}{x^2\left[1-e^{-\theta /x}\right]\left\{2-{\left[1-e^{-\theta /x}\right]}^{\beta }\right\}},\hspace{1em}x>0.$$

(9)

We thus introduce a new three-parameters lifetime distribution, with potential new features in probability and statistics. Among them, we claim that the TIIPTLIEx distribution possesses flexible functions. Since this aspect is hard to handle with theoretical tools, illustrations are proposed in Figure 1 and Figure 2, with plots of the pdf and hrf.

Figure 1 reveals that the pdf of the TIIPTLIEx distribution is reverse J, left skewed, near symmetrical and right skewed. Figure 2 shows that the hrf of the TIIPTLIEx distribution is increasing, decreasing and upside down bathtub shaped. All these observations are strong signs that the TIIPTLIEx distribution enjoys a great flexibility in the modelling of various lifetime data sets.

3. Some Properties of the TIIPTL-G Family

This section shows important distributional and structural properties satisfied by the TIIPTL-G family.

3.1. Quantile Function

The quantile function (qf) $Q(u;\alpha ,\beta ,\xi )$ of the TIIPTL-G family satisfies the nonlinear equation

$$Q\left(F\right(u;\alpha ,\beta ,\xi );\alpha ,\beta ,\xi )=u,\hspace{1em}u\in (0,1).$$

After some algebra, it comes:

$$Q(u;\alpha ,\beta ,\xi )=Q_G\left\{1-{\left[1-\sqrt{1-{(1-u)}^{1/\alpha }}\right]}^{1/\beta };\xi \right\},\hspace{1em}u\in (0,1),$$

where $Q_G(u;\xi )$ is the quantile function corresponding to $G(x;\xi )$. The closed-form of the qf is one of the advantages of the TIIPTL-G family. Indeed, the qf plays a central role; it allows to determine the three first quartiles of the TIIPTL-G family, including the median defined by

$$M=Q(0.5;\alpha ,\beta ,\xi )=Q_G\left\{1-{\left[1-\sqrt{1-{0.5}^{1/\alpha }}\right]}^{1/\beta };\xi \right\}.$$

The qf is also useful to generate values from the TIIPTL-G family at a given baseline cdf $G(x;\xi )$. Indeed, for any independent realizations $u_1,\dots ,u_n$ from a random variable U following the uniform distribution over the unit interval, then $x_1,\dots ,x_n$ with $x_i=Q(u_i;\alpha ,\beta ,\xi )$ are independent realizations of a random variable X following corresponding TIIPTL-G distribution.

Finally, let us precise the qf of the TIIPTLIEx distribution; after some algebra, it expressed as

$$Q(u;\alpha ,\beta ,\theta )=-\theta {\left[\log \left\{1-{\left[1-\sqrt{1-{(1-u)}^{1/\alpha }}\right]}^{1/\beta }\right\}\right]}^{-1},\hspace{1em}u\in (0,1).$$

(10)

From this expression, the simulation of values from the TIIPTLIEx distribution is possible. This result will be used in Section 4.

3.2. Mixture Representation

The following result presents a mixture representation of the cdf and pdf of the TIIPTL-G family.

Theorem 1.

Let x such that$G(x;\xi )\in (0,1)$(x such that$G(x;\xi )=1$is excluded). Let us introduce the cdf and pdf of the exponentiated-G family defined by, respectively,$G_{\gamma }(x;\xi )=G{(x;\xi )}^{\gamma }$and$g_{\gamma }(x;\xi )=\gamma g(x;\xi )G{(x;\xi )}^{\gamma -1}$. Then

• we have the following expansion for$F(x;\alpha ,\beta ,\xi )$:

  $$F(x;\alpha ,\beta ,\xi )=1+\sum _{k,\ell =0}^{+\infty }{a}_{k,\ell }{G}_{\ell }(x;\xi )$$

  where

  $$a_{k,\ell }=\left(\genfrac{}{}{0pt}{}{\alpha }{k}\right)\left(\genfrac{}{}{0pt}{}{\beta (k+\alpha )}{\ell }\right){(-1)}^{k+\ell +1}{2}^{\alpha -k}.$$
• we have the following expansion for$f(x;\alpha ,\beta ,\xi )$:

  $$f(x;\alpha ,\beta ,\xi )=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{+\infty }{a}_{k,\ell }{g}_{\ell }(x;\xi ).$$

Proof. 

Since $G(x;\xi )\in (0,1)$, implying that ${\left[1-G(x;\xi )\right]}^{\beta }/2\in (0,1)$, the generalized binomial formula can applied and gives

$$\begin{array}{ll}F(x;\alpha ,\beta ,\xi )& =1-{\left[1-G(x;\xi )\right]}^{\alpha \beta }{\displaystyle \sum _{k=0}^{+\infty }}\left(\genfrac{}{}{0pt}{}{\alpha }{k}\right)2^{\alpha -k}{(-1)}^k{\left[1-G(x;\xi )\right]}^{\beta k}\\ & =1+{\displaystyle \sum _{k=0}^{+\infty }}\left(\genfrac{}{}{0pt}{}{\alpha }{k}\right)2^{\alpha -k}{(-1)}^{k+1}{\left[1-G(x;\xi )\right]}^{\beta (k+\alpha )}.\end{array}$$

By applying again the generalized binomial formula, we get

$${\left[1-G(x;\xi )\right]}^{\beta (k+\alpha )}=\sum _{\ell =0}^{+\infty }\left(\genfrac{}{}{0pt}{}{\beta (k+\alpha )}{\ell }\right){(-1)}^{\ell }G{(x;\xi )}^{\ell }.$$

By combining all the above equalities, we obtain the desired mixture expansion for $F(x;\alpha ,\beta ,\xi )$. The one for $f(x;\alpha ,\beta ,\xi )$ is derived upon differentiation, excluding the term in $\ell =0$ in the sum since its vanishes. This completes the proof of Theorem 1. □

3.3. Some Kinds of Moments

Here, we derive some kinds of the moments for the TIIPTL-G family. It is supposed that all the introduced quantities are well-defined (convergent if any…), depending on $G(x;\xi )$, $\alpha$, $\beta$ and other introduced functions-parameters.

3.3.1. Moments and Central Moments

First of all, for any positive integer r, the r-th moment is given by

$${\mu }_r^{\prime }={\int }_{-\infty }^{+\infty }{x}^{r}f(x;\alpha ,\beta ,\xi )dx.$$

This integral can be calculated numerically by using any scientific software. A series expression is possible by applying Theorem 1; we have

$${\mu }_r^{\prime }=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{+\infty }{a}_{k,\ell }{\omega }_{\ell ,r},$$

(11)

where ${\omega }_{\ell ,r}={\int }_{-\infty }^{+\infty }{x}^r{g}_{\ell }(x;\xi )dx=\ell {\int }_0^1{u}^{\ell -1}{\left[Q_G(u;\xi )\right]}^{r}du$.

The r-th central moment is given by

$${\mu }_r={\int }_{-\infty }^{+\infty }{(x-{\mu }_1^{\prime })}^{r}f(x;\alpha ,\beta ,\xi )dx=\sum _{m=0}^r\left(\genfrac{}{}{0pt}{}{r}{m}\right){(-1)}^m{\left({\mu }_1^{\prime }\right)}^m{\mu }_{r-m}^{\prime }.$$

From this formula, one can deduce the mean, the variance, the standard deviation, the cumulants, the coefficients of skewness and kurtosis, and so on.

3.3.2. Inverted Moments

When the moments are not well defined, inverted moments can be of interest. Here, the r-th inverted moment is given by

$${\mu }_r^{\ast }={\int }_{-\infty }^{+\infty }{x}^{-r}f(x;\alpha ,\beta ,\xi )dx.$$

Then, the previous arguments hold; by applying Theorem 1, we have

$${\mu }_r^{\ast }=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{+\infty }{a}_{k,\ell }{\rho }_{\ell ,r},$$

where ${\rho }_{\ell ,r}={\int }_{-\infty }^{+\infty }{x}^{-r}{g}_{\ell }(x;\xi )dx=\ell {\int }_0^1{u}^{\ell -1}{\left[Q_G(u;\xi )\right]}^{-r}du$.

In the context of the TIIPTLIEx distribution, we have

$${\rho }_{\ell ,r}={\int }_{-\infty }^{+\infty }{x}^{-r}{g}_{\ell }(x;\xi )dx=\ell \theta {\int }_0^{+\infty }{x}^{-r-2}{e}^{-\ell \theta /x}dx={(\ell \theta )}^{-r}r!,$$

implying that

$${\mu }_r^{\ast }={\theta }^{-r}r!\sum _{k=0}^{+\infty }\sum _{\ell =1}^{+\infty }{a}_{k,\ell }{\ell }^{-r}.$$

3.3.3. Incomplete Moments

For any positive integer r and $t\in \mathbb{R}$, the r-th incomplete moment is given by

$${\mu }_r^{\prime }\left(t\right)={\int }_{-\infty }^t{x}^{r}f(x;\alpha ,\beta ,\xi )dx.$$

Again, one can determine it numerically. A series expression of it follows from Theorem 1; we have

$${\mu }_r^{\prime }\left(t\right)=\sum _{k=0}^{+\infty }\sum _{\ell =1}^{+\infty }{a}_{k,\ell }{\omega }_{\ell ,r}\left(t\right),$$

where ${\omega }_{\ell ,r}\left(t\right)={\int }_{-\infty }^t{x}^r{g}_{\ell }(x;\xi )dx=\ell {\int }_0^{G(t;\xi )}{u}^{\ell -1}{\left[Q_G(u;\xi )\right]}^{r}du$. From this formula, one can deduce the mean deviations about the mean and the median, the mean residual life function, the Bonferroni and Lorenz curves, and so on.

In the context of the TIIPTLIEx distribution, for any $t>0$, we have

$${\omega }_{\ell ,r}\left(t\right)={\int }_{-\infty }^t{x}^r{g}_{\ell }(x;\xi )dx=\ell \theta {\int }_0^t{x}^{r-2}{e}^{-\ell \theta /x}dx={(\ell \theta )}^r{\int }_{\ell \theta /t}^{+\infty }{y}^{-r}{e}^{-y}dy={(\ell \theta )}^r\Gamma (1-r,\ell \theta /t),$$

where $\Gamma (s,x)={\int }_x^{+\infty }{y}^{s-1}{e}^{-y}dy$ (the so-called upper incomplete gamma function). Hence, in this case, we can write

$${\mu }_r^{\ast }\left(t\right)={\theta }^r\sum _{k=0}^{+\infty }\sum _{\ell =1}^{+\infty }{a}_{k,\ell }{\ell }^r\Gamma (1-r,\ell \theta /t).$$

3.4. Stochastic Ordering

When we deal with a general family of distributions, for practical purposes, it is of interest to identify the inherent stochastic ordering of these members according to the parameters. In this regard, one can use some distributional functions, as the cdf, hrf, likelihood ratio function…. Here, we focus on the likelihood ratio order defined as follows. For two random variables X and Y, we say that $X{⪯}_{lr}Y$ if and only if the ratio of the two corresponding pdfs (the one of X divided by the one of Y) is a decreasing function in x. For the complete theory, we refer the reader to [26]. The following result is about the likelihood ratio order related to the TIIPTL-G family, with fixed $\beta$.

Proposition 1.

Let$X_1$and$X_2$be two random variables such that$X_1$and$X_2$have the pdfs of the TIIPTL-G family given by$f(x;{\alpha }_1,\beta ,\xi )$and$f(x;{\alpha }_2,\beta ,\xi )$, respectively. Then, we have$X_1{⪯}_{lr}{X}_2$.

Proof. 

By using (4), we have

$$\frac{f(x;{\alpha }_1,\beta ,\xi )}{f(x;{\alpha }_2,\beta ,\xi )}=\frac{{\alpha }_1}{{\alpha }_2}{\left[1-G(x;\xi )\right]}^{\beta ({\alpha }_1-{\alpha }_2)}{\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}^{{\alpha }_1-{\alpha }_2}.$$

Hence, we get

$$\begin{array}{ll}\log \left[\frac{f(x;{\alpha }_1,\beta ,\xi )}{f(x;{\alpha }_2,\beta ,\xi )}\right]=& \log \left({\alpha }_1\right)-\log \left({\alpha }_2\right)+\beta ({\alpha }_1-{\alpha }_2)\log \left[1-G(x;\xi )\right]\\ & +({\alpha }_1-{\alpha }_2)\log \left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}\end{array}$$

and

$$\begin{array}{ll}{\left\{\log \left[\frac{f(x;{\alpha }_1,\beta ,\xi )}{f(x;{\alpha }_2,\beta ,\xi )}\right]\right\}}^{\prime }& =-\beta ({\alpha }_1-{\alpha }_2)\frac{g(x;\xi )}{1-G(x;\xi )}+\beta ({\alpha }_1-{\alpha }_2)\frac{g(x;\xi ){\left[1-G(x;\xi )\right]}^{\beta -1}}{2-{\left[1-G(x;\xi )\right]}^{\beta }}\\ & =\beta ({\alpha }_1-{\alpha }_2)\frac{g(x;\xi )}{1-G(x;\xi )}\left[\frac{{\left[1-G(x;\xi )\right]}^{\beta }}{2-{\left[1-G(x;\xi )\right]}^{\beta }}-1\right]\\ & =2\beta ({\alpha }_2-{\alpha }_1)\frac{g(x;\xi )}{1-G(x;\xi )}\frac{1-{\left[1-G(x;\xi )\right]}^{\beta }}{2-{\left[1-G(x;\xi )\right]}^{\beta }},\end{array}$$

which is negative if ${\alpha }_2<{\alpha }_1$. Therefore, $\log \left[f(x;{\alpha }_1,\beta ,\xi )/f(x;{\alpha }_2,\beta ,\xi )\right]$ is decreasing, implying that $f(x;{\alpha }_1,\beta ,\xi )/f(x;{\alpha }_2,\beta ,\xi )$ is decreasing. This proves the desired likelihood ratio. □

3.5. Reliability

One of the most common measure in the context of reliability is the coefficient R given by

$$R=P(X_1>X_2),$$

where $X_1$ and $X_2$ are two random variables modeling the lifetime of a component in two different states. Numerous statistical applications have been investigated, pioneered by [27]. Here, we determine R in the context of the TIIPTL-G family. The first result is given in the following proposition.

Proposition 2.

Let$X_1$and$X_2$be two independent random variables such that$X_1$and$X_2$have the cdfs of the TIIPTL-G family given by$F(x;{\alpha }_1,\beta ,\xi )$and$F(x;{\alpha }_2,\beta ,\xi )$, respectively. Then, we have

$$R=\frac{{\alpha }_2}{{\alpha }_1+{\alpha }_2}.$$

Proof. 

Since $X_1$ and $X_2$ are independent, by using (2) and (4), after some algebra, we have

$$\begin{array}{ll}R& ={{\displaystyle \int }}_{-\infty }^{+\infty }F(x;{\alpha }_2,\beta ,\xi )f(x;{\alpha }_1,\beta ,\xi )dx\\ & =1-{{\displaystyle \int }}_{-\infty }^{+\infty }2{\alpha }_1\beta g(x;\xi ){\left[1-G(x;\xi )\right]}^{({\alpha }_1+{\alpha }_2)\beta -1}{\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}^{{\alpha }_1+{\alpha }_2-1}\left\{1-{\left[1-G(x;\xi )\right]}^{\beta }\right\}dx\\ & =1-\frac{{\alpha }_1}{{\alpha }_1+{\alpha }_2}{{\displaystyle \int }}_{-\infty }^{+\infty }f(x;{\alpha }_1+{\alpha }_2,\beta ,\xi )dx=1-\frac{{\alpha }_1}{{\alpha }_1+{\alpha }_2}=\frac{{\alpha }_2}{{\alpha }_1+{\alpha }_2}.\end{array}$$

The proof of Proposition 2 is ended. □

We have $R=0.5$ by taking ${\alpha }_1={\alpha }_2$, the standard value immediately obtained by the definition of R and the fact that $X_1$ and $X_2$ are independent and identically distributed.

The following result generalizes Proposition 2, but with a less tractable series expression.

Proposition 3.

Let$X_1$and$X_2$be two independent random variables such that$X_1$and$X_2$have the cdfs of the TIIPTL-G family given by$F(x;{\alpha }_1,{\beta }_1,\xi )$and$F(x;{\alpha }_2,{\beta }_2,\xi )$, respectively. Then, we have

$$R=1+\sum _{k,\ell ,m=0}^{+\infty }\sum _{q=1}^{+\infty }{a}_{k,\ell }^{\left(2\right)}{a}_{m,q}^{\left(1\right)}\frac{q}{\ell +q},$$

where$a_{m,q}^{\left(1\right)}=\left(\genfrac{}{}{0pt}{}{{\alpha }_1}{m}\right)(\genfrac{}{}{0pt}{}{{\beta }_1(m+{\alpha }_1)}{q}){(-1)}^{m+q+1}{2}^{{\alpha }_1-m}$and$a_{k,\ell }^{\left(2\right)}=\left(\genfrac{}{}{0pt}{}{{\alpha }_2}{k}\right)(\genfrac{}{}{0pt}{}{{\beta }_2(k+{\alpha }_2)}{\ell }){(-1)}^{k+\ell +1}{2}^{{\alpha }_2-k}$.

Proof. 

By applying Theorem 1, we can write

$$F(x;{\alpha }_2,{\beta }_2,\xi )=1+\sum _{k,\ell =0}^{+\infty }{a}_{k,\ell }^{\left(2\right)}{G}_{\ell }(x;\xi ),\hspace{1em}f(x;{\alpha }_1,{\beta }_1,\xi )=\sum _{m=0}^{+\infty }\sum _{q=1}^{+\infty }{a}_{m,q}^{\left(1\right)}{g}_q(x;\xi ).$$

Hence, since $X_1$ and $X_2$ are independent, by using these expressions, we have

$$R={\int }_{-\infty }^{+\infty }F(x;{\alpha }_2,{\beta }_2,\xi )f(x;{\alpha }_1,{\beta }_1,\xi )dx=1+\sum _{k,\ell ,m=0}^{+\infty }\sum _{q=1}^{+\infty }{a}_{k,\ell }^{\left(2\right)}{a}_{m,q}^{\left(1\right)}{\int }_{-\infty }^{+\infty }{g}_q(x;\xi )G_{\ell }(x;\xi )dx,$$

with

$${\int }_{-\infty }^{+\infty }{g}_q(x;\xi )G_{\ell }(x;\xi )dx=\frac{q}{\ell +q}{\int }_{-\infty }^{+\infty }{g}_{\ell +q}(x;\xi )dx=\frac{q}{\ell +q}.$$

The proof of Proposition 3 is completed. □

3.6. Order Statistics

We now provide some distributional results on order statistics in the setting of the TIIPTL-G family. Let $X_1,\dots ,X_n$ be a random sample from the TIIPTL-G family, i.e., $X_1,\dots ,X_n$ are independent and identically distributed having the common cdf given by (2), and $X_{i:n}$ be the i-th order statistic. The following result shows that the pdf of $X_{i:n}$ can be expressed as a finite mixture of pdfs of the TIIPTL-G family.

Proposition 4.

Let$f_{i:n}(x;\alpha ,\beta ,\xi )$be the pdf of$X_{i:n}$. Then, we can write

$$f_{i:n}(x;\alpha ,\beta ,\xi )=\sum _{j=0}^{i-1}{b}_{j}f(x;\alpha (j+n-i+1),\beta ,\xi ),$$

where

$$b_j=\frac{n!}{(i-1)!(n-i)!}\left(\genfrac{}{}{0pt}{}{i-1}{j}\right){(-1)}^j\frac{1}{j+n-i+1}.$$

Proof. 

By using a well-known general result, the pdf of $X_{i:n}$ is given by

$$f_{i:n}(x;\alpha ,\beta ,\xi )=\frac{n!}{(i-1)!(n-i)!}f(x;\alpha ,\beta ,\xi ){\left[F(x;\alpha ,\beta ,\xi )\right]}^{i-1}{\left[S(x;\alpha ,\beta ,\xi )\right]}^{n-i},\hspace{1em}x\in \mathbb{R}.$$

By applying the standard binomial formula, we get

$$f_{i:n}(x;\alpha ,\beta ,\xi )=\frac{n!}{(i-1)!(n-i)!}\sum _{j=0}^{i-1}\left(\genfrac{}{}{0pt}{}{i-1}{j}\right){(-1)}^j\left\{f(x;\alpha ,\beta ,\xi ){\left[S(x;\alpha ,\beta ,\xi )\right]}^{j+n-i}\right\}.$$

Now, owing to (4) and (3), let us notice that

$$\begin{array}{l}f(x;\alpha ,\beta ,\xi ){\left[S(x;\alpha ,\beta ,\xi )\right]}^{j+n-i}\\ =2\alpha \beta g(x;\xi ){\left[1-G(x;\xi )\right]}^{\alpha (j+n-i+1)\beta -1}{\left\{2-{\left[1-G(x;\xi )\right]}^{\beta }\right\}}^{\alpha (j+n-i+1)-1}\left\{1-{\left[1-G(x;\xi )\right]}^{\beta }\right\}\\ =\frac{1}{j+n-i+1}f(x;\alpha (j+n-i+1),\beta ,\xi ).\end{array}$$

By putting the above equalities together, the proof of Proposition 4 is completed. □

Some properties of $X_{i:n}$ can be easily derived to Proposition 4 and the already shown properties of the TIIPTL-G family in Section 3. As example, the r-th moment of $X_{i:n}$ is defined by

$${\mu }_r^o={\int }_{-\infty }^{+\infty }{x}^r{f}_{i:n}(x;\alpha ,\beta ,\xi )dx.$$

Then, owing to Proposition 4, we have

$${\mu }_r^o=\sum _{j=0}^{i-1}{b}_j{\mu }_{j,r}^{\prime },$$

where ${\mu }_{j,r}^{\prime }={\int }_{-\infty }^{+\infty }{x}^{r}f(x;\alpha (j+n-i+1),\beta ,\xi )dx$ can be expressed as in (11).

4. Estimation and Simulation

In this section, we discuss the inferential properties of the TIIPTLIEx model (see Section 2.4). The model parameters, i.e., $\alpha$, $\beta$ and $\theta$, are investigated by three different methods: the maximum likelihood, percentile and right-tail Anderson-Darling methods, with a simulation study illustrating their convergence properties. Hereafter, we consider a random variable X following the TIIPTLIEx distribution, as well as n independent realizations $x_1,\dots ,x_n$ of X and their rearrangements in increasing order denoted by $x_{\left(1\right)},\dots x_{\left(n\right)}$.

4.1. Maximum Likelihood Method of Estimation

In the context of the TIIPTLIEx model, by using (7), the likelihood function is given by

$$\begin{array}{l}L(\alpha ,\beta ,\theta )={\displaystyle \prod _{i=1}^n}f(x_i;\alpha ,\beta ,\xi )\\ =2^n{\alpha }^n{\beta }^n{\theta }^n{\displaystyle \prod _{i=1}^n}\frac{1}{x_i^2}{e}^{-\theta /x_i}{\left[1-e^{-\theta /x_i}\right]}^{\alpha \beta -1}{\left\{2-{\left[1-e^{-\theta /x_i}\right]}^{\beta }\right\}}^{\alpha -1}\left\{1-{\left[1-e^{-\theta /x_i}\right]}^{\beta }\right\}.\end{array}$$

The maximum likelihood estimates (MLEs) are given by maximizing this function according to $\alpha$, $\beta$ and $\theta$. They are also defined as the maximum of the log-likelihood function defined by

$$\begin{array}{l}\ell (\alpha ,\beta ,\theta )=\log \left[L(\alpha ,\beta ,\theta )\right]\\ =n\log \left(2\right)+n\log \left(\alpha \right)+n\log \left(\beta \right)+n\log \left(\theta \right)-2{\displaystyle \sum _{i=1}^n}\log \left(x_i\right)-\theta {\displaystyle \sum _{i=1}^n}{x}_i^{-1}+(\alpha \beta -1){\displaystyle \sum _{i=1}^n}\log \left[1-e^{-\theta /x_i}\right]\\ +(\alpha -1){\displaystyle \sum _{i=1}^n}\log \left\{2-{\left[1-e^{-\theta /x_i}\right]}^{\beta }\right\}+{\displaystyle \sum _{i=1}^n}\log \left\{1-{\left[1-e^{-\theta /x_i}\right]}^{\beta }\right\}.\end{array}$$

That is, the MLEs are the solutions of the three following equations: $\partial \ell (\alpha ,\beta ,\theta )/\partial \alpha =0$, $\partial \ell (\alpha ,\beta ,\theta )/\partial \beta =0$ and $\partial \ell (\alpha ,\beta ,\theta )/\partial \theta =0$, where

$$\frac{\partial \ell (\alpha ,\beta ,\theta )}{\partial \alpha }=\frac{n}{\alpha }+\beta {\displaystyle \sum _{i=1}^n}\log \left[1-e^{-\theta /x_i}\right]+{\displaystyle \sum _{i=1}^n}\log \left\{2-{\left[1-e^{-\theta /x_i}\right]}^{\beta }\right\},$$

$$\begin{array}{ll}\frac{\partial \ell (\alpha ,\beta ,\theta )}{\partial \beta }=& \frac{n}{\beta }+\alpha {\displaystyle \sum _{i=1}^n}\log \left[1-e^{-\theta /x_i}\right]-(\alpha -1){\displaystyle \sum _{i=1}^n}\frac{{\left[1-e^{-\theta /x_i}\right]}^{\beta }\log \left[1-e^{-\theta /x_i}\right]}{2-{\left[1-e^{-\theta /x_i}\right]}^{\beta }}\\ & -{\displaystyle \sum _{i=1}^n}\frac{{\left[1-e^{-\theta /x_i}\right]}^{\beta }\log \left[1-e^{-\theta /x_i}\right]}{1-{\left[1-e^{-\theta /x_i}\right]}^{\beta }}\end{array}$$

and

$$\begin{array}{ll}\frac{\partial \ell (\alpha ,\beta ,\theta )}{\partial \theta }=& \frac{n}{\theta }-{\displaystyle \sum _{i=1}^n}{x}_i^{-1}+(\alpha \beta -1){\displaystyle \sum _{i=1}^n}\frac{e^{-\theta /x_i}}{x_i(1-e^{-\theta /x_i})}\\ & -(\alpha -1)\beta {\displaystyle \sum _{i=1}^n}\frac{e^{-\theta /x_i}{\left[1-e^{-\theta /x_i}\right]}^{\beta -1}}{x_i\left\{2-{\left[1-e^{-\theta /x_i}\right]}^{\beta }\right\}}-\beta {\displaystyle \sum _{i=1}^n}\frac{e^{-\theta /x_i}{\left[1-e^{-\theta /x_i}\right]}^{\beta -1}}{x_i\left\{1-{\left[1-e^{-\theta /x_i}\right]}^{\beta }\right\}}.\end{array}$$

The solutions of these equations have no close form; mathematical software must be used to have a numerical evaluation of the MLEs. In this study, we use the R software (see [28]).

4.2. Percentile Method of Estimation

We now explore the percentile method of estimation pioneered by [29]. By using the qf of the TIIPTLIEx distribution given by (10), we introduce the following function:

$$\begin{array}{ll}U(\alpha ,\beta ,\theta )& ={\displaystyle \sum _{i=1}^n}{\left[x_{\left(i\right)}-Q(p_i;\alpha ,\beta ,\theta )\right]}^2\\ & ={\displaystyle \sum _{i=1}^n}{\left[x_{\left(i\right)}+\theta {\left[\log \left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}\right]}^{-1}\right]}^2,\end{array}$$

where $p_i=i/(n+1)$. Then, the percentile estimates (PCEs) of $\alpha$, $\beta$ and $\theta$ are obtained by minimizing $U(\alpha ,\beta ,\theta )$ according to $\alpha$, $\beta$ and $\theta$, which is equivalent to solve the three following equations simultaneously: $\partial U(\alpha ,\beta ,\theta )/\partial \alpha =0$, $\partial U(\alpha ,\beta ,\theta )/\partial \beta =0$ and $\partial U(\alpha ,\beta ,\theta )/\partial \theta =0$, where

$$\frac{\partial U(\alpha ,\beta ,\theta )}{\partial \alpha }=2{\displaystyle \sum _{i=1}^n}{\upsilon }_i^{\left(1\right)}(\alpha ,\beta ,\theta )\left[x_{\left(i\right)}+\theta {\left[\log \left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}\right]}^{-1}\right],$$

$$\frac{\partial U(\alpha ,\beta ,\theta )}{\partial \beta }=2{\displaystyle \sum _{i=1}^n}{\upsilon }_i^{\left(2\right)}(\alpha ,\beta ,\theta )\left[x_{\left(i\right)}+\theta {\left[\log \left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}\right]}^{-1}\right]$$

and

$$\frac{\partial U(\alpha ,\beta ,\theta )}{\partial \theta }=2{\displaystyle \sum _{i=1}^n}{\upsilon }_i^{\left(3\right)}(\alpha ,\beta ,\theta )\left[x_{\left(i\right)}+\theta {\left[\log \left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}\right]}^{-1}\right],$$

with

$$\begin{array}{ll}{\upsilon }_i^{\left(1\right)}(\alpha ,\beta ,\theta )& =\frac{\partial Q(p_i;\alpha ,\beta ,\theta )}{\partial \alpha }\\ & =-\frac{\theta {(1-p_i)}^{1/\alpha }\log (1-p_i){\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta -1}}{2{\alpha }^2\beta \sqrt{1-{(1-p_i)}^{1/\alpha }}\left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}{\left[\log \left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}\right]}^2},\end{array}$$

$$\begin{array}{ll}{\upsilon }_i^{\left(2\right)}(\alpha ,\beta ,\theta )& =\frac{\partial Q(p_i;\alpha ,\beta ,\theta )}{\partial \beta }\\ & =-\frac{\theta {\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\log \left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}{{\beta }^2\left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}{\left[\log \left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}\right]}^2}\end{array}$$

and

$${\upsilon }_i^{\left(3\right)}(\alpha ,\beta ,\theta )=\frac{\partial Q(p_i;\alpha ,\beta ,\theta )}{\partial \theta }={\left[\log \left\{1-{\left[1-\sqrt{1-{(1-p_i)}^{1/\alpha }}\right]}^{1/\beta }\right\}\right]}^{-1}.$$

For practical purposes, these PCEs can evaluated numerically.

4.3. Right-Tail Anderson-Darling Method of Estimation

We now discuss the right-tail Anderson-Darling estimates (RTADEs) of $\alpha$, $\beta$ and $\theta$ pioneered by [30]. First of all, by using the cdf and chrf of the TIIPTLIEx distribution given by (6) and (8), respectively, we introduce the following function:

$$\begin{array}{ll}R(\alpha ,\beta ,\theta )& =\frac{n}{2}-2{\displaystyle \sum _{i=1}^n}F(x_{\left(i\right)};\alpha ,\beta ,\theta )+\frac{1}{n}{\displaystyle \sum _{i=1}^n}(2i-1)H(x_{(n+1-i)};\alpha ,\beta ,\theta )\\ & =\frac{n}{2}-2{\displaystyle \sum _{i=1}^n}\left\{1-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\alpha \beta }{\left\{2-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\beta }\right\}}^{\alpha }\right\}\\ & -\alpha \frac{1}{n}{\displaystyle \sum _{i=1}^n}(2i-1)\left[\beta \log \left[1-e^{-\theta /x_{(n+1-i)}}\right]+\log \left\{2-{\left[1-e^{-\theta /x_{(n+1-i)}}\right]}^{\beta }\right\}\right].\end{array}$$

Then, the RTADEs can be obtained by minimizing $R(\alpha ,\beta ,\theta )$ according to $\alpha$, $\beta$ and $\theta$, which is equivalent to solve the three following equations simultaneously: $\partial R(\alpha ,\beta ,\theta )/\partial \alpha =0$, $\partial R(\alpha ,\beta ,\theta )/\partial \beta =0$ and $\partial R(\alpha ,\beta ,\theta )/\partial \theta =0$, where

$$\frac{\partial R(\alpha ,\beta ,\theta )}{\partial \alpha }=-2{\displaystyle \sum _{i=1}^n}{\eta }_i^{\left(1\right)}(\alpha ,\beta ,\theta )+\frac{1}{n}{\displaystyle \sum _{i=1}^n}(2i-1)\frac{{\eta }_{n+1-i}^{\left(1\right)}(\alpha ,\beta ,\theta )}{S(x_{(n+1-i)};\alpha ,\beta ,\theta )},$$

$$\frac{\partial R(\alpha ,\beta ,\theta )}{\partial \beta }=-2{\displaystyle \sum _{i=1}^n}{\eta }_i^{\left(2\right)}(\alpha ,\beta ,\theta )+\frac{1}{n}{\displaystyle \sum _{i=1}^n}(2i-1)\frac{{\eta }_{n+1-i}^{\left(2\right)}(\alpha ,\beta ,\theta )}{S(x_{(n+1-i)};\alpha ,\beta ,\theta )}$$

and

$$\frac{\partial R(\alpha ,\beta ,\theta )}{\partial \theta }=-2{\displaystyle \sum _{i=1}^n}{\eta }_i^{\left(3\right)}(\alpha ,\beta ,\theta )+\frac{1}{n}{\displaystyle \sum _{i=1}^n}(2i-1)\frac{{\eta }_{n+1-i}^{\left(3\right)}(\alpha ,\beta ,\theta )}{S(x_{(n+1-i)};\alpha ,\beta ,\theta )},$$

with

$$\begin{array}{ll}{\eta }_i^{\left(1\right)}(\alpha ,\beta ,\theta )& =\frac{\partial F(x_{\left(i\right)};\alpha ,\beta ,\theta )}{\partial \alpha }\\ & =-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\alpha \beta }{\left\{2-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\beta }\right\}}^{\alpha }\left[\beta \log \left[1-e^{-\theta /x_{\left(i\right)}}\right]+\log \left\{2-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\beta }\right\}\right],\end{array}$$

$$\begin{array}{ll}{\eta }_i^{\left(2\right)}(\alpha ,\beta ,\theta )& =\frac{\partial F(x_{\left(i\right)};\alpha ,\beta ,\theta )}{\partial \beta }\\ & =-2\alpha \left\{1-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\beta }\right\}\log \left[1-e^{-\theta /x_{\left(i\right)}}\right]{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\alpha \beta }{\left\{2-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\beta }\right\}}^{\alpha -1},\end{array}$$

$$\begin{array}{ll}{\eta }_i^{\left(3\right)}(\alpha ,\beta ,\theta )& =\frac{\partial F(x_{\left(i\right)};\alpha ,\beta ,\theta )}{\partial \theta }\\ & =-2\alpha \beta \frac{1}{x_{\left(i\right)}}{e}^{-\theta /x_{\left(i\right)}}\left\{1-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\beta }\right\}{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\alpha \beta -1}{\left\{2-{\left[1-e^{-\theta /x_{\left(i\right)}}\right]}^{\beta }\right\}}^{\alpha -1}\end{array}$$

and

$$S(x_{(n+1-i)};\alpha ,\beta ,\theta )={\left[1-e^{-\theta /x_{(n+1-i)}}\right]}^{\alpha \beta }{\left\{2-{\left[1-e^{-\theta /x_{(n+1-i)}}\right]}^{\beta }\right\}}^{\alpha }.$$

The quantities ${\eta }_{n+1-i}^{\left(1\right)}(\alpha ,\beta ,\theta )$, ${\eta }_{n+1-i}^{\left(2\right)}(\alpha ,\beta ,\theta )$ and ${\eta }_{n+1-i}^{\left(3\right)}(\alpha ,\beta ,\theta )$ are defined in a similar manner to ${\eta }_i^{\left(1\right)}(\alpha ,\beta ,\theta )$, ${\eta }_i^{\left(2\right)}(\alpha ,\beta ,\theta )$ and ${\eta }_i^{\left(3\right)}(\alpha ,\beta ,\theta )$, respectively, with $x_{(n+1-i)}$ instead of $x_{\left(i\right)}$.

Numerical solutions are available in R to evaluate these RTADEs.

4.4. A Simulation Study

Here, we perform a simulation study giving numerical results to compare the performance of the previously presented estimation methods. Our methodology is described as follows. By using the corresponding qf, we generate $N=1000$ random samples of size $n=50$, 100, 200 and 500 from the TIIPTLIEx distribution. Then, four sets of the parameters are assigned as: Set1: $(\alpha =2,\theta =1.5,\beta =2)$, Set2: $(\alpha =3,\theta =1.5,\beta =2)$, Set3: $(\alpha =2,\theta =1.5,\beta =3)$ and Set4: $(\theta =3,\theta =1.5,\beta =3)$. Then, we consider the following measures: the (mean) estimates and the corresponding mean squared errors (MSEs) defined as follows:

$${\widehat{Estimate}}_{ϵ}\left(n\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\widehat{ϵ}}_i,\hspace{1em}{\widehat{MSE}}_{ϵ}\left(n\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{({\widehat{ϵ}}_i-ϵ)}^2,$$

where $ϵ=\alpha$, $\theta$ or $\beta$, and ${\widehat{ϵ}}_i$ is the estimates of ${ϵ}_i$ for $i=1,\dots ,N$ via the considered method: MLE, PCE or RTADE. The obtained numerical results are documented in

Table 2. Estimates and MSEs of TIIPTLIEx distribution for MLE, PCand RTADestimates for Set1: $(\alpha =2,\theta =1.5,\beta =2)$.

	MLEs		PCEs		RTADEs
$\mathit{n}$	Estimates	MSEs	Estimates	MSEs	Estimates	MSEs
50	2.143	0.291	2.094	0.662	1.599	0.801
	1.528	0.067	1.392	0.102	1.115	0.585
	2.022	0.271	1.857	0.370	1.572	0.707
100	2.115	0.106	2.176	0.480	1.668	0.786
	1.519	0.033	1.405	0.072	1.142	0.570
	1.960	0.066	1.826	0.286	1.567	0.673
200	2.088	0.074	2.003	0.393	1.626	0.759
	1.511	0.011	1.452	0.033	1.143	0.550
	1.981	0.042	1.968	0.142	1.585	0.653
500	2.105	0.047	2.089	0.221	1.813	0.488
	1.499	4.844 *	1.428	0.017	1.282	0.344
	1.948	0.025	1.846	0.133	1.741	0.406

* Indicates that the value multiply ${10}^{-3}$.

,

Table 3. Estimates and MSEs of TIIPTLIEx distribution for MLE, PC and RTAD estimates for Set2: $(\alpha =3,\theta =1.5,\beta =2)$.

	MLEs		PCEs		RTADEs
$\mathit{n}$	Estimates	MSEs	Estimates	MSEs	Estimates	MSEs
50	2.489	0.365	2.448	1.084	1.863	2.770
	1.573	0.050	1.315	0.177	1.078	0.814
	2.441	0.324	1.984	0.611	1.795	1.210
100	2.505	0.315	2.346	1.008	1.803	2.512
	1.572	0.034	1.395	0.062	1.083	0.687
	2.451	0.270	2.177	0.330	1.765	0.944
200	2.466	0.307	2.339	0.804	1.920	2.136
	1.539	0.013	1.468	0.025	1.147	0.573
	2.364	0.161	2.317	0.289	1.835	0.789
500	2.482	0.279	2.218	0.638	1.919	2.127
	1.559	7.459 *	1.470	0.016	1.165	0.572
	2.384	0.156	2.325	0.188	1.874	0.799

* Indicates that the value multiply ${10}^{-3}$.

,

Table 4. Estimates and MSEs of TIIPTLIEx distribution for MLE, PC and RTAD estimates for Set3: $(\alpha =2,\theta =1.5,\beta =3)$.

	MLEs		PCEs		RTADEs
$\mathit{n}$	Estimates	MSEs	Estimates	MSEs	Estimates	MSEs
50	2.630	0.525	2.439	0.463	2.661	0.620
	1.536	0.040	1.389	0.121	1.489	0.060
	2.589	0.318	2.453	0.821	2.481	0.469
100	2.585	0.432	2.334	0.250	2.626	0.469
	1.517	0.019	1.395	0.074	1.452	0.022
	2.627	0.312	2.465	0.704	2.429	0.386
200	2.534	0.310	2.344	0.239	2.593	0.389
	1.474	0.012	1.363	0.050	1.429	0.013
	2.507	0.285	2.319	0.694	2.368	0.383
500	2.524	0.292	2.344	0.164	2.619	0.376
	1.454	6.626 *	1.406	0.027	1.449	7.531*
	2.481	0.283	2.432	0.444	2.392	0.382

* Indicates that the value multiply ${10}^{-3}$.

and

Table 5. Estimates and MSEs of TIIPTLIEx distribution for MLE, PC and RTAD estimates for Set4: $(\alpha =3,\theta =1.5,\beta =3)$.

	MLEs		PCEs		RTADEs
$\mathit{n}$	Estimates	MSEs	Estimates	MSEs	Estimates	MSEs
50	3.224	0.652	2.711	0.464	3.120	0.318
	1.567	0.058	1.421	0.099	1.514	0.047
	3.193	0.494	3.022	0.911	3.082	0.266
100	3.336	0.431	2.582	0.311	3.082	0.221
	1.542	0.016	1.369	0.053	1.510	0.027
	3.027	0.187	2.838	0.436	3.022	0.148
200	3.280	0.309	2.705	0.159	3.019	0.099
	1.522	7.876 *	1.418	0.027	1.511	0.013
	2.965	0.118	2.912	0.248	3.030	0.073
500	3.225	0.196	2.760	0.091	3.091	0.082
	1.480	3.803 *	1.476	8.344 *	1.513	5.006 *
	2.817	0.117	3.065	0.099	2.995	0.050

* Indicates that the value multiply ${10}^{-3}$.

.

One can observe from

Table 6. Ranks of all the three methods of estimation for the considered sets of parameters.

Sets	n	MLEs	PCEs	RTADEs
Set1: $(\alpha =2,\theta =1.5,\beta =2)$	50	1.0	2.0	3.0
	100	1.0	2.0	3.0
	200	1.0	2.0	3.0
	500	1.0	2.0	3.0
Set2: $(\alpha =3,\theta =1.5,\beta =2)$	50	1.0	2.5	2.5
	100	1.0	2.0	3.0
	200	1.0	2.0	3.0
	500	1.0	2.0	3.0
Set3: $(\alpha =2,\theta =1.5,\beta =3)$	50	1.0	2.5	2.5
	100	1.0	2.5	2.5
	200	1.0	2.5	2.5
	500	1.0	2.5	2.5
Set4: $(\alpha =3,\theta =1.5,\beta =3)$	50	2.0	3.0	1.0
	100	2.0	3.0	1.0
	200	2.0	3.0	1.0
	500	2.5	2.5	1.0
Sum of the partial ranks		20.5	38.0	37.5
Final rank		1.0	3.0	2.0

that the maximum likelihood method outperforms the other methods (with the final score of 20.5). Therefore, the use of the MLEs to estimate the TIIPTLIEx model parameters is justified.

5. Applications

This section shows the potential of the TIIPTL-G family distribution in a practical setting. We consider the TIIPTLIEx model and all the consider model parameters will be estimated by the maximum likelihood method, with the use of the R software. We compare the TIIPTLIEx model with seven three(or less)-parameter models connected to the IEx model, namely: the Kumaraswamy inverse exponential (KIEx) model (see [31]), beta inverse exponential (BIEx) model (see [32]) by keeping shape parameter is equal to one, alpha-power inverse Weibull (AIW) model (see [33]), logistic inverse exponential (LIEx) model (see [34]), inverse Weibull inverse exponential (IWIEx) model (see [35]), type II Topp-Leone generalized inverse Rayleigh (TIR) model (see [36]) and standard IEX model.

Two practical data sets are analyzed. The first data set contains the ball bearing data, which indicates the number of revolutions before failure for ball bearing (see [37]). The data are as follows: 33.00, 68.64, 173.40, 41.52, 42.12, 68.64, 68.88, 45.60, 48.48, 84.12, 93.12, 98.64, 105.12, 105.84, 51.84, 51.96, 54.12, 17.88, 55.56, 127.92, 128.04, 67.80, 67.80, 28.92.

The second considered data set contains the waiting times (in seconds), between 65 successive eruptions of the Kiama Blowhole. These values were recorded by Jim Irish on July 12, 1998, and recently has been referenced by [38]. The data are as follows: 83, 51, 87, 60, 28, 95, 8, 27, 15, 10, 18, 16, 29, 54, 91, 8, 17, 55, 10, 35, 47, 77, 36, 17, 21, 36, 18, 40, 10, 7, 34, 27, 28, 56, 8, 25, 68, 146, 89, 18, 73, 69, 9, 37, 10, 82, 29, 8, 60, 61, 61, 18, 169, 25, 8, 26, 11, 83, 11, 42, 17, 14, 9, 12.

The MLEs of the model parameters are documented in

Table 7. MLEs and their standard errors (in parentheses) for the first data set.

Model	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$	a	b
TIIPTLIEx	46.4917	0.2570	58.4781	-	-	-
	(2.0811)	(0.4493)	(3.7038)	-	-	-
KIEx	15.5780	5.6385	8.6130	-	-	-
	(2.7977)	(2.2527)	(0.5530)	-	-	-
BIEx	-	-	11.6360	-	16.9072	3.8280
	-	-	(0.9004)	-	(0.1398)	(1.0557)
AIW	35.4934	1.2320	-	33.8531	-	-
	(3.0404)	(0.1345)	-	(6.8240)	-
LIEx	-	-	-	-	4.2022	28.3120
	-	-	-	-	(0.7476)	(2.9606)
IWIEx	1.7362	1.8178	27.5001	-	-	-
	(2.4572)	(0.2659)	(9.7337)	-	-	-
TIR	14.5765	5.6554	1.0716	-	-	-
	(0.6273)	(1.38163)	(0.3041)	-	-	-
IEx	-	-	55.4934	-	-	-
	-	-	(11.3275)	-	-	-

and

Table 8. MLEs and their standard errors (in parentheses) for the second data set.

Model	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\theta }$	$\mathit{\lambda }$	a	b
TIIPTLIEx	28.7430	0.1522	10.9219	-	-	-
	(0.4839)	(0.1831)	(2.4038)	-	-	-
KIEx	21.3327	1.7608	1.3437	-	-	-
	(1.9516)	(0.3244)	(7.9917)	-	-	-
BIEx	-	-	11.7217	-	2.8252	1.6669
	-	-	(0.1304)	-	(0.2676)	(0.9539)
AIW	3.6810	49.2020	-	1.4616	-	-
	(4.6113)	(0.0244)	-	(0.1661)	-
LIEx	-	-	-	-	2.4594	11.2381
	-	-	-	-	(0.2792)	(1.2269)
IWIEx	1.2470	1.2812	14.3304	-	-	-
	(2.1153)	(0.1442)	(5.3741)	-	-	-
TIR	16.8288	0.2966	0.5422	-	-	-
	(9.7095)	(3.8675)	(0.0809)	-	-	-
IEx	-	-	20.4026	-	-	-
	-	-	(2.5503)	-	-	-

for the first and second data sets, respectively. The standard goodness-of-fit measures are computed in

Table 9. The $-\widehat{\ell }$, AIC, CAIC, BIC, HQIC, W* and A* values for the first data set.

Model	$-\widehat{\mathit{\ell }}$	AIC	CAIC	BIC	HQIC	W*	A*
TIIPTLIEx	117.7402	241.4803	242.6803	245.0145	242.4180	0.0343	0.2247
KIEx	118.0351	242.0702	243.2702	245.6044	243.0078	0.0373	0.2561
BIEx	118.7151	243.4301	244.6301	246.9643	244.3677	0.0499	0.3567
AIW	125.6581	257.3162	258.5162	260.8504	258.2539	0.0399	0.2780
LIEx	119.1395	242.2790	242.8504	245.6351	242.9043	0.0526	0.3747
IWIEx	120.6731	247.3462	248.5462	250.8804	248.2838	0.0910	0.6401
TIR	120.6591	247.3182	248.5182	250.8524	248.2558	0.0947	0.6639
IEx	126.9634	255.9268	256.1086	257.1049	256.2394	0.0498	0.3562

and

Table 10. The $-\widehat{\ell }$, AIC, CAIC, BIC, HQIC, W* and A* values for the second data set.

Model	$-\widehat{\mathit{\ell }}$	AIC	CAIC	BIC	HQIC	W*	A*
TIIPTLIEx	293.7982	593.5963	593.9963	600.0730	596.1478	0.1211	0.8804
KIEx	294.761	595.5237	595.9237	602.0003	598.0751	0.1512	1.0674
BIEx	294.8518	595.7036	596.1036	602.1802	598.2557	0.1575	1.1037
AIW	294.9399	595.8798	596.2798	602.3565	598.4313	0.1591	1.1133
LIEx	299.3795	602.7589	602.9556	607.0767	604.4599	0.2466	1.6523
IWIEx	295.5628	597.1256	597.5256	603.6023	599.6771	0.1889	1.28434
TIR	296.7181	599.4362	599.8362	605.9128	601.9876	0.2378	1.5590
IEx	299.1754	600.3507	600.4152	602.5096	601.2012	0.1566	1.0983

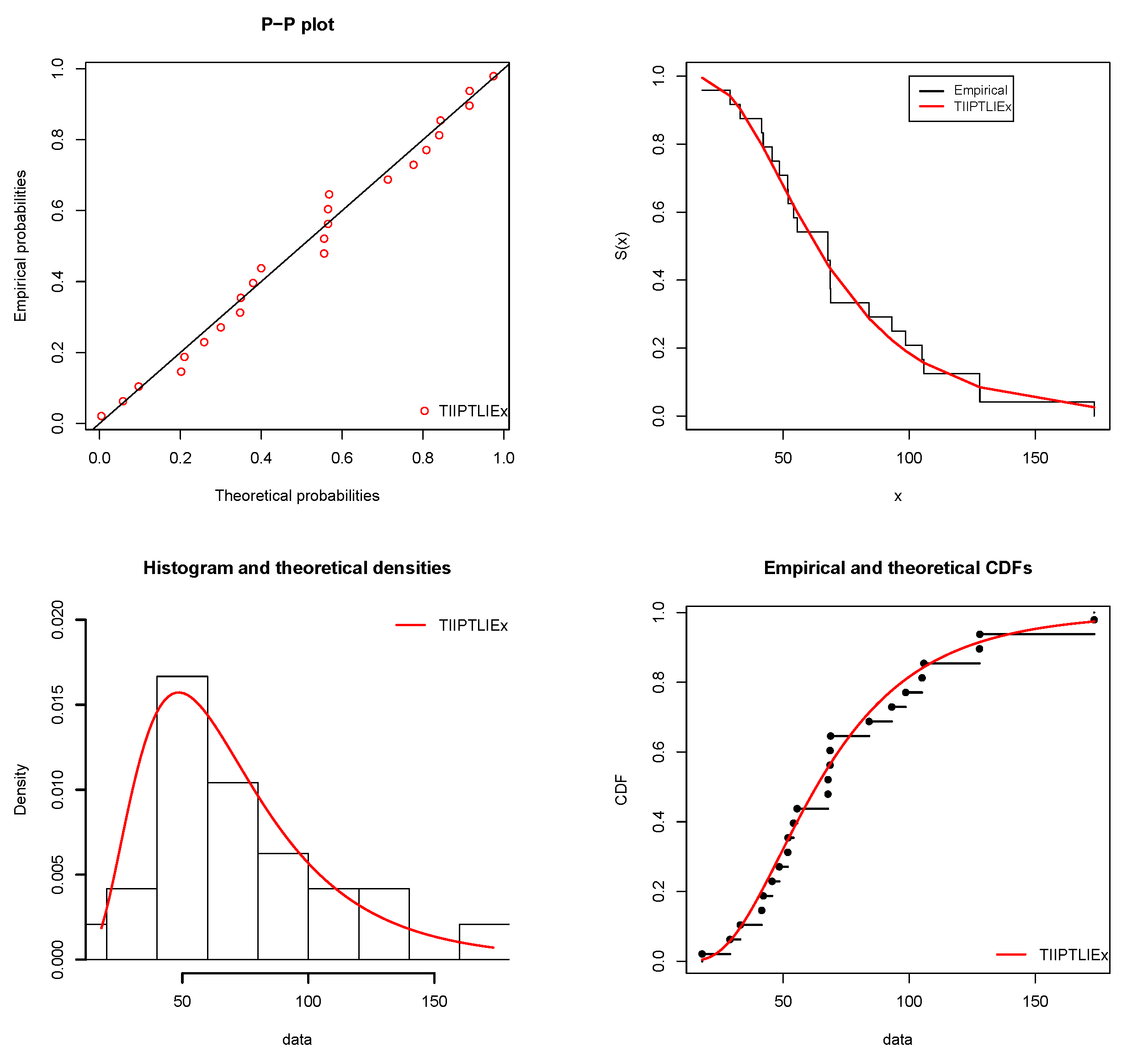
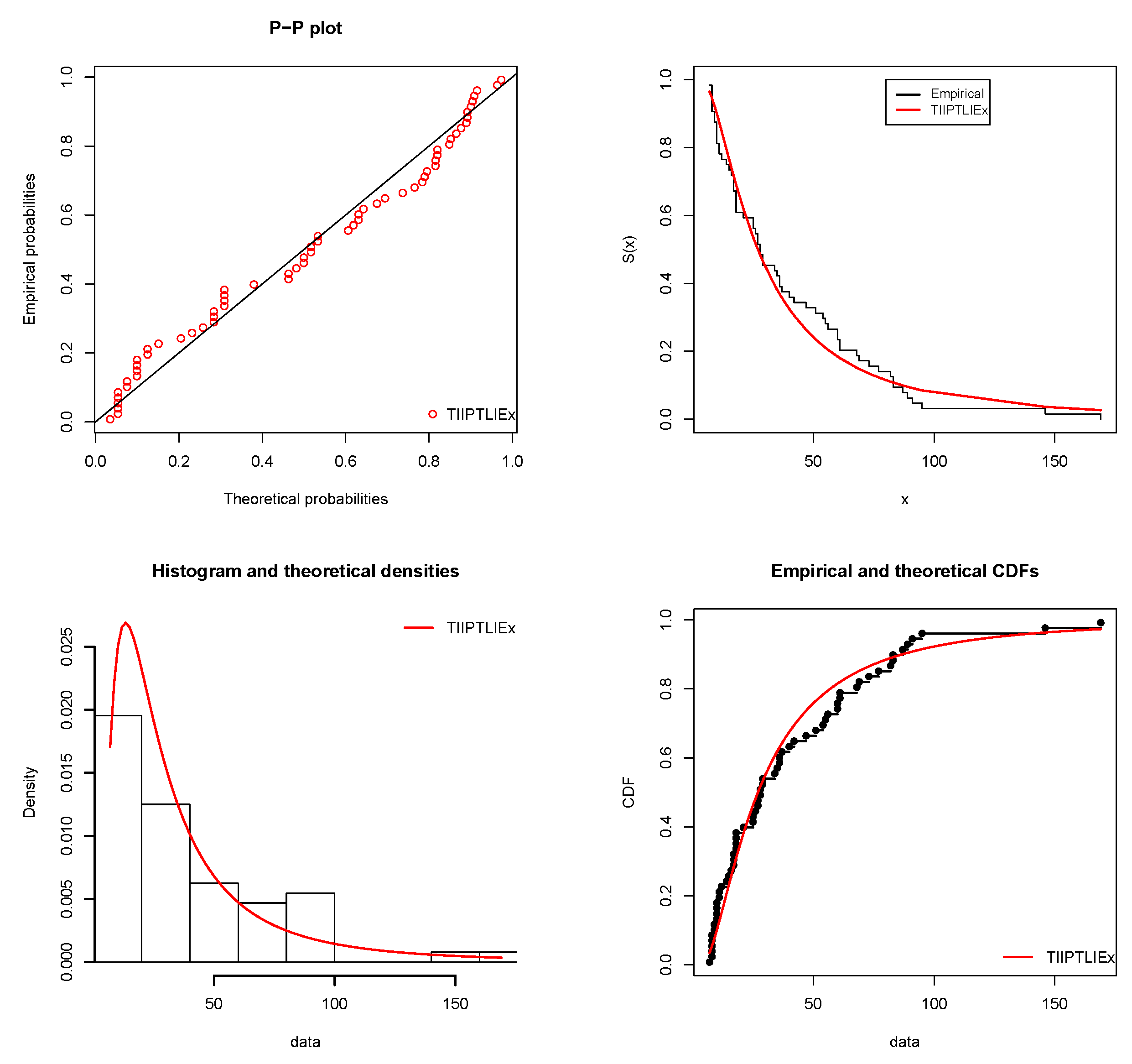
, indicating the estimated log-likelihood $(\widehat{\ell })$, Akaike information criterion (AIC), corrected Akaike information criterion (CAIC), Bayesian information criterion (BIC), Hannan-Quinn information criterion (HQIC), Cramer-von Mises (W*) statistic and Anderson-Darling (A*) statistic. The lower the values of these numerical criteria, the better the fit. We thus see that the TIIPTLIEx model is the best. With a focus on the TIIPTLIEx model, the P-P (Probability-Probability) plot and various fits involving estimated cdfs, sfs and pdfs over for the first and second data sets can be seen in Figure 3 and Figure 4. All of them illustrate the nice fits of the TIIPTLIEx model, showing its potential of interest for the practitioner in an analysis of data setting. 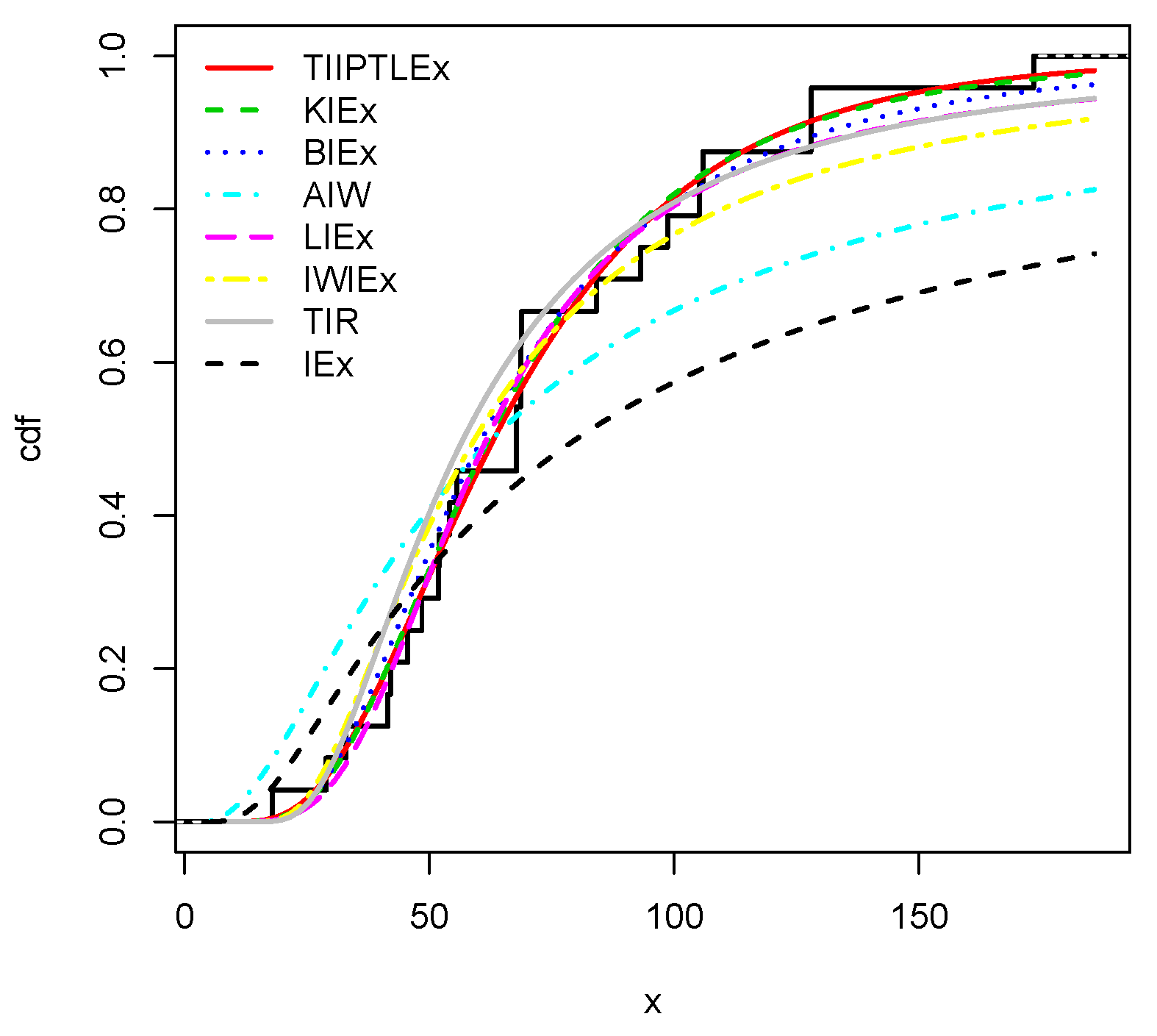We complete these analyzes by showing the fits of the estimated pdfs in Figure 5 and Figure 6 over the histograms of the first and second data sets, respectively. On the other hand, estimated cdfs over the empirical cdf can be seen in Figure 7 and Figure 8 for the first and second data sets, respectively. As remark, from the fits of the plain red line (TIIPTLIEx) and the dashed black line (IEx) in the above figures, one can notice that the TIIPTLIEx model significantly increases the flexible properties of the former IEx model, reaching new perspectives of statistical modelling for various kinds of data sets.

6. Conclusions

A new family of distributions is proposed in this paper, called the type II power Topp-Leone-G (TIIPTL-G) family. It extends, in some senses, the so-called type II Topp-Leone-G family by the add of a new shape parameter. The main properties of the TIIPTL-G family are discussed, proving several essential results on the quantile function, mixture representation of the cdf and pdf, moments, stochastic ordering, reliability and order statistics. A focus is put on the special member defined with the inverse exponential distribution as baseline, introducing a new three-parameter lifetime distribution. We perform an inferential study on the related model, called the TIIPTLIEx model, including the use of several estimation methods for the model parameters. Then, we apply this new model to two practical data sets, by adopting the maximum likelihood method of estimation. Seven competitors models are considered but no one perform better to the TIIPTLIEx model in terms of standard goodness-of-fit measures. Thus, the TIIPTL-G family of distribution has a straightforward utilization within the errors-in-variables models, especially for an application in calibration (see [39]) or within the change-point analysis (see [40]). We therefore believe that the TIIPTL-G family has a promising usefulness for future applications beyond the scope of this paper.