Abstract
Proof of ownership on multimedia data exposes users to significant threats due to a myriad of transmission channel attacks over distributed computing infrastructures. In order to address this problem, in this paper, an efficient blind symmetric image watermarking method using singular value decomposition (SVD) and the fast Walsh-Hadamard transform (FWHT) is proposed for ownership protection. Initially, Gaussian mapping is used to scramble the watermark image and secure the system against unauthorized detection. Then, FWHT with coefficient ordering is applied to the cover image. To make the embedding process robust and secure against severe attacks, two unique keys are generated from the singular values of the FWHT blocks of the cover image, which are kept by the owner only. Finally, the generated keys are used to extract the watermark and verify the ownership. The simulation result demonstrates that our proposed scheme is highly robust against numerous attacks. Furthermore, comparative analysis corroborates its superiority among other state-of-the-art methods. The NC of the proposed method is numerically one, and the PSNR resides from 49.78 to 52.64. In contrast, the NC of the state-of-the-art methods varies from 0.7991 to 0.9999, while the PSNR exists in the range between 39.4428 and 54.2599.
1. Introduction
The flow of multimedia data increases manifold with the recent infrastructural development of computer networks. Accordingly, the proof of ownership issue for multimedia data has come to the surface as an impending challenge. In a bid to negotiate with this problem, the watermarking approach might be used as an indispensable tool. Since multimedia data often suffer from different types of transmission channel attacks, the technique should be immune to such maladies. Hence, the watermarking approach is used for hiding the digital information during transmission. The watermark is typically used to prove the ownership of such host signals. Several algorithms have been proposed in the literature to create robust and imperceptible watermarks. In general, watermarking methods can be divided into three main categories: (i) blind methods [1,2,3,4,5,6,7,8,9,10,11,12,13], (ii) semi-blind methods [14,15,16,17] (iii) non-blind methods [18,19,20,21,22,23,24]. A blind watermarking framework for high dynamic range images (HDRIs) is proposed in [1]. In this method, the artificial bee colony algorithm is employed to select the best block for the embedding watermark. Then, the watermark is inserted in the first level approximation sub-band of the discrete wavelet transform (DWT) of each selected block. This method provides good quality watermarked images, although it is not robust against geometric attacks such as rotation and scaling. In [2], a new blind error diffusion-based halftone visual watermarking method called content aware double-sided embedding error diffusion (CaDEED) is introduced. By adopting the problem formulation of CaDEED, the optimization problem is solved in order to achieve an optimal solution. Although it shows good results for imperceptibility and robustness, the performance of this system is highly dependent on the content of the host image and watermark. A blind integer wavelet-based watermarking scheme for inserting the compressed version of the binary watermark is presented in [3]. The peak signal-to-noise ratio (PSNR) result of this method is quite satisfactory. However, the robustness against compression attacks is not significant. The authors in [4] proposed a blind geometrically invariant image watermarking method by employing connected objects and a gravity center. This framework has proven resistant against geometrical attacks, such as rotation and scaling. However, it has low robustness against other regular noise attacks such as Gaussian or speckle noise. Furthermore, a contrast-adaptive strategy as a removal solution for visible watermarks is presented in [5] where a sub-sampling technique is adopted to propose such a blind system. The imperceptibility results of this method are very good. However, it shows low robustness against some attacks. In addition to this, a blind watermarking scheme based on singular value decomposition (SVD) is introduced in [6]. Initially, they analyzed the orthogonal matrix U via SVD. This work utilizes the concept of finding a strong similarity correlation existing between the second-row first column element and the third-row first column element. At the final stage, the color watermark is embedded by slightly modifying the value of the second-row first column element and the third-row first column element of the U matrix. The technique performs well against various attacks, although it demonstrates very poor performance under median filtering of the watermarked image. Furthermore, the authors in [7] proposed a robust watermarking scheme using discrete cosine transform (DCT) and SVD for lossless copyright protection. Its imperceptibility result is significantly good. However, its robustness result against cropping attacks is quite low. A blind simple watermarking algorithm for image authentication is presented using fractional wavelet packet transform (FRWPT) and SVD in [8]. The proposed algorithm performs the embedding operation on singular values of the host image. To improve the fidelity, the perceptual quality of the watermarked images is exhibited. Although this method is highly secured, it shows low robustness against various attacks for some watermarked images. For estimation of the original coefficients, a blind watermarking method is placed in [9]; the authors used a trained SVR there. Additionally, the particle swarm optimization (PSO) is further utilized to optimize the proposed scheme. It provides high imperceptibility; however, it could not show excellent robustness against several attacks. A blind self-synchronized watermarking method in the cepstrum domain is suggested in [10]. This method does not provide a good trade-off between imperceptibility and robustness. Furthermore, a blind scheme is proposed in [11] in a bid to obtain minimal image distortion. This method provides high-quality watermarked images, albeit low robustness against various attacks. In [12], hamming codes are used to embed the authentication information in a cover image. The watermark extraction process of this method is blind and provides satisfactory results in imperceptibility. However, the robustness result against various attacks is not reported there. The authors of [13] suggested a blind watermarking algorithm based on lower-upper (LU) decomposition. The watermark is embedded into the first-column second-row element and the first-column third-row element of the lower triangular matrix obtained from LU decomposition. It provides good quality watermarked images despite the low robustness against compression attacks. A semi-blind self-reference image watermarking method using discrete cosine transform (DCT) and singular value decomposition (SVD) is proposed in [14]. Initially, essential blocks are fetched by using a threshold on the number of edges in each block. Using these essential blocks, a reference image is created and then transformed into the DCT and SVD domain. Embedding the watermark is done by modifying singular values of the host image using singular values of the watermark image. This method yields good quality watermarked images. However, it shows low robustness against the scaling operation. To embed the watermark, the concepts of vector quantization (VQ) and association rules in data mining are employed in [15]. The approach is semi-blind, which hides the association rules of the watermark instead of the whole watermark. This method shows good robustness against various attacks with poor performance on imperceptibility. In addition, a reference watermarking scheme with semi-blind is proposed in [16] based on DWT and SVD for copyright protection and authenticity. The method has high imperceptibility showing the low robustness against cropping and rotation attacks. An image watermarking method using DWT, all phase discrete cosine bi-orthogonal transform (APDCBT), and SVD is proposed in [17]. This method shows high imperceptibility; however, it provides low robustness against combined cropping and compression attacks. A non-blind image watermarking algorithm based on the Hadamard transform is proposed in [18]. In this method, the breadth first search (BFS) technique is used to embed the watermark. Notably, it shows good performance in imperceptibility. However, it has the limitation of relatively poor performance against compression attacks. The authors in [19] introduced a non-blind robust watermarking technique using DCT and a normalization procedure. They used image normalization for calculating the affine transform parameters so that the watermark embedding and detection processes can be performed in the original coordinate system. However, this method shows low robustness against some attacks. In [20], a non-blind digital watermarking algorithm using wavelet-based contourlet transform (WBCT) is presented. To select the position for inserting the watermark, the texture information of the image is used. It has good robustness against numerous attacks, albeit low robustness against filtering attacks. Moreover, the imperceptibility result of this method is not reported there. A non-blind hybrid image watermarking scheme based on DWT and SVD is proposed in [21]. In this approach, the watermark is embedded to the elements of singular values of the cover image of DWT sub-bands. The imperceptibility result of this method is quite high, having low the robustness against cropping attacks. A non-blind SVD-based digital watermarking scheme for ownership protection is proposed in [22]. In this method, a meaningful text message is used rather than using a randomly generated Gaussian sequence. However, the robustness of this method against attacks is low. A non-blind image watermarking using DCT and DWT is proposed in [23]. The DCT coefficients of the watermark image are embedded into four DWT bands of the color components of the host image. The imperceptibility result of this method is quite satisfactory. However, the robustness against rotation attacks is a little low. A non-blind color image watermarking method using SVD and QR code is suggested in [24]. This method shows good results in imperceptibility; the robustness result against poison and speckle noise attack is not reported.
From the above studies, we can conclude that some methods have low robustness, whereas some methods have less imperceptible or less secured. Further, some methods are non-blind and semi-blind. To overcome these limitations, an SVD-based blind symmetric image watermarking method using fast Walsh–Hadamard transform (FWHT) with key mapping and coefficient ordering for ownership protection is proposed in this paper. In symmetric watermarking, the same keys are used for embedding and detecting the watermark. The major contributions of this research work are subjected:
- A blind image watermarking method is proposed that is highly robust and secured against numerous attacks while providing good quality watermarked images;
- To safeguard the unauthorized detection, the Gaussian mapping is used to scramble the watermark;
- To facilitate authentic and errorless extraction of the watermark image by generating the keys from the singular values the FWHT blocks of the cover image;
- It provides a good trade-off among robustness, security, and imperceptibility.
Simulation results indicated that our proposed method is highly robust against numerous attacks. The normalized correlation (NC) of the proposed method is numerically one, whereas the NC of the recent methods [13,23,24] vary from 0.7991 to 0.9999. The peak signal-to-noise ratio (PSNR) of the proposed method varies from 49.78 to 52.64, whereas the PSNR of the recent methods [13,23,24] vary from 39.4428 to 54.2599. In other words, the proposed method outperforms state-of-the-art methods in terms of robustness, security, and imperceptibility.
2. Background Information
2.1. Singular Value Decomposition
For an square matrix with rank , its SVD is represented by Equation (1):
where and are orthogonal matrices, and is a singular diagonal matrix with diagonal elements . These diagonal elements are unique for image data. Therefore, these values are used to generate unique keys for the errorless and authentic extraction of the watermarks.
2.2. Fast Walsh-Hadamard Transform
General Hadamard transform is performed by a Hadamard matrix with the size defined in Equation (2). It is an orthogonal square matrix with only +1 and −1 values. Furthermore, it has a unique sequence that is counted on the basis of the changes of the values in a row.
The Hadamard transform concentrates most of the energy into the upper left corner of the transformed matrix. The direct current (DC) and alternating current (AC) coefficients of the transform matrix are arranged in zigzag order from low-frequency components to high-frequency components. In this study, the low-frequency components are used for embedding the watermark, since they are less sensitive to noise. Additionally, the Hadamard matrix has a different form called Walsh matrix , which is defined in Equation (3).
In this proposed method, fast Walsh–Hadamard transform (FWHT) is utilized, which is a technique of calculating a discrete Walsh–Hadamard transform with less computation time.
3. Proposed Method
Let be the original host image and be the watermark image to be embedded into the original image.
3.1. Watermark Preprocessing
It is essential to preprocess the watermark for enhancing its security. Preprocessing includes the scrambling of the watermark image. In this proposed method, we utilize Gaussian mapping to scramble the watermark. To implement the Gaussian mapping on the watermark, the following steps are performed:
- Step 1.
- The watermark image W is reshaped into a one-dimensional sequence Q = {q(r), }.
- Step 2.
- Initially, a reference pattern is generated using a Gaussian map, which is defined in Equation (4).where a, b, and are predefined constants and are used as key as shown in Figure 1.
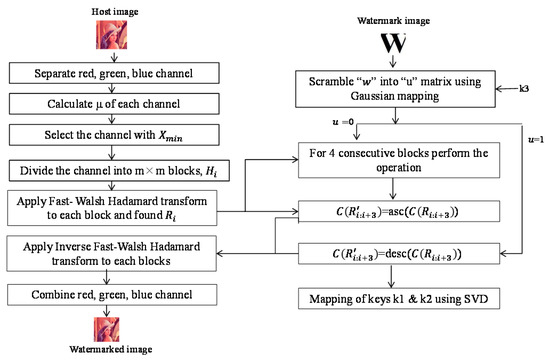 Figure 1. Proposed embedding algorithm.
Figure 1. Proposed embedding algorithm. - Step 3.
- Then, the binary reference pattern is calculated using the following equation:where T is a predefined threshold.
- Step 4.
- Finally, the watermark sequence q(r) is scrambled with z(r) using Equation (6):where denotes the bitwise XOR operation.
3.2. Watermark Embedding Process
The proposed watermark embedding process is shown in Figure 1. The pseudo code of the watermark embedding process is presented in Algorithm 1. The embedding process is described in the following steps:
- Step 1.
- The original host image is first divided into three channels , where represent the red, green, and blue channels of the original image, respectively. Then, the mean of the pixel values of each channel is calculated using Equation (7).where indicate the mean of the pixel values of the red, green, and blue channels, respectively. After that, the channel with minimum mean is selected, which is either .
- Step 2.
- The selected channel is further divided into m × m non-overlapping blocks, n}, where is the block number and m is the length of the row and column of each block.
- Step 3.
- FWHT is applied in each block to obtain the transformed block , where Ri contains the FWHT coefficients.
- Step 4.
- Among all theblocks, each set of four consecutive blocks Ri, Ri+1, Ri+2, and Ri+3 is selected to embed a watermark bit. The main idea of the embedding process is to sort the coefficients of the first row represented by of each set of selected blocks Ri, Ri+1, Ri+2, and Ri+3 except the DC value. If the watermark bit is 1, the selected low-frequency coefficients are sorted in descending order; otherwise, they are sorted in ascending order. The concept of embedding the watermark bit in ascending and descending order with a block size of 4 × 4 where, m = 4, is shown in Figure 2.
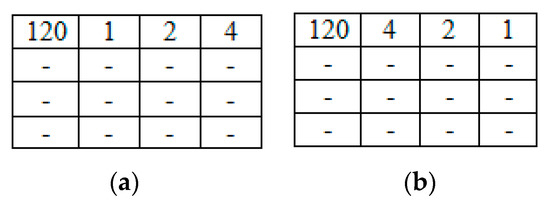 Figure 2. (a) Sorting in ascending order to embed 0 bits and (b) sorting in descending order to embed 1 bit.
Figure 2. (a) Sorting in ascending order to embed 0 bits and (b) sorting in descending order to embed 1 bit.
In this step, two keys k1 and k2 are also used in order to make the watermarking method more secured. The key k1 is generated from the singular values of each block of the selected channel of host image. The key k2 is generated from key k1, which is used to authenticate key k1 in the watermark extraction process. The following operation is performed for embedding a watermark bit into each selected block.
where asc and desc represent sorting the data in ascending order and descending order, respectively. The process of mapping the keys k1 and k2 are described in the next section.
: In this section, the process of mapping keys k1 and k2 is explained, which is defined in Equation (8). This step is introduced to strengthen the proposed algorithm under severe attack. To map the keys initially, SVD is applied in each block to generate the necessary information. To perform the operation, the following steps are used:
- (1)
- Each block of the selected channel is decomposed into three matrices:using Equation (9).where are the singular values of the matrix Di of each block . These singular values are unique for each block Hi. The keys k1 and k2 are calculated using these singular values. Thus, unauthorized people could not map the keys without the host image to prove fake ownership. To do this, initially, a null key is defined. Then, is generated using these singular values as defined in Equation (10) below:where i indicates the block number, j m} indicates the singular values of each block, asc and desc represent sorting the data in ascending order and descending order, respectively, and indicates the concatenation operation The singular values are sorted according to the watermark bit 0 or 1.
- (2)
- Finally, k1 is converted into a one-dimensional sequence of length L = , where n is the total number of blocks and m is the total number of singular values in each block.
- (3)
- To generate key k2, define a null key with length S, where S = n/m. Then, is generated from key using the following Equation (11):where is the mean of consecutive t values of key and the length of key k2 is (n/m) + 1. Although the first key can be generated by the owner only, the second key is generated to authenticate the first key in the extraction process.
- Step 5.
- Inverse FWHT is applied to each transformed block and the watermarked blocks are found.
- Step 6.
- Finally, three watermarked channels are combined to generate the watermarked image .
| Algorithm 1: Watermark Insertion |
| Variable Declaration: X: Host image : Mean intensity value of each channel of host image (Lena) : Channel with minimum mean : Non-overlapping blocks of (size 4 × 4) FWHT, SVD: Transformation and decomposition used in the algorithm : FWHT transformed block of : Three coefficients of first row (except DC value) of the consecutive transformed block : Coefficients in ascending or descending order W: Watermark image u: Scrambled watermark sequence Watermark Embedding Procedure: 1. Watermark preprocess: scramble W to obtain u using Gaussian mapping 2. Read the host image and calculate of each channel (Red, Green, Blue) X.bmp (host image with size of 256 × 256) W.bmp (watermark image with size of 32 × 32) 3. Select channel and divide it into 4 × 4 blocks 4. Apply FWHT to each block and found 5. Watermark Insertion // Use SVD to map keys 6. Perform inverse FWHT and combine the channels to get the Watermarked Image |
3.3. Watermark Detection Process
The watermark extraction process has two main phases: (1) modify the degree of ascendant/descendant of the attacked watermarked image with key, and (2) authenticate key with key. In addition, the pseudo code of the watermark detection process is presented in Algorithm 2. The overall process is described below and shown in Figure 3:
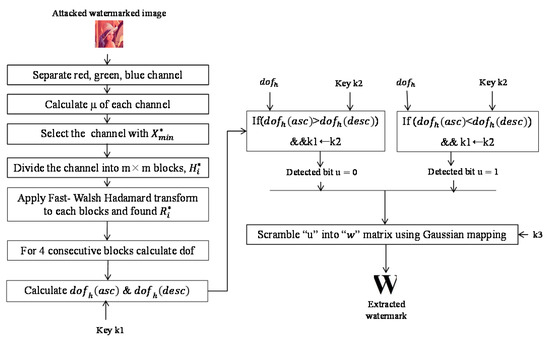
Figure 3.
Proposed extraction algorithm.
- Step 1.
- The attacked watermarked image is first divided into three channels, {}. Then, the mean value of the pixels of the red, green, and blue channels represented by are calculated. Thereafter that, the channel with minimum mean is selected for extracting the watermark.
- Step 2.
- The selected channel is further divided into m × m non-overlapping blocks, where is the block number.
- Step 3.
- FWHT is carried out on each block. After applying this operation, the transformed blocks are found.
- Step 4.
- The degree of ascendant/descendant denoted by dof is calculated for four consecutive transformed blocks }. Therefore, dof(asc) represents the number of times that the low-frequency coefficients in the first rowof each transformed block except for the DC value are in ascending order. Similarly, the dof(desc) represents the number of times that the low-frequency coefficients in the first row of each transformed block except the DC value are in descending order.
Later, is modified with key . This phase assists the system to resist when the noise attack is severe. Initially, the of the first t values of key is calculated to extract the first watermark bit using Equations (12) and (13). Thus, consecutive t values of the key are considered each time for extracting a one-bit watermark. We found another two matrices, and , with values, where is the length of key , .
Finally, we modify the with by a simple addition operation, as shown in Equations (14) and (15), and found two matrices, and .
Authenticatewith: This operation is carried out to authenticate key using k2. For this purpose, the average of the consecutive t values of is calculated and compared with one value of . This operation is represented using Equations (16) and (17) given below:
where means is authenticated by and means is not authenticated by . If is authenticated, then the watermark would be extracted accordingly.
- Step 5.
- The hidden binary sequence is found using the following rule:
If
then
else If
then - Step 6.
- The binary watermark sequence q*(r) is extracted with key k3 using the following equation:
Finally, the watermark image W* is found by arranging the watermark sequence q*(r) into the N×N matrix.
| Algorithm 2: Watermark Extraction |
| Variable Declaration: : Attacked watermarked image : Mean intensity value of each channel of : Channel with minimum mean : Non-overlapping blocks of (size 4 × 4) FWHT: Transformations used in the algorithm : FWHT transformed block of : Three coefficients of first row (except DC value) of four consecutive transformed block W: Watermark image u: Scrambled watermark sequence dof(asc/desc): The number of times low-frequency coefficients in the first row of each transformed block except the DC value are in ascending/descending order. Watermark Extraction Procedure: 1. Read and calculate of each channel (Red, Green, Blue) 2. Select channel and divide into 4 × 4 blocks 3. Apply FWHT to each block and found 4. Watermark extraction (a) Modifying dof(asc/desc) into dof′(asc/desc) with key // Consecutive t values of the key are considered each time for extracting a one-bit watermark, where and means mean of these t values (c) Watermark extraction If then else If then where, (d) Re-scramble u to get W |
4. Experimental Results and Discussions
In this section, the performance of our proposed method is evaluated in terms of imperceptibility and robustness. The proposed method used various images, including Lena, Peppers, Baboon, and Fruit, with the size 256 × 256 as host images shown in Figure 4. The size of the binary watermark image is 32 × 32, as shown in Figure 5. It performs well for all the host images in term of imperceptibility and robustness. In this study, the selected values for m and t are 4 and 16, respectively, as the size of each block Hi is 4 × 4. Therefore, the total number blocks is 4096. Thus, the length of the key k1 is 16384. The main reason for selecting a smaller value for m to embed the watermark bit is that sorting larger blocks causes greater degradation in the quality of the watermarked image.

Figure 4.
The host images: (a) Lena, (b) Peppers, (c) Baboon, and (d) Fruit.

Figure 5.
Watermark images: (a) original, (b) scrambled with a = 10, b = 0.05, and y0 = 20, and (c) scrambled with a = 30, b = 0.01, and y0 = 10.
Imperceptibility test: The imperceptibility of the watermarked images can be evaluated in terms of the peak signal-to-noise ratio (PSNR), as given in Equation (19).
where X and X’ are the original and watermarked images, respectively. Higher values of PSNR indicate the better quality of the watermarked image. Figure 4 shows the original and scrambled images with different values of a, b, and y0.
To test the imperceptibility of the proposed framework, the PSNR values are calculated and compared with those values of the existing methods, as shown in Table 1. From this table, it is observed that the PSNR of the proposed method varies from 49.78 to 52.64, whereas the PSNR of the recent methods [13,23,24] varies from 47.1961 to 47.1836, 54.2577 to 54.2599, and 39.4428 to 40.8216. Therefore, it is evident that the PSNRs of the recent methods [23,24] are quite high, whereas the PSNRs of the recent method [13] are low compared to all other methods. In other word, the PSNR of the proposed method is higher than that of the methods reported in [13]. However, it is slightly lower than that of the method reported in [24]. This comparison justifies that the suggested method outperforms the other recent techniques. Since in each 4 4 block, only three AC values are shuffled, and the DC value remains in its position, low image degradation took place. However, low image degradation results in high imperceptibility.

Table 1.
Comparison between the proposed and recent methods in terms of peak signal-to-noise ratio (PSNR).
Security analysis: For a secured watermarking method, how it performs against various attacks is very important. The proposed method utilizes a Gaussian map to enhance the security. To encrypt the watermark image, some predefined constants are used such as a, b, and , which are considered as secret key k3. If the selected value for a, b, and are wrong, in that case, the watermark will not be extracted properly. Further, in order to make the watermarking method more secured, the two keys k1 and k2 are used. The key k1 is generated from the singular values of each block of the selected channel of host image. Moreover, it is observed that these singular values are floating point numbers, and it is not possible to find out these singular values without the host image. Therefore, it is not possible to generate key k1 without the host image. The key k2 is generated from key k1, which is used to authenticate the key k1 in the watermark extraction process. Therefore, it is not possible to generate the key k2 without k1. These keys (k1, k2, k3) are used in the watermark detection process to extract the embedded watermark. The correct watermark can be extracted when all the keys (k1, k2, and k3) are correct. In other words, if any one of the keys is wrong, then the watermark will not be extracted correctly. This phenomenon is illustrated in Figure 6. Moreover, the size of each block Hi of the selected channel of the host image is 4 × 4; therefore, the total number of blocks in each host image is 4096. Thus, the length of the key k1 is 4096 × 4 = 16,384, and the length of the key k2 is (4096/4) + 1 = 1025, which are quite long, indicating that the key space is large enough. As the key k1, k2, and k3 are floating point numbers, therefore, the value of these keys cannot be determined. Hence, the probability of extracting the right watermark is near to 0. Therefore, the attacker cannot detect the correct watermark without the right key, which enhances the security of the proposed watermarking method.
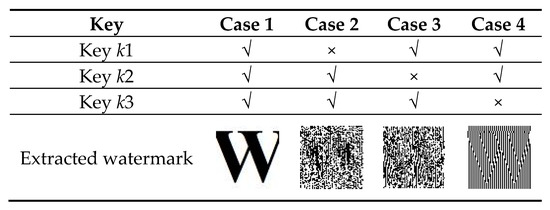
Figure 6.
The extracted watermark with right and different wrong keys.
Robustness test: To measure the robustness of the proposed algorithm, the normalized correlation (NC) is calculated between the original watermark image and the extracted watermark image. The NC value is calculated using Equation (20):
where and W* are the original watermark and extracted watermark, respectively.
Now, the main fact is to consider the different types of noise attacks on the watermarked image. The results are illustrated in such a way as to identify the effect of keys on the NC values. Figure 7, Figure 8 and Figure 9 show the effect of keys in a pictorial way, including the PSNR and NC values.
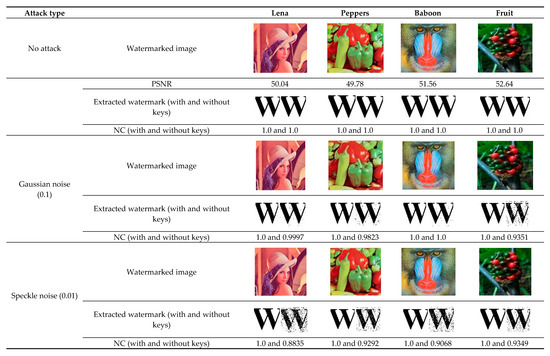

Figure 7.
Analysis of proposed method under No attack, Gaussian noise (0.01), Speckle noise, and Salt and Pepper noise (0.01). NC: normalized correlation.


Figure 8.
Analysis of proposed method under Adjustment, Cropping (50%), Sharpening (0.1), and Weiner filtering.


Figure 9.
Analysis of the proposed method under Poison noise, Median filtering, Compression (quality factor: 50%), and Rotation.
Furthermore, Table 2 and Table 3 show an overview of the NC values of the proposed scheme with keys and without keys, respectively. Notably, the NC values shown in Table 2 reflect better results than Table 3. This is because severe noise attacks affect the degree of ascendant/descendant (dof). This dof is derived without key and is vulnerable to noise attack until it is modified with as defined in Equations (14) and (15). Since the keys make the system effectively resistant against noise, Table 3 shows better results in terms of NC. Further, the extracted watermarks from four different watermarked images under Gaussian noise with tolerance 0.1 are shown in Figure 7. The extracted watermark using only dof (without key) for the “Fruit” cover image provides lower NC values than the others. Since the color variation in this host image is not very high, dof (without keys) is more vulnerable under additive noise attack. This is also applicable for other attacks, such as adjustment and sharpening, as shown in Figure 8. This problem is overcome in the proposed framework with the concept of key mapping. In spite of the high noise attack, extracting the watermark using dofk (with keys) could reconstruct the watermark image successfully with a unity of NC values, as shown in Figure 7, Figure 8 and Figure 9. We observed that the NC of the proposed method against various attacks is numerically one. It is because the keys (k1, k2 and k3) that contain the necessary information of the watermark are not affected by various attacks. Hence, this proposed technique ensures high robustness.

Table 2.
NC values after applying various noise attacks (with keys).

Table 3.
NC values after applying various noise attacks (without keys).
Table 4 shows a comparative analysis between the proposed and several recent state-of-the-art methods [13,23,24] for NC against different attacks. From this table, it is observed that the NC of the proposed method is numerically one against various attacks using keys, in contrast to state-of-the-art methods whose NC vary from 0.7991 to 0.9999. It should be mentioned that Ahmed et al. [23] shows low robustness against rotation and salt and pepper noise attack, and Su et al. [13] shows low robustness against median filtering and JPEG compression attack. In all other cases, these two methods show good robustness. Moreover, Patvardhar et al. [24] shows good robustness against various attacks.

Table 4.
A comparative analysis between the proposed and several recent methods in terms of NC.
In other words, this proposed algorithm with its unique key approach is much more robust than any other existing method. In addition, our method utilizes the key mapping concept with singular values of the host image. This concept improves the performance of the proposed method against severe noise attack. This approach also ensures ownership with high robustness. Furthermore, Gaussian mapping enhances the security of the watermark. Finally, coefficient ordering in the smaller block provides high imperceptibility. The concatenation of smaller blocks into the larger block provides high robustness against noise attack. In a nutshell, it can be concluded that our proposed method outperforms recent state-of-the-art methods in terms of robustness, security, and imperceptibility.
5. Conclusions
This paper presented an image watermarking scheme using FWHT, SVD, key mapping, and coefficient ordering. FWHT is chosen because of its low computational complexity. To enhance the robustness of the proposed method against severe attacks, key mapping is introduced using SVD. It is used because unique keys are generated from the singular values of the FWHT blocks of the cover image. Furthermore, Gaussian mapping is used to scramble the watermark. This makes the system secured against unauthorized detection. Thus, the proposed method ensures high robustness as well as high security against numerous attacks. Experimental results indicated that the proposed scheme shows better results than the recent methods in terms of robustness and security. Moreover, it yielded high-quality watermarked images. The NC value of the proposed method is numerically one, while the PSNR of it lies between 49.78 and 52.64. In contrast, the recent state-of-the-art methods show that the NC varies from 0.7991 to 0.9999, while the PSNR resides between 39.4428 and 54.2599. These results verified that the proposed method could be effectively utilized for image copyright protection and proof of ownership. We will extend the proposed method for video watermarking in the future.
Author Contributions
All authors contributed equally to the conception of the idea, the design of experiments, the analysis and interpretation of results, and the writing and improvement of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry and Energy (MOTIE) of the Republic of Korea (20192510102510, 20172510102130)
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bakhsh, F.Y.; Moghaddam, M.E. A robust HDR images watermarking method using artificial bee colony algorithm. J. Inf. Secur. Appl. 2018, 41, 12–27. [Google Scholar]
- Guo, Y.; Au, O.C.; Wang, R.; Fang, L.; Cao, X. Halftone image watermarking by content aware double-sided embedding error diffusion. IEEE Trans. Image Process. 2018, 27, 3387–3402. [Google Scholar] [CrossRef] [PubMed]
- Chetan, K.R.; Nirmala, S. An efficient and secure robust watermarking scheme for document images using Integer wavelets and block coding of binary watermarks. J. Inf. Secur. Appl. 2015, 24, 13–24. [Google Scholar] [CrossRef]
- Wanga, H.; Yina, B.; Zhoub, L. Geometrically invariant image watermarking using connected objects and gravity centers. KSII Trans. Internet Inf. Syst. 2013, 7, 2893–2912. [Google Scholar]
- Lin, P.Y.; Chen, Y.H.; Chang, C.C.; Lee, J.S. Contrast adaptive removable visible watermarking (CARVW) mechanism. Image Vis. Comput. 2013, 31, 311–321. [Google Scholar] [CrossRef]
- Su, Q.; Niu, Y.; Zou, H.; Liu, X. A blind dual color images watermarking based on singular value decomposition. Appl. Math. Comput. 2013, 219, 8455–8466. [Google Scholar] [CrossRef]
- Wu, X.; Sun, W. Robust copyright protection scheme for digital images using overlapping DCT and SVD. Appl. Soft Comput. 2013, 13, 1170–1182. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Wua, Q.M.J.; Raman, B. A new robust adjustable logo watermarking scheme. Comput. Secur. 2012, 31, 40–58. [Google Scholar] [CrossRef]
- Tsai, H.H.; Huang, Y.J.; Lai, Y.S. An SVD-based image watermarking in wavelet domain using SVR and PSO. Appl. Soft Comput. 2012, 12, 2442–2453. [Google Scholar] [CrossRef]
- Hun, H.T.; Chen, W.H. A dual cepstrum based watermarking scheme with self-synchronization. Signal Process. 2012, 92, 1109–1116. [Google Scholar]
- Lin, C.C. An information hiding scheme with minimal image distortion. Comput. Stand. Interfaces 2011, 33, 477–484. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, H.; Park, Y. A new data hiding scheme for binary image authentication with small image distortion. Inf. Sci. 2009, 179, 3866–3884. [Google Scholar] [CrossRef]
- Su, Q.; Wang, G.; Zhang, X. A new algorithm of blind color image watermarking based on LU decomposition. Multidimens. Syst. Signal Process. 2018, 29, 1055–1074. [Google Scholar] [CrossRef]
- Murty, P.S.; Kumar, S.D.; Kumar, P.R. A semi blind self reference image watermarking in DCT using Singular Value Decomposition. Int. J. Comput. Appl. 2013, 62, 29–36. [Google Scholar]
- Shen, J.J.; Ren, J.M. A robust associative watermarking technique based on vector quantization. Digit. Signal Process. 2010, 20, 1408–1423. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Raman, B. A new robust reference watermarking scheme based on DWT-SVD. Comput. Stand. Interfaces 2009, 31, 1002–1013. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, H.; Wang, C. A robust image watermarking technique based on DWT, APDCBT, and SVD. Symmetry 2018, 10, 77. [Google Scholar] [CrossRef]
- Sarker, M.I.H.; Khan, M.I. An efficient image watermarking scheme using BFS technique based on Hadamar Transform. Smart Comput. Rev. 2013, 3, 298–308. [Google Scholar]
- Kumar, A.; Luhach, A.K.; Pal, D. Robust digital image watermarking technique using image normalization and Discrete Cosine Transformation. Int. J. Comput. Appl. 2013, 65, 5–13. [Google Scholar]
- Liua, J.; Liub, G.; Hea, W.; Lia, Y. A new digital watermarking algorithm based on WBCT. Procedia Eng. 2012, 29, 1559–1564. [Google Scholar] [CrossRef][Green Version]
- Lai, C.C.; Tsai, C.C. Digital image watermarking using Discrete Wavelet Transform and Singular Value Decomposition. IEEE Trans. Instrum. Meas. 2010, 59, 3060–3063. [Google Scholar] [CrossRef]
- Mohammad, A.A.; Alhaj, A.; Shaltaf, S. An improved SVD-based watermarking scheme for protecting rightful ownership. Signal Process. 2008, 88, 2158–2180. [Google Scholar] [CrossRef]
- Ahmed, K.A.; Ozturk, S. A novel hybrid DCT and DWT based robust watermarking algorithm for color images. Multimed. Tools Appl. 2019, 78, 17027–17049. [Google Scholar]
- Patvardhan, C.; Kumar, P.; Lakshmi, C.V. Effective color image watermarking scheme using YCbCr color space and QR code. Multimed. Tools Appl. 2018, 77, 12655–12677. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



