Abstract
The formation of a skyrmion crystal and its phase transition are studied, taking into account the Dzyaloshinskii–Moriya (DM) interaction at the interface between a ferroelectric layer and a magnetic layer in a superlattice. Frustration is introduced in both magnetic and ferroelectric films. The films have a simple cubic lattice structure. The spins inside the magnetic layers are Heisenberg spins interacting with each other via nearest-neighbor (NN) exchange and next-nearest-neighbor (NNN) exchange . The polarizations in the ferroelectric layers are assumed to be of Ising type with NN and NNN interactions and . At the magnetoelectric interface, a DM interaction between spins and polarizations is supposed. The spin configuration in the ground state is calculated by the steepest descent method. In an applied magnetic field perpendicular to the layers, we show that the formation of skyrmions at the magnetoelectric interface is strongly enhanced by the frustration brought about by the NNN antiferromagnetic interactions and . Various physical quantities at finite temperatures are obtained by Monte Carlo simulations. We show the critical temperature, the order parameters of magnetic and ferroelectric layers as functions of the interface DM coupling, the applied magnetic field, and and . The phase transition to the disordered phase is studied in detail.
1. Introduction
The localized topological spin textures called “magnetic skyrmions” currently attract intensive research due to their fundamental properties and practical applications [1,2,3,4,5,6]. Indeed, skyrmions are promising structures for future digital technologies [7,8,9,10,11,12,13,14,15]. In addition, next-generation spintronic devices can be based on metastable isolated skyrmions guided along magnetic stripes [14,16,17,18]. Skyrmions have been experimentally observed in many materials, particularly in magnetic materials [2,4,5,7,19,20,21,22,23,24,25,26,27], multiferroic materials [28], ferroelectric materials [29], and semiconductors [30]. Skyrmions have been seen also in helimagnets [2,20]. Under an applied magnetic field, it has been shown that the helical spin configuration is transformed into a skyrmion lattice with a triangular structure [31]. In a strong magnetic field, the spin ordering is ferromagnetic (FM), but there exist isolated stable skyrmions as topological defects [32,33].
Real magnetic materials have complicated interactions; there are large families of frustrated systems, such as the heavy lanthanides metals (holmium, terbium, and dysprosium) [34,35] and helical MnSi [36]. Other interesting properties of skyrmions in magnetically frustrated systems have also been investigated [31,37,38,39,40,41,42,43,44,45,46]. Multiferroics and superlattices of multiferroics (for example, and ) currently attract many research activities on these materials because of the coexistence of ferroelectric and magnetic orderings. A large number of investigations was devoted to the non-uniform states in magneto-ferroelectric superlattices both theoretically [47] and experimentally [48,49,50,51,52,53,54]. In Ref. [55,56], Janssen et al. proposed a new model for the interaction between polarizations and spins in magneto-ferroelectric superlattices. Using this model, the dynamics and configurations of domain walls for the unidimensional case were simulated. Li et al. [57] proposed an algorithm based on the Monte Carlo method for a two-dimensional (2D) lattice. Recently, magneto-ferroelectric superlattices have drawn as much attention as magneto-electric (ME) materials. This is due to the intrinsic magneto-electric effects stemming from the spin–orbit interaction [52] as well as from the spin charge–orbital coupling [58]. It has been shown that surface ME effects appear due to the charge and spin accumulation [53,59]. The enhancement of magnetoelectric effects due to phase separation was shown in Ref. [60]. Many microscopic interaction mechanisms for different materials have been suggested. Among these, we can mention the lone skyrmion pair mechanism [61], the ferroelectricity in manganites [62], the multiferroicity induced by the spiral spin ordering [63], and the off-center shifts in geometrically frustrated magnets [64]. In Ref. [65], it was shown that magnetic frustration results in a phase competition, which is the origin of the magnetoelectric response. A possible experimental realization of an isolated skyrmion as well as a skyrmion lattice has been suggested [66]. In Ref. [15], the 2D Heisenberg exchange model with Dzyaloshinskii–Moriya (DM) interaction was used to study the lifetimes of antiferromagnetic skyrmions. Spin waves and skyrmions in magnetoelectric superlattices with a DM interface coupling have been studied [47]. Yadav et al. [67] have produced complex topologies of electrical polarizations—namely, nanometer-scale vortex–antivortex structures—using the competition between charge, orbital, and lattice degrees of freedom in superlattices of alternate lead titanate and strontium titanate films. They showed that the vortex state is the low-energy state for various superlattice periods. In Ref. [19], the authors explored skyrmions and antiskyrmions in a 2D frustrated ferromagnetic system with competing exchange interactions based on the classical Heisenberg model on a simple square lattice [38] with dipole–dipole interaction, which was neglected in previous works [37,68]. Dipole–dipole interaction has been shown to cause frustration in systems of skyrmions. The interface-induced skyrmions have been investigated. The superstructures are obviously the best for creating interactions of skyrmions on different interfaces causing very particular dynamics compared to interactions between skyrmions of the same interface. We can mention a theoretical study of two skyrmions on two-layer systems [69] using micromagnetic modeling and an analysis based on the Thiele equation. It has been found that there is a reaction between them, such as the collision and bound state formation. The dynamics of these skyrmions depends on the sign of the DM interaction; the number of two skyrmions is well described by the Thiele equation. Another interesting aspect is a colossal spin-transfer torque effect of bound skyrmion pairs, revealed in antiferromagnetically coupled bilayer systems. Note that the study of current-induced motion using the Thiele equation was carried out in a skyrmion lattice using two models of the pinning potential [70]. Shi-Zeng Lin et al. [71] studied the dynamics of skyrmions in chiral magnets in the presence of a spin-polarized current. They also showed that skyrmions can be created by increasing the current in the magnetic spiral state. Numerical simulations of the Landau–Lifshitz–Gilbert equation were performed in Ref. [72], which reveals a remarkably robust and universal current–velocity relation of the skyrmion motion driven by the spin-transfer torque. This is unaffected by impurities and non-adiabatic effects, in sharp contrast to the case of the domain wall or spin helix.
Note that in Ref. [47], we studied the effects of Dzyaloshinskii–Moriya (DM) magneto-ferroelectric coupling in a superlattice formed by “unfrustrated” magnetic and ferroelectric films. In a zero field, we showed that the ground state (GS) spin configuration is periodically non-collinear. Through the use of a Green’s function technique, we calculated the spin wave spectrum in a monolayer and in a bilayer sandwiched between ferroelectric films. In particular, we showed that the DM interaction strongly affects the long-wavelength spin wave mode. In a magnetic field applied in the z direction perpendicular to the layers, we showed that skyrmions are arranged to form a crystalline structure at the interface.
In this paper, we study a superlattice composed of alternating “frustrated” magnetic films and “frustrated” ferroelectric films. The frustration due to competing interactions has been extensively investigated over the last four decades. The reader is referred to Ref. [73] for reviews on theories, simulations, and experiments on various frustrated systems. Our present aim is to investigate the effect of the frustration in the presence of the DM interaction at the magnetoelectric interface. It turns out that the frustration gives rise to an enhancement of skyrmions created by the DM interaction in a field applied perpendicularly to the films. Monte Carlo simulations are carried out to study the skyrmion phase transition in the superlattice as a function of the frustration strength.
The paper is presented as follows. In Section 2, we describe our model and show how to determine the ground-state spin structure. The skyrmion crystal is shown with varying frustration parameters. Section 3 is devoted to the presentation of the Monte Carlo results for the phase transition in the system as a function of the frustration, in the presence of the interface DM coupling. These results show that the skyrmion crystalline structure is stable up to a transition temperature . Concluding remarks are given in Section 4.
2. Model and Skyrmion Crystal
2.1. Model
The superlattice that we study here is shown in Figure 1a. It is composed of magnetic and ferroelectric films with a simple cubic lattice. The Hamiltonian of this magneto-ferroelectric superlattice is given by:
where and indicate the magnetic and ferroelectric parts, respectively. denotes the Hamiltonian of magnetoelectric interaction at the interface of two adjacent films. We are interested in the frustrated regime. Therefore, we consider the following magnetic Hamiltonian with the Heisenberg spin model:
where is the spin occupying the i-th lattice site, denotes the magnetic field applied along the z axis, and denotes the magnetic interaction between two spins and . We shall take into account both the nearest neighbor (NN) interaction, denoted by , and the next-nearest neighbor (NNN) interaction, denoted by . We consider to be the same everywhere in the magnetic film. To introduce the frustration, we shall consider —namely, antiferromagnetic interaction—as the same everywhere. The interactions between spins and polarizations at the interface are given below.
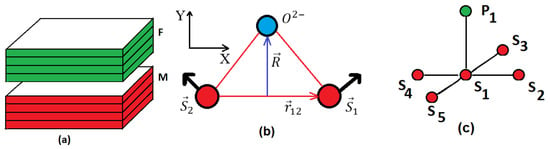
Figure 1.
(a) Magneto-ferroelectric superlattice; (b) positions of the spins in the plane and the position of the non-magnetic ion Oxygen, defining the Dzyaloshinskii-Moriya (DM) vector (see text); (c) interfacial coupling between a polarization P with five spins in a DM interaction.
Before introducing the DM interface interaction, let us emphasize that the bulk model on the simple cubic lattice has been studied with Heisenberg spins [74] and the Ising model [75], where and are both antiferromagnetic (). The critical value ; above this, the bipartite antiferromagnetic ordering changes into a frustrated ordering, where a line of spins up is surrounded by its neighboring lines of spins down. In the cases of (ferro) and , it is easy to show that the critical value where the ferromagnetic becomes antiferromagnetic is . Below this value, the antiferromagnetic ordering replaces the ferromagnetic ordering.
For the ferroelectric film, we assume that electric polarizations are of an Ising model of magnitude 1, pointing in the direction. The Hamiltonian reads
where is the polarization on the i-th lattice site and is the interaction parameter between polarizations at sites i and j. Similarly to with the magnetic subsystem, we will take the same for all NN pairs, and for NNN pairs.
We know that the DM interaction is written as
where is the spin at the i-th magnetic site, while denotes the Dzyaloshinskii–Moriya vector which is defined as , where is the displacement of the ligand ion (oxygen) and is the unit vector along the axis connecting and (see Figure 1b). One then has
We define
where D is a constant, is the unit vector on the z axis, and .
For the magnetoelectric interaction at the interface, we choose the interface Hamiltonian following Ref. [47]:
where is the polarization at the site k of the ferroelectric interface layer, while and belong to the interface magnetic layer (see Figure 1c). In this expression, is defined as the DM vector which is along the z axis, given by Equation (6). When summing the neighboring pairs , attention should be paid to the signs of and (see example in Ref. [47]).
Hereafter, we suppose independently of .
Since is in the z direction, i.e., the DM vector is in the z direction, in the absence of an applied field, the spins in the magnetic layers will lie in the plane to minimize the interface interaction energy, according to Equation (7).
In Equation (7), the magnetoelectric interaction favors a non-collinear spin structure in competition with the exchange interactions and , which favor collinear (ferro and antiferro) spin configurations. In ferroelectric layers, only collinear, ferro-, or antiferromagnetic ordering is possible because of the assumed Ising model for the polarizations. In historical demonstrations, the DM interaction was supposed to be small with respect to the exchange terms in the Hamiltonian. However, in superlattices, the magnetoelectric interaction is necessary to create non-collinear spin ordering. It has been shown that Rashba spin–orbit coupling can lead to a strong DM interaction at the interface [76,77], where the broken inversion symmetry at the interface can change the magnetic states. The DM interaction has been identified as a key ingredient in the creation and stabilization of skyrmions and chiral domain walls.
2.2. Ground State
From Equation (7), we see that the interface interaction is at its minimum when and lie in the interface plane and are perpendicular to each other in the absence of exchange interactions. When the exchange interactions are turned on, the collinear configuration will compete with the DM perpendicular configuration. This results in a non-collinear configuration, as will be shown below.
We note that when the magnetic film has more than one layer, the angle between NN spins in each magnetic layer is different. The determination of the angles is analytically difficult. We have to recourse to the numerical method known as the “steepest descent method” to minimize the energy to get the ground state (GS): We calculate the local field acting on a spin and align it in the direction of the local field. We go to another spin and do the same thing until all spins are visited. We repeat the operation many times until the total energy reaches its minimum.
In the simulations, a sample size of was used, with the linear lateral size and thickness , where ( is the magnetic layer’s thickness and is the ferroelectric layer’s thickness). We use the periodic boundary conditions in the plane.
For simplicity, we take exchange parameters between NN spins and NN polarizations equal to 1—namely, —for the simulations. We investigate the effects of the interaction parameters and . We note that the steepest descent method calculates the GS down to the value . For values lower than this, the DM interaction is so strong that the spin–spin angle tends towards so that magnetic exchange terms are zero.
We now consider a case with the frustrated regime for , namely above the critical value of ‒0.5, as mentioned above.
The spin configuration in the case where is shown in Figure 2 for the interface magnetic layer. We observe here a stripe phase with long islands and domain walls. The inside magnetic layers have the same texture.
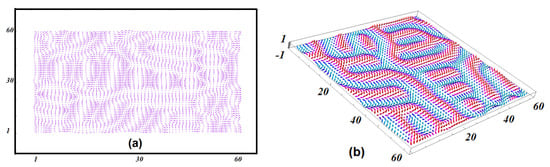
Figure 2.
(a) Two-dimensional (2D) view of the ground state (GS) configuration of the interface for with , , and ; (b) Three-dimensional (3D) view.
When H is increased, we observe the skyrmion crystal, as seen in Figure 3: The GS configuration of the interface and beneath the magnetic layers was obtained for , with and external magnetic field . A zoom of the skyrmion shown in Figure 3c and the z-components across the skyrmion shown in Figure 3d indicate that the skyrmion is of a Bloch type.
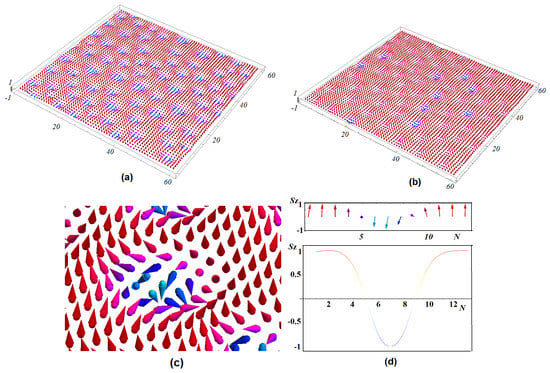
Figure 3.
(a) 3D view of the GS configuration of the interface for moderate frustration . (b) 3D view of the GS structure of the interior magnetic layers; (c) zoom of a skyrmion on the interface layer: Red denotes up spin, the four spins with clear blue color are down spin, and other colors correspond to spin orientations between the two. The skyrmion is of the Bloch type; (d) z-components of spins across the skyrmion shown in (c). Other parameters: , , and .
At this field strength of , if we increase the frustration—for example, —the skyrmion structure is enhanced: We can observe a clear 3D skyrmion crystal structure not only in the interface layer, but also in the interior layers. This is shown in Figure 4, where the interface and the second layer are displayed.
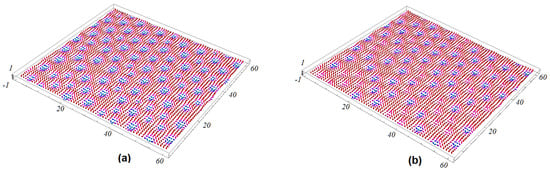
Figure 4.
3D view of the GS configuration of (a) the interface and (b) the second layer, for stronger frustration . , , , and .
The highest value of frustration where the skyrmion structure can be observed is when close to the critical value ‒0.5. We show this case in Figure 5: The GS configuration of the interface (a) and second (interior) (b) magnetic layers are presented. Other parameters are the same as in the previous figures, namely and . We can observe a clear 3D skyrmion crystal structure in all magnetic layers, not only near the interface layer. Unlike in the case where we did not take into account the interaction between [47], in the present case, where the frustration is very strong, we see that a large number of skyrmions are distributed over the all magnetic layers with a certain periodicity close to that of a perfect crystal.
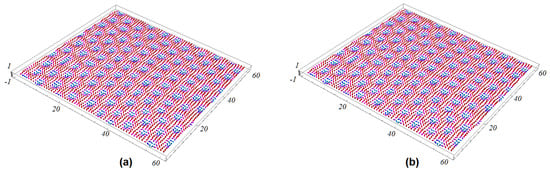
Figure 5.
Strongest frustration with (a) 3D view of the GS configuration of the interface and (b) 3D view of the GS configuration of the second magnetic layers. Other parameters: , , and .
Though we take the same values for and in the figures shown above, it is obvious that only the magnetic frustration is important for the skyrmion structure. The ferroelectric frustration affects only the stability of the polarizations at the interface. As long as does not exceed ‒0.5, the skyrmions are not affected by . In Figure 6, we show the GS configuration of the interface and the second magnetic layers for and (other parameters: , ). We see that the skyrmion structure is not different from the case (), shown in Figure 4.
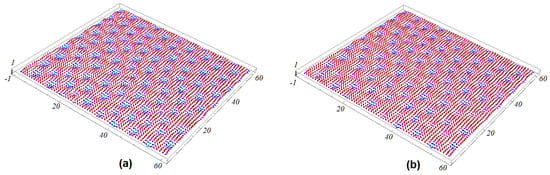
Figure 6.
(a) 3D view of the GS configuration of the interface for , , , and and (b) 3D view of the GS configuration of the second magnetic layers, for and . Other parameters: , , and .
Figure 7 shows the GS configuration of the interface and second (interior) magnetic layers for (, and ); it is not visibly different from the case () shown in Figure 5. We conclude here that, when the magnetic frustration is strong enough, the ferroelectric frustration does not affect the skyrmion structure.
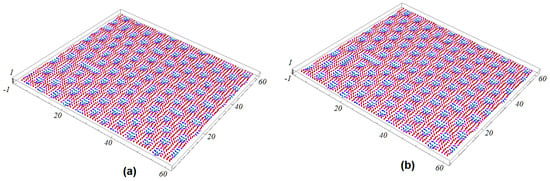
Figure 7.
(a) 3D view of the GS configuration of the interface and ; (b) 3D view of the GS configuration of the interface for and . Other parameters: , , and .
Now, if the magnetic frustration is not strong enough, the ferroelectric frustration plays an important role: Figure 8a shows the GS configuration of the interface magnetic layer for (, ) and Figure 8a shows the case of (, ). We see that skyrmions disappear when . Comparing this to the case (, ), where skyrmions are clearly formed, we conclude that while magnetic frustration enhances the formation of skyrmions, the ferroelectric frustration in the weak magnetic frustration tends to suppress skyrmions. The mechanism of these parameters when acting together seems to be very complicated.
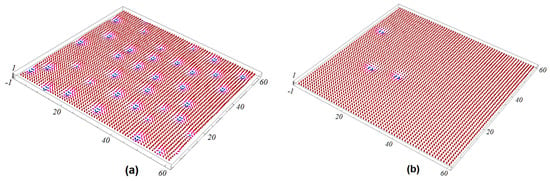
Figure 8.
(a) 3D view of the GS configuration of the interface for and ; (b) 3D view of the GS configuration of the interface for and . Other parameters: , , and .
Let us now show the effect of H. In the case of zero frustration, skyrmions disappear with an external field larger than [47]. In the case in which we take into account the negative interaction between neighbors, the skyrmion structure is stable with an external field of up to (see Figure 9). The spins are almost aligned in the direction of the field.
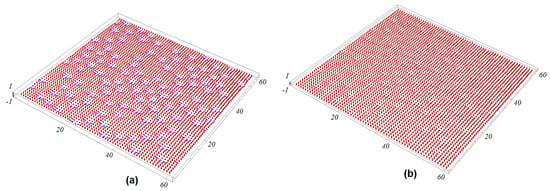
Figure 9.
: 3D view of the GS configuration of (a) the magnetic interface and (b) the second magnetic layers. Other parameters: , , , and .
The phase diagram in the plane—for the case , , and —is shown in Figure 10a. We can see that in region , skyrmions are not formed at any value of . In region , skyrmions are formed at non-zero values of . The smaller is, the larger the values of should be for the formation of skyrmions at the interface. With , skyrmions are formed without frustration at zero values of . When we introduce frustration in the magnetic layers at magneto-ferroelectric interaction , skyrmions form a perfect crystalline structure. Figure 10b shows the dependence of the ratio of the number of skyrmions on the interior layer to that on the interface layer . We see that, as the frustration becomes stronger, the ratio tends towards 1.
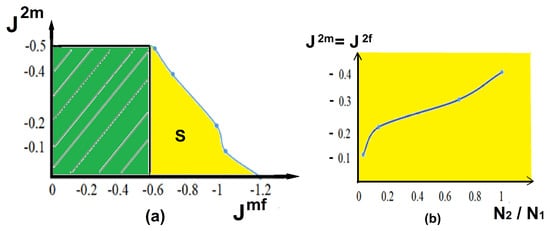
Figure 10.
(a) Phase diagram in the plane for the case , , and . The skyrmion phase is indicated by S (the yellow region). See the text for comments; (b) dependence of the ratio of the number of skyrmions on the interior layer to that on the interface layer .
Let us discuss about some theoretical observations of skyrmions in frustrated magnets [31,37,38,39,40,41,42,43,46]. Each of these works used a different model, so comparison is impossible. However, all show very similar skyrmion textures. For experiments, many observations have been made in various magnetic materials [2,4,5,7,19,20,21,22,23,24,25,26,27], in multiferroic materials [28], in ferroelectric materials [29], in semiconductors [30], and in helimagnets [2,20]. Again, as each real material corresponds to a particular microscopic mechanism, the comparison is not simple. However, one can observe many similar topological textures.
3. Skyrmion Phase Transition
The magnetic transition is driven by the competition between T, the DM interaction (namely ), the field H, and the magnetic texture (skyrmions). The stronger and/or is, the higher the transition temperature of the skyrmion structure will be. As mentioned above, strong DM interaction helps stabilize the skyrmion crystal [76,77] at the superlattice interface. We used a strong , as in the previous section.
We used the Metropolis algorithm [78,79] to simulate the system at . We performed calculations for systems with different sizes , where N varied from 40 to 100 and the thickness L varied from 2 to 16. It should be noted that changing the lateral size of N does not affect the results on skyrmions shown in the article. However, the influence of the total thickness L of the magnetic and ferroelectric layers is very significant: With an increase in the thickness of the magnetic and ferroelectric layers from to 8, skyrmions were formed only near the interface, not on layers far inside. In most calculations, we used and . With this thickness, skyrmions were observed in the two interior layers, as seen in the previous section. Usually, we discard Monte Carlo steps (MCS) per spin in order to equilibrate the system and average physical quantities over the next MCS/spin. Such long Monte Carlo times are needed, since it has been tested for the skyrmion crystal similar to that of the present model [31].
For the ferroelectric layers, the order parameter of layer n is given by
where indicates the thermal average.
For the magnetic layers where the spin configuration is not collinear, the definition of an order parameter is not easy. One way to proceed is to heat the system from a selected GS configuration. At a given T, we compare the actual spin configuration observed at the time t with its GS. The comparison is made by projecting that configuration onto the GS. The order parameter of layer n can be thus calculated by
where is the i-th spin at the time t and at T, and denotes its orientation at . We see that is close to 1 at very low T, where each spin is close to its orientation in the GS. At high T, where every spin strongly fluctuates, becomes zero.
Note that is defined in a similar way to the Edwards–Anderson (EA) order parameter in spin glasses (SG) [80]. The EA order parameter is calculated by taking the time average of each spin. When it is frozen at low T, its time average is not zero. At high T, it fluctuates greatly with time so that its time average is zero. The EA order parameter is just the sum of the squares of each spin average. It expresses the degree of freezing, but does not express the kind of ordering.
Note that if the system makes a global rotation during the simulation, then for a long time average. To check this, the most efficient way to proceed is to calculate the relaxation time to obtain properties at the infinite time, in the same spirit as the finite-size scaling used to calculate properties at the infinite system size. We have calculated the relaxation time of the 2D skyrmion crystal [31] using the order parameter defined by Equation (9). We have found that skyrmions need more than MCS/spin to relax to equilibrium, and the order parameter follows a stretched exponential law as in SG for .
Another way to check the stability of the skyrmion crystal is to numerically count the topological charges around each skyrmion [81]. If there is a phase transition, the charge number, which plays the role of an order parameter, evolves with T and goes to zero at the phase transition.
The total order parameters and are the sum of the layer order parameters, namely and .
In Figure 11, we display the magnetic energy and the magnetic order parameter vs. T in an external magnetic field for various sets of NNN interaction. Note that the phase transition occurs at the energy curvature changes, namely at the maximum of the specific heat. The red curve in Figure 11a is for both sets and . The change of curvature takes place at . This means that the ferroelectric frustration does not affect the magnetic skyrmion transition at such a strong magnetic frustration . For —i.e., no magnetic frustration—the transition takes place at a much higher temperature .
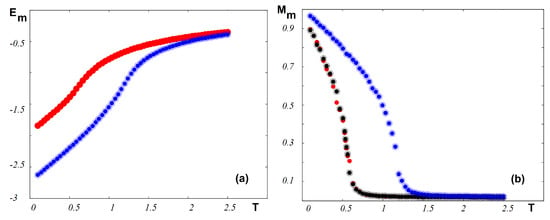
Figure 11.
(a) Energy of the magnetic films versus temperature T for (red), coinciding with the curve for (black, hidden behind the red curve). The blue curve is for . (b) Order parameter of the magnetic films versus temperature T for (red), (black), and (blue). Other used parameters: , .
At this stage, we note that the above results are shown in the dimensionless unit: Energy in the unit of and temperature in the unit of . Our results can be used for materials with different . For example, if one experimentally observes that the skyrmion phase transition occurs at K, we can calculate the effective exchange using, for example, the mean-field equation
where (simple cubic lattice), (spin magnitude), and Joules/Kelvin have been used. is a combination of , , and . Knowing the GS, we can deduce these interactions. We can then calculate the energy in units of Joules by multiplying the value of in Figure 11a by the value of . Unfortunately, at the time being, there is no experimental energy measurement for comparison.
The magnetic order parameters shown in Figure 11b confirm the skyrmion transition temperatures seen by the curvature change of the energy in Figure 11a.
In Figure 12a, we show the ferroelectric energy and ferroelectric order parameters for the same sets of frustration parameters: (), (, ), (, ). As seen, the first and second sets where the magnetic frustration is strong give and 0.90, respectively. This means that the ferroelectric frustration which does not affect the skyrmion transition strongly affects the ferroelectric transition. The third set with no magnetic frustration () gives the transition at . Figure 12b shows the ferroelectric order parameters for the three sets of NNN interactions shown in Figure 12a. These curves confirm the transition temperatures given above.
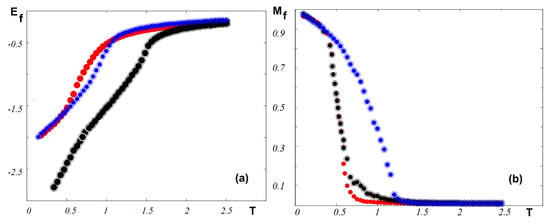
Figure 12.
(a) Energy of the ferroelectric films versus temperature T for (red), (black), () (blue), (b) Order parameter of the ferroelectric films versus temperature T for (red), (black), (blue). Other used parameters: , .
4. Conclusions
In this paper, we have studied the effect of the NNN interactions in both magnetic and ferroelectric layers of a magneto-ferroelectric superlattice. A Dzyaloshinskii–Moriya (DM) interaction was assumed for the magneto-ferroelectric interface coupling.
We found the formation of a skyrmion crystal in the GS under an applied magnetic field in a large region of parameters in the space (. As expected, the magnetic frustration enhances the creation of skyrmions while, when strong enough, the ferroelectric frustration destabilizes skyrmions if the magnetic frustration is weak.
We have studied the phase transition of the skyrmion crystal through the use of Monte Carlo method. Skyrmions have been shown to be stable at finite temperatures. While the magnetic frustration helps enhance the creation of skyrmions, it reduces the transition temperature considerably.
The existence of very stable skyrmions confined at the magneto-ferroelectric interface at finite T is very interesting and may have potential applications in spintronics. Many applications using skyrmions have been mentioned in the Introduction. As a last remark, let us mention that the present magneto-ferroelectric superlattice model can be used in the cases of magnetic monolayers or bilayers to study the dynamics of the skyrmions driven by a spin-polarized current or by a spin-transfer torque. Due to the small thickness, the skyrmions created by the interface are as well confined as in 2D. Our model is therefore suitable for creating skyrmion pinning by using an electric field acting on the ferroelectric polarizations. This is the subject of our future investigations.
Author Contributions
Conceptualization, H.T.D. and I.F.S.; methodology, H.T.D.; software, I.F.S.; validation, H.T.D. and I.F.S.; formal analysis, H.T.D.; investigation, I.F.S.; writing—original draft preparation, I.F.S.; writing— review and editing, H.T.D. All authors have read and agreed to the published version of the manuscript.
Funding
No external funding received for this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bogdanov, A.N.; Yablonskii, D. Thermodynamically stable vortices in magnetically ordered crystals. The mixed state of magnets. Z. Eksp. Teor. Fiz 1989, 95, 178. [Google Scholar]
- Yu, X.; Onose, Y.; Kanazawa, N.; Park, J.; Han, J.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Heinze, S.; Von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.E.; Wolter, B.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and deleting single magnetic skyrmions. Science 2013, 341, 636–639. [Google Scholar] [CrossRef]
- Rosch, A. Skyrmions: Moving with the current. Nat. Nanotechnol. 2013, 8, 160. [Google Scholar] [CrossRef]
- Leonov, A.; Togawa, Y.; Monchesky, T.; Bogdanov, A.; Kishine, J.; Kousaka, Y.; Miyagawa, M.; Koyama, T.; Akimitsu, J.; Koyama, T.; et al. Chiral surface twists and skyrmion stability in nanolayers of cubic helimagnets. Phys. Rev. Lett. 2016, 117, 087202. [Google Scholar] [CrossRef]
- Moreau-Luchaire, C.; Moutafis, C.; Reyren, N.; Sampaio, J.; Vaz, C.; Van Horne, N.; Bouzehouane, K.; Garcia, K.; Deranlot, C.; Warnicke, P.; et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotechnol. 2016, 11, 444–448. [Google Scholar] [CrossRef]
- Soumyanarayanan, A.; Raju, M.; Oyarce, A.G.; Tan, A.K.; Im, M.Y.; Petrović, A.P.; Ho, P.; Khoo, K.; Tran, M.; Gan, C.; et al. Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers. Nat. Mater. 2017, 16, 898–904. [Google Scholar] [CrossRef]
- Dupé, B.; Bihlmayer, G.; Böttcher, M.; Blügel, S.; Heinze, S. Engineering skyrmions in transition-metal multilayers for spintronics. Nat. Commun. 2016, 7, 11779. [Google Scholar] [CrossRef]
- Müller, J.; Rosch, A.; Garst, M. Edge instabilities and skyrmion creation in magnetic layers. New J. Phys. 2016, 18, 065006. [Google Scholar] [CrossRef]
- Rosch, A. Spintronics: Electric control of skyrmions. Nat. Nanotechnol. 2017, 12, 103–104. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Xia, J.; Zhao, G.; Zhang, X.; Ezawa, M.; Tretiakov, O.A.; Liu, X.; Zhou, Y. Spin torque nano-oscillators based on antiferromagnetic skyrmions. Appl. Phys. Lett. 2019, 114, 042402. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Bessarab, P.; Yudin, D.; Gulevich, D.; Wadley, P.; Titov, M.; Tretiakov, O.A. Stability and lifetime of antiferromagnetic skyrmions. Phys. Rev. B 2019, 99, 140411. [Google Scholar] [CrossRef]
- Tomasello, R.; Martinez, E.; Zivieri, R.; Torres, L.; Carpentieri, M.; Finocchio, G. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 2014, 4, 6784. [Google Scholar] [CrossRef]
- Koshibae, W.; Kaneko, Y.; Iwasaki, J.; Kawasaki, M.; Tokura, Y.; Nagaosa, N. Memory functions of magnetic skyrmions. Jpn. J. Appl. Phys. 2015, 54, 053001. [Google Scholar] [CrossRef]
- Kang, W.; Huang, Y.; Zheng, C.; Lv, W.; Lei, N.; Zhang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Voltage controlled magnetic skyrmion motion for racetrack memory. Sci. Rep. 2016, 6, 23164. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, J.; Zhou, Y.; Liu, X.; Zhang, H.; Ezawa, M. Skyrmion dynamics in a frustrated ferromagnetic film and current-induced helicity locking-unlocking transition. Nat. Commun. 2017, 8, 1717. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Du, H.; Che, R.; Kong, L.; Zhao, X.; Jin, C.; Wang, C.; Yang, J.; Ning, W.; Li, R.; Jin, C.; et al. Edge-mediated skyrmion chain and its collective dynamics in a confined geometry. Nat. Commun. 2015, 6, 8504. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Upadhyaya, P.; Zhang, W.; Yu, G.; Jungfleisch, M.B.; Fradin, F.Y.; Pearson, J.E.; Tserkovnyak, Y.; Wang, K.L.; Heinonen, O.; et al. Blowing magnetic skyrmion bubbles. Science 2015, 349, 283–286. [Google Scholar] [CrossRef] [PubMed]
- Leonov, A.; Monchesky, T.; Romming, N.; Kubetzka, A.; Bogdanov, A.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. New J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- Woo, S.; Litzius, K.; Krüger, B.; Im, M.Y.; Caretta, L.; Richter, K.; Mann, M.; Krone, A.; Reeve, R.M.; Weigand, M.; et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 2016, 15, 501–506. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, X.; Yu, G.; Zhang, W.; Wang, X.; Jungfleisch, M.B.; Pearson, J.E.; Cheng, X.; Heinonen, O.; Wang, K.L.; et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 2017, 13, 162–169. [Google Scholar] [CrossRef]
- Litzius, K.; Lemesh, I.; Krüger, B.; Bassirian, P.; Caretta, L.; Richter, K.; Büttner, F.; Sato, K.; Tretiakov, O.A.; Förster, J.; et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat. Phys. 2017, 13, 170–175. [Google Scholar] [CrossRef]
- Woo, S.; Song, K.M.; Han, H.S.; Jung, M.S.; Im, M.Y.; Lee, K.S.; Song, K.S.; Fischer, P.; Hong, J.I.; Choi, J.W.; et al. Spin-orbit torque-driven skyrmion dynamics revealed by time-resolved X-ray microscopy. Nat. Commun. 2017, 8, 15573. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef]
- Nahas, Y.; Prokhorenko, S.; Louis, L.; Gui, Z.; Kornev, I.; Bellaiche, L. Discovery of stable skyrmionic state in ferroelectric nanocomposites. Nat. Commun. 2015, 6, 8542. [Google Scholar] [CrossRef]
- Kézsmárki, I.; Bordács, S.; Milde, P.; Neuber, E.; Eng, L.; White, J.; Rønnow, H.M.; Dewhurst, C.; Mochizuki, M.; Yanai, K.; et al. Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV 4 S 8. Nat. Mater. 2015, 14, 1116–1122. [Google Scholar] [CrossRef]
- El Hog, S.; Bailly-Reyre, A.; Diep, H.T. Stability and phase transition of skyrmion crystals generated by Dzyaloshinskii-Moriya interaction. J. Magn. Magn. Mater. 2018, 455, 32–38. [Google Scholar] [CrossRef]
- Butenko, A.; Leonov, A.; Rößler, U.; Bogdanov, A. Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets. Phys. Rev. B 2010, 82, 052403. [Google Scholar] [CrossRef]
- Rößler, U.K.; Leonov, A.A.; Bogdanov, A.N. Chiral skyrmionic matter in non-centrosymmetric magnets. J. Phys. Conf. Ser. 2011, 303, 012105. [Google Scholar] [CrossRef]
- Zverev, V.; Tishin, A.; Chernyshov, A.; Mudryk, Y.; Gschneidner, K.A., Jr.; Pecharsky, V.K. Magnetic and magnetothermal properties and the magnetic phase diagram of high purity single crystalline terbium along the easy magnetization direction. J. Phys. Condens. Matter 2014, 26, 066001. [Google Scholar] [CrossRef] [PubMed]
- Zverev, V.; Tishin, A.; Min, Z.; Mudryk, Y.; Gschneidner, K., Jr.; Pecharsky, V. Magnetic and magnetothermal properties, and the magnetic phase diagram of single-crystal holmium along the easy magnetization direction. J. Phys. Condens. Matter 2015, 27, 146002. [Google Scholar] [CrossRef] [PubMed]
- Stishov, S.M.; Petrova, A.E.; Khasanov, S.; Panova, G.K.; Shikov, A.A.; Lashley, J.C.; Wu, D.; Lograsso, T.A. Magnetic phase transition in the itinerant helimagnet MnSi: Thermodynamic and transport properties. Phys. Rev. B 2007, 76, 052405. [Google Scholar] [CrossRef]
- Leonov, A.; Mostovoy, M. Edge states and skyrmion dynamics in nanostripes of frustrated magnets. Nat. Commun. 2017, 8, 14394. [Google Scholar] [CrossRef]
- Lin, S.Z.; Hayami, S. Ginzburg-Landau theory for skyrmions in inversion-symmetric magnets with competing interactions. Phys. Rev. B 2016, 93, 064430. [Google Scholar] [CrossRef]
- Hayami, S.; Lin, S.Z.; Batista, C.D. Bubble and skyrmion crystals in frustrated magnets with easy-axis anisotropy. Phys. Rev. B 2016, 93, 184413. [Google Scholar] [CrossRef]
- Hayami, S.; Lin, S.Z.; Kamiya, Y.; Batista, C.D. Vortices, skyrmions, and chirality waves in frustrated Mott insulators with a quenched periodic array of impurities. Phys. Rev. B 2016, 94, 174420. [Google Scholar] [CrossRef]
- Lin, S.Z.; Hayami, S.; Batista, C.D. Magnetic vortex induced by nonmagnetic impurity in frustrated magnets. Phys. Rev. Lett. 2016, 116, 187202. [Google Scholar] [CrossRef] [PubMed]
- Batista, C.D.; Lin, S.Z.; Hayami, S.; Kamiya, Y. Frustration and chiral orderings in correlated electron systems. Rep. Prog. Phys. 2016, 79, 084504. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Gomonay, O.; Kläui, M. Skyrmions and multisublattice helical states in a frustrated chiral magnet. Phys. Rev. B 2017, 96, 134415. [Google Scholar] [CrossRef]
- Rózsa, L.; Deák, A.; Simon, E.; Yanes, R.; Udvardi, L.; Szunyogh, L.; Nowak, U. Skyrmions with attractive interactions in an ultrathin magnetic film. Phys. Rev. Lett. 2016, 117, 157205. [Google Scholar] [CrossRef]
- Rózsa, L.; Palotás, K.; Deák, A.; Simon, E.; Yanes, R.; Udvardi, L.; Szunyogh, L.; Nowak, U. Formation and stability of metastable skyrmionic spin structures with various topologies in an ultrathin film. Phys. Rev. B 2017, 95, 094423. [Google Scholar] [CrossRef]
- Sutcliffe, P. Skyrmion knots in frustrated magnets. Phys. Rev. Lett. 2017, 118, 247203. [Google Scholar] [CrossRef]
- Sharafullin, I.F.; Kharrasov, M.K.; Diep, H.T. Dzyaloshinskii-Moriya interaction in magnetoferroelectric superlattices: Spin waves and skyrmions. Phys. Rev. B 2019, 99, 214420. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, J.; Lofland, S.; Ma, Z.; Mohaddes-Ardabili, L.; Zhao, T.; Salamanca-Riba, L.; Shinde, S.; Ogale, S.; Bai, F.; et al. Multiferroic batio3-cofe2o4 nanostructures. Science 2004, 303, 661–663. [Google Scholar] [CrossRef]
- Bibes, M.; Barthélémy, A. Multiferroics: Towards a magnetoelectric memory. Nat. Mater. 2008, 7, 425–426. [Google Scholar] [CrossRef]
- Mathur, N. Materials science: A desirable wind up. Nature 2008, 454, 591–592. [Google Scholar] [CrossRef]
- Nan, C.W. Magnetoelectric effect in composites of piezoelectric and piezomagnetic phases. Phys. Rev. B 1994, 50, 6082–6088. [Google Scholar] [CrossRef] [PubMed]
- Sergienko, I.A.; Dagotto, E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 2006, 73, 094434. [Google Scholar] [CrossRef]
- Udalov, O.; Beloborodov, I. The Coulomb based magneto-electric coupling in multiferroic tunnel junctions and granular multiferroics. AIP Adv. 2018, 8, 055810. [Google Scholar] [CrossRef]
- Ortiz-Álvarez, H.; Bedoya-Hincapié, C.; Restrepo-Parra, E. Monte Carlo simulation of charge mediated magnetoelectricity in multiferroic bilayers. Phys. B Condens. Matter 2014, 454, 235–239. [Google Scholar] [CrossRef]
- Janssen, T. Dynamics of (anti) ferromagnetic/electric domain walls. Ferroelectrics 1994, 162, 265–273. [Google Scholar] [CrossRef]
- Janssen, T.; Tjon, J. Microscopic model for incommensurate crystal phases. Phys. Rev. B 1982, 25, 3767–3785. [Google Scholar] [CrossRef]
- Li, Q.; Chen, X.; Gao, X.; Liu, J.M.; Liu, Z. Monte-carlo study on phase transitions of ferroelectromagnets. Ferroelectrics 2002, 279, 67–81. [Google Scholar] [CrossRef]
- Pyatakov, A. Magnetoelectricity goes local: From bulk multiferroic crystals to ferroelectricity localized on magnetic topological textures. Phys. B Condens. Matter 2018, 542, 59–62. [Google Scholar] [CrossRef]
- Maruyama, T.; Shiota, Y.; Nozaki, T.; Ohta, K.; Toda, N.; Mizuguchi, M.; Tulapurkar, A.; Shinjo, T.; Shiraishi, M.; Mizukami, S.; et al. Large voltage-induced magnetic anisotropy change in a few atomic layers of iron. Nat. Nanotechnol. 2009, 4, 158–161. [Google Scholar] [CrossRef]
- Alberca, A.; Munuera, C.; Azpeitia, J.; Kirby, B.; Nemes, N.; Perez-Muñoz, A.; Tornos, J.; Mompean, F.; Leon, C.; Santamaria, J.; et al. Phase separation enhanced magneto-electric coupling in La 0.7 Ca 0.3 MnO 3/BaTiO 3 ultra-thin films. Sci. Rep. 2015, 5, 17926. [Google Scholar] [CrossRef]
- Karthik, T.; Rao, T.D.; Srinivas, A.; Asthana, S. A-Site Cation disorder and Size variance effects on the physical properties of multiferroic Bi0. 9RE0. 1FeO3 Ceramics (RE = Gd3+, Tb3+, Dy3+). arXiv 2012, arXiv:1206.5606. [Google Scholar]
- Garcia-Castro, A.C.; Spaldin, N.A.; Romero, A.; Bousquet, E. Geometric ferroelectricity in fluoroperovskites. Phys. Rev. B 2014, 89, 104107. [Google Scholar] [CrossRef]
- Xiang, H.; Kan, E.; Zhang, Y.; Whangbo, M.H.; Gong, X. General theory for the ferroelectric polarization induced by spin-spiral order. Phys. Rev. Lett. 2011, 107, 157202. [Google Scholar] [CrossRef] [PubMed]
- Balents, L. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Pei, H.; Guo, S.; Ren, L.; Chen, C.; Luo, B.; Dong, X.; Jin, K.; Ren, R.; Zeeshan, H.M. The Frustration-induced Ferroelectricity of a Manganite Tricolor Superlattice with Artificially Broken Symmetry. Sci. Rep. 2017, 7, 6201. [Google Scholar] [CrossRef] [PubMed]
- Göbel, B.; Mook, A.; Henk, J.; Mertig, I. Antiferromagnetic skyrmion crystals: Generation, topological Hall, and topological spin Hall effect. Phys. Rev. B 2017, 96, 060406. [Google Scholar] [CrossRef]
- Yadav, A.; Nelson, C.; Hsu, S.; Hong, Z.; Clarkson, J.; Schlepütz, C.; Damodaran, A.; Shafer, P.; Arenholz, E.; Dedon, L.; et al. Observation of polar vortices in oxide superlattices. Nature 2016, 530, 198–201. [Google Scholar] [CrossRef]
- Leonov, A.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef]
- Koshibae, W.; Nagaosa, N. Theory of skyrmions in bilayer systems. Sci. Rep. 2017, 7, 42645. [Google Scholar] [CrossRef]
- Martinez, J.; Jalil, M. Topological dynamics and current-induced motion in a skyrmion lattice. New J. Phys. 2016, 18, 033008. [Google Scholar] [CrossRef]
- Lin, S.Z.; Reichhardt, C.; Batista, C.D.; Saxena, A. Driven Skyrmions and Dynamical Transitions in Chiral Magnets. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef] [PubMed]
- Iwasaki, J.; Mochizuki, M.; Nagaosa, N. Universal current-velocity relation of skyrmion motion in chiral magnets. Nat. Commun. 2013, 4, 1463. [Google Scholar] [CrossRef] [PubMed]
- Diep, H.T. Frustrated Spin Systems; World Scientific: Singapore, 2013; 648p. [Google Scholar]
- Pinettes, C.; Diep, H.T. Phase transition and phase diagram of the J1-J2 Heisenberg model on a simple cubic lattice. J. Appl. Phys. 1998, 83, 6317. [Google Scholar] [CrossRef]
- Hoang, D.T.; Magnin, Y.; Diep, H.T. Spin Resistivity in the Frustrated J1-J2 Model. Mod. Phys. Lett. 2011, 25, 937–945. [Google Scholar] [CrossRef]
- Yang, H.; Chen, G.; Cotta, A.A.C.; N’ Diaye, A.T.; Nikolaev, S.A.; Soares, E.A.; Macedo, W.A.A.; Liu, K.; Schmid, A.K.; Fert, A.; et al. Significant Dzyaloshinskii-Moriya interaction at graphene-ferromagnet interfaces due to the Rashba effect. Nat. Mater. 2018, 17, 605–609. [Google Scholar] [CrossRef]
- Manchon, A.; Koo, H.C.; Nitta, J.; Frolov, S.; Duine, R. New perspectives for rashba spin-orbit coupling. Nat. Mater. 2015, 14, 871–882. [Google Scholar] [CrossRef]
- Landau, D.P.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: London, UK, 2009. [Google Scholar]
- Brooks, S.; Gelman, A.; Jones, S.L.; Meng, X.L. Handbook of Markov Chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Mézard, M.; Parisi, M.; Virasoro, M. Spin Glass Theory and Beyond An Introduction to the Replica Method and Its Applications; World Scientific: Singapore, 1986. [Google Scholar]
- El Hog, S.; Kato, F.; Koibuchi, H.; Diep, H.T. Skyrmions on 2D Elastic Surfaces with Fixed Boundary Frame. J. Mag. Mag. Mat. 2019, in press. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).