Monte Carlo Study of Rubber Elasticity on the Basis of Finsler Geometry Modeling †
Abstract
1. Introduction
2. Models and Simulation Technique
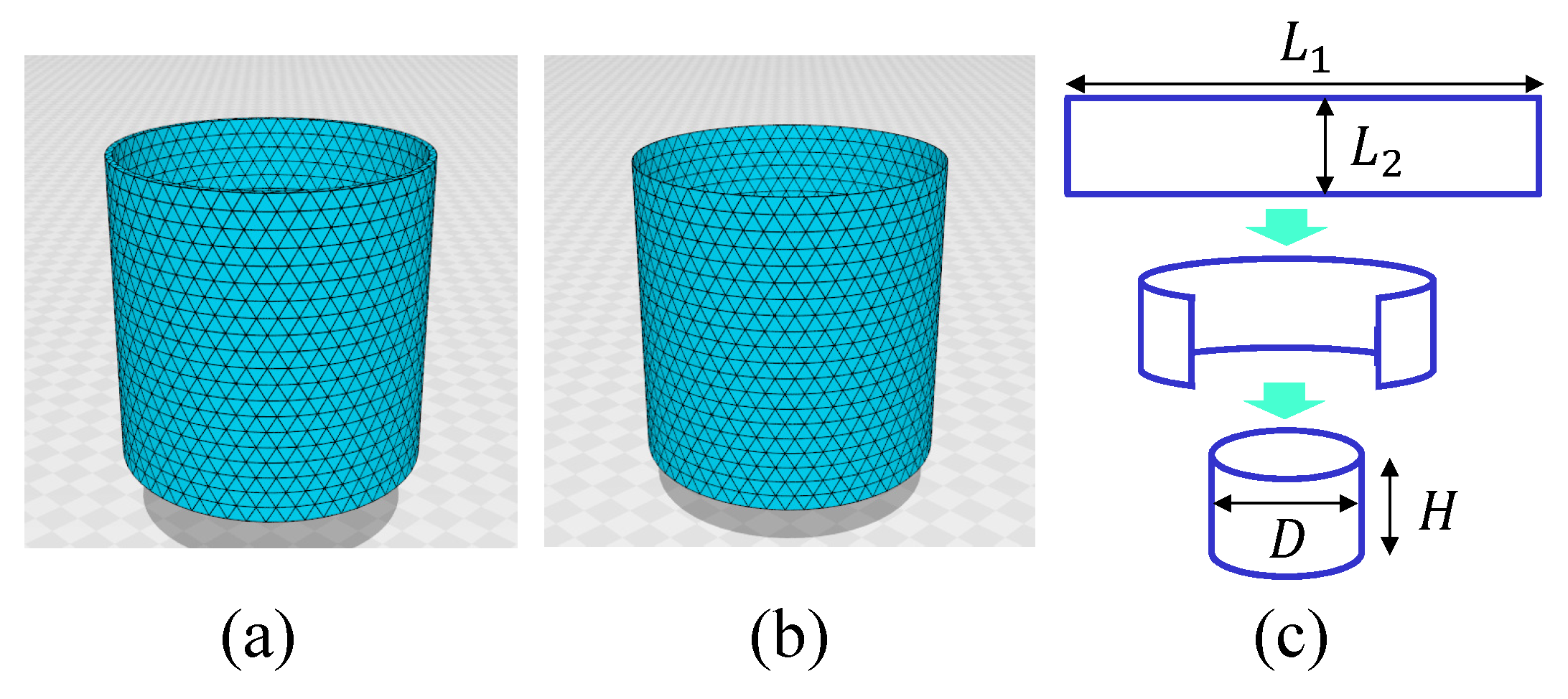
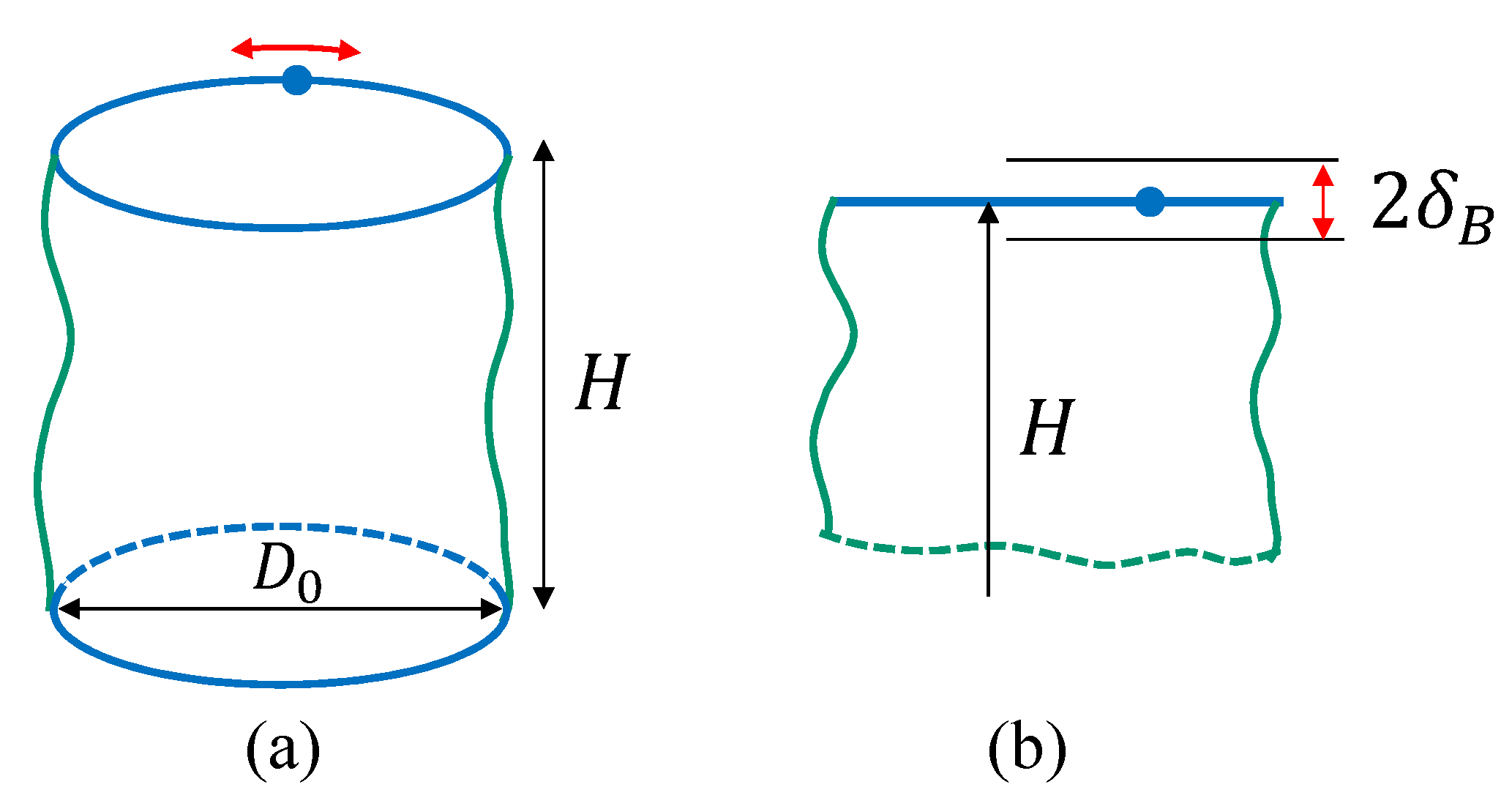
2.1. Lattices and the Monte Carlo Technique
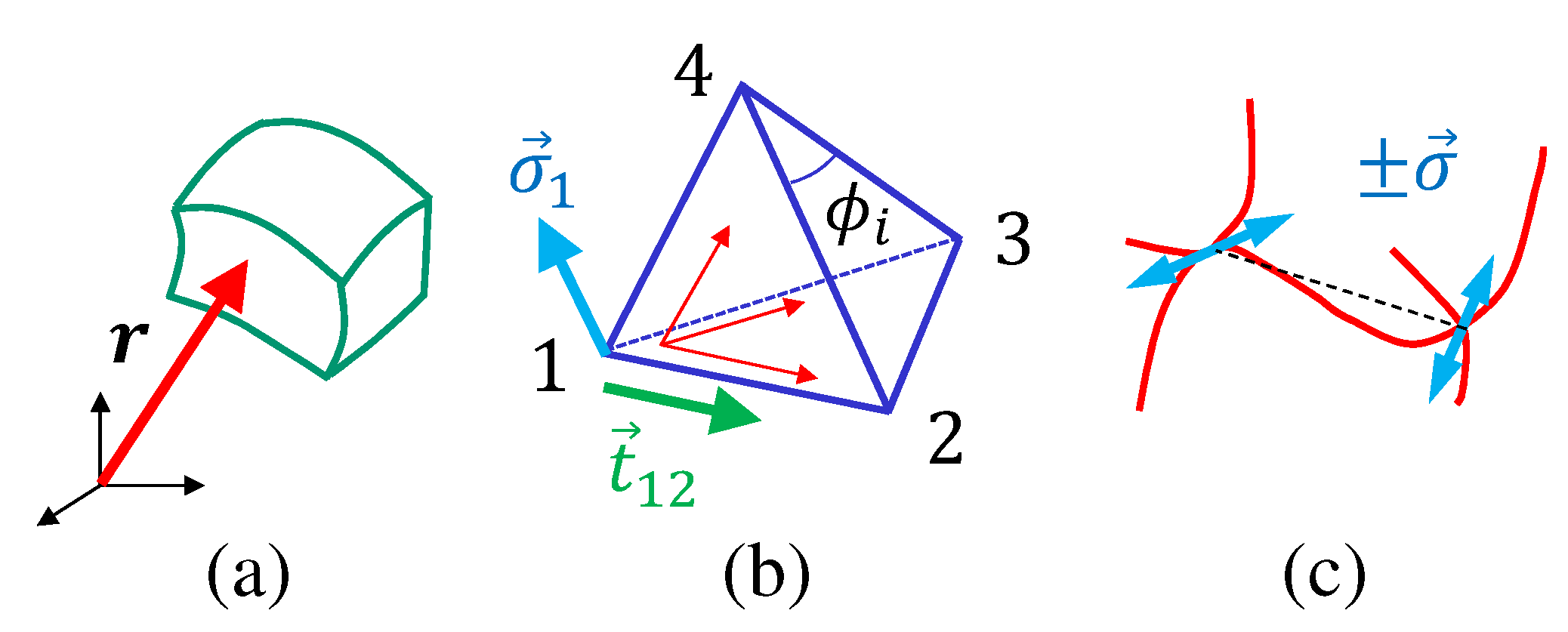
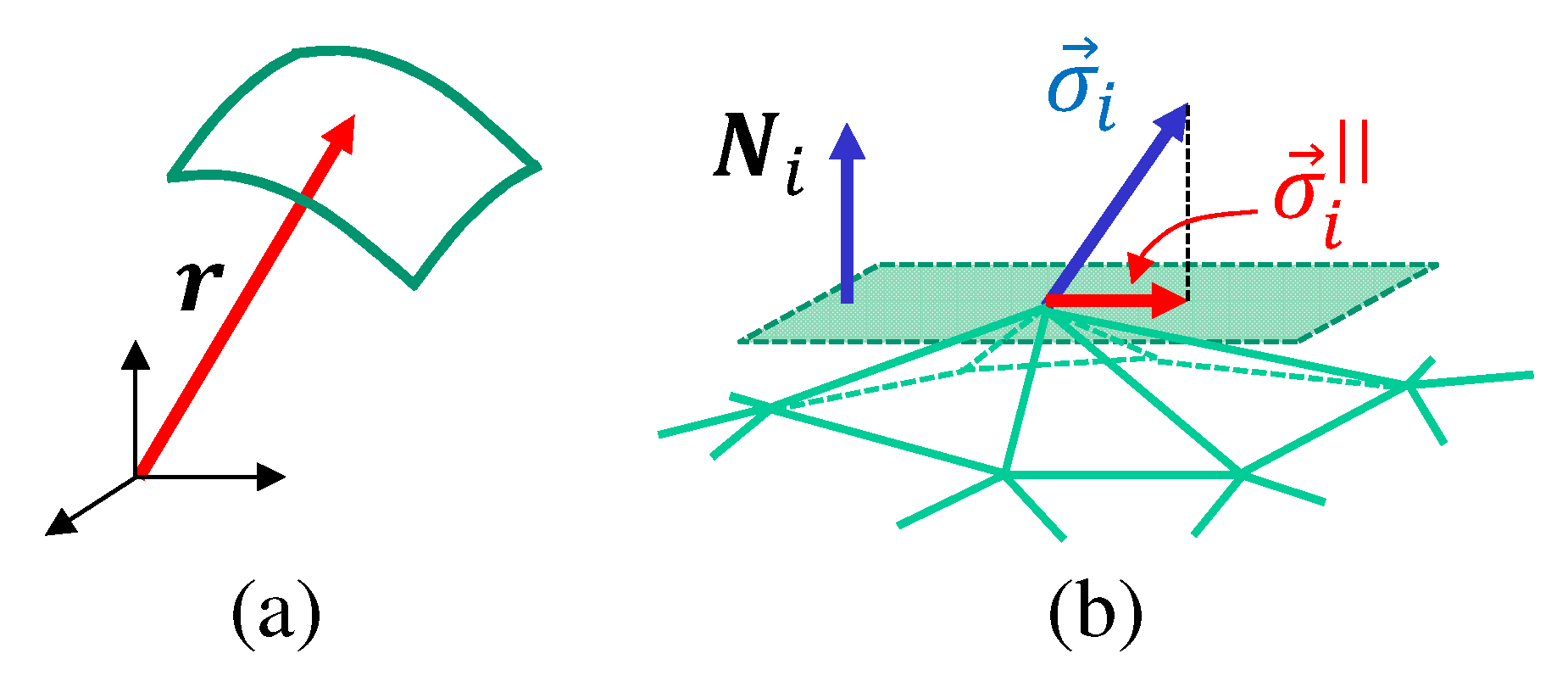
2.2. 3D Model
2.3. 2D Model
2.4. Formula for the Frame Tension
2.5. Physical Unit of the Frame Tension
2.6. Monte Carlo Simulations
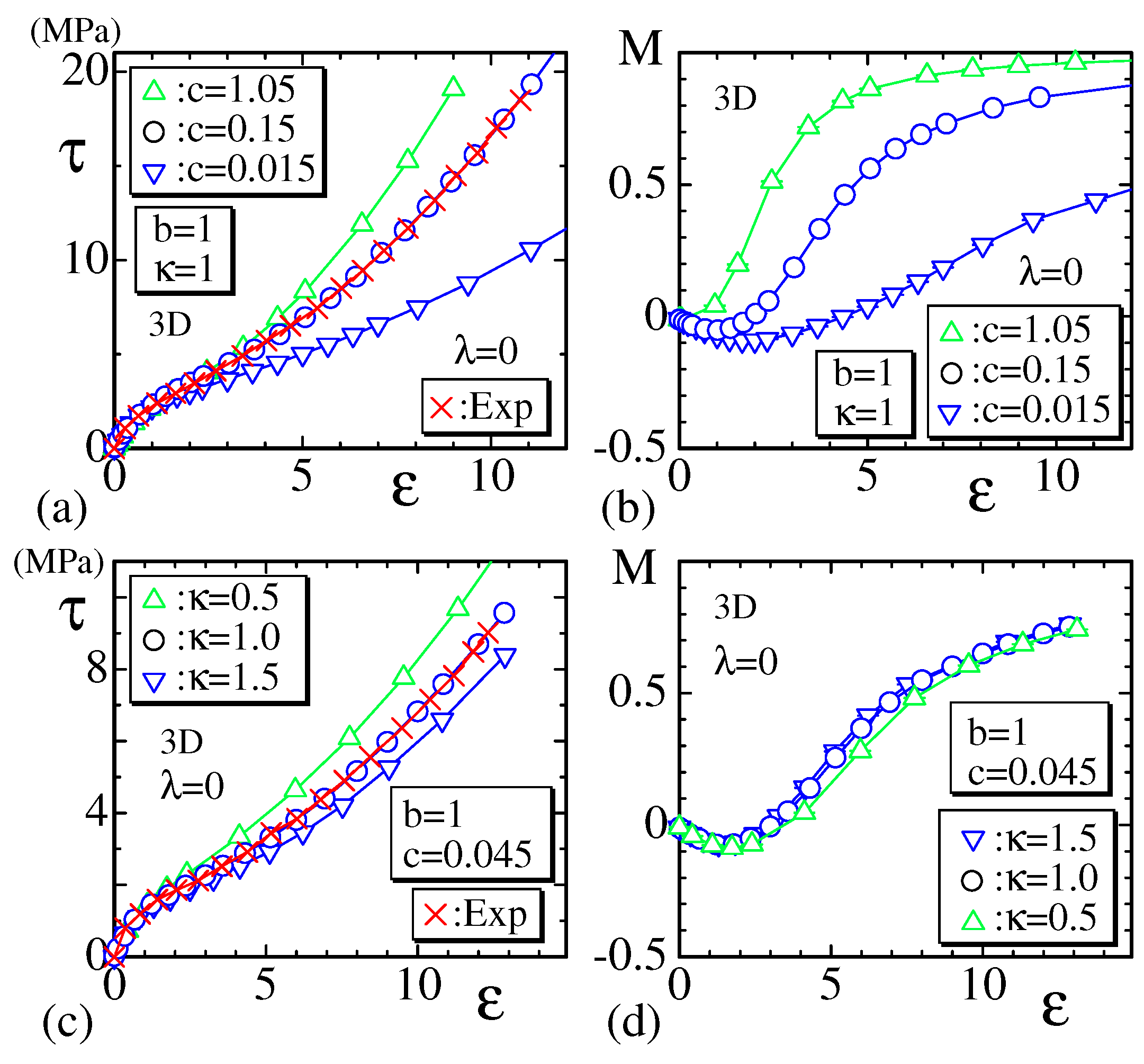
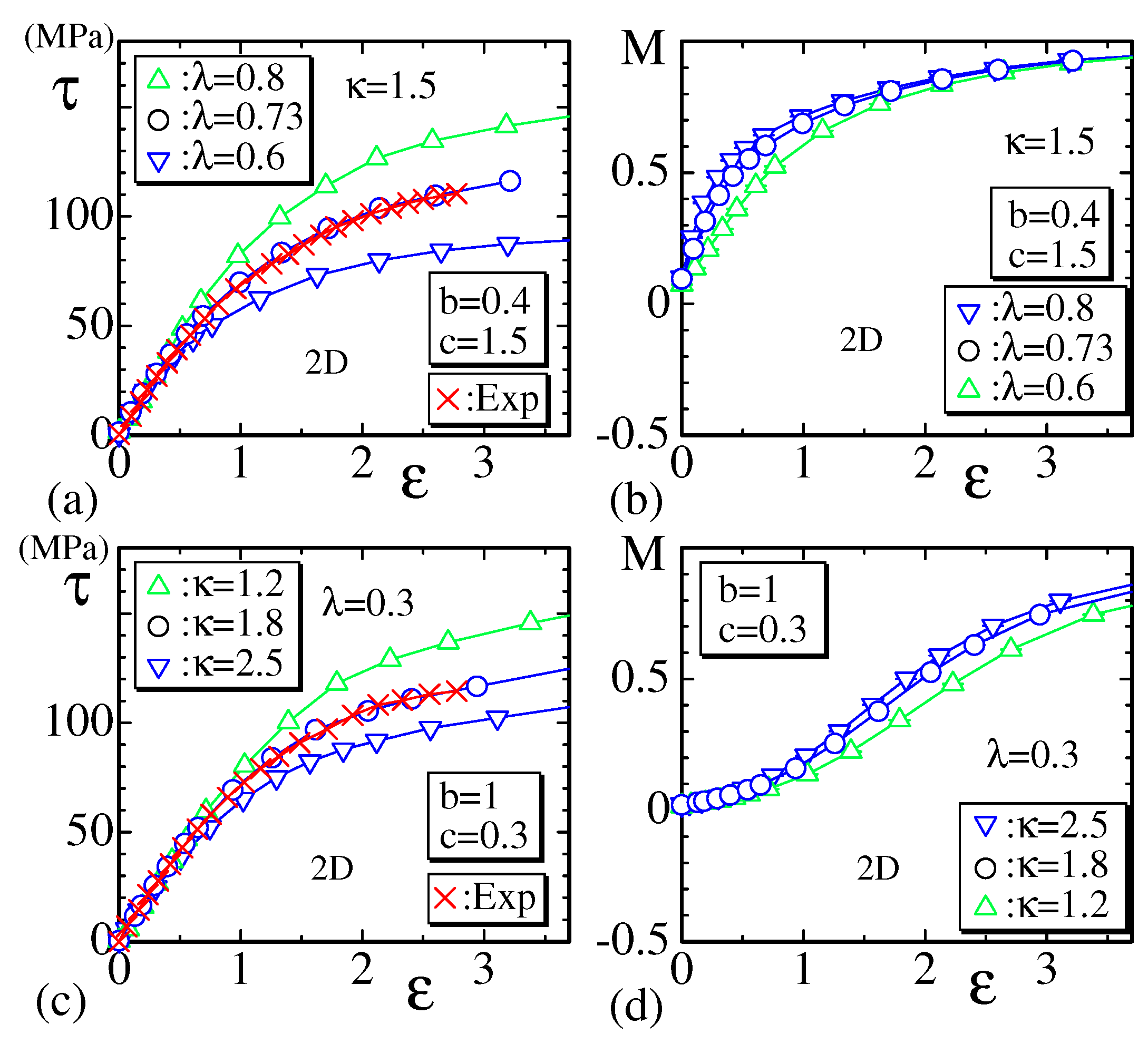
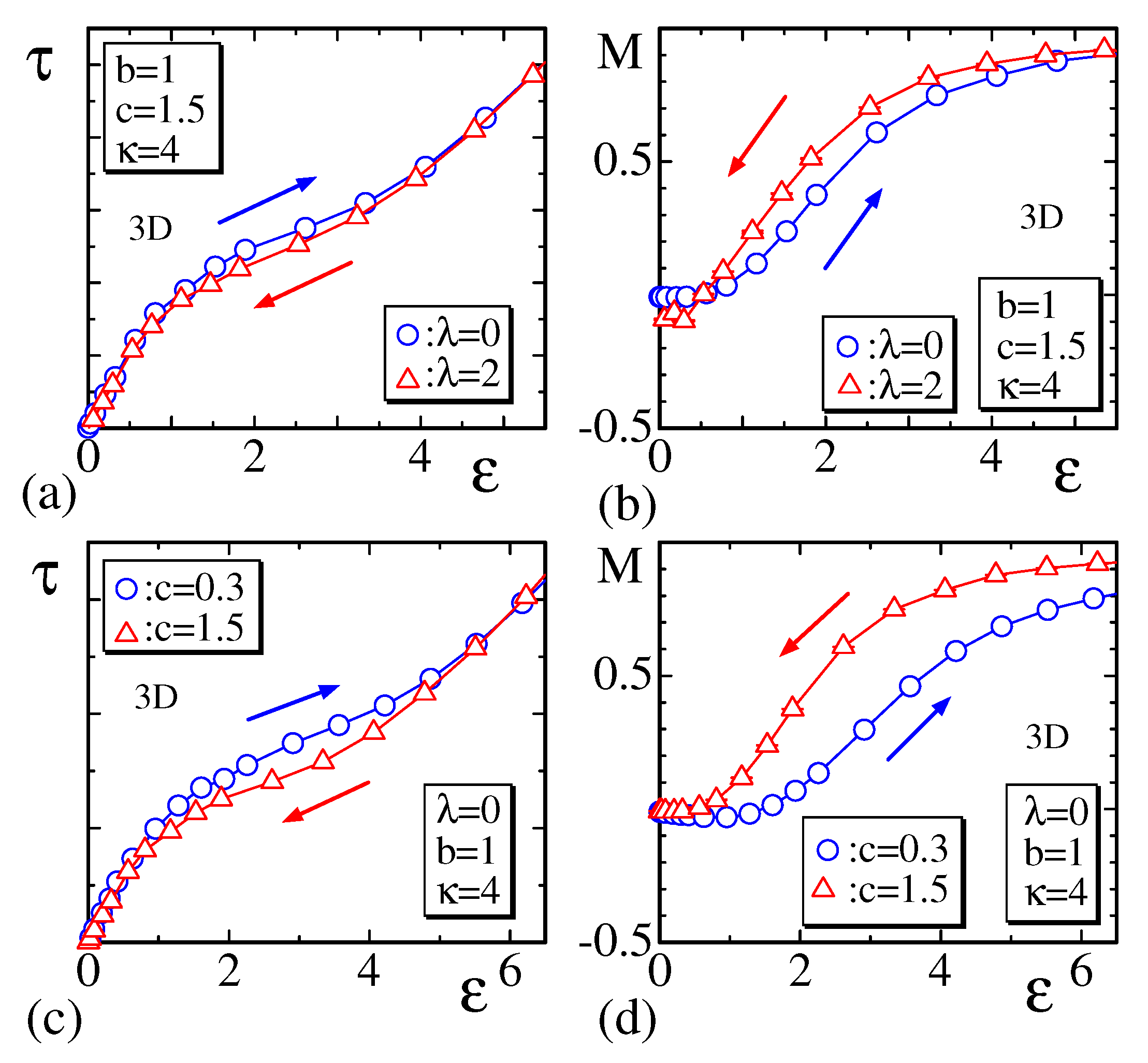
3. Numerical Results
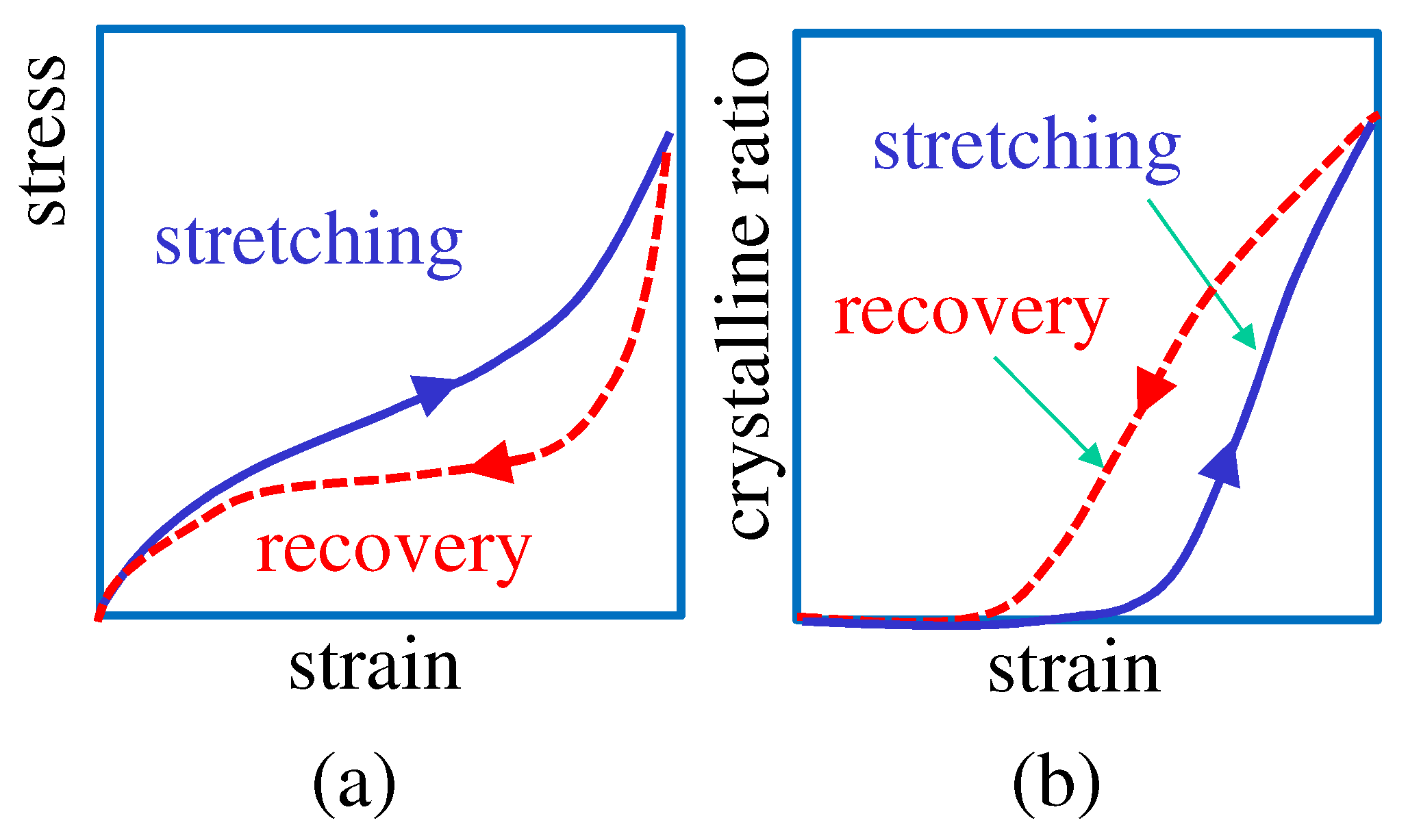
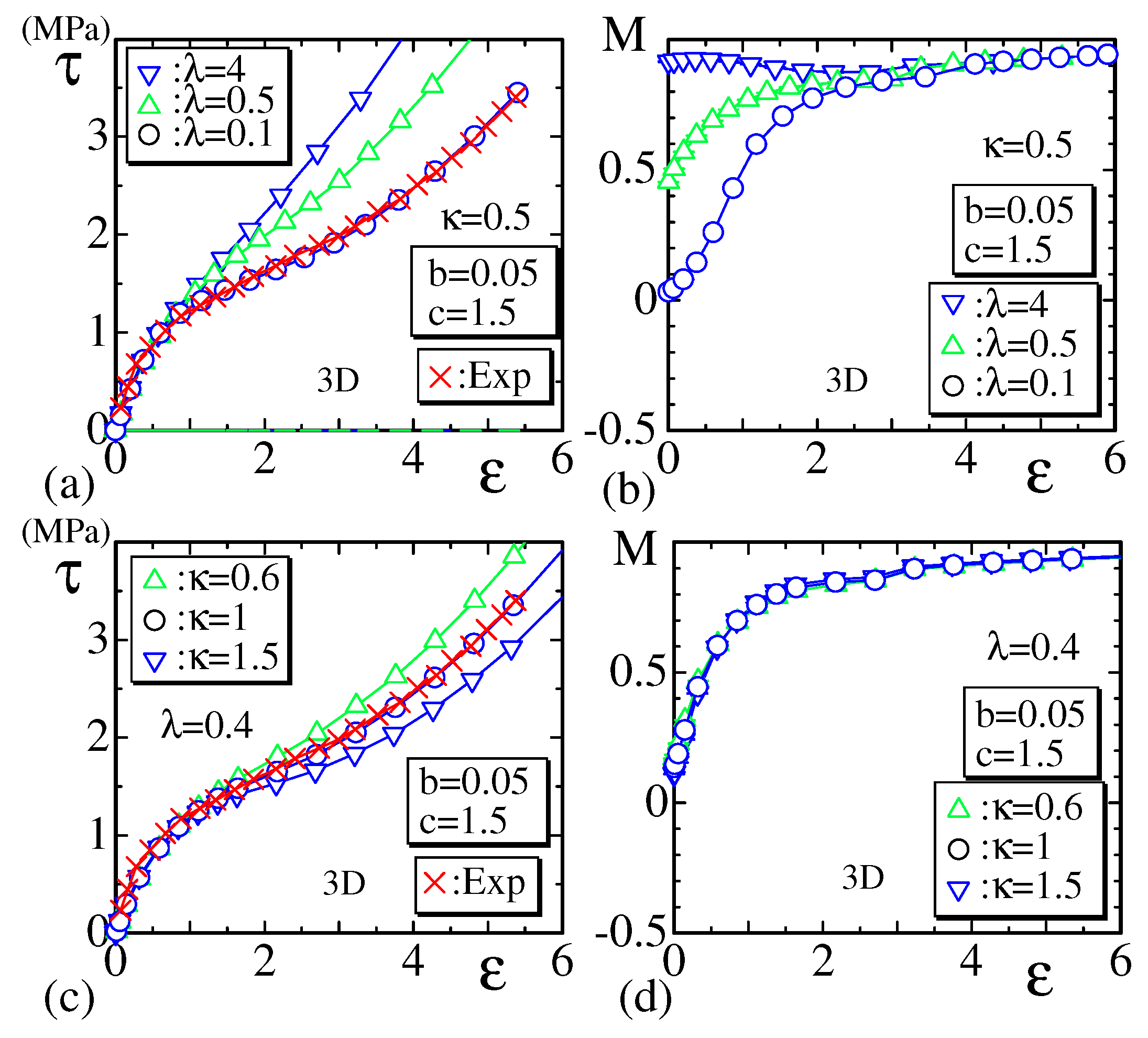
3.1. Stress–Strain Curve and the Order Parameter
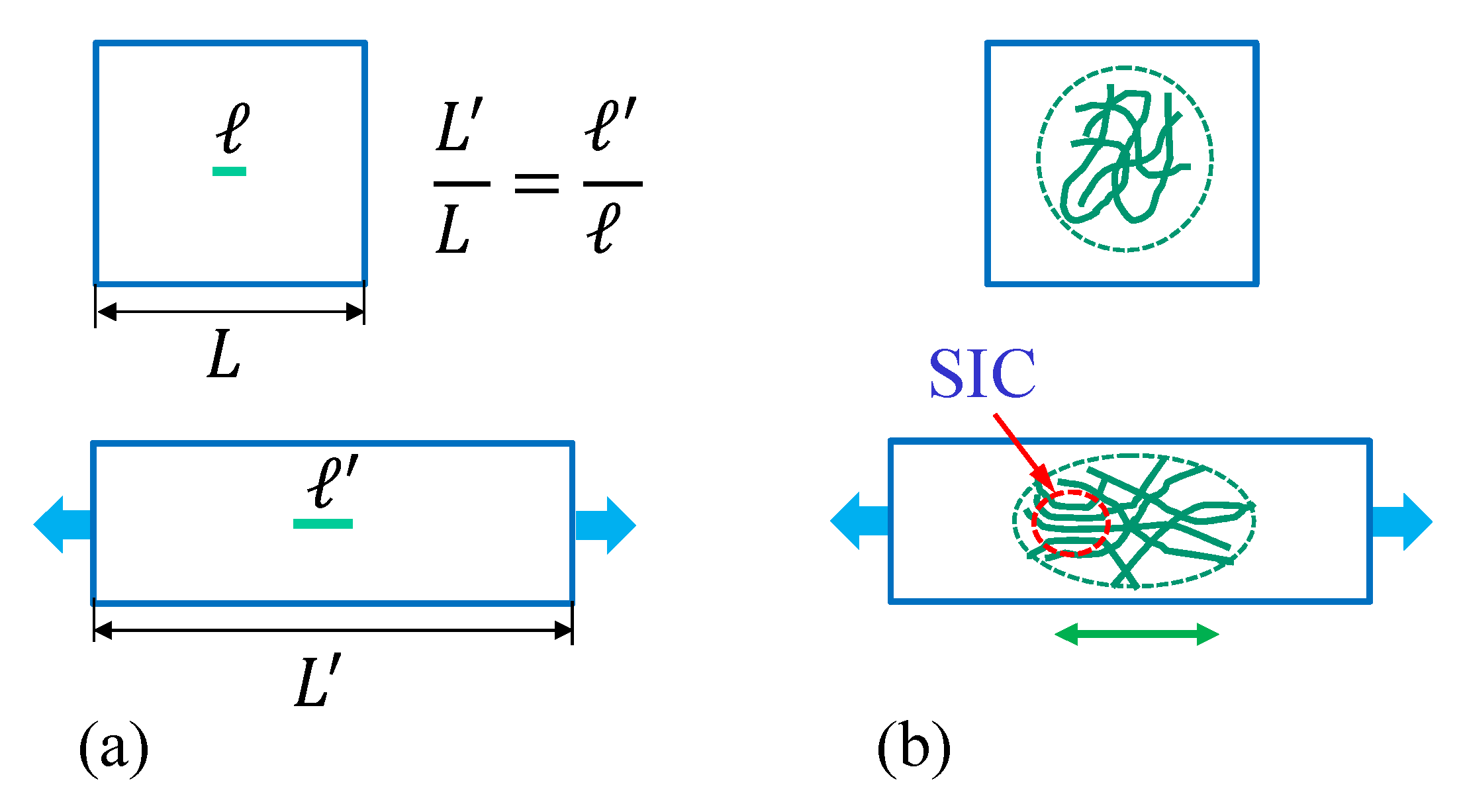
3.2. Simulations for Strain-Induced Crystallization
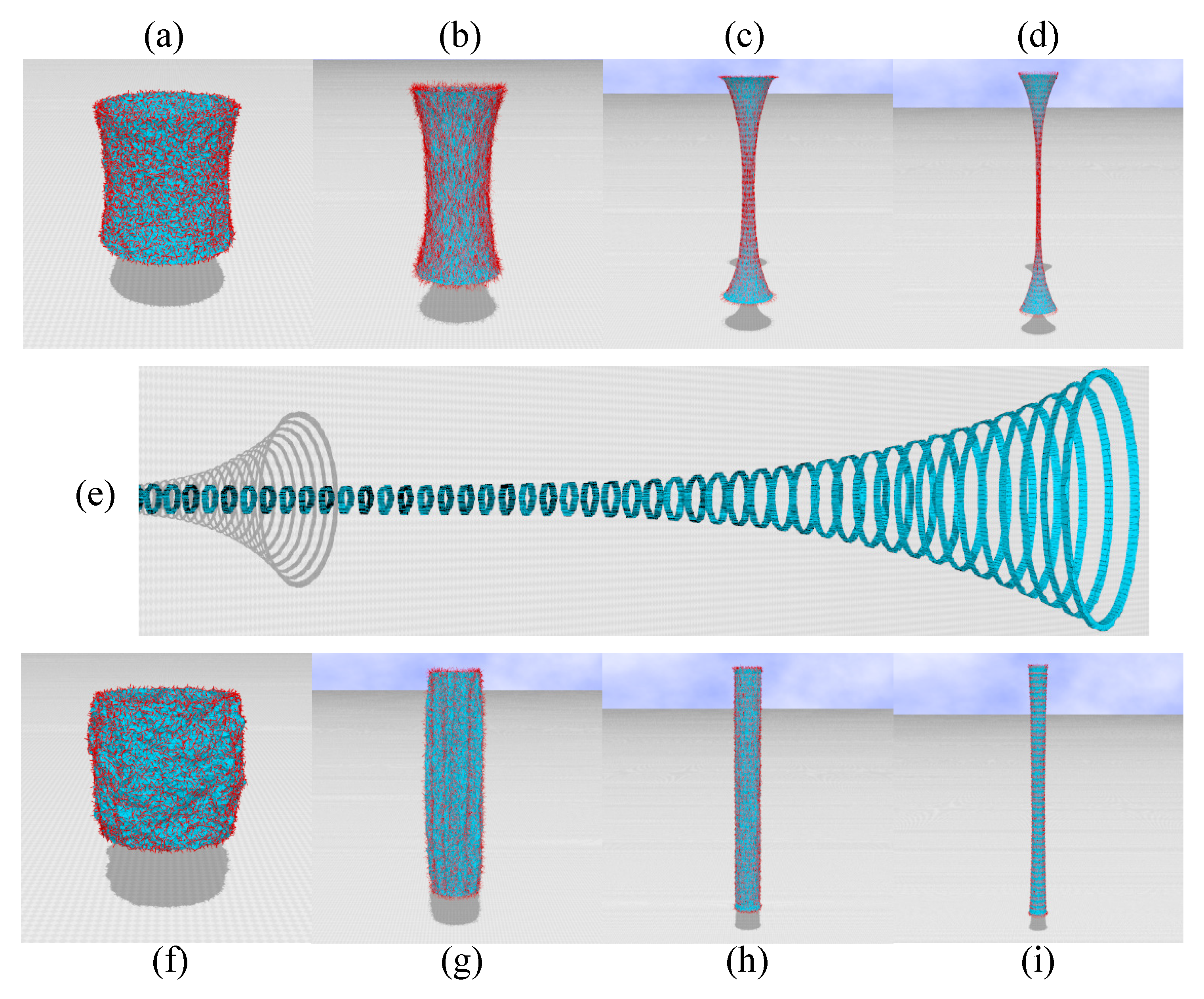
3.3. Lattice Spacing and Snapshots
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
Appendix A. Discretization of the Tensile Energy for the 3D Model
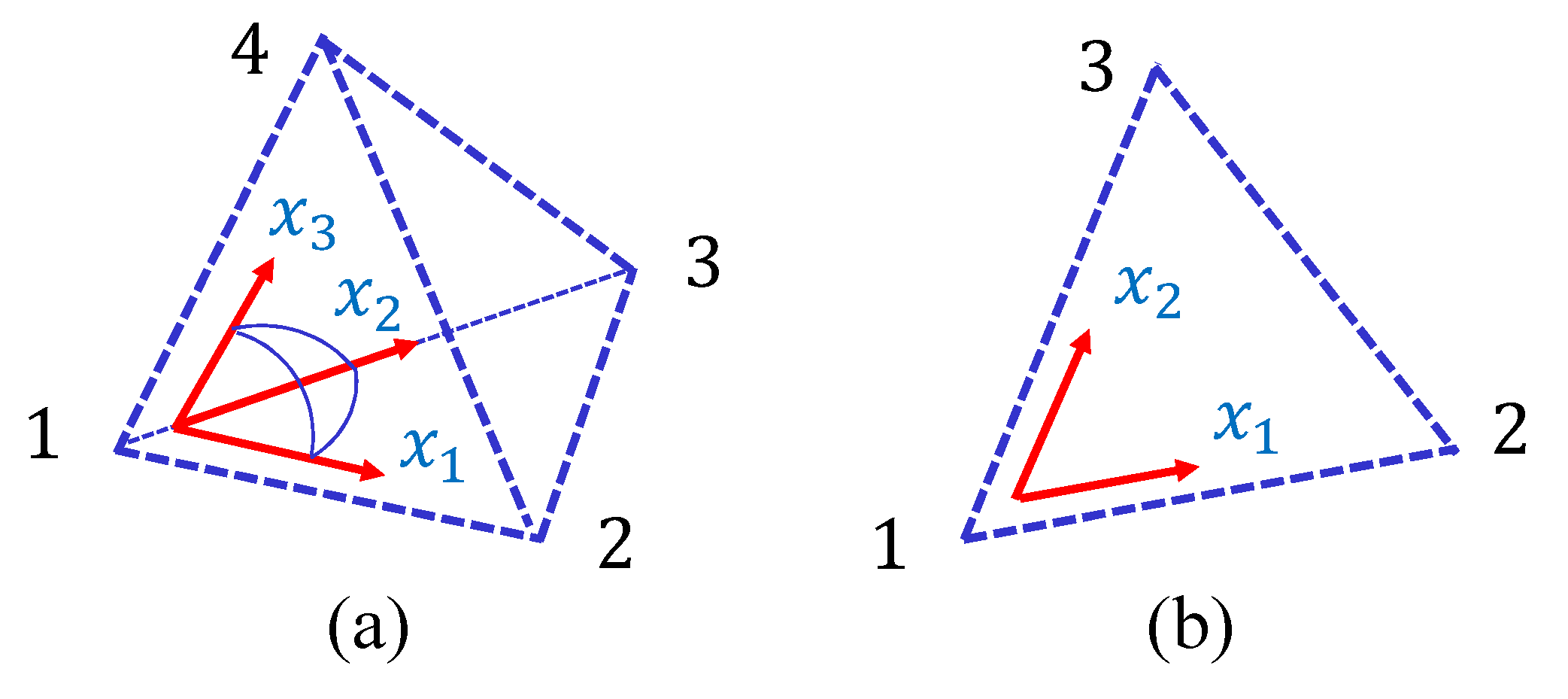
Appendix B. Discretization of the Tensile and Bending Energies for the 2D Model
References and Notes
- Albouy, P.-A. The conformation of poly (dimethylsiloxane) in the crystalline state. Polymer 2000, 41, 3083–3086. [Google Scholar] [CrossRef]
- Imbernon, L.; Puachet, R.; Pire, M.; Albouy, P.-A.; Tencé-Giraut, S.; Norves, S. Strain-induced crystallization in sustainably crosslinked epoxidizednatural rubber. Polymer 2016, 93, 189–197. [Google Scholar] [CrossRef]
- Candau, N.; Chazeau, L.; Chenal, J.-M.; Gauthier, C.; Ferreira, J.; Munch, E.; Rochas, C. Characteristic time of strain induced crystallization of crosslinked natural rubber. Polymer 2012, 53, 2540–2543. [Google Scholar] [CrossRef]
- Toki, S.; Sics, I.; Hsiao, B.S.; Murakami, S.; Tosaka, M.; Poompradub, S.; Kohjiya, S.; Ikeda, Y. Structural developments in synthetic rubbers during uniaxial deformation by in situ synchrotron X-ray diffraction. J. Polym. Sci. B 2004, 42, 956–964. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 3rd ed.; Claredon Press: Oxford, UK, 1975. [Google Scholar]
- Treloar, L.R.G. Rubber elasticity. Contemp. Phys. 1971, 12, 33–56. [Google Scholar] [CrossRef]
- Kuhn, W. Dependence of the average transversal on the longitudinal dimensions of statistical coils formed by chain molecules. J. Polym. Sci. 1946, 1, 380–388. [Google Scholar] [CrossRef]
- Kuhn, W. Beziehungen zwischen Molekülgröse, statistischer Molekülgestalt und elastischen Eigenschaften hochpolymerer Stoffe. Kolloid Z. 1936, 76, 258–271. [Google Scholar] [CrossRef]
- Flory, P.J. Network topology and the theory of rubber elasticity. Polym. Int. 1985, 17, 96–102. [Google Scholar] [CrossRef]
- Tanaka, F. Polymer Physics: Applications to Molecular Association and Thermoreversible Gelation; Cambridge Univ. Press Ithaca: Cambridge, UK, 2011. [Google Scholar]
- James, H.M.; Guth, E. Statistical Thermodynamics of Rubber Elasticity. J. Chem. Phys. 1953, 21, 1039–1048. [Google Scholar] [CrossRef]
- Wall, F.T. Statistical Thermodynamics of Rubber. III. J. Chem. Phys. 1943, 11, 527–530. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical thermodynamics of random networks. Proc. Roy. Soc. Lond. A 1976, 351, 351–380. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell Univ. Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Wall, F.T.; Flory, P.J. Statistical Thermodynamics of Rubber Elasticity. J. Chem. Phys. 1951, 19, 1435–1439. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Mechanics of Swelling of Network Structures. J. Chem. Phys. 1950, 18, 108–111. [Google Scholar] [CrossRef]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials I. Fundamental concepts. Phil. Trans. R. Soc. Lond. Soc. A 1948, 240, 459–490. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. Further depelopements of the general theory. Phil. Trans. R. Soc. Lond. Soc. A 1948, 241, 379–397. [Google Scholar] [CrossRef]
- Deam, R.T.; Edwards, F.R.S. The theory of rubber elasticity. Phil. Trans. Roy. Soc. Lond. 1976, 280, 317–353. [Google Scholar] [CrossRef]
- Urayama, K. An experimentalist’s view of the physics of rubber elasticity. J. Polym. Sci. B 2006, 44, 3440–3444. [Google Scholar] [CrossRef]
- Koibuchi, H.; Sekino, H. Monte Carlo studies of a Finsler geometric surface model. Phys. A 2014, 393, 37–50. [Google Scholar] [CrossRef]
- Osari, K.; Koibuchi, H. Finsler geometry modeling and Monte Carlo study of 3D liquid crystal elastomer. Polymer 2017, 114, 355–369. [Google Scholar] [CrossRef]
- Takano, Y.; Koibuchi, H. J-shaped stress–strain diagram of collagen fibers: Frame tension of triangulated surfaces with fixed boundaries. Phys. Rev. E 2017, 95, 042411. [Google Scholar] [CrossRef]
- Mitsuhashi, K.; Ghosh, S.; Koibuchi, H. Mathematical modeling and simulations for large-strain J-shaped diagrams of soft biological tissues. Polymers 2018, 10, 715. [Google Scholar] [CrossRef] [PubMed]
- Koibuchi, H.; Bernard, C.; Chenal, J.M.; Diguet, G.; Sebald, G.; Cavaille, J.Y.; Takagi, T.; Chazeau, L. Mathematical Modeling of Rubber Elasticity. J. Phys. Conf. Ser. 2018, 1142, 012081. [Google Scholar] [CrossRef]
- Lebwohl, P.A.; Lasher, G. Nematic-Liquid-Crystal Order?A Monte Carlo Calculation. Phys. Rev. A 1972, 6, 426–429. [Google Scholar] [CrossRef]
- Wheater, J.F. Random surfaces: From polymer membranes to strings. J. Phys. A Math. Gen. 1994, 27, 3323–3354. [Google Scholar] [CrossRef]
- Fournier, J.-B.; Barbetta, C. Direct Calculation from the Stress Tensor of the Lateral Surface Tension of Fluctuating Fluid Membranes. Phys. Rev. Lett. 2008, 100, 078103. [Google Scholar] [CrossRef] [PubMed]
- Foty, R.A.; Forgacs, G.; Pfleger, C.M.; Steinberg, M.S. Liquid properties of embryonic tissues: Measurement of interfacial tensions. Phys. Rev. Lett. 1994, 72, 2298–2301. [Google Scholar] [CrossRef] [PubMed]
- Creutz, M. Quarks, Gluons and Lattices; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Schoeberl, J. Netgen Mesh Generator, a Free Software for 3D Meshing. Available online: https://ngsolve.org/ (accessed on 1 January 2016).
- Chern, S.-S. Finsler Geometry Is Just Riemannian Geometry without the Quadratic Restriction. In Notices of the AMS; American Mathematical Society: Providence, RI, USA, 1996; pp. 959–963. [Google Scholar]
- Matsumoto, M. Foundations of Finsler Geometry and Special Finsler Spaces; Kaiseisya: Tokyo, Japan, 1986. [Google Scholar]
- Matsumoto, M. Keiryou Bibun Kikagaku; Shokabo: Tokyo, Japan, 1975. (In Japanese) [Google Scholar]
- Bao, D.; Chern, S.-S.; Shen, Z. An Introduction to Riemann-Finsler Geometry, GTM 200; Springer: New York, NY, USA, 2000. [Google Scholar]
- The variable represents the “mean value” of the direction of the polymer chains at a given point in the material, and this mean direction is identical to that expressed by . For this reason, the directions are represented by the left-right arrows in Figure 4c.
- Helfrich, W. Elastic Properties of Lipid Bilayers: Theory and Possible Experiments. Z. Naturforsch C 1973, 28, 693–703. [Google Scholar] [CrossRef]
- Polyakov, A.M. Fine structure of strings. Nucl. Phys. B 1986, 268, 406–412. [Google Scholar] [CrossRef]
- Kantor, Y.; Karder, M.; Nelson, D.R. Tethered surfaces: Statics and dynamics. Phys. Rev. A 1987, 35, 3056–3071. [Google Scholar] [CrossRef] [PubMed]
- Kantor, Y.; Nelson, D.R. Phase Transitions in Flexible Polymeric Surfaces. Phys. Rev. A 1987, 36, 4020–4032. [Google Scholar] [CrossRef] [PubMed]
- Bowick, M.; Travesset, A. The statistical mechanics of membranes. Phys. Rep. 2001, 344, 255–308. [Google Scholar] [CrossRef]
- Wiese, K.J. Polymerized Membranes, a Review. In Phase Transitions and Critical Phenomena 19; Domb, C., Lebowitz, J.L., Eds.; Academic Press: London, UK, 2000; pp. 253–498. [Google Scholar]
- Nelson, D. The Statistical Mechanics of Membranes and Interfaces. In Statistical Mechanics of Membranes and Surfaces, 2nd ed.; Nelson, D., Piran, T., Weinberg, S., Eds.; World Scientific: Singapore, 2004; pp. 1–17. [Google Scholar]
- Gompper, G.; Kroll, D.M. Triangulated-surface Models of Fluctuating Membranes. In Statistical Mechanics of Membranes and Surfaces, 2nd ed.; Nelson, D., Piran, T., Weinberg, S., Eds.; World Scientific: Singapore, 2004; pp. 359–426. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- David, F. Geometry and Field Theory of Random Surfaces and Membranes. In Statistical Mechanics of Membranes and Surfaces, 2nd ed.; Nelson, D., Piran, T., Weinberg, S., Eds.; World Scientific: Singapore, 2004; pp. 149–209. [Google Scholar]
- Stress is normally expressed by the symbol σ, however, this symbol σ is already used for the directional degree of freedom of polymers. For this reason, the symbol τ is used instead of σ for stress in this paper.
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Landau, D.P. Finite-size behavior of the Ising square lattice. Phys. Rev. B 1976, 13, 2997–3011. [Google Scholar] [CrossRef]
- Pradhan, S.; Costa, F.R.; Wagenknecht, U.; Jehnichen, D.; Bhowmick, A.K.; Heinrich, G. Elastomer/LDH nanocomposites: Synthesis and studies on nanoparticle dispersion, mechanical properties and interfacial adhesion. Eur. Polym. J. 2008, 44, 3122–3132. [Google Scholar] [CrossRef]
- The high-precision number assumed for c does not always imply that the results are very sensitive to c. In the simulation program, the parameter c′(=(2/3)c) was used instead of c. As a result, the simple input numbers c′ = 0.7 and c′ = 0.03 turn to be c = 1.05 and c = 0.045, respectively.
- Shahedifar, V.; Rezadoust, A.M. Thermal and mechanical behavior of cotton/vinyl ester composites: Effects of some flame retardants and fiber treatment. J. Reinf. Plast. Compos. 2013, 32, 681–688. [Google Scholar] [CrossRef]
- Kawano, Y.; Wang, Y.; Palmer, R.A.; Aubuchon, S.R. Stress-Strain Curves of Nafion Membranes in Acid and Salt Forms. Polim. Cienc. Tecnol. 2002, 12, 96–101. [Google Scholar] [CrossRef]
- In the hysteresis simulation for the variation of the strain ϵ, the final configuration of the previous simulation is used as an input of the following simulation, where the total number of Monte Carlo sweep is always kept small so that the configuration may not be convergent.
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koibuchi, H.; Bernard, C.; Chenal, J.-M.; Diguet, G.; Sebald, G.; Cavaille, J.-Y.; Takagi, T.; Chazeau, L. Monte Carlo Study of Rubber Elasticity on the Basis of Finsler Geometry Modeling. Symmetry 2019, 11, 1124. https://doi.org/10.3390/sym11091124
Koibuchi H, Bernard C, Chenal J-M, Diguet G, Sebald G, Cavaille J-Y, Takagi T, Chazeau L. Monte Carlo Study of Rubber Elasticity on the Basis of Finsler Geometry Modeling. Symmetry. 2019; 11(9):1124. https://doi.org/10.3390/sym11091124
Chicago/Turabian StyleKoibuchi, Hiroshi, Chrystelle Bernard, Jean-Marc Chenal, Gildas Diguet, Gael Sebald, Jean-Yves Cavaille, Toshiyuki Takagi, and Laurent Chazeau. 2019. "Monte Carlo Study of Rubber Elasticity on the Basis of Finsler Geometry Modeling" Symmetry 11, no. 9: 1124. https://doi.org/10.3390/sym11091124
APA StyleKoibuchi, H., Bernard, C., Chenal, J.-M., Diguet, G., Sebald, G., Cavaille, J.-Y., Takagi, T., & Chazeau, L. (2019). Monte Carlo Study of Rubber Elasticity on the Basis of Finsler Geometry Modeling. Symmetry, 11(9), 1124. https://doi.org/10.3390/sym11091124







