Fully Automatic Facial Deformation Transfer

Abstract

Facial Animation is a serious and ongoing challenge for the Computer Graphic industry. Because diverse and complex emotions need to be expressed by different facial deformation and animation, copying facial deformations from existing character to another is widely needed in both industry and academia, to reduce time-consuming and repetitive manual work of modeling to create the 3D shape sequences for every new character. But transfer of realistic facial animations between two 3D models is limited and inconvenient for general use. Modern deformation transfer methods require correspondences mapping, in most cases, which are tedious to get. In this paper, we present a fast and automatic approach to transfer the deformations of the facial mesh models by obtaining the 3D point-wise correspondences in the automatic manner. The key idea is that we could estimate the correspondences with different facial meshes using the robust facial landmark detection method by projecting the 3D model to the 2D image. Experiments show that without any manual labelling efforts, our method detects reliable correspondences faster and simpler compared with the state-of-the-art automatic deformation transfer method on the facial models.

1. Introduction

Character modeling, especially character facial modeling, plays a pivotal role in computer graphics and computer animation. Copying facial deformations from one character to another is widely needed in both industry and academia, to replace time consuming modeling work to create the shape sequences for every new character. The main limitation of current deformation transfer methods is the dependence on tedious work to get the reliable correspondence map between the source character and the new target character. The existing state-of-the-art method introduced by Sumner et al. [1] for geometry-based deformation transfer reply on the point-wise correspondences between source and target models.

Therefore, the research on automatically detecting the correspondences between source and target characters, then employing the skin deformation method [1] to fully automatically obtain high-quality deformation transfer results becomes very important in computer modeling and animation to reuse the existing dataset for generating new shapes and reduce tedious time cost of artists. To achieve this, [2] exploits the learning capability of deep neural networks to learn how shapes deform naturally from a given dataset, provide a differentiable metric measuring visual similarity and build reliable mapping between the latent spaces with cycle-consistency, including proposes a mesh-based convolutional variational auto-encoder (VAE) to encode a shape set with flexible deformations in a compact latent space, a differentiable network to measure visual similarity, and a cycle-consistent GAN for reliable mapping between latent spaces. The automatic deformation transfer method by VC-GAN neural networks introduced in Gao et al. [2] is able to copy deformations from source shapes to a given target mesh, but sometimes causes obvious artefacts and is less accurate in localized areas of detailed facial deformations, as shown in Figure 6c, the artefacts highlighted in boxes are caused by Gao et al. [2] when it transfers the localized subtle face deformation from source character.

To tackle the above problem for transferring subtle detailed facial deformations, in this paper, we propose one straight forward approach to automatically obtain the 3d point-wise correspondences on source and target faces without any manual work. Two mapping processes are employed to obtain the 3D point-wise correspondences, (1) we project the 3D source and target character to 2D images, which are produced by the front view orthographic projection, then the facial feature detection technique is employed to extract the same set of 2D landmarks on both source and target character; (2) these 2D landmarks are inversely mapped back with accurate corrections for the eye and mouth areas, to finally obtain the 3D point-wise correspondences.

Aimed at facial deformation transfer, experiments show that our method fully automatically creates high-quality correspondences between source and target faces, is able to obtain believable deformations transferred much faster, and is simpler than the state-of-the-art automatic deformation transfer method presented in [2].

2. Related Work

Shape deformation plays a very critical role in character modeling and animation filed, especially facial shape deformation, how to quickly create high fidelity expressions for different characters is still one active research topic and in great demand from industry. A comprehensive review about different facial modeling and animation approaches are introduced by Noh et al. [3] and Li et al. [4]. The research to improve face modeling and animation generally includes: (1) produce realistic face animation, (2) can reach real-time performance, (3) reduce manual work by automatic approach, and (4) can be transferred and adapted to different faces.

Mastering facial animation is a long-standing challenge in computer animation and computer graphics. The face is a very important part in expressing one character’s emotions, their state of mind, and to indicate their future actions. Audiences are naturally and particularly trained to notice subtle characteristics of faces and identify different hint from faces (Cao et al. [5]). Research of facial modeling and animation includes two major types, one type is geometric manipulations-based and the other is image manipulation-based. Geometric manipulations include key-framing and geometric interpolations, parameterizations Cohen et al. [6], finite element methods Basu et al. [7], muscle-based modeling Pieper et al. [8], visual simulation using pseudo muscles (Magnenat et al. [9]), spline models (Wang et al. [10]) and free-form deformations (Kalra et al. [11]). Image manipulations include image morphing between photographic images (Ucicr et al. [12]), image blending (Pighin et al. [13]), and vascular expressions (Kalra et al. [14]).

Presently, facial deformation and animation are often produced by feature tracking (Li et al. [15]) or performance driven. In the research of face modelling, analysis and reconstruction, the landmark papers of Eigenfaces Turk et al. [16] and Active Shape Models Cootes et al. [17] were to define the research landscape for years to come. Romdhani et al. [18] present a novel algorithm aiming to estimate the 3D shape, the texture of a human face, along with the 3D pose and the light direction from a single photograph by recovering the parameters of a 3D morphable model. Generally, the algorithms tackling the problem of 3D shape estimation from image data use only the pixels intensity as input to drive the estimation process. Bas et al. [19] explores the problem of fitting a 3D morphable model to single face images using only sparse geometric features (edges and landmark points). Hu et al. [20] present an efficient stepwise 3DMM-to-2D image-fitting procedure by the optimisation process involves all the pixels of the input image, rather than randomly selected subsets, which enhances the accuracy of the fitting.

Sumner et al. [1] performed pioneering work for deformation transfer between different meshes. Local shape deformation is represented using deformation gradients, which are transferred from the source to the target shapes. This proposed approach brings one piratical approach to clone facial expressions to new characters but requires point-wise correspondences between source and target shapes. Semantic deformation transfer introduced in Baran et al. [21] preserves the semantic characteristics of the motion instead of its literal deformation with a shape space that enables interpolation and projection with standard linear algebra. Given several example mesh pairs, semantic deformation transfer infers a correspondence between the shape spaces of the two characters. This enables automatic transfer of new poses and animations. However, it needs paired source and target shapes. Chu et al. [22] present an example-based deformation transfer method to solve the above limitation. With the aid of a few target examples, the characteristic deformations of transferred target models are recovered. To minimize manual effort on the correspondences, Yang et al. [23] also proposes a novel algorithm by adapting a biharmonic weight deformation framework which is able to produce plausible deformation even with only a few key points, although the corresponding points on the target shape still require to be manually specified. Therefore, the research on fully automatic skin deformation method to obtain high-quality deformation transfer results becomes very important in computer modeling and animation to reuse the existing dataset for generating new shapes and reduce tedious time cost of artists. To achieve this, one state-of-the-art automatic algorithm to deform target shapes by VC-GAN neural networks is introduced in Gao et al. [2] to obtain high-quality deformation transfer results for a given character.

3. Our Approach

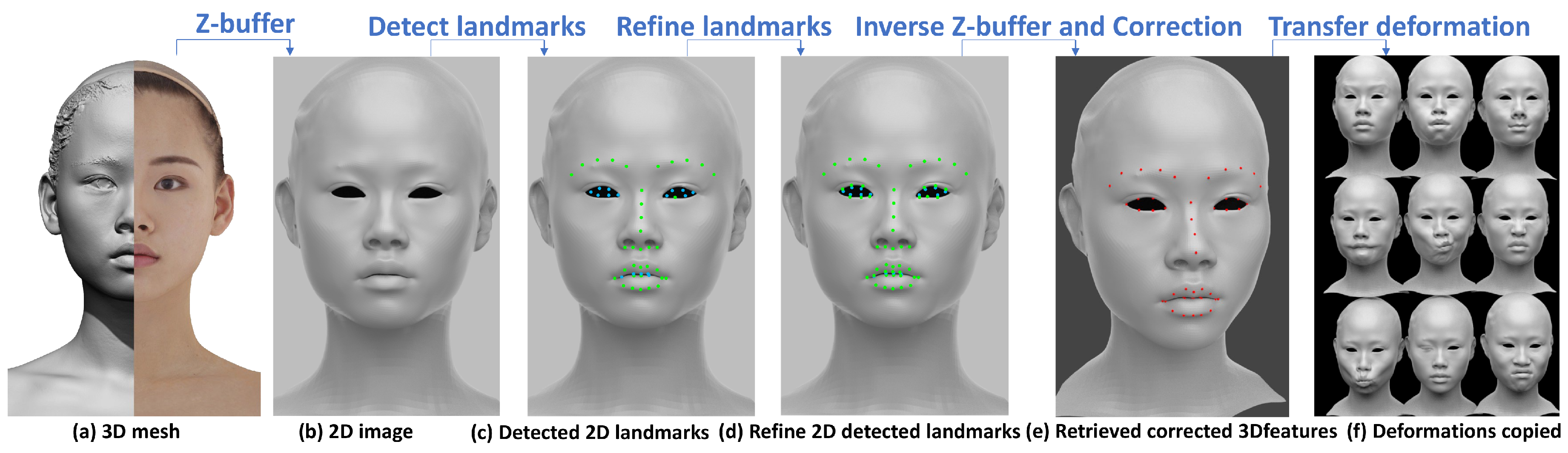
Our approach consists of three steps to extract the point-wise correspondences from the source facial mesh to the target facial mesh, including: project 3D mesh to 2D space; detect and refine to valid 2D facial landmarks; retrieve 3D point-wise correspondences and correct the eyes and mouth feature points, as shown in Figure 1a–e.

Figure 1a shows one girl’s scanned 3D model, after non-rigid registration, we obtain one cleaned mesh and the scaled orthographic projection is employed to project this mesh to one front view image, as shown in Figure 1b. Then, 68 face landmarks are detected by the OpenCV cascade facial landmark detector, according to experiments, our approach only use 46 points of them as shown in Figure 1c to avoid noise and keep transfer quality. In Figure 1c, the green landmarks are viewed as valid pixels which has corresponding vertex information and is a point on the 3D model surface. But the blue landmarks are viewed as invalid pixels, which need to be refined and find the nearest valid pixel instead, the refinement result of landmarks are shown in Figure 1d, especially the eye and mouth area. Then, inverse Z-buffer are used to retrieve the feature points on the 3D model surface from each landmark in 2D image after the refinement. The feature points obtained so far are not reasonable, for example, the eye corner point. In this case, Principal component analysis (PCA) is used to obtain the principle axes of the eye feature points to correct the eye corner feature points’ position, as shown form Figure 1d,e.

After that, the same set of feature points of another different characters’ face are obtained by the same process and the point-wise correspondence between different character face is achieved for deformation transfer. The deformations copied from our existing expression dataset to this girl face model is showed in Figure 1f. More experiments of deformation transfered from existing dataset to different characters can be seen in Figure 4.

3.1. Convert 3D Mesh to 2D Space

Several projection approaches can be employed to convert 3D facial shapes to 2D images, but here we chose the scaled orthographic projection, because it constrains the space of possible transformations to the space of rigid motions in Euclidean space and additionally allows for scaling [24].

We use $\mathcal{S}$ to denote the source shape or the target shape. Let $\mathcal{F}$ be the faces of source or target shape, here the source and target shape can have a different topology.

Then, we compute the 2D space pixel information ${\mathit{z}}_{ij}=\{f_k,L_0,L_1,L_2\}$ by Z-buffer algorithm, where ${\mathit{z}}_{ij}$ stores the face $f_k$ and barycentric coordinates $L_0$, $L_1$ and $L_2$ on the face where $\mathcal{Z}$ is satisfied with Equation (1).

$$\mathcal{Z}(L_0{\mathit{x}}_0+L_1{\mathit{x}}_1+L_2{\mathit{x}}_2)<=\mathcal{Z}\left(\mathit{x}\right),\forall \mathit{x}\in \partial \mathcal{S}$$

(1)

Here, ${\mathit{x}}_0,{\mathit{x}}_1$ and ${\mathit{x}}_2$ are vertices of $f_k$, and $\mathit{x}$ is a point on the surface $\partial \mathcal{S}$. If a pixel is not projected by any point, we simply let ${\mathit{z}}_{ij}=\{-1,0,0,0\}$. And these pixels are viewed as invalid pixels.

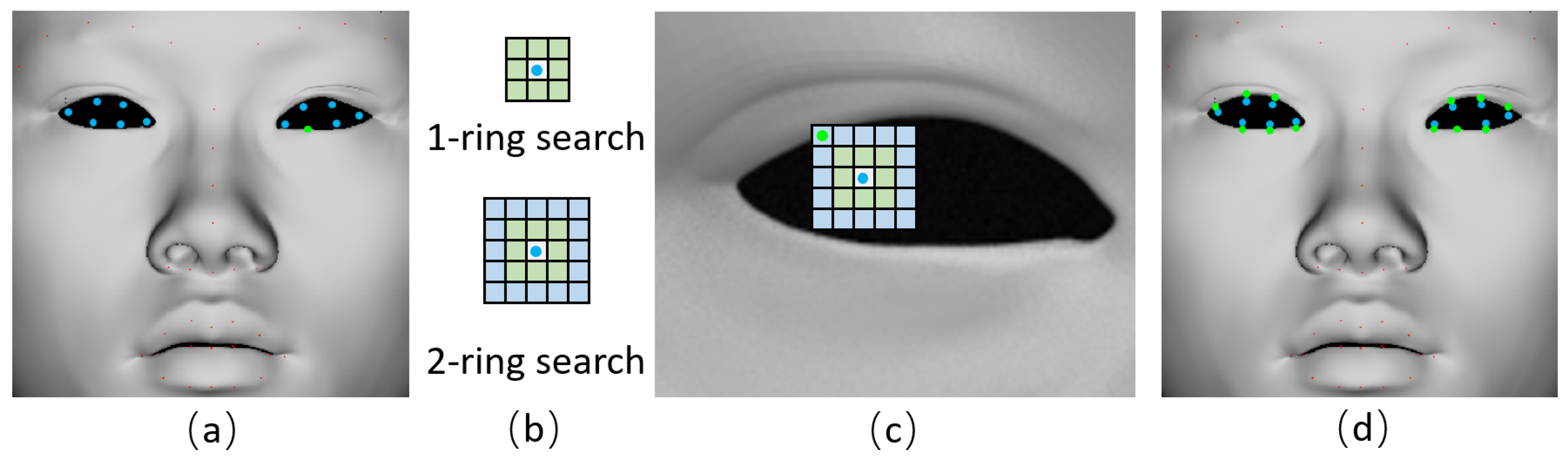
3.2. Detect and Refine the 2D Facial Landmarks

In Section 3.1, we get the 2D orthographic-view images of source and target shape. Here, the Supervised Descent Method [25] is used to detect the 2D facial landmarks [26], as shown in Figure 1c. We can see some detected 2D landmarks are located at invalid pixels like the blue pixels in Figure 2a, in this case, we need to refine them to valid pixels by the nearest search, starting from $1-\mathrm{ring}$ search to $n-\mathrm{ring}$, until finding the valid pixel satisfying $f_k\ne -1,f_k\in {\mathit{z}}_{ij}$, as shown in Figure 2b,c. Figure 2d shows that the initial detected invalid pixels (blue dots) are refined to valid facial landmarks (green dots).

3.3. Retrieve 3D Point-Wise Correspondences

After moving every detected 2D landmark $l_i$ to valid pixel ${\widehat{l}}_i$, we use the inverse Z-buffer process to get projection information of each pixel $p_{ij}$:

$$\{f_k,L_0,L_1,L_2\}={\mathcal{Z}}^{-1}\left(p_{ij}\right),p_{ij}\in \widehat{\mathcal{L}}$$

(2)

The 3D point-wise feature ${\mathit{v}}_i$ is the vertex within $f_k$ and has the largest coefficient of $max(L_0,L_1,L_2)$. Therefore, ${\mathit{v}}_i$ is the 3D feature point index calculated from each valid 2D landmark $\widehat{\mathcal{L}}$.

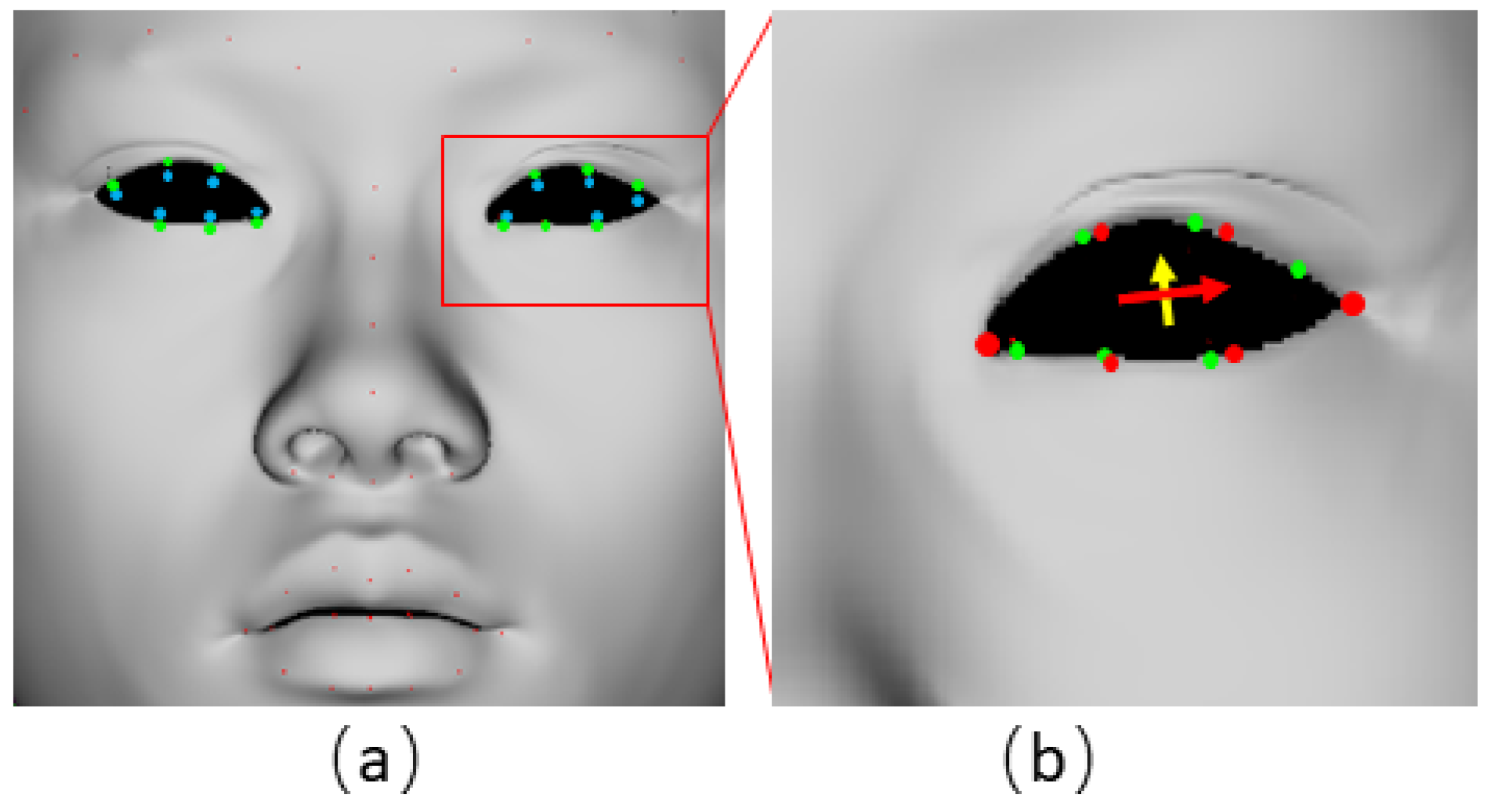
Figure 3a shows some obtained 3D feature points (green dots) obtained are still not all in the reasonable locations, especially around the eyes and mouth. In order to correct these feature points, firstly we calculate the current green features’ center of each eye or mouth, to search the closest edge circle.

Then Principal component analysis (PCA) is utilized to obtain the principle axes of the circle vertices. As shown in Figure 3b, the first principle vector (red arrow) is regarded as the width axis of the eye, which is used to determine the two eye corner feature points (large red dots). And among the other two vectors, the one has smaller angle with the circle plane is regarded as the height axis (yellow arrow) to determine the other interval feature points (red dots). After the correction, all 3D facial feature points $\mathcal{V}$ are obtained correctly from green dots to red dots, shown as Figure 3b. The same correction process are applied for both eye circles and mouth circle, the final 3D facial feature points retrieved can be seen in Figure 1e.

The same set of 3D facial feature points obtained on both source and target face shapes are regarded as the point-wise correspondence for transferring the deformations of existing source dataset to the target face.

3.4. Deformation Transfer

Our approach utilizes one mesh-based effective deformation transfer algorithm introduced by Sumner et al. [1] to copy deformations from one model onto another, regardless of topology or vertices’ number. This algorithm treat the shape deformation as a set of affine transformations of each vertex on the source model as below:

$$Q{v}_i+d={\tilde{v}}_i,i\in 1\dots 4$$

(3)

where Q denotes the rotation matrix and d denotes the translation vector. $v_i$ and ${\tilde{v}}_i$ represent vertices of each triangle face on original and deformed mesh, with $v_4$ is introduced in the direction perpendicular to the triangle. The forth vertex $v_4$ is computed by

$$v_4=v_1+(v_2-v_1)\times (v_3-v_1)/\sqrt{|(v_2-v_1)\times (v_3-v_1)|}$$

(4)

Here, Equation (3) can be written as $QV=\tilde{V}$, therefore, the affine transformation Q can be computed by

$$Q=\tilde{V}{V}^{-1}$$

(5)

Then $S_1,\dots ,S_{\left|s\right|}$ are used to encode the affine transformation of each triangle face on source mesh, and $T_1,\dots T_{\left|t\right|}$ encode the deformations of target mesh. In order to transfer the deformations of source mesh onto the target mesh. One constrained optimization problem for the target affine transformations need to be solved:

$$\underset{T_1+d_1...T_{\left|T\right|}+d_{\left|T\right|}}{min}\sum _{j=1}^{\left|M\right|}\left|\right|S_{s_j}-T_{t_j}{\left|\right|}_F^2,subjectto:T_j{v}_i+d_j=T_k{v}_i+d_k\vee i,\vee j,k\in p\left(v_i\right).$$

(6)

It means the target triangle face indexed with $t_i$ will deform like the source triangle $s_j$, where the mapping between source mesh $S_{s_j}$ and target mesh $T_{t_j}$ can be computed by the point-wise correspondences from a small set of user selected marker points on source and target meshes. However manually selecting marker points is very time-consuming repetitive work which makes the deformation transfer algorithm inconvenient for general use.

In our approach, we solve the above problem using the robust facial landmark detection method by projecting the 3D model to the 2D image, to automatically estimate the correspondences with different facial meshes. Specifically, the same feature points pattern is detected both on source and target character to obtain the 3D point-wise correspondences. Then, the deformation transfer algorithm introduced by Sumner et al. [1] is utilized to copy the deformations from source mesh onto target mesh.

4. Experiments and Comparisons

Our experiments to evaluate the quality of the 3D correspondence feature points obtained by our method are carried out on a computer with an i7 8650U CPU, 16GB RAM, and Intel(R) UHD Graphics 620.

Figure 4 shows the facial movements copied to three target characters whose number of vertices are 28,426, 11,780 and 11,676 from source shape (9127 verts). The first row in Figure 4 shows the existing character expression dataset used as source shapes, the second to forth rows in Figure 4a illustrate three target characters’ neutral pose and point-wise feature correspondence obtained (red dots), the second to forth rows in Figure 4b demonstrate the deformations copied automatically from source dataset. Without any multi-threading, our running time of detecting 3D correspondences of the target faces from the second row to forth row in Figure 4a are 0.343 s, 0.335 s and 0.327 s respectively. Then, 2.228 s, 1.218 s, and 1.159 s to transfer 9 deformations, as shown in

Table 1. The running time of detecting 3D correspondence on different faces with different topology and the running time of deformation transfer for each expression.

Models	Source Face	Girl Face	Female Face	Male Face
Polygon Verts	9127	28,426	11,780	11,676
Detecting 3D correspondence	0.115 s	0.343 s	0.335 s	0.327 s
Deformation transfer	–	0.248 s	0.135 s	0.129 s

.

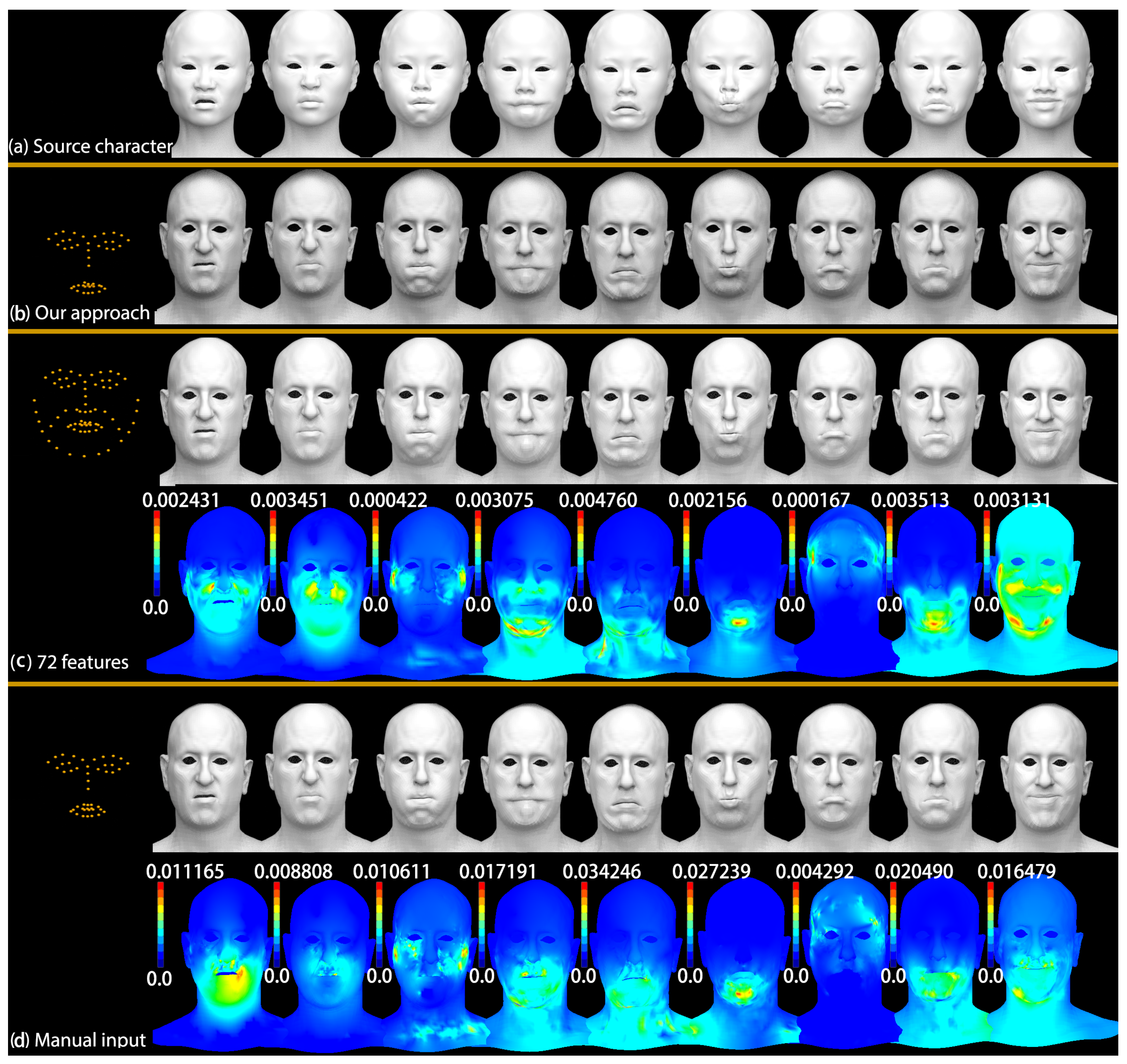
We compare the deformation transfer results obtained from the 46 features determined by our algorithm, manual corrected features (46 features), and more features (72 features), as shown in Figure 5. Figure 5a shows the source character shapes. Figure 5b shows the deformation transfer results by our proposed approach with automatically detected 46 corresponding feature points. The first row of Figure 5c shows the results created by supervised selection of more corresponding points (72 features); the color map for each expression in the second row is the quantitative comparison to show the differences between our approach and supervised selection of 72 features, the Maximum Vertex Errors (MVEs) between them are 0.002431, 0.003451, 0.000422, 0.003075, 0.004760, 0.002156, 0.000167, 0.003513 and 0.003131 respectively. Figure 5d shows the results produced by the manually labeling 46 corresponding feature points; the color map for each expression in the second row is also the quantitative comparison to show the differences between our approach and manually labeling 46 features, the Maximum Vertex Errors (MVEs) between them are 0.011165, 0.008808, 0.010611, 0.017191, 0.034246, 0.027239, 0.004292, 0.020490, and 0.016479, respectively. The above experiments illustrate that our approach can produce competitive results with manual efforts, and much more feature points can not promote the effect significantly, the differences between them can hardly be seen visually.

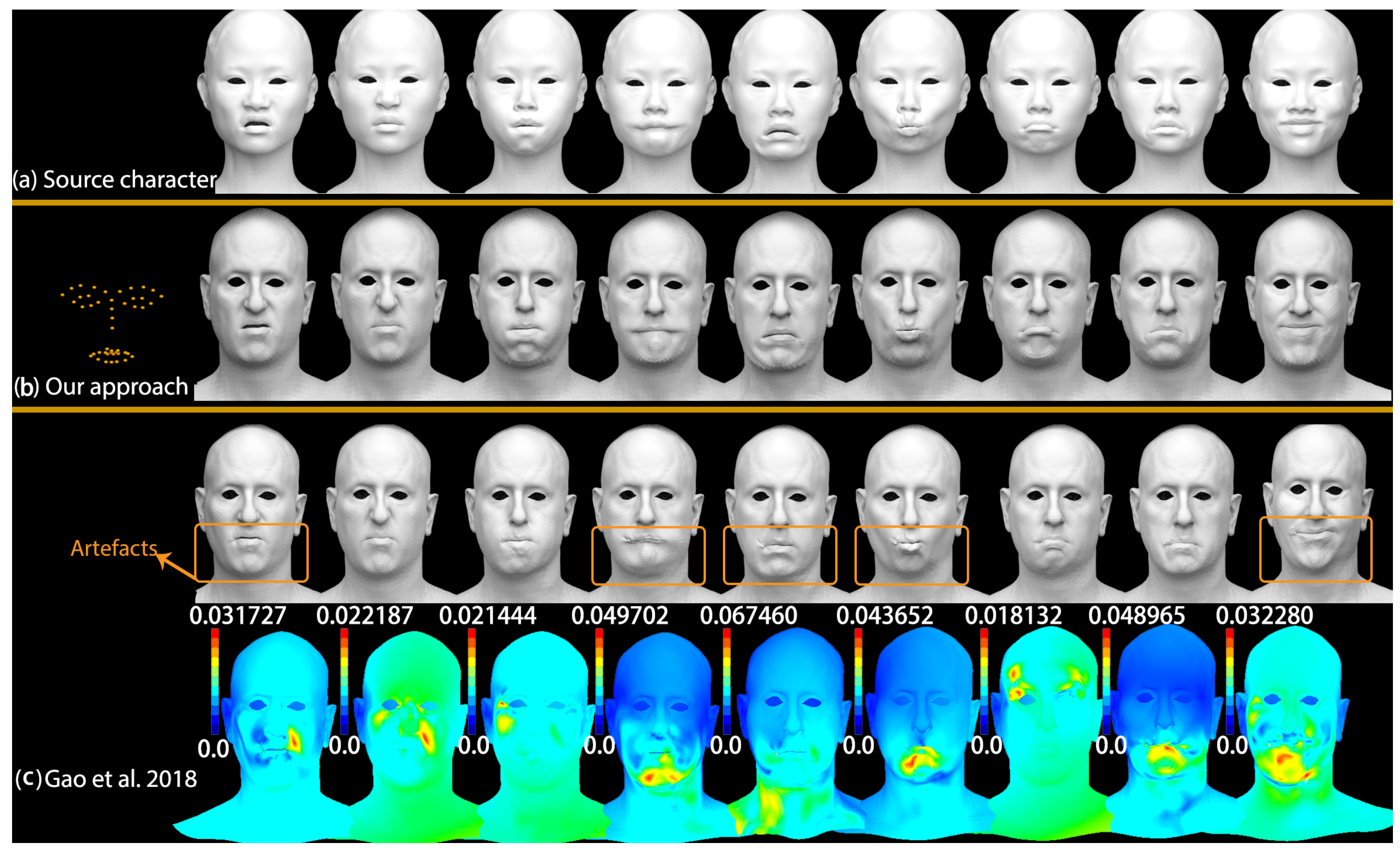
One state-of-the-art automatic algorithm to deform target shapes by VC-GAN neural networks introduced in Gao et al. [2] can obtain high-quality global deformation transfer results for a given character’s deformations, but causes obvious artefacts and is less accurate with the localized subtle detailed facial deformations as shown in Figure 6. Figure 6a shows the source character shapes. Figure 6b shows the deformation transfer results by our proposed approach with automatically detected 46 corresponding feature points. The first row of Figure 6c shows the results created by Gao et al. [2], the artefacts can be seen in several localized areas; the color map for each expression in the second row shows the differences between our approach and Gao et al. [2], the Maximum Vertex Errors (MVEs) between them are 0.031727, 0.022187, 0.021444, 0.049702, 0.067460, 0.043652, 0.018132, 0.048965 and 0.032280 respectively.

In this experiment, using the same source (28,426 vertices) mesh with 14 training examples and target (8150 vertices) mesh with 12 training examples, Gao et al. [2] takes more than one hour to train the VAE, SimNet and CycleGAN. After this off-line training, it can do the deformation transfer for each mesh in 10 ms. In contrast, without any optimization, our method does not need a training process with hours, and the computing time to detect the 3D feature correspondences of source (28,426 vertices) and target (8150 vertices) in Figure 6 is 0.670 s totally.

5. Conclusions

Facial Animation is a serious and ongoing challenge for the Computer Graphic industry. Because diverse and complex emotions need to be expressed by different facial deformation and animation, copying facial deformations from existing character to another is widely needed in both industry and academia to reduce time-consuming and repetitive manual work.

In this paper, we focused on the specific topic of feasible facial deformation transfer, in order to reuse the existing face expressions dataset and full automatically copy the deformations to new characters, we employ the facial image landmark detection algorithm to find the 3D facial feature correspondences between source and target characters by projecting the 3D face orthogonally 2D and establish the correspondence in 2D first and then map back to 3D.

The experiments demonstrate that our proposed method provides a very simple and effective way to achieve high-quality, believable and competitive deformation transfer results without any manual work. Several improvements can be made in the future. First, we will extend our method to more generic model, for example human body, hand or animal model. And iterations will be introduced to approach and approximate the real deformations to reduce errors.