Parametric Jensen-Shannon Statistical Complexity and Its Applications on Full-Scale Compartment Fire Data
Abstract
1. Introduction
2. Theoretical Background and Remarks
2.1. Entropy and Statistical Complexity
2.2. Extraction of the Underlying Probability Distribution
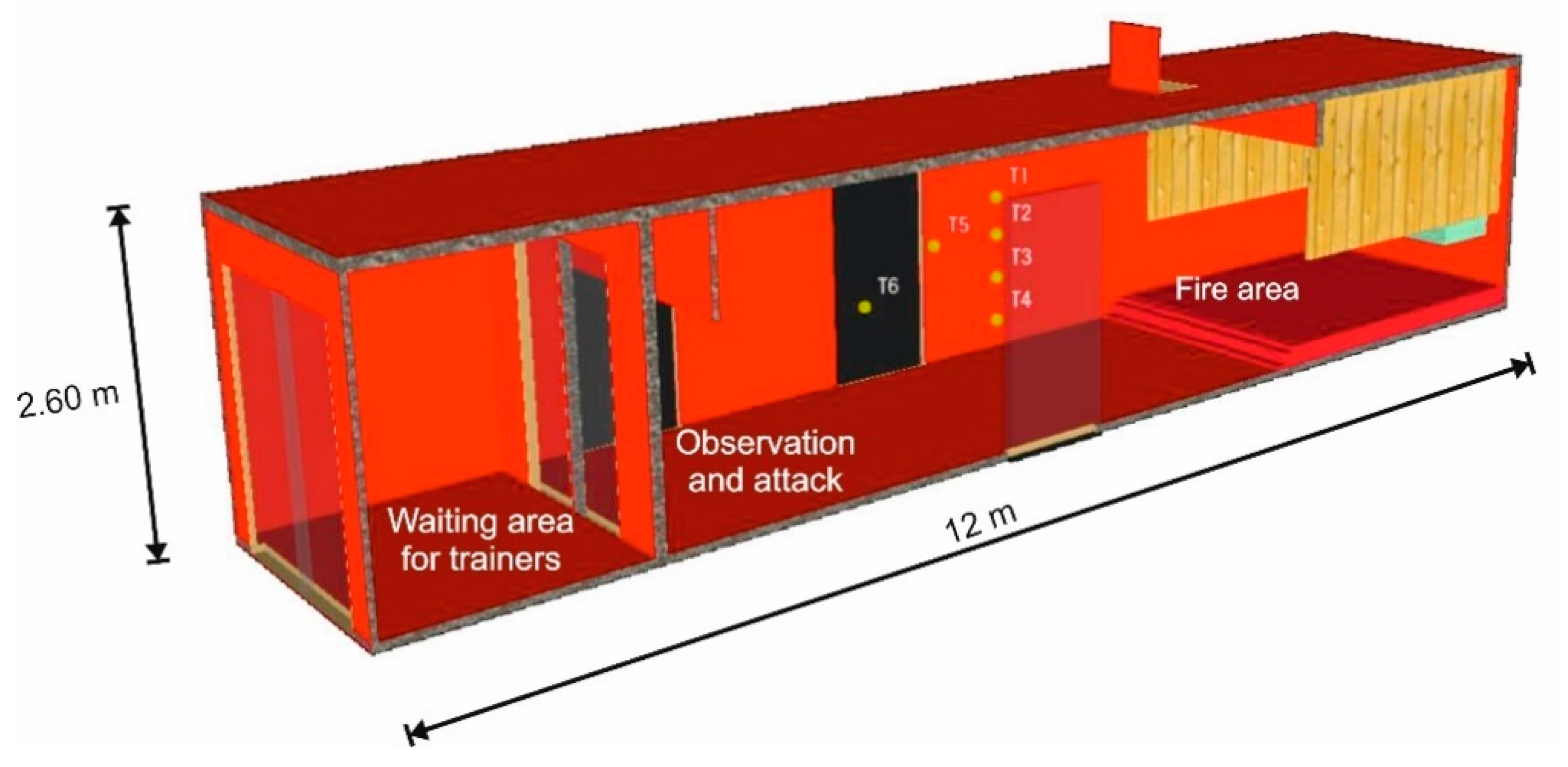
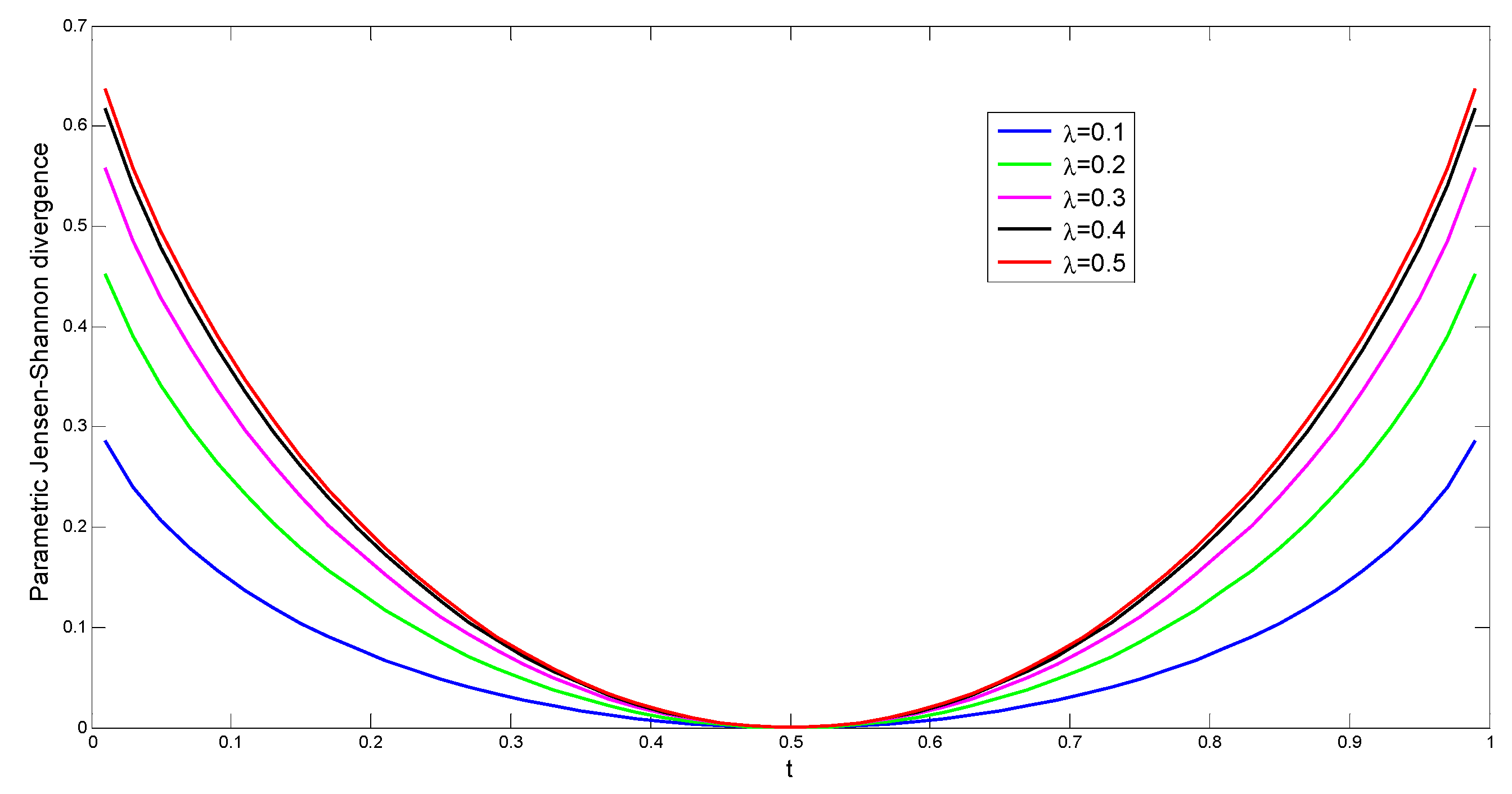
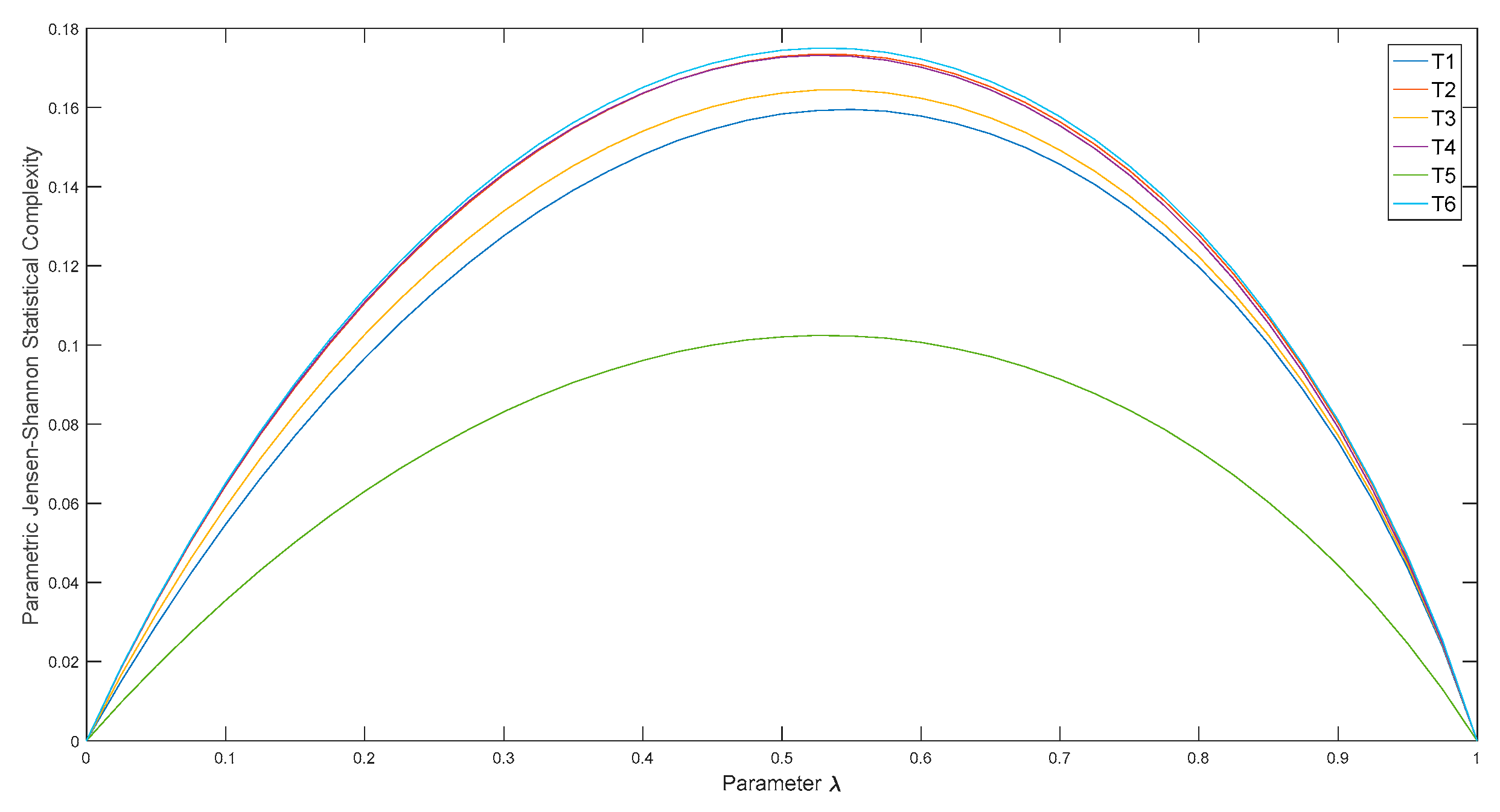
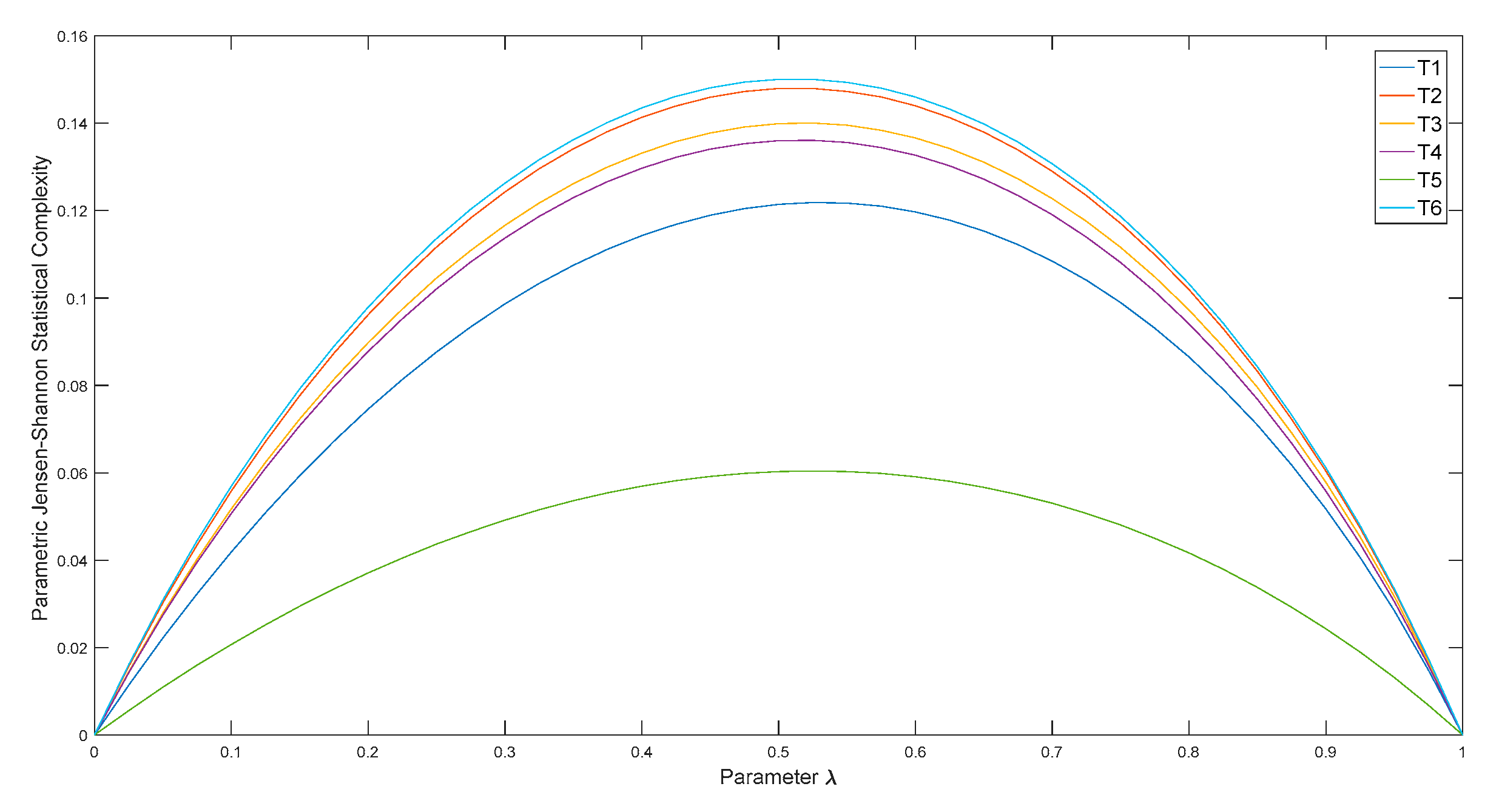
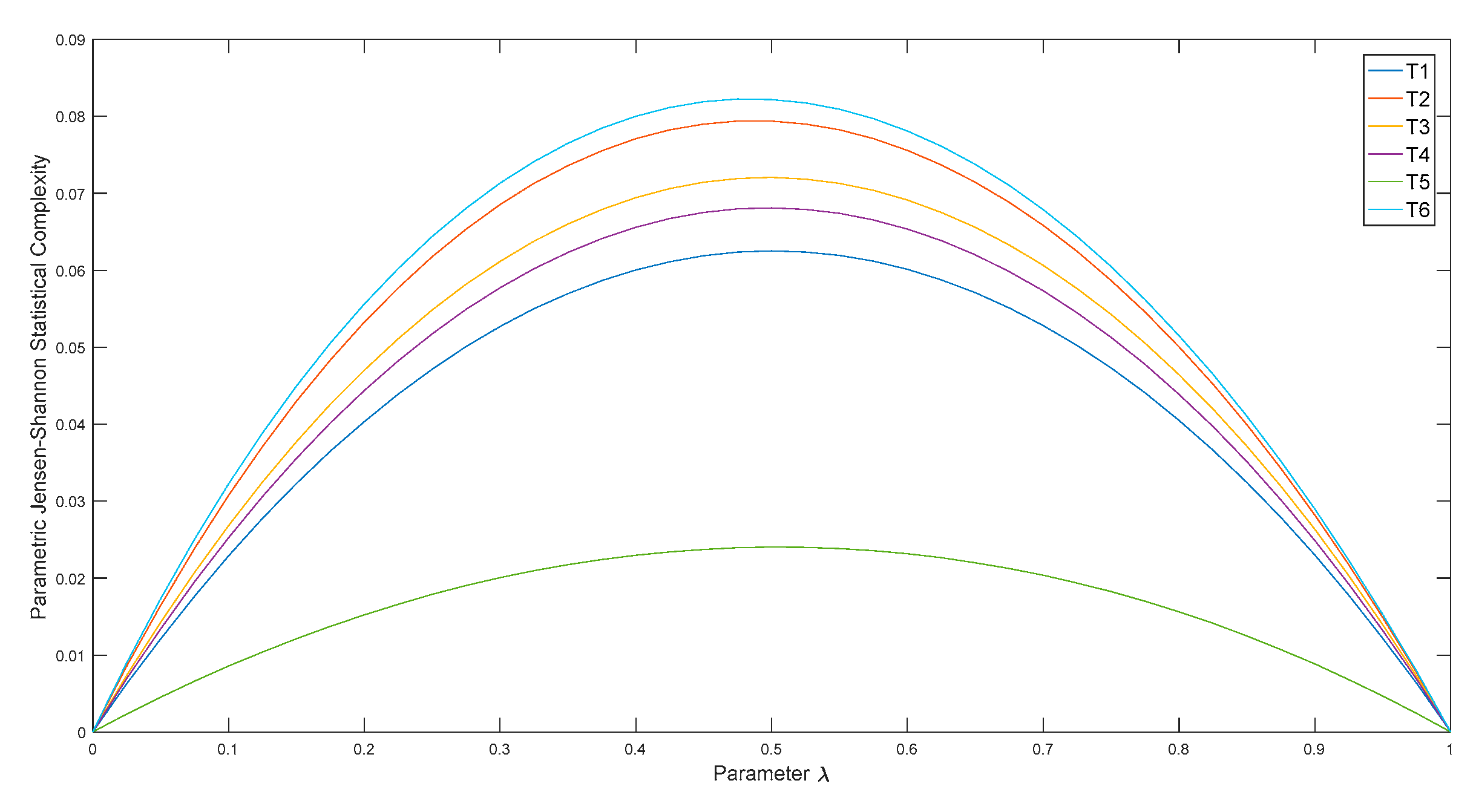
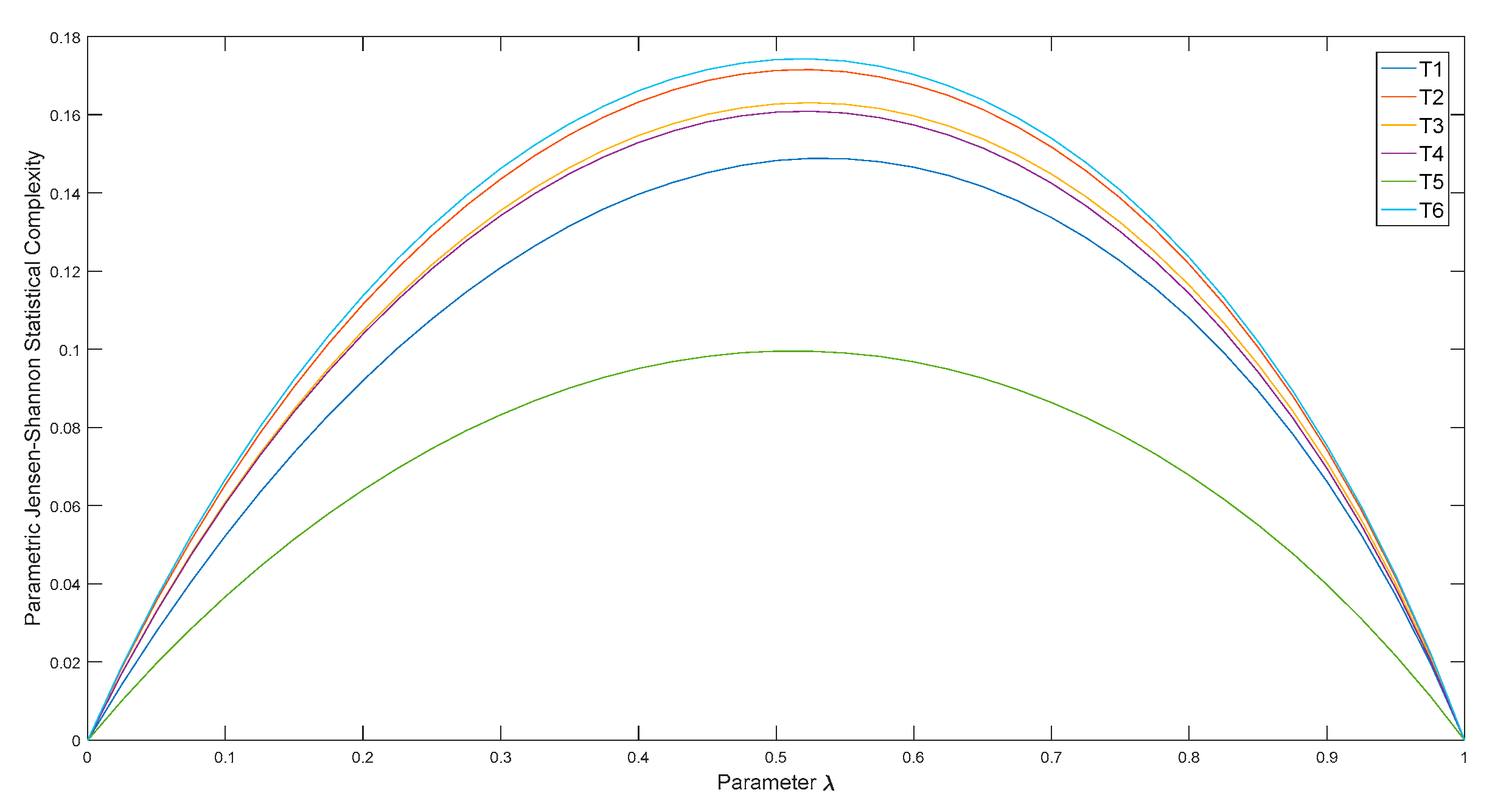
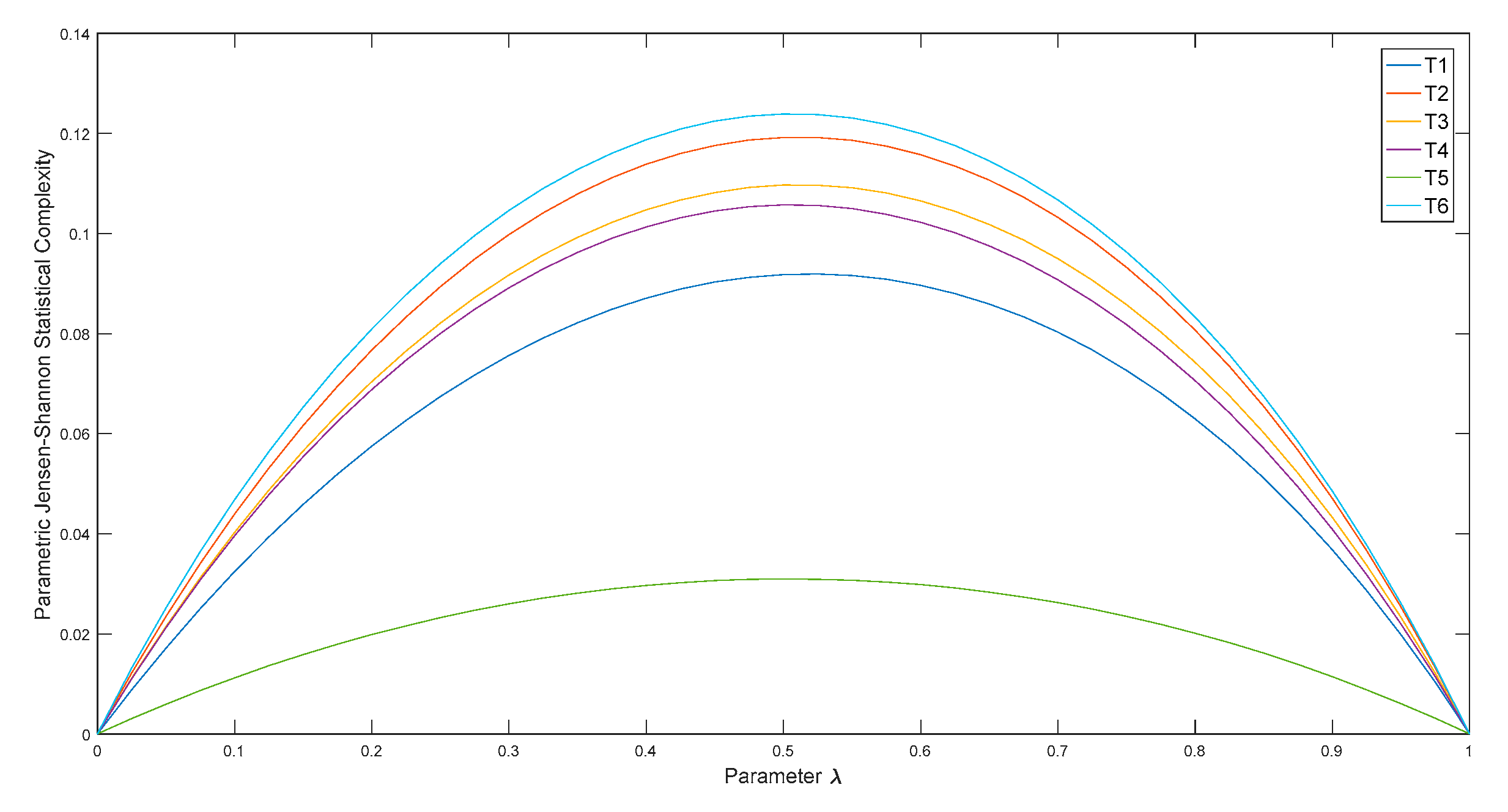
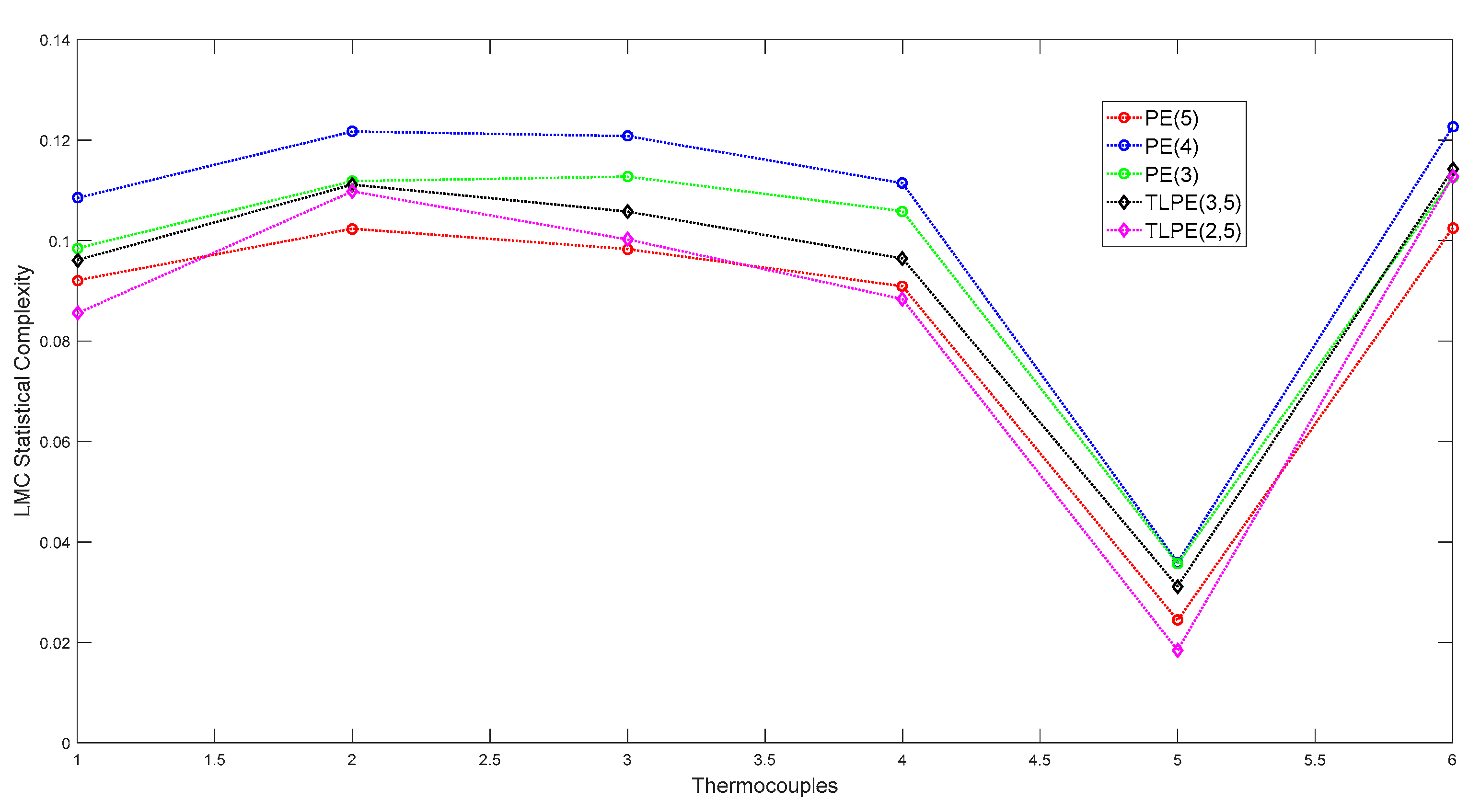
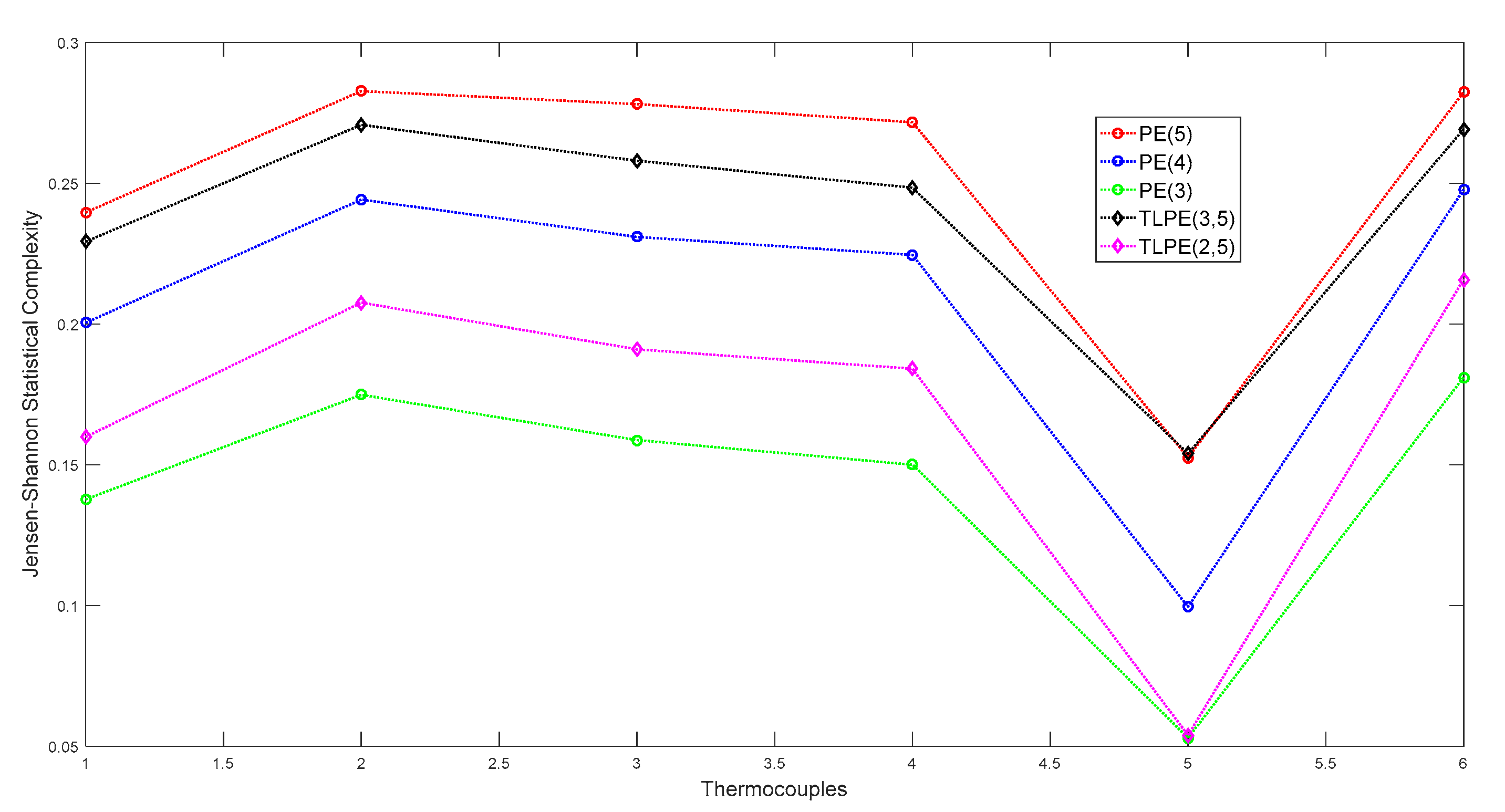
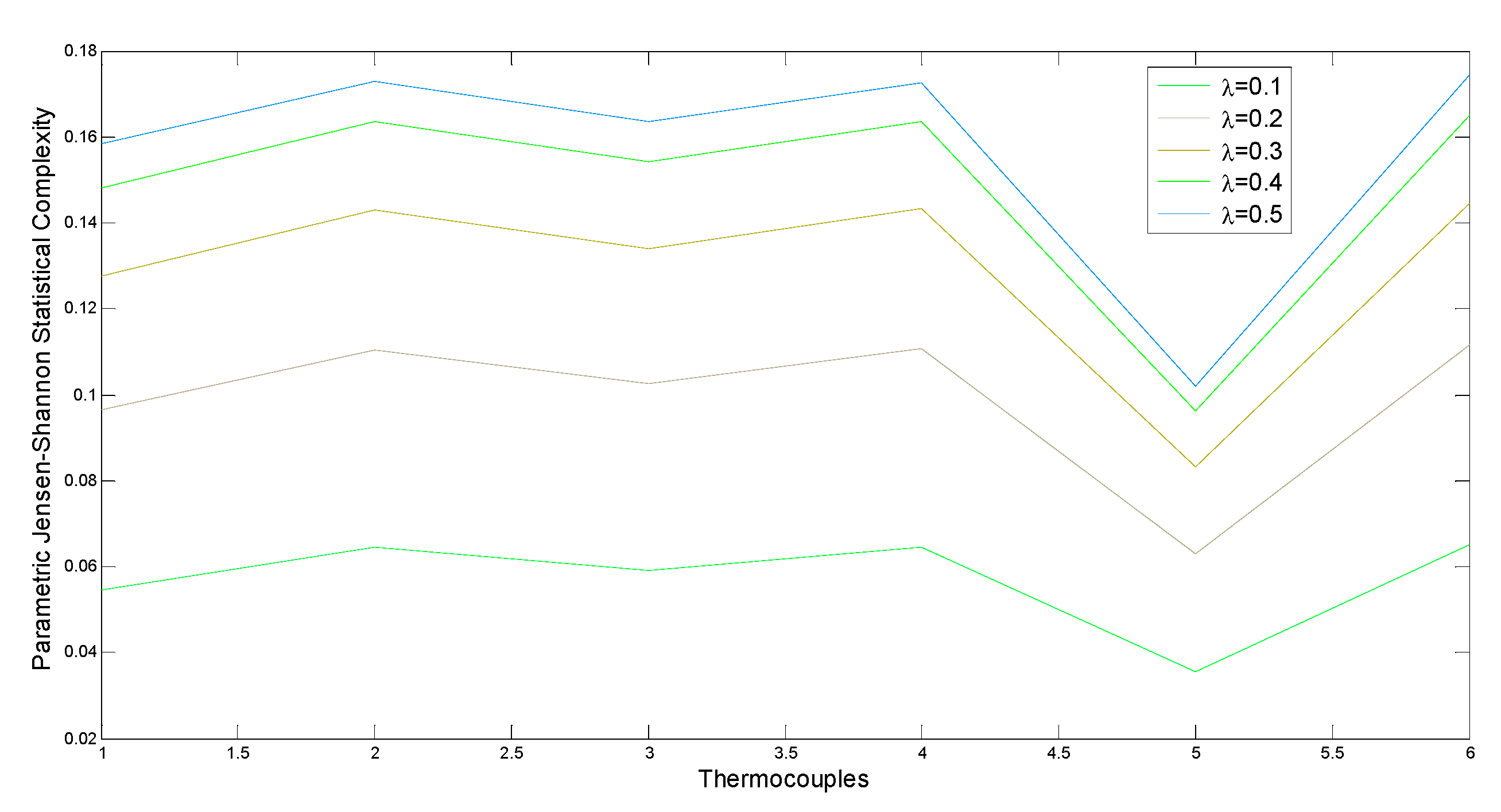
3. Raw Data Analysis
4. Concluding Remarks on the Limitations of Our Study
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Takagi, K.; Gotoda, H.; Tokuda, I.T.; Miyano, T. Dynamic behavior of temperature field in a buoyancy-driven turbulent fire. Phys. Lett. A 2018, 382, 3181–3186. [Google Scholar] [CrossRef]
- Murayama, S.; Kaku, K.; Funatsu, M.; Gotoda, H. Characterization of dynamic behavior of combustion noise and detection of blowout in a laboratory-scale gas-turbine model combustor. Proc. Combust. Inst. 2019, 37, 5271–5278. [Google Scholar] [CrossRef]
- Mitroi-Symeonidis, F.-C.; Anghel, I.; Lalu, O.; Popa, C. The permutation entropy and its applications on fire tests data. arXiv 2019, arXiv:1908.04274. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, L.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE-Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Rao, C.R.; Nayak, T.K. Cross entropy, dissimilarity measures, and characterizations of quadratic entropy. IEEE Trans. Inform. Theory 1985, 31, 589–593. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Lamberti, P.W.; Martin, M.T.; Plastino, A.; Rosso, O.A. Intensive entropic non-triviality measure. Phys. A Stat. Mech. Appl. 2004, 334, 119–131. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Rosso, O.A. Distinguishing chaotic and stochastic dynamics from time series by using a multiscale symbolic approach. Phys. Rev. E 2012, 86, 046210. [Google Scholar] [CrossRef]
- Niculescu, C.P.; Persson, L.-E. Convex Functions and their Applications. A Contemporary Approach, 2nd ed.; CMS Books in Mathematics; Springer-Verlag: New York, NY, USA, 2018; Volume 23. [Google Scholar]
- Donald, M.J. Further results on the relative entropy. Math. Proc. Camb. Philos. Soc. 1987, 101, 363–373. [Google Scholar] [CrossRef]
- Mitroi-Symeonidis, F.-C. About the precision in Jensen-Steffensen inequality. Ann. Univ. Craiova Ser. Mat. Inform. 2010, 37, 73–84. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Cao, T.; Tung, W.W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 046217. [Google Scholar] [CrossRef]
- Duan, S.; Wang, F.; Zhang, Y. Research on the biophoton emission of wheat kernels based on permutation entropy. Optik 2019, 178, 723–730. [Google Scholar] [CrossRef]
- Watt, S.J.; Politi, A. Permutation entropy revisited. Chaos Solitons Fractals 2019, 120, 95–99. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Mitroi-Symeonidis, F.-C.; Anghel, I.; Furuichi, S. Encodings for the calculation of the permutation hypoentropy and their applications on full-scale compartment fire data. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2019, 62, 607–616. [Google Scholar]
- Furuichi, S.; Mitroi-Symeonidis, F.-C.; Symeonidis, E. On some properties of Tsallis hypoentropies and hypodivergences. Entropy 2014, 16, 5377–5399. [Google Scholar] [CrossRef]
- Araujo, F.H.A.; Bejan, L.; Rosso, O.A.; Stosic, T. Permutation entropy and statistical complexity analysis of Brazilian agricultural commodities. Entropy 2019, 21, 1220. [Google Scholar] [CrossRef]
- Song, Y.; Ju, Y.; Du, K.; Liu, W.; Song, J. Online road detection under a shadowy traffic image using a learning-based illumination-independent image. Symmetry 2018, 10, 707. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitroi-Symeonidis, F.-C.; Anghel, I.; Minculete, N. Parametric Jensen-Shannon Statistical Complexity and Its Applications on Full-Scale Compartment Fire Data. Symmetry 2020, 12, 22. https://doi.org/10.3390/sym12010022
Mitroi-Symeonidis F-C, Anghel I, Minculete N. Parametric Jensen-Shannon Statistical Complexity and Its Applications on Full-Scale Compartment Fire Data. Symmetry. 2020; 12(1):22. https://doi.org/10.3390/sym12010022
Chicago/Turabian StyleMitroi-Symeonidis, Flavia-Corina, Ion Anghel, and Nicușor Minculete. 2020. "Parametric Jensen-Shannon Statistical Complexity and Its Applications on Full-Scale Compartment Fire Data" Symmetry 12, no. 1: 22. https://doi.org/10.3390/sym12010022
APA StyleMitroi-Symeonidis, F.-C., Anghel, I., & Minculete, N. (2020). Parametric Jensen-Shannon Statistical Complexity and Its Applications on Full-Scale Compartment Fire Data. Symmetry, 12(1), 22. https://doi.org/10.3390/sym12010022





