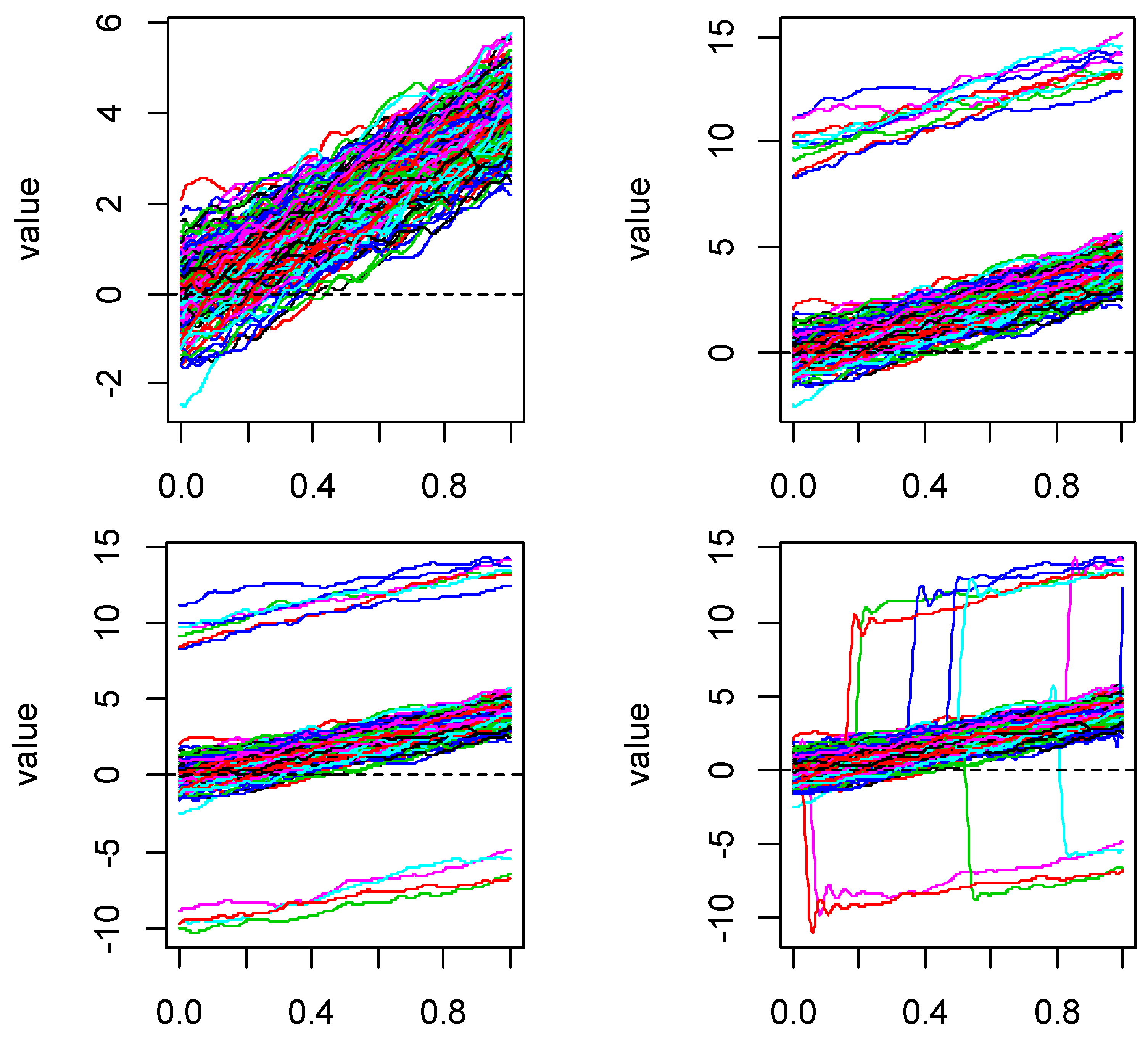
4.1. Simulation
In order to compare the robustness to outliers of L1-norm functional principal components (L1-FPCs) that are proposed in this paper and the classical L2-norm functional principal components (L2-FPCs), we performed this simulation. We referred to the simulation setting given by Fraiman and Muniz (2001) [
38]. Here, we considered that functional data
are the implementations of squared integrable stochastic process
, and the function curves were generated from different model. There was no contamination in Model 1, and several other models suffered from different types contamination based on Model 1.
Model 1 (no contamination): , where error term is a stochastic Gaussian process with zero mean and covariance function and ,.
Model 2 (asymmetric contamination): , where is the sample of the 0–1 distribution with the parameter , and is the contamination constant.
Model 3 (symmetric contamination): , where and are defined as in Model 2 and is a sequence of random variables with values of 1 and −1 with a probability of 1/2 that is independent of .
Model 4 (partially contaminated): ,
where is a random number generated from a uniform distribution on [0,1].
Model 5 (peak contamination): ,
where and is a random number generated from a uniform distribution on .
Figure 1 shows the simulated curves of these five models. For each model, we set 100 equal-interval sampling points in [0,1] and generated 200 replications. For Model 1, the parameter
was 0 and the contamination constant
was 0. For several other contaminated models, we considered several levels of contamination, with q = 5% and 10% and contamination constants M = 5 and 10. When fitting function curves, we use generalized cross validation (GCV) to obtain the number of bases. The results showed that the number of bases of Model 1–3 were the same, while those of Models 4 and 5 were different. However, due to the need of calculating the change of principal component coefficient, we had to calculate it on the same basis. Therefore, for comparison purposes, in Models 4 and 5, we selected the same number of bases as that of Model 1.
Classical L2-norm FPCA and L1-norm FPCA were used for the simulated functional data corresponding to these five models. We focused on their robust to various abnormal disturbances. When implementing L1-norm FPCA on Model 1, by comparing the value of objective function, the initial value was chosen as the first L2-norm functional principal component weight function, i.e., , where is the eigenfunction corresponding to the largest eigenvalue of the sample covariance function of the functional data in Model 1. Because the L1-norm FPCA of the following several disturbance models should be compared with Model 1, in order to ensure the consistency of conditions when calculating the L1-norm FPCA of the following several disturbance models, the initialization values also adopted the eigenfunction corresponding to the largest eigenvalue of the sample covariance function of the corresponding functional data.
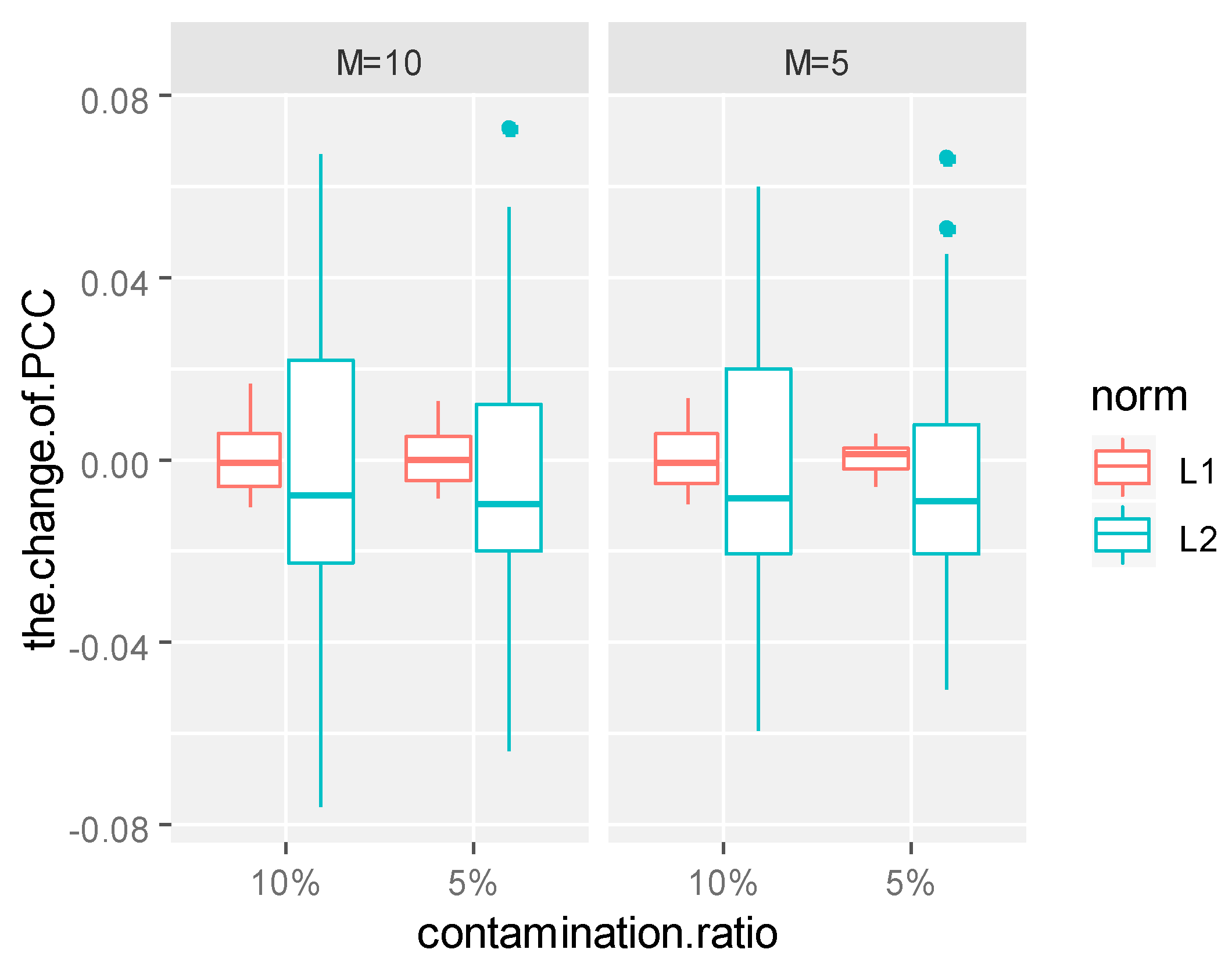
The sums of absolute values of the coefficient differences of several principal components under non-contamination and contamination were compared and analyzed. The sum of the absolute values of the corresponding coefficient changes are given in
Table 1,
Table 2,
Table 3 and
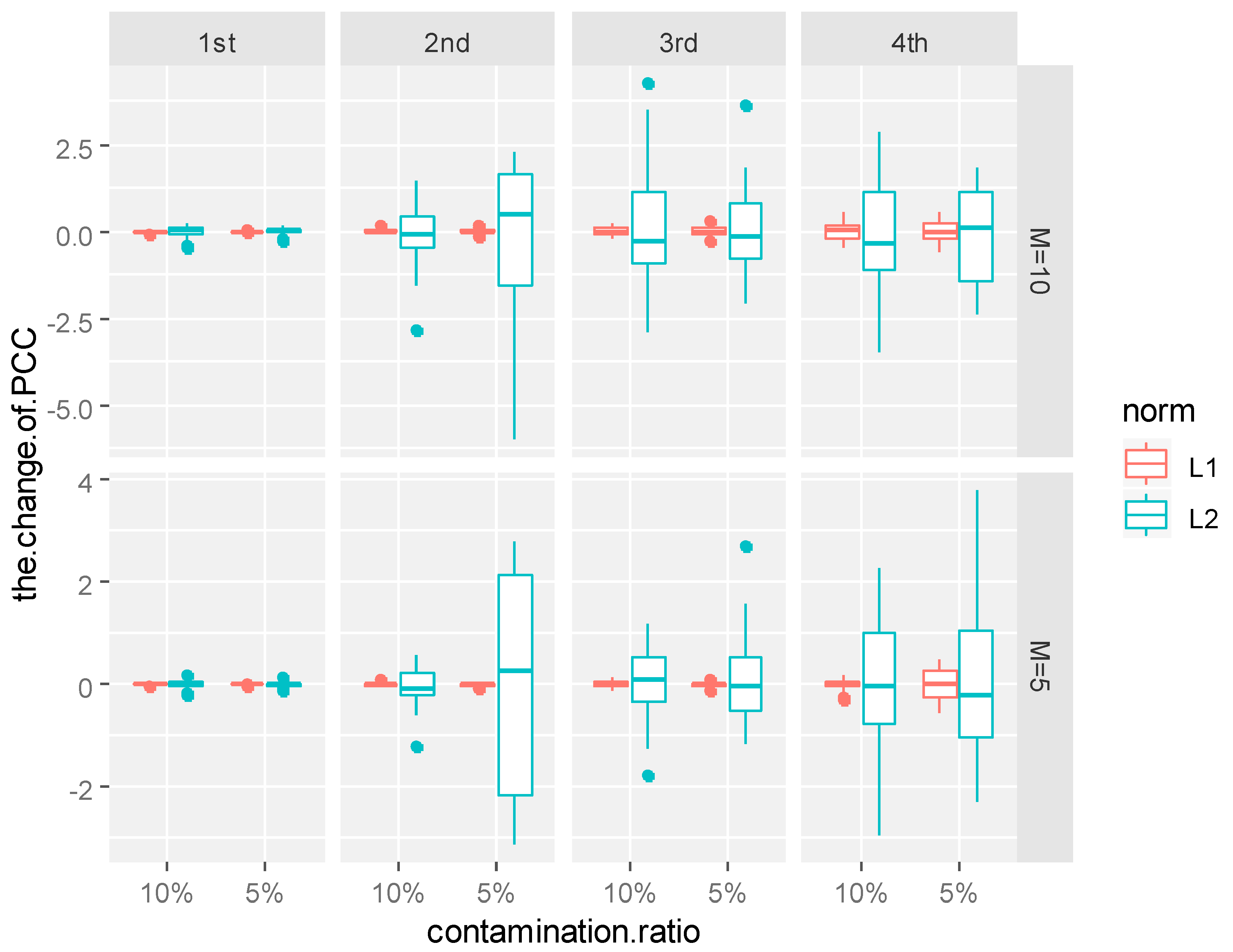
Table 4. Since the variance contribution rate of the first principal component reached 80%, only the first principal component function was taken in Models 1, 2, 3 and 4. However, in order to achieve a similar variance contribution rate, at least four principal components were needed in Model 5. Thus, for Models 1, 2, 3 and 4, we only show the changes of the first principal component function. For Model 5, we show the changes of the first four principal component functions.
It can be seen from
Table 1,
Table 2,
Table 3 and
Table 4 that under the same contamination ratio and contamination size, the coefficient changes of the principal component weight functions of the L1-norm were significantly smaller than those of the L2-norm, which shows that the functional principal components of the L1-norm were more stable than those of the L2-norm, no matter which form of contamination was received. This conclusion can also be confirmed from the boxplots of the coefficient changes of the principal component weight functions.
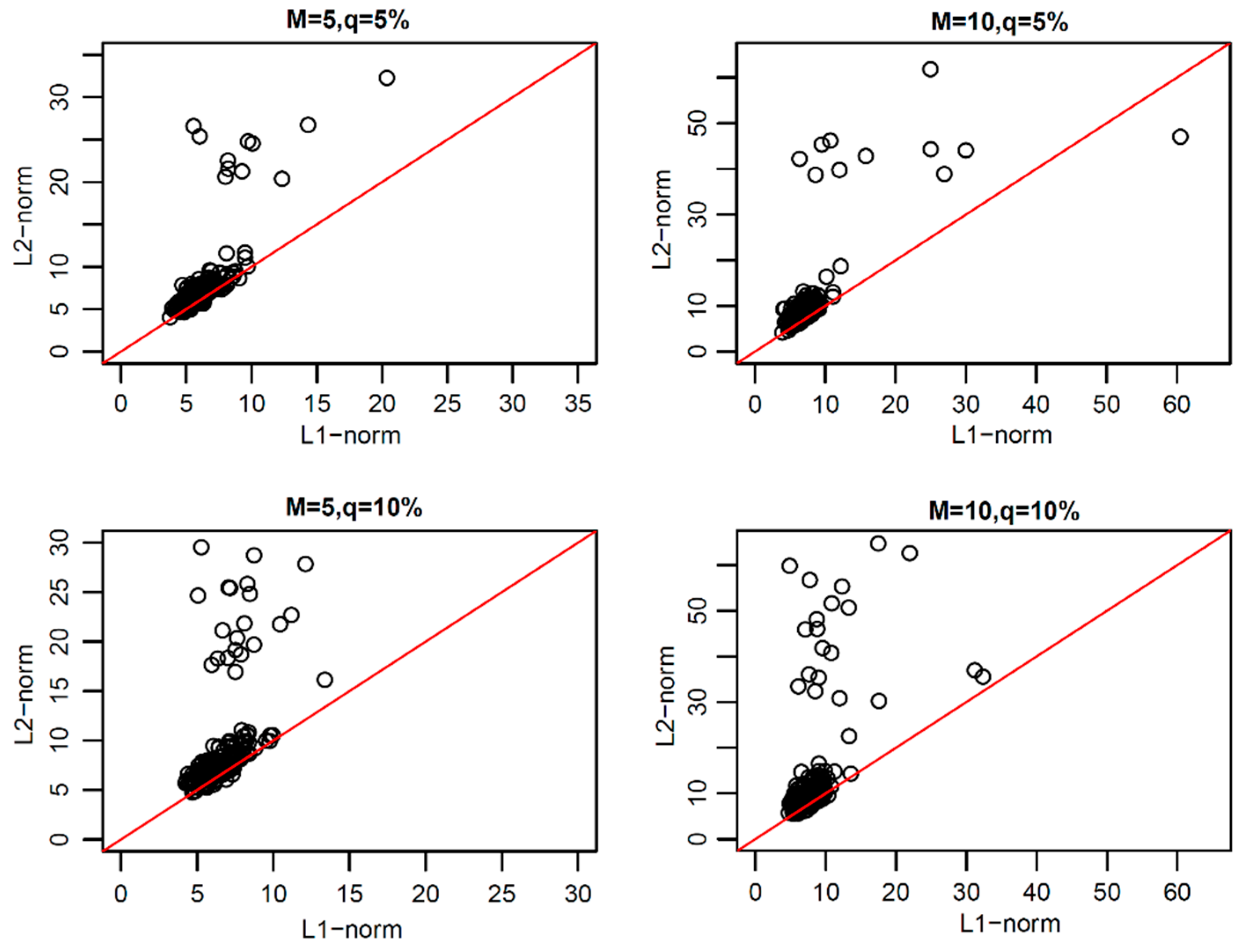
As can be seen from
Figure 2,
Figure 3,
Figure 4 and
Figure 5, in the same contamination ratio and size, the changes of L1-norm principal component coefficient are more concentrated near zero compared with the changes of the L2-norm principal component coefficient, which shows that under the same contamination mode, L1-norm functional principal components were more robust to outliers and more reliable.
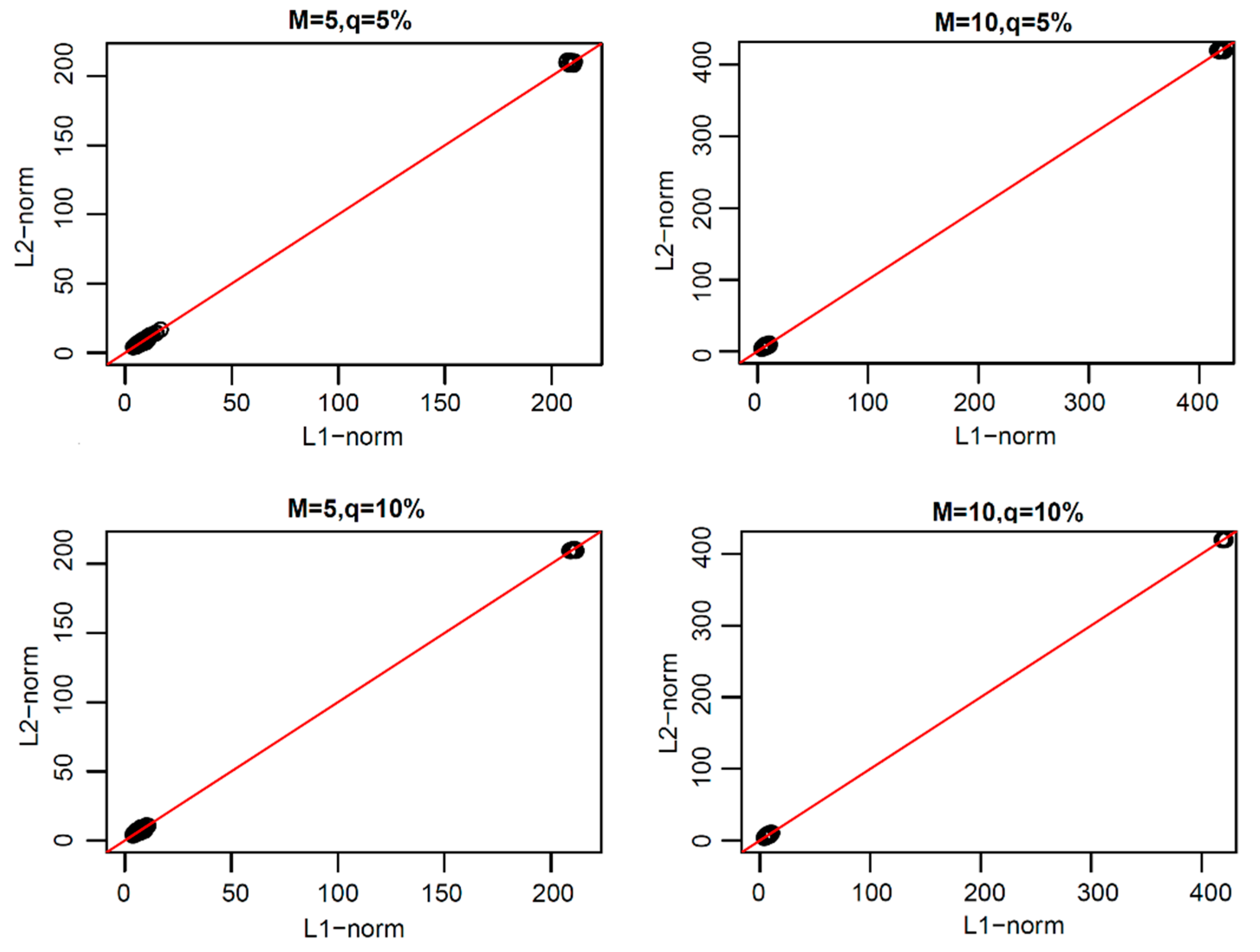
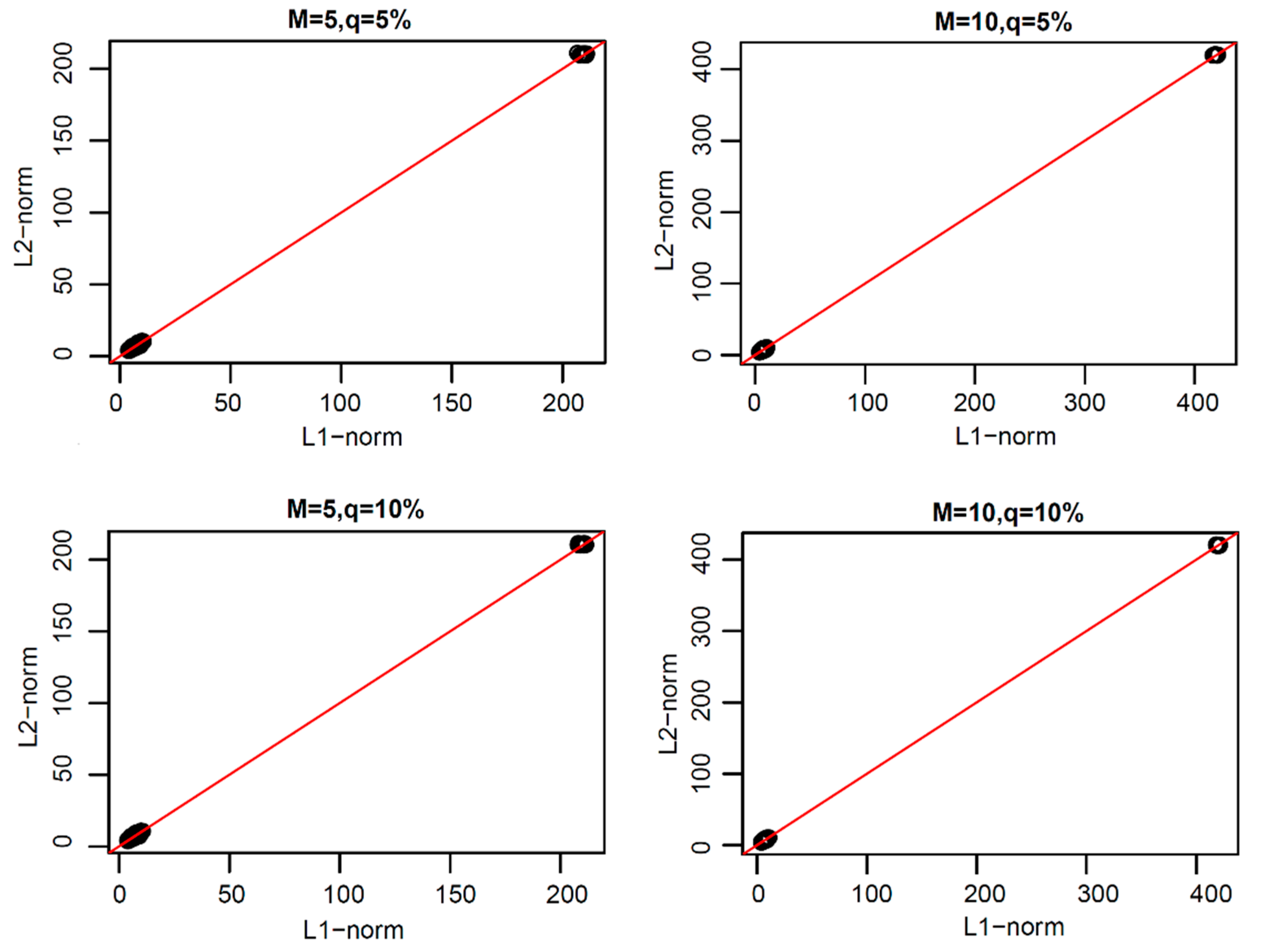
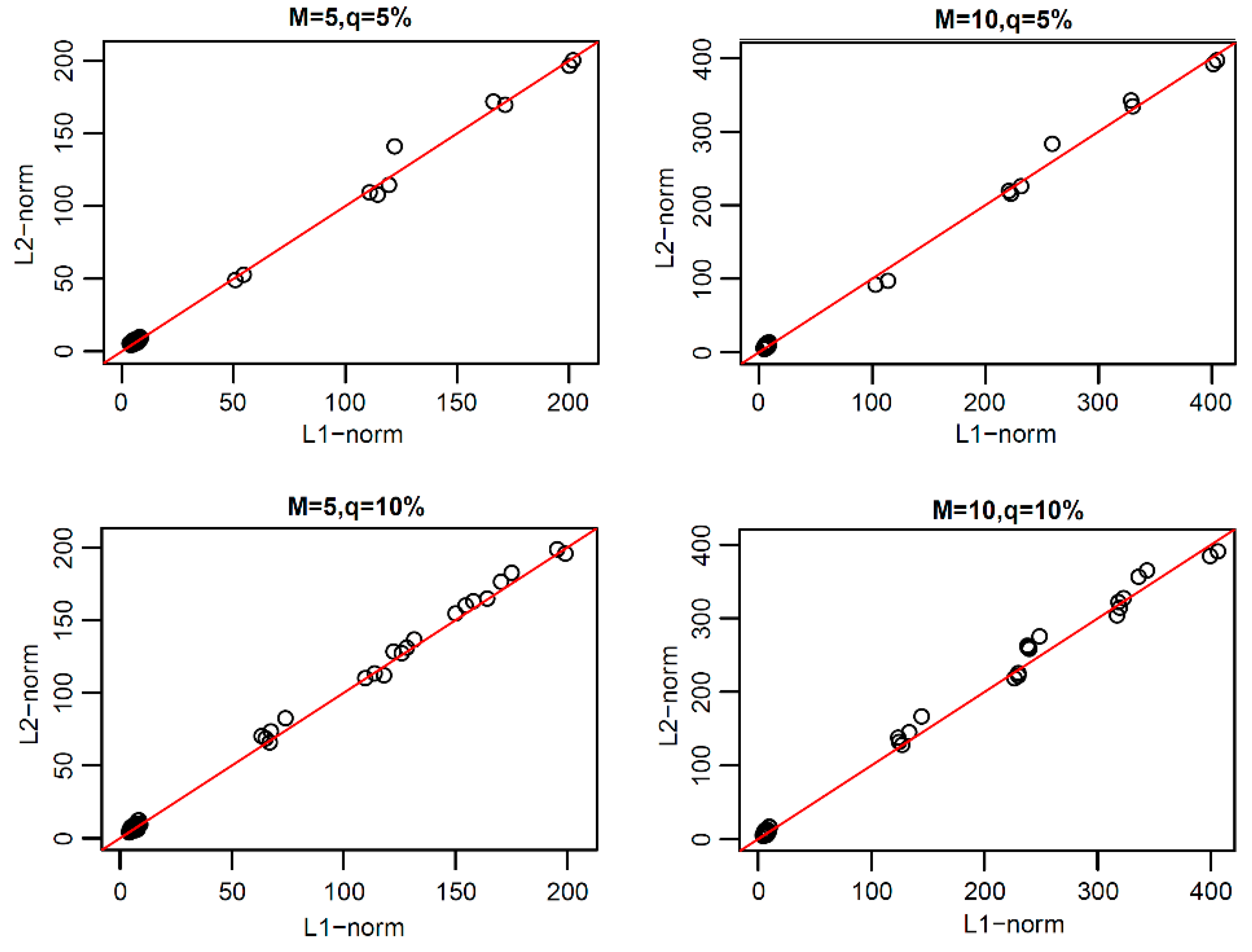
From the above research, we found that the L1-norm functional principal components were more robust than L2-norm functional principal components. Thus, how can one reconstruct the original functional data with these two types of principal components? In order to study this problem, we reconstructed the original uncontaminated functional data with the same number of functional principal components of L1-norm and L2-norm under each model. The scatter plots of the coefficients of the two types of reconstructed error curves are shown in
Figure 6,
Figure 7,
Figure 8 and
Figure 9.
In
Figure 6,
Figure 7,
Figure 8 and
Figure 9, we can see that the scatter plots of the reconstruction error curve coefficients of L1-norm and L2-norm were always near the line y = x under the first three pollution models, and under peak pollution, the reconstruction error of the L1-norm was smaller than that of the L2-norm. When using the paired one-sided
T-test, the
p-values were found to all be close to 1, indicating that the reconstruction error curve coefficients of the L1-norm were not greater than those of the L2-norm. Thus, the reconstruction ability of the L1-norm principal components to the original uncontaminated functional data was not worse than that of the L2-norm principal components. The results of the paired one-sided
T-test are shown in
Table 5,
Table 6,
Table 7 and
Table 8.
The above experiments showed that the functional principal component of the L1-norm was not just stable and reliable, it also had the same reconstruction ability as the L2-norm.
4.2. Canadian Weather Data
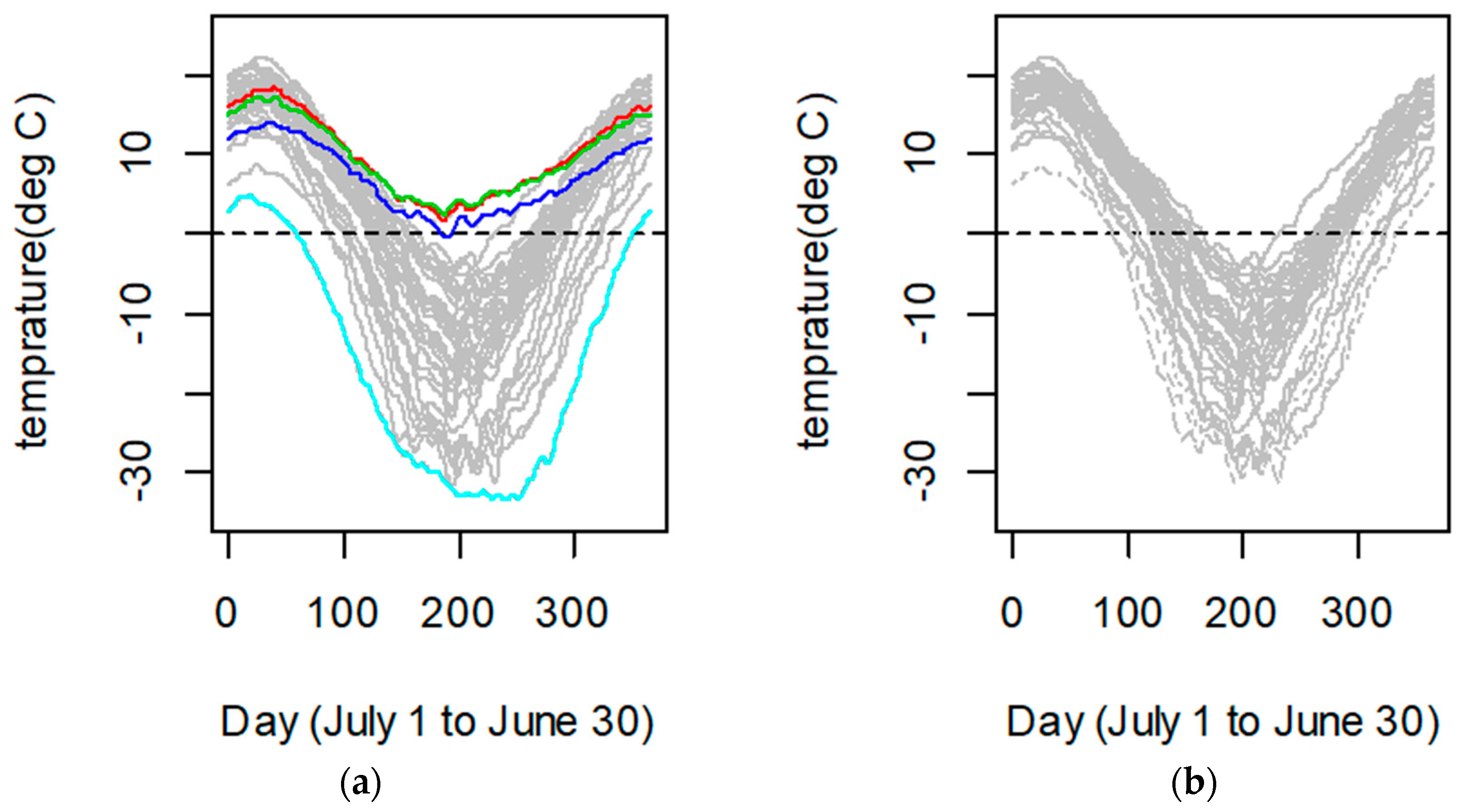
We used Canadian weather data, which provide daily temperatures at 35 different locations in Canada averaged over 1960–1994, in order to compare the robust to outliers of the L1-norm functional principal components and L2-norm functional principal components when the functional data were contaminated by abnormal data. Firstly, by considering the periodic characteristics of the data, the discrete temperature observation data were fitted into 35 functional curves by a Fourier basis function, and the number of the basis functions was 65. The fitting curves are shown in
Figure 10a. As can be seen when using the function data outlier detection method [
39], the temperature modes of the four stations of Vancouver, Victoria, Pr. Rupert and Resolute were different from those of the other stations.
Figure 10b shows this function after removing the data from these four observatories. The functional data of the 35 observatories were called the whole data, and the functional data after removing Vancouver, Victoria, Pr. Rupert and Resolute were normal data, so the whole data can be understood as the addition of abnormalities to the normal data.
In order to compare the robustness between the L2-norm functional principal component weighting functions and the L1-norm functional principal component weighting functions to outliers, the L2-norm functional principal components and L1-norm functional principal components were, respectively, used for normal data and data added with outliers. For each method, the results of the two cases were compared, because the variance contribution rate of the first two principal components reached 90%, though the latter analysis only focused on the first two functional principal components.
Figure 11 shows the change of the first principal component weight function before and after adding outliers by using two functional principal component analysis methods.
Figure 11a is a graph of the first principal component weight function that was obtained by using the L2-norm functional principal component method. The solid line is the result of normal data, and the dashed line is the result of adding four abnormal curves.
Figure 11b is a graph of the first principal component weight function that was obtained by using the proposed L1-norm functional principal component method. After comparing the objective function, the initial value was chosen as the first L2-norm functional principal component weight function, i.e.,
, where
is the eigenfunction corresponding to the largest eigenvalue of the sample covariance function of normal functional data and the same method for whole functional data. The solid line is the result of normal data, and the dashed line is the result of adding four abnormal curves. By comparing the coefficients of the two first functional principal component weighting functions, it was found that the sum of the absolute change of the coefficients of the first principal component weighting functions that were obtained by the L1-norm method before and after adding abnormal values was 0.16, which was less than the 0.18 corresponding to the L2-norm. Next, the performance of the second principal component weight function is discussed.
Figure 12 shows the change of the second principal component weight function before and after the addition of outliers by using two functional principal component analysis methods.
Figure 12a is a graph of the second principal component weight function that was obtained by using the L2-norm function principal component method. The solid line is the result of normal data, and the dashed line is the result of adding four abnormal curves.
Figure 12b is a graph of the second principal component weight function that was obtained by using the proposed L1-norm function principal component method. The solid line is the result of normal data, and the dashed line is the result of adding four abnormal curves. By comparing the coefficients of the two second function principal component weighting functions, it was found that the sum of absolute change of the coefficients of the second principal component weighting functions that were obtained by the L1-norm method before and after adding abnormal values was 0.33, which was less than the 0.76 corresponding to the L2-norm. the sums of the absolute values of the coefficient change of the principal component weight functions under the two methods are shown in
Table 5.
Table 9 shows that the classical L2-norm principal components weight functions greatly changed before and after removing outliers, reflecting its sensitivity to outliers. However, the L1-norm functional principal components weight functions presented in this paper had little change before and after adding abnormal values. Therefore, that the L1-norm principal component weight function proposed in this paper has a strong anti-noise ability and a good stability.
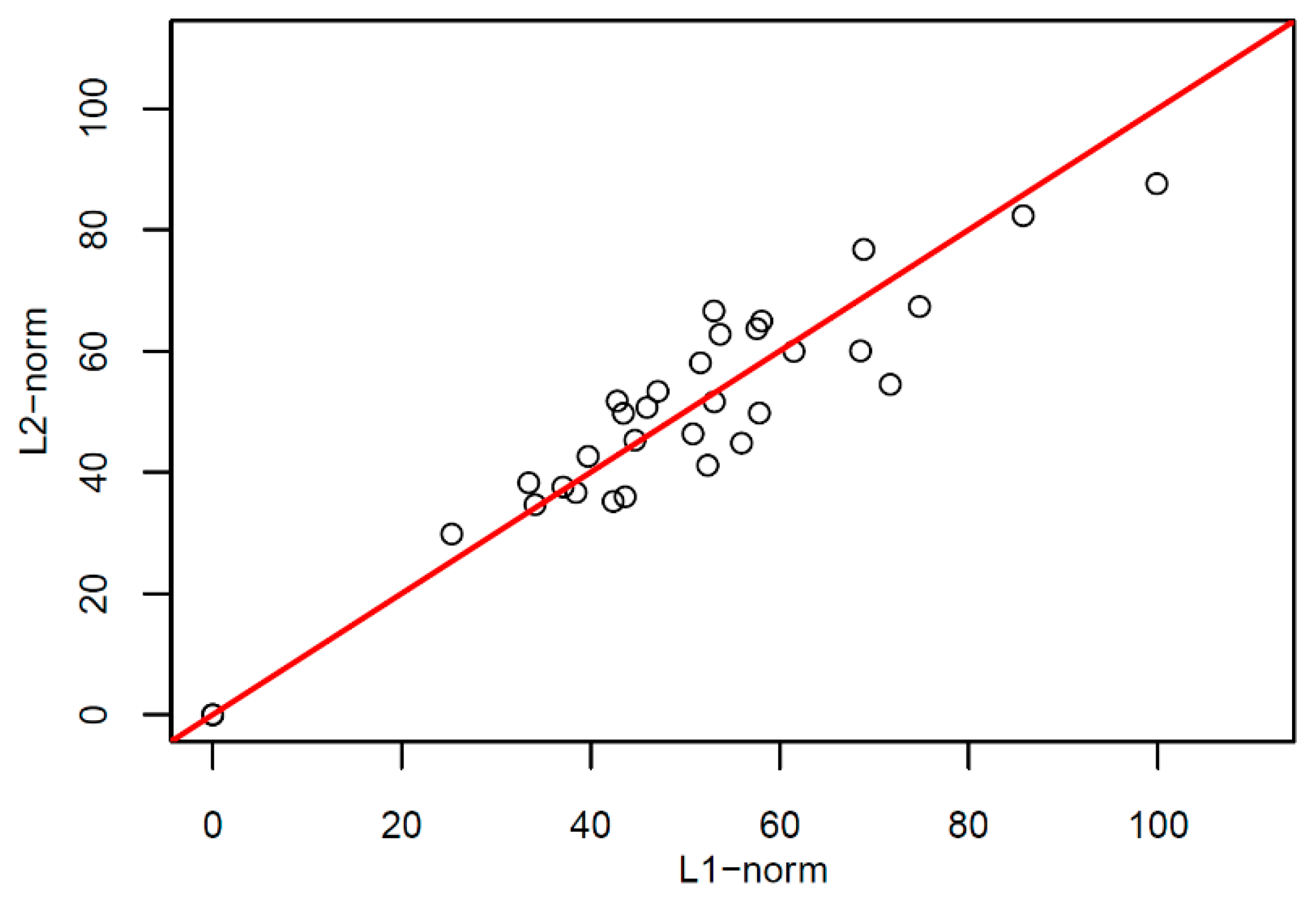
We also compared the reconstruction ability of two types of principal components to normal data. The scatter plots of the coefficients of the two types of reconstructed error curves are shown in
Figure 13.
From
Figure 13, it can be seen the scatter plots of the reconstruction error curve coefficients of L1-norm and L2-norm were always near the line y = x; When we performed a paired one-sided
T-test for the two groups of reconstruction error curve coefficients, the t value was found to 1.0323, the degree of freedom for the t-statistic was 33, and the
p-value was 0.1547, which indicates that the reconstruction error curve coefficients of L1-norm were not greater than those of L2-norm. Thus, the reconstruction ability of the L1-norm principal components to the original uncontaminated functional data was not worse than the L2-norm principal components.