Abstract
Incremental feature extraction algorithms are designed to analyze large-scale data streams. Many of them suffer from high computational cost, time complexity, and data dependency, which adversely affects the processing of the data stream. With this motivation, this paper presents a novel incremental feature extraction approach based on the Discrete Cosine Transform (DCT) for the data stream. The proposed approach is separated into initial and sequential phases, and each phase uses a fixed-size windowing technique for processing the current samples. The initial phase is performed only on the first window to construct the initial model as a baseline. In this phase, normalization and DCT are applied to each sample in the window. Subsequently, the efficient feature subset is determined by a particle swarm optimization-based method. With the construction of the initial model, the sequential phase begins. The normalization and DCT processes are likewise applied to each sample. Afterward, the feature subset is selected according to the initial model. Finally, the k-nearest neighbor classifier is employed for classification. The approach is tested on the well-known streaming data sets and compared with state-of-the-art incremental feature extraction algorithms. The experimental studies demonstrate the proposed approach’s success in terms of recognition accuracy and learning time.
1. Introduction
The rapid growth of technology increases application areas day by day. In recent years, the developed application areas such as social networks [1], electronic business [2], cloud computing [3,4], computer networks measurement [5,6,7], internet of things applications [8], etc. are generating large volume data [9]. Such large volume data are known as data streams, and they have different characteristics. The data stream is an infinitive sequence. The probability distribution of the data stream may change over time dynamically. It is processed in real-time without intermission. Besides, each instance arrives as continuous streams. Therefore, all data are not available from scratch, and the arriving data order cannot be controlled. Each instance has a vast scale and can be analyzed only once. Collecting true class labels of all instances in-stream is infeasible for real-time scenarios. The characteristics of the data streams have brought a huge challenge to processing them [10].
Feature extraction is one of the main processing steps of data mining and machine learning applications. It aims to extract useful features by projecting data into lower dimensional space from high dimensional space. The extraction of features helps to reach accurate results in large-scale data stream classification applications. However, traditional feature extraction techniques fail to satisfy the requirements of the data stream. Therefore, the incremental feature extraction techniques have been designed to facilitate the feature extraction of the data stream [11]. They aim to solve the problems of traditional methods for data streams. Although incremental feature extraction techniques can answer various problems, some techniques are not suitable for high-dimensional data streams in terms of time complexity and computational costs.
The large majority of unsupervised approaches can be easily applied to the data stream. However, most of them have problems such as data dependency and high computation cost in determining the eigenspace for large scale data. Moreover, they require a long time to instantly processing each incoming data. These problems make the incremental feature extraction algorithms complicated for data streams. This difficulty causes to use of alternative unsupervised approaches such as Discrete Cosine Transform (DCT) [12].
In this paper, the DCT-based feature extraction approach is presented for the data stream. The study aims to show the DCT-based algorithm being superior to well-known incremental feature extraction algorithms for data stream feature extraction. The well-known incremental Principal Component Analysis (IPCA) based feature extraction approaches are employed for performance comparison. The main contributions of the paper are as follows.
- A novel, efficient incremental feature extraction approach-based DCT is developed for the data stream to overcome the computation cost and time complexity problems.
- The proposed approach is based on DCT and PSO. To our knowledge, it is the first time using DCT and PSO for the data stream feature extraction algorithm.
The remainder of this paper is organized as follows. Section 2 briefly introduces a quick review of the well-known IPCA algorithms and DCT-based data stream approaches. Section 3 presents the proposed DCT-based data stream feature extraction approach in detail. The experimental settings and performance evaluations are given in Section 4. Conclusions and future works are presented in Section 5.
Notation—The bold letters denote vectors; x is spatial coordinate in sample domain; denotes a 1-D input vector with N data; u is frequency coordinate in transform domain; denotes the 1-D DCT coefficients vector with N values; is constant whose value depends on u; denotes ith sample of data stream.
2. Related Work
In this section, unsupervised incremental feature extraction algorithms and DCT-based data stream studies are reviewed.
The basis of the most popular incremental feature extraction algorithms is based on PCA. PCA [13] was proposed to use as a dimensionality reduction and feature extraction algorithm for traditional data. Many incremental versions of PCA (IPCA) were proposed to perform PCA in incremental learning manner. In the literature, IPCA algorithms are divided into two categories [14]: The first category algorithms are based on calculating eigenvectors and eigenvalues for each new incoming sample. The different representations of the covariance matrix in an incremental manner are the main reason for the variation of the IPCA algorithms in this category. Due to the characteristic of incremental learning, the covariance matrix must be updated with each new data. However, as the scale and the number of features increase, the computation cost correspondingly increases. The updating of the covariance matrix and calculation of new eigenspace becomes difficult for each new data. Besides, these algorithms have an unpredicted approximation error problem.
The first IPCA algorithm was proposed by Hall and Martin in the literature [15]. The algorithm updates the covariance matrix for each data using the residue estimating method. The authors later improved their studies using a chunk structure instead of using only one data. The study is based on merging and splitting the eigenspace using the chunk structure [16]. Liu and Chen [17] proposed an approach based on incremental updating of the eigenspace to detect video shot boundary. The algorithm computes histogram representation as soon as the new frame arrives. Afterward, the determined eigenspace utilizes the features of new frames to detect the shot boundary. Finally, the eigenspace is updated by PCA-based incremental algorithm. Li [18] developed an incremental and robust subspace learning algorithm. This algorithm has two eigendecompositions steps for computing the eigenvalues and eigenvectors. First, the algorithm calculates the initial principal components with the first observations. Afterward, the main eigenvectors are obtained by using previous eigenvectors and eigenvalues for new observations. Although the algorithm is easy to implement, it suffers from the time complexity, and computational and compilation cost; this applies to other PCA algorithms as well. In another study, Ozawa [19] proposed an extended IPCA algorithm based on the accumulation ratio. The eigenspace is updated using the rotation of the eigen-axes and the dimensional augmentation in IPCA algorithms. The dimensional augmentation is obtained when the norm of residue vector is larger than a threshold value. If the threshold value is too small, redundant eigenspace is obtained. This causes to decrease in computational efficiency and performance. Therefore, determining the best threshold value is a challenge for the existing algorithms. Due to the need for determining the best threshold value, the extended IPCA uses the accumulation ratio. Later, Ozawa et al. [20] enhanced their extended IPCA by adding chunk structure to algorithm and called as chunk IPCA. The chunk IPCA uses a chunk model instead of a one-pass data model. The eigenspace is incrementally updated for the chunk of samples at a time. Zhao et al. [14] developed an incremental learning and feature extraction algorithm called SVDU-IPCA. The algorithm uses the SVD updating algorithm, and it does not require to recompute the eigenspace from scratch. Rosas-Arias [21] proposed an online learning methodology for counting vehicles in video sequences. The approach is based on IPCA, which employs SVD algorithm. Fujiwara [22] presented incremental dimensionality reduction algorithm based on IPCA for visualizing streaming multidimensional data. The presented approach uses SVD for computing eigenspace. All IPCA algorithms and applications in the first category [23,24,25] suffer from high computational cost and time complexity in the requirement of determining or updating eigenspace for each data stream. IPCA algorithms are not suitable for the data stream, which requires an instant response, due to having data dependency, high computational cost, and time complexity.
The second category IPCA algorithms are based on computing the eigenspace without using the covariance matrix. The eigenvectors are calculated one by one using the higher-order principal components. Therefore, it is necessary to be known in advance how many eigenvectors must be calculated. In addition to these problems, the traditional PCA and its incremental versions have data dependency problems. When adding new data to the database, the recomputation of the covariance matrix and eigenspace is required. Candid Covariance-Free IPCA (CCIPCA) [26] is a well-known and fast incremental algorithm in this category. CCIPCA does not require to reconstruct the covariance matrix for each new data using the SVD based algorithm. It determines the eigenspace sequentially. The current principal component is a base of the next principal component in CCIPCA. The most dominant principal components are first computed, and then the second can be obtained by using the first one. CCIPCA is a suitable algorithm for the data stream, and it attracts researchers’ attention to develop feature extraction algorithms for data stream [10,27]. Wei [27] proposed covariance-free incremental covariance decomposition of compositional data (C-CICD) for data stream, which is based on the idea of CCIPCA. However, the increase in the number of samples and features does not affect the time complexity of the algorithm linearly. Moreover, the error is propagated and CCIPCA does not estimate the last eigenvectors accurately due to the incremental computation of principal components [14].
PCA and IPCA algorithms are linear transformations, and they linearly extract features. However, the linear transformation could not satisfy the needs. In such circumstances, the kernel structure could obtain more accurate results. In the literature, Kernel PCA (KPCA)-based incremental algorithms are proposed for extracting features of data stream [28,29,30,31,32,33,34]. Incremental KPCA (IKPCA) algorithms suffer from the same problems as IPCA. Moreover, choosing the best kernel type for the data stream is a challenge in IKPCA.
The discussed problems make IPCA algorithms difficult to utilize for data streams. This difficulty causes researchers to use alternative approaches for incremental feature extraction. The most popular approach is DCT [12]. DCT is successfully used in many different research areas for feature extraction [35,36]. Although DCT has been reported in the literature as the best transformation approach after PCA with energy compaction [37], it gains an advantage over PCA in many aspects [38]. The DCT is not a data-dependent algorithm. It does not require recomputation when adding new data to the database. Therefore, computational cost and time complexity are no problems for the DCT. Moreover, DCT can be easily implemented using fast algorithms. The advantages and structure of the DCT show that the algorithm can respond more quickly to the streaming data in comparison with PCA. In the literature, there are limited DCT-based data stream studies. The existing DCT-based studies are about data stream clustering [39], analysis of concept drift problem [40], and analysis of data stream [41]. Apart from these studies, Sharma [42] proposed a visual object tracking method based on sparse 2-D DCT coefficients as discriminative features and incremental learning. The discriminative DCT features are selected by using feature probability and ratio classifier criteria in this study. However, this study needs to perform IPCA for subspace learning, and the authors did not tackle the problem as a data stream manner. There is no DCT-based data stream feature extraction and dimensionality reduction study in literature. Existing studies are based on processing feature extraction in real-time [43,44,45]. However, real-time applications need a collected training set to construct a model. This need points batch learning, and it conflicts the nature of the streaming data.
3. Metarials and Methods
A novel, simpler, and effective feature extraction approach based on DCT and swarm intelligence is proposed in this paper to meet the requirements of the data stream. The proposed study is shown in Figure 1.
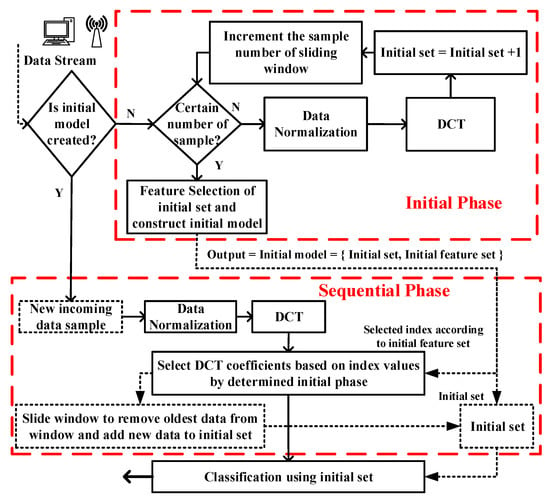
Figure 1.
Flowchart of the proposed approach.
As can be seen in the flow chart, the proposed approach consists of two stages. Both stages utilize the fixed-sized sliding window that consists of a certain number of data stream samples. In the first stage, an initial model is first created by using the window includes certain stream samples. Normalization and DCT process are first applied on each stream sample, then added to the into the window. The first window is called as initial set. The certain number stream samples are collected into the initial set; afterward, the feature selection step is activated. In this step, the best features are selected on all DCT coefficients by using Swarm Intelligent techniques. The selected features and corresponding indexes are assigned as the initial feature set. The initial model includes the initial and feature sets, as shown in Figure 1. Then, the sequential phase is started. This phase tackles new data stream samples sequentially and updates the initial model. First, the data normalization technique is applied on current sample. Afterward, DCT is performed for feature extraction of the sample. The 1-D DCT coefficient is obtained after the feature extraction process. The feature subset selection process is then applied on the DCT coefficients based on selected indexes by the determined initial phase. At the end of the algorithm, the processed data stream sample is added to the initial set, and the first sample of the initial set is deleted according to the sliding window technique. Thus, the proposed approach gains robustness against the concept drift problem. Finally, the Euclidean Distance based the K-Nearest Neighbor classifier is adopted for the classification task.
3.1. Initial Phase
3.1.1. Data Normalization
In this paper, the normalization is employed to remove the measurement differences between the attributes of the current data stream sample obtained by reading from sensors. The sample attributes indicate different cases, and the attribute values may be at different intervals. Therefore, the standard deviation normalization [46] is applied to each incoming data stream sample separately to bring the attribute values into the same range.
3.1.2. Discrete Cosine Transform
DCT is commonly used to transform images, time-series signals, or sequence of finite data points into basic frequency components. The DCT is a method to show data as a sum of cosine functions oscillating at different frequencies. The 1-D DCT coefficients are calculated as follows,
where is defined by
is a 1-D input vector with N data values, and denotes the 1-D DCT coefficients vector with N values. The DCT coefficients consist of low- and high-frequency components. The first parts of the DCT vector are low-frequency coefficients, and the first one is referred to as the DC coefficient. It holds average information of the signal. The rest coefficients are called AC components. The last elements of the DCT vector are high-frequency components, which give detailed information about the signal. In this paper, DCT is employed to extract features of data stream samples, due to the reasons discussed in Section 2. After the measurement differences of attributes of samples are removed using data normalization, the 1-D DCT is separately applied to each data stream sample in the window. A 1-D DCT coefficient vector with N frequency values is obtained for each data stream sample by the end of DCT processing. Thus, the data stream sample is transmitted to frequency space in which data samples can be more distinguishable by dividing the sample into low and high components.
3.1.3. Feature Selection
Due to the large-scale nature and inconsistent features of the data stream, a feature selection technique is required. The feature selection process is based on selecting the most consistent, proper, and accurate features subset from feature vectors. In the proposed approach, the feature selection step is carried out during the initial phase. The selected features and their indexes are kept in the initial feature set. They have an important place in determining the subfeature set of each incoming data stream in the sequential phase. In this paper, two different feature selection mechanisms are employed. The first one is experimentally feature selection. The experimental selection aims to demonstrate the rapidness of DCT-based feature extraction approach without additional modules, which increase time and computational cost. The other is automatically feature selection through PSO [47] and APSO [48]. Both algorithms are used to increase the performance of DCT by determining the best feature set automatically with optimization techniques. The automatic feature selection process searches the best feature subset that can give higher performance. The inputs of experimental and automatic subset selection are called the initial set, which consists of DCT coefficient vectors for the first sliding window, and the outputs are the initial feature set. The initial set and feature set to form the initial model.
3.1.3.1. Experimentally Feature Selection
The experimental selection aims to demonstrate the performance of the DCT-based feature extraction approach without extra computational cost and time complexity. The best feature interval is determined by selecting first m DCT coefficients. m corresponds to the size of interval and it is decreased one by one in each experiment. For instance, the initial interval is the entire DCT coefficient with N size, and the second one includes first N-1 coefficients. The last interval includes only the DC coefficient. The experimental feature selection process is shown in Figure 2.
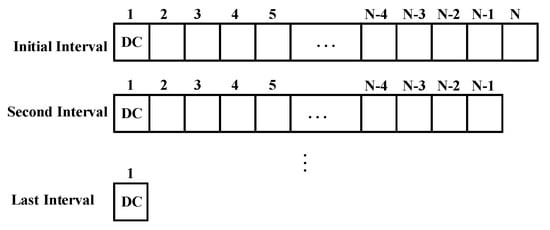
Figure 2.
Experimental feature selection process.
3.1.3.2. Automatic Feature Selection
The experimental feature selection needs an expert to determine the best feature set for different data sets. However, there is not enough time for experimental analysis in data stream applications. The approach must search the best subset without an expert. Therefore, the automatic feature selection mechanism is employed in this study. In the literature, there are various PSO- and APSO-based automatic feature selection applications of streaming data. These applications demonstrate the success of automatic feature selection using swarm intelligence [49,50,51,52].
Initially, the best feature subset is selected by PSO using the initial set. PSO is a popular optimization algorithm, and it was proposed by Dr. Eberhart and Dr. Kennedy in 1995 [47]. Nowadays, it is used as a feature selection technique in many studies. PSO is based on a swarm search strategy, and it is used to find optimal features recursively with local and global searches in the feature selection area. In the algorithm, the swarm consists of a random group of particles, and it uses an objective function to reach the optimum solution.
The individual best values in PSO (pbest) are used to increase diversity for qualified solutions. However, the diversity can be obtained using different way randomness; consequently, APSO [48] was proposed to accelerate convergence only using global best value (gbest). The velocity and position vectors are made simpler to accelerate the algorithm in APSO. All the above reasons enable the APSO algorithm to convergence faster than PSO. It can be seen in the literature that the APSO algorithm is more suitable to use for data stream due to the convergence speed [49]. Therefore, the APSO algorithm is also used for feature selection in this study. The usage of the APSO, feature selection schema, and objective function are the same as PSO in this approach.
In this study, a K-Fold Cross-Validation-based technique is employed as the objective function of PSO and APSO. The objective function takes the class label of the data stream, the K value, and the subset matrix of the initial set for currently selected features as inputs. The output of the objective function is called an average score, and it is obtained using Euclidean Distance based Nearest Neighbor classifier. The score array is a dissimilarity rate. Therefore, the classifier aims to detect feature subset which gives a minimum score. The obtained accuracy results are averaged for every subset according to the K value. The averaged result is the output value of the objective function, and the result is also the fitness value of the current particle. The algorithm of the objective function is illustrated in Algorithm 1. The outputs of PSO and the APSO algorithm are the best features sets that represent the data stream. Therefore, the algorithm is performed only in the initial phase. After the initial phase, the determined feature set is used for feature selection of new incoming samples.
| Algorithm 1: Objective Function | |
| Input: label, k, data | |
| Output: score | |
| 1 | Divide data into k parts |
| 2 | for each i in k parts do |
| 3 | Set ith part as test data and initialize score as zero |
| 4 | Set remainder parts as training data |
| 5 | for each x in test data do |
| 6 | Calculate Euclidean Distances between x and train data |
| 7 | Find minimum distance and related index of train data |
| 8 | If label of the related indexed train data not equal to the label of x then |
| 9 | Increment score |
| 10 | end if |
| 11 | end for |
| 12 | Assign score to ith value of score array |
| 13 | end for |
| 14 | Average score array and set score as output of average score array. |
3.2. Sequential Phase
The sequential phase incrementally tackles data stream samples, analyzes the current sample by using the initial model, and updates the initial model. The analysis has three steps: data normalization, DCT, and feature subset selection. Data normalization and the DCT steps are performed on the current data stream sample as same as the initial phase. Afterward, the subset feature selection process is performed on the 1-D DCT coefficients of current sample. DCT coefficients are selected based on index values using the determined initial feature subset in the initial phase. Finally, the current data stream sample is then added to the initial set to update the initial model and the last training sample is ejected according to the sliding window technique as shown in Figure 3.
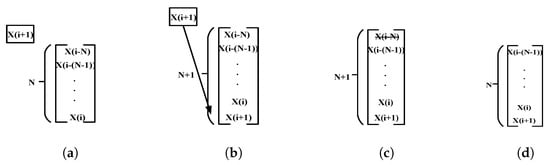
Figure 3.
The sliding window technique (M1). (a) ()th data is the current data stream sample, the initial model consists of N data, and N is the sample number of the initial model. (b) The current sample is added at the end of the initial model. (c) The first sample of the initial model is ejected from the model. (d) Updated initial model with the current sample.
To demonstrate the robustness and efficiency of the proposed approach, Euclidean Distance based KNN classifier is employed for classification. KNN does not need to build a classifier model in advance [53]. This characteristic makes the KNN suitable and easily applicable to the data stream [54,55].
4. Results and Discussion
In this section, the evaluation of the DCT-based data stream feature extraction approach is presented on real and synthetic data sets with respect to PCA and IPCA algorithms. The linear and nonlinear feature extraction algorithms are employed for comparison. The linear algorithms are the traditional PCA [13], IPCA proposed by Li [18] (IPCA-Li), IPCA proposed by Ozawa [19] (IPCA-Ozawa), and CCFIPCA [26]; the nonlinear algorithm is CIKPCA [30]. The proposed approach, PCA and IPCA algorithms have been implemented in MATLAB (R2016b) under Windows 10 (64-bit OS). The CPU of the computer is an Intel® CoreTM i7-7500 (2.70 GHz) with 8 GB of random-access memory. All algorithms have been implemented as reported in their original papers. The result CIKPCA is used as reported in their original papers. Three main experiments are focused in this study. The first one is to investigate the influence of the proposed feature extraction approach on classification. The accuracy rate (Acc) [%], the number of the data stream that classified correctly (NDSCC), and F-score are evaluation metrics in the first experiment. Another experiment is to examine the influence of variation of the DCT coefficients. The last experiment is to investigate the effect of automatic feature selection in the proposed DCT-based feature selection approach. PSO and APSO algorithms have been implemented in MATLAB (R2016b) to handle automatic feature selection.
4.1. Data Sets
The evaluation of the proposed approach is performed on real and synthetic numeric data sets. The Forest Cover Type is a real data set, and it is available on the UCI Machine Learning Repository [56]. The Forest Cover Type data set contains 581.012 observations of seven forest cover types in 30 × 30 m cell, and each observation consists of 54 geological and geographical variables. The data set includes ten quantitative variables, forty binary soil type variables, and four binary wilderness areas for describing the environment. A randomly generated subset of 100,000 data from Forest Cover Type is used in this paper.
The Poker-Hand is a real data set and available on the UCI Machine Learning Repository [56]. The data set consists of a poker hand of five cards, which drawn from a standard deck of 52. It contains one million instances, eleven attributes, and two class information. The last attribute describes the class information. In this paper, a randomly generated subset of 100,000 data from Poker-Hand is used as in Forest Cover Type.
The ElecNormNews is real data set described by M. Harries and analyzed by Gama [56]. The data set is a normalized version of the Electricity data set. It consists of 45,312 instances and eight attributes. The last attribute of each instance describes class information, and the data set consists of two classes. ElecNormNews was obtained from the Australian New South Wales Electricity Market.
The Optic-digits is optical character recognition data set. It contains 5620 instances, 64 classes, and 10 attributes. The Optic-digits is available on the UCI Machine Learning Repository [56].
The DS1 and Waveform are synthetic data sets and were generated through Massive Online Analysis (MOA) [57]. The DS1 data set consists of 26,733 instances, 10 attributes, and two classes; The Waveform data set consists of 5000 instances, 21 attributes, and three classes. The summary of data sets as used in this paper is given in Table 1.

Table 1.
Data sets description.
4.2. The Classification Performance
In this section, the performance of the proposed method is evaluated by comparing with linear and nonlinear feature extraction algorithms. Three different methods are employed to evaluate the classification performance. The first one (M1) is a sliding window model that is given as Figure 3, and it has a traditional structure used in incremental learning approaches for the data stream in the literature. The second one (M2) is to use only the first certain number of the data stream samples for the initial model. A new incoming streaming data sample is used for the only classification. This method has similar structure with batch learning. Therefore, only traditional PCA is performed with M2 as in Table 2. The last method (M3) is based on adding a new sample to the initial model without eliminating the old and outdated samples. Thus, the sample number of the initial model is increased as the time going by. The usage of the model is shown in Figure 4.

Table 2.
Accuracy Ratio (Acc), The Number of the Data Stream that Classified Correctly (NDSCC), and F-scores for Principal Component Analysis (PCA) and the proposed approach.
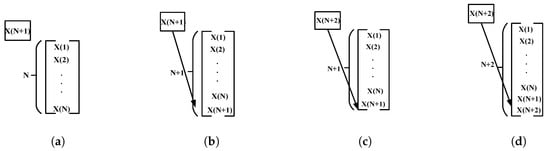
Figure 4.
The M3 technique. (a) th data is the current sample, the initial model consists of N data, and N is the sample number of the initial model. (b) The current sample is added to the end of the initial model. (c) th data comes for processing. (d) th data is added at the end of the initial model. The sample number of the initial model is increased to .
Table 2, Table 3 and Table 4 show the accuracy rates and the NDSCC scores for the traditional PCA, IPCA-Li, CCFIPCA, CIKPCA, and the proposed method. CIKPCA uses Waveform and Optical-digit data sets in its original paper. Therefore, Table 4 only includes the results of Waveform and Optical-digit data sets.

Table 3.
Acc and NDSCC scores for IPCA-Li, CCFIPCA, and the proposed approach.

Table 4.
Accuracy for CIKPCA and the proposed approach.
In this experiment, the sliding window size is determined as 1000 according to experimental results, and so the first 1000 samples of all data sets are used for the initial model. After the initial phase, entire samples are used in the test stage and processed one by one. Table 2 and Table 3 demonstrate that the proposed DCT-based approach almost obtains the best accuracy rates and NDSCC scores for all data sets. On the one hand, the traditional PCA algorithm reaches a higher result than the proposed approach only for the Poker and DS1 data set. The fact that the M2 method has the same structure as PCA, and the proposed approach is designed as an incremental learning approach causes PCA to be more successful. On the other hand, the proposed approach achieves better F-score measure. These results demonstrate how precise the proposed approach is, as well as how robust it is in comparison with the traditional PCA. The fact that the M2 method has the same structure as PCA, and the proposed approach is designed as an incremental learning approach, cause PCA to be more successful. The ForestCovType is a huge and sparse data set. It is reported that [58] processing the data set is difficult. Nevertheless, the proposed DCT-based approach can achieve the best results compared with the other three methods. All approaches have almost the same Acc and the NDSCC scores for data set DS1. The processing of DS1 is easier in comparison with others due to being a synthetic data set. The Acc and NDSCC scores reach a higher percent for four approaches. However, the proposed approach achieves the best results among the four approaches. The reason for the proposed approach’s success is to extract features in the frequency domain. The DCT extracts the best representative and distinctive features in the frequency domain. The use of frequency-domain representation of data streams provides better discrimination of different classes. Consequently, the proposed approach obtains significant results for all data sets. Moreover, PCA, IPCA-Li, and CCFIPCA are linear transformation techniques. The distribution and complexity of data sets are not suitable for transforming data stream linearly.
CIKPCA is an nonlinear data stream feature extraction algorithm. According to Table 4, CIKPCA has higher results obtained on kernel space for Waveform and Optical-digit. The positive effects of kernel space can be seen in Table 4. However, the proposed approach is more successful than CIKPCA. This demonstrates that the processing in frequency domain is more efficient than processing in kernel space. Moreover, the concept of data stream can be changed in time. The used kernel type can remain ineffective due to concept drift problem. To decide the best kernel type is a challenge for data stream. In contrast, the concept drift does not affect the proposed DCT-based data stream feature extraction approach.
4.3. The Analysis of the Variation of DCT Coefficients
The effects of dimension reduction and variation of DCT coefficients are examined in this experiment. The experiment is carried out by taking first or last N features from the coefficient vectors called an interval. The intervals are determined as experimentally. The first interval corresponds to the whole DCT coefficient vector. Afterward, the length of intervals is decreased one by one until half of the vector length remained. To do this, the new one is constructed by removing the last element of the previous interval. This process is carried out to see the effect of the last parts (high-frequency components). To observe the effect of the first part (low-frequency components) as opposed to the method of examining the influence of the last elements, the first elements of the previous interval are removed. In both cases, the NDSCC score is used as an evaluation metric, and the scores are obtained by performing M1 on five data sets.
Figure 5 shows the NDSCC scores for five data sets by performing M1. M1-LH and M1-FH refer to the results of the M1 method for the last half and first half. Based on Figure 5, some interesting observations can be made as follows. It is observed that when the length of the interval is reduced, the NDSCC scores show a tendency to decrease. However, the decrease of NDSCC scores does not occur monotonically for all data sets in some cases. For example, case 6 achieves higher performance than case 7 for ElecNormNews data set on M1-LH. The same situation can be seen in the results of Poker and DS1 data sets according to Figure 5. The reason is that all the features cannot contribute in the same way. Some features negatively affect the results.
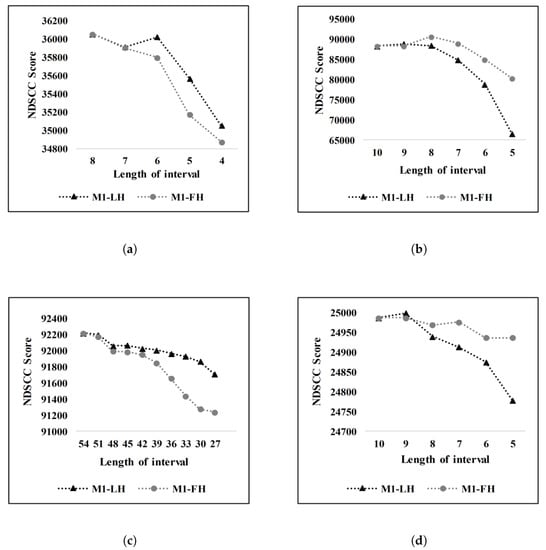
Figure 5.
Examining the influence of the interval length for five data sets: (a) ElecNormNews (b), Poker (c), and Forest CovType (d) DS1.
Furthermore, it seems that the influence of the coefficients is tended to exhibit the same behavior for M1-LH and M1-FH on all data sets. When the length of the interval is reduced, the NDSCC scores tend to decrease as expected, and the performance of both intervals becomes different. With the reduction of the interval length, the last coefficients of the DCT vector are tended to be more efficient for data sets ForestCovType and ElecNormNews; the first elements of the DCT vector become efficient for Poker and DS1 data sets. The NDSCC scores vary at different interval levels for all data sets. This situation demonstrates the necessity of automatic feature selection for best representing the characteristics of the data set.
4.4. The Analysis of the Automatic Feature Selection
In this section, an automatic feature selection is evaluated. The purpose is to make a positive contribution to the results by selecting the best representative features and discarding ineffective features from the feature set. PSO and APSO algorithms are implemented to perform an automatic feature selection. The objective function of PSO and APSO is described in Section 3.1.3.2. The k value in the objective function is selected as 3 according to the experimental results. In this experiment, only the M1 method is used.
Figure 6 shows the comparison of DCT, PSO-DCT, and APSO-DCT. It is observed from Figure 6 that there is a slight difference between PSO and APSO. Both automatic feature selection methods can select the best features from the feature set. However, when the number of selected features is reduced, the performance of PSO-DCT is increased on ElecNormNews data sets. The performance of APSO-DCT is better in all cases for Poker data set. Although using only global best value in APSO contribute for the Poker data set in all cases, it does not affect the ElecNormNews positively in all cases. Furthermore, both automatic feature selection methods achieve higher results than experimentally feature selection based DCT according to Figure 6. This is because the PSO- and APSO-based methods automatically select features by evaluating the structure of the data sets. However, these two methods have a longer learning time disadvantage than DCT.
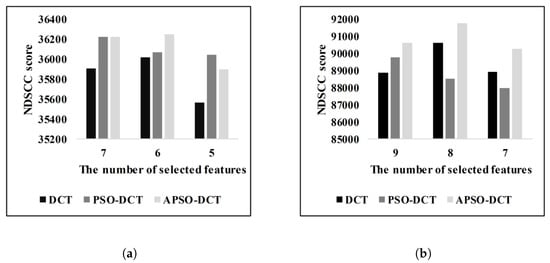
Figure 6.
Comparison of DCT, PSO-DCT, and APSO-DCT: (a) ElecNormNews and (b) Poker.
The last experiment is accuracy and average learning time comparison between the proposed method and IPCA-Ozawa. IPCA-Ozawa performs by increasing the size of the eigenvector space with every incoming data. The size of the eigenvector space is considerably larger than the first example at the end of the process, so the algorithm ends in a gradually increasing time. Therefore, the APSO-DCT method is compared IPCA-Ozawa to show the performing faster than the IPCA-Ozawa even when the DCT algorithm has an additional workload. Table 5 demonstrates the ACC and learning time of algorithms. It is observed that the DCT-based method with additional load (APSO-DCT) is processed in a shorter average learning time than the IPCA-Ozawa method. Moreover, the proposed approach obtains higher accuracy rates. It can be seen from Table 5 that the proposed approach is the best method in comparison with IPCA-Ozawa. The gradually increasing time performance of IPCA-Ozawa is not preferable for data stream environment.

Table 5.
Comparison of APSO and IPCA-Ozawa.
Finally, the time complexity of the proposed approach is lower than IPCA as summarized in Table 5. In another way, the recomputation of the covariance matrix is first required in IPCA algorithms. The eigenvalue and eigenvector are then calculated. In the proposed approach, only the fast-discrete cosine transformation is required. Suppose that the data stream has N attributes. In IPCA N*N, the covariance matrix is first produced then the eigenvalues and eigenvectors are computed. The proposed approach requires only 1-D DCT transformation process for feature extraction. Furthermore, the automatic feature selection step based on PSO/APSO slightly increases the computations. Because PSO/APSO is only performed in the initial phase for a couple of samples to determine an efficient feature set and never be repeated. This does not yield a high computational complexity to the algorithm.
5. Conclusions
Incremental feature extraction approaches are used to facilitate feature extraction from large-scale streaming data. The aim is to address the needs of the data stream for feature extraction. The most popular incremental feature extraction algorithms are the incremental versions of PCA. However, IPCA algorithms have some problems, and these problems make algorithms challenging for the data stream. In this paper, the DCT and swarm intelligence-based feature extraction approach is presented for the data stream as an alternative incremental feature extraction algorithm. The proposed approach has a simple and applicable structure for the data stream. The objective of the proposed study is to demonstrate the superiority of the DCT algorithm to PCA and IPCA algorithms for feature extraction of the data stream. The proposed approach is compared with the traditional PCA, IPCA-Li, CCFIPCA, IPCA-Ozawa, and CIKPCA on six real and synthetic data sets. The experimental results prove the success of DCT-based feature extraction approach and its advantage over PCA and incremental versions. Moreover, DCT-based approach has a less computational cost and time complexity, and so DCT requires less additional workload than PCA and IPCA algorithms. Additionally, the performance of the proposed approach with automatic feature selection is examined. The obtained results confirm the positive effect of automatic feature selection to data stream feature extraction. Therefore, feature selection that considers the structure of the data sets plays an essential role to be obtained higher classification accuracy. Furthermore, although the proposed approach uses an automatic selection mechanism that increases the learning time in the initial phase, the learning time is shorter than Ozawa’s IPCA method.
In this study, the number of the data stream instance using in the learning phase is determined experimentally and constantly for all data sets. As future work, the sample number of the data stream using in the learning phase will be determined dynamically according to the structure of data sets.
Author Contributions
All authors contributed equally and significantly in writing this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This research has no acknowledgments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DCT | Discrete Cosine Transform |
| PSO | Particle Swarm Optimization |
| APSO | Accelerated Particle Swarm Optimization |
| PCA | Principal Component Analysis |
| IPCA | Incremental Feature Extraction |
| CCFIPCA | Candid Covariance Free Incremental Principal Component Analysis |
| CIKPCA | Chunk Incremental Kernel Principal Component Analysis |
| MOA | Massive Online Analysis |
| Acc | Accuracy Ratio |
| NDSCC | The Number of the Data Stream that Classified Correctly |
References
- Tso, F.; Cu, L.; Zhang, L. Dragonnet: A robust mo-bile Internet service system for long-distance trains. IEEE Trans. Mob. Comput. 2013, 12, 2206–2218. [Google Scholar]
- Atzori, L.; Iera, A.; Morabit, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Armbrust, M.; Fox, A.; Griffith, R. A view of cloud computing. Commun. ACM 2010, 53, 50–58. [Google Scholar] [CrossRef]
- Fu, Z.; Sun, X.; Liu, Q.; Zhou, L.; Shu, J. Achieving efficient cloud search services: Multi-keyword ranked search over encrypted cloud data supporting parallel computing. IEICE Trans. Commun. 2015, E98-B, 190–200. [Google Scholar] [CrossRef]
- Lall, A.; Sekar, V.; Ogihara, M.; Xu, J.; Zhang, H. Data streaming algorithms for estimating entropy of network traffic. ACM Sigmetrics 2006, 34, 145–156. [Google Scholar] [CrossRef]
- Aceto, G.; Ciuonzo, D.; Montieri, A.; Pescapé, A. Mobile encrypted traffic classification using deep learning: Experimental evaluation, lessons learned, and challenges. IEEE Trans. Netw. Serv. 2019, 16, 445–458. [Google Scholar] [CrossRef]
- Gupta, A.; Birkner, R.; Canini, M.; Feamster, N.; Mac-Stoker, C.; Willinger, W. Network monitoring as a streaming analytics problem. In Proceedings of the 15th ACM Workshop on Hot Topics in Networks, Atlanta, GA, USA, 9–10 November 2016; pp. 106–112. [Google Scholar]
- Amini, A.; Saboohi, H.; Ying, W.T.; Herawan, T. A fast density-based clustering algorithm for real-time internet of things stream. Sci. World J. 2014, 2014, 926020. [Google Scholar] [CrossRef]
- Tan, C.; Ji, G. Semi-supervised incremental feature extraction for large-scale data stream. Concurr. Comp-Pract. E 2017, 29, e3914. [Google Scholar] [CrossRef]
- Zeng, X.Q.; Li, G.Z. Incremental partial least squares analysis of big streaming data. Pattern Recognit. 2014, 47, 3726–3735. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, B.; Liu, N.; Yan, S.; Cheng, Q.; Fan, W.; Yang, Q.; Xi, W.; Chen, Z. Effective and efficient dimensionality reduction for large-scale and streaming data preprocessing. TKDE 2006, 18, 320–333. [Google Scholar]
- Ahmed, N.; Natarajan, T.; Rao, K.R. Discrete cosine transform. IEEE Trans. Comput. 1974, C-23, 90–93. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal component analysis and factor analysis. In Principal Component Analysis; Springer: New York, NY, USA, 1986; pp. 115–128. [Google Scholar]
- Zhao, H.; Yuen, P.C.; Kwok, J.T. A novel incremental principal component analysis and its application for face recognition. IEEE Trans. Syst. Man. Cybern. B Cybern. 2006, 36, 873–886. [Google Scholar] [CrossRef] [PubMed]
- Hall, P.; Martin, R. Incremental Eigenanalysis for Classification. In Proceedings of the British Machine Vision Conference, Southampton, UK, 14–17 September 1998; pp. 286–295. [Google Scholar]
- Hall, P.; Marshall, D.; Martin, R. Merging and splitting eigenspace model. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1042–1049. [Google Scholar] [CrossRef]
- Liu, X.; Chen, T. Shot boundary detection using temporal statistics modeling. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; p. IV-3389. [Google Scholar]
- Li, Y. On incremental and robust subspace learning. Pattern Recognit. 2004, 37, 1509–1518. [Google Scholar] [CrossRef]
- Ozawa, S.; Pang, S.; Kasabov, N. A modified incremental principal component analysis for online learning of feature space and classifier. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence, Auckland, New Zealand, 9–13 August 2004; pp. 231–240. [Google Scholar]
- Ozawa, S.; Pang, S.; Kasabov, N. Incremental learning of chunk data for online pattern classification systems. IEEE Trans. Neural Netw. 2008, 19, 1061–1074. [Google Scholar] [CrossRef][Green Version]
- Rosas-Arias, L.; Portillo-Portillo, J.; Hernandez-Suarez, A.; Olivares-Mercado, J.; Sanchez-Perez, G.; Toscano-Medina, K.; Perez-Meana, H.; Orozco, A.L.S.; García Villalba, L.J. Vehicle Counting in Video Sequences: An Incremental Subspace Learning Approach. Sensors 2019, 19, 2848. [Google Scholar] [CrossRef]
- Fujiwara, T.; Chou, J.K.; Shilpika, S.; Xu, P.; Ren, L.; Ma, K.L. An incremental dimensionality reduction method for visualizing streaming multidimensional data. IEEE Trans. Vis. Comput. Graph. 2019, 26, 418–428. [Google Scholar] [CrossRef]
- Jain, P.; Jin, C.; Kakade, S.M.; Netrapalli, P.; Sidford, A. Streaming PCA: Matching Matrix Bernstein and Near-Optimal Finite Sample Guarantees for Oja’s Algorithm. In Proceedings of the 29th Annual Conference on Learning Theory, New-York City, NY, USA, 23–36 June 2016; pp. 1147–1164. [Google Scholar]
- Kuncheva, L.I.; Faithfull, W.J. Pca feature extraction for change detection in multidimensional unlabelled streaming data. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba Science City, Japan, 11–15 November 2012; pp. 1140–1143. [Google Scholar]
- Qahtan, A.A.; Alharbi, B.; Wang, S.; Zhang, X. A pca-based change detection framework for multidimensional data streams: Change detection in multidimensional data streams. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 935–944. [Google Scholar]
- Weng, J.; Zhang, Y.; Hwang, W.S. Candid covariance-free incremental principal component analysis. IEEE Trans. Pattern Anal. 2003, 25, 1034–1040. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, H.; Wang, S.; Saporta, G. Incremental modelling for compositional data streams. Commun. Stat-Simul. C 2019, 48, 2229–2243. [Google Scholar] [CrossRef]
- Tokumoto, T.; Ozawa, S. A fast incremental kernel principal component analysis for learning stream of data chunks. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 2881–2888. [Google Scholar]
- Ghashami, M.; Perry, D.J.; Phillips, J. Streaming kernel principal component analysis. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; pp. 1365–1374. [Google Scholar]
- Joseph, A.A.; Tokumoto, T.; Ozawa, S. Online feature extraction based on accelerated kernel principal component analysis for data stream. Evol. Syst. 2016, 7, 15–27. [Google Scholar] [CrossRef]
- Chin, T.J.; Suter, D. Incremental kernel principal component analysis. IEEE Trans. Image Process. 2007, 16, 1662–1674. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Ozawa, S.; Abe, S. An efficient incremental kernel principal component analysis for online feature selection. In Proceedings of the International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007; pp. 2346–2351. [Google Scholar]
- Fredrik, H.; Paul, N. Incremental kernel PCA and the Nyström method. arXiv 2018, arXiv:1802.00043. [Google Scholar]
- Liu, J.; Zhang, J.; Lee, S.W.; Zhao, F.; Rekik, I.; Shen, D. Two-Phase Incremental Kernel PCA for Learning Massive or Online Datasets. Complexity 2019, 2019, 5937274. [Google Scholar]
- Dabbaghchian, S.; Ghaemmaghami, M.P.; Aghag-olzadeh, A. Feature extraction using discrete cosine transform and discrimination power analysis with a face recognition technology. Pattern Recognit. 2010, 43, 1431–1440. [Google Scholar] [CrossRef]
- Nassih, B.; Amine, A.; Ngadi, M.; Hmina, N. DCT and HOG Feature Sets Combined with BPNN for Efficient Face Classification. Procedia Comput. Sci. 2019, 148, 116–125. [Google Scholar] [CrossRef]
- Tjahyadi, R.; Liu, W.; Venkatesh, S. Application of the DCT energy histogram for face recognition. In ICITA 2004: Proceedings of the Second International Conference on Information Technology and Applications; IEEE: Sydney, Australia, 2004; pp. 314–319. [Google Scholar]
- Er, M.J.; Chen, W.; Wu, S. High-speed face recognition based on discrete cosine transform and RBF neural networks. IEEE Trans. Neural Netw. 2005, 16, 679–691. [Google Scholar] [CrossRef]
- Yu, F.; Oyana, D.; Hou, W.C.; Wainer, M. Approximate Clustering on Data Streams Using Discrete Cosine Transform. JIPS 2010, 6, 67–78. [Google Scholar] [CrossRef]
- Hayat, M.Z.; Hashemi, M.R. A dct based approach for detecting novelty and concept drift in data streams. In Proceedings of the 2010 International Conference of Soft Computing and Pattern Recognition, Paris, France, 7–10 December 2010; pp. 373–378. [Google Scholar]
- Yan, F.; Hou, W.C.; Jiang, Z.; Huan, Y.; Che, D. Selectivity estimation of range queries over data streams using cosine transform. Int. J. Comput. Sci. 2007, 1, 422–439. [Google Scholar]
- Sharma, V.K.; Mahapatra, K.K.; Acharya, B. Visual object tracking based on discriminant DCT features. DSP 2019, 95, 102572. [Google Scholar] [CrossRef]
- Cho, H.; Han, S.; Hwang, S.Y. Design of an Efficient Real-Time Algorithm Using Reduced Feature Dimension for Recognition of Speed Limit Signs. Sci. World J. 2013, 2013, 135614. [Google Scholar] [CrossRef]
- Rashidi, S.; Fallah, A.; Towhidkhah, F. Feature extraction based DCT on dynamic signature verification. Scientia Iranica 2012, 19, 1810–1819. [Google Scholar] [CrossRef]
- Wijaya, I.G.P.S.; Husodo, A.Y.; Arimbawa, I.W.A. Real time face recognition using DCT coefficients based face descriptor. In Proceedings of the 2016 International Conference on Informatics and Computing (ICIC), Mataram, Indonesia, 28–29 October 2016; pp. 142–147. [Google Scholar]
- Loizou, C.P.; Pantziaris, M.; Pattichis, C.S.; Seimenis, I. Brain MR Image Normalization in Texture Analysis of Multiple Sclerosis. JBGC 2013, 3. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 Novenber–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Fong, S.; Wong, R.; Vasilakos, A.V. Accelerated PSO swarm search feature selection for data stream mining big data. IEEE Trans. Serv. Comput. 2015, 9, 33–45. [Google Scholar] [CrossRef]
- Cheng, X.; Ciuonzo, D.; Rossi, P.S. Multi-bit decentralized detection through fusing smart & dumb sensors based on rao test. IEEE Trans. Aerosp. Electr. Syst. 2019. [Google Scholar] [CrossRef]
- Cheng, X.; Ciuonzo, D.; Rossi, P.S. Multi-bit decentralized detection of a weak signal in wireless sensor networks with a rao test. In Proceedings of the 2018 IEEE 23rd International Conference on Digital Signal Processing (DSP), Shanghai, China, 19–21 November 2018; pp. 1–5. [Google Scholar]
- Fong, S.; Liang, J.; Fister, I.; Mohammed, S. Gesture recognition from data streams of human motion sensor using accelerated PSO swarm search feature selection algorithm. J. Sens. 2015, 2015, 205707. [Google Scholar] [CrossRef]
- Deshpande, M.; Karypis, G. Evaluation of techniques for classifying biological sequences. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Taipei, Taiwan, 6–8 May 2002; pp. 417–431. [Google Scholar]
- Kong, X.; Philip, S.Y. An ensemble-based approach to fast classification of multi-label data streams. In Proceedings of the 7th International Conference on Collaborative Computing: Networking Applications and Worksharing (CollaborateCom), Orlanda, FL, USA, 15–18 October 2011; pp. 95–104. [Google Scholar]
- Khan, M.; Ding, Q.; Perrizo, W. k-nearest neighbor classification on spatial data streams using P-trees. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Taipei, Taiwan, 6–8 May 2002; pp. 517–528. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2019. [Google Scholar]
- Bifet, A.; Holmes, G.; Kirkby, R.; Pfahringer, B. Moa: Massive online analysis. JMLR 2010, 11, 1601–1604. [Google Scholar]
- Laohakiat, S.; Phimoltares, S.; Lursinsap, C. A clustering algorithm for stream data with LDA-based unsupervised localized dimension reduction. Inf. Sci. 2017, 381, 104–123. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).