Small Wind Turbine Blade Design and Optimization
Abstract
1. Introduction
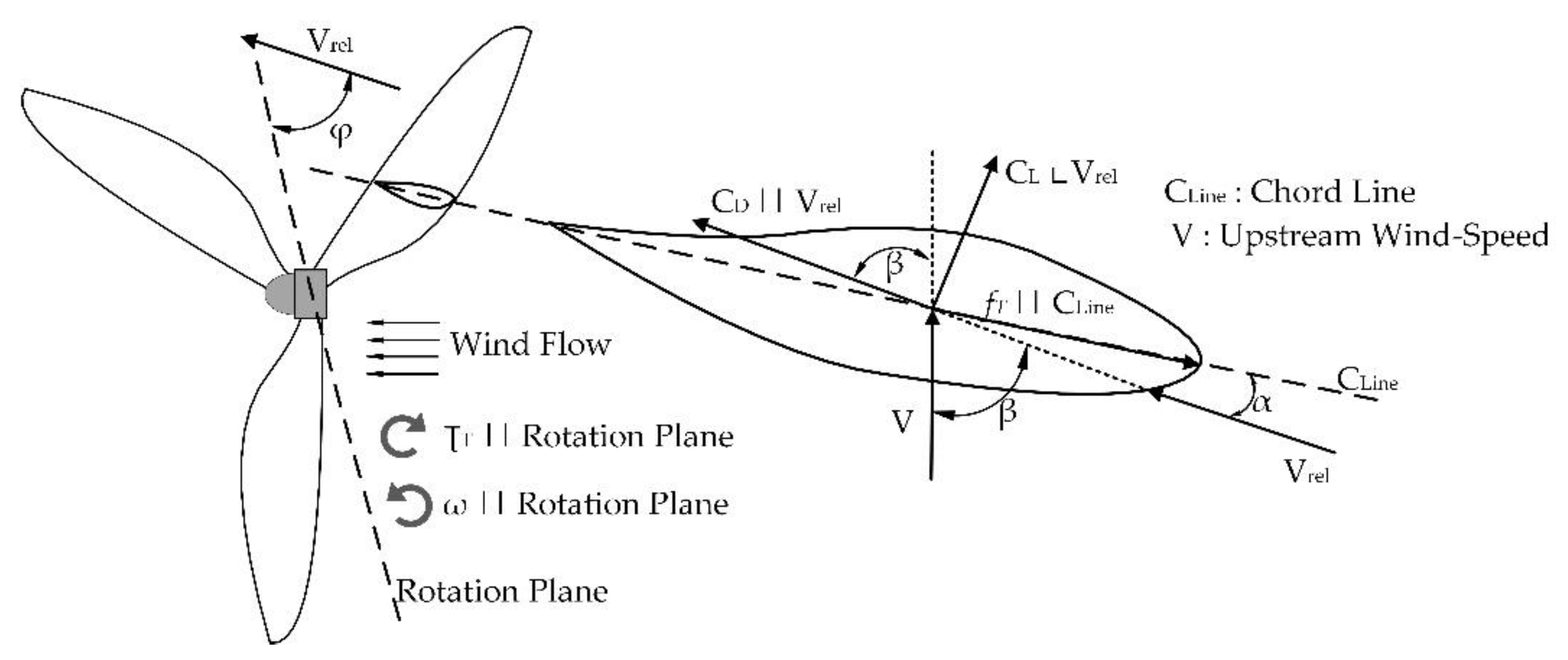
2. Subject Theory
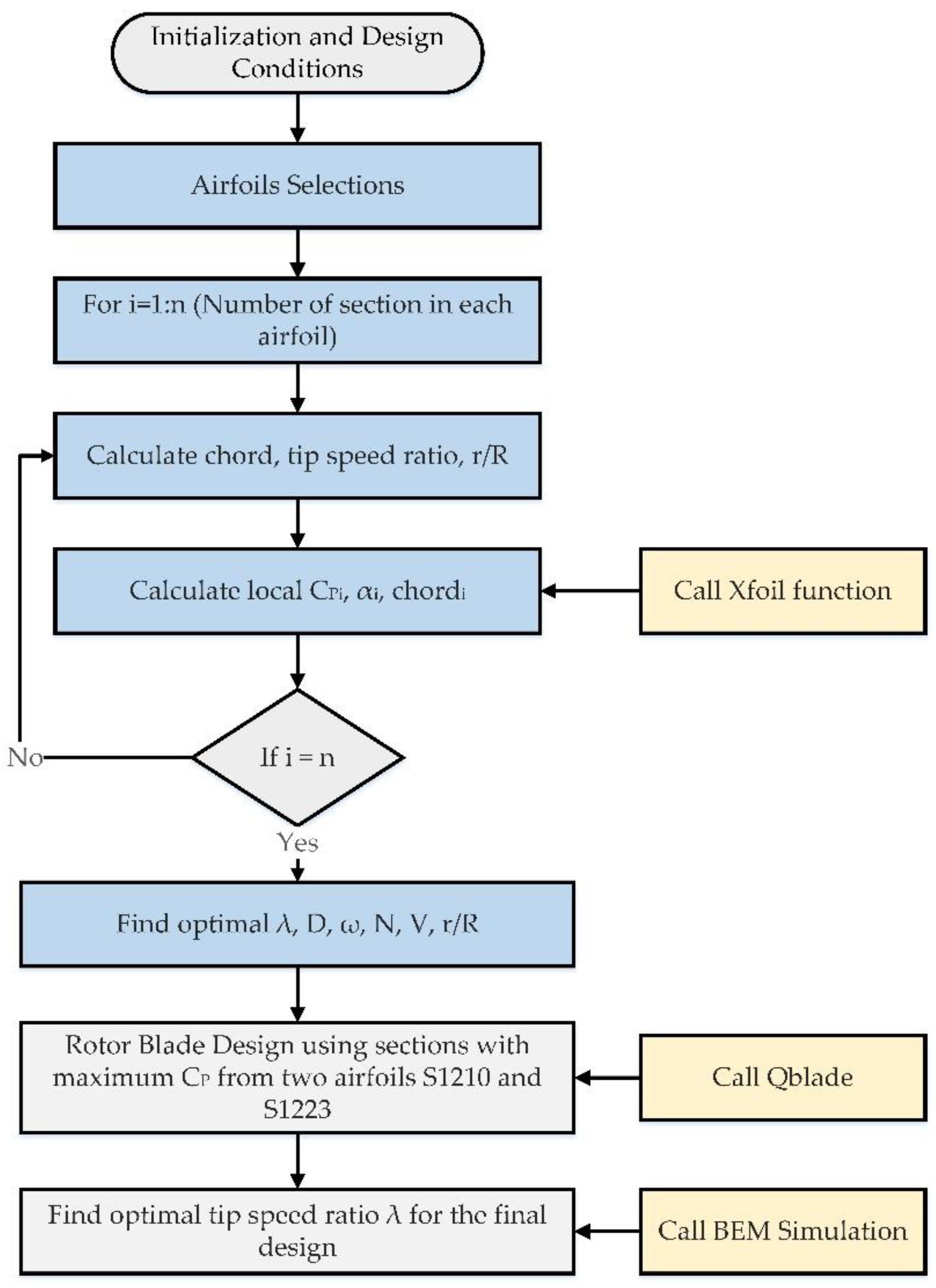
3. Design Methodology
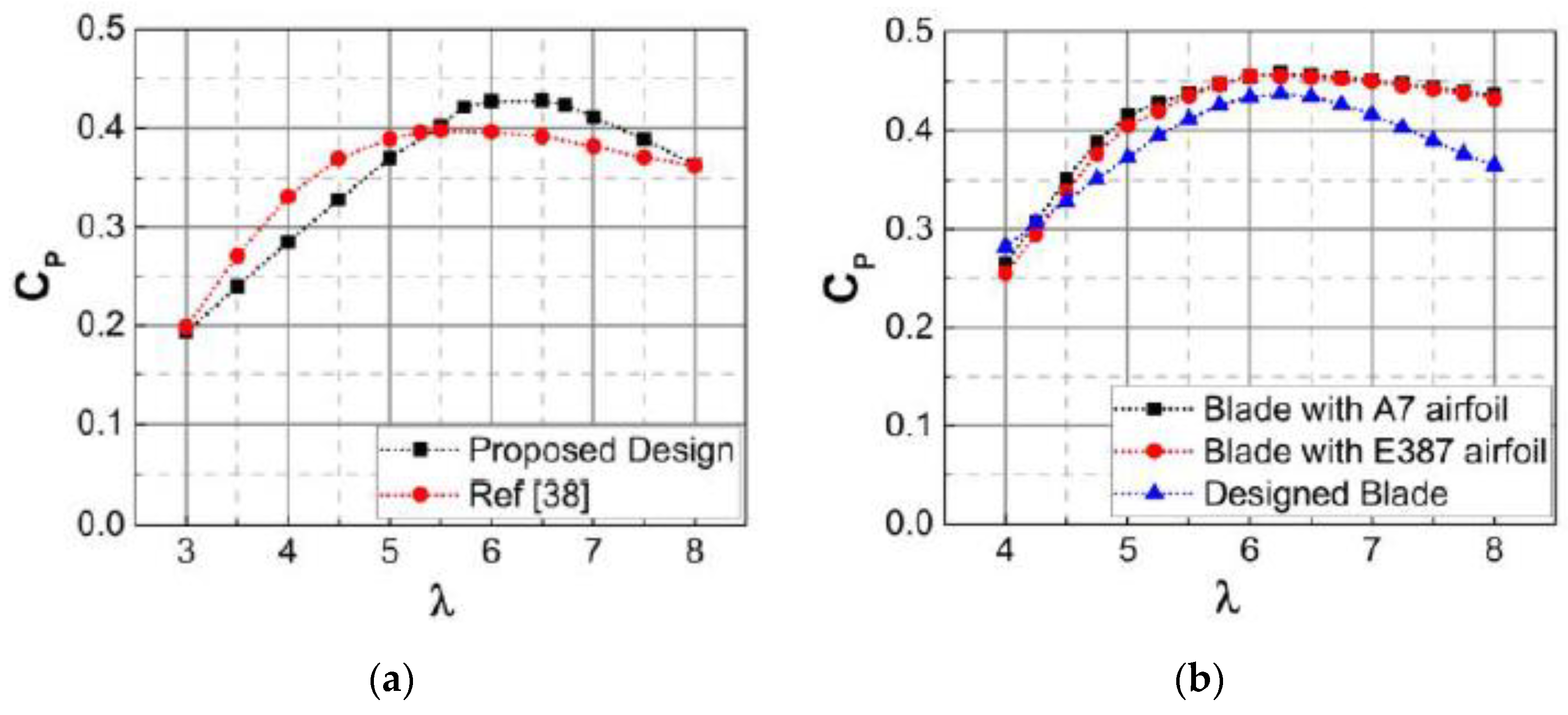
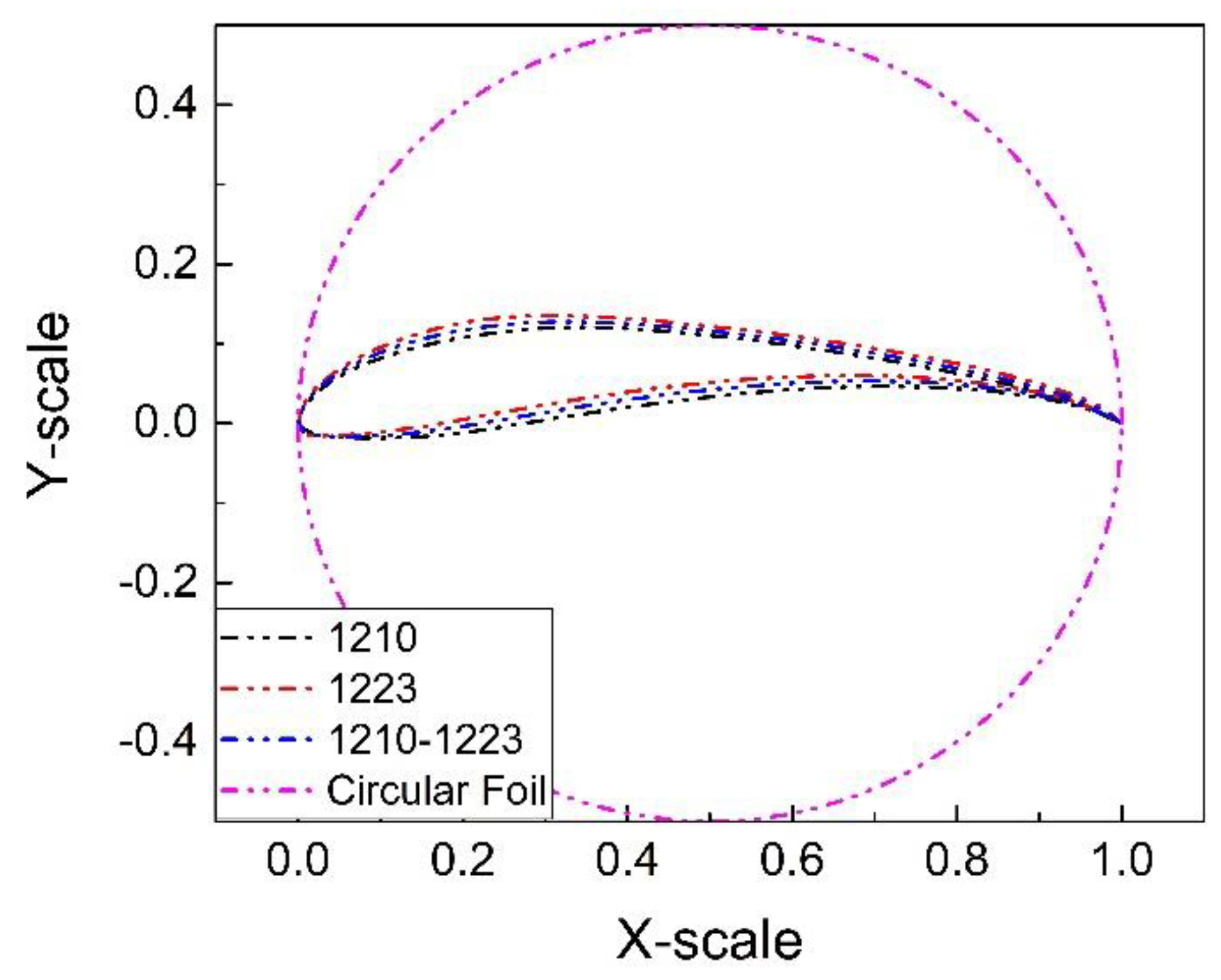
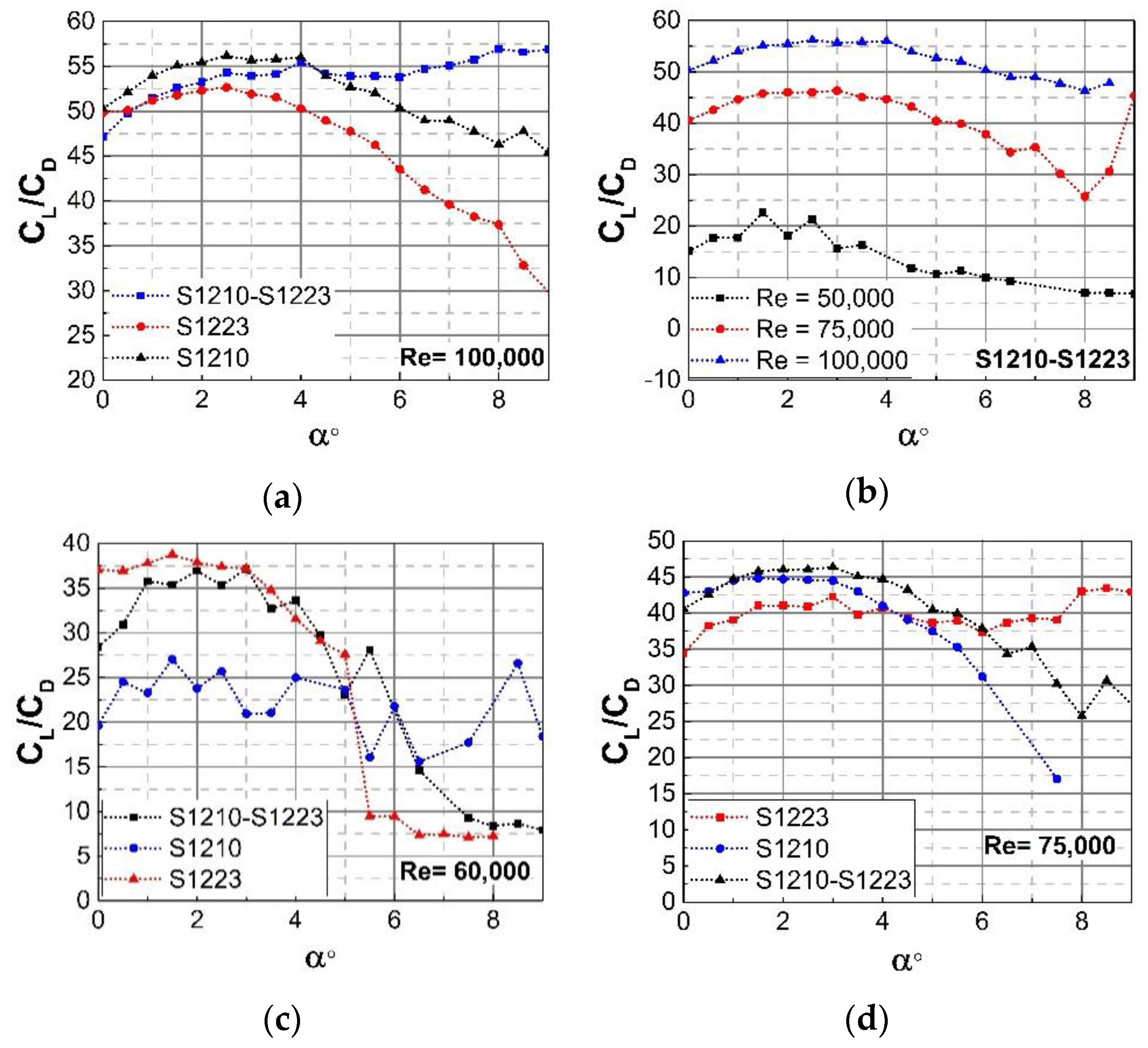
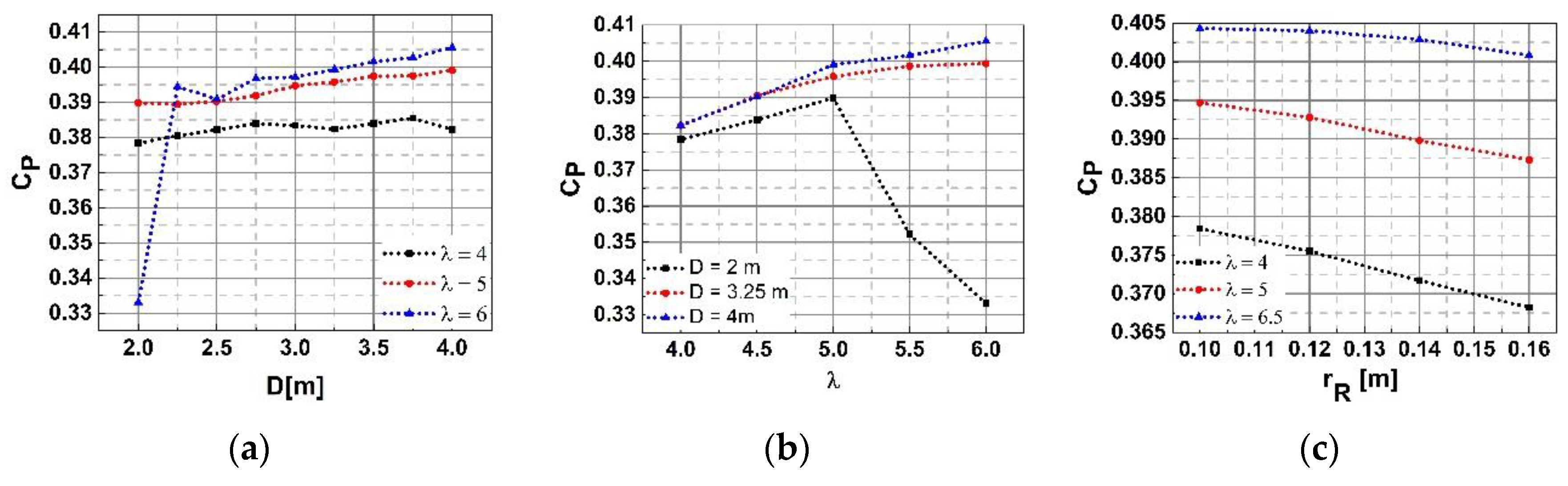
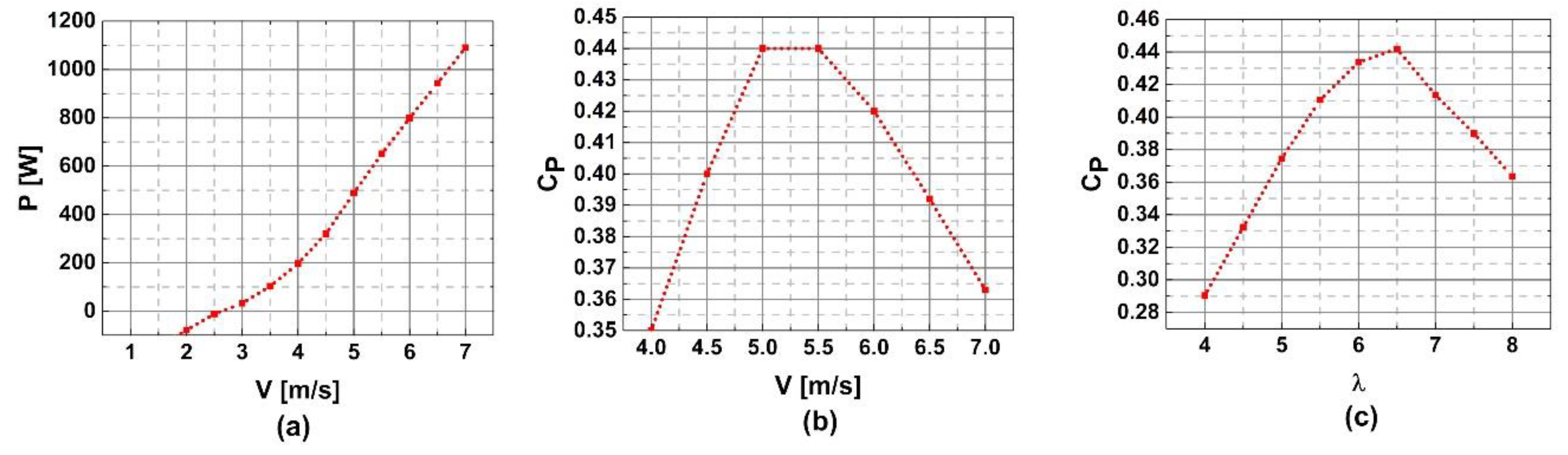
4. Results and Discussion
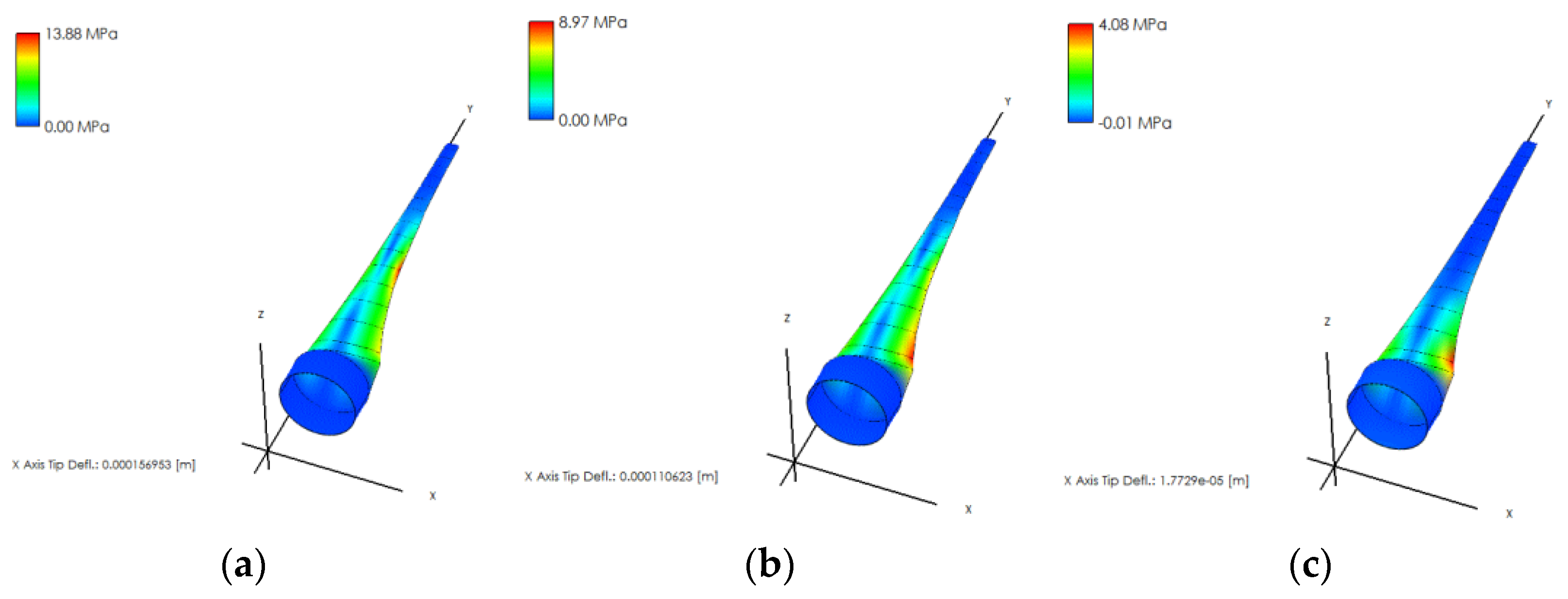
5. Validation of the Proposed Approach
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ρ | Density of air (1.22 kg/m3) |
| N | Number of blades |
| D | Blade Diameter (m) |
| P | Mechanical Power (W) |
| V | Upstream wind-speed (m/s) |
| CP | Power coefficient |
| CQ | Torque coefficient |
| c | Cross section Area at radius r (m2) |
| λ, λ0 | tip-speed ratio, optimum |
| FL | Lift force (N) |
| FD | Drag force (N) |
| CL | Lift coefficient |
| CD | Drag coefficient |
| FT | Tangential force (N) |
| τr | Torque per unit-length (N) |
| Vrel | Relative wind speed (m/s) |
| R | Radius of the rotor (m) |
| Φ | Angle of relative wind (deg) |
| β | Pitch angle (deg) |
| ⍵ | Rotational Speed (rad/s) |
| A | Area (m2) |
| Rr | External radius to internal radius ratio (r / R) |
| V | Average wind speed (m/s) |
| a | Axial Induction factor |
| a’ | Radial Induction factor |
| Cline | Chord line |
| AoA | Angle of Attack |
| r | Internal radius (Distance between the axis of rotation and the blade section) (m) |
| Re | Reynolds number |
References
- Hau, E. Wind Turbines: Fundamentals, Technologies, Application, Economics; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Carbon, T. Small-Scale Wind Energy-Policy Insights and Practical Guidance; Carbon Trust: London, UK, 2008. [Google Scholar]
- World Wind Energy Association. Wind Power Capacity Reaches 539 GW, 52.6 GW Added in 2017. Available online: https://wwindea.org/blog/2018/02/12/2017-statistics/ (accessed on 20 February 2018).
- Sessarego, M.; Wood, D. Multi-dimensional optimization of small wind turbine blades. Renew. Wind Water Sol. 2015, 2, 9. [Google Scholar] [CrossRef]
- Al-Abadi, A.; Özgür, E.; Horst, W.; Antonio, D. A design and optimization method for matching the torque of the wind turbines. J. Renew. Sustain. Energy 2015, 7, 1–11. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Hassanabad, A.H.; Dadvand, A. Aerodynamic shape optimization and analysis of small wind turbine blades employing the Viterna approach for post-stall region. Alex. Eng. J. 2016, 55, 2035–2043. [Google Scholar] [CrossRef]
- El-Mouhsine, S.; Oukassou, K.; Ichenial, M.M.; Kharbouch, B.; Hajraoui, A. Aerodynamics and structural analysis of wind turbine blade. Procedia Manuf. 2018, 22, 747–756. [Google Scholar] [CrossRef]
- Lanzafame, R.; Mauro, S.; Messina, M. HAWT Design and Performance Evaluation: Improving the BEM Theory Mathematical Models. Energy Procedia 2015, 82, 172–179. [Google Scholar] [CrossRef]
- Ribeiro, A.F.P.; Awruch, A.M.; Gomes, H.M. An airfoil optimization technique for wind turbines. Appl. Math. Model. 2012, 36, 4898–4907. [Google Scholar] [CrossRef]
- Nada, A.A.; Al-Shahrani, A.S. Shape Optimization of Low Speed Wind Turbine Blades using Flexible Multibody Approach. Energy Procedia 2017, 134, 577–587. [Google Scholar] [CrossRef]
- Jeong, J.; Park, K.; Jun, S. Design optimization of a wind turbine blade to reduce the fluctuating unsteady aerodynamic load in turbulent wind. J. Mech. Sci. Technol. 2012, 26, 827. [Google Scholar] [CrossRef]
- Erfort, G.; Von Backstrom, T.W.; Venter, G. Numerical optimization of a small-scale wind turbine through the use of surrogate modelling. J. Energy S. Afr. 2017, 28, 79–91. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mohammadi, A.; Mohammadi, M.; Minaei, H.N. Optimization of Small-Scale Wind Turbine Blades for Low Speed Conditions. JOCET 2016, 4, 140–143. [Google Scholar] [CrossRef]
- Tenguria, N.; Mittal, N.D.; Ahmed, S. Review on Horizontal Axis Wind Turbine Rotor Design and Optimization. Trends Appl. Sci. Res. 2011, 6, 309–344. [Google Scholar] [CrossRef]
- Vivek, C.M.; Gopikrishnan, P.; Murugesh, R.; Mohamed, R.R. A Review on Vertical and Horizontal Axis Wind Turbine. IJRET 2017, 4, 247–250. [Google Scholar]
- Jureczko, M.; Pawlak, M.; Mezyk, A. Optimization of wind turbine blades. J. Mater. Process. Technol. 2005, 167, 463–471. [Google Scholar] [CrossRef]
- Benini, E.; Toffolo, A. Optimal Design of Horizontal-Axis Wind Turbines Using Blade-Element Theory and Evolutionary Computation. J. Sol. Energy Eng. 2002, 124, 357–363. [Google Scholar] [CrossRef]
- Chehouri, A.; Younes, R.; Ilinca, A.; Perron, J. Wind Turbine Design: Multi-Objective Optimization. arXiv 2016, arXiv:1610.00975. [Google Scholar]
- Thumthae, C. Optimum Blade Profiles for a Variable-Speed Wind Turbine in Low Wind Area. Energy Procedia 2015, 75, 651–657. [Google Scholar] [CrossRef]
- Tang, X.; Huang, X.; Peng, R.; Liu, X. A Direct Approach of Design Optimization for Small Horizontal Axis Wind Turbine Blades. Procedia CIRP 2015, 36, 12–16. [Google Scholar] [CrossRef]
- Lin, Y.T.; Chiu, P.H.; Huang, C.C. An experimental and numerical investigation on the power performance of 150 kW horizontal axis wind turbine. Renew. Energy 2017, 113, 85–93. [Google Scholar] [CrossRef]
- Pourrajabian, A.; Afshar, P.A.N.; Ahmadizadeh, M.; Wood, D. Aero-structural design and optimization of a small wind turbine blade. Renew. Energy 2016, 87, 837–848. [Google Scholar] [CrossRef]
- Tahir, A.; Elgabaili, M.; Rajab, Z.; Buaossa, N.; Khalil, A.; Mohamed, F. Optimization of small wind turbine blades using improved blade element momentum theory. Wind Eng. 2019, 43, 1–12. [Google Scholar] [CrossRef]
- Battisti, L.; Benini, E.; Brighenti, A.; Dell’Anna, S.; Castelli, M.R. Small wind turbine effectiveness in the urban environment. Renew. Energy 2018, 129, 102–113. [Google Scholar] [CrossRef]
- Karthikeyan, N.; Murugavel, K.K.; Kumar, S.A.; Rajakumar, S. Review of aerodynamic developments on small horizontal axis wind turbine blade. Renew. Sustain. Energy Rev. 2015, 42, 801–822. [Google Scholar] [CrossRef]
- Singh, R.K.; Ahmed, M.R. Blade design and performance testing of a small wind turbine rotor for low wind speed applications. Renew. Energy 2013, 50, 812–819. [Google Scholar] [CrossRef]
- Song, D.; Fan, X.; Yang, J.; Liu, A.; Chen, S.; Joo, Y.H. Power extraction efficiency optimization of horizontal-axis wind turbines through optimizing control parameters of yaw control systems using an intelligent method. Appl. Energy 2018, 224, 267–279. [Google Scholar] [CrossRef]
- Sarkar, M.; Julai, S.; Wen Tong, C.; Toha, S.F. Effectiveness of Nature-Inspired Algorithms using ANFIS for Blade Design Optimization and Wind Turbine Efficiency. Symmetry 2019, 11, 456. [Google Scholar] [CrossRef]
- Bianchi, F.D.; De Battista, H.; Mantz, R.J. Wind Turbine Control Systems: Principles, Modeling and Gain Scheduling Design; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Ingram, G. Wind Turbine Blade Analysis Using the Blade Element Momentum Method; Version 1.1.; Durham University: Durham, NC, USA, 2011. [Google Scholar]
- Sriti, M. Improved blade element momentum theory (BEM) for predicting the aerodynamic performances of horizontal Axis wind turbine blade (HAWT). Tech. Mech. Sci. J. Fundam. Appl. Eng. Mech. 2018, 38, 191–202. [Google Scholar]
- Kavari, G.; Tahani, M.; Mirhosseini, M. Wind shear effect on aerodynamic performance and energy production of horizontal axis wind turbines with developing blade element momentum theory. J. Clean. Prod. 2019, 219, 368–376. [Google Scholar] [CrossRef]
- Dehouck, V.; Lateb, M.; Sacheau, J.; Fellouah, H. Application of the Blade Element Momentum Theory to Design Horizontal Axis Wind Turbine Blades. J. Sol. Energy Eng. 2018, 140, 014501. [Google Scholar] [CrossRef]
- Fingersh, L.; Hand, M.; Laxson, A. Wind Turbine Design Cost and Scaling Model; No. NREL/TP-500-40566; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2006.
- Selig, M.S.; Guglielmo, J.J.; Broeren, P.; Giguere, P. Summary of Low-Speed Airfoil Data; Volume 1; SoarTech Publications: Virginia Beach, VA, USA, 1995. [Google Scholar]
- Selig, M.S.; McGranahan, B.D. Wind Tunnel Aerodynamic Tests of Six Airfoils for Use on Small Wind Turbines Period of Performance; NREL/SR-500-34515; Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2003; p. 1188.
- Probst, O.; Martínez, J.; Elizondo, J.; Monroy, O. Small Wind Turbine Technology Wind Turbines; Al-Bahadly, I., Ed.; InTech: Rijejka, Croatia, 2011; ISBN 978-953-307-221-0. [Google Scholar] [CrossRef]
- Bai, C.J.; Wang, W.C.; Chen, P.W.; Chong, W.T. System integration of the horizontal-axis wind turbine: The design of turbine blades with an axial-flux permanent magnet generator. Energies 2014, 7, 7773–7793. [Google Scholar] [CrossRef]
- Shen, X.; Avital, E.; Paul, G.; Rezaienia, M.A.; Wen, P.; Korakianitis, T. Experimental study of surface curvature effects on aerodynamic performance of a low Reynolds number airfoil for use in small wind turbines. J. Renew. Sustain. Energy 2016, 8, 053303. [Google Scholar] [CrossRef]
| Number of Variables and Output Parameters | Symbol | Description |
|---|---|---|
| 1 | Number of Blades | |
| 2 | Tip speed ratio (unitless) | |
| 3 | Rotor diameter (m) | |
| 4 | Angular velocity (rad/s) | |
| 5 | Induction factor (unitless) | |
| 6 | Wind speed (m/s) | |
| 7 | Power coefficient (%) | |
| 8 | Watts | |
| 9 | /R | Internal-to-external radius ratio |
| λ | No. of Blades | D (m) | ⍵ (rad/s) | a | V (m/s) | r/R | CP(trap) | CP(sim) |
|---|---|---|---|---|---|---|---|---|
| 6 | 3 | 4 | 16.5 | 0.275 | 5.5 | 0.1 | 0.391876 | 0.405566 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhsen, H.; Al-Kouz, W.; Khan, W. Small Wind Turbine Blade Design and Optimization. Symmetry 2020, 12, 18. https://doi.org/10.3390/sym12010018
Muhsen H, Al-Kouz W, Khan W. Small Wind Turbine Blade Design and Optimization. Symmetry. 2020; 12(1):18. https://doi.org/10.3390/sym12010018
Chicago/Turabian StyleMuhsen, Hani, Wael Al-Kouz, and Waqar Khan. 2020. "Small Wind Turbine Blade Design and Optimization" Symmetry 12, no. 1: 18. https://doi.org/10.3390/sym12010018
APA StyleMuhsen, H., Al-Kouz, W., & Khan, W. (2020). Small Wind Turbine Blade Design and Optimization. Symmetry, 12(1), 18. https://doi.org/10.3390/sym12010018