Constitutive Model of Stress-Dependent Seepage in Columnar Jointed Rock Mass
Abstract
1. Introduction
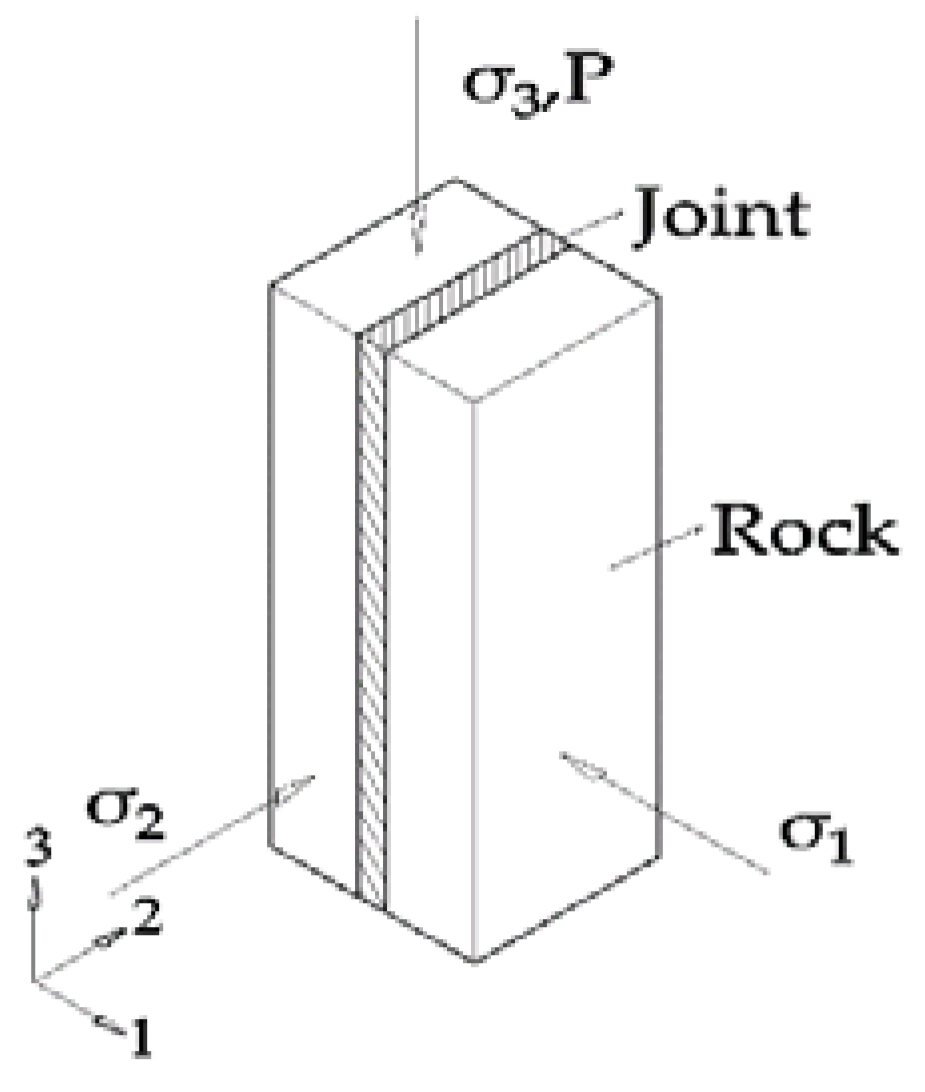
2. Establishment of Seepage Model for Stress-Dependent Fractured Rock Mass
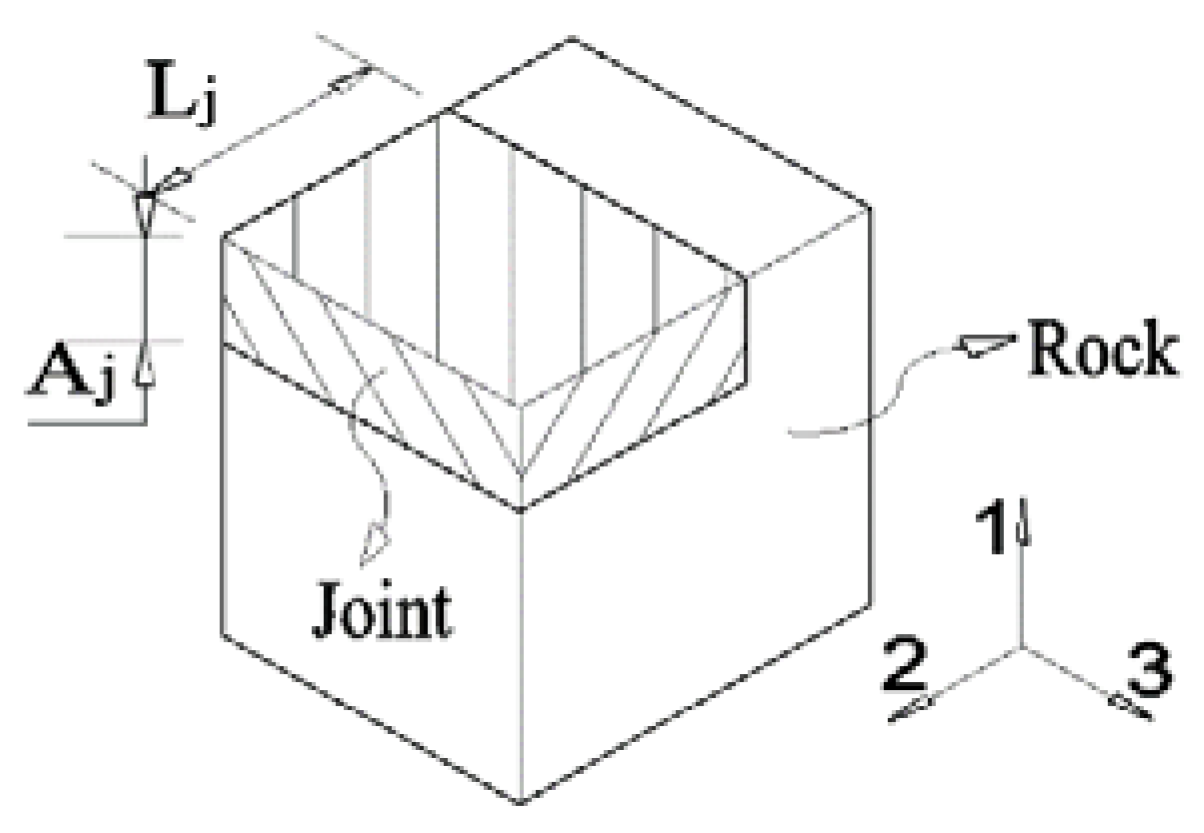
2.1. Seepage Model
2.2. Stress-Dependent Seepage Model
3. Establishment of Seepage Model for Stress-Dependent Fractured Rock Mass
3.1. Stress-Dependent Seepage Model
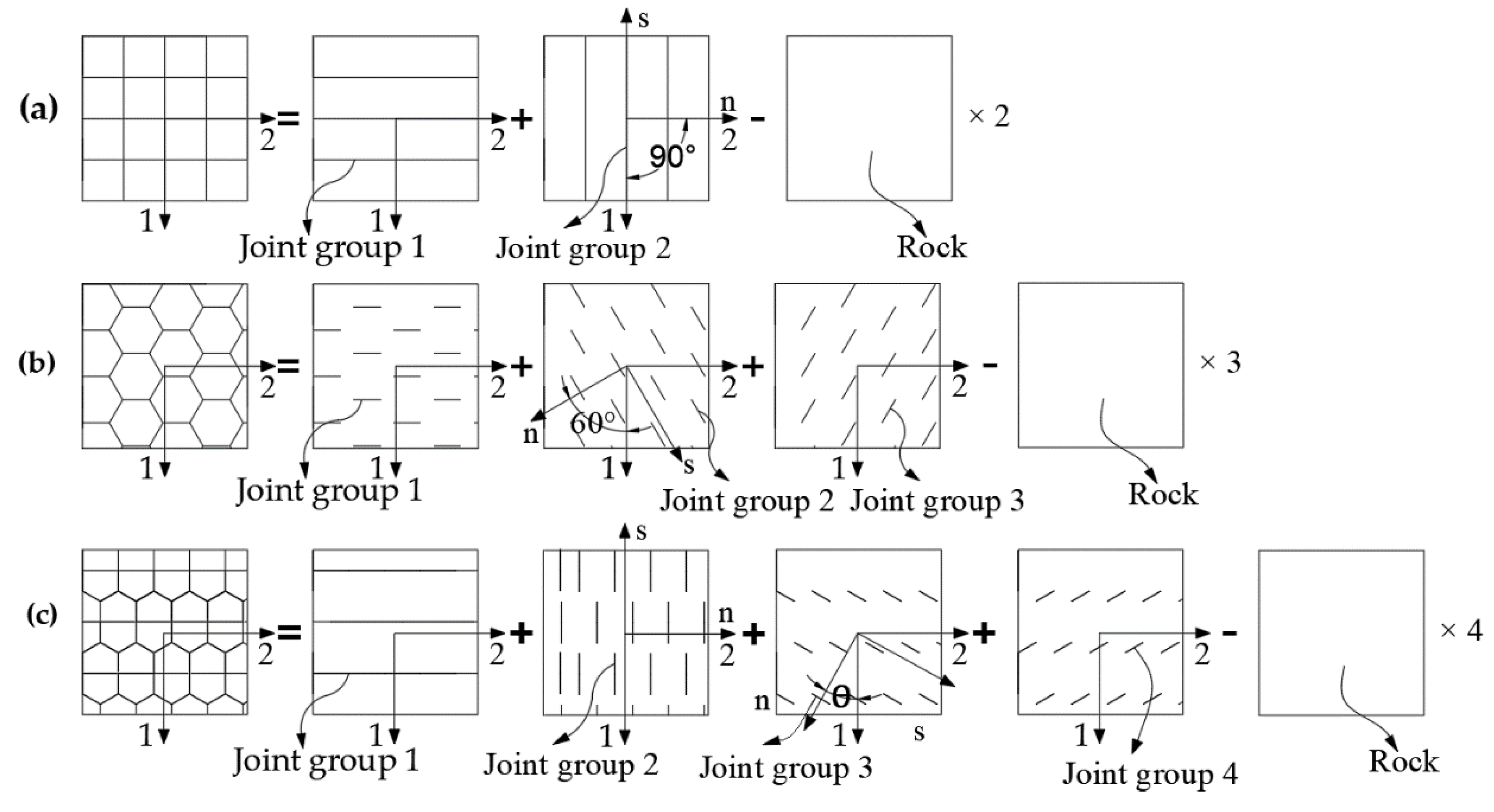
3.2. Constitutive Equation of Joint in the 1-2 Plane
3.3. Establishment of Three-Dimensional Joint Flexibility Matrix
3.4. Establishment of Permeability Coefficient KZZ of the Column-Axis Equation
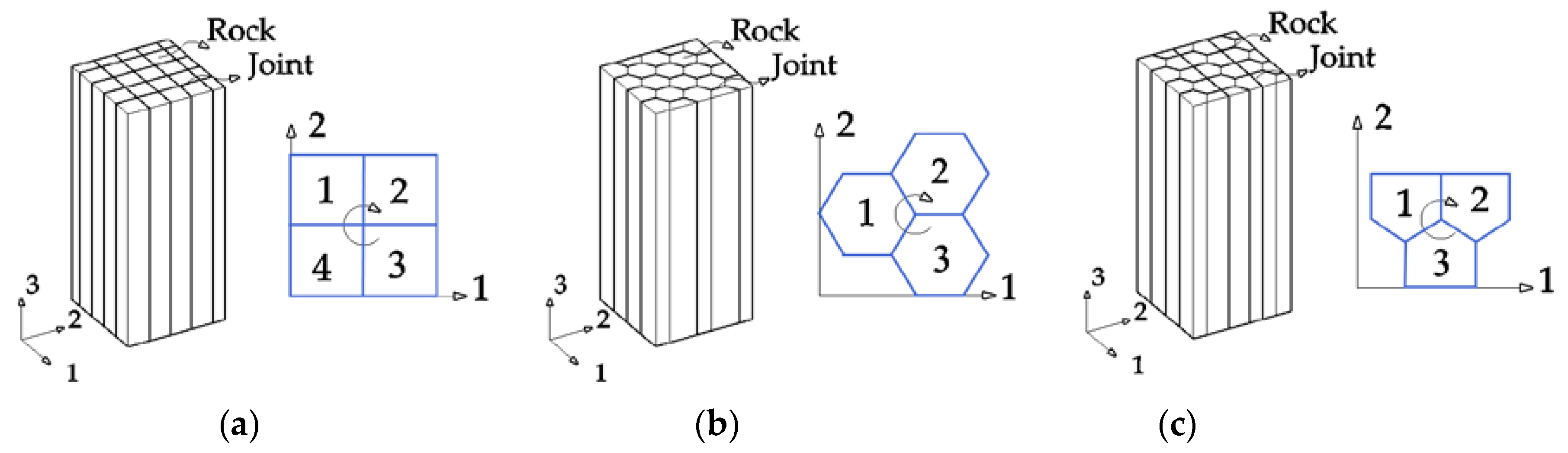
4. Verification and Comparison of CJRM Seepage Constitutive Models
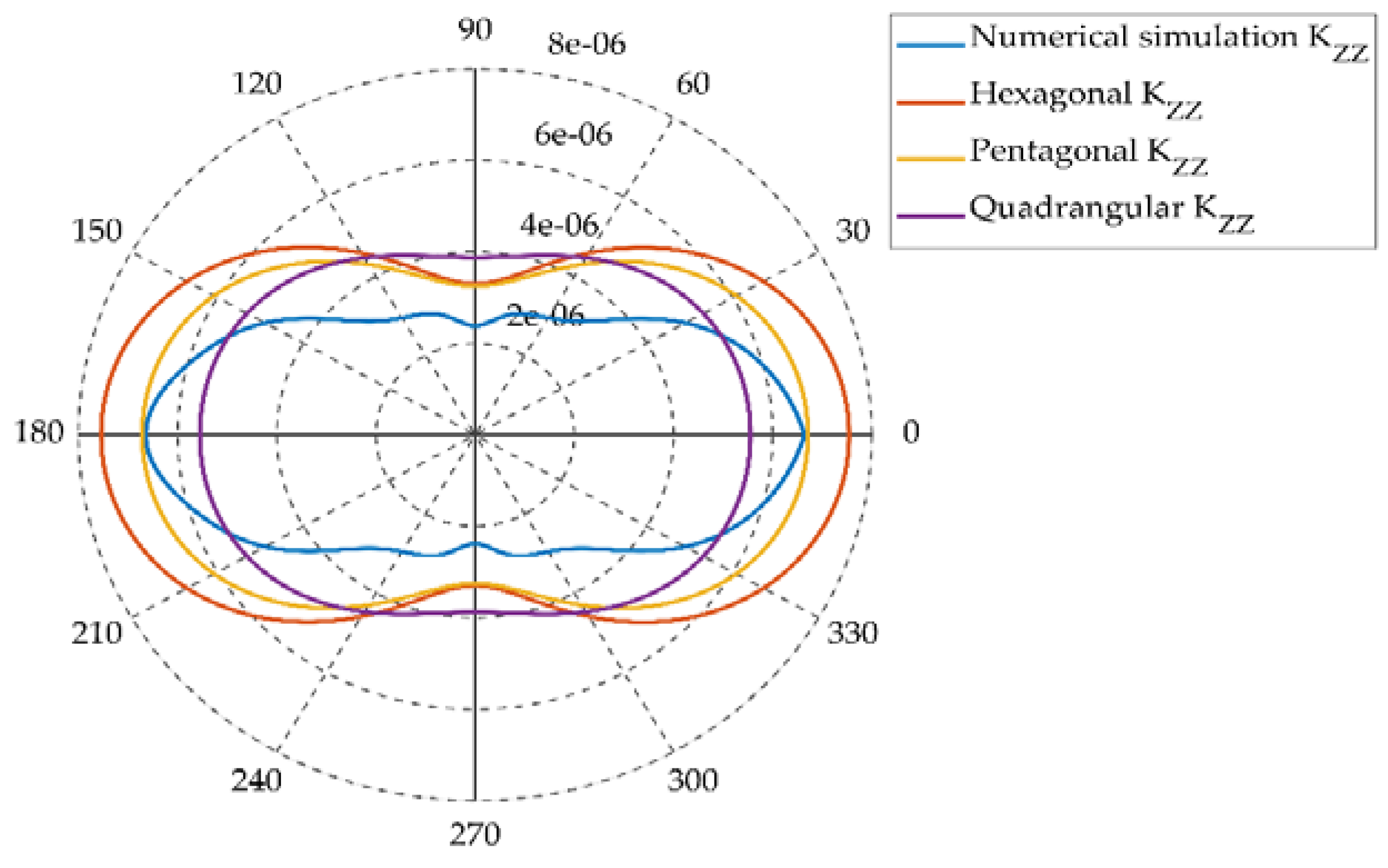
4.1. Comparison and Analysis of Three Constitutive Models and Numerical Simulation Results
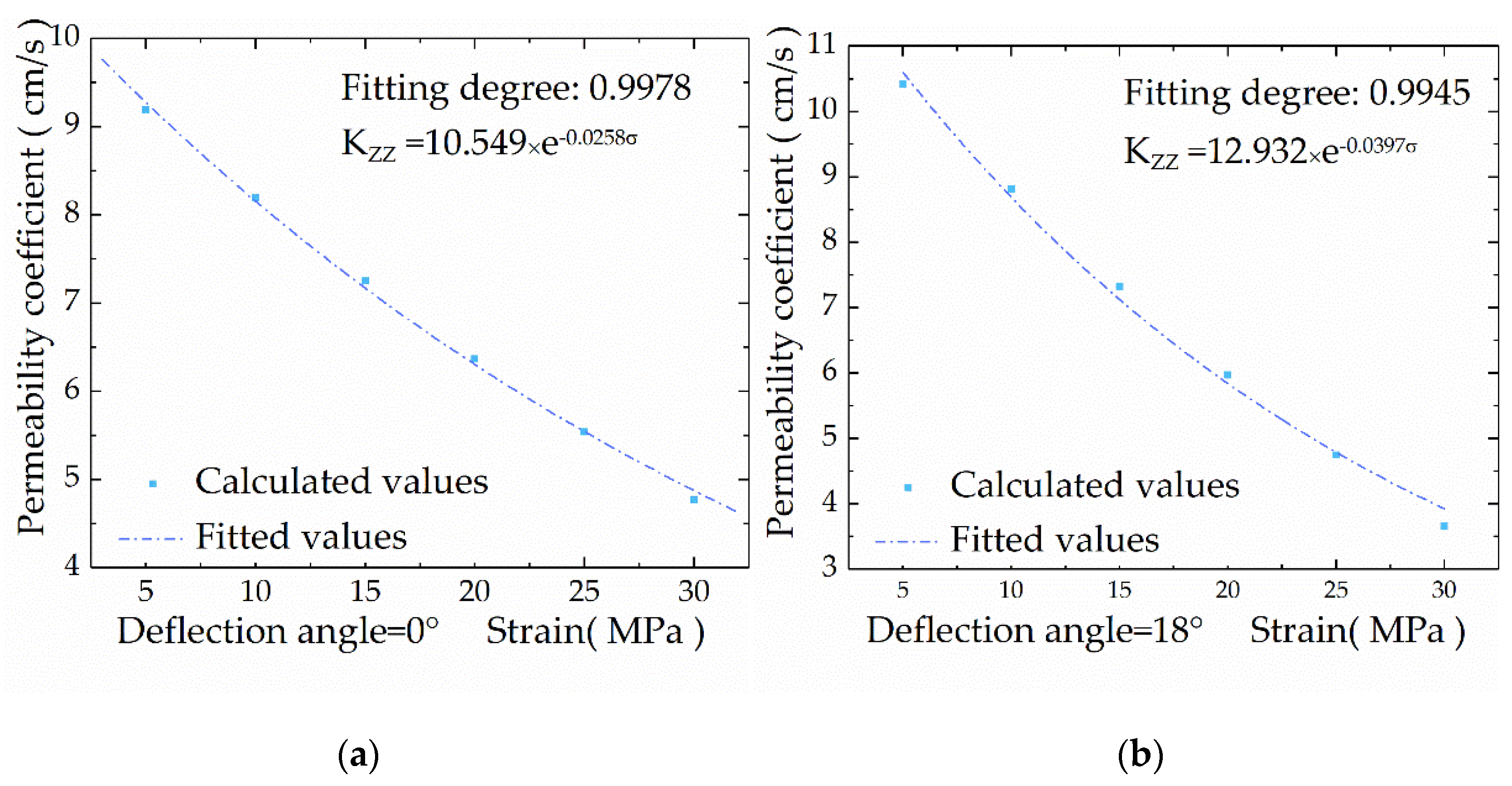
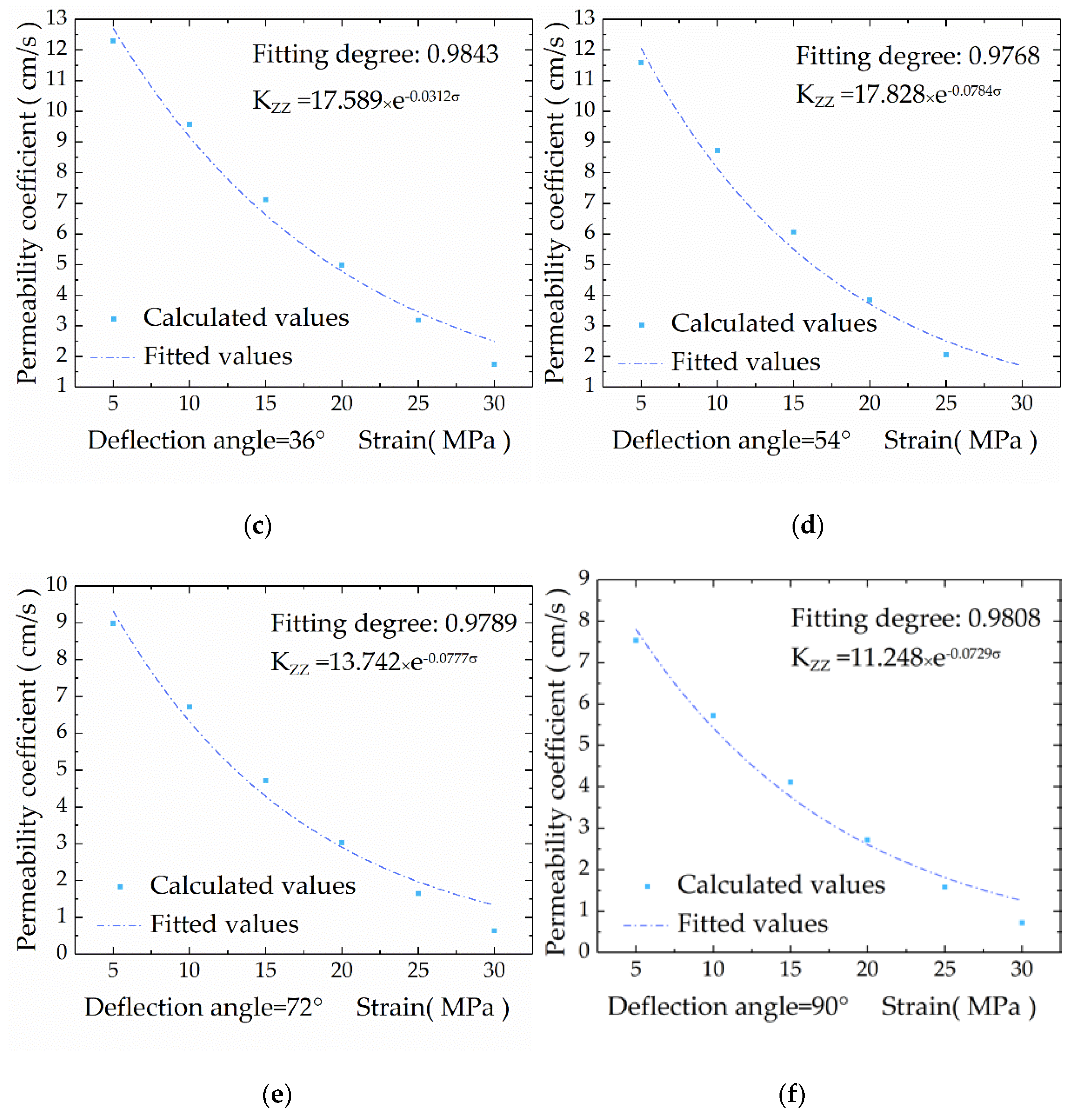
4.2. The Variation Law of Permeability Coefficient of Pentagonal Prism Model with Confining Pressure
5. Conclusions
- The three models applied to the Baihetan project were able to reflect the basic seepage characteristics. Compared with the Quadrangular prism and the Hexagonal prism model, the calculation results of the Pentagonal prism model were most consistent with the numerical simulation results. This is because the Pentagonal prism model not only has a completely penetrating joint, but also a mutual bite between the prisms, which is able to truly reflect the seepage characteristics of the columnar jointed rock mass.
- The permeability coefficients calculated by the seepage constitutive model of the three columnar jointed rock masses reached their minimum when the deflection angle of the prism was β = n∙90°(n = 1,3), and reached their maximum when the deflection angle of the cylinder was β = (n − 1)∙90°(n = 1,3). This is because at β = n∙90°(n = 1,3), the confining pressure of the column is completely converted into normal stress, and the joint strain is high. As the deflection angle gradually decreases to β = (n − 1)∙90°(n = 1,3), the partial confining pressure causes the joint shear slip, and the joint strain becomes smaller, leading to a larger permeability coefficient of the joint.
- The law of permeability coefficient with the change of confining pressure calculated by the seepage constitutive models proposed in this paper can be expressed as a negative exponential function, which conforms to the general law of seepage of jointed rock mass, and expands the solution method for the permeability coefficient of columnar jointed rock mass under stress field.
Author Contributions
Funding
Conflicts of Interest
References
- Meng, Q.; Yan, L.; Chen, Y.; Zhang, Q. Generation of Numerical Models of Anisotropic Columnar Jointed Rock Mass Using Modified Centroidal Voronoi Diagrams. Symmetry 2018, 10, 618. [Google Scholar] [CrossRef]
- Hao, X.; Feng, X.; Yang, C.; Jiang, Q.; Li, S. Analysis of EDZ Development of Columnar Jointed Rock Mass in the Baihetan Diversion Tunnel. Rock Mech. Rock Eng. 2016, 49, 1289–1312. [Google Scholar] [CrossRef]
- Li, B.; Tao, L.; Xu, N.; Dai, F.; Tan, Y. Stability assessment of the left bank slope of the baihetan hydropower station. Int. J. Rock Mech. Min. Sci. 2018, 104, 34–44. [Google Scholar] [CrossRef]
- Dai, F.; Jiang, P.; Xu, N.; Chen, W.; Tan, Y. Focal mechanism determination for microseismic events and its application to the left bank slope of the baihetan hydropower station in china. Environ. Earth Sci. 2018, 77, 268. [Google Scholar] [CrossRef]
- Yan, D.; Xu, W.; Wang, W.; Shi, C.; Wu, G. Research of size effect on equivalent elastic modulus of columnar jointed rock mass. Chin. J. Geotech. Eng. 2012, 34, 243–250. (In Chinese) [Google Scholar]
- Kim, J.W.; Chong, S.H.; Cho, G.C. Experimental Characterization of Stress- and Strain-Dependent Stiffness in Grouted Rock Masses. Materials 2018, 11, 524. [Google Scholar] [CrossRef]
- Min, K.B.; Rutqvist, J.; Tsang, C.F.; Jing, L. Stress-dependent permeability of fractured rock masses: A numerical study. Int. J. Rock Mech. Min. Sci. 2004, 41, 1191–1210. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Stress effects on permeability in a fractured rock mass with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2008, 45, 1320–1334. [Google Scholar] [CrossRef]
- Lu, T.; Xu, R.; Zhou, B.; Wang, Y.; Zhang, F.; Jiang, P. Improved Method for Measuring the Permeability of Nanoporous Material and Its Application to Shale Matrix with Ultra-Low Permeability. Materials 2019, 12, 1567. [Google Scholar] [CrossRef]
- Pan, D.; Zhang, N.; Xie, Z.; Feng, X.; Kong, Y. Laboratory Testing of Silica Sol Grout in Coal Measure Mudstones. Materials 2016, 9, 940. [Google Scholar] [CrossRef]
- Singh, B. Continuum characterization of jointed rock masses: Part I-The constitutive equations. Int. J. Rock Mech. Min. Sci. 1973, 10, 311–335. [Google Scholar] [CrossRef]
- Singh, B. Continuum characterization of jointed rock masses: Part II-Significance of low shear modulus. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1973, 10, 337–349. [Google Scholar] [CrossRef]
- Gerrard, C.M. Elastic models of rock masses having one, two and three sets of joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1982, 19, 15–23. [Google Scholar] [CrossRef]
- Gerrard, C.M. Equivalent elastic moduli of a rock mass consisting of orthorhombic layers. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1982, 19, 9–14. [Google Scholar] [CrossRef]
- Yan, S.; Huang, Y.; Chen, C.Y. An equivalent model for jointed rock mass with persistent joint and its elastic parameters. J. Huazhong Univ. Sci. Technol. 2001, 29, 60–63. [Google Scholar]
- Meng, G.T. Geomechanical Analysis of Anisotropic Columnar Jointed Rock Mass and Its Application in Hydropower Engineering; Hohai University: Nanjing, China, 2007. [Google Scholar]
- Zou, L.; Tarasov, B.; Dyskin, A.V.; Adhikary, D.; Pasternak, E.; Xu, W. Physical modeling of stress-dependent permeability infractured rocks. Rock Mech. Rock Eng. 2013, 46, 67–81. [Google Scholar] [CrossRef]
- Xiong, G. Seepage Tensor Study and Engineering Application on Column Jointed Rock Mass of Dam Foundation. Master’s Thesis, Hohai University, Nanjing, China, 2017. [Google Scholar]
- Wang, H.; Xu, W.; Zuo, J.; Shao, J.; Jia, C. Evolution law of the permeability and porosity for low-permeability rock based on gas permeability test. J. Hydraul. Eng. 2015, 46, 208–216. (In Chinese) [Google Scholar]
- Chao, Z.; Wang, H.; Xu, W.; Jia, C.; Xia, J. Model tests on permeability of columnar jointed rock mass. Chin. J. Geotech. Eng. 2016, 38, 1407–1416. (In Chinese) [Google Scholar]
- Que, X.; Zhu, Z.; Lu, W. Anisotropic constitutive model of pentagonal prism columnar jointed rock mass. Bull Eng. Geol. Environ. 2020, 79, 269–286. [Google Scholar] [CrossRef]
- Lomize, G.M. Flow in Fractured Rock; Gosemergoizdat: Moscow, Russia, 1951; pp. 127–129. (In Russian) [Google Scholar]
- Louis, C. A Study of Groundwater Flow in Jointed Rock and Its Influence on the Stability of Rock Masses (Rock Mech. Res.Rep.10); Imperial College: London, UK, 1969. [Google Scholar]
- Louis, C.; Maini, Y.N.T. Determination of in situ hydraulic parameters in jointed rock. In Proceedings of the 2nd Congress ISRM, Beograd, Yugoslavia, 25–27 September 1970; pp. 235–245. [Google Scholar]
- Nelson, R.A. An experimental study of fracture permeability in porous rock. In Proceedings of the 17th U.S. Symposium on Rock Mechanics, Snow Bird, UT, USA, 25–27 August 1976; pp. 2A6–12A6-1. [Google Scholar]
- Bandis, S.C.; Lumsden, A.C.; Barton, N.R. Fundamentals of rock joint deformation. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Yang, T.; Jia, P.; Shi, W.; Wang, P.; Liu, H.; Yu, Q. Seepage–stress coupled analysis on anisotropic characteristics of the fractured rock mass around roadway. Tunn. Undergr. Space Technol. 2014, 43, 11–19. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Z.; Zhu, S.; He, Z.; Zhu, D.; Liu, J.; Meng, S. Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory. Materials 2019, 12, 1505. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Jiang, Q.; Feng, X.; Li, S.; Liu, J.; Chen, W.; Zhang, J.; Pei, S. Insights into statistical structural charactestics and deformation properties of columnar jointed basalts: Field investigation in the Baihetan dam base, China. Bull. Eng. Geol. Environ. 2017, 77, 775–790. [Google Scholar] [CrossRef]


| Location and Country | Shape of Column Section | ||
|---|---|---|---|
| Quadrilateral | Pentagon | Hexagon | |
| Craters of Moon (USA) (CAN) | 28% | 56% | 16% |
| Dunsmuir (CAN) | 14.5% | 46% | 33.5% |
| Lewiston (USA) | 7.5% | 45% | 41.5% |
| Devils Tower (USA) | 17% | 42% | 35% |
| BaihetanP2β33 (CHN) | 49% | 46% | 5% |
| kn (GPa/m) | ks (GPa/m) | Kf0 (cm/s) | tj (m) | Er (GPa) | Gr (GPa) | vr | l (m) | s3 (m) | s (m) |
|---|---|---|---|---|---|---|---|---|---|
| 100 | 50 | 8.599 | 1 × 10−3 | 65.1 | 25 | 0.23 | 0.2 | 2 | 0.05 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Z.; Zhu, Z.; Que, X. Constitutive Model of Stress-Dependent Seepage in Columnar Jointed Rock Mass. Symmetry 2020, 12, 160. https://doi.org/10.3390/sym12010160
Niu Z, Zhu Z, Que X. Constitutive Model of Stress-Dependent Seepage in Columnar Jointed Rock Mass. Symmetry. 2020; 12(1):160. https://doi.org/10.3390/sym12010160
Chicago/Turabian StyleNiu, Zihao, Zhende Zhu, and Xiangcheng Que. 2020. "Constitutive Model of Stress-Dependent Seepage in Columnar Jointed Rock Mass" Symmetry 12, no. 1: 160. https://doi.org/10.3390/sym12010160
APA StyleNiu, Z., Zhu, Z., & Que, X. (2020). Constitutive Model of Stress-Dependent Seepage in Columnar Jointed Rock Mass. Symmetry, 12(1), 160. https://doi.org/10.3390/sym12010160




