A Selective Overview of Skew-Elliptical and Related Distributions and of Their Applications
Abstract
1. Context and Motivation
1.1. The Wider Perspective
1.2. The Specific Target
2. Background Concepts
2.1. Basics of Elliptical Distributions
2.2. The Multivariate Skew-Normal Distribution
2.3. A General Result
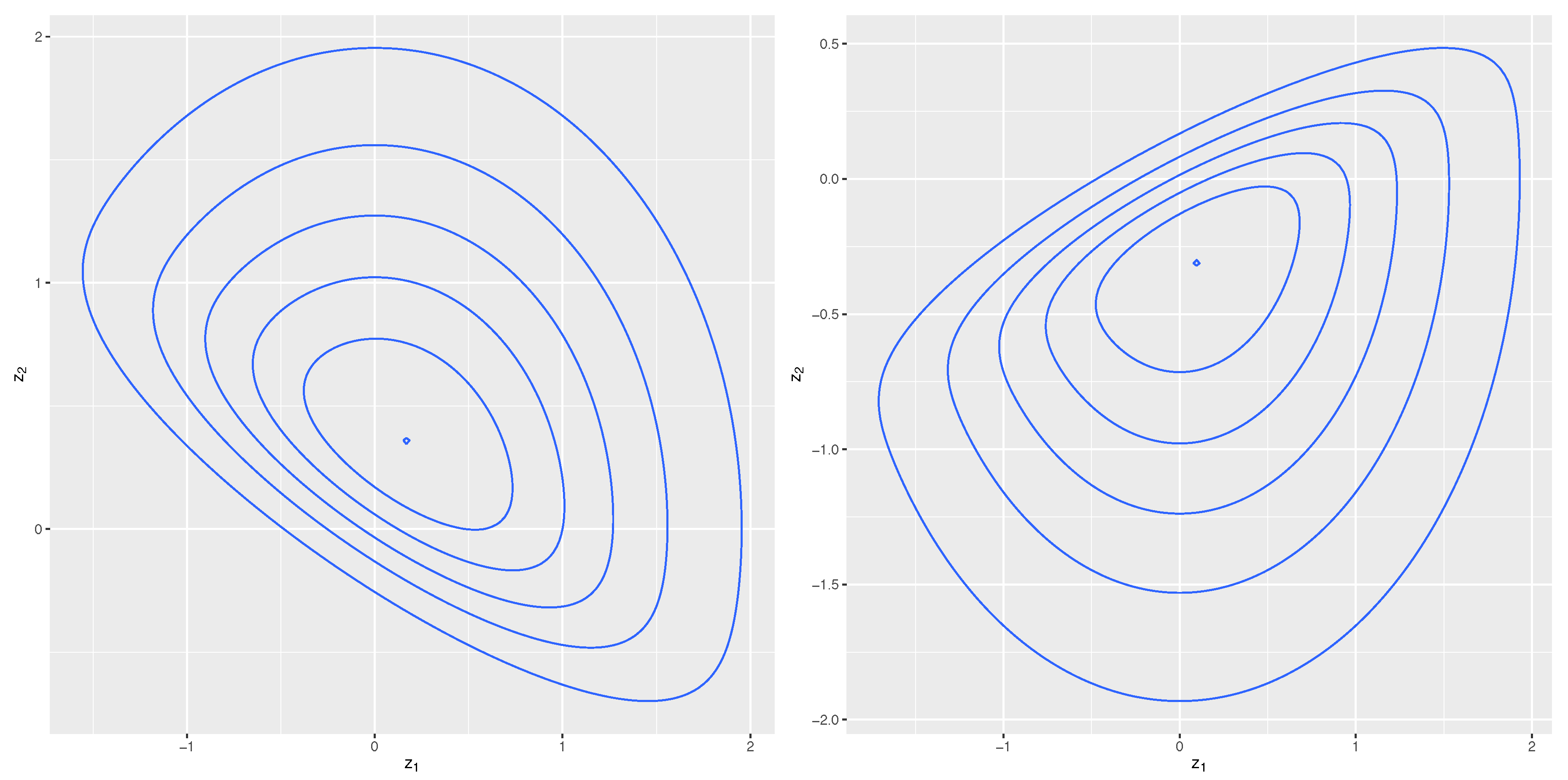
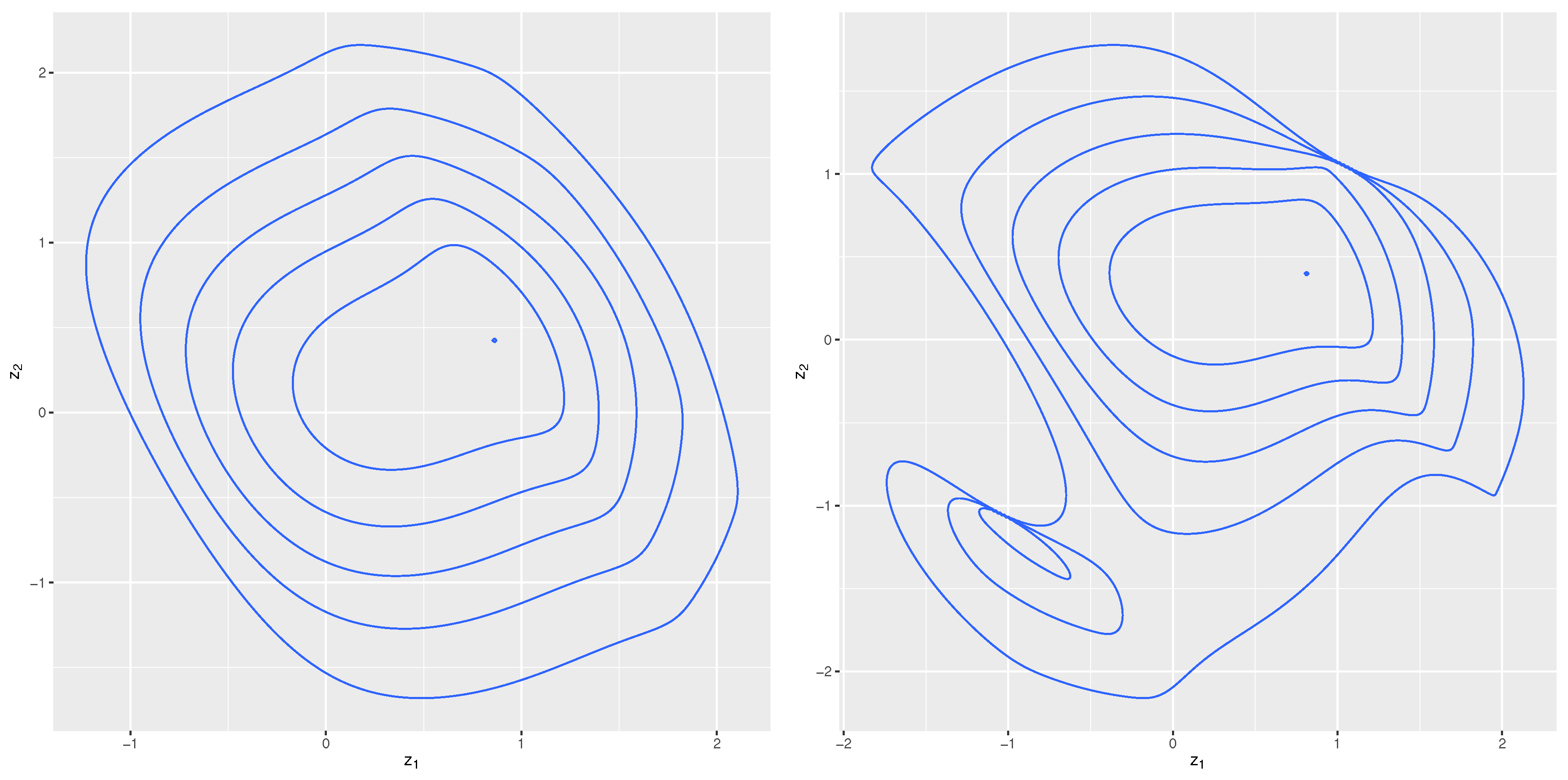
2.4. Symmetry-Modulated Distributions
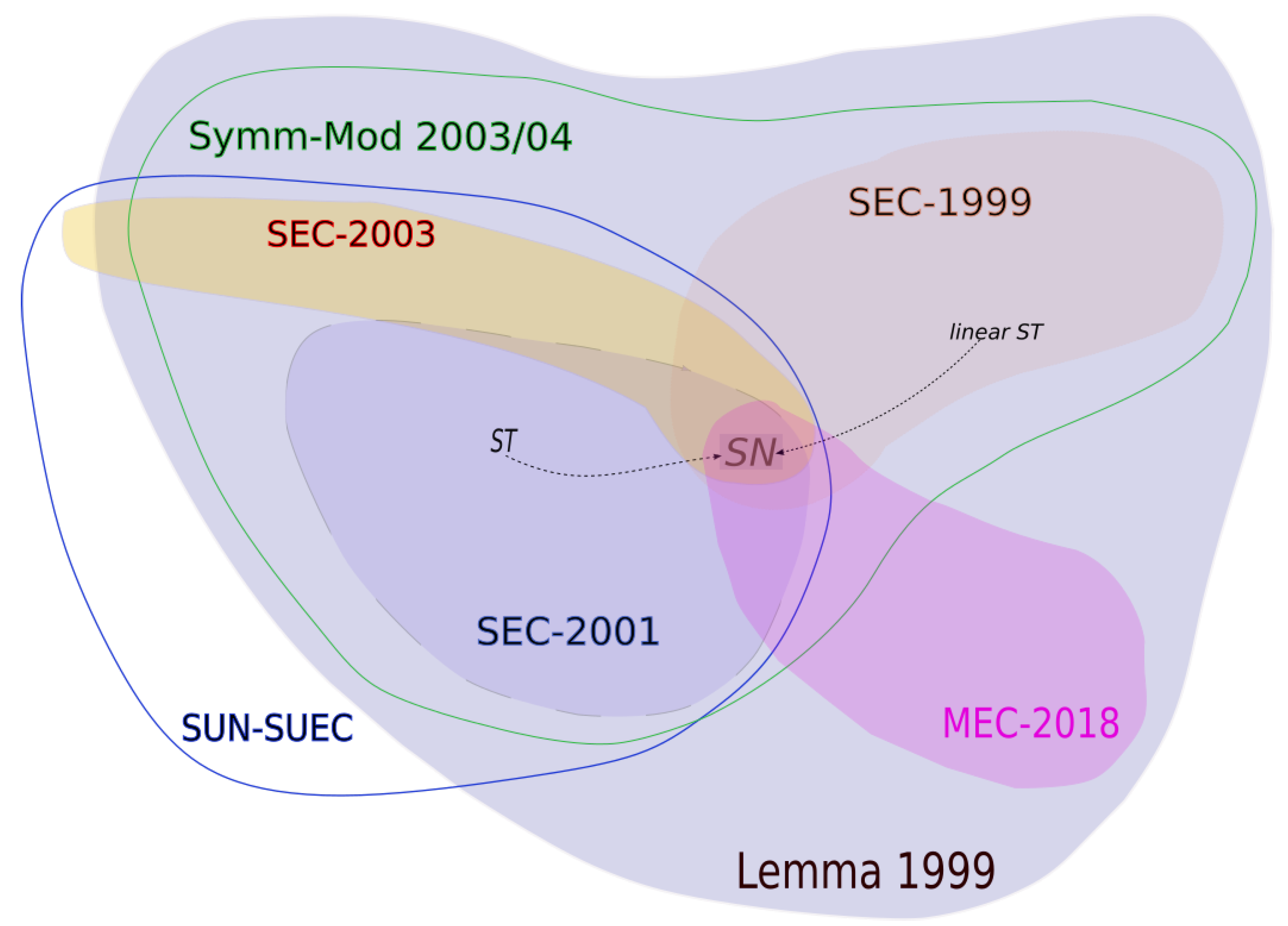
3. SEC and Other Modulations of EC Distributions
3.1. SEC Distributions with a Linear-Combination Argument
3.2. SEC Distributions via Conditioning
3.3. Constructions Based on Several Latent Variables
3.4. Other Mixtures of SN Variables
3.5. Miscellanea
3.6. Cave Nomina
4. Applications as Methodological Developments
4.1. Regression Models and Variants
4.2. Finite Mixtures and Model-Based Clustering
4.3. Spatial and Spatio-Temporal Models
4.4. Methods for Biostatistics and Medical Statistics
4.5. Methods for Observational Studies and the Social Sciences
4.6. A Popular Benchmark
5. Applications to Real Problems
5.1. Economics and Applied Financial Economics
5.2. Quantitative Finance
5.3. Risk
5.4. Biology and Life Sciences
5.5. Environmental Issues
5.6. Industrial and Technological Applications
6. Two Illustrations in Applied Domains
6.1. A Finance Application
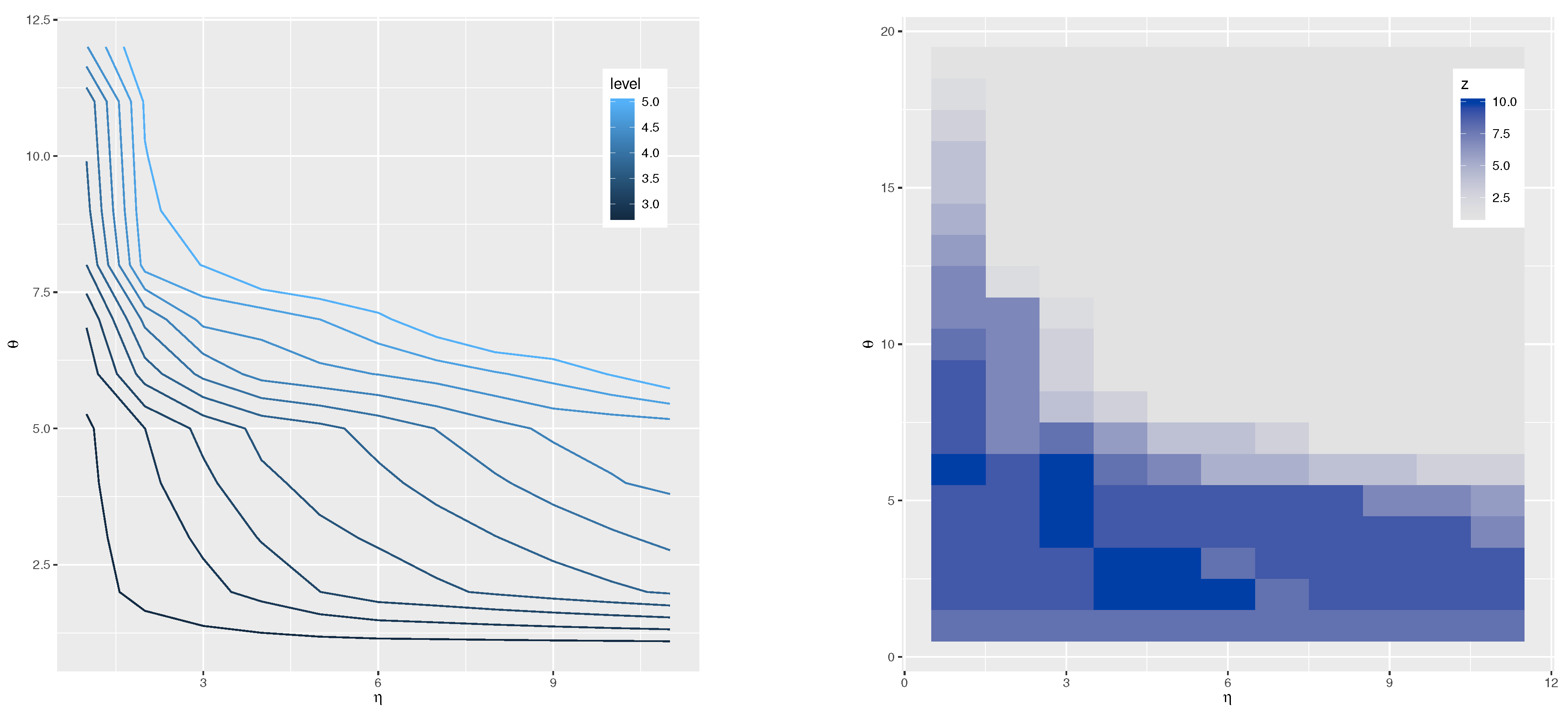
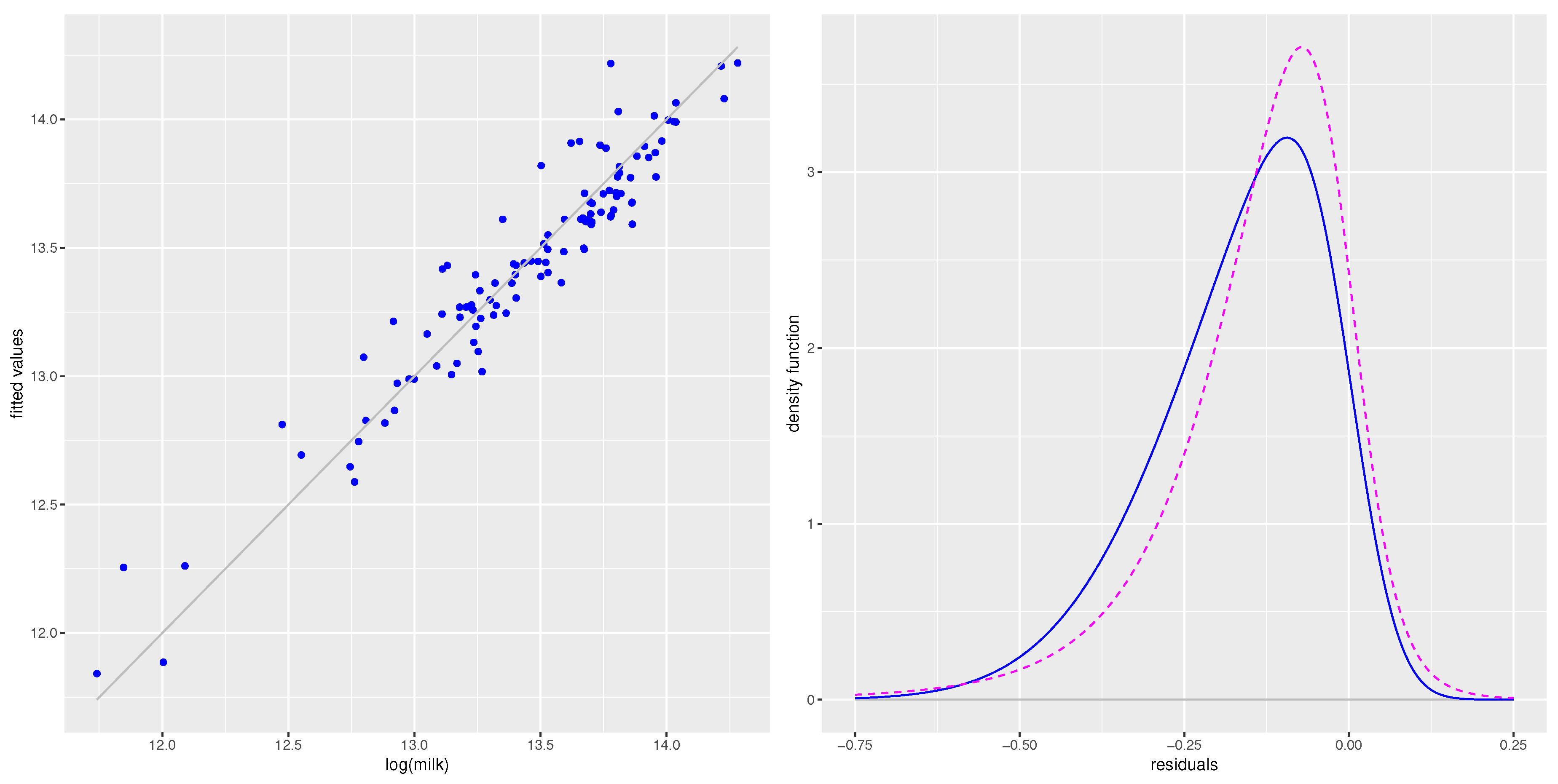
6.2. Stochastic Frontier Analysis: An Simple Case
7. Final Comments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pretorious, S.J. Skew bivariate frequency surfaces, examined in the light of numerical illustrations. Biometrika 1930, 22, 109–223. [Google Scholar] [CrossRef]
- Schols, C.M. Over de Theorie der Fouten in de Ruimte en in Het Platte Vlak; Verhandelingen der Koninklijke Akademie van Wetenschappen: Amsterdam, The Netherlands, 1875; Volume XV, Part VI; pp. 1–67, Reprinted as ‘Théorie des erreurs dans le plan et dans l’espace’; Ann. de l’École Polytechnique de Delft: Delft, The Netherlands, 1886; pp. 123–175. [Google Scholar]
- Perozzo, L. Nuove applicazioni del calcolo delle probabilità allo studio dei fenomeni statistici, e distribuzione dei matrimoni secondo l’età degli sposi. In Reale Accademia dei Lincei, Serie 3a, Memorie Classe di Scienze Morali, Storiche e Filologiche; Reale Accademia dei Lincei: Rome, Italy, 1882; Volume X, pp. 1–22. [Google Scholar]
- Jones, M.C. On families of distributions with shape parameters (with discussion). Int. Stat. Rev. 2015, 83, 175–227. [Google Scholar] [CrossRef]
- Babić, S.; Ley, C.; Veredas, D. Comparison and classification of flexible distributions for multivariate skew and heavy-tailed data. Symmetry 2019, 11, 1216. [Google Scholar] [CrossRef]
- Genton, M.G. (Ed.) Skew-Elliptical Distributions and Their Applications: A Journey Beyond Normality; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Azzalini, A.; Capitanio, A. The Skew-Normal and Related Families; IMS Monographs; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Fang, K.T.; Kotz, S.; Ng, K.W. Symmetric Multivariate and Related Distributions; Chapman & Hall: London, UK, 1990. [Google Scholar]
- Kano, Y. Consistency property of elliptical probability density functions. J. Multivar. Anal. 1994, 51, 139–147. [Google Scholar] [CrossRef]
- Azzalini, A.; Dalla Valle, A. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Statistical applications of the multivariate skew normal distribution. J. R. Stat. Soc. Ser. B 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Genton, M.G.; He, L.; Liu, X. Moments of skew-normal random vectors and their quadratic forms. Stat. Probab. Lett. 2001, 51, 319–325. [Google Scholar] [CrossRef]
- Capitanio, A. On the canonical form of scale mixtures of skew-normal distributions. arXiv 2012, arXiv:1207.0797. [Google Scholar]
- Balakrishnan, N.; Scarpa, B. Multivariate measures of skewness for the skew-normal distribution. J. Multivar. Anal. 2012, 104, 73–87. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Capitanio, A.; Scarpa, B. A test for multivariate skew-normality based on its canonical form. J. Multivar. Anal. 2014, 128, 19–32. [Google Scholar] [CrossRef]
- Rao, C.R. Weighted distributions arising out of methods of ascertainment: What population does a sample represent. In A Celebration of Statistics: The ISI Centenary Volume; Atkinson, A.C., Fienberg, S.E., Eds.; Springer: Berlin, Germany, 1985; Chapter 24; pp. 543–569. [Google Scholar]
- Arellano-Valle, R.B.; Branco, M.D.; Genton, M.G. A unified view on skewed distributions arising from selections. Canad. J. Stat. 2006, 34, 581–601. [Google Scholar] [CrossRef]
- Jupp, P.E.; Regoli, G.; Azzalini, A. A general setting for symmetric distributions and their relationship to general distributions. J. Multivar. Anal. 2016, 148, 107–199. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t distribution. J. R. Stat. Soc. Ser. B 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Wang, J.; Boyer, J.; Genton, M.G. A skew-symmetric representation of multivariate distributions. Stat. Sin. 2004, 14, 1259–1270. [Google Scholar]
- Gupta, A.K.; Chang, F.C.; Huang, W.J. Some skew-symmetric models. Random Oper. Stoch. Equ. 2002, 10, 133–140. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. Skew models I. Acta Appl. Math. 2007, 98, 1–28. [Google Scholar] [CrossRef]
- Branco, M.D.; Dey, D.K. A general class of multivariate skew-elliptical distributions. J. Multivar. Anal. 2001, 79, 99–113. [Google Scholar] [CrossRef]
- Azzalini, A.; Regoli, G. Some properties of skew-symmetric distributions. Ann. Inst. Stat. Math. 2012, 64, 857–879. [Google Scholar] [CrossRef]
- Gupta, A.K. Multivariate skew t-distribution. Statistics 2003, 37, 359–363. [Google Scholar] [CrossRef]
- Kim, H.M.; Mallick, B.K. Moments of random vectors with skew t distribution and their quadratic forms. Stat. Probab. Lett. 2003, 63, 417–423, Corrigendum at 2009, 79, 2098–2099. [Google Scholar] [CrossRef]
- Kim, H.M. A note on scale mixtures of skew normal distribution. Stat. Probab. Lett. 2008, 78, 1694–1701, Corrigendum at 2013, 83, 1937. [Google Scholar] [CrossRef]
- Giorgi, E. Indici Non Parametrici per Famiglie Parametriche Con Particolare Riferimento Alla t Asimmetrica. Tesi di Laurea Magistrale, Università di Padova. 2012. Available online: http://tesi.cab.unipd.it/40101/ (accessed on 6 January 2020).
- Arevalillo, J.M.; Navarro, H. A note on the direction maximizing skewness in multivariate skew-t vectors. Stat. Probab. Lett. 2015, 96, 328–332. [Google Scholar] [CrossRef]
- Kim, H.M.; Zhao, J. Multivariate measures of skewness for the scale mixtures of skew-normal distributions. Commun. Stat. Appl. Methods. 2018, 25, 109–130. [Google Scholar] [CrossRef]
- Azzalini, A.; Genton, M.G. Robust likelihood methods based on the skew-t and related distributions. Int. Stat. Rev. 2008, 76, 106–129. [Google Scholar] [CrossRef]
- Wang, J.; Genton, M.G. The multivariate skew-slash distribution. J. Stat. Plan. Inference 2006, 136, 209–220. [Google Scholar] [CrossRef]
- Kim, H.M.; Genton, M.G. Characteristic functions of scale mixtures of multivariate skew-normal distributions. J. Multivar. Anal. 2011, 102, 1105–1117. [Google Scholar] [CrossRef]
- Shushi, T. A proof for the conjecture of characteristic function of the generalized skew-elliptical distributions. Stat. Probab. Lett. 2016, 119, 301–304. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Contreras-Reyes, J.E.; Genton, M.G. Shannon entropy and mutual information for multivariate skew-elliptical distributions. Scand. J. Stat. 2013, 40, 42–62. [Google Scholar] [CrossRef]
- Adcock, C.J. Asset pricing and portfolio selection based on the multivariate extended skew-Student-t distribution. Ann. Oper. Res. 2010, 176, 221–234. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Genton, M.G. Multivariate extended skew-t distributions and related families. Metron 2010, LXVIII, 201–234. [Google Scholar] [CrossRef]
- Lee, S.; Genton, M.G.; Arellano-Valle, R.B. Perturbation of numerical confidential data via skew-t distributions. Manag. Sci. 2010, 56, 318–333. [Google Scholar] [CrossRef]
- Marchenko, Y.V.; Genton, M.G. A Heckman selection-t model. J. Am. Stat. Assoc. 2012, 107, 304–317. [Google Scholar] [CrossRef]
- Adcock, C.J. Mean-variance-skewness efficient surfaces, Stein’s lemma and the multivariate extended skew-Student distribution. Eur. J. Oper. Res. 2014, 234, 392–401. [Google Scholar] [CrossRef]
- Sahu, K.; Dey, D.K.; Branco, M.D. A new class of multivariate skew distributions with applications to Bayesian regression models. Can. J. Stat. 2003, 31, 129–150, Corrigendum: 2009, 37, 301–302. [Google Scholar] [CrossRef]
- González-Farías, G.; Domínguez-Molina, J.A.; Gupta, A.K. Additive properties of skew normal random vectors. J. Stat. Plan. Inference 2004, 126, 521–534. [Google Scholar] [CrossRef]
- González-Farías, G.; Domínguez-Molina, J.A.; Gupta, A.K. The closed skew-normal distribution. In Skew-elliptical Distributions and Their Applications: A Journey Beyond Normality; Genton, M.G., Ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; Chapter 2; pp. 25–42. [Google Scholar]
- Liseo, B.; Loperfido, N. A Bayesian interpretation of the multivariate skew-normal distribution. Stat. Probab. Lett. 2003, 61, 395–401. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Genton, M.G. On fundamental skew distributions. J. Multivar. Anal. 2005, 96, 93–116. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Azzalini, A. On the unification of families of skew-normal distributions. Scand. J. Stat. 2006, 33, 561–574. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Genton, M.G. Multivariate unified skew-elliptical distributions. Chil. J. Stat. 2010, 1, 17–33. [Google Scholar]
- Arellano-Valle, R.B.; Jamalizadeh, A.; Mahmoodian, H.; Balakrishnan, N. L-statistics from multivariate unified skew-elliptical distributions. Metrika 2014, 77, 559–583. [Google Scholar] [CrossRef]
- Abtahi, A.; Towhidi, M. The new unified representation of multivariate skewed distributions. Statistics 2013, 47, 126–140. [Google Scholar] [CrossRef]
- Aziz, M.A.; Gupta, A.K. Quadratic forms in unified skew normal random vectors. J. Probab. Stat. Sci. 2013, 11, 1–15. [Google Scholar]
- Gupta, A.K.; Aziz, M.A.; Ning, W. On some properties of the unified skew normal distribution. J. Stat. Theory Pract. 2013, 7, 480–495. [Google Scholar] [CrossRef]
- Richter, W.D.; Venz, J. Geometric representations of multivariate skewed elliptically contoured distributions. Chil. J. Stat. 2014, 5, 71–90. [Google Scholar]
- Arellano-Valle, R.B.; Castro, L.M.; Genton, M.G.; Gómez, H.W. Bayesian inference for shape mixtures of skewed distributions, with application to regression analysis. Bayesian Anal. 2008, 3, 513–539. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Genton, M.G.; Loschi, R.H. Shape mixtures of multivariate skew-normal distributions. J. Multivar. Anal. 2009, 100, 91–101. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Ferreira, C.S.; Genton, M.G. Scale and shape mixtures of multivariate skew-normal distributions. J. Multivar. Anal. 2018, 166, 98–110. [Google Scholar] [CrossRef]
- Tamandi, M.; Jamalizadeh, A. Finite mixture modeling using shape mixtures of the skew scale mixtures of normal distributions. Commun. Stat. Simul. Comput. 2019. [Google Scholar] [CrossRef]
- Arslan, O. Variance-mean mixture of the multivariate skew normal distribution. Stat. Pap. 2015, 56, 353–378. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.; Kent, J.; Sørensen, M. Normal variance-mean mixtures and z distributions. Int. Stat. Rev. 1982, 50, 145–159. [Google Scholar] [CrossRef]
- Genton, M.G. Discussion of “The skew-normal”. Scand. J. Stat. 2005, 32, 189–198. [Google Scholar] [CrossRef]
- Kim, H.J. A class of weighted multivariate normal distributions and its properties. J. Multivar. Anal. 2008, 99, 1758–1771. [Google Scholar] [CrossRef]
- Jamalizadeh, A.; Kundu, D. A multivariate Birnbaum-Saunders distribution based on the multivariate skew normal distribution. J. Jpn. Stat. Soc. 2015, 45, 1–20. [Google Scholar] [CrossRef][Green Version]
- Azzalini, A.; Regoli, G. On symmetry-modulated distributions: Revisiting an old result and a step further. Stat 2018, 7, e171. [Google Scholar] [CrossRef]
- Gupta, A.K.; Varga, T.; Bodnar, T. Elliptically Contoured Models in Statistics and Portfolio Theory, 2nd ed.; Springer: Berlin, Germany, 2013. [Google Scholar] [CrossRef]
- Giorgi, E.; McNeil, A.J. On the computation of multivariate scenario sets for the skew-t and generalized hyperbolic families. Comput. Stat. Data Anal. 2016, 100. [Google Scholar] [CrossRef]
- Bolfarine, H.; Montenegro, L.C.; Lachos, V.H. Influence diagnostics for skew-normal linear mixed models. Sankhyā 2007, 69, 648–670. [Google Scholar]
- Ferreira, C.S.; Arellano-Valle, R.B. Estimation and diagnostic analysis in skew-generalized-normal regression models. J. Stat. Comput. Simul. 2018, 88, 1039–1059. [Google Scholar] [CrossRef]
- Labra, F.V.; Garay, A.M.; Lachos, V.H.; Ortega, E.M.M. Estimation and diagnostics for heteroscedastic nonlinear regression models based on scale mixtures of skew-normal distributions. J. Stat. Plan. Inference 2012, 142, 2149–2165. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Ozán, S.; Bolfarine, H.; Lachos, V.H. Skew-normal measurement error models. J. Multivar. Anal. 2005, 96, 265–281. [Google Scholar] [CrossRef]
- Figueiredo, C.C.; Bolfarine, H.; Sandoval, M.C.; Lima, C.R.O.P. On the skew-normal calibration model. J. Appl. Stat. 2010, 37, 435–451. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Castro, L.M.; Loschi, R.H. Change point detection in the skew-normal model parameters. Commun. Stat. Theory Methods 2013, 42, 603–618. [Google Scholar] [CrossRef]
- Lachos, V.H.; Labra, F.V.; Bolfarine, H.; Ghosh, P. Multivariate measurement error models based on scale mixtures of the skew-normal distribution. Statistics 2010, 44, 541–556. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Azzalini, A.; Ferreira, C.S.; Santoro, K. A two-piece normal measurement error model. Comput. Stat. Data Anal. 2020, 144. [Google Scholar] [CrossRef]
- Chen, M.H.; Dey, D.K.; Shao, Q.M. A new skewed link model for dichotomous quantal response data. J. Am. Stat. Assoc. 1999, 94, 1172–1186. [Google Scholar] [CrossRef]
- Bazán, J.L.; Bolfarine, H.; Branco, M.D. A framework for skew-probit links in binary regression. Commun. Stat. Theory Methods 2010, 39, 678–697. [Google Scholar] [CrossRef]
- Bazán, J.L.; Branco, M.D.; Bolfarine, H. A skew item response model. Bayesian Anal. 2006, 1, 861–892. [Google Scholar] [CrossRef]
- Bazán, J.L.; Branco, M.D.; Bolfarine, H. Extensions of the skew-normal ogive item response model. Braz. J. Probab. Stat. 2014, 28, 1–23. [Google Scholar] [CrossRef]
- Sanros, J.R.S.; Azevedo, C.L.N.; Bolfarine, H. A multiple group item response theory model with centered skew-normal latent trait distributions under a Bayesian framework. J. Appl. Stat. 2013, 40, 2129–2149. [Google Scholar]
- Durante, D. Conjugate Bayes for probit regression via unified skew-normal distributions. Biometrika 2019, 106, 765–779. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Peel, D. Finite Mixture Models; Description John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Lin, T.I.; Lee, J.C.; Yen, S.Y. Finite mixture modelling using the skew normal distribution. Stat. Sin. 2007, 17, 909–927. [Google Scholar]
- Lin, T.I.; Lee, J.C.; Hsieh, W.J. Robust mixture modeling using the skew t distribution. Stat. Comput. 2007, 17, 81–92. [Google Scholar] [CrossRef]
- Otiniano, C.E.G.; Rathie, P.N.; Ozelim, L.C.S.M. On the identifiability of finite mixture of skew-normal and skew-t distributions. Stat. Probab. Lett. 2015, 106, 103–108. [Google Scholar] [CrossRef]
- Lin, T.I. Maximum likelihood estimation for multivariate skew normal mixture models. J. Multivar. Anal. 2009, 100, 257–265. [Google Scholar] [CrossRef]
- Lin, T.I. Robust mixture modeling using multivariate skew t distributions. Stat. Comput. 2010, 20, 343–356. [Google Scholar] [CrossRef]
- Pyne, S.; Hu, X.; Wang, K.; Rossin, E.; Lin, T.I.; Maier, L.M.; Baecher-Alland, C.; McLachlan, G.J.; Tamayo, P.; Hafler, D.A.; et al. Automated high-dimensional flow cytometric data analysis. Proc. Natl. Acad. Sci. USA 2009, 106, 8519–8524. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, S.; Pyne, S. Bayesian inference for finite mixtures of univariate and multivariate skew-normal and skew-t distributions. Biostatistics 2010, 11, 317–336. [Google Scholar] [CrossRef]
- Vrbik, I.; McNicholas, P. Analytic calculations for the EM algorithm for multivariate skew t-mixture model. Stat. Probab. Lett. 2012, 82, 1169–1174. [Google Scholar] [CrossRef]
- Vrbik, I.; McNicholas, P.D. Parsimonious skew mixture models for model-based clustering and classification. Comput. Stat. Data Anal. 2014, 71, 196–210. [Google Scholar] [CrossRef]
- Lachos Dávila, V.H.; Cabral, C.R.B.; Zeller, C.B. Finite Mixture of Skewed Distributions; Briefs in Statistics; Springer: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Lee, S.X.; McLachlan, G.J. Finite mixtures of canonical fundamental skew t-distributions. Stat. Comput. 2016, 26, 573–596. [Google Scholar] [CrossRef]
- Lee, S.X.; McLachlan, G.J. EMMIXcskew: An R package for the fitting of a mixture of canonical fundamental skew t-distributions. J. Stat. Softw. 2018. [Google Scholar] [CrossRef]
- Liu, M.; Lin, T.I. A skew-normal mixture regression model. Educ. Psychol. Meas. 2014, 74, 139–162. [Google Scholar] [CrossRef]
- Zeller, C.B.; Cabral, C.R.B.; Lachos, V.H. Robust mixture regression modeling based on scale mixtures of skew-normal distributions. Test 2016, 25, 375–396. [Google Scholar] [CrossRef]
- Doğru, F.Z.; Arslan, O. Robust mixture regression based on the skew t distribution. Rev. Colomb. Estad. 2017, 40, 45–64. [Google Scholar] [CrossRef]
- Kim, H.M.; Mallick, B.K. A Bayesian prediction using the skew Gaussian distribution. J. Stat. Plan. Inference 2004, 120, 85–101. [Google Scholar] [CrossRef]
- Minozzo, M.; Ferracuti, L. On the existence of some skew-normal stationary processes. Chil. J. Stat. 2012, 3, 159–172. [Google Scholar]
- Zhang, H.; El-Shaarawi, A. On spatial skew-Gaussian processes and applications. Environmetrics 2010, 21, 33–47. [Google Scholar] [CrossRef]
- Schmidt, A.M.; Gonçalves, K.C.M.; Velozo, P.L. Spatiotemporal models for skewed processes. Environmetrics 2017, 28, e2411. [Google Scholar] [CrossRef]
- Genton, M.G.; Hering, A.S. Comments on: Spatiotemporal models for skewed processes. Environmetrics 2017, 28, e2430. [Google Scholar] [CrossRef]
- Hering, A.S.; Genton, M.G. Powering up with space-time wind forecasting. J. Am. Stat. Assoc. 2010, 105, 92–104. [Google Scholar] [CrossRef]
- Hosseini, F.; Eidsvik, J.; Mohammadzadeh, M. Approximate Bayesian inference in spatial GLMM with skew normal latent variables. Comput. Stat. Data Anal. 2011, 55, 1791–1806. [Google Scholar] [CrossRef]
- Karimi, O.; Mohammadzadeh, M. Bayesian spatial regression models with closed skew normal correlated errors and missing. Stat. Pap. 2012, 53, 205–218. [Google Scholar] [CrossRef]
- Zareifard, H.; Jafari Khaledi, M. Non-Gaussian modeling of spatial data using scale mixing of a unified skew Gaussian process. J. Multivar. Anal. 2013, 114, 16–28. [Google Scholar] [CrossRef]
- Ahmad, O.S.; Pinoli, J.C. Lipschitz-Killing curvatures of the excursion sets of skew Student’s t random fields. Stoch. Models 2013, 29, 273–289. [Google Scholar] [CrossRef]
- Rimstad, K.; Omre, H. Skew-Gaussian random fields. Spat. Stat. 2014, 10, 43–62. [Google Scholar] [CrossRef]
- Rezaie, J.; Eidsvik, J.; Mukerji, T. Value of information analysis and Bayesian inversion for closed skew-normal distributions: Applications to seismic amplitude variation with offset data. Geophysics 2014, 79, R151–R163. [Google Scholar] [CrossRef]
- Boojari, H.; Khaledi, M.J.; Rivaz, F. A non-homogeneous skew-Gaussian Bayesian spatial model. Stat. Methods Appl. 2016, 25, 55–73. [Google Scholar] [CrossRef]
- Baghfalaki, T.; Ganjali, M.; Khounsiavash, M. A non-random dropout model for analyzing longitudinal skew-normal response. J. Iran. Stat. Soc. 2012, 11, 101–129. [Google Scholar]
- Huang, Y.; Dagne, G.A. Simultaneous Bayesian inference for skew-normal semiparametric nonlinear mixed-effects models with covariate measurement errors. Bayesian Anal. 2012, 7, 189–210. [Google Scholar] [CrossRef]
- Chang, S.C.; Zimmerman, D.L. Skew-normal antedependence models for skewed longitudinal data. Biometrika 2016, 103, 363–376. [Google Scholar] [CrossRef]
- Jana, S.; Balakrishnan, N.; Hamid, J.S. Estimation of the parameters of the extended growth curve model under multivariate skew normal distribution. J. Multivar. Anal. 2018, 166, 111–128. [Google Scholar] [CrossRef]
- Barrett, J.; Diggle, P.; Henderson, R.; Taylor-Robinson, D. Joint modelling of repeated measurements and time-to-event outcomes: Flexible model specification and exact likelihood inference. J. R. Stat. Soc. Ser. B 2015, 77, 131–148. [Google Scholar] [CrossRef] [PubMed]
- Baghfalaki, T.; Ganjali, M. A Bayesian approach for joint modeling of skew-normal longitudinal measurements and time to event data. Rev. Stat. Stat. J. 2015, 13, 169–191. [Google Scholar]
- Shun, Z.; Gordon Lan, K.K.; Soo, Y. Interim treatment selection using the normal approximation approach in clinical trials. Stat. Med. 2008, 27, 597–618. [Google Scholar] [CrossRef] [PubMed]
- Azzalini, A.; Bacchieri, A. A prospective combination of phase II and phase III in drug development. Metron 2010, LXVIII, 347–369. [Google Scholar] [CrossRef]
- Heckman, J.J. Sample selection bias as a specification error. Econometrica 1979, 47, 153–161. [Google Scholar] [CrossRef]
- Grilli, L.; Rampichini, C. Selection bias in linear mixed models. Metron 2010, LXVIII, 309–329. [Google Scholar] [CrossRef]
- Azzalini, A.; Kim, H.M.; Kim, H.J. Sample selection models for discrete and other non-Gaussian response variables. Stat. Methods Appl. 2019, 28, 27–56. [Google Scholar] [CrossRef]
- Fabrizi, E.; Trivisano, C. Robust models for mixed effects in linear mixed models applied to small area estimation. J. Stat. Plan. Inference 2010, 140, 433–443. [Google Scholar] [CrossRef]
- Ferraz, V.R.S.; Moura, F.A.S. Small area estimation using skew normal models. Comput. Stat. Data Anal. 2012, 56, 2864–2874. [Google Scholar] [CrossRef]
- Ferrante, M.R.; Pacei, S. Small domain estimation of business statistics by using multivariate skew normal models. J. R. Stat. Soc. Ser. A 2017, 180, 1057–1088. [Google Scholar] [CrossRef]
- Diallo, M.S.; Rao, J.N.K. Small area estimation of complex parameters under unit-level models with skew-normal errors. Scand. J. Stat. 2018, 45, 1092–1116. [Google Scholar] [CrossRef]
- Montanari, A.; Viroli, C. A skew-normal factor model for the analysis of student satisfaction towards university courses. J. Appl. Stat. 2010, 37, 473–487. [Google Scholar] [CrossRef]
- Liu, M.; Lin, T.I. Skew-normal factor analysis models with incomplete data. J. Appl. Stat. 2015, 42, 789–805. [Google Scholar] [CrossRef]
- Lin, T.I.; Wu, P.H.; McLachlan, G.J.; Lee, S.X. A robust factor analysis model using the restricted skew-t distribution. TEST 2015, 24, 510–531. [Google Scholar] [CrossRef]
- Lin, T.I.; McLachlan, G.J.; Lee, S.X. Extending mixtures of factor models using the restricted multivariate skew-normal distribution. J. Multivar. Anal. 2016, 143, 398–413. [Google Scholar] [CrossRef]
- Wang, W.L.; Castro, L.M.; Chang, Y.T.; Lin, T.I. Mixtures of restricted skew-t factor analyzers with common factor loadings. Adv. Data Anal. Classifi. 2018. [Google Scholar] [CrossRef]
- Azzalini, A. The R Package sn: The Skew-Normal and Related Distributions Such Ss the Skew-t (Version 1.5-4); Università di Padova: Padova, Italia, 2019; Available online: https://cran.r-project.org/package=sn (accessed on 6 January 2020).
- Marchenko, Y.V.; Genton, M.G. A suite of commands for fitting the skew-normal and skew-t models. Stata J. 2010, 10, 507–539. [Google Scholar] [CrossRef]
- Harvey, C.R.; Liechty, J.C.; Liechty, M.; Müller, P. Portfolio selection with higher moments. Quant. Financ. 2010, 10, 469–485. [Google Scholar] [CrossRef]
- Barbi, M.; Romagnoli, S. Skewness, basis risk, and optimal futures demand. Int. Rev. Econ. Financ. 2018, 58, 14–29. [Google Scholar] [CrossRef]
- Carmichael, B.; Coën, A. Asset Pricing with Skewed Returns. Financ. Res. Lett. 2013, 10, 50–57. [Google Scholar] [CrossRef]
- Alodaat, M.; Al-Rawwash, M.Y. The extended skew Gaussian process for regression. Metron 2014, 72, 317–330. [Google Scholar] [CrossRef]
- Adcock, C.J. Capital asset pricing for UK stocks under the multivariate skew-normal distribution. In Skew Elliptical Distributions and Their Applications: A Journey Beyond Normality; Genton, M., Ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; Chapter 11; pp. 191–204. [Google Scholar]
- Adcock, C.J. Stein’s Lemma For Skew-Normal Distributions: A Comment and an Example. J. Appl. Probab. Stat. 2013, 8, 58–64. [Google Scholar]
- Abanto-Valle, C.A.; Lachos, V.H.; Dey, D.K. Bayesian estimation of a skew-t stochastic volatility model. Methodol. Comput. Appl. Probab. 2015, 17, 721–738. [Google Scholar] [CrossRef]
- Heston, S.L. Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- De Luca, G.; Loperfido, N. Modelling Multivariate Skewness in Financial Returns: A SGARCH Approach. Eur. J. Financ. 2015, 21, 1113–1132. [Google Scholar] [CrossRef]
- Chen, L.; Pourahmadi, M.; Maadooliat, M. Regularized Multivariate Regression Models with Skew-t Error Distributions. J. Stat. Plan. Inference 2014, 149, 125–129. [Google Scholar] [CrossRef]
- Panagiotelis, A.; Smith, M. Bayesian density forecasting of intraday electricity prices using multivariate skew t distributions. Int. J. Forecast. 2008, 24, 710–727. [Google Scholar] [CrossRef]
- Brito, P.; Duarte Silva, A.P. Modelling interval data with Normal and Skew-Normal distributions. J. Appl. Stat. 2012, 39, 3–20. [Google Scholar] [CrossRef]
- Ozaki, V.A.; Silva, R.S. Bayesian ratemaking procedure of crop insurance contracts with skewed distribution. J. Appl. Stat. 2009, 36, 443–452. [Google Scholar] [CrossRef]
- Coelli, T.J.; Prasada Rao, D.S.; O’Donnell, C.; Battese, G.E. An Introduction to Efficiency and Productivity Analysis, 2nd ed.; Springer: Berlin, Germany, 2005. [Google Scholar]
- Domínguez-Molina, J.A.; González-Farías, G.; Ramos-Quiroga, R. Skew-normality in stochastic frontier analysis. In Skew-elliptical Distributions and Their Applications: A Journey Beyond Normality; Genton, M.G., Ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; Chapter 13; pp. 223–242. [Google Scholar]
- Domínguez-Molina, J.A.; González-Farías, G.; Ramos-Quiroga, R.; Gupta, A.K. A matrix variate closed skew-normal distribution with applications to stochastic frontier analysis. Commun. Stat. Theory Methods 2007, 36, 1671–1703. [Google Scholar] [CrossRef]
- Tchumtchoua, S.; Dey, D.K. Bayesian estimation of stochastic frontier models with multivariate skew t error terms. Commun. Stat. Theory Methods 2007, 36, 907–916. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.K.; Schmidt, P. Formulation and Estimation of Stochastic Production Function Model. J. Econ. 1977, 12, 21–37. [Google Scholar] [CrossRef]
- Colombi, R. Closed skew normal stochastic frontier models for panel data. In Advances in Theoretical and Applied Statistics; Torelli, N., Pesarin, F., Bar-Hen, A., Eds.; Studies in Theoretical and Applied Statistics; Springer: Berlin, Germany, 2013; Chapter 17; pp. 177–186. [Google Scholar] [CrossRef]
- Brorsen, B.W.; Kim, T. Data aggregation in stochastic frontier models: The closed skew normal distribution. J. Product. Anal. 2013, 39, 27–34. [Google Scholar] [CrossRef]
- Colombi, R.; Kumbhakar, S.C.; Martini, G.; Vittadini, G. Closed-skew normality in stochastic frontiers with individual effects and long/short-run efficiency. J. Product. Anal. 2014, 42, 123–136. [Google Scholar] [CrossRef]
- Filippini, M.; Greene, W. Persistent and transient productive inefficiency: A maximum simulated likelihood approach. J. Product. Anal. 2016, 45, 187–196. [Google Scholar] [CrossRef]
- Adcock, C.J.; Shutes, K. Portfolio Selection Based on The Multivariate Skew-Normal Distribution. In Financial Modelling; Skulimowski, A., Ed.; Progress and Business Publishers: Kraków, Poland, 1999. [Google Scholar]
- Fama, E.F. Efficient Capital Markets II. J. Financ. 1991, 46, 1575–1617. [Google Scholar] [CrossRef]
- Adcock, C.J. Extensions of Stein’s Lemma for the Skew-Normal Distribution. Commun. Stat. Theory Methods 2007, 36, 1661–1671. [Google Scholar] [CrossRef]
- Simaan, Y. Portfolio Selection and Asset Pricing-Three-Parameter Framework. Manag. Sci. 1993, 39, 568–577. [Google Scholar] [CrossRef]
- Stein, C.M. Estimation of The Mean of a Multivariate Normal Distirbution. Ann. Stat. 1981, 9, 1135–1151. [Google Scholar] [CrossRef]
- Landsman, Z.; Nešlehová, J. Stein’s Lemma for elliptical random vectors. J. Multivar. Anal. 2008, 99, 912–927. [Google Scholar] [CrossRef][Green Version]
- Roch, O.; Valdez, E.A. Lower convex order bound approximations for sums of log-skew normal random variables. Appl. Stoch. Models Bus. Ind. 2011, 27, 487–502. [Google Scholar] [CrossRef]
- Dhaene, J.; Denuit, M.; Goovaerts, M.J.; Kaas, R.; Vyncke, D. The concept of comonotonicity in actuarial science and finance: Applications. Insur. Math. Econ. 2002, 31, 133–161. [Google Scholar] [CrossRef]
- Dhaene, J.; Denuit, M.; Goovaerts, M.J.; Kaas, R.; Vyncke, D. The concept of comonotonicity in actuarial science and finance: Theory. Insur. Math. Econ. 2002, 31, 1–33. [Google Scholar] [CrossRef]
- Blasi, F.; Scarlatti, S. From Normal vs Skew-Normal Portfolios: FSD and SSD Rules. J. Math. Financ. 2012, 2, 90–95. [Google Scholar] [CrossRef][Green Version]
- Bodnar, T.; Gupta, A.K. Robustness of the inference procedures for the global minimum variance portfolio weights in a skew-normal model. Eur. J. Financ. 2015, 21, 1176–1194. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. The Cross-section of expected stock returns. J. Financ. 1992, 47, 427–465. [Google Scholar] [CrossRef]
- Bernardi, M.; Maruotti, A.; Lea, P. Skew mixture models for loss distributions: A Bayesian approach. Insur. Math. Econ. 2012, 51, 617–623. [Google Scholar] [CrossRef]
- McNeil, A. Estimating the tails of loss severity distributions using extreme value theory. ASTIN Bull. 1997, 27, 117–137. [Google Scholar] [CrossRef]
- Bernardi, M. Risk measures for Skew Normal mixtures. Stat. Probab. Lett. 2013, 83, 1819–1824. [Google Scholar] [CrossRef]
- Pigeon, M.; Antonio, K.; Denuit, M. Individual Loss Reserving with the Multivariate Skew Normal Framework. ASTIN Bull. J. Int. Actuar. Assoc. 2013, 43, 399–428. [Google Scholar] [CrossRef]
- Gupta, A.K.; Chen, J. A class of multivariate skew normal models. Ann. Inst. Stat. Math. 2004, 56, 305–315. [Google Scholar] [CrossRef]
- Eling, M. Fitting Insurance Claims to Skewed Distributions: Are the Skew-Normal and Skew-Student Good Models? Insur. Math. Econ. 2012, 51, 239–248. [Google Scholar] [CrossRef]
- Antonio, K.; Plat, R. Micro-level stochastic loss reserving for general insurance. Scand. Actuar. J. 2014, 2014, 649–669. [Google Scholar] [CrossRef]
- Vernic, R. Multivariate skew-normal distributions with applications in insurance. Insur. Math. Econ. 2006, 38, 413–426. [Google Scholar] [CrossRef]
- Adcock, C.J.; Eling, M.; Loperfido, N. Skewed Distributions in Finance and Actuarial Science: A Review. Eur. J. Financ. 2015, 21, 1253–1281. [Google Scholar] [CrossRef]
- Tian, W.; Wang, T.; Baokun, L. Risk Measures with Wang Transforms under Flexible Skew-generalized Settings. Int. J. Intell. Technol. Appl. Stat. 2014, 7, 185–205. [Google Scholar]
- Wang, S.S. A Class of Distortion Operators for Pricing Financial and Insurance Risks. J. Risk and Insur. 2000, 67, 15–36. [Google Scholar] [CrossRef]
- Wang, S.S. A universal framework for pricing financial and insurance risks. Astin Bull. 2002, 32, 213–234. [Google Scholar] [CrossRef]
- Kollo, T.; Pettere, G.; Valge, M. Tail Dependence of Skew t-Copulas. Commun. Stat. Simul. Comput 2017, 46, 1024–1034. [Google Scholar] [CrossRef]
- Pettere, G.; Kollo, T. Risk Modeling for Future Cash Flow using Skew T-Copula. Commun. Stat. Theory Methods 2011, 40, 2919–2925. [Google Scholar] [CrossRef]
- Padoan, S. Multivariate extreme models based on underlying skew-t and skew-normal distributions. J. Multivar. Anal. 2011, 102, 977–991. [Google Scholar] [CrossRef]
- Lysenko, N.; Roy, P.; Waeber, R. Multivariate Extremes of Generalized Skew-normal Distributions. Stat. Probab. Lett. 2009, 79, 525–533. [Google Scholar] [CrossRef][Green Version]
- Lin, T.I.; Wang, W.L. Multivariate skew-normal linear mixed models for multi-outcome longitudinal data. Stat. Model. 2013, 13, 199–221. [Google Scholar] [CrossRef]
- Huang, Y.; Dagne, G. A Bayesian Approach to Joint Mixed-Effects Models with a Skew-Normal Distribution and Measurement Errors in Covariates. Biometrics 2011, 69, 260–269. [Google Scholar] [CrossRef]
- Goldman, A.I.; Carlin, B.P.; Crane, L.R.; Launer, C.; Korvick, J.A.; Deyton, L.; Abrams, D.L. Response of CD4+ and Clinical Consequences to Treatment Using ddI or ddC in Patients with Advanced HIV Infection. J. Acquir. Immune Defic. Syndr. Hum. Retrovirol. 1996, 11, 161–169. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, J.; Yan, C. Mixed-Effects Joint Models with SkewNormal Distribution for HIV Dynamic Response with Missing and Mismeasured Time-Varying Covariate. Int. J. Biostat. 2012, 8, 1–28. [Google Scholar] [CrossRef]
- Lederman, M.; Connick, E.; Landay, A.; Kuritzkes, D.R.; Spritzler, J.; Clair, S.M.; Kotzin, B.L.; Fox, L.; Chiozzi, M.H.; Leonard, J.M.; et al. Immunologic responses associated with 12 weeks of combination antiretroviral therapy consisting of zidovudine, lamivudine, and ritonavir: Results of AIDS Clinical Trials Group Protocol 315. J. Infect. Dis. 1998, 178, 70–79. [Google Scholar] [CrossRef]
- Yu, B.; O’Malley, A.J.; Ghosh, P. Linear mixed models for multiple outcomes using extended multivariate skew-t distributions. Stat. Interface 2014, 7, 101–111. [Google Scholar] [CrossRef]
- Ghosh, P.; Hanson, T. A semiparametric Bayesian approach to multivariate longitudinal data. Aust. N. Z. J. Stat. 2010, 52, 275–288. [Google Scholar] [CrossRef]
- Zadkarami, M.R.; Rahimi, A. Factors Associated with Birthweight: An Application of the Multiple Skew-Normal Regression. Res. J. Obs. Gynecol. 2008, 1, 9–17. [Google Scholar] [CrossRef][Green Version]
- Mahmud, S.; Lou, W.; Johnston, N. A probit- log- skew-normal mixture model for repeated measures data with excess zeros, with application to a cohort study of paediatric respiratory symptoms. BMC Med. Res. Methodol. 2010, 55, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ho, R.; Fong, T.C.T.; Cheung, I.K.M. Cancer-related fatigue in breast cancer patients: Factor mixture models with continuous non-normal distributions. Qual. Life Res. 2014, 23, 2909–2916. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Jamalizadeh, A.; Balakrishnan, N.; Salehi, M. Order statistics and linear combination of order statistics arising from a bivariate selection normal distribution. Stat. Probab. Lett. 2010, 80, 445–451. [Google Scholar] [CrossRef]
- Fishman, G.; Baca, W.; Alexander, K.R.; Derlacky, D.J.; Glenn, A.M.; Viana, M.A.G. Visual acuity in patients with best vitelliform macular dystrophy. Ophthalmology 1993, 100, 1665–1670. [Google Scholar] [CrossRef]
- Mansourian, M.; Mahdiyeh, Z.; Park, J.J.; Haghjooyejavanmard, S. Skew-symmetric Random Effect Models with Application to a Preventive Cohort Study: Improving Outcomes in Low Back Pain Patients. Int. J. Prev. Med. 2013, 4, 279–285. [Google Scholar]
- Ismail, S.; Sun, W.; Nathoo, F.S.; Babul, A.; Moiseev, A.; Beg, M.; Virji-Babul, N. A Skew-t space-varying regression model for the spectral analysis of resting state brain activity. Stat. Methods Med Res. 2012, 22, 422–438. [Google Scholar] [CrossRef]
- Kline, B.; Tobias, J.L. The Wages of BMI: Bayesian Analysis of a Skewed Treatment—Response Model with Nonparametric Endogeneity. J. Appl. Econ. 2008, 23, 767–793. [Google Scholar] [CrossRef]
- Fernandes, E.; Pacheco, A.; Penha-Gonçalves, C. Mapping of quantitative trait loci using the skew-normal distribution. J. Zhejiang Univ. Sci. 2007, 8, 792–801. [Google Scholar] [CrossRef]
- Chai, H.; Bailey, K.R. Use of log-skew-normal distribution in analysis of continuous data with a discrete component at zero. Stat. Med. 2008, 27, 3643–3655. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Lachos, V.H.; Abanto-Valle, C.A.; Ghosh, P. Linear Mixed Models for Skew-Normal Independent bivariate responses with an application to Periodontal Disease. Stat Med. 2010, 10, 2643–2655. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Lachos, V.H.; Castro, L.M.; Dey, D.K. Skew-normal/independent linear mixed models for censored responses with applications to HIV viral loads. Biom. J. 2012, 54, 405–425. [Google Scholar] [CrossRef] [PubMed]
- Dagne, G.A. NIH Bayesian Inference for Skew-Normal Mixture Models With Left Censoring. J. Biopharm. Stat. 2013, 23, 1023–1041. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ho, H.; Lin, T.I.; Chang, H.H.; Haase, S.B.; Huang, S.; Pyne, S. Parametric modeling of cellular state transitions as measured with flow cytometry. BMC Bioinform. 2012, 13, S5. [Google Scholar] [CrossRef] [PubMed]
- Diggle, P.J.; Kenward, M.G. Informative dropout in longitudinal data analysis (with discussion). Appl. Stat. 1994, 43, 49–94. [Google Scholar] [CrossRef]
- Contreras-Reyes, J. Analyzing Fish Condition Factor Index Through Skew-Gaussian Information Theory Quantifiers. Fluct. Noise Lett. 2016, 15, 1–15. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E.; Arellano-Valle, R.B.; Canales, T.M. Comparing growth curves with asymmetric heavy-tailed errors: Application to the southern blue whiting (Micromesistius australis). Fish. Res. 2014, 159, 88–94. [Google Scholar] [CrossRef]
- Lee, M.S.Y.; Skinner, A. Testing fossil calibrations for vertebrate molecular trees. Zool. Scr. 2011, 40, 538–543. [Google Scholar] [CrossRef]
- Stoy, P.C.; Williams, M.; Disney, M.; Prieto-Blanco, A.; Huntley, B.; Baxter, R.; Lewis, P. Upscaling as ecological information transfer: A simple framework with application to Arctic ecosystem carbon exchange. Landsc. Ecol. 2009, 24, 971–986. [Google Scholar] [CrossRef]
- Simolo, C.; Brunetti, M.; Maugeri, M.; Nanni, T. Evolution of extreme temperatures in a warming climate. Geophys. Res. Lett. 2011, 38, 1–6. [Google Scholar] [CrossRef]
- Anagreh, Y.; Bataineh, A.; Al-Odat, M. Assessment of renewable energy potential, at Aqaba in Jordan. Renew. Sustain. Energy Rev. 2010, 14, 1347–1351. [Google Scholar] [CrossRef]
- Bartoletti, S.; Loperfido, N. Modelling air pollution data by the skew-normal distribution. Stoch. Environ. Res. Risk Assess. 2010, 24, 513–517. [Google Scholar] [CrossRef]
- Morris, S.A.; Reich, B.J.; Thibaud, E.; Cooley, D. A space-time skew-t model for threshold exceedances. Biometrics 2017, 73, 749–758. [Google Scholar] [CrossRef] [PubMed]
- Guttorp, P.; Loperfido, N. Network bias in air quality monitoring design. Environmetrics 2008, 19, 661–671. [Google Scholar]
- Hashemi, F.; Amirzadeh, V.; Jamalizadeh, A. An Extension of the Birnbaum-Saunders Distribution Based on Skew-Normal-t Distribution. J. Stat. Res. Iran 2015, 12, 1–37. [Google Scholar]
- Zakaria, R.; Metcalfe, A.V.; Howlett, P.; Piantadosi, J.; Boland, J. Using the skew-t copula to model bivariate rainfall distribution. Anziam J. 2010, 51, C231–C246. [Google Scholar] [CrossRef]
- Nathoo, F.S. Space–time regression modeling of tree growth using the skew-t distribution. Environmetrics 2010, 21, 817–833. [Google Scholar] [CrossRef]
- Li, C.I.; Su, N.C.; Su, P.F.; Shyr, Y. The design of and R control charts for skew normal distributed data. Commun. Stat. Theory Methods 2014, 43, 4908–4924. [Google Scholar] [CrossRef]
- Figueiredo, F.; Gomes, M.I. The Skew-Normal Distribution in SPC. Rev. Stat. J. 2013, 11, 83–104. [Google Scholar]
- Rendao, Y.; Longquan, Z.; Kun, L. An Empirical Study on the Energy Intensity in China Based on the Skew-normal Distribution. Int. J. Smart Home 2015, 9, 73–82. [Google Scholar] [CrossRef]
- Youssef, M. Outlier Detection Technique Based on Skew-Normal Distribution. Int. J. Res. Wirel. Syst. 2013, 2, 7–16. [Google Scholar]
- Zadkarami, M.R.; Rowhani, M. Application of Skew-normal in Classification of Satellite Image. J. Data Sci. 2010, 8, 597–606. [Google Scholar]
- Balef, H.A.; Kamal, M.; Afzali-Kusha, A.; Pedram, M. All-Region Statistical Model for Delay Variation Based on Log-Skew-Normal Distribution. IEEE Trans. Comput. Aided Des. Integr. Circ. Syst. 2016, 35, 1503–1508. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lin, C.T. Lifetime inference for highly reliable products based on skew-normal accelerated destructive degradation test model. IEEE Trans. Reliab. 2015, 64, 1340–1355. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, Y. Use of Skew-Normal and Skew-t Distributions for Mixture Modeling of Freeway Speed Data. J. Transp. Res. Board 2011, No. 2260, 67–75. [Google Scholar] [CrossRef]
- Ramprasath, S.; Vijaykumar, M.; Vasudevan, V. A skew-normal canonical model for statistical static timing analysis. IEEE Trans. VLSI Syst. 2016, 24, 2359–2368. [Google Scholar] [CrossRef]
- Müller, P.; José, A.; del Peral-Rosado, R.P.; Seco-Granados, G. Statistical trilateration with skew-t distributed errors in LTE Networks. IEEE Trans. Wirel. Commun. 2016, 15, 7114–7127. [Google Scholar] [CrossRef]
- Eyer, L.; Genton, M.G. An astronomical distance determination method using regression with skew-normal errors. In Skew-Elliptical Distributions and Their Applications: A Journey Beyond Normality; Genton, M.G., Ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; Chapter 18; pp. 309–319. [Google Scholar]
- Simola, U.; Dumusque, X.; Cisewski-Kehe, J. Measuring precise radial velocities and cross-correlation function line-profile variations using a skew normal density. Astron. Astrophys. 2019, 622, A131. [Google Scholar] [CrossRef]
- Lu, X.; Liu, Q.; Xue, F. Unique closed-form solutions of portfolio selection subject to mean-skewness-normalization constraints. Oper. Res. Perspect 2019, 6, 1–15. [Google Scholar] [CrossRef]
- Bekaert, G.; Harvey, C.R.; Erb, C.B.; Viskantam, T.E. Distributional Characteristics of Emerging Market Returns & Asset Allocation. J. Portf. Manag. 1998, 24, 201–216. [Google Scholar]
- Bogetoft, P.; Otto, L. Benchmarking with DEA and SFA; R Package Version 0.27; 2018; Available online: https://cran.r-project.org/package=Benchmarking (accessed on 6 January 2020).
- Tancredi, A. Accounting for Heavy Tails in Stochastic Frontier Models; Working Paper 2002.16; Dipartimento di Scienze Statistiche, Università di Padova: Padova, Italia, 2002. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adcock, C.; Azzalini, A. A Selective Overview of Skew-Elliptical and Related Distributions and of Their Applications. Symmetry 2020, 12, 118. https://doi.org/10.3390/sym12010118
Adcock C, Azzalini A. A Selective Overview of Skew-Elliptical and Related Distributions and of Their Applications. Symmetry. 2020; 12(1):118. https://doi.org/10.3390/sym12010118
Chicago/Turabian StyleAdcock, Chris, and Adelchi Azzalini. 2020. "A Selective Overview of Skew-Elliptical and Related Distributions and of Their Applications" Symmetry 12, no. 1: 118. https://doi.org/10.3390/sym12010118
APA StyleAdcock, C., & Azzalini, A. (2020). A Selective Overview of Skew-Elliptical and Related Distributions and of Their Applications. Symmetry, 12(1), 118. https://doi.org/10.3390/sym12010118




