Routing for Hazardous Materials Transportation in Urban Areas

Abstract

Hazardous materials (HAZMAT) are important for daily production in cities, which usually have a high population. To avoid the threat to public safety and security, the routes for HAZMAT transportation should be planned legitimately by mitigating the maximum risk to population centers. For the objective of min-max local risk in urban areas, this study has newly proposed an optimization model where the service of a link for HAZMAT transportation was taken as the key decision variable. Correspondingly, the symmetric problem of min-max optimization takes significant meanings. Moreover, in consideration of the work load of solving the model under a lot of decision variables, a heuristic algorithm was developed to obtain an optimal solution. Thereafter, a case study was made to test the proposed model and algorithm, and the results were compared with those generated by deterministic solving approaches. In addition, this research is able to be an effective reference for authorities on the management of HAZMAT transportation in urban areas.

1. Introduction

Hazardous materials (HAZMAT) are important for the daily production of cities, while the undesirable harmfulness they represent cannot be neglected. Many incidents of HAZMAT contamination have occurred during the processes of transportation, leading to serious consequences to the society. According to the statistics of the US Department of Transportation [1], there were 140,742 HAZMAT transportation incidents on roads in the decade 2004–2013. Hence, it is rather essential to mitigate risk in the process of HAZMAT transportation, especially for urban areas with many population centers. These centers include schools, hospitals, resident communities, and so on. For a HAZMAT transportation route, the risk to population centers along the way should be reduced as much as possible. Hence, it is necessary to solve the routing problem using accurate mathematical methods in which optimization approaches take the majority of research field.

In fact, there have been quite a few studies on routing for HAZMAT transportation by different modes. For the design of HAZMAT transportation networks, Kara and Verter proposed a linear integer bi-level programming model that could be transformed to a single mixed integer form by Kuhn-Tucker constraints [2]. For the mitigation of global risk, Erkut and Alp proposed a spanning tree to cover the large gathering area [3]. In a bi-level programming model solved by a heuristic algorithm, two optimization objectives were risk and transit cost [4]. Moreover, a path-based approach for HAZMAT transport network design was proposed by Verter and Kara [5]. Bianco et al. studied a bi-level programming model, in which the upper level was to minimize the maximum risk among certain links and the lower level was minimizing the total risk [6]. Xie et al. proposed the multi-modal HAZMAT routing problem based on an integrated model consisting of practical constraints [7]. Furthermore, a game-theoretic approach for regulating HAZMAT transportation was developed [8]. Fan et al. made an urban HAZMAT transportation model with road closure consideration to deal with traffic restrictions [9]. Bronfman et al. developed the max-min HAZMAT routing problem to ensure security along transport routes [10].

In addition, there has been some research on transportation network optimization by economic measures, such as studies on social welfare and toll policies [11,12,13]. To facilitate capacity planning, assessment, and querying activities in multi-modal HAZMAT transportation systems, Bevrani et al. developed a comprehensive linear programming model that includes congestion functions, analytical, structural and parametric changes [14]. Similarly, an improved multi-commodity network flow (MCNF) model was introduced to holistically assess a multi modal transportation system and to identify the optimal flows achievable [15]. Taking uncertainty scenarios into consideration, a reliable multi-modal multi-commodity model was made by Mohammadi et al. [16]. Taslimi et al. designed a comprehensive modelling framework for HAZMAT transport network design, HAZMAT response team location and equity of risk [1]. Moreover, Hosseini and Verma proposed a Value-at-Risk approach to routing rail HAZMAT shipments [17]. Fontaine and Minner introduced the method of Benders decomposition to solve complicated HAZMAT transport network design problems [18]. To address the impact of time windows and fuzzy demands on route selection, Fazayeli et al. presented a two-part genetic algorithm to obtain the optimal scheme [19]. Ghaderi and Burdett developed an integrated location and routing approach for transporting hazardous materials in a bi-modal transportation network with stochastic restrictions on reliability [20]. Jabbarzadeh et al. introduced an optimization approach to planning rail HAZMAT shipments in the presence of random disruptions [21]. To deal with traffic restriction constraints in HAZMAT transportation networks, Hu et al. made a multi-objective location-routing model for hazardous materials logistics [22].

These studies involve various kinds of optimization objectives and decision measures. However, there has not been a study that specializes in the problem of total risk under the condition of maximum local risk in urban areas. Furthermore, the most closely related work with routing for HAZMAT transportation in cities was performed by Bronfman et al., who focused on a single transportation route for HAZMAT and the maximum distance for security [10]. In light of the demonstrated advantage of the minimum local consequence model over previous catastrophic avoidance techniques, here we make the first attempt to develop a method for minimizing the maximum local risk framework for urban road HAZMAT shipments. It is important that the proposed framework is distinct from that in Bronfman et al. in the following ways: 1) characteristics of risk criteria—for example, affected population due to HAZMAT release in transportation incidents; 2) compared with single route planning, the application of multiple shipments with various origin-destination pairs is a more realistic scenario; and 3) for an optimal heuristic algorithm used for large real instances, it is necessary to incorporate iterative characteristics in computation. Thereafter, this paper will propose an optimization method where all transportation routes of HAZMAT were considered and the maximum local risk to population centers was mitigated. Hence, it is necessary to make comprehensive analysis for the symmetric problem of min-max optimization. The remaining parts of this paper are organized as follows. In Section 2, a linear integer optimization model is established. Moreover, the corresponding heuristic algorithm for the proposed model is made in Section 3. Furthermore, Section 4 describes a case study. Finally, Section 5 provides the conclusions of this study and discusses future research issues.

2. An Optimization Model

In the routing for HAZMAT transportation, all routes should be planned by the authority that focuses on the risk in urban areas. For such a practical problem, comprehensive factors are involved under the constraints of application. Hence, some necessary hypotheses should be presented before the description of the optimization model.

2.1. Problem Hypotheses

In this section, the relevant factors and conditions were assumed to facilitate modelling analysis and quantitative research. In practical applications such as decision support, this method can be further extended by combining specific limited factors to ensure the accuracy and universality of basic theories.

Hypothesis 1:

Time dimension of the problem. This optimization problem is assumed to be static, and the time-dependent conditions are simplified. For a purpose of reasonable abstract definition, the values of dynamic parameters are assumed to be averaged, for example, affected population due to HAZMAT shipments. If necessary, the basic conditions are able to be expanded for more complicated planning of HAZMAT transportation.

Hypothesis 2:

Connectivity of the transportation network. In this study, the basic road network is a completely connected graph. For any shipment of HAZMAT, there is at least one path from the origin to the destination (OD pair).

Hypothesis 3:

Impact of the geographic shape. All population centers are assumed to be points in the calculation while the corresponding sizes are ignored. Moreover, the distance from a population center to a transport link is assumed as the Euclidean distance between the center point and the closest point on the link.

Hypothesis 4:

Impact of incident possibility. It is assumed that all vehicles are in stable condition and the probabilities of incident are unknown in the transportation network. Hence, the risk caused by HAZMAT only consists of threatened consequences to population centers.

Hypothesis 5:

Traffic conditions in the network. From a perspective of macro modelling, this study focuses on the optimization effect of the relevant network characteristics. For the incident risk, the traffic conditions are assumed to be optimistic. Furthermore, the probability of incident is not incorporated in the risk assessment of this study. Moreover, the traffic conditions can be analyzed further in future studies with perspectives of micro modelling.

2.2. Model Establishment

$$\min Z={\displaystyle \sum _{s\in S}{R}^s}.$$

(1)

where,

$S$: 

Set of HAZMAT shipments, indexed by $s$, and the number of shipments is $\lambda$.

$R^s$: 

Auxiliary decision variable, maximum local risk caused by the closest link of shipment $s$ to population centers, unit: persons per kilometer.

$${\displaystyle \sum _{(i,j)\in A}{n}^s{\rho }^c(1/d_{cs}^{ij})v_{cs}^{ij}}\le R^s \forall c\in N^c,s\in S.$$

(2)

where,

$n^s$: 

Transportation demand of shipment $s$, measured by the number of standardized vehicles;

$i,j$: 

Nodes of road transportation network in the urban area, and the number of nodes is $\epsilon$;

$A$: 

Set of links of road transportation network in the urban area, $(i,j)\in A$, and the number of links is $\phi$;

$N^c$: 

Set of population centers, indexed by $c$;

${\rho }^c$: 

Population quantity of center $c$, unit: persons, and the number of centers is $\mu$;

$d_{cs}^{ij}$: 

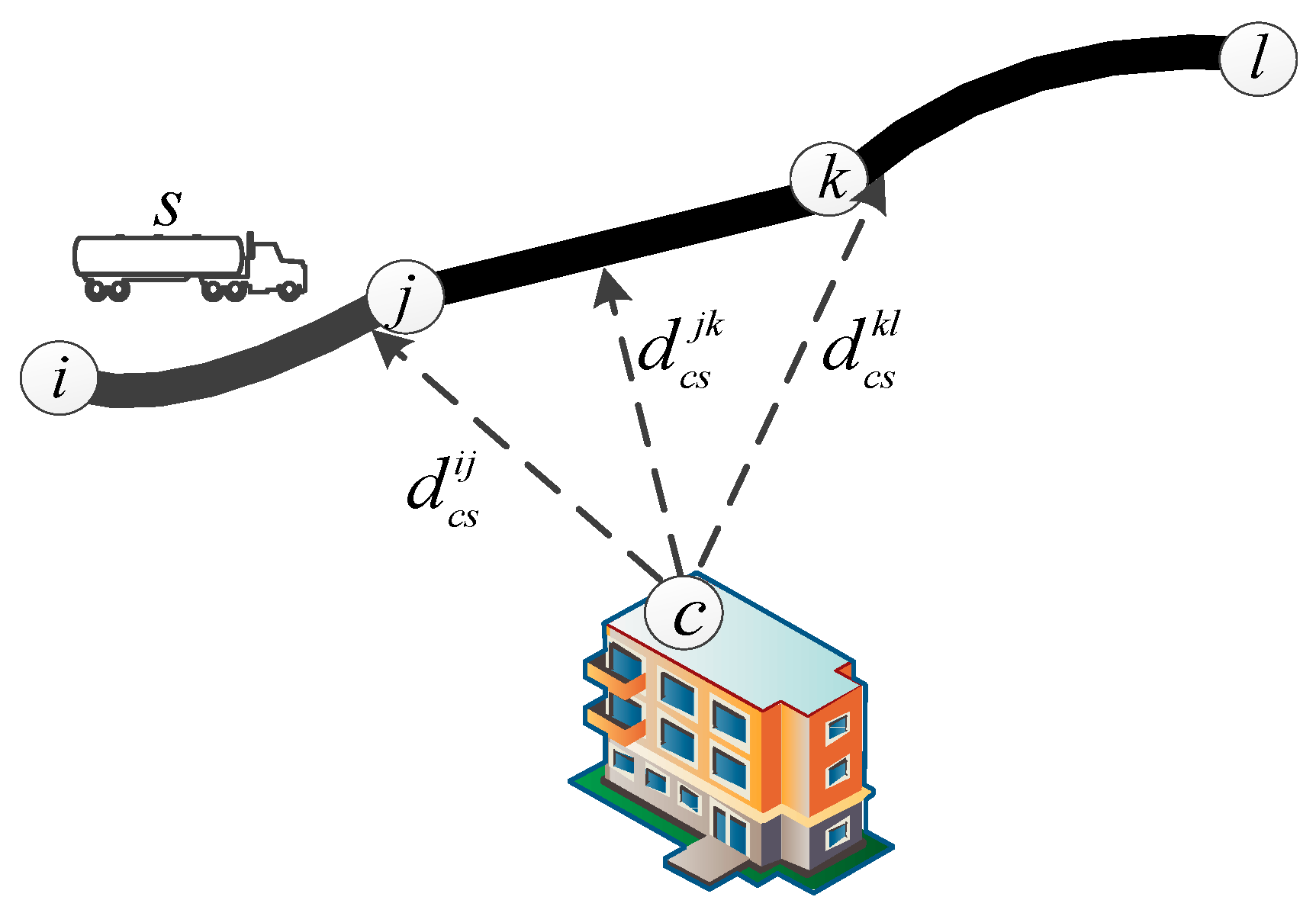
Euclidean distance between center $c$ and its closest point on link $(i,j)$ of shipment $s$, illustrated in Figure 1, unit: kilometers;

$v_{cs}^{ij}$: 

Decision variable, which is equal to 1 if link $(i,j)$ used for HAZMAT shipment $s$ is the closest link to $c$, 0 otherwise.

$$v_{cs}^{ij}\le x_s^{ij} \forall (i,j)\in A,c\in N^c,s\in S.$$

(3)

where,

$x_s^{ij}$: 

Decision variable, which is equal to 1 if link $(i,j)$ is used for HAZMAT shipment $s$, 0 otherwise.

$${\displaystyle \sum _{(i,j)\in A}{v}_{cs}^{ij}}\le 1 \forall c\in N^c,s\in S.$$

(4)

where,

$v_{cs}^{ij}$: 

This notation has been explained in Formula (2).

$$x_s^{ij}-{\displaystyle \sum _{(m,n)\in A|d_{cs}^{mn}\le d_{cs}^{ij}}{v}_{cs}^{mn}\le }{v}_{cs}^{ij} \forall (i,j)\in A,c\in N^c,s\in S.$$

(5)

where,

$v_{cs}^{mn}$: 

Referring to the definition of $v_{cs}^{ij}$;

$d_{cs}^{mn}$: 

Referring to the definition of $d_{cs}^{ij}$.

Formula (6) offers the constraint of transit flow conservation for a link, which divides the nodes into three types. Furthermore, Formula (7) delimits the auxiliary decision variable, and the maximum local risk caused by the closest link of a shipment to a population center is nonnegative. Finally, it is necessary to describe the binary constraints of decision variables in Formula (8) and Formula (9).

$${\displaystyle \sum _{(i,j)\in A}{x}_s^{ij}}-{\displaystyle \sum _{(j,i)\in A}{x}_s^{ji}}=\{\begin{array}{ll}1& \mathrm{if}i=o(s)\\ -1& \mathrm{if}i=d(s)\\ 0& \mathrm{otherwise}\end{array} \forall i\in N,s\in S.$$

(6)

where,

$o(s)$: 

Origin of HAZMAT shipment $s$;

$d(s)$: 

Destination of HAZMAT shipment $s$.

$$R^s\ge 0.$$

(7)

where,

$R^s$: 

Nonnegative constraint for auxiliary decision.

$$x_s^{ij}\in \left\{0,1\right\} \forall (i,j)\in A,s\in S.$$

(8)

where,

$x_s^{ij}$: 

Constrained to be binary.

$$v_{cs}^{ij}\in \left\{0,1\right\} \forall (i,j)\in A,c\in N^c,s\in S.$$

(9)

where,

$v_{cs}^{ij}$: 

Constrained to be binary.

3. Algorithm Design

Although there are continuous variables (i.e., $R^s$ for all shipments) in the proposed model, they only play the role of auxiliary decision variables. This problem is a linear integer program which can be solved by common techniques theoretically, and it does not belong to the NP-hard class. However, the complexity of the problem not only depends on the types of variables, but also lies with the numbers of variables and constraints. From the formulations in Section 2, it is able to be found that there are $\lambda +\lambda \phi \mu +\lambda \phi$ decision variables and $2\lambda \mu +2\lambda \phi \mu +\lambda \epsilon +\lambda$ constraints. Thereafter, the work load of computation is rather heavy, even for small instances in simple urban areas. Moreover, the complexity of calculation leads to the limited application in practical operation, although the linear model with integer variables could be theoretically solved by commercial software such as CPLEX [1]. Hence, there is a need to explore more effective solving approaches, and feasible heuristic algorithms are also able to be considered in depth [10]. In addition, this study has developed a heuristic calculation under principles of minimizing the maximum local risk for all HAZMAT shipments in the urban area.

The main concept behind this heuristic algorithm is that a risk radius can be used to control the searching step for an optimal HAZMAT shipment route. Moreover, the structure of the road network is reconstructed in iterations where the undesirable links are eliminated one after one. Finally, an optimal HAZMAT shipment route would be determined in the unchanged network. The item ${\omega }_{cs}^{ij}=n^s{\rho }^c(1/d_{cs}^{ij})$ is denoted as the equivalent local risk under the inverse impact of distance. For a certain type of HAZMAT transported in urban areas, when there is a disruption in the shipment $s$, much of the consequence would be within the zone with a certain radius ${\gamma }^s$ illustrated in Figure 2. Thus, the valid local risk is represented as ${\omega }_{cs}^{ij}=n^s{\rho }^c(1/d_{cs}^{ij})|d_{cs}^{ij}\le {\gamma }^s$. Furthermore, the maximum local risk along the route of a shipment is ${\omega }_s^{ij}=\underset{c\in N^c}{\max }{\omega }_{cs}^{ij}|d_{cs}^{ij}\le {\gamma }^s$.

In addition, the solution of routing for HAZMAT shipments is to search for feasible route schemes when the objective and constraints are taken into consideration. Thereafter, for a HAZMAT shipment $s$, $F_s^t$ is denoted as the $t_{th}$ candidate route in the transportation network. Thus, the maximum local risk to population centers along route $F_s^t$ is ${\omega }^{F_s^t}=\underset{(i,j)\in F_s^t}{\min }{\omega }_s^{ij}$, and the calculation is in accordance with the optimization objective of minimizing the maximum local risk for all shipments. The flow chart of the heuristic algorithm is illustrated in Figure 3, and the corresponding detailed steps are as follows.

Step 1: 

Initialization. List the structure of the transportation network $\left(N,A\right)$ including nodes and links, OD pairs for HAZMAT shipments and population centers in the area.

Step 1-1: 

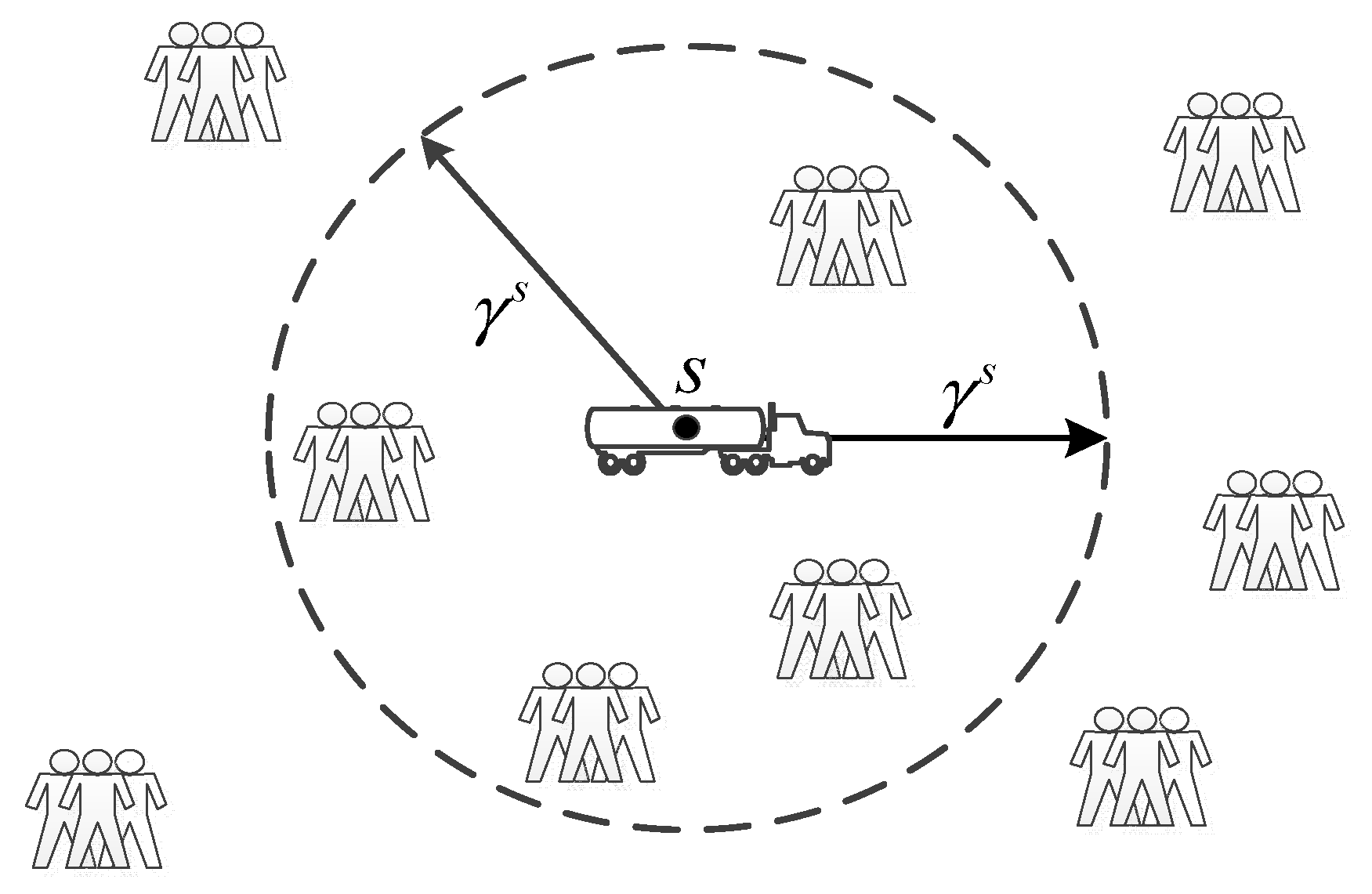
Set the counter $t=0$, and determine the risk radius ${\gamma }^s$ according to the type of HAZMAT for all shipments.

Step 1-2: 

$\forall s\in S,c\in N^c,(i,j)\in A|d_{cs}^{ij}\le {\gamma }^s$, compute the local risk along the route of shipment $s$ as ${\omega }_{cs}^{ij}$. While $\forall s\in S,c\in N^c$, $(i,j)\in A|d_{cs}^{ij}>{\gamma }^s$, set ${\omega }_{cs}^{ij}=0$.

Step 1-3: 

For all $s\in S,(i,j)\in A$ in the HAZMAT transportation network, compute the maximum local risk along the route of shipment $s$ as ${\omega }_s^{ij}$.

Step 2: 

Initial Route. For all $s\in S$, the Dijkstra algorithm is used to search for a shortest route between $o(s)$ and $d(s)$ [23], and the route is denoted as $F_s^0$ for shipment $s$. Thereafter, the maximum local risk to population centers along route $F_s^0$ is calculated as ${\omega }^{F_s^0}$.

Step 2-1: 

If ${\omega }^{F_s^0}=0$, $F_s^0$ is an optimal solution route for shipment $s$, and $R^s=0$. The computation for shipment $s$ stops, turn to next shipment until all shipments are checked.

Step 2-2: 

If ${\omega }^{F_s^0}>0$, there is possible to search for a better route. For the corresponding $s\in S$ turn to Step 3 for computation.

Step 3: 

Route update. The initial route is improved by the following sub-steps.

Step 3-1: 

$\forall s\in S$, the set of links is obtained as $A_s^t=A-\left\{(i,j)\in A|{\omega }_s^{ij}\ge {\omega }^{F_s^t}\right\}$. When $t=0$, $A_s^{t-1}=A$. Denote $N_s^t$ as the set of relevant nodes, and the candidate graph in $t_{th}$ iteration for shipment $s$ is $\left(N_s^t,A_s^t\right)$. Thereafter, the counter $t=t+1$.

Step 3-2: 

$\forall s\in S$, search for a feasible route $F_s^t$ over $\left(N_s^t,A_s^t\right)$ between $o(s)$ and $d(s)$.

Step 3-2-1: 

If no feasible route $F_s^t$ is found, the candidate graph in $t_{th}$ iteration for shipment $s$ is disconnected, $F_s^{t-1}$ is an optimal solution route for shipment $s$, and $R^s={\omega }^{F_s^{t-1}}$. The computation for shipment $s$ stops, turn to next shipment until all shipments are checked.

Step 3-2-2: 

If a feasible route $F_s^t$ is found, turn to Step 3-1.

Step 4: 

Scheme check. In the completely connected transportation network, any shipment is able to be assigned an optimal route, and all optimal routes are the final output.

It is worth pointing out that the calculation process in the algorithm is convergent, as all steps would be finished in finite iterations. As a convergence principle, the maximum local risk to population centers along a route should be under the condition ${\omega }_s^{ij}\ge {\omega }^{F_s^t}$. Hence, no matter how complicated the transportation network is, the optimal route is feasible when the network is completely connected. In addition, the application of the shortest route ensures the uniqueness of a solution, avoiding “multi-route” generation in the iterations [24].

4. Case Study

To test the effectiveness of the proposed model and algorithm, the local area of a city in North China was taken as the research subject. In the studied area, there were 337 nodes (numbered from N1 to N337) and 614 directed links (numbered from L1 to L614) to make up the transportation network. Moreover, 16 population centers (including universities, large residence communities and railway stations, numbered from C1 to C16) are regulated to be protected from undesired risk due to HAZMAT transportation, and the relevant population values are shown in

Table 1. Population centers in the case network.

Center	C1	C2	C3	C4	C5	C6	C7	C8
Population	4270	4910	5180	7100	6850	5190	6230	10020
Center	C9	C10	C11	C12	C13	C14	C15	C16
Population	9470	5960	8030	12030	7310	7210	5540	14640

. Furthermore, there were 12 shipments (numbered from S1 to S12) with different transportation demand and OD pairs listed in

Table 2. Shipments in the case network.

Shipment	S1	S2	S3	S4	S5	S6
OD pair	N1-N226	N2-N305	N3-N271	N4-N225	N5-N193	N6-N236
Demand	10	15	20	25	10	15
Shipment	S7	S8	S9	S10	S11	S12
OD pair	N7-N164	N8-N322	N9-N150	N10-N297	N11-N148	N12-N249
Demand	20	25	10	15	20	25

. The original assignment of computational data was taken as a reference for further calculation and analysis.

The experimental results were organized into two parts. The first part shows analysis of a brief comparison between the deterministic solving method by commercial software and the proposed heuristic algorithm. The second part shows detailed sensitivity analysis with respect to the value of risk radius due to HAZMAT transportation. In addition, the proposed model is optimally solved by CPLEX 12.8 solver, and the heuristic algorithm is coded and implemented in MATLAB R2018b. All solving processes were based on a PC with 4 GB of RAM. Thereafter, the main features of the proposed model and algorithm were as follows.

Figure 4 shows the convergence of a computation process by the heuristic algorithm where the risk radius was set as 1.0 km. As an illustration of the changing line, the objective remains unchanged after certain descending iterations, indicating that the computation was convergent. Furthermore, for the problem of searching for feasible routes in a connected graph, the number of links to be eliminated was finite, and the links had to be eliminated at each step [10]. The computation converged on the optimum solution, because it either finds a route with $R^s=0$, or there is no best feasible solution than the last route found right before the problem becomes unsolvable. Moreover, the computation was polynomial, as at every iteration the Dijkstra algorithm for the shortest route was used, which is polynomial. Hence, the maximum number of iterations is the number of links, that is, 337 in the case network.

Illustrated in

Table 3. Comparison between deterministic solving and the heuristic algorithm. (Risk radius = 1.0 km).

Index	Shipment Set	Deterministic Solving by CPLEX 12.8	The Proposed Heuristic Algorithm	Gap
Optimal objective (persons/km)	S1–S4	0.6335 × 106	0.7156 × 106	12.97%
	S1–S8	1.3371 × 106	1.5075 × 106	12.74%
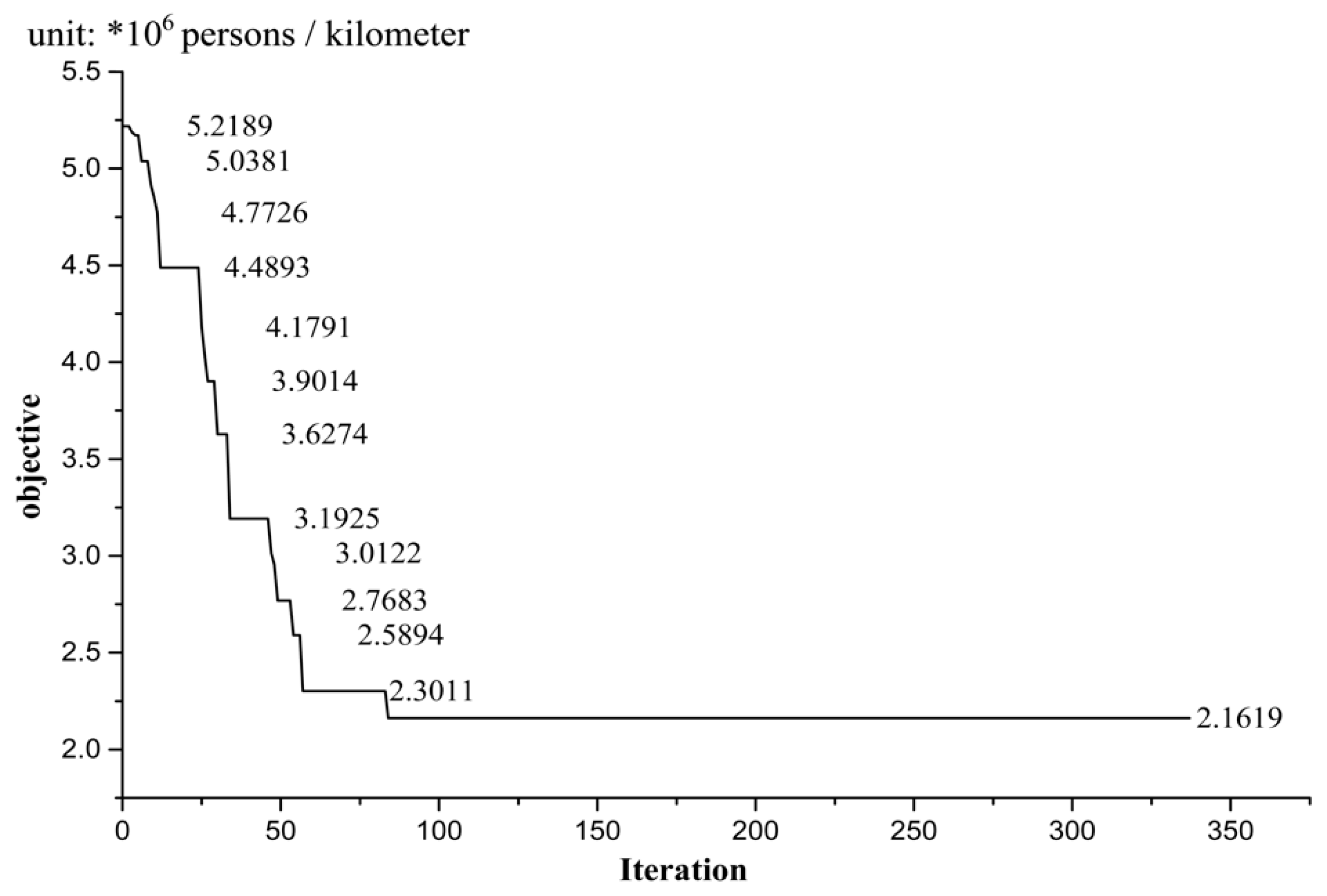
	S1–S12	1,9268 × 106	2.1619 × 106	12.20%
Max Rs (persons/km)	S1–S4	2.5083 × 105	2.6241 × 105	4.62%
	S1–S8	2.5083 × 105	2.6241 × 105	4.62%
	S1–S12	2.7358 × 105	2.7358 × 105	0.00%
Run time (s)	S1–S4	1.8729 × 104	0.8461 × 104	121.36%
	S1–S8	3.6114 × 104	1.3715 × 104	163.32%
	S1–S12	5.3782 × 104	1.9295 × 104	178.73%

, three indices were calculated for the comparison between deterministic solving and the heuristic algorithm. To highlight the different impacts on computation workload, three groups of shipments were taken into consideration. For the comparison of optimal objective, the results by deterministic solving were better than the ones generated by the proposed heuristic algorithm. However, the gap of calculated results tended to be smaller when the shipments are increased. For the maximum risk of a route, the difference between deterministic solving and the heuristic algorithm was not obvious. For the maximum risk with shipments S1–S12, there was no gap between the two solving methods. Furthermore, it was clear that the heuristic algorithm takes less run time for computation. In addition, the more the shipments were, the long run time was. On the whole, the deterministic solving by CPLEX 12.8 achieved better solutions than the proposed heuristic algorithm, but the gap was reduced when the shipping demand increased. Meanwhile, the proposed heuristic algorithm has an advantage on run time compared to the deterministic solving, and the difference was rather obvious when there are more shipments.

As shown in

Table 4. Impact of risk radius on optimal indices (Shipment set S1–S12).

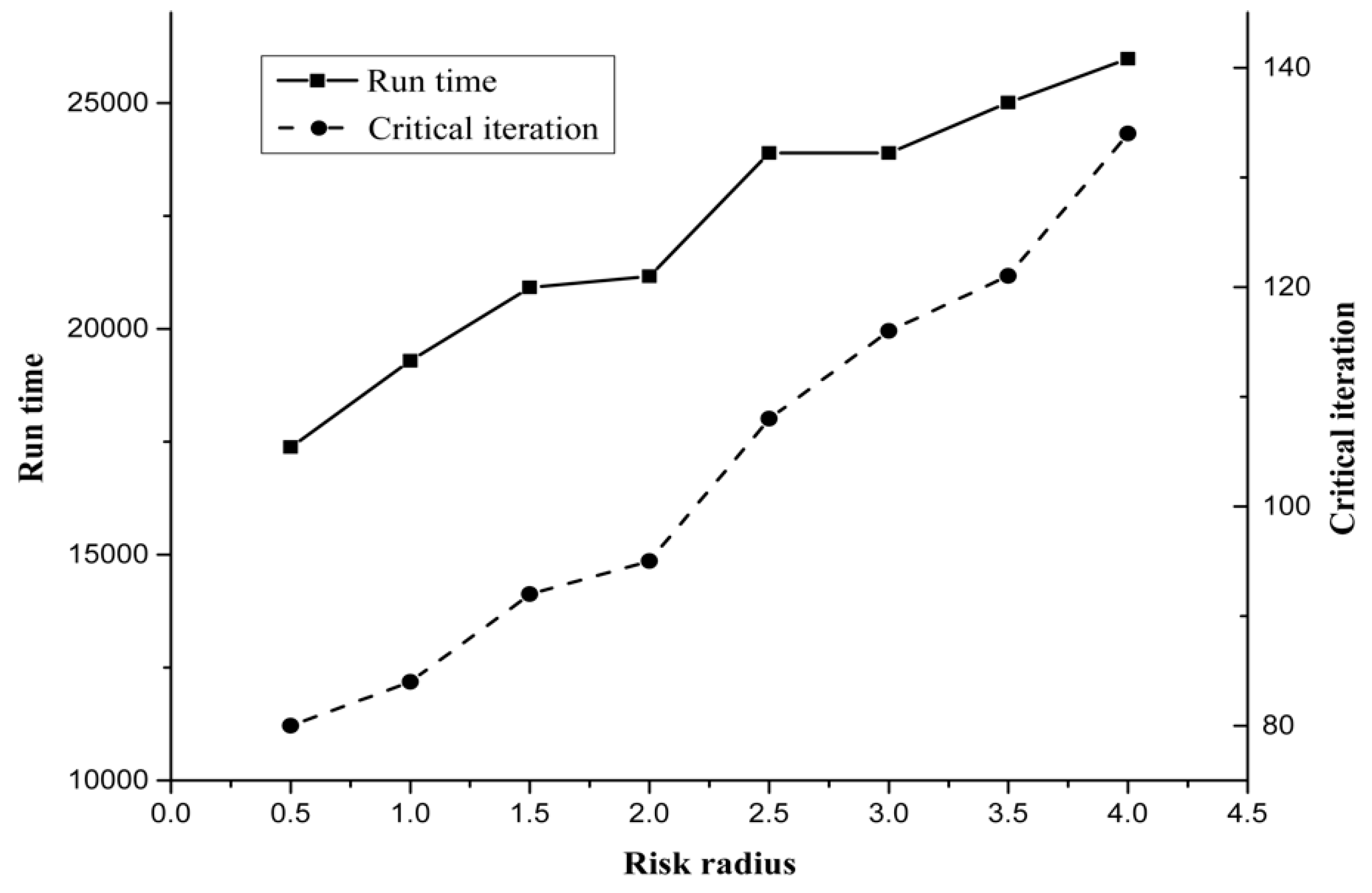
Risk Radius (km)	Optimal Objective (persons/km)	Max Rs (persons/km)
0.5	2.2348 × 106	3.0155 × 105
1.0	2.1619 × 106	2.7358 × 105
1.5	2.0862 × 106	2.5183 × 105
2.0	2.0047 × 106	2.4924 × 105
2.5	1.9490 × 106	2.4418 × 105
3.0	1.9205 × 106	2.3561 × 105
3.5	1.9205 × 106	2.3561 × 105
4.0	1.9205 × 106	2.3561 × 105

, the risk radius ${\gamma }^s$ takes significant impact on the calculated results by the proposed heuristic algorithm. From the general trend, both the optimal objective and the maximum local risk decreased with the increasing risk radius. The results indicate that when the value of risk radius was very large, more population centers were likely to be influenced by the risk due to HAZMAT transportation, thus the relevant routes of shipments should be planned away from the population centers as far as possible. Thereafter, the corresponding results would be better than the ones with smaller risk radiuses. However, when the risk radius was ${\gamma }^s>2.5$, the results remained unchanged, as there was no feasibility for planning more optimal routes. In addition, the following analysis will focus on the impact of risk radius on computation efficiency.

The illustration in Figure 5 shows the impact of risk radius on computation efficiency, including run time and critical iteration in the computing process. It can be inferred that the computation efficiency decreased with the increasing risk radius, as the difficulty of searching for optimal routes was raised. Moreover, the risk radius for calculation should be determined in accordance with practical demands. Furthermore, it is worth pointing out that computational experiments with parallel values of risk radius are able to be taken into consideration.

5. Conclusions

For the problem of routing for HAZMAT shipments in urban areas, this study develops an optimization model with a heuristic algorithm. To ensure the safety and security of population centers, the maximum risk due to HAZMAT transportation should be mitigated as much as possible. Thus, the objective of min-max local risk is proposed, and the service of a link for HAZMAT transportation is taken as the key decision variable. Moreover, in consideration of the work load of solving the model under a lot of decision variables, a heuristic algorithm was designed to obtain an optimal solution. Thereafter, a case study was made to testify the proposed model and algorithm, and the results were compared with the ones by deterministic solving approaches. This paper makes a three-fold contribution: 1) this is the first work that incorporates the characteristics of maximum local risk to population centers, and then outlines a min-max optimization model to mitigate risk from road HAZMAT shipments in urban areas; 2) this is the only effort that proposes multiple shipments with multiple routes to plan urban HAZMAT transportation using the optimal configuration of avoiding local consequence; and 3) this is the only work that demonstrates that the proposed methodology not only facilitates single population-averse routing of urban HAZMAT shipments, but can also deal with more kinds of risk based on the criteria preference (or tolerance) of the decision makers. In addition, this research is able to be effective reference for authorities on the management of HAZMAT transportation in urban areas.

In this research, more kinds of deterministic solving approaches are able to be considered. Furthermore, the proposed modelling method has not achieved the impact of some factors, such as vehicle type and geographic shape of population centers. This situation should be improved in future studies. Moreover, applying the emergency response is worthy of exploration, including relevant location and service assignment. In addition, incident probabilities could be analyzed in depth, in order to describe the problem comprehensively.