High-Precision Authentication Scheme Based on Matrix Encoding for AMBTC-Compressed Images
Abstract
1. Introduction
2. Related Works
2.1. AMBTC Compression
2.2. The Matrix Encoding
- Step 1:
- Compute to derive vector M.
- Step 2:
- Calculate the syndrome vector, .
- Step 3:
- Search for the same syndrome value as z in Table 2, then the gth column can be located, where . The corresponding identifier (ID) is also g, which is the to-be-flipped bit-location later in this paper. At the same time, the corresponding coset leader vector is mapped as eg.
- Step 4:
- Change the gth bit of the cover vector CV by . Note that if the syndrome value, z = (000) or g = 0, then there is nothing to be changed; that is, CV′ = CV.
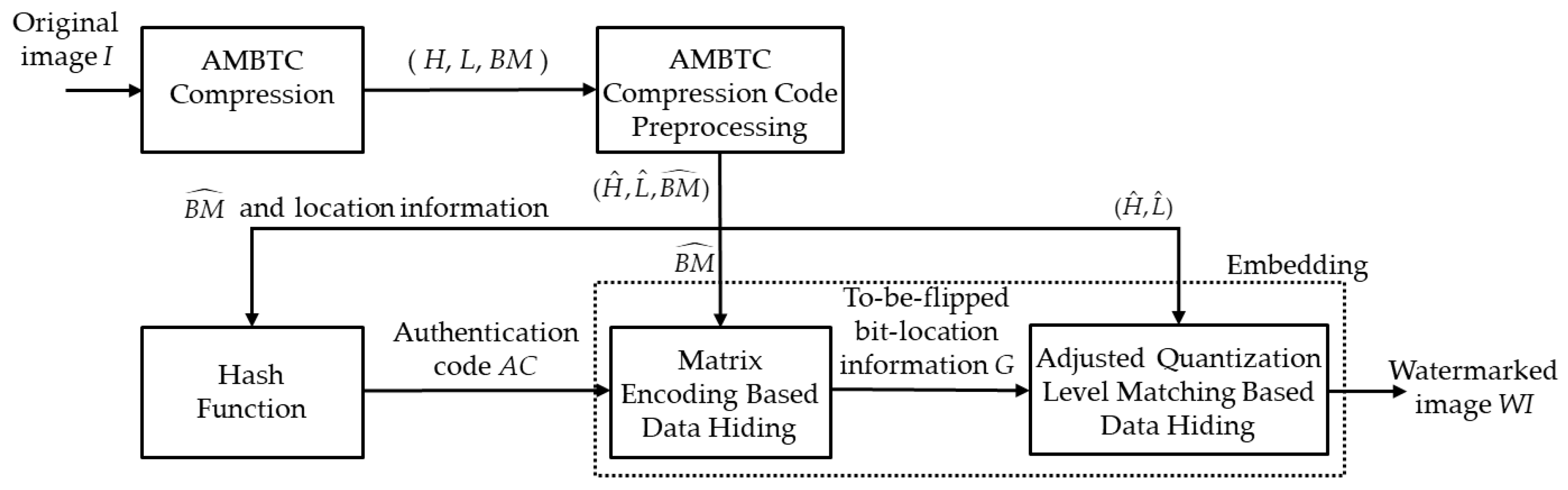
3. Proposed Scheme
3.1. AMBTC Compression and Preprocessing Phase
3.2. Authentication Code Generation Phase
3.3. Embedding Phase
3.3.1. The Matrix Encoding Based Data Hiding
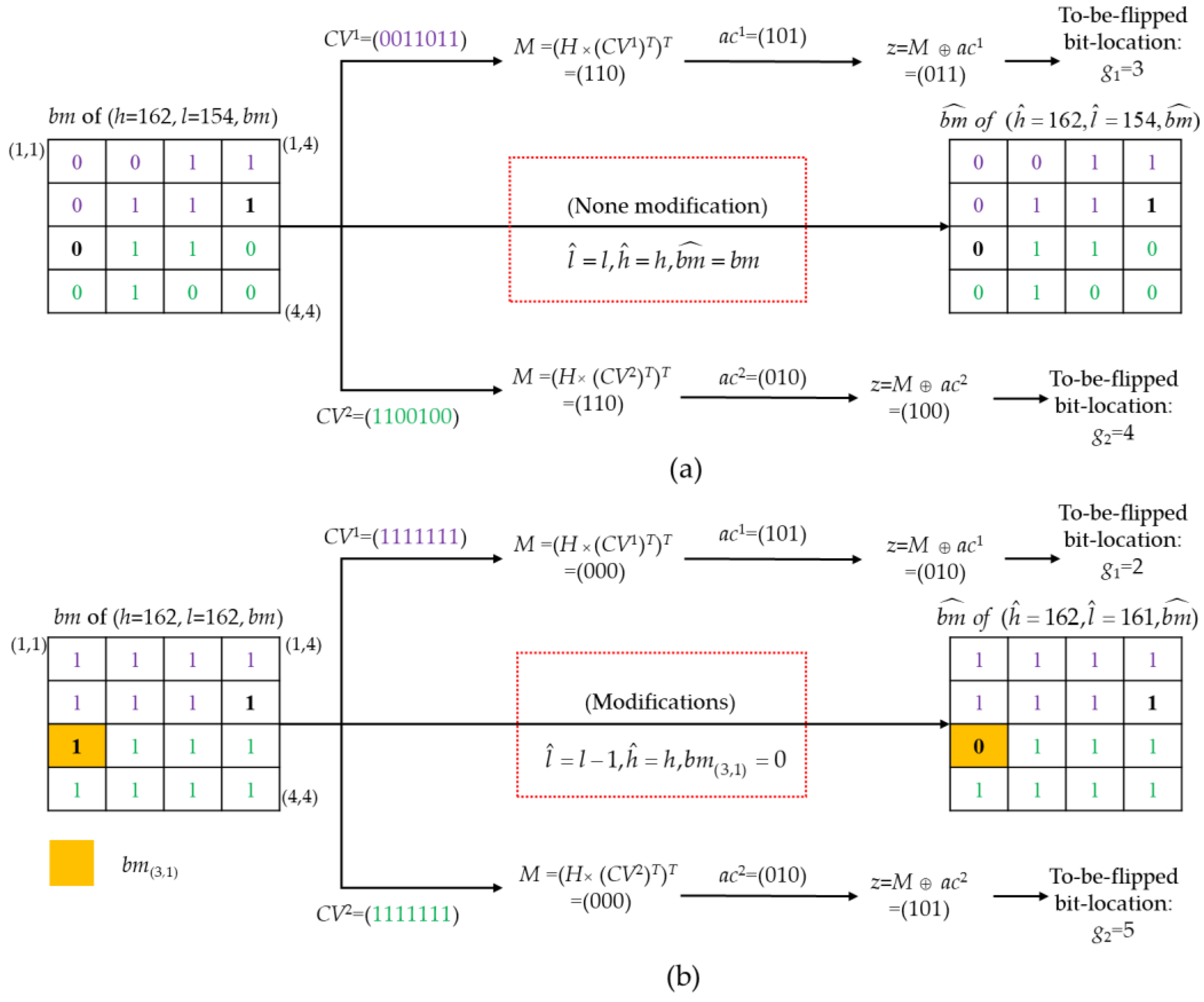
- Step 1.
- Divide the original image, I, into non-overlapping blocks by a size of 4 × 4 pixels.
- Step 2.
- Generate the AMBTC compression codes (H, L, BM) for the image, I, as explained in Section 2.1. For each block, assume its preprocessed AMBTC compression code is .
- Step 3.
- Generate the authentication code, AC, as explained in Section 3.2. For each block, assume the first three-bit sub-code is and the second three-bit sub-code is .
- Step 4.
- Extract the first seven bits of bm as the first cover vector, CV1 = = (bm(1, 1), bm(1, 2), bm(1, 3), bm(1, 4), bm(2, 1), bm(2, 2), bm(2, 3)). Extract the last seven bits of bm as the second cover vector, CV2 = = (bm(3, 2), bm(3, 3), bm(3, 4), bm(4, 1), bm(4, 2), bm(4, 3), bm(4, 4)).
- Step 5.
- Perform matrix encoding, as explained in Section 2.2, to embed the first three-bit sub-code, ac1, into the first cover vector, CV1, then derive the to-be-flipped bit-location, g1. The second three-bit sub-code, ac2, is embedded into the second cover vector, CV2, and then used to derive the to-be-flipped bit-location, g2. Note that we only record the to-be-flipped bit-location information but nothing is modified for the bm. Hence, for each block, two-tuple location information (g1, g2) can be derived.
- Step 6.
- Perform Steps 2 to 5 until all blocks have been processed.
- Step 7.
- Output all location information (g1, g2) for each block to the to-be-flipped bit-location information, G.
- Step 8.
- End.
3.3.2. Adjusted Quantization Levels Matching Based Data Hiding
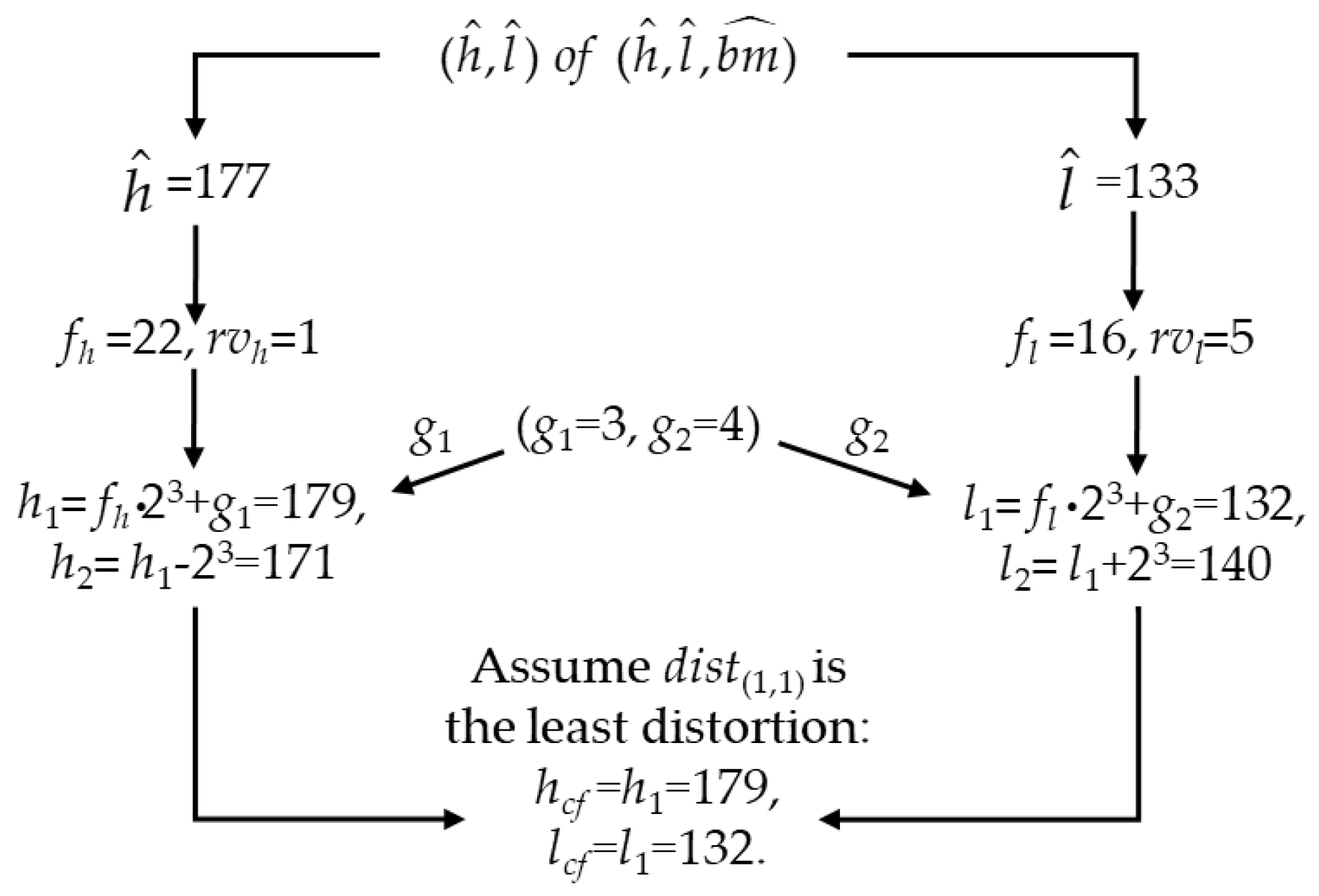
- Step 1.
- Get a triple for one block from preprocessed AMBTC compression codes .
- Step 2.
- Get the corresponding to-be-flipped bit-location information (g1, g2) for this block from G.
- Step 3.
- Calculate the factors for and for the current block by:where fh and fl represent the factors of and , respectively.
- Step 4.
- Calculate the remaining values for and for the current block by:where rvh and rvl represent the remainder values of and , respectively.
- Step 5.
- Perform adjusted quantization level matching-based data hiding. If the remainder, rvh, is equal to g1, the matching work of is done; otherwise, the candidates at the quantization level, , should be adjusted by:where h1 and h2 are the candidates at the quantization level, . Here, if h2 is lower than zero or higher than 255, h2 must be set to h1. Similarly, if the remainder, rvl, is equal to g2, the matching work of is done; otherwise, the candidates at the quantization level, , should be adjusted by:where l1 and l2 are the candidates at quantization level . l2 must be set to l1 if l2 is lower than zero or higher than 255.
- Step 6.
- Let hcf = ha and lcf = lb be the final, selected solution under the constraint of the least distortion, dist(a,b), which can be calculated by:where , , . Besides, in a few cases, this situation may happen, that is, hcf will be equal to lcf, then hcf or lcf will be forced to be justified once again by the following rule:
- Step 7.
- Perform Steps 1 to 6 until all blocks have been processed.
- Step 8.
- Output the watermarked AMBTC compression code for each block, and the watermarked image, WI, is achieved.
- Step 9.
- End.
3.4. Tampering Detection Phase
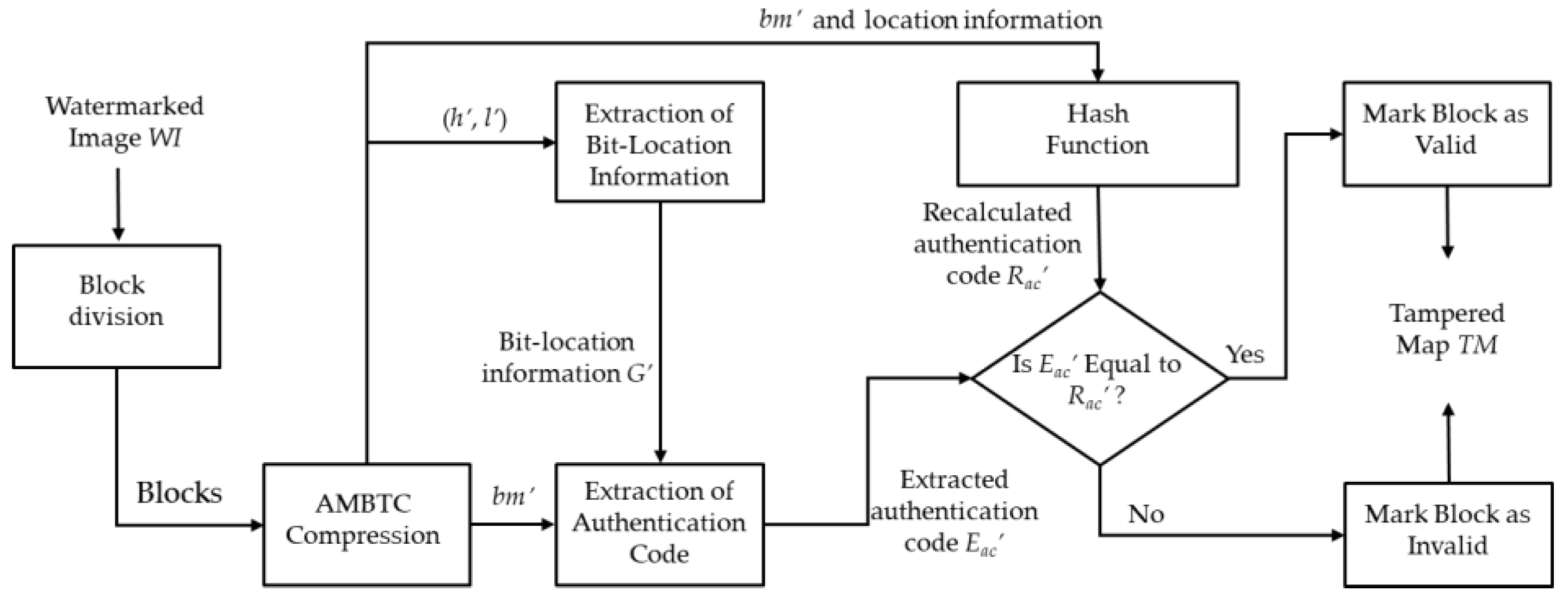
3.4.1. Extraction of Bit-Location Information
- Step 1.
- Divide the watermarked image, WI, into non-overlapping blocks by a size of 4 × 4 pixels.
- Step 2.
- Perform the AMBTC compression technique for one block to derive the corresponding AMBTC compression code (h’, l’, bm’).
- Step 3.
- Extract the bit-location information (, ) for this block by the following equation:
- Step 4.
- Perform Steps 2 and 3 until all blocks have been processed.
- Step 5.
- Output all location information (, ) for each block to provide the bit-location information, G′.
- Step 6.
- End.
3.4.2. Extraction of the Authentication Code
- Step 1.
- Get a triple (h’, l’, bm’) for one block from AMBTC compression codes (H’, L’, BM’).
- Step 2.
- Get a tuple bit-location information (, ) for the corresponding block from G′.
- Step 3.
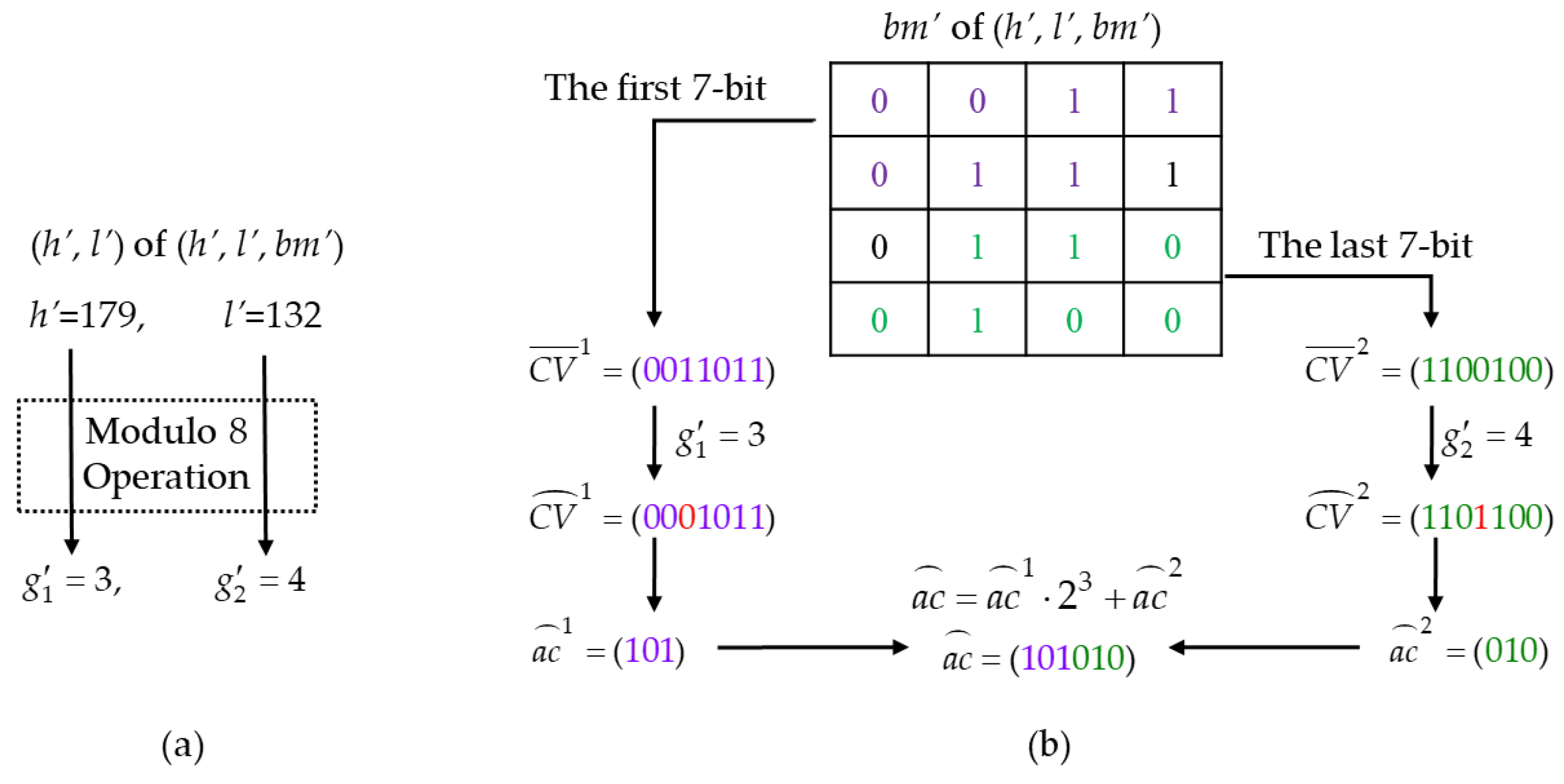
- Recombine the first seven bits of bm’ as the first cover vector, = . Recombine the last seven bits of bm’ as the second cover vector, .
- Step 4.
- Flip the th bit for the first cover vector, , and denoted as , then flip the th bit for the first cover vector, , and denoted as . Note that if or is equal to zero, the corresponding flipping operation is skipped. In Figure 5b, the red digit represents the flipped bit-location.
- Step 5.
- Extract the authentication code. Two three-bit sub-codes (, ) can be computed by:Then, the six-bit authentication code, , can be derived by:
- Step 6.
- Perform Steps 1 to 5 until all blocks have been processed.
- Step 7.
- Output the authentication code, , for each block to provide the extracted authentication code, EAC.
- Step 8.
- End.
3.4.3. Tampering Detection
- Step 1.
- Generate the authentication code, as mentioned in Section 3.2, and denote it as RAC.
- Step 2.
- Get an authentication code for one block from RAC and denote it as Rac’.
- Step 3.
- Get an authentication code for the corresponding block from EAC and denote it as Eac’.
- Step 4.
- Mark the tampered map, TM, according to the comparison results of Rac’ and Eac’. If they are equal, the corresponding position of TM is marked as ‘0’, which means the current block is valid; otherwise, it is marked as ‘1’, which indicates the current block is invalid.
- Step 5.
- Perform Steps 2 to 4 until all blocks have been processed.
- Step 6.
- Output the tampered map, TM.
- Step 7.
- End.
4. Experimental Results
4.1. Statistical Metrics
4.2. Tampering Detection Analyses
4.2.1. Cropping Attack
4.2.2. Constant Average Attack
4.2.3. Collage Attack
4.2.4. AMBTC Compression Codes’ Attacks
4.3. Performance Comparisons
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schneider, M.; Chang, S.F. A robust content based digital signature for image authentication. In Proceedings of the 3rd IEEE International Conference on Image Processing, Lausanne, Switzerland, 19 September 1996; pp. 227–230. [Google Scholar]
- Tabatabaei, S.A.H.; Ur-Rehman, O.; Zivic, N.; Ruland, C. Secure and robust two-phase image authentication. IEEE Trans. Multimed. 2015, 17, 945–956. [Google Scholar] [CrossRef]
- Yan, C.P.; Pun, C.M. Multi-scale difference map fusion for tamper localization using binary ranking hashing. IEEE Trans. Inf. Forensics Secur. 2017, 12, 2144–2158. [Google Scholar] [CrossRef]
- Chen, Z.; Li, L.; Peng, H.; Liu, Y.; Yang, Y. A novel digital watermarking based on general non-negative matrix factorization. IEEE Trans. Multimed. 2018, 20, 1973–1986. [Google Scholar] [CrossRef]
- Walton, S. Image authentication for a slippery new age. Dr. Dobb's J. 1995, 20, 18–26. [Google Scholar]
- Wong, P.W.; Memon, N. Secret and public key image watermarking schemes for image authentication and ownership verification. IEEE Trans. Image Process. 2001, 10, 1593–1601. [Google Scholar] [CrossRef] [PubMed]
- Haouzia, A.; Noumeir, R. Methods for image authentication: A survey. Multimed. Tools Appl. 2008, 39, 1–46. [Google Scholar] [CrossRef]
- Ozyurt, F.; Tuncer, T.; Avci, E. A novel probabilistic image authentication method based on universal hash function for RGB images. In Proceedings of the 2018 International Conference on Computing Sciences and Engineering (ICCSE), Kuwait City, Kuwait, 11–13 March 2018; pp. 1–6. [Google Scholar]
- Holliman, M.; Memon, N. Counterfeiting attacks on oblivious block-wise independent invisible watermarking schemes. IEEE Trans. Image Process. 2000, 9, 432–441. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, S.; Qian, Z.; Feng, G. Reference sharing mechanism for watermark self-embedding. IEEE Trans. Image Process. 2011, 20, 485–495. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xiao, Y.; Zhao, Z. Self-embedding fragile watermarking based on DCT and fast fractal coding. Multimed. Tools Appl. 2015, 74, 5767–5786. [Google Scholar] [CrossRef]
- Chang, C.C.; Lu, T.C.; Zhu, Z.H.; Tian, H. An effective authentication scheme using DCT for mobile devices. Symmetry 2018, 10, 13. [Google Scholar] [CrossRef]
- Dadkhah, S.; Manaf, A.A.; Hori, Y.; Hsssanien, A.E.; Sadeghi, S. An effective SVD-based image tampering detection and self-recovery using active watermarking. Signal Process. Image Commun. 2014, 29, 1197–1210. [Google Scholar] [CrossRef]
- Shehab, A.; Elhoseny, M.; Muhammad, K.; Sangaiah, A.K.; Yang, P.; Huang, H.; Hou, G. Secure and robust fragile watermarking scheme for medical images. IEEE Access 2018, 6, 10269–10278. [Google Scholar] [CrossRef]
- Qin, C.; Ji, P.; Wang, J.; Chang, C.C. Fragile image watermarking scheme based on VQ index sharing and self-embedding. Multimed. Tools Appl. 2017, 76, 2267–2287. [Google Scholar] [CrossRef]
- Fan, M.; Wang, H. An enhanced fragile watermarking scheme to digital image protection and self-recovery. Signal Process. Image Commun. 2018, 66, 19–29. [Google Scholar] [CrossRef]
- Qi, X.; Xin, X. A singular-value-based semi-fragile watermarking scheme for image content authentication with tamper localization. J. Vis. Commun. Image Represent. 2015, 30, 312–327. [Google Scholar] [CrossRef]
- Preda, R.O.; Vizireanu, D.N. Watermarking-based image authentication robust to JPEG compression. Electron. Lett. 2015, 51, 1873–1875. [Google Scholar] [CrossRef]
- Chuang, J.C.; Hu, Y.C. An adaptive image authentication scheme for vector quantization compressed image. J. Vis. Commun. Image Represent. 2011, 22, 440–449. [Google Scholar] [CrossRef]
- Tu, S.F.; Hsu, C.S. A BTC-based watermarking scheme for digital images. Int. J. Inf. Secur. 2004, 15, 216–228. [Google Scholar] [CrossRef]
- Jiang, M.F.; Zhu, N.B. Image fragile watermarking algorithm based on BTC domain. Sci. Technol. Eng. 2009, 9, 717–720. [Google Scholar]
- Yang, C.N.; Lu, Z.M. A Blind image watermarking scheme utilizing BTC bitplanes. Int. J. Digi. Crime Forensics 2011, 3, 42–53. [Google Scholar] [CrossRef][Green Version]
- Hu, Y.C.; Lo, C.C.; Chen, W.L. Joint image coding and image authentication based on absolute moment block truncation coding. J. Electron. Imaging 2013, 22, 013012. [Google Scholar] [CrossRef]
- Yang, H.; Kot, A.C. Pattern-based data hiding for binary image authentication by connectivity-preserving. IEEE Trans. Multimed. 2007, 9, 475–486. [Google Scholar] [CrossRef]
- Hu, Y.C.; Lo, C.C.; Wu, C.M.; Chen, W.L.; Wen, C.H. Probability-based tamper detection scheme for BTC-compressed images based on quantization levels modification. Int. J. Secur. Its Appl. 2013, 7, 11–32. [Google Scholar]
- Nguyen, T.S.; Chang, C.C.; Chung, T.F.A. Tamper-detection scheme for BTC-compressed images with high-quality images. KSII Trans. Internet Inf. Syst. 2014, 8, 2005–2021. [Google Scholar]
- Lin, C.C.; Huang, Y.; Tai, W.L. A high-quality image authentication scheme for AMBTC-compressed images. KSII Trans. Internet Inf. Syst. 2014, 8, 4588–4603. [Google Scholar]
- Li, W.; Lin, C.C.; Pan, J.S. Novel image authentication scheme with fine image quality for BTC-based compressed images. Multimed. Tools Appl. 2016, 75, 4771–4793. [Google Scholar] [CrossRef]
- Lin, C.C.; Huang, Y.; Tai, W.L. A novel hybrid image authentication scheme based on absolute moment block truncation coding. Multimed. Tools Appl. 2017, 76, 463–488. [Google Scholar] [CrossRef]
- Hong, W.; Chen, M.; Chen, T.S.; Huang, C.C. An efficient authentication method for AMBTC compressed images using adaptive pixel pair matching. Multimed. Tools Appl. 2018, 77, 4677–4695. [Google Scholar] [CrossRef]
- Hong, W.; Zhou, X.; Lou, D.C.; Huang, X.; Peng, C. Detectability improved tamper detection scheme for absolute moment block truncation coding compressed images. Symmetry 2018, 10, 318. [Google Scholar] [CrossRef]
- Nasrabadi, N.M.; King, R.A. Image coding using vector quantization: A review. IEEE Trans. Commun. 1988, 36, 957–971. [Google Scholar] [CrossRef]
- Lema, M.; Mitchell, R. Absolute moment block truncation coding and its application to color images. IEEE Trans. Commun. 1984, 32, 1148. [Google Scholar] [CrossRef]
- Delp, E.J.; Mitchell, O.R. Image compression using block truncation coding. IEEE Trans. Commun. 1979, 27, 1335. [Google Scholar] [CrossRef]
- Zhang, X. Reversible data hiding in encrypted image. IEEE Signal Process. Lett. 2011, 18, 255–258. [Google Scholar] [CrossRef]
- Nguyen, D.V.; Vasic, B. Two-bit bit flipping algorithms for LDPC codes and collective error correction. IEEE Trans. Commun. 2014, 62, 1153–1163. [Google Scholar] [CrossRef]
- Hamming, R.W. Error Detecting and Error Correcting Codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]
- Chen, K.; Chang, C.C. Real-time error-free reversible data hiding in encrypted images using (7, 4) hamming code and most significant bit prediction. Symmetry 2019, 11, 51. [Google Scholar] [CrossRef]
- Liu, S.; Fu, Z.; Yu, B. Rich QR codes with three-layer information using hamming code. IEEE Access 2019, 7, 78640–78651. [Google Scholar] [CrossRef]





| Methods | Tampering Detection Result for First Stage (%) | Requirement of Reference Matrix | Main Limitation |
|---|---|---|---|
| Scheme in [23] | 93.75 | No | Compression codes’ attack, Collage attack |
| Scheme in [25] | 96.87 | No | |
| Scheme in [26] | 93.75 | Yes | |
| Scheme in [27] | 93.75 | No | |
| Scheme in [28] | 93.75 | Yes | |
| Scheme in [29] | 93.75 | Yes | Compression codes’ attack |
| Scheme in [30] | 93.75 | Yes | More computation |
| Scheme in [31] | 98.50/99.61 | No | Collage attack |
| Proposed scheme | 99.85 | No | - |
| ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Syndrome | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| Coset leader | 0000000 | 1000000 | 0100000 | 0010000 | 0001000 | 0000100 | 0000010 | 0000001 |
| Symbols | Definitions | Symbols | Definitions |
|---|---|---|---|
| I | Original image | WI | Watermarked image |
| H | Parity check matrix | TM | Tampered map |
| h | High quantization level for a block in I | H | A set of h |
| l | Low quantization level for a block in I | L | A set of l |
| bm | Bitmap for a block in I | BM | A set of bm |
| Preprocessed high quantization level | A set of | ||
| Preprocessed low quantization level | A set of | ||
| Preprocessed bitmap | A set of | ||
| h′ | High quantization level for a block in WI | H′ | A set of h′ |
| l′ | Low quantization level for a block in WI | L′ | A set of l′ |
| bm′ | Bitmap for a block in WI | BM′ | A set of bm′ |
| g1, g2 | Bit-location information of a block | ac | Authentication code for a block |
| Original Images | Number of Tampered Blocks (4 × 4) | The First Hierarchical Tampering Detection Results (%) | The Second Hierarchical Tampering Detection Results (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | First Hierarchy | Second Hierarchy | TDR | FPR | FNR | TDR | FPR | FNR | |
| Lena | 961 | 949 | 961 | 98.75 | 0 | 0.0777 | 100 | 0 | 0 |
| Elaine | 5700 | 5620 | 5698 | 98.60 | 0 | 0.7432 | 99.96 | 0 | 0.0187 |
| Woman | 296 | 293 | 296 | 98.99 | 0 | 0.0186 | 100 | 0 | 0 |
| Average | 98.78 | 0 | 0.3356 | 99.99 | 0 | 0.0063 | |||
| Size of Blocks | Original Images | Number of Tampered Blocks | The First Hierarchical Tampering Detection Results (%) | The Second Hierarchical Tampering Detection Results (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total | First Hierarchy | Second Hierarchy | TDR | FPR | FNR | TDR | FPR | FNR | ||
| 4 × 4 | Zelda | 1225 | 1196 | 1225 | 97.63 | 0 | 0.1909 | 100 | 0 | 0 |
| Baboon | 1225 | 1213 | 1225 | 99.02 | 0 | 0.0791 | 100 | 0 | 0 | |
| 2 × 2 | Zelda | 1369 | 1320 | 1367 | 96.42 | 0 | 0.3253 | 99.85 | 0 | 0.0133 |
| Baboon | 1369 | 1333 | 1368 | 97.37 | 0 | 0.2392 | 99.93 | 0 | 0.0067 | |
| Average | 97.61 | 0 | 0.2086 | 99.95 | 0 | 0.0050 | ||||
| Original Mages | Number of Tampered Blocks (4 × 4) | The First Hierarchical Tampering Detection Results (%) | The Second Hierarchical Tampering Detection Results (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | First Hierarchy | Second Hierarchy | TDR | FPR | FNR | TDR | FPR | FNR | |
| Lake | 4126 | 4062 | 4121 | 98.45 | 0 | 0.5194 | 99.88 | 0.0485 | 0.0408 |
| Boat | 1350 | 1331 | 1350 | 98.59 | 0 | 0.1262 | 100 | 0 | 0 |
| Average | 98.52 | 0 | 0.3228 | 99.94 | 0.0243 | 0.0204 | |||
| Original image | Kinds of Attacks | Number of Tampered Blocks (4 × 4) | The First Hierarchical Tampering Detection Results (%) | The Second Hierarchical Tampering Detection Results (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total | First Hierarchy | Second Hierarchy | TDR | FPR | FNR | TDR | FPR | FNR | ||
| Lena | (H or L) | 961 | 961 | 961 | 100 | 0 | 0 | 100 | 0 | 0 |
| (H or L) and flower | 1211 | 1204 | 1208 | 99.42 | 0 | 0.0461 | 99.75 | 0.0827 | 0.0198 | |
| BM | 651 | 651 | 651 | 100 | 0 | 0 | 100 | 0 | 0 | |
| BM and flower | 901 | 894 | 898 | 99.22 | 0 | 0.0452 | 99.67 | 0.1112 | 0.0194 | |
| Average | 99.66 | 0 | 0.0228 | 99.86 | 0.0485 | 0.0098 | ||||
| Original Images | PSNRs (dB) | |
|---|---|---|
| AMBTC | Proposed Scheme | |
| Couple | 31.27 | 30.38 |
| Boat | 31.87 | 30.89 |
| Zelda | 37.99 | 35.07 |
| Lena | 33.23 | 31.99 |
| Woman | 37.98 | 35.03 |
| Elaine | 33.91 | 32.41 |
| Baboon | 28.30 | 27.78 |
| Lake | 29.88 | 29.21 |
| Peppers | 33.43 | 32.15 |
| Average | 33.10 | 31.66 |
| Methods | Number of Authentication Bits | Hierarchy of Detection Strategies | TDR of First Hierarchy (%) | TDR of Multi-Hierarchy (%) | Average PSNRs (dB) |
|---|---|---|---|---|---|
| Lin et al. [29] | 4 | 2 | 93.75 | 98.19 | 33.07 |
| Hong et al. [30] | 4 | 2 | 93.75 | 99.83 | 32.33 |
| Hong et al. [31] (LSBP)/(MSBP) | 6 | 2 | 98.50 | 99.66 | 31.27/31.73 |
| 8 | 99.61 | 28.92/29.84 | |||
| Proposed scheme | 6 | 2 | 98.55 | 99.85 | 31.66 |
| Compared Lists | Lin et al.’s Scheme [29] | Hong et al.’s Scheme [30] | Hong et al.’s Scheme [31] | Proposed Scheme |
|---|---|---|---|---|
| Components to embed AC | Quantization levels or bitmap | Quantization levels | Quantization levels | Quantization levels and bitmap |
| Generation of AC | Pseudo-random generator | Hash function | Hash function | Hash function |
| Detection of the special modification of bitmap | No | Yes | Yes | Yes |
| Detection of the special modification of quantization levels | No | Yes | Yes | Yes |
| Detection of the cropping attack | Yes | Yes | Yes | Yes |
| Detection of the constant average attack | Yes | Yes | Yes | Yes |
| Detection of the collage attack | Yes | Yes | No | Yes |
| Authentication for AMBTC compression codes | Yes | Yes | Yes | Yes |
| Authentication for AMBTC compressed image | Yes | No | No | Yes |
| Methods | Compression Methodology | Domain | Detectable Block Size | Length of AC for a Block | PSNR (dB) |
|---|---|---|---|---|---|
| Scheme in [17] | JPEG | Frequency | 4 × 4 | 1 | [40.33, 44.12] |
| Scheme in [18] | JPEG | Frequency | 8 × 8 | 3 | 44.63 |
| Scheme in [19] | VQ | Space | 4 × 4, 8 × 8 | [1, 3] | ≈[29.00, 31.50] |
| Proposed scheme | AMBTC | Space | 4 × 4 | [1, 6] | [31.66, 33.10] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, G.-D.; Chang, C.-C.; Lin, C.-C. High-Precision Authentication Scheme Based on Matrix Encoding for AMBTC-Compressed Images. Symmetry 2019, 11, 996. https://doi.org/10.3390/sym11080996
Su G-D, Chang C-C, Lin C-C. High-Precision Authentication Scheme Based on Matrix Encoding for AMBTC-Compressed Images. Symmetry. 2019; 11(8):996. https://doi.org/10.3390/sym11080996
Chicago/Turabian StyleSu, Guo-Dong, Chin-Chen Chang, and Chia-Chen Lin. 2019. "High-Precision Authentication Scheme Based on Matrix Encoding for AMBTC-Compressed Images" Symmetry 11, no. 8: 996. https://doi.org/10.3390/sym11080996
APA StyleSu, G.-D., Chang, C.-C., & Lin, C.-C. (2019). High-Precision Authentication Scheme Based on Matrix Encoding for AMBTC-Compressed Images. Symmetry, 11(8), 996. https://doi.org/10.3390/sym11080996







