Abstract
Beauty judgments for regular polygon tessellations were examined in two experiments. In experiment 1 we tested the three regular and eight semi-regular tilings characterized by a single vertex. In experiment 2 we tested the 20 demi-regular tilings containing two vertices. Observers viewed the tessellations at different random orientations inside a circular aperture and rated them using a numeric 1–7 scale. The data from the first experiment show a peak in preference for tiles with two types of polygons and for five polygons around a vertex. Triangles were liked more than other geometric shapes. The results from the second experiment demonstrate a preference for tessellations with a greater number of different kinds of polygons in the overall pattern and for tiles with the greatest difference in the number of polygons between the two vertices. Ratings were higher for tiles with circular arrangements of elements and lower for those with linear arrangements. Symmetry group p6m was liked the most and groups cmm and pmm were liked the least. Taken as a whole the results suggest a preference for complexity and variety in terms of both vertex qualities and symmetric transformations. Observers were sensitive to both the underlying mathematical properties of the patterns as well as their emergent organization.
1. Introduction
We are surrounded by geometric patterns. These can be seen in the tiles on floors, in wallpaper patterns on our walls, and in the clothes we wear. They are also found in decorative artwork that adorns the outside of buildings and in signs, advertising, and in graphic and web design [1]. All major cultures have produced and enjoyed them [2,3]. What is the allure of these patterns? Why have we been compelled to create and view them over the course of human history? In this paper, we will examine these questions by looking at a group of tessellations, also known as tilings, whose geometric and mathematical properties are well defined. We will use these properties to predict and help explain their aesthetic appeal. In what follows, we outline the different types of tessellations, showing that they can be categorized by the types of polygons they contain, the way they are arranged around defining vertices, and their symmetry properties.
A plane tessellation is a pattern made up of one or more shapes, completely covering a surface without any gaps or overlaps [4,5]. All tessellations can be extended in the plane infinitely in every direction. Tilings are made up of closed figures that form the overall design. Closed figures all have a perimeter and area. The simplest type of closed figure is a polygon, made of straight-line segments and defined by number of sides and angles. Any regular triangle, quadrilateral, or hexagon will tessellate the plane by itself. Regular in this instance means that all sides and angles are equal. Regular pentagons, heptagons, or any other regular polygon will not tile the plane. These three types of tilings are called regular. Any other tiling of the plane by regular polygons must occur through a combination of two or more polygons. There are eight such types, known as semi-regular tilings.
Every regular tiling is defined by a vertex point. This vertex is surrounded by a group of polygons that in sequence serve as a signature for its identification. The first group of 11 regular and semi-regular tilings are defined by one vertex point and are studied in experiment 1 (shown in Figure 1). These are known as 1-uniform patterns. The second group of regular tilings are defined by two different vertices and are explored in experiment 2. All of these tessellations are edge-to-edge, meaning the polygons share common edges and vertices. However, it is possible to tessellate the plane with regular polygons that are not arranged this way. These are called non-congruent tilings. In addition, one can tile the plane with polygons that are not regular and do not have equal sides and angles. These tessellations are referred to as irregular. Non-congruent and irregular tilings will not be examined in the current study.
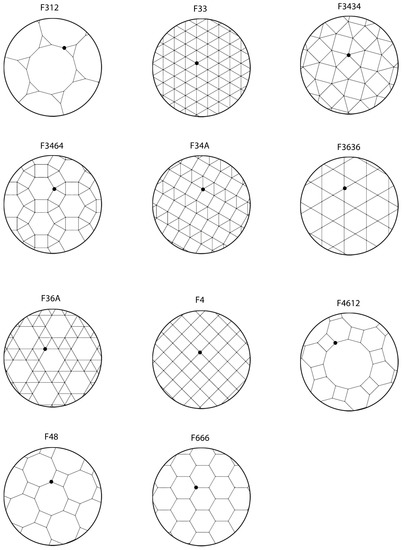
Figure 1.
The 11 types of regular polygon tessellations shown in experiment 1. The black dot indicates a defining vertex.
Regular and semi-regular tilings are characterized by a set of rules first formulated in 1785 by The Rev. Mr. Jones [6]. The first is that these tilings must have polygon angles meeting at a vertex that sum to exactly 360°. The second is that they must have at least three polygons and no more than six meeting at each vertex. The third is that no semi-regular tiling can have four different types of polygons meeting at a vertex. The study provides a more extended and technical discussion of these rules [6]. The polygons in a shape are clearly visible and may have an impact on their perceived beauty. People may prefer certain polygons over others or may prefer patterns with certain types of vertices.
Another way to characterize tessellations is by their symmetry properties [7]. There are four basic symmetry transformations that when applied can transform a shape in a tessellation upon itself or another identical shape. These are translation, reflection, rotation, and glide reflection. In translation a shape is simply moved. In reflection it is mirror-imaged about an axis. In rotation it is rotated or spun about a point. When shapes are rotated, they can be described by their order of rotation. If a shape has an order of rotation of 2 it has 2-fold rotational symmetry and can be rotated into congruence with itself by a 180° spin. Order 3 is 3-fold (120°), order 4 is 4-fold (90°), and order 6 is 6-fold, (60°). In glide reflection, the shape is both translated and then reflected. All of these symmetries are present in polygon tessellations. When looking at tile patterns, one can consciously or subconsciously perceive these transformations and so they may play a role in determining their visual beauty.
Despite their ubiquity, there is remarkably little research on the aesthetic qualities of tessellations. Much of the work in this area has focused on individual polygons and dates from the 19th and 20th centuries [8,9,10,11,12,13]. According to a recent study, participants judged the perceived attractiveness for all basic types of squares and quadrilaterals [14]. There was a preference for regularity. Triangles with smaller side length standard deviations (more equal sides) were found to be more beautiful. Observers in that study liked equilateral triangles more than any other type of triangle. The same result was found for quadrilaterals. As four-sided shapes become more regular, they are preferred more. Symmetry also predicted liking for these polygons but could not completely account for all of the ranked preferences.
Symmetry is a major property affecting preference for two-dimensional geometric pattern. In one study, participants were asked to judge the subjective beauty of novel graphic patterns [15]. Symmetry correlated highly with aesthetic assessments as did stimulus complexity. However, they also found individual differences, in which some of the participants preferred non-symmetric patterns. Their data fit both a group model and an individual case model, indicating universal and particular tastes. Another study similarly found individual differences in preferences for single polygons [16].
Recent work found that geometric symmetrical patterns are used most frequently in life, but are also produced spontaneously in the lab [17]. In addition, they are rated significantly more attractive than random patterns. In prior work, the researchers looked at the spatial distribution characteristics of “Crazy Quilts” and ordered quilt patterns [18]. Crazy quilts, first created in the 1870s, are intended to appear haphazard and unstructured. They found that these two quilt types belong to separate classes, the first corresponding to randomness and the second to ordered production methods. The ordered patterns were based on regular pattern motifs that repeated in the designs. Preference for random patterns however, appear to be an exception, with most decorative arts of this nature being highly ordered [19].
In a different study, researchers interviewed six fourth-grade children as to how they conceptualized tessellations and compared their responses with those of two adult mathematicians [20]. Preference tasks showed the students had a slight preference for symmetric over random patterns but judged on a number of other criteria such as color, complexity and motif. Although children agreed on the criteria, there were substantial individual differences on which criteria determined appeal for a given pattern. The children rarely created random tilings if they could make a symmetric one and often pointed out the “patterns” in random tilings they had constructed. The mathematicians disliked tessellations with only one interesting dimension and thus seemed to have a preference for complexity. They also enjoyed tessellations that surprised them or were thought provoking. In addition, mathematicians preferred tilings whose aesthetic qualities aligned with those identified by previous researchers. Children focused on some themes the adults did not like variety of color and real-world connections. This study shows that even young children have a sense of aesthetics and that they can apply this to both evaluating and creating tessellations.
The current study is exploratory rather than confirmatory in nature. We thus make no a priori predictions about which tessellations will be considered more beautiful than others. This is because each tiling differs considerably in the kind and complexity of both the polygons that make it up and the symmetry transformations that map these polygons onto themselves and one another. We instead analyze a number of polygon and symmetry features to see if these can predict preference. The main variables measured are the kind of polygons, the number of polygons around each vertex, their symmetry group and lattice type, the kind of symmetries, their rotation order, and other characteristics, such as the location of rotation centers. In experiment 1, we look at the 11 regular and semi-regular tile types defined by a single vertex. In experiment 2, we test the 20 types defined by two vertices, sometimes called demi-regular tessellations.
2. Experiment 1
2.1. Participants
Thirty-two Manhattan College undergraduates participated to fulfill a class requirement. There were 17 males and 15 females. Vision was normal or corrected to normal. Average age of the students was approximately 19 years. All participants volunteered to participate and signed a consent form prior to running in the experiment. American Psychological Association ethical standards and data confidentiality were adhered to.
2.2. Stimuli
All of the tiling patterns used in both experiments are regular, meaning they consist only of regular convex polygons whose sides and angles are equal. The types of polygons that occur in these tessellations are equilateral triangles, squares, hexagons, octagons, and dodecagons. All of the tiles are edge-to-edge, in which every side of every tile is an edge of the tiling, and each side of a tile is also a side of precisely one other tile. There are 11 distinct edge-to-edge tilings by regular polygons. These are shown in Figure 1.
One of these patterns, (F36A or 34.6) has an enantiomorphic, or mirror image form. The two versions of these are difficult to distinguish perceptually and so only one of these versions was included in the study. Each of these regular tessellations is identified by a unique type of vertex surrounded by a circular sequence of polygons. For example, the purely triangular tiling F33 is defined by the vertex (36), in the expanded notation (3.3.3.3.3.3) because the vertex is surrounded by six equilateral triangles. The pattern F3434 or (3.3.4.3.4) has a vertex surrounded by two equilateral triangles, a square, an equilateral triangle, and a square.
Patterns F33, F4, and F66 (36), (44), and (63) are labeled as regular tilings or tessellations. These three are regular if the symmetry group of the tiling acts transitively on the flags of the tiling [21]. A flag is a triple consisting of a mutually incident vertex, edge, and tile of the tiling. For every pair of flags there is a symmetry operation mapping the first flag to the second. The remaining eight tilings are known as Archimedean, uniform, or semi-regular tilings. These are characterized by vertex-transitivity, meaning that for every pair of vertices, there is a symmetry operation mapping the first vertex to the second. In vertex-transitivity each vertex is surrounded by the same kinds of face in the same or reverse order and with the same angles between corresponding faces.
Each pattern can also be categorized by its symmetry group that lists the type of symmetry operations mapping motifs or elements of the pattern onto themselves and one another. For example, the triangular tiling (36) belongs to group p6m, characterized by rotations of orders 2 (180°), 3 (120°), and 6 (60°), as well as reflections and glide-reflections. The pattern F3434 or (32·4·3·4) belongs to symmetry group p4g. This has reflections and rotations of orders 2 and 4 and four axes of reflection. Table 1 lists the notations, symmetry group and polygon features for each of the 11 patterns, listed by the preference rank determined in experiment 1. Table 2 lists the properties of each symmetry group for the tilings used in both experiments.

Table 1.
Notations, Symmetry Group and Polygon Properties for the Tilings of Experiment 1.

Table 2.
Symmetry Group Properties for the Tilings in Experiments 1 and 2.
2.3. Procedure
The tilings were presented within a circular aperture that measured 16 cm in diameter. This was done to prevent familiarity and any framing effects where the lines in the pattern may have aligned with prominent orientations such as gravitational vertical or the sides of the computer monitor. Five versions of each tiling were generated. Each version corresponded to a different random orientation. This yielded 55 trials per block. Six blocks were presented for a total of 330 trials in an experimental session. Trial order within a block was randomized. Observers were given as much time as they needed to respond. On average a session took about 25 min to complete.
Participants judged the beauty of each tiling using a 7-point rating scale. A “7” on the scale corresponded to “Very Beautiful”, while a “1” corresponded to “Very Ugly”. The students were encouraged to use the entire range of the scale, including “4”, which indicated a neutral response of no preference. They used the number keys that ran across the top of the computer keyboard. Participants were additionally instructed that there was no right or wrong answer and to rate the tessellations in any manner they wanted. This was done in order to reduce experiment-induced judgment criteria or demand characteristics. If any number other than 1–7 was entered, the participant would not be able to advance to the next trial. In this case, they were told to re-enter an appropriate value.
Following the experiment, all participants completed a questionnaire to compile basic demographic information. They were also asked to respond personally as to what tilings they liked and what features of the patterns may have affected their responding. They read a written debrief form and any remaining questions they had concerning the study were answered by the research assistant.
2.4. Results and Discussion
Any responses that exceeded seven seconds were considered moments of inattention and removed from the data prior to analysis. These constituted about less than 3% of all the responses. Beauty ratings were normalized by the formula of (score − min)/(max − min) where the minimum and maximum were determined across subjects. Reaction time measures were also taken but did not produce any interpretable results so are not reported here.
One-way analysis of variance (ANOVA) tests were performed for number of unique polygons in the overall tile pattern (Polygons in Pattern), number of polygons around the vertex (Polygons Around Vertex), symmetry group (Symmetry Group) and for type of tile pattern (Tile Pattern). There was a significant effect of Polygons in Pattern, F(2, 93) = 114.03, p < 0.01, with peak responding found for tilings with two polygons (Figure 2). Effect size as Eta Squared was (η2 = 0.05). Polygons Around Vertex was also significant, F(3, 124) = 320.16, p < 0.01, (η2 = 0.14) with peak mean beauty ratings for five polygons (Figure 3). Symmetry Group was analyzed next, F(4, 155) = 254.73, p < 0.01, (η2 = 0.22) with the highest rating for tiles with group p4g (Figure 4). Finally, we looked at mean ratings for Tile Pattern, F(10, 341) = 136.39, p < 0.01, (η2 = 0.17)with peak responding found for tile F3434 (32·4·3·4). This is shown in Figure 5.
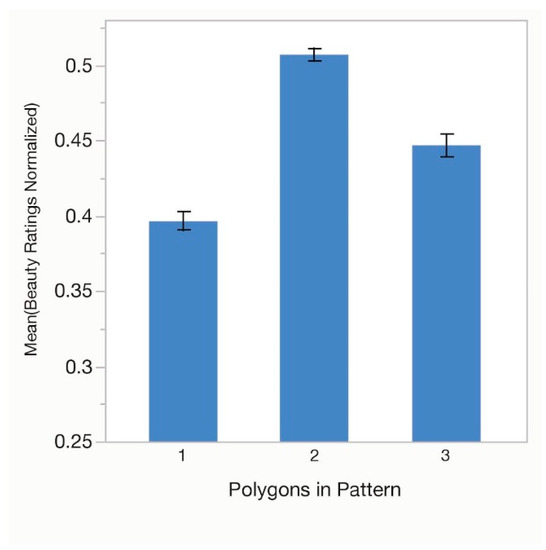
Figure 2.
Average normalized beauty ratings based on the total number of different polygons in the tessellations for experiment 1. Error bars indicate ±1 standard error of the mean.
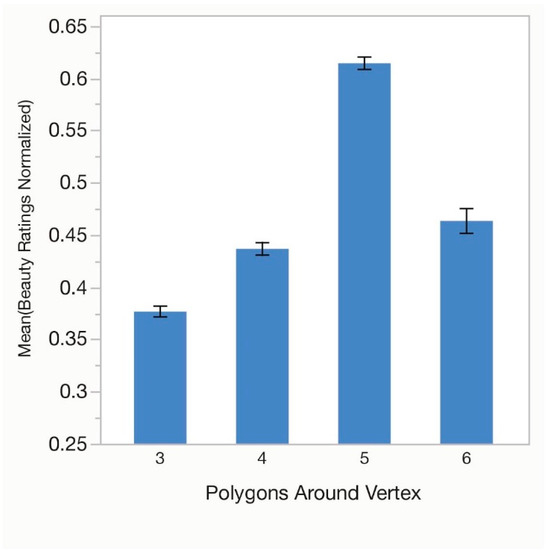
Figure 3.
Average normalized beauty ratings for the number of different polygons around the defining vertex for the tessellations in experiment 1. Error bars indicate ±1 standard error of the mean.
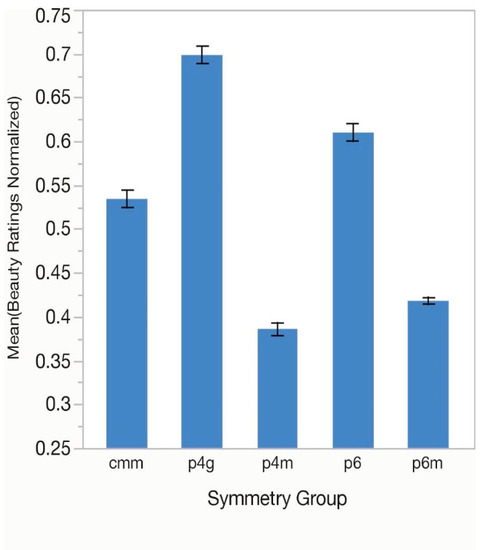
Figure 4.
Average normalized beauty ratings for the symmetry groups of the tessellations in experiment 1. Error bars indicate ±1 standard error of the mean. See Table 2 for the defining features of each group.
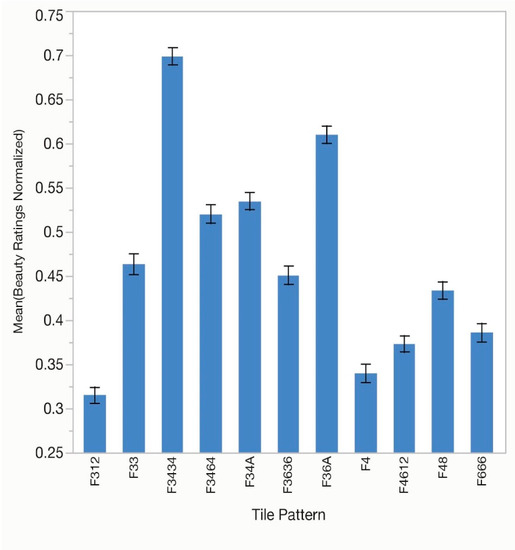
Figure 5.
Average normalized beauty ratings for each of the 11 tile pattern types in experiment 1. Error bars indicate ±1 standard error of the mean.
The results show that participants preferred tiles with the second greatest number of different polygons. One might have predicted a variety effect, in which ratings increased continuously on this variable, but this was not obtained suggesting a moderate preference for polygonal variety. Preference also increased with number of polygons around the vertex, but only up to five. This may indicate a limit to liking how tightly packed a pattern is with polygons, as polygon density increases with number around the vertex. Average angle and size of polygons around the vertex are also correlated with number. The greater the number the lower the average angle and the smaller in area the polygons become.
Figure 5 shows mean beauty ratings by each of the 11 tessellation types. These were analyzed in terms of the type of polygons they contained to see if participants preferred certain polygons. Looking at ranked preference in Table 1 we see that tilings with triangles dominated the top of the list. Excluding F312 tiles triangles occupied the top six positions. Tiles with dodecagons (F4612 and F312) were near the bottom of the list, at positions nine and eleven respectively. These preferences were independent of the number of different polygons around the vertex.
Preference for symmetry groups ranked high to low was as follows: p4g, p6, cmm, p6m, and p4m. We can evaluate these rankings looking at some of the basic symmetry properties shown in Table 2. Each tiling is characterized by an underlying lattice type. Each lattice type has a geometric cell structure that contains the tiling’s basic pattern or motifs and which when fit together will tile that pattern to completely fill the two-dimensional plane. Lattice type did not predict rankings. The p4g tiling has a square lattice and was preferred the most. The p4m tiling also has a square lattice but was preferred the least.
We can also examine the type of symmetry operations in each tiling. It was not the case that tessellations with more symmetries were rated higher. Tile p4g has rotation, reflection, and glide-reflection and was liked the most. But tile p4m also has these three symmetries and was ranked lowest. Rotation order additionally did not predict liking. Tiles with the greatest number of rotation orders (2, 3, 6) were not liked more than those that had only two (2, 4) or one (2) order of rotation. Tile p6 and tile p6m have three rotation orders but were not liked equivalently, ranked at positions two and four respectively. One explanation for tile p4g’s popularity is that it has reflections in two perpendicular directions and order 2 rotation centers that are at the intersections of reflection axes. So, the type and location of rotation centers for this pattern may be meaningful.
3. Experiment 2
The first experiment examined the 11 regular and semi-regular tiles. These are designated as 1-uniform because they are characterized by a single vertex. However, there is another class of regular tiles that are 2-uniform, meaning they are defined uniquely by two different vertices. There are 20 distinct types of 2-uniform edge-to-edge tilings by regular polygons. These are shown in Figure 6 with the two dots indicating the vertices. These patterns allow us to potentially replicate and generalize the findings from experiment 1 to a larger class of similar patterns. They also allow us to examine the relationship between two vertices and how those might affect beauty judgments.
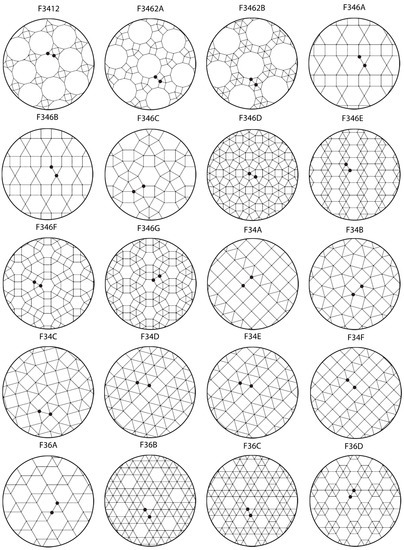
Figure 6.
The 20 types of regular polygon tessellations shown in experiment 2. The two black dots indicate the defining vertices.
3.1. Participants
Thirty-three Manhattan College undergraduates participated to fulfill a class requirement. There were 18 males and 15 females. Vision was normal or corrected to normal. Average age of the students was approximately 19 years. All participants volunteered to participate and signed a consent form prior to running in the experiment. American Psychological Association ethical standards and data confidentiality were followed.
3.2. Stimuli
All of the tiling patterns were again regular containing polygons of equal sides and angles. This time however there were 20 tilings characterized by having two defining vertices. Each of these are shown in Figure 6. Table 3 lists the notation, symmetry group, and polygon features for these 20 patterns, listed by their order of preference from the second experiment data. Table 2 lists the properties for each of the symmetry groups including the two new groups of pgg and pmm. It should be noted that there are several tilings among the two-uniform grouping that have equivalent vertex designations but that differ in their appearance. These differences are explored in the data analysis.

Table 3.
Notations, Symmetry Group and Polygon Properties for the Tilings of Experiment 2.
3.3. Procedure
The procedure was identical to that in the first study. The tilings were presented within the same-sized circular aperture. Five versions of each tiling were generated. Each version corresponded to a different randomly determined orientation. This yielded 100 trials per block. Three blocks were presented for a total of 300 trials in an experimental session. Trial order within a block was randomized. Observers were given as much time as they needed to respond. On average a session took about 25 min to complete. Participants judged the beauty of each tiling using the same 7-point rating scale and the same set of instructions described previously. Following the experiment, all participants completed a demographic questionnaire and debrief form.
3.4. Results and Discussion
Any responses that exceeded seven seconds were considered moments of inattention and removed prior to analysis. These constituted about less than 2% of all the responses. Beauty ratings were normalized by the formula of (score − min)/(max − min) where the minimum and maximum were determined across subjects. Reaction time measures did not produce meaningful results and are not reported.
One-way ANOVAs were performed for number of unique polygons in the overall tile pattern (Polygons in Pattern), the difference in the number of polygons between the two vertices (Polygons Vertex 1 − Vertex 2, where vertex 1 contained the larger number), the tessellations symmetry group (Symmetry Group) and for type of tile pattern (Tile Pattern). There was a significant effect of Polygons in Pattern, F(2, 96) = 84.46, p < 0.01, (η2 = 0.09) with ratings increasing with the number of polygons (Figure 7). Ratings for the difference in the number of polygons between the two vertex centers was also significant, F(2, 96) = 51.97, p < 0.01, (η2 = 0.06) with mean beauty ratings at a minimum for tilings with equal numbers of polygons and rising as the difference increases (Figure 8). Symmetry Group was analyzed next, F(6, 224) = 247.32, p < 0.01, (η2 = 0.10) with the highest rating for tiles with group p6m, followed by p4m, p4g, pgg, p6, pmm, and cmm (see Figure 9). Finally, we looked at mean ratings for each of the 20 unique patterns, what we call Tile Pattern, F(19, 640) = 104.60, p < 0.01, (η2 = 0.26) with peak responding found for four tiles in the F346 group, intermediate level responding for several tiles in the F36 group and lowered ratings for some of the F34 group of tiles. This is depicted in Figure 10.
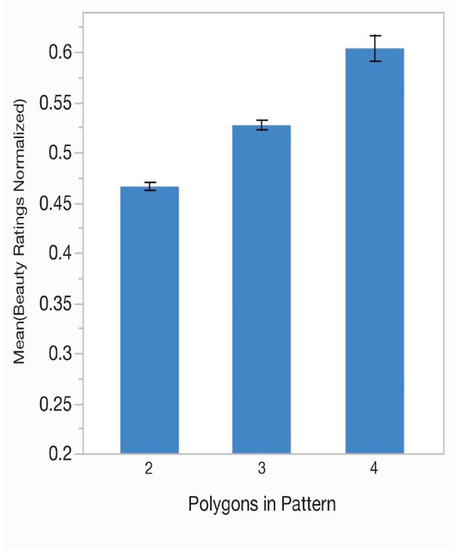
Figure 7.
Average normalized beauty ratings based on the total number of different polygons in the tessellations used in experiment 2. Error bars indicate ±1 standard error of the mean.
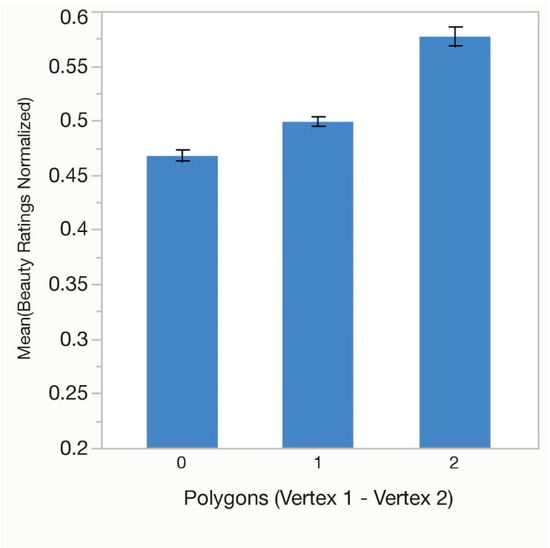
Figure 8.
Average normalized beauty ratings for the difference in the number of polygons between the two defining vertices for the tessellations in experiment 2. Error bars indicate ±1 standard error of the mean.
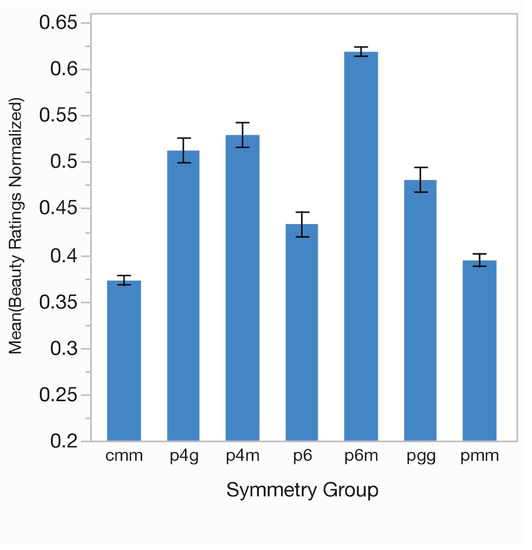
Figure 9.
Average normalized beauty ratings for the symmetry groups of the tessellations in experiment 2. Error bars indicate ±1 standard error of the mean. See Table 2 for the defining features of each group.
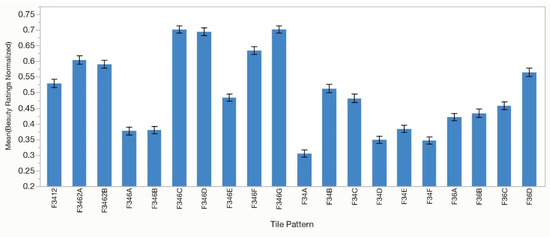
Figure 10.
Average normalized beauty ratings for each of the 20 tile pattern types in experiment 2. Error bars indicate ±1 standard error of the mean.
Participants preferred tiles with the greatest number of different polygons. Unlike experiment 1, in this study ratings increased continuously on this variable. In fact, going from 2–4 polygons the effect looks quite linear. The results suggest a preference for either complexity or variety of basic polygon shapes. Perhaps the difference between the two experiments has to do with the range of polygons presented. When a greater number of types are present, there may be a preference shift towards increased complexity.
In this experiment the patterns are categorized based on two vertex centers with different numbers and types of polygons. In order to capture whether participants are sensitive to the presence of these centers we took the difference in the number of polygons between them and used this to predict ratings. The results show a clear preference for centers that differ from each other in polygon number. Patterns in which the number was the same were liked the least with an upward trend as the difference increased. Patterns with different centers are less homogenous so this result could again indicate a preference for variety or complexity. These results show that participants are sensitive to vertices and that they do seem to affect aesthetic judgments.
We compared tiles that had equivalent vertex designations but varying similarity. Some of these equivalents are nearly identical to one another in appearance while others are more dissimilar. If there is no difference in responding between such equivalents then the underlying vertices play a more important role in determining perceived beauty. If there is a difference between equivalents that is discernible, then surface appearance should be the more important factor. A Least Squared Means Differences analysis (Tukey HSD) was performed for all pair-wise tiles (α = 0.05, Q = 3.54). There was no significant difference in mean ratings between any of the vertex equivalent pairs (F36B–F36C, F34D–F34E, F34B–F34C, F34A–F34F, F346A–F346B). We conclude that the vertices, although less obvious than some of the larger features in these patterns, affected responding more. This result corroborates the vertex difference findings reported above and shows that our observers are sensitive to vertex properties.
Unlike in experiment 1 it is difficult to determine a preference for triangles, since all of the patterns contain them. Looking at the rankings for polygon type in Table 3 there doesn’t seem to be a preference either for patterns with a particular collection of polygons. To illustrate, patterns containing triangles, squares, and hexagons (TSH) are in positions 1, 2, 4, 16, and 17, which are at both the top and bottom of the list.
However, there are some clusters present in the rankings related to specific types of tile patterns. F346G, F346C, F346D, and F346F are all in the top four positions. These tiles all have a global motif consisting of a hexagon surrounded by triangles and squares, indicating that the holistic configuration of polygons is important for aesthetic evaluation. The result implies that participants were perceiving emergent collections of shapes within the tiles and not just processing them at the individual vertex or polygon level. Tiles F3462A and F3462B were also ranked high, at positions five and six as was F3412 at position eight. These tessellations are characterized by large dodecagons surrounded by interconnecting collections of triangles, squares and hexagons. These patterns can be characterized as having prominent, more circular central spaces.
The tessellations at the bottom of the rankings are also informative. F34D, F34F and F34A were the least preferred at positions 18, 19, and 20, respectively. They all have linear stripes of squares that run through them along with stripes of interlocking triangles. The same can be said for F34E, F346B and F346A at positions 15, 16 and 17. Emergent linear formations thus seem to be less liked than other configurations.
The results with regard to symmetry group based on Table 3 fall into roughly three categories. First, tiles with symmetry group p6m were preferred the most. These tessellations made up the top seven rankings and position 12. p6m tiles have a hexagonal lattice, contain all three symmetry operations (Rf, Rt, Gl) and rotation orders of 2, 3, and 6. As such they appear to have the highest degree of symmetric complexity. Second, tessellations in group cmm and pmm were liked the least. These were in the bottom seven positions and at ranking number ten. cmm have rhombic lattices, contain reflections and rotations and a rotation order of 2. pmm have rectangular lattices, reflections and rotations, with a rotation order of 2. Third, the remaining symmetry groups p4m, p4g, pgg, and p6 were in approximately intermediary locations in the list.
4. Conclusions
In this study, we examined preference for tessellations containing regular polygons. In experiment 1 we tested the three regular and eight semi-regular (Archimedean) tilings characterized by a single vertex, excluding the single enantiomorphic alternate. In experiment 2 we tested the 20 demi-regular tessellations defined by two vertices. The data from the first experiment show a peak in preference for tiles with two types of polygons and for five polygons around a vertex. Triangles were preferred more than other geometric shapes. There was no clear-cut effect of symmetry group and no preference for tiles with a greater number of symmetry operations. The results from experiment 2 show a preference for tessellations with a greater number of different kinds of polygons in the overall pattern and for tiles with the greatest difference in the number of polygons around the two vertices. There was increased preference for tessellations with hexagonal and dodecagonal centers and decreased preference for those with linear square striping. Symmetry group p6m was liked the most and groups cmm and pmm were liked the least.
There are several themes that emerge from the results. The first of these is complexity. This is notoriously difficult to define in a visual stimulus and can vary based on a number of factors [22]. Nevertheless, in our study we will define it based on several features. Tessellations with a greater number of polygon types may be considered more complex since they contain a greater variety of different geometric shapes. We see a preference for this in experiment 2. Another form of complexity may be the number of polygons around the defining vertices. This peaked at the second highest number in experiment 1 but showed a linear increasing effect in experiment 2. We measured this as the difference between the two vertices in the second study. The greater this difference the more heterogeneous the pattern becomes. This was also found to drive responses demonstrating a complexity preference.
Complexity can also be demonstrated in terms of the symmetry group. Pattern p6m appears to be the most complex. It has all three types of symmetric transformations, all three rotation orders and reflection in six different directions. p4g and p4m have the three symmetry types but only two rotation orders. p6 has all three rotation orders but only one type of symmetry. p6m was the number one preferred type in experiment 2. In contrast, cmm and pmm were least liked in that study and may be considered the least complex. They have two symmetry types but only one rotation order. However, this result must be interpreted with some caution. Pgg shares these properties but has no reflections, which may reduce its complexity. It is not clear how to interpret lattice types in terms of complexity but hexagonal lattices were liked the most overall, followed by square lattices. Rhombic lattices were liked the least with square and rectangular lattices occupying the middle ground.
One of the earliest studies examining fractal patterns varied dimension, recursion, and number of segments in starting generator lines [23]. Ratings of complexity were affected most by recursion and fractal dimension. More recent work has shown that preference for fractal patterns increases with these same measures of stimulus complexity [24]. This study presented artificially generated fractals to observers who evaluated them aesthetically. Preference ratings for most of the participants went up with an increase in fractal dimension. The presence of symmetry interacted with the other variables in their study. Preference for patterns at low levels of recursion were increased by the presence of symmetry. Most of those tested required a high level of recursion to increase liking for patterns lacking in symmetry. Some but not all of the patterns with high rankings in our study had high estimated dimensionality. Pattern F346D and F36B both have lots of space-filling curves, but only the former was rated highly. Although our patterns did not have exact repeating structures at different scales, there was approximate repetition for some shapes. For example, F3462A, F3462B, F346D, F346G and F36D all have recursive circular formations by individual polygons or collections of polygons at different sizes and were highly ranked but F36D, which was also highly rated, does not.
A second major theme regards centers. In experiment 2 the preference for vertex centers differing in number of polygons was somewhat surprising because these centers are not always easy to locate, even when one is aware of their presence. Our participants were naïve with regard to the mathematical properties of the patterns and average response time was often quick, around one second. The data therefore suggest that observers were able to rapidly process information about the two vertex centers and that these vertex centers had a clear influence on their aesthetic judgments. This finding is corroborated by the vertex equivalent pairs, which were responded to similarly despite cases where their outward appearances were different. It is probable that our participants did not locate these centers analytically or count the number and type of polygons around them, as they had little knowledge of their existence. Instead they were able to perceptually detect the difference somehow by noting changes in the arrangement of polygons across the pattern.
Based on the experiment 2 results our participants showed a preference for tiles containing hexagonal and dodecagonal centers and did not seem to like as much tiles with linear arrangements of squares or triangles. Centers in this sense refer not to vertex centers but to prominent polygons that other polygons organize around. For example, pattern F346C has prominent hexagons with triangles and squares around it. It also has salient triangles with other triangles and squares around it. In comparison pattern F34F has no perceptually noticeable centers. It appears to consist of alternating linear bands of squares two rows thick interspersed with single linear rows of triangles.
To further determine the role of circular and linear arrangements we assigned each of the 20 tessellations in experiment 2 one of three rankings, “C” if it contained a primarily circular configuration of elements, “L” if it had a mostly linear arrangement and “M” if it contained a mixture of circular and linear elements. 71% of the upper third of rankings were circular, 57% of the middle third were mixed, and 100% of the bottom third were linear. This suggests a preference for tessellations with rotational rather than linear configurations. It also strongly demonstrates that emergent structures made of multiple individual polygons are affecting perceived beauty. It may be that recursive spatial scales are more detectable with circular arrangements and that this could be driving preference in these patterns.
It is not clear how to reconcile some of the differences between the two experiments. In experiment 1 there appears to be a preference for moderate complexity in terms of preference for number of polygons in the pattern and around the vertex. More complex symmetry groups were not predictive in that study and there was no preference for circular vs. linear arrangements (a linear configurations appears at ranking position 3 and 10). In contrast, for experiment 2 there were trends towards increased complexity based on polygons and symmetry, and a distinct circular arrangement preference. One explanation may concern the variety of tilings viewed. If the viewing set is small and the range of pattern examples is limited in terms of complexity and variety, participants may correspondingly limit their preference to lower levels of these measures. When the viewing set is larger and contains a greater variety of different examples, then there may be a shift toward preference for greater complexity.
There is much further fruitful ground for study. Many different categories of tessellations exist that have yet to be examined from an aesthetics standpoint. These include three-uniform patterns with regular polygons defined by three vertices, mixtures of regular and non-regular polygons, tessellations with star and diamond polygons, monohedral tessellations made from a single shapes like triangles, quadrilaterals, and pentagons, N-morphic monohedral tilings in which the same shape can tile the plane in different ways, homohedral tiles that are similar but not identical, polyiamonds, polyominoes, and polyhexes, Escher and Penrose tilings, and many more [25,26,27,28]. The aesthetics of tessellations and the properties that determine their appeal has hopefully just begun.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Weil, C.; Weil, T. Geometric Ornament in Architecture, Art, and Design; Schiffer Publishing: Atglen, PA, USA, 2009. [Google Scholar]
- Washburn, D.K.; Crowe, D.W. Symmetries of Culture. Theory and Practice of Plane Pattern Analysis; University of Washington Press: Seattle, WA, USA, 1988. [Google Scholar]
- Washburn, D.K.; Crowe, D.W. Symmetry Comes of Age: The Role of Pattern in Culture; University of Washington Press: Seattle, WA, USA, 2004. [Google Scholar]
- Beyer, J. The Secrets of Interlocking Patterns: Designing Tessellations; Contemporary Books: Chicago, IL, USA, 1999. [Google Scholar]
- Seymour, D.; Britton, J. Introduction to Tessellations; Dale Seymour Publications: Palo Alto, CA, USA, 1989. [Google Scholar]
- Kinsey, L.C.; Moore, T.E. Symmetry, Shape, and Space: An Introduction to Mathematics Through Geometry; Springer/Key College Publishing: New York, NY, USA, 2002. [Google Scholar]
- Stevens, P.S. Handbook of Regular Patterns: An Introduction to Symmetry in Two Dimensions; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Arnheim, R. Art and Visual Perception. A Psychology of the Creative Eye; University of California Press: Berkeley, CA, USA, 1974. [Google Scholar]
- Berlyne, D.E. Studies in the New Experimental Aesthetics: Steps Toward an Objective Psychology of Aesthetic Appreciation; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Birkhoff, G.D. Aesthetic Measure; Harvard University Press: Cambridge, MA, USA, 1932. [Google Scholar]
- Day, H. Evaluation of subjective complexity, pleasingness and interestingness for a series of random polygons varying in complexity. Percept. Psychophys. 1967, 2, 281–286. [Google Scholar] [CrossRef]
- Fechner, G. Vorschule der Aesthetic; Breitkopf und Hartel: Leipzig, Germany, 1876. [Google Scholar]
- Valentine, C.W. An Introduction to the Experimental Psychology of Beauty; Nelson & Sons: Edinburgh, UK, 1919. [Google Scholar]
- Friedenberg, J. Geometric regularity, symmetry and the perceived beauty of simple shapes. Empir. Stud. Arts 2018, 36, 71–89. [Google Scholar] [CrossRef]
- Jacobsen, T.; Höfel, L. Aesthetic judgments of novel graphic patterns: Analyses of individual judgments. Percept. Mot. Ski. 2002, 95, 755–766. [Google Scholar] [CrossRef] [PubMed]
- McManus, I.C.; Cook, R.; Hunt, A. Beyond the Golden Section and normative aesthetics: Why do individuals differ so much in their aesthetic preferences for rectangles? Psychol. Aesthet. 2010, 4, 113–126. [Google Scholar] [CrossRef]
- Westphal-Fitch, G.; Fitch, W.T. Beauty for the eye of the beholder: Plane pattern perception and production. Psychol. Aesthet. 2017, 11, 451–456. [Google Scholar] [CrossRef]
- Westphal-Fitch, G.; Fitch, W.T. Spatial analysis of “crazy quilts,” a class of potentially random aesthetic artefacts. PLoS ONE 2013, 8, e74005. [Google Scholar] [CrossRef] [PubMed]
- Gombrich, E.H. The Sense of Order: A Study in the Psychology of Decorative Art; Phaidon Press: London, UK, 1984. [Google Scholar]
- Eberle, R.S. Children’s Mathematical Understandings of Tessellations: A Cognitive and Esthetic Synthesis. Dissertation Abstracts International Section A: Humanities and Social Sciences; ProQuest Information & Learning: Ann Arbor, MI, USA, 2011. [Google Scholar]
- Grünbaum, B.; Shephard, G.C. Tilings and Patterns; W.H. Freeman and Company: New York, NY, USA, 1987. [Google Scholar]
- Nadal, M.; Munar, E.; Marty, G.; Cela-Conde, C.J. Visual complexity and beauty appreciation: Explaining the divergence of results. Empir. Stud. Arts 2010, 28, 173–191. [Google Scholar] [CrossRef]
- Cutting, J.E.; Garvin, J.J. Fractal curves and complexity. Percept. Psychophys. 1987, 42, 365–370. [Google Scholar] [CrossRef] [PubMed]
- Bies, A.J.; Blanc-Goldhammer, D.R.; Boydston, C.R.; Taylor, R.P.; Sereno, M.E. Aesthetic responses to exact fractals driven by physical complexity. Front. Hum. Neurosci. 2016, 10, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Coxeter, H.S.M. Regular Polytopes, 3rd ed.; Dover Publications: Mineola, NY, USA, 1973. [Google Scholar]
- Escher, M.C. Escher: His Life and Complete Graphic Work; Locher, J.L., Ed.; Abrams: New York, NY, USA, 1982. [Google Scholar]
- Golomb, S.W. Polyominoes. Puzzles, Patterns, Problems, and Packings, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Penrose, R. Pentaplexity. Eureka 1978, 39, 16–22. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).