Column Generation Accelerated Algorithm and Optimisation for a High-Speed Railway Train Timetabling Problem
Abstract
1. Introduction
2. Problem Formulation
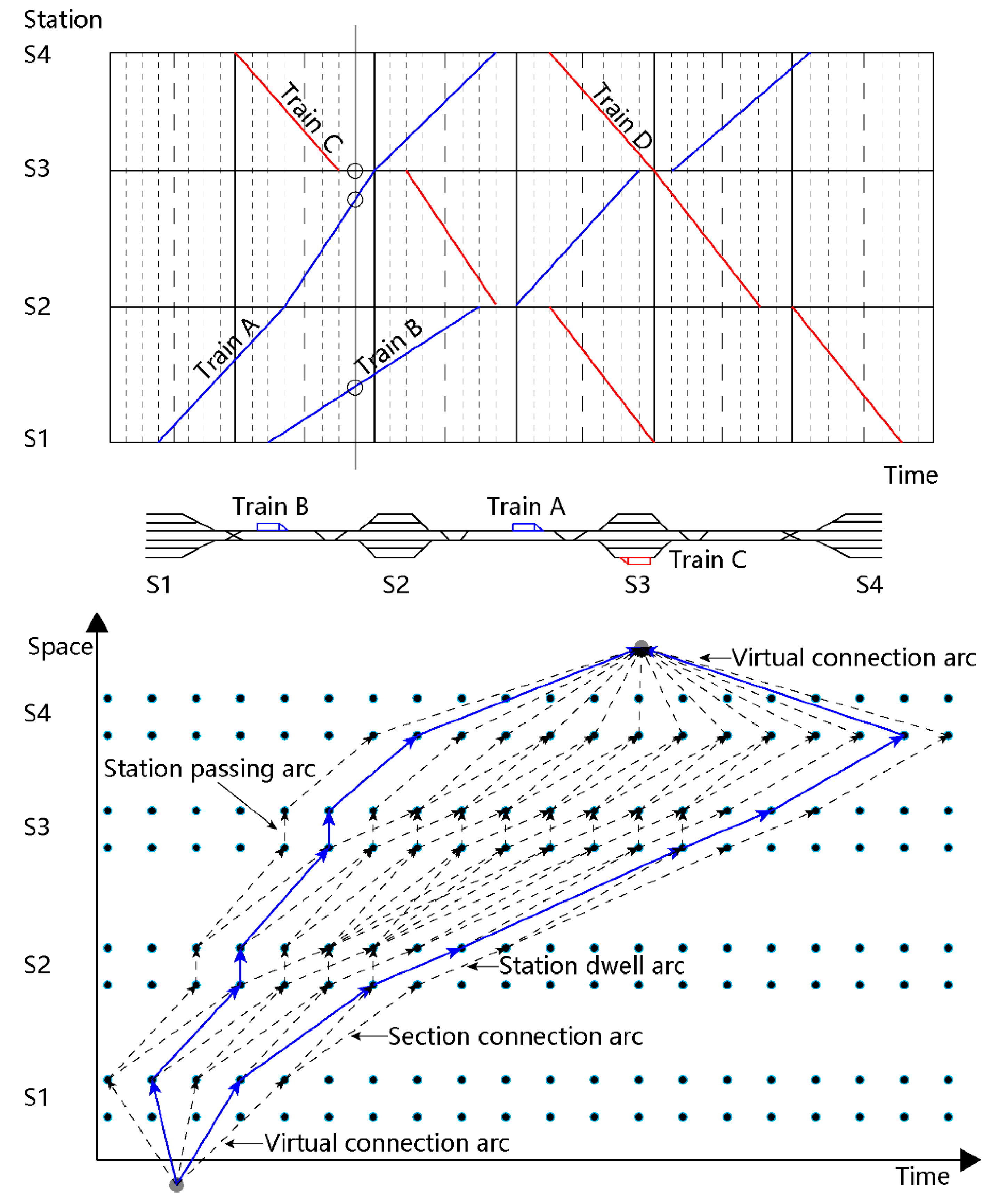
2.1. Problem Description
2.2. Notation
2.3. Mathematical Model
3. Column Generation-Based Algorithm
3.1. Column Generation Algorithm
3.2. Branching Strategies
- Step 1
- Construct a space-time network. Generate an initial path set as the root node of the branch tree and add it to . Set and .
- Step 2
- Judge whether is an empty set. If it is, the algorithm stops; otherwise, go to Step 3.
- Step 3
- Judge whether is true or not. If it is true, the algorithm stops; otherwise, go to Step 4.
- Step 4
- Judge whether the minimum objective function value of the nodes in is greater than . If it is, update . Sort according to the depth-first strategy, select the first node , and remove it from . Judge whether node is the root node. If it is, go to Step 6; otherwise, go to Step 5.
- Step 5
- Judge whether of node is empty. If it is, go to Step 2; otherwise, the first variable to be branched is selected from and added to . Each branch variable in is circulated, and is added to the model as the constraint. Remove from , and go to Step 6.
- Step 6
- The column generation algorithm is used to solve the linear relaxation problem of node .
- Step 6.1
- The initial feasible solution of the RMP is generated. Suppose that .
- Step 6.2
- The dual variables are obtained by solving the RMP. If an integer solution is obtained and is less than , update .
- Step 6.3
- The dual variables are used to update the weights of the space-time arcs and calculate the shortest path of each sub-problem. The path satisfying the requirement of reduced cost is added to set .
- Step 6.4
- Judge whether is empty. If it is, go to Step 7; otherwise, add the paths in to the RMP. Remove the paths from , and go to Step 6.2.
- Step 7
- Judge whether the objective function of is less than . If it is, the new active node is added to , is added to , the fractional variables in the results are sorted according to certain rules, and a certain number of variables are selected and added to according to the beam search algorithm. Delete the variable from , and go to Step 5. Otherwise, pruning is conducted, and the variable is deleted from . Then, go to Step 5.
4. Acceleration Strategies of the Column Generation-Based Algorithm
4.1. Preprocessing Stage
4.2. RMP Stage
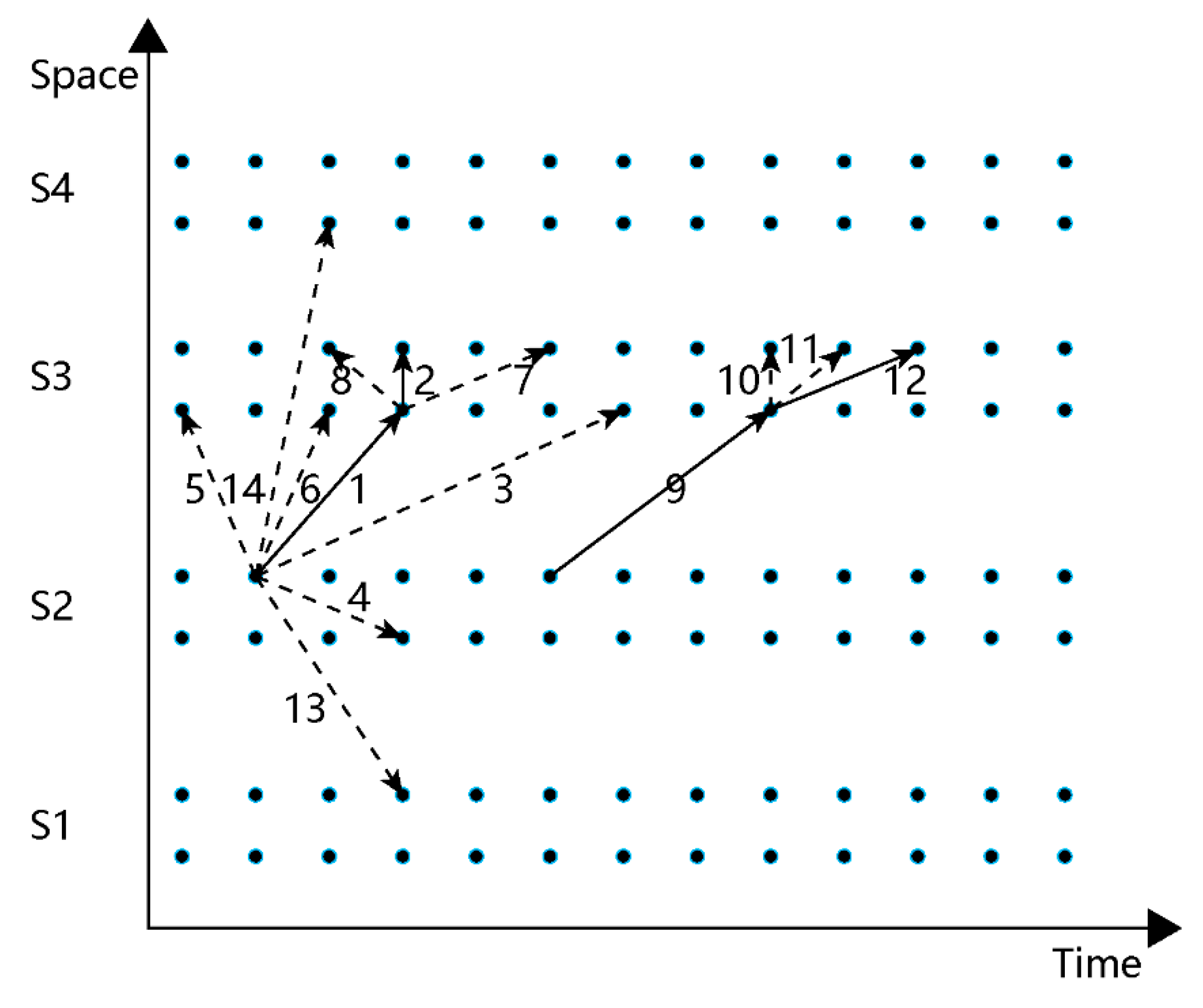
4.2.1. Column Management Strategy
4.2.2. Initial Solution Iteration Strategy
4.3. PP Stage
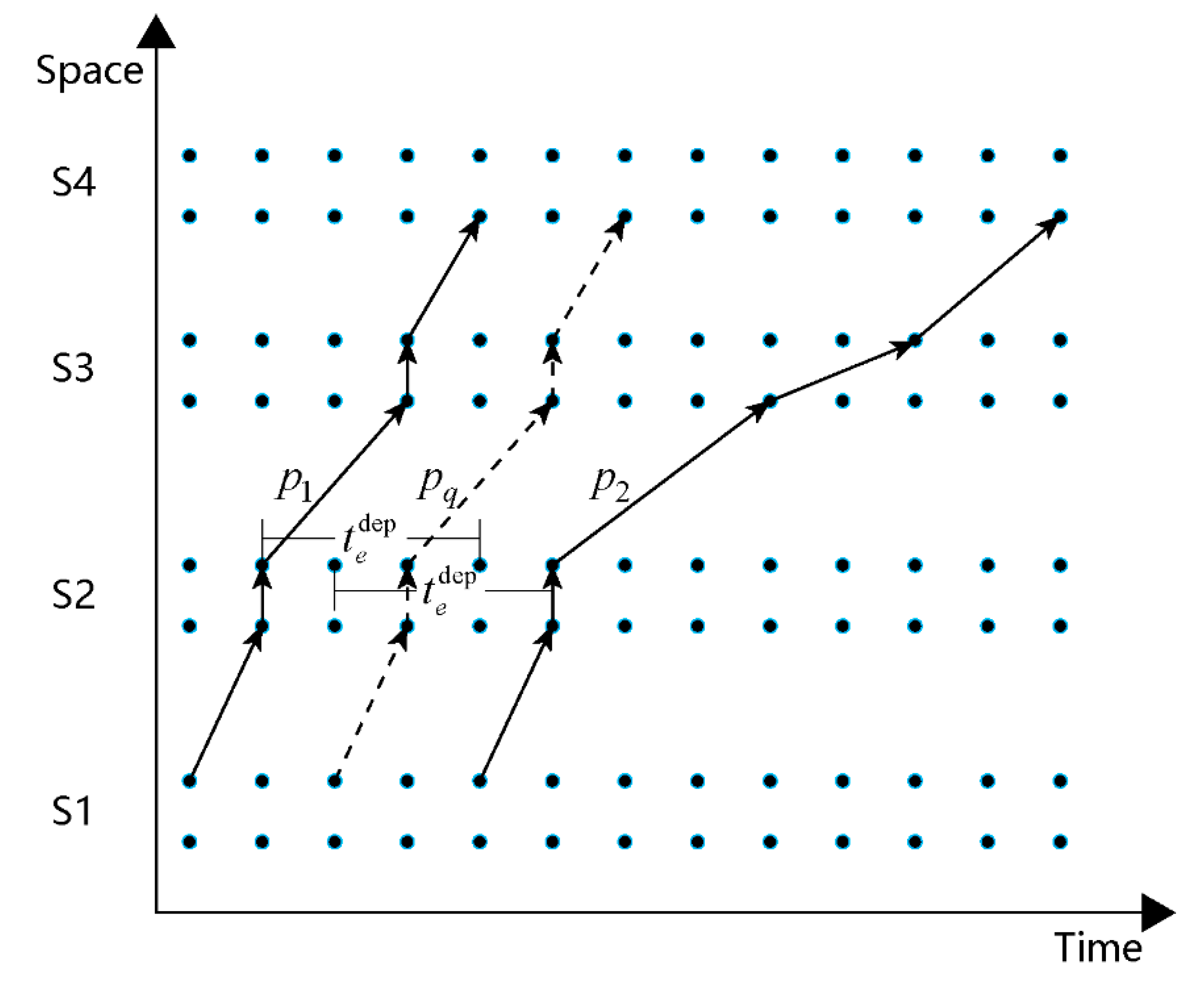
4.3.1. Partial Pricing Strategy
4.3.2. Multiple Paths Strategy
4.3.3. Delayed Constraint Strategy
4.4. Branch-and-Bound Stage
4.4.1. Early Branching Strategy
4.4.2. Column Replacement Strategy
4.5. Postprocessing Stage
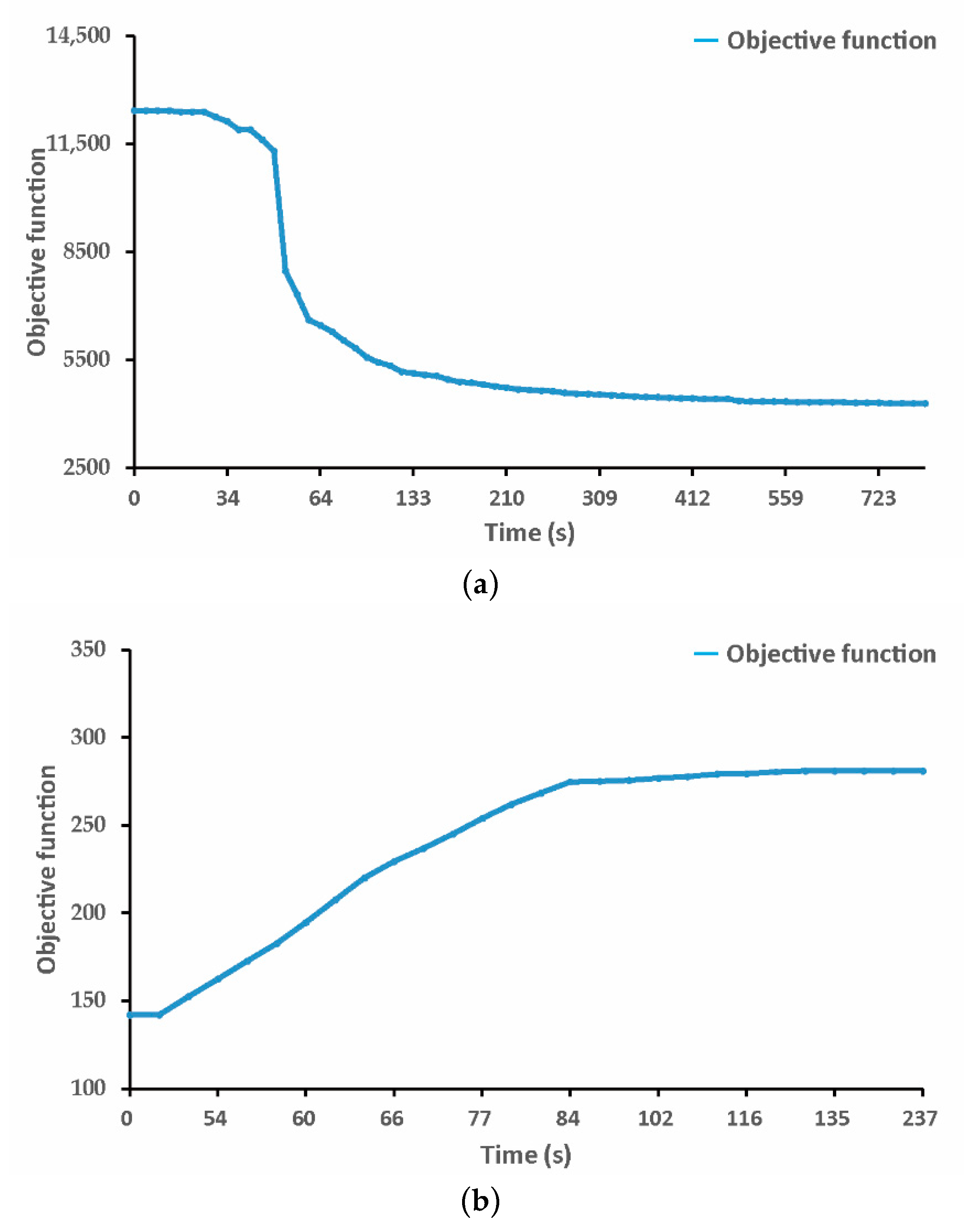
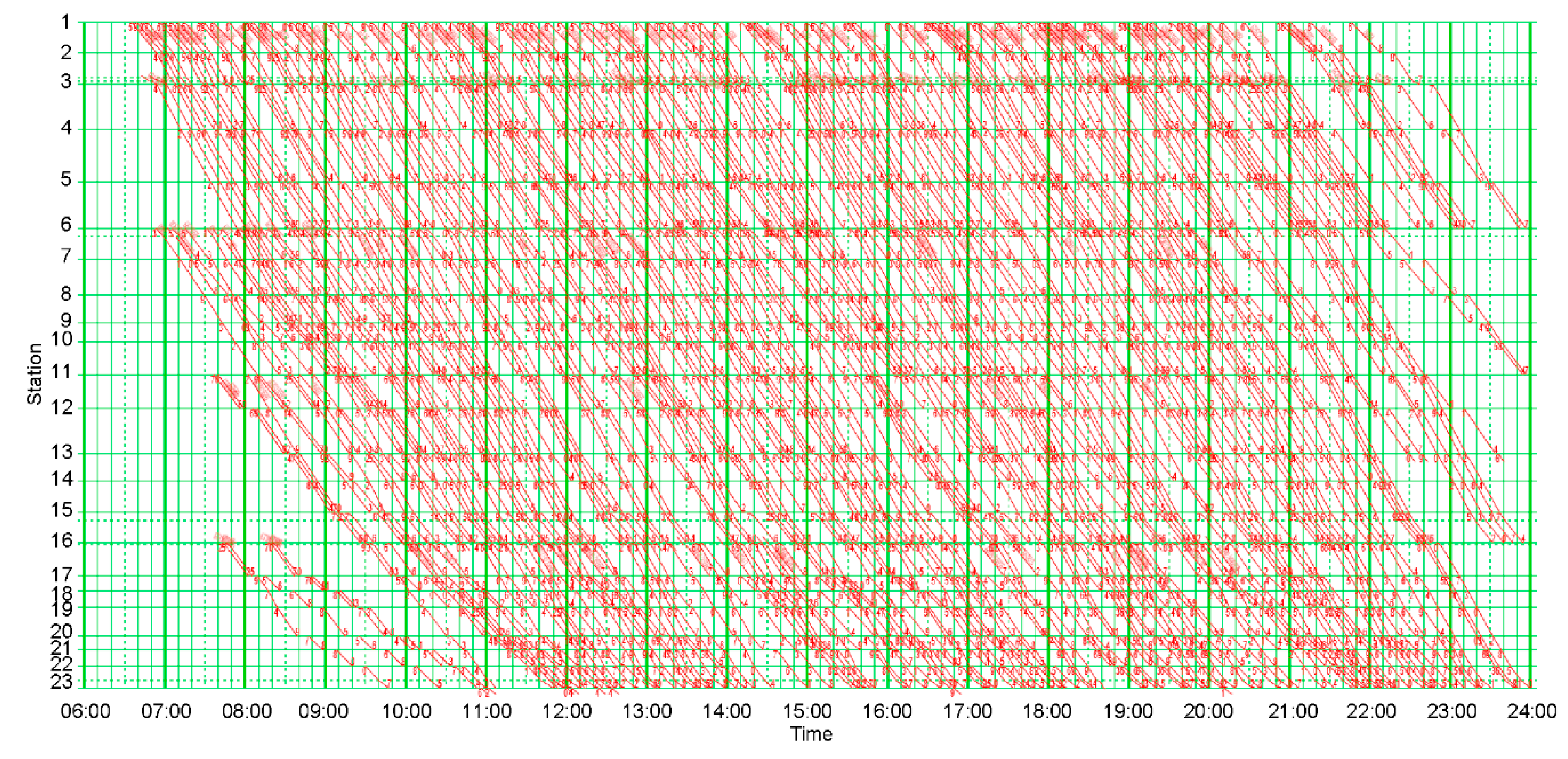
5. Case Study
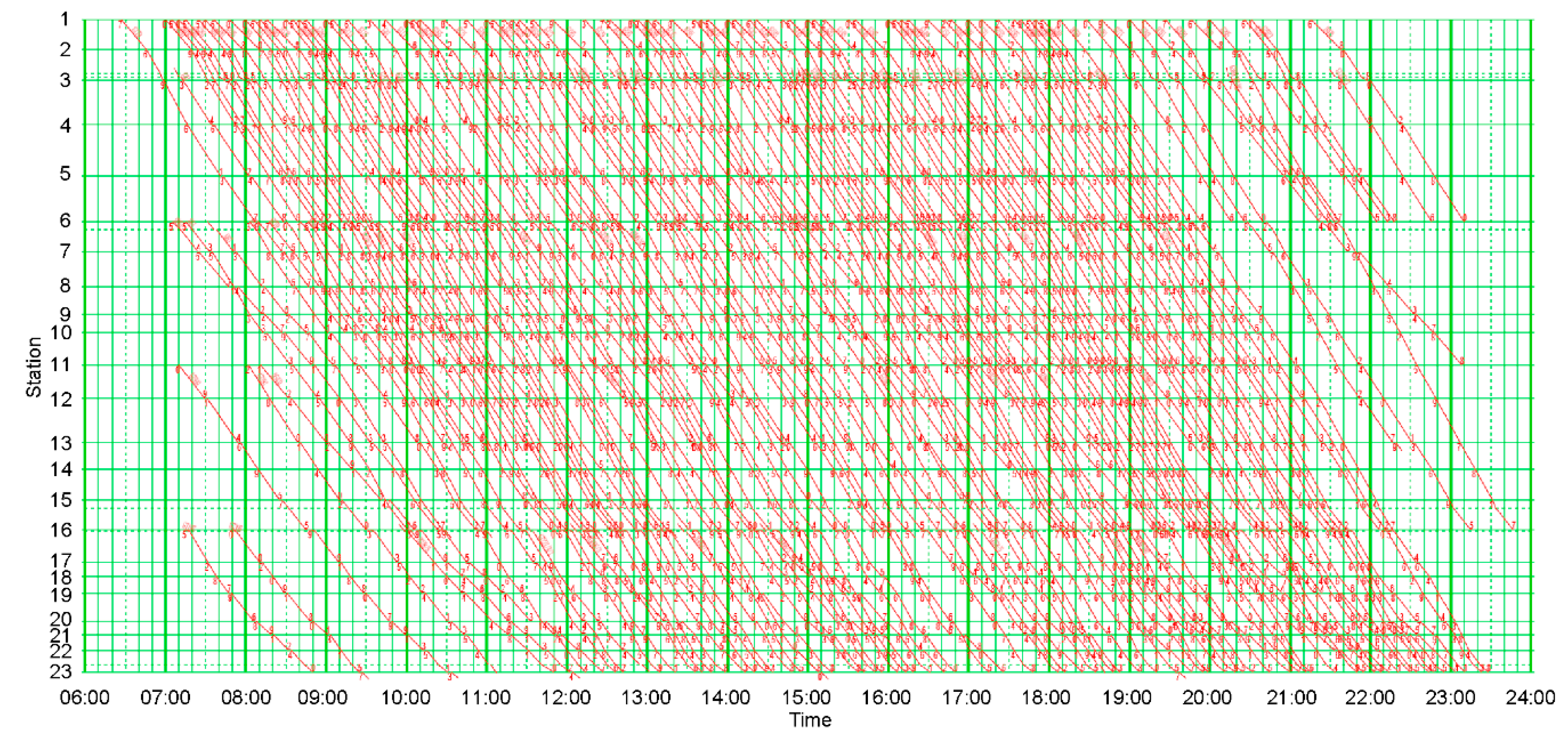
- Case 1
- A train timetable calculated using the original column generation-based algorithm.
- Case 2
- A train timetable calculated using the improved column generation-based algorithm with the acceleration strategies of the column management strategy and initial solution iteration strategy.
- Case 3
- A train timetable calculated using the improved column generation-based algorithm with the acceleration strategies of the early branching strategy and column replacement strategy.
- Case 4
- A train timetable calculated using the improved column generation-based algorithm with the acceleration strategies of the delayed constraint strategy and neighbourhood search strategy.
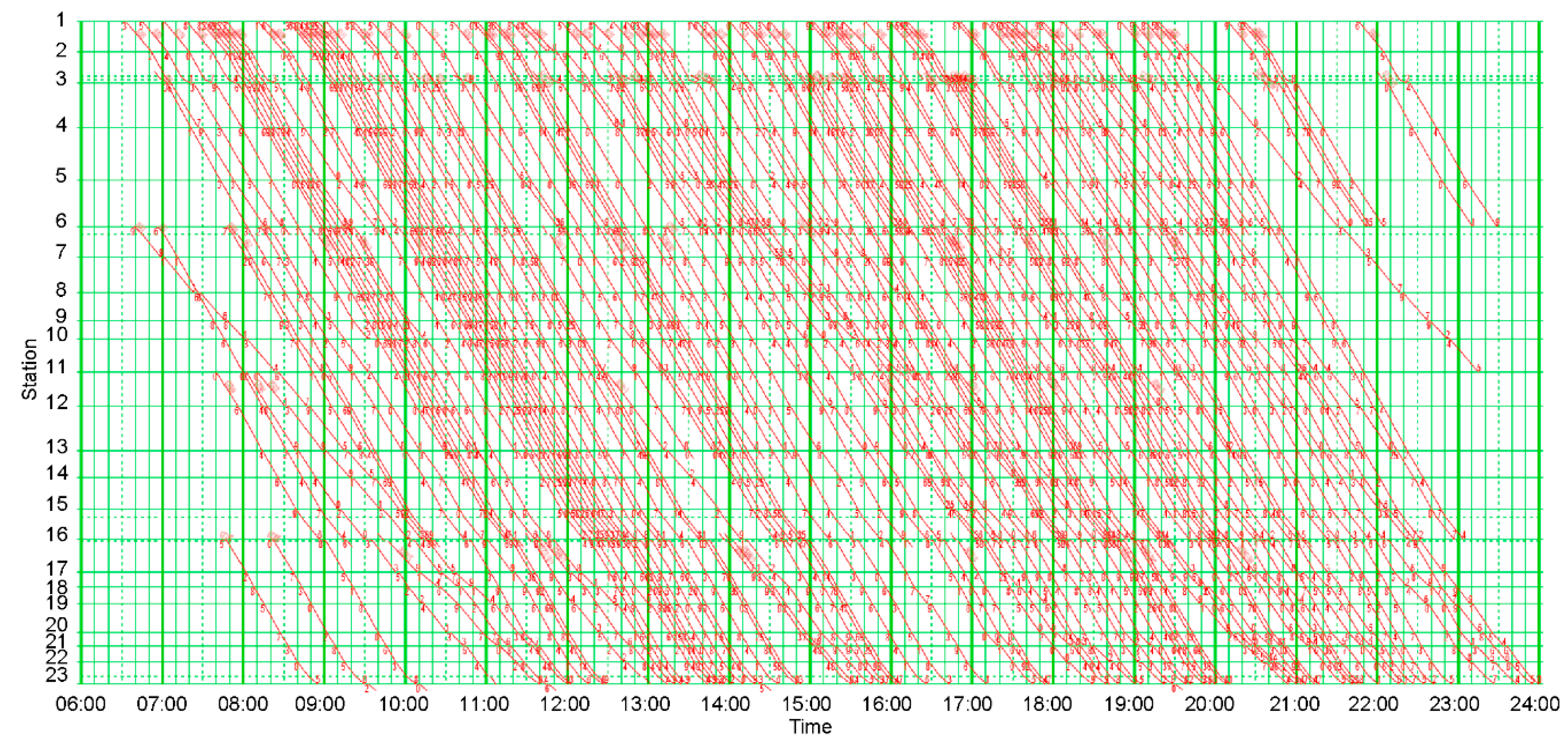
- Case 5
- A train timetable calculated using the improved column generation-based algorithm with all nine acceleration strategies.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dulebenets, M.A. A comprehensive multi-objective optimization model for the vessel scheduling problem in liner shipping. Int. J. Prod. Econ. 2018, 196, 293–318. [Google Scholar] [CrossRef]
- Jalalian, M.; Gholami, S.; Ramezanian, R. Analyzing the trade-off between CO2 emissions and passenger service level in the airline industry: Mathematical modeling and constructive heuristic. J. Clean. Prod. 2019, 206, 251–266. [Google Scholar] [CrossRef]
- Liu, L.; Chen, R.C. A novel passenger flow prediction model using deep learning methods. Trans. Res. Part C Emerg. Technol. 2017, 84, 74–91. [Google Scholar] [CrossRef]
- Wagenaar, J.; Kroon, L.; Fragkos, I. Rolling stock rescheduling in passenger railway transportation using dead-heading trips and adjusted passenger demand. Trans. Res. Part B Methodol. 2017, 101, 140–161. [Google Scholar] [CrossRef]
- Han, P.; Nie, L.; Fu, H.; Gong, Y.; Wang, G. A Multiobjective Integer Linear Programming Model for the Cross-Track Line Planning Problem in the Chinese High-Speed Railway Network. Symmetry 2019, 11, 670. [Google Scholar] [CrossRef]
- Liu, S.; Lin, B.; Wu, J.; Zhao, Y. Modeling the service network design problem in railway express shipment delivery. Symmetry 2018, 10, 391. [Google Scholar] [CrossRef]
- Qu, Z.; He, S. A Time-Space Network Model Based on a Train Diagram for Predicting and Controlling the Traffic Congestion in a Station Caused by an Emergency. Symmetry 2019, 11, 780. [Google Scholar] [CrossRef]
- Niu, H.; Zhou, X.; Gao, R. Train scheduling for minimizing passenger waiting time with time-dependent demand and skip-stop patterns: Nonlinear integer programming models with linear constraints. Trans. Res. Part B Methodol. 2015, 76, 117–135. [Google Scholar] [CrossRef]
- Yue, Y.; Wang, S.; Zhou, L.; Tong, L.; Saat, M.R. Optimizing train stopping patterns and schedules for high-speed passenger rail corridors. Trans. Res. Part C Emerg. Technol. 2016, 63, 126–146. [Google Scholar] [CrossRef]
- Zhou, L.; Tong, L.C.; Chen, J.; Tang, J.; Zhou, X. Joint optimization of high-speed train timetables and speed profiles: A unified modeling approach using space-time-speed grid networks. Trans. Res. Part B Methodol. 2017, 97, 157–181. [Google Scholar] [CrossRef]
- Jiang, F.; Cacchiani, V.; Toth, P. Train timetabling by skip-stop planning in highly congested lines. Trans. Res. Part B Methodol. 2017, 104, 149–174. [Google Scholar] [CrossRef]
- Adenso-Dıaz, B.; González, M.O.; González-Torre, P. On-line timetable re-scheduling in regional train services. Trans. Res. Part B Methodol. 1999, 33, 387–398. [Google Scholar] [CrossRef]
- Kroon, L.G.; Dekker, R.; Vromans, M.J. Cyclic railway timetabling: A stochastic optimization approach. In Algorithmic Methods for Railway Optimization; Springer: Berlin, Germany, 2007; pp. 41–66. [Google Scholar] [CrossRef]
- Zhou, L.; Hu, S.; Ma, J.; Yue, Y. Network Hierarchy Parallel Algorithm of Automatic Train Scheduling. J. China Railw. Soci. 1998, 20, 15–21. [Google Scholar]
- Shi, F.; Wei, T.; Zhou, W.; Luo, X. Optimization method for train diagram of high-speed railway considering the turnover of multiple units and the utilization of arrival-departure tracks. China Railw. Sci. 2012, 33, 107–114. [Google Scholar] [CrossRef]
- Caprara, A.; Monaci, M.; Toth, P.; Guida, P.L. A Lagrangian heuristic algorithm for a real-world train timetabling problem. Discret. Appl. Math. 2006, 154, 738–753. [Google Scholar] [CrossRef]
- He, B.; Song, R.; He, S.; Xu, Y. High-speed rail train timetabling problem: A time-space network based method with an improved branch-and-price algorithm. Math. Problems Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Lu, C.; Zhou, L.; Chen, R. Optimization of high-speed railway timetabling based on maximum utilization of railway capacity. J. Railw. Sci. Eng. 2018, 15, 32–40. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, L.; Yue, Y.; Tang, J.; Bai, Z. Optimizing High-Speed Railroad Timetable with Passenger and Station Service Demands: A Case Study in the Wuhan-Guangzhou Corridor. J. Adv. Trans. 2018, 2018. [Google Scholar] [CrossRef]
- Chen, S.; Shen, Y. Accelerating Column Generation for Solving Crew Scheduling Problems. J. Trans. Syst. Eng. Inf. Technol. 2014, 14, 144–149. [Google Scholar] [CrossRef]
- Desaulniers, G.; Desrosiers, J.; Solomon, M.M. Accelerating strategies in column generation methods for vehicle routing and crew scheduling problems. In Essays and Surveys in Metaheuristics; Springer: New York, NY, USA, 2002; pp. 309–324. [Google Scholar] [CrossRef]
- Gamache, M.; Soumis, F.; Marquis, G.; Desrosiers, J. A column generation approach for large-scale aircrew rostering problems. Oper. Res. 1999, 47, 247–263. [Google Scholar] [CrossRef]
- Ryan, D.; Foster, B. An Integer Programming Approach to Scheduling. Comput. Sched. Public Trans. 1981, 82, 269–280. [Google Scholar]
- Danna, E.; Pape, C. Branch-and-price heuristics: A case study on the vehicle routing problem with time windows. In Column Generation; Springer: Boston, MA, USA, 2005; pp. 99–129. [Google Scholar] [CrossRef]
- Savelsbergh, M. A branch-and-price algorithm for the generalized assignment problem. Oper. Res. 1997, 45, 831–841. [Google Scholar] [CrossRef]
- Sigurd, M.M.; Ulstein, N.L.; Nygreen, B.; Ryan, D.M. Ship scheduling with recurring visits and visit separation requirements. In Column Generation; Springer: Boston, MA, USA, 2005; pp. 225–245. [Google Scholar] [CrossRef]
- Sol, M.; Savelsbergh, M.W.P. A Branch-and-Price Algorithm for the Pickup and Delivery Problem with Time Windows; Eindhoven University of Technology, Department of Mathematics and Computing Science: Lyngby, Denmark, 1994. [Google Scholar]
- Zhou, X.; Zhong, M. Bicriteria train scheduling for high-speed passenger railroad planning applications. Eur. J. Oper. Res. 2005, 167, 752–771. [Google Scholar] [CrossRef]
- Goffin, J.L.; Vial, J.P. Multiple cuts in the analytic center cutting plane method. SIAM J. Optim. 2000, 11, 266–288. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, X.; Wang, L. Track Allocation Optimization in Multi-Direction High-Speed Railway Stations. Symmetry 2019, 11, 459. [Google Scholar] [CrossRef]

| Symbol | Definition |
|---|---|
| Subscripts | |
| Index of times, , where is the set of time intervals, ; | |
| Index of stations, , where is the set of stations; | |
| Index of trains, , where is the set of trains, ; | |
| Index of paths, , where is the set of paths; | |
| Index of sections, , where is the set of sections; | |
| Sets | |
| Space-time path set belonging to train ; | |
| Space-time path set passing section ; | |
| Input parameters | |
| Cost of a space-time path for different mathematical models; | |
| Time when a train enters and leaves section ; | |
| Minimum departure headway and minimum arrival headway of section ; | |
| Arrival time and departure time of station in path ; | |
| Minimum and maximum dwell time requirements for station ; | |
| Number of side tracks at station ; | |
| Stop index, which is equal to 1 if path stops at station and is equal to 0 otherwise; | |
| Coupled-stop index, which is equal to 1 if path stops at both station and station and is equal to 0 otherwise, ; | |
| Penalty coefficient of the number of train stops, the unit is 1/num; | |
| Penalty coefficient of the stopping time, the unit is 1/min; | |
| Minimum number of direct trains serving the passenger flow from station to station ; | |
| Average passenger flow OD matrix from station to station over a period of time counted by the passenger ticket department, the unit is one person; | |
| Passenger capacity of a train, the unit is one person; | |
| Average attendance rate of the trains from station to station . |
| Station Name | Station ID | Distance (km) | Number of Tracks | ||
|---|---|---|---|---|---|
| Downward Direction | Upward Direction | All | |||
| Beijing South | 1 | 0 | 20 | 20 | 24 |
| Langfang | 2 | 59 | 6 | 6 | 12 |
| Tianjin South | 3 | 131 | 4 | 4 | 6 |
| Cangzhou West | 4 | 219 | 6 | 6 | 8 |
| Dezhou East | 5 | 327 | 8 | 8 | 12 |
| Jinan West | 6 | 419 | 10 | 11 | 17 |
| Taian | 7 | 462 | 6 | 6 | 8 |
| Qufu East | 8 | 533 | 6 | 6 | 8 |
| Tengzhou East | 9 | 589 | 3 | 3 | 4 |
| Zaozhuang | 10 | 625 | 6 | 6 | 8 |
| Xuzhou East | 11 | 688 | 9 | 10 | 15 |
| Suzhou East | 12 | 767 | 6 | 6 | 8 |
| Bengbu South | 13 | 844 | 10 | 11 | 14 |
| Dingyuan | 14 | 897 | 3 | 3 | 4 |
| Chuzhou | 15 | 959 | 4 | 4 | 6 |
| Nanjing South | 16 | 1018 | 6 | 6 | 10 |
| Zhenjiang South | 17 | 1087 | 6 | 6 | 8 |
| Danyang North | 18 | 1112 | 3 | 3 | 4 |
| Changzhou North | 19 | 1144 | 6 | 6 | 8 |
| Wuxi East | 20 | 1201 | 6 | 6 | 8 |
| Suzhou North | 21 | 1227 | 6 | 6 | 8 |
| Kunshan South | 22 | 1259 | 4 | 4 | 6 |
| Shanghai Hongqiao | 23 | 1302 | 10 | 11 | 19 |
| Adjacent Station Pair | Section Travel Time (min) | |
|---|---|---|
| Grade G | Grade D | |
| 1–2 | 19 | 22 |
| 2–3 | 13 | 16 |
| 3–4 | 18 | 22 |
| 4–5 | 22 | 26 |
| 5–6 | 20 | 23 |
| 6–7 | 13 | 15 |
| 7–8 | 15 | 18 |
| 8–9 | 12 | 14 |
| 9–10 | 8 | 9 |
| 10–11 | 14 | 16 |
| 11–12 | 14 | 17 |
| 12–13 | 18 | 22 |
| 13–14 | 12 | 14 |
| 14–15 | 13 | 16 |
| 15–16 | 16 | 19 |
| 16–17 | 17 | 20 |
| 17–18 | 6 | 7 |
| 18–19 | 7 | 8 |
| 19–20 | 12 | 14 |
| 20–21 | 6 | 7 |
| 21–22 | 7 | 8 |
| 22–23 | 15 | 17 |
| Station | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | — | 8 | 11 | 8 | 8 | 14 | 8 | 8 | 8 | 8 | 11 | 8 | 11 | 2 | 8 | 14 | 9 | 5 | 8 | 8 | 10 | 8 | 14 |
| 2 | — | 5 | 2 | 2 | 8 | 2 | 2 | 2 | 2 | 5 | 2 | 5 | 1 | 2 | 8 | 1 | 2 | 2 | 2 | 4 | 2 | 8 | |
| 3 | — | 5 | 5 | 11 | 5 | 5 | 5 | 5 | 8 | 3 | 8 | 0 | 4 | 11 | 1 | 2 | 5 | 3 | 7 | 3 | 11 | ||
| 4 | — | 2 | 8 | 2 | 2 | 2 | 2 | 5 | 2 | 5 | 2 | 2 | 8 | 3 | 2 | 2 | 2 | 4 | 2 | 8 | |||
| 5 | — | 8 | 2 | 2 | 2 | 2 | 5 | 2 | 5 | 2 | 2 | 8 | 3 | 1 | 2 | 2 | 4 | 2 | 8 | ||||
| 6 | — | 8 | 8 | 8 | 8 | 11 | 8 | 11 | 3 | 8 | 14 | 9 | 7 | 8 | 8 | 10 | 8 | 14 | |||||
| 7 | — | 2 | 2 | 2 | 5 | 2 | 5 | 1 | 2 | 8 | 3 | 1 | 2 | 2 | 4 | 2 | 8 | ||||||
| 8 | — | 2 | 2 | 5 | 2 | 5 | 0 | 2 | 8 | 3 | 2 | 2 | 2 | 4 | 2 | 8 | |||||||
| 9 | — | 2 | 5 | 2 | 5 | 2 | 2 | 8 | 3 | 2 | 2 | 2 | 4 | 2 | 8 | ||||||||
| 10 | — | 5 | 2 | 5 | 1 | 2 | 8 | 3 | 2 | 2 | 2 | 4 | 2 | 8 | |||||||||
| 11 | — | 5 | 8 | 5 | 5 | 11 | 6 | 5 | 5 | 5 | 7 | 5 | 11 | ||||||||||
| 12 | — | 5 | 2 | 2 | 8 | 3 | 2 | 2 | 2 | 4 | 2 | 8 | |||||||||||
| 13 | — | 3 | 5 | 11 | 6 | 5 | 5 | 5 | 7 | 5 | 11 | ||||||||||||
| 14 | — | 2 | 6 | 2 | 2 | 2 | 2 | 4 | 2 | 5 | |||||||||||||
| 15 | — | 8 | 3 | 2 | 2 | 2 | 4 | 2 | 8 | ||||||||||||||
| 16 | — | 9 | 8 | 8 | 8 | 10 | 8 | 14 | |||||||||||||||
| 17 | — | 3 | 3 | 3 | 5 | 3 | 9 | ||||||||||||||||
| 18 | — | 2 | 2 | 4 | 2 | 8 | |||||||||||||||||
| 19 | — | 2 | 4 | 2 | 8 | ||||||||||||||||||
| 20 | — | 4 | 2 | 8 | |||||||||||||||||||
| 21 | — | 4 | 10 | ||||||||||||||||||||
| 22 | — | 8 | |||||||||||||||||||||
| 23 | — |
| Parameters | Actual Case | M1 | M2 |
|---|---|---|---|
| Number of trains | 142 | 142 | 200 |
| Average travel speed (km/h) | 216.1 | 238.2 | 213.2 |
| Average number of stops | 5.2 | 2.8 | 5.2 |
| Average dwell time (min) | 16.2 | 6.8 | 15.8 |
| Overtaking | 124 | 38 | 281 |
| Max dwell time of Grade G (min) | 12 | 7 | 12 |
| Max dwell time of Grade D (min) | 34 | 25 | 28 |
| Station | Instance | Station | Instance | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | ||
| 1 | N | N | N | N | N | 13 | N | Y | Y | N | Y |
| 2 | N | Y | Y | N | Y | 14 | Y | N | Y | N | Y |
| 3 | N | Y | Y | N | Y | 15 | N | Y | Y | N | Y |
| 4 | N | Y | Y | N | Y | 16 | Y | N | Y | N | Y |
| 5 | Y | N | Y | N | Y | 17 | N | Y | Y | N | Y |
| 6 | N | Y | Y | N | Y | 18 | N | Y | Y | N | Y |
| 7 | N | Y | Y | N | Y | 19 | N | Y | Y | N | Y |
| 8 | Y | N | Y | N | Y | 20 | N | Y | Y | N | Y |
| 9 | N | Y | Y | N | Y | 21 | N | Y | Y | N | Y |
| 10 | N | Y | Y | N | Y | 22 | N | Y | Y | N | Y |
| 11 | N | Y | Y | N | Y | 23 | N | N | N | N | N |
| 12 | N | Y | Y | N | Y | — | — | — | — | — | — |
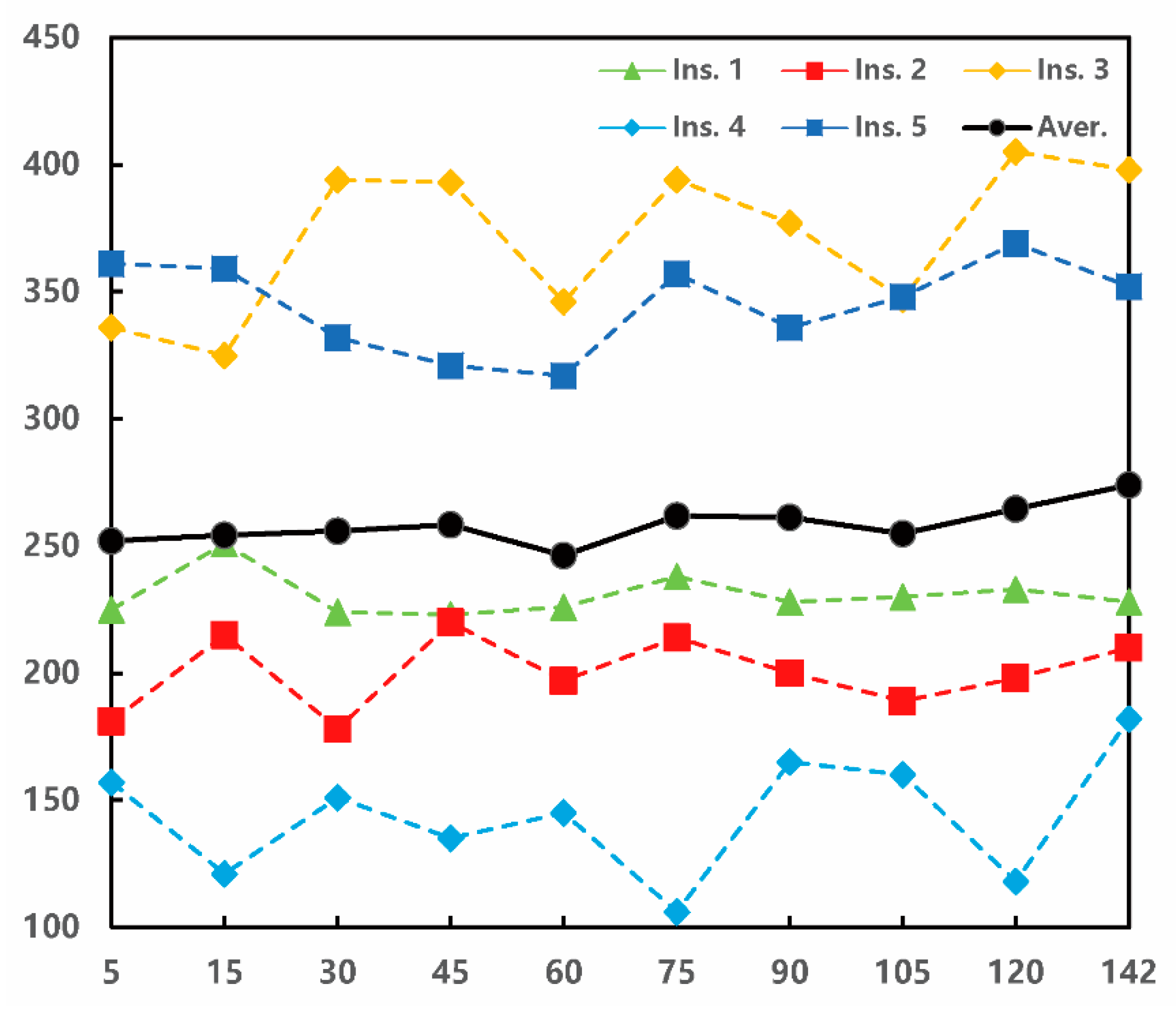
| Instance | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Time | Gap | Time | Gap | Time | Gap | Time | Gap | Time | Gap | |
| 1 | 2564 | 0.302 | 1847 | 0.282 | 1215 | 0.287 | 780 | 0.125 | 223 | 0.109 |
| 2 | 2441 | 0.63 | 2187 | 0.522 | 1015 | 0.522 | 2301 | 0.515 | 178 | 0.162 |
| 3 | 4019 | 0.61 | 1945 | 0.600 | 2164 | 0.600 | 1364 | 0.184 | 325 | 0.154 |
| 4 | 2028 | 0.455 | 1327 | 0.455 | 907 | 0.460 | 544 | 0.345 | 106 | 0.363 |
| 5 | 2575 | 0.463 | 2319 | 0.463 | 1520 | 0.470 | 867 | 0.325 | 317 | 0.288 |
| Average | 2725 | 0.492 | 1925 | 0.464 | 1364 | 0.468 | 1171 | 0.299 | 230 | 0.215 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhou, L.; Yue, Y. Column Generation Accelerated Algorithm and Optimisation for a High-Speed Railway Train Timetabling Problem. Symmetry 2019, 11, 983. https://doi.org/10.3390/sym11080983
Wang J, Zhou L, Yue Y. Column Generation Accelerated Algorithm and Optimisation for a High-Speed Railway Train Timetabling Problem. Symmetry. 2019; 11(8):983. https://doi.org/10.3390/sym11080983
Chicago/Turabian StyleWang, Jin, Leishan Zhou, and Yixiang Yue. 2019. "Column Generation Accelerated Algorithm and Optimisation for a High-Speed Railway Train Timetabling Problem" Symmetry 11, no. 8: 983. https://doi.org/10.3390/sym11080983
APA StyleWang, J., Zhou, L., & Yue, Y. (2019). Column Generation Accelerated Algorithm and Optimisation for a High-Speed Railway Train Timetabling Problem. Symmetry, 11(8), 983. https://doi.org/10.3390/sym11080983






