The Solutions of Non-Integer Order Burgers’ Fluid Flowing through a Round Channel with Semi Analytical Technique
Abstract
:1. Introduction
2. Governing Equations
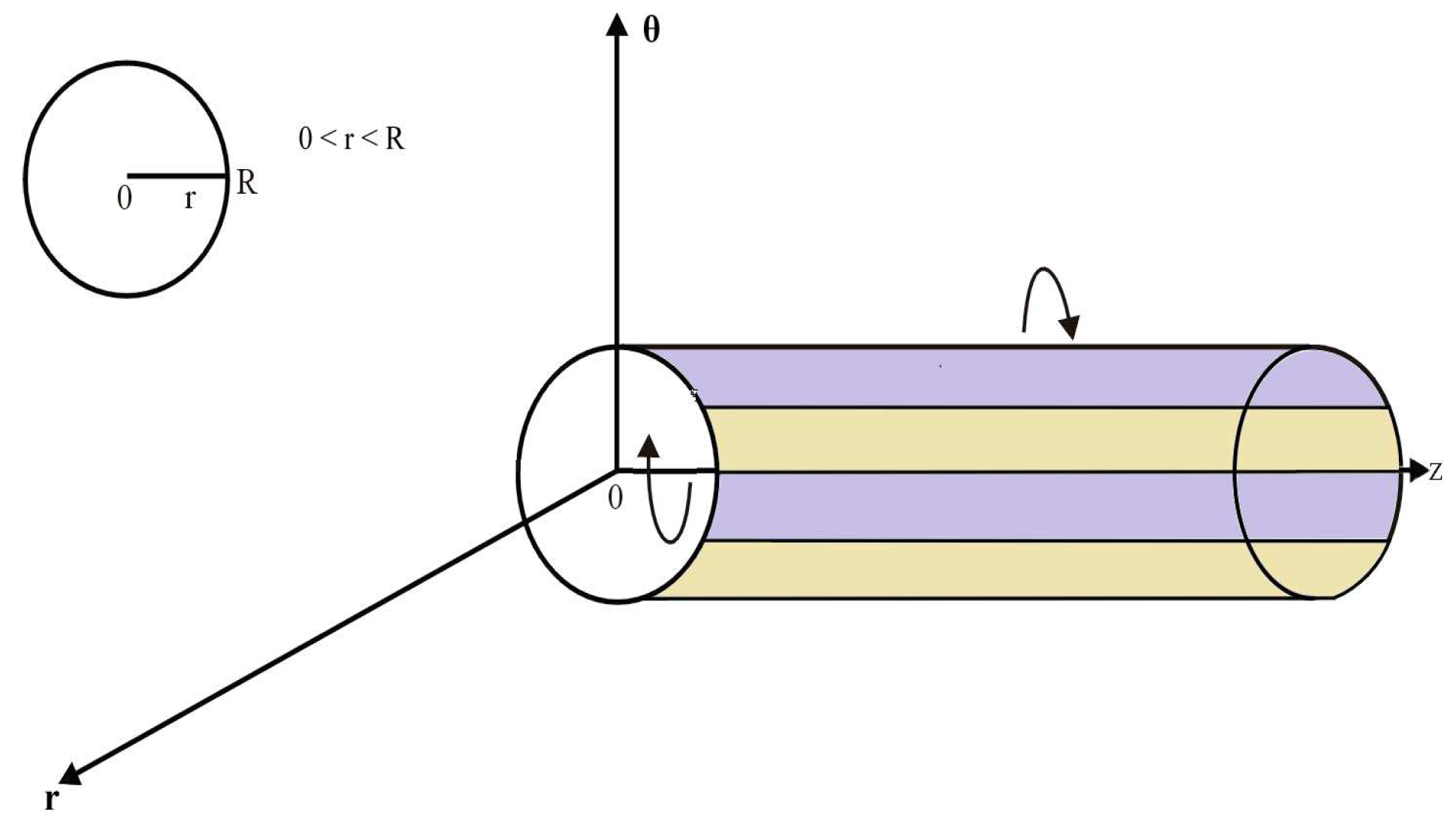
3. Imposing Condition and Geometry
3.1. Velocity Field Due to Rotating Circular Pipe
3.2. Shear Stress Due to Rotating Circular Cylinder
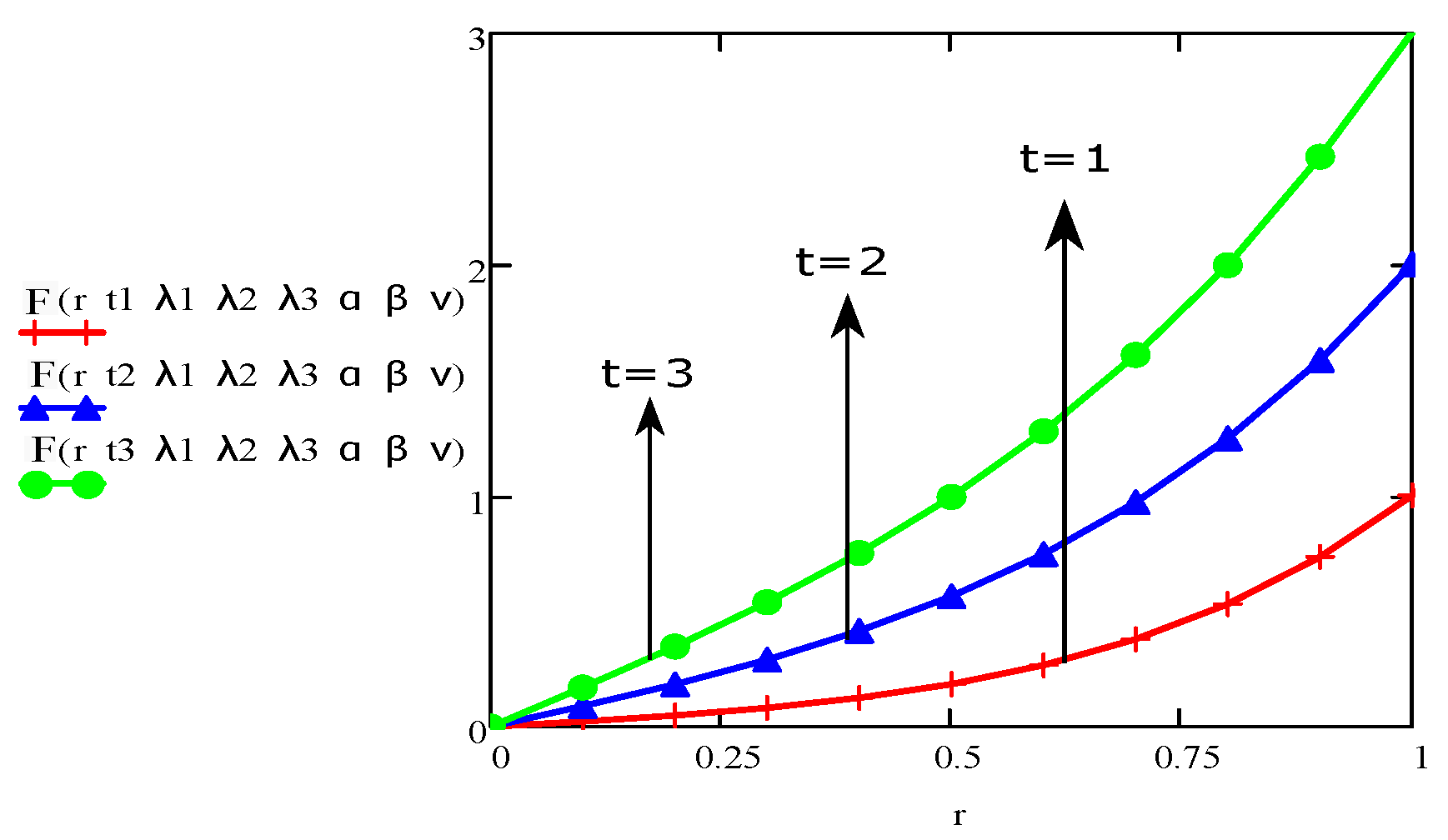
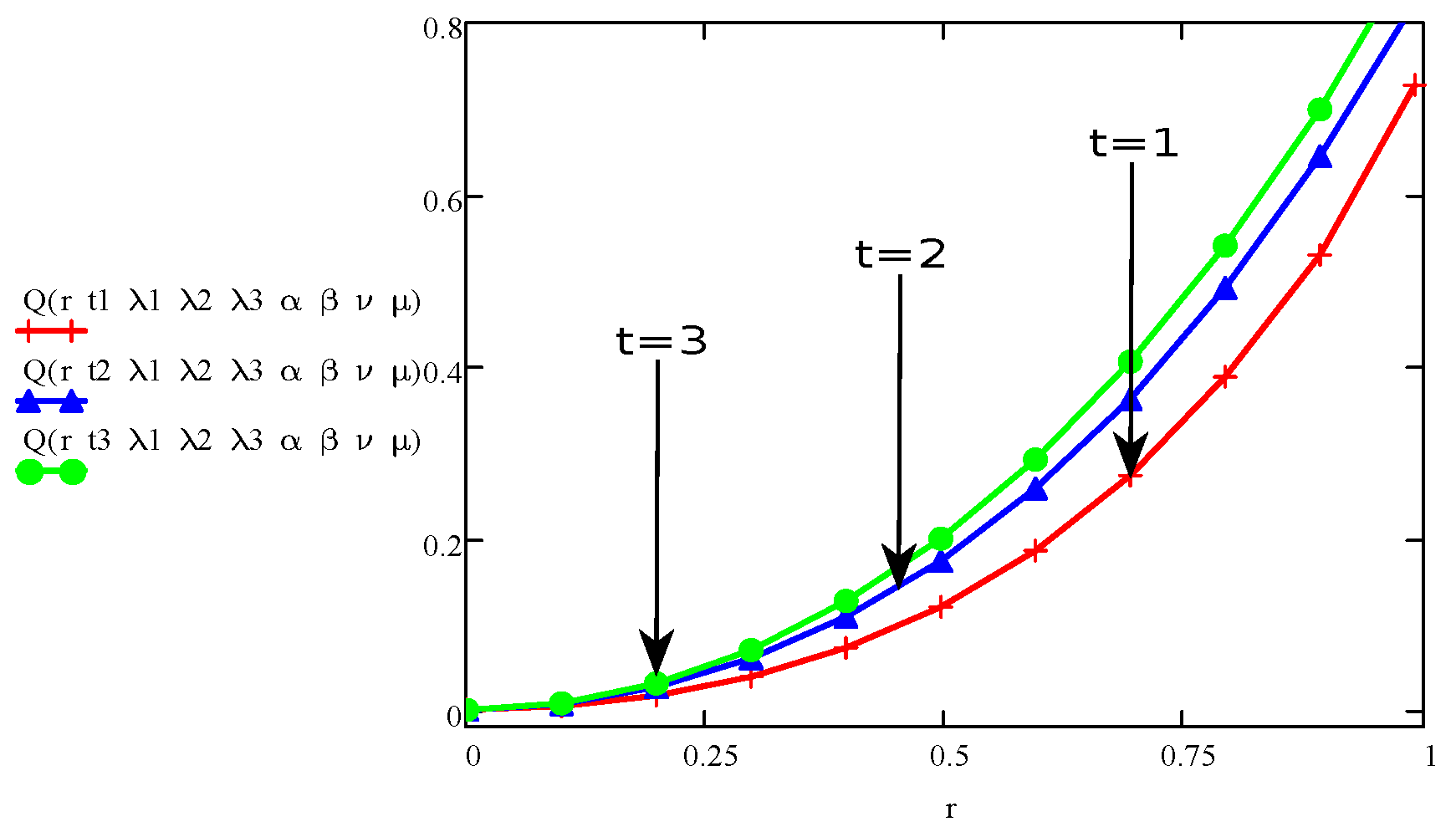
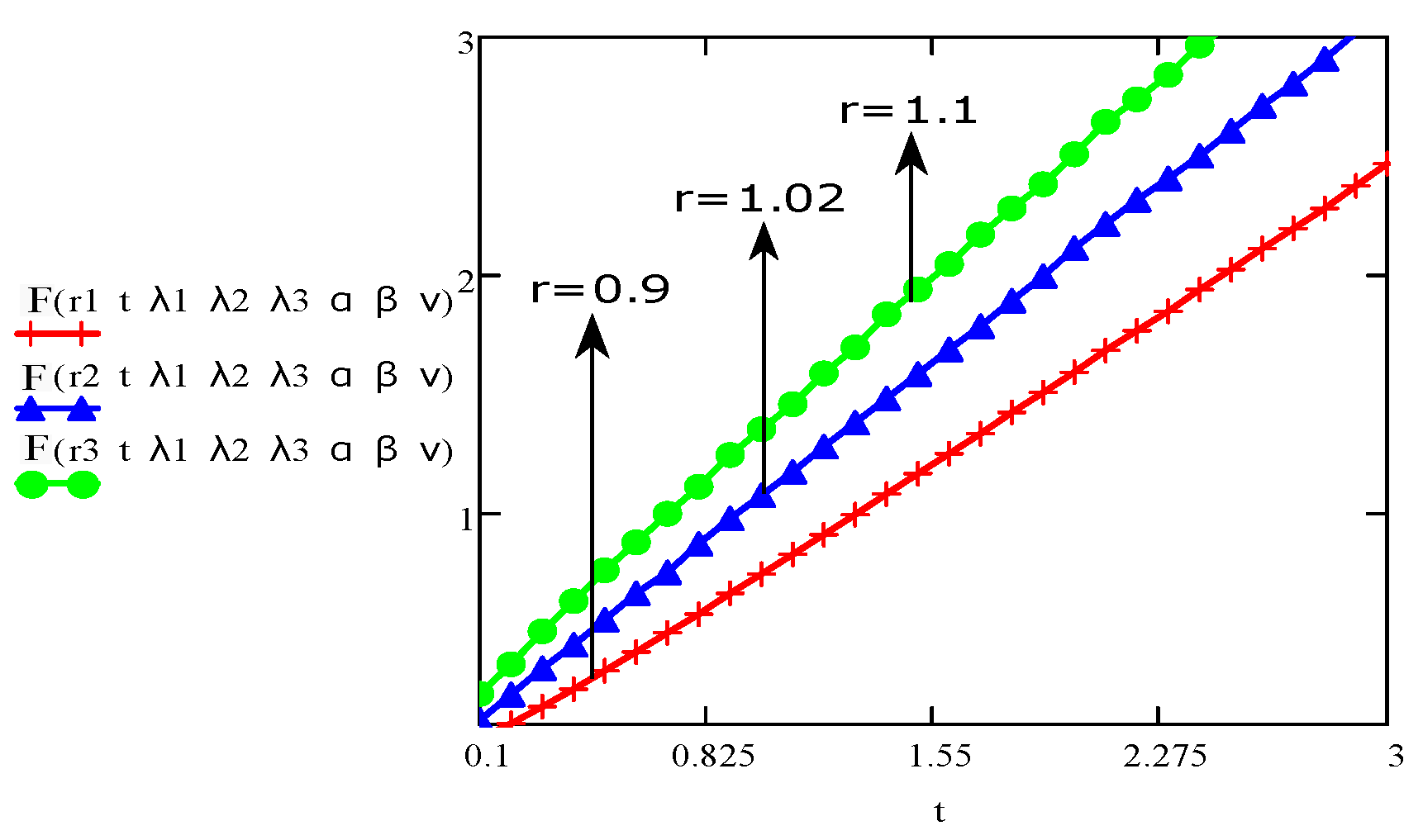
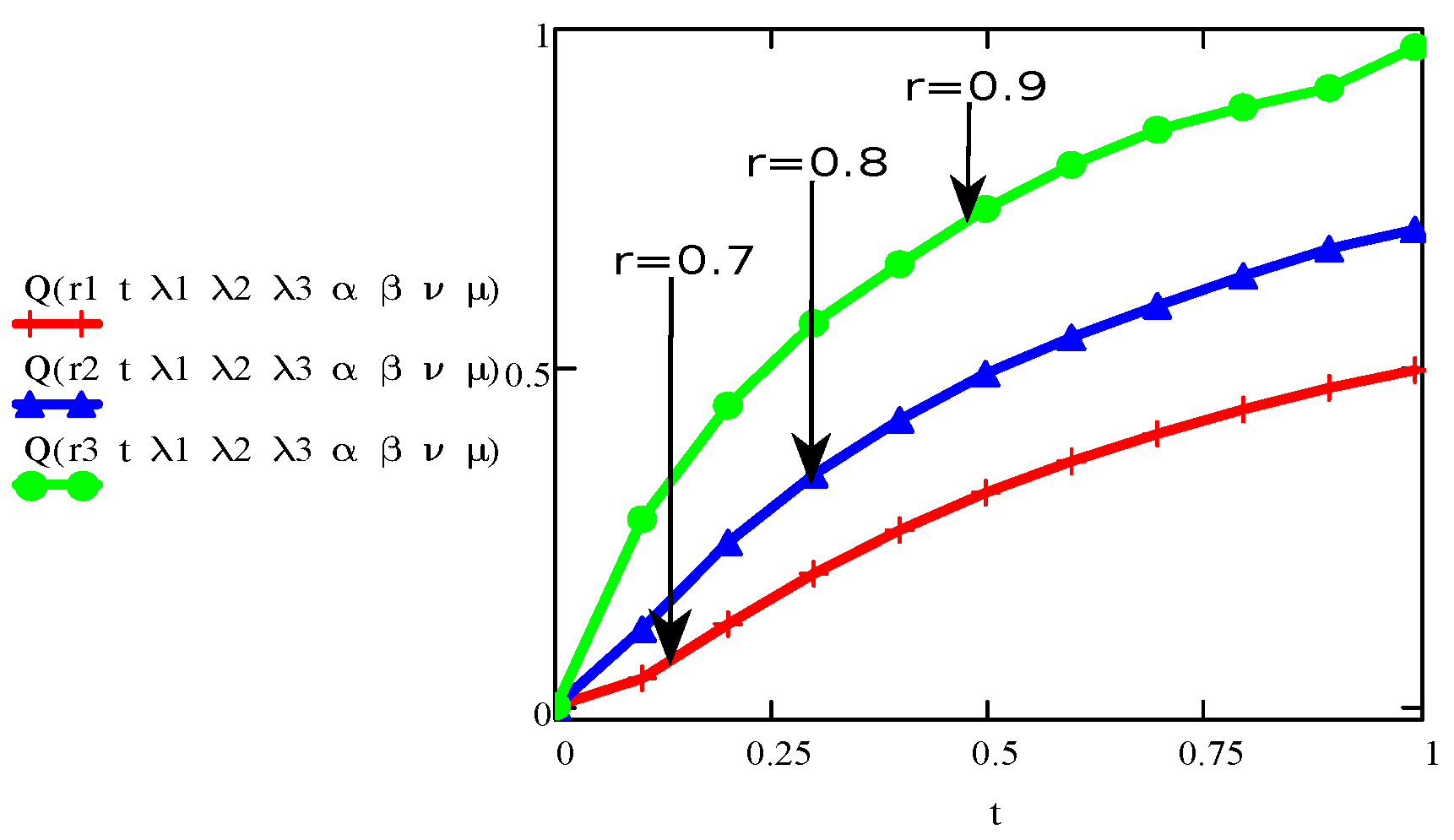
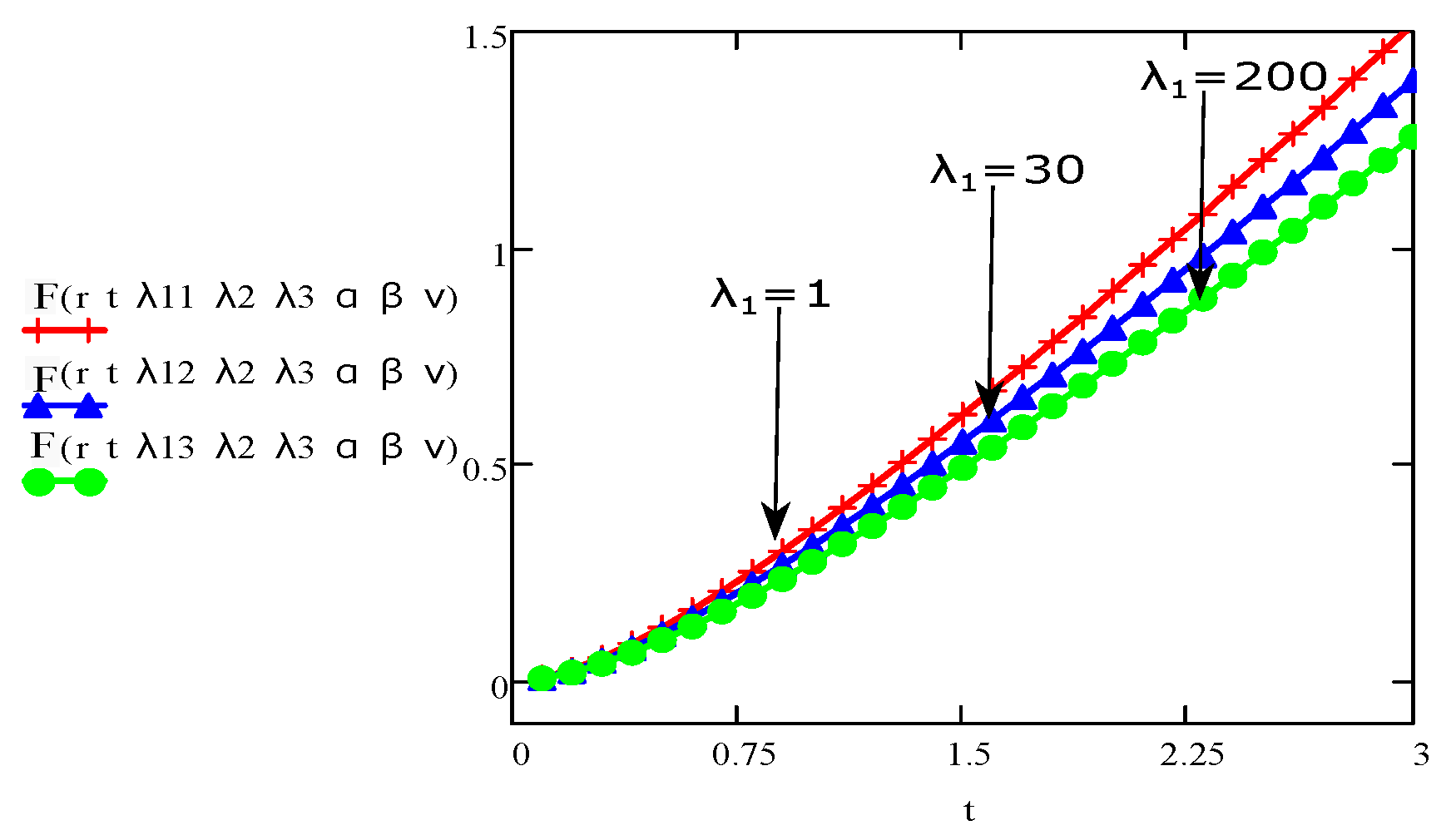
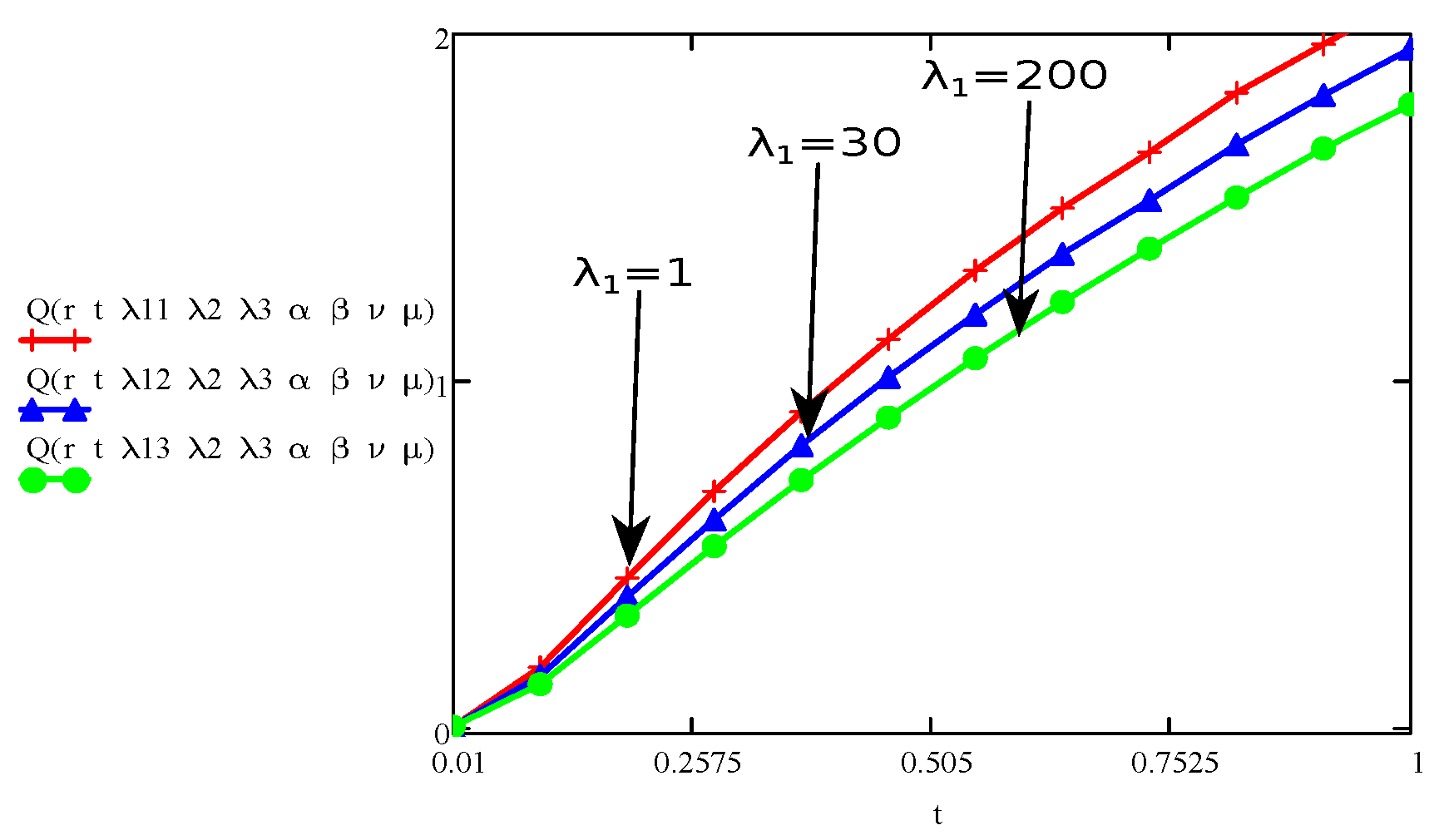
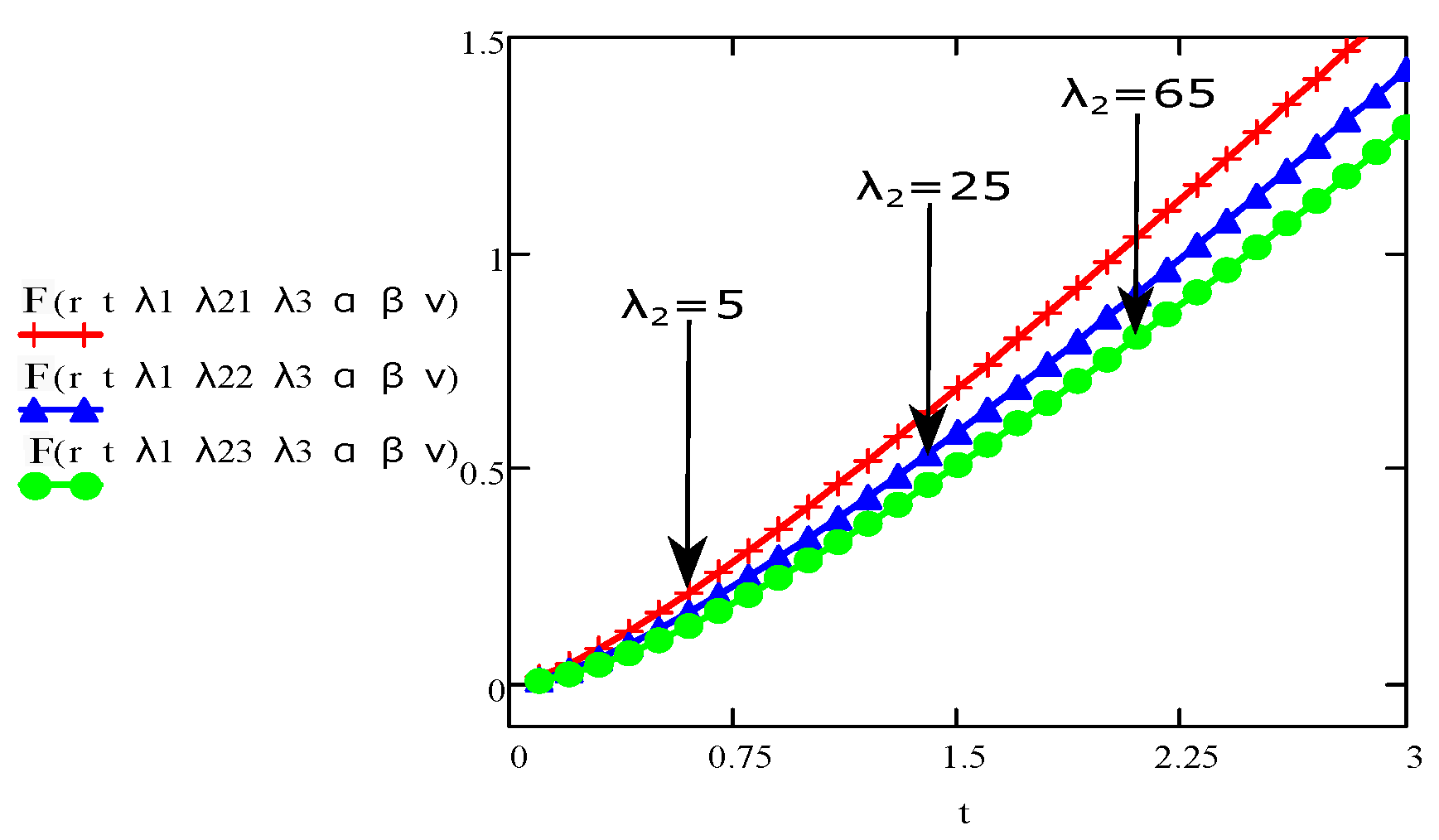
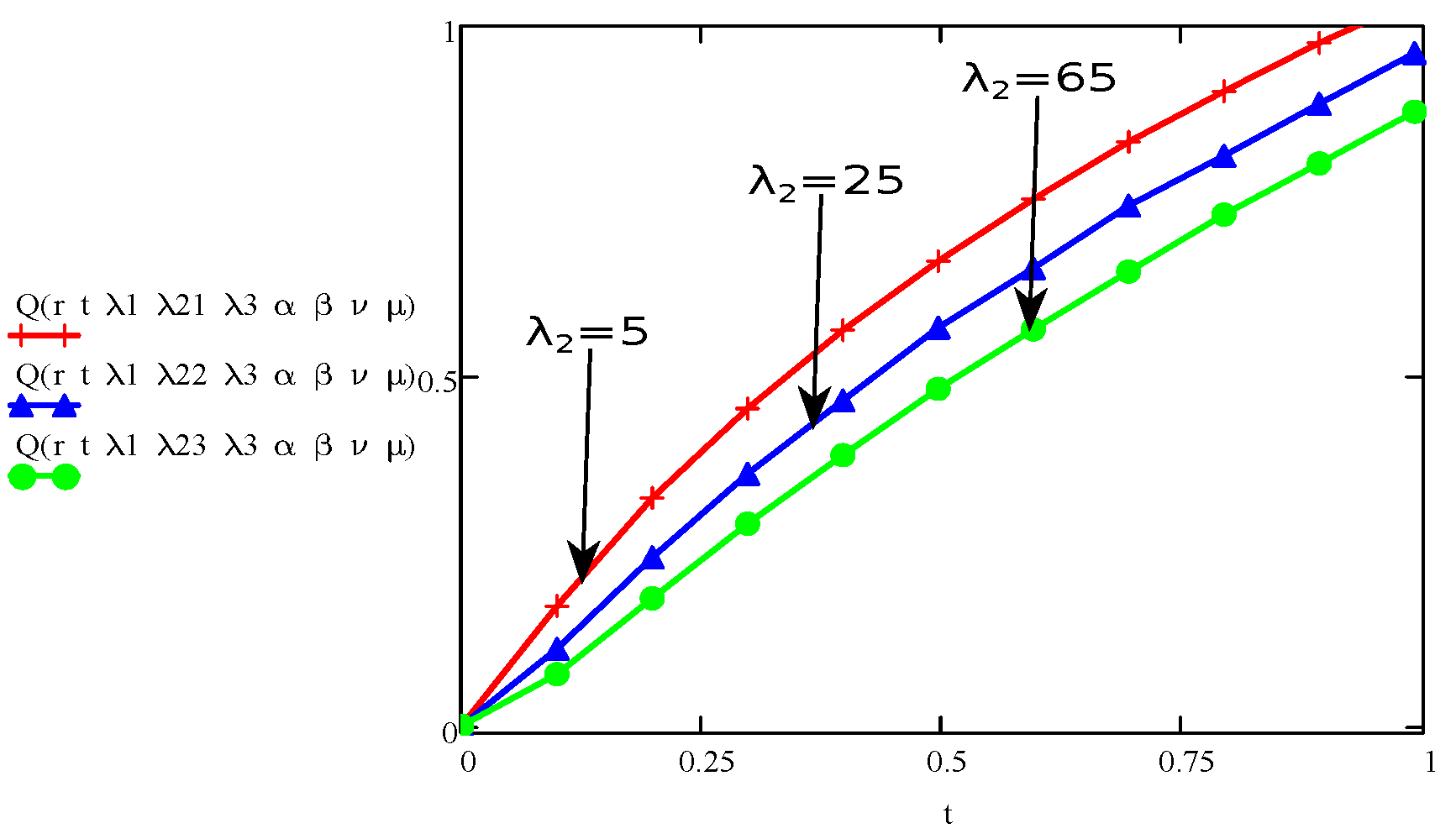
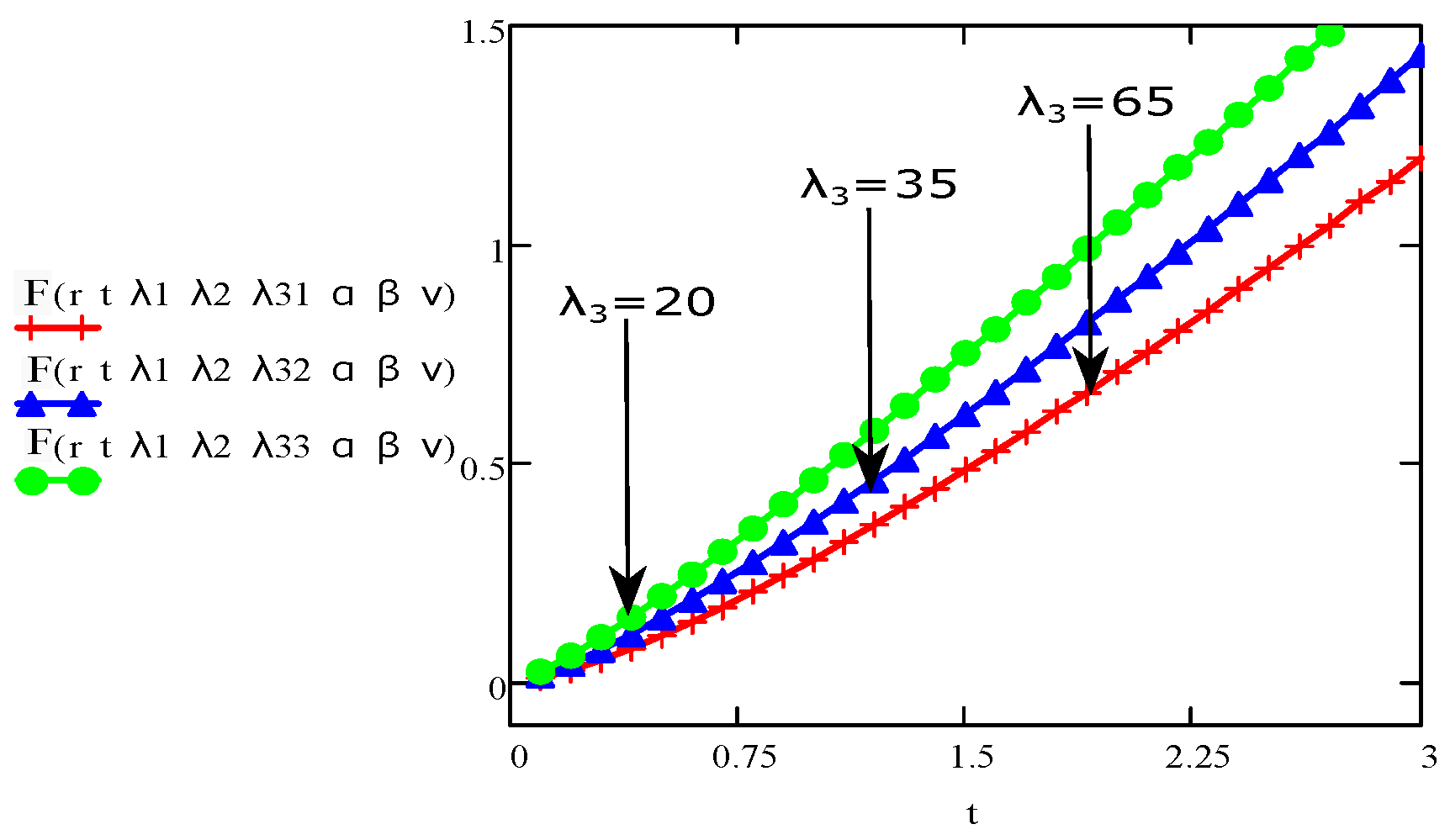
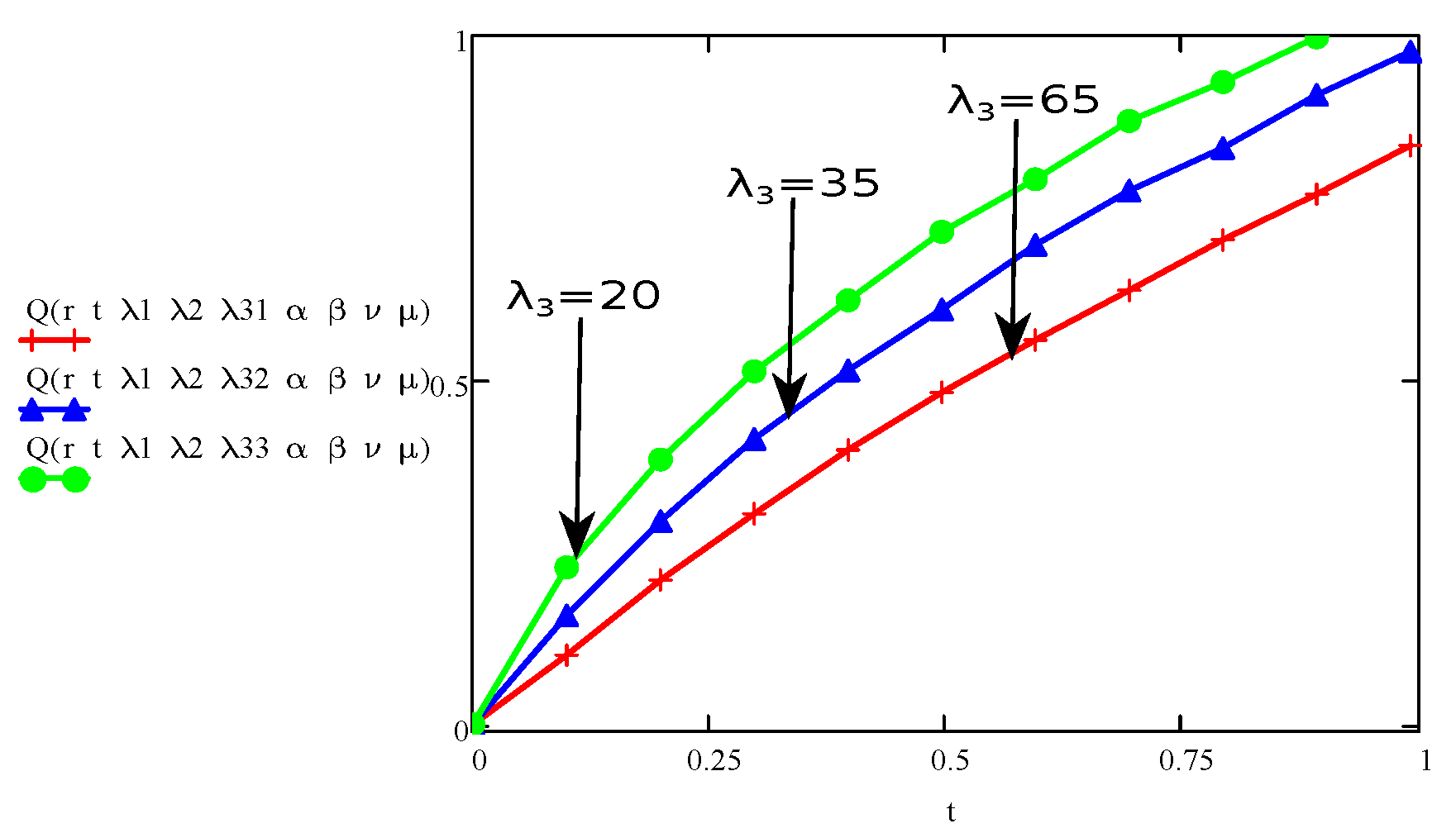
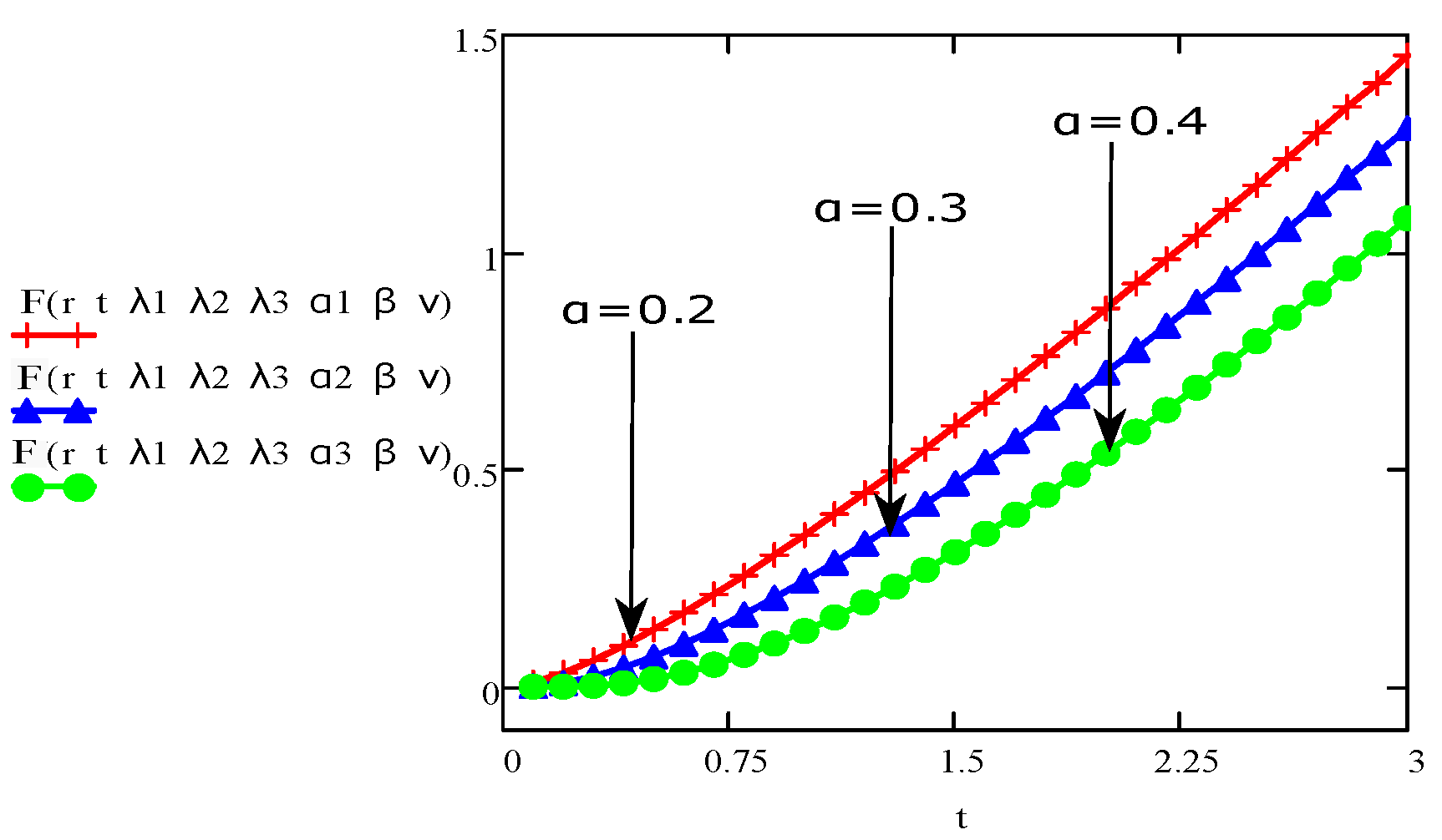
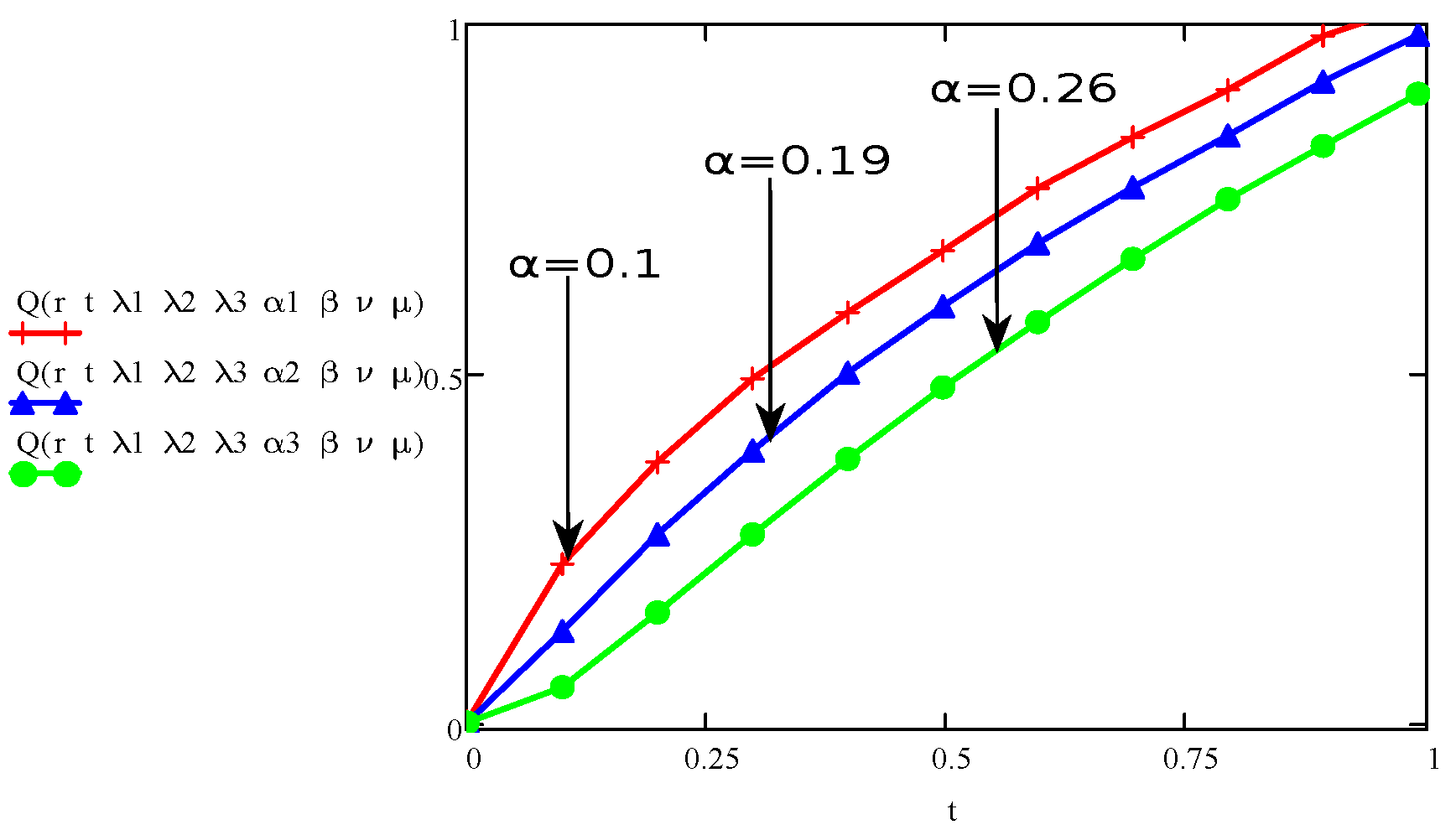
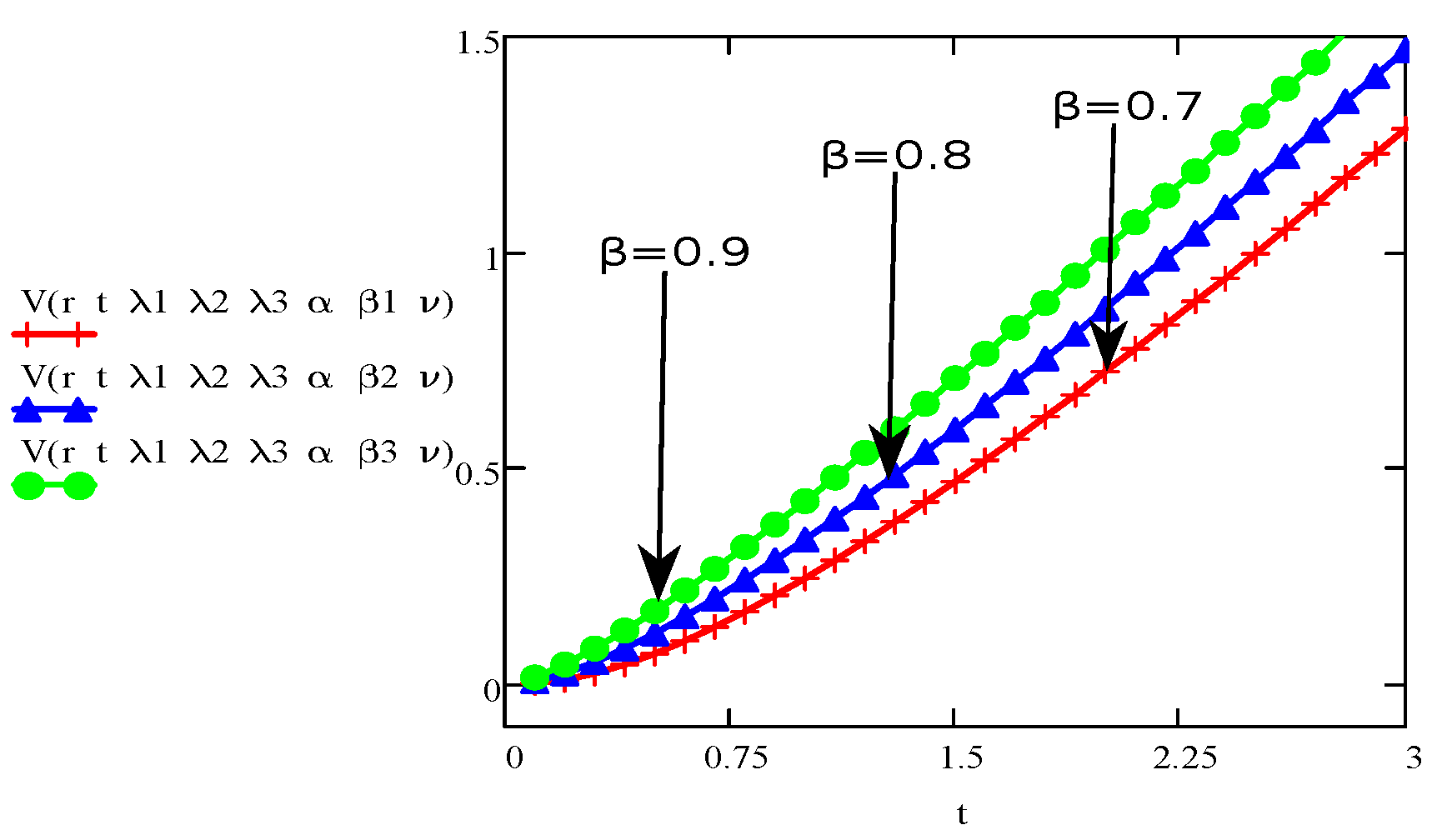
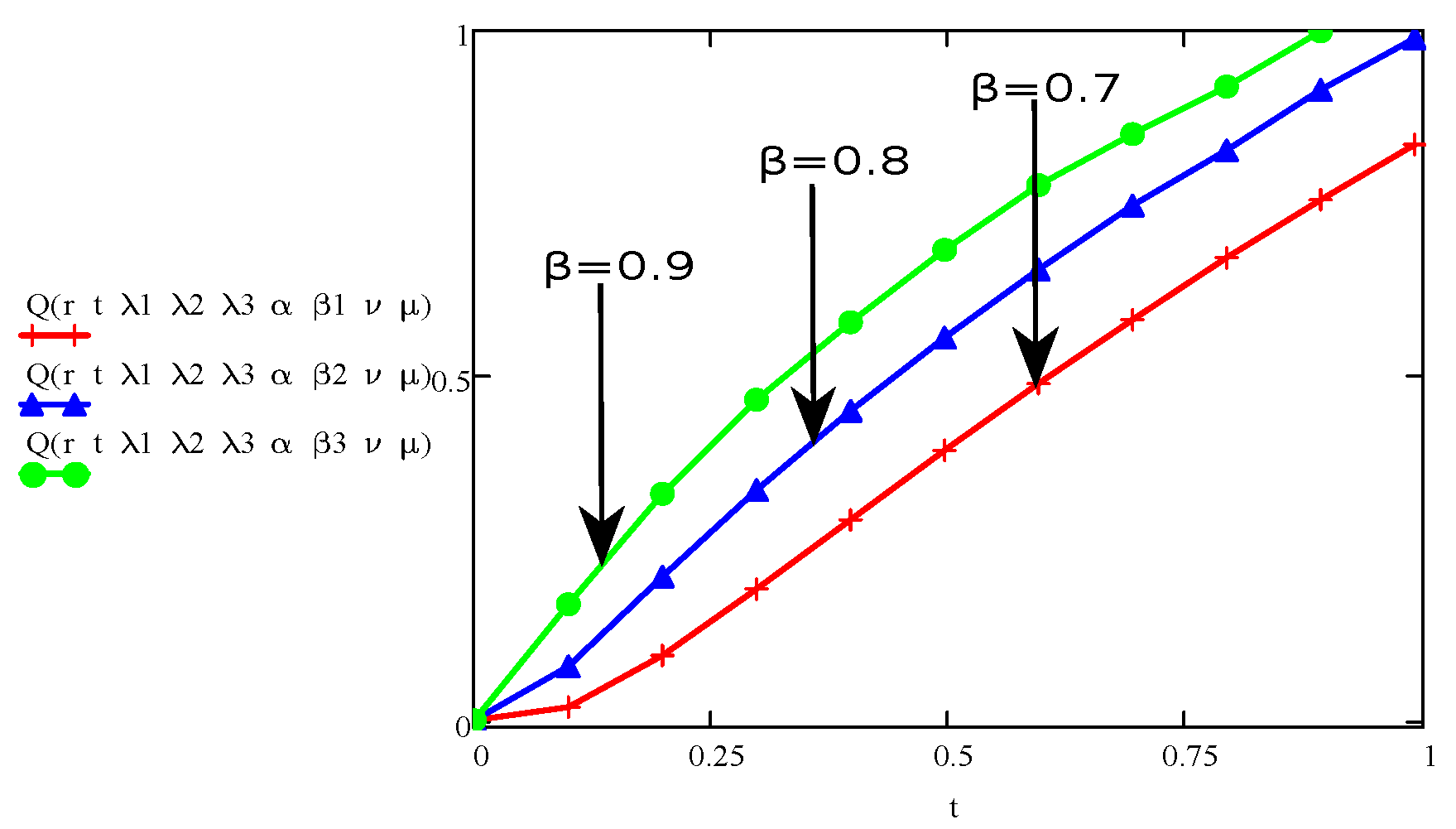
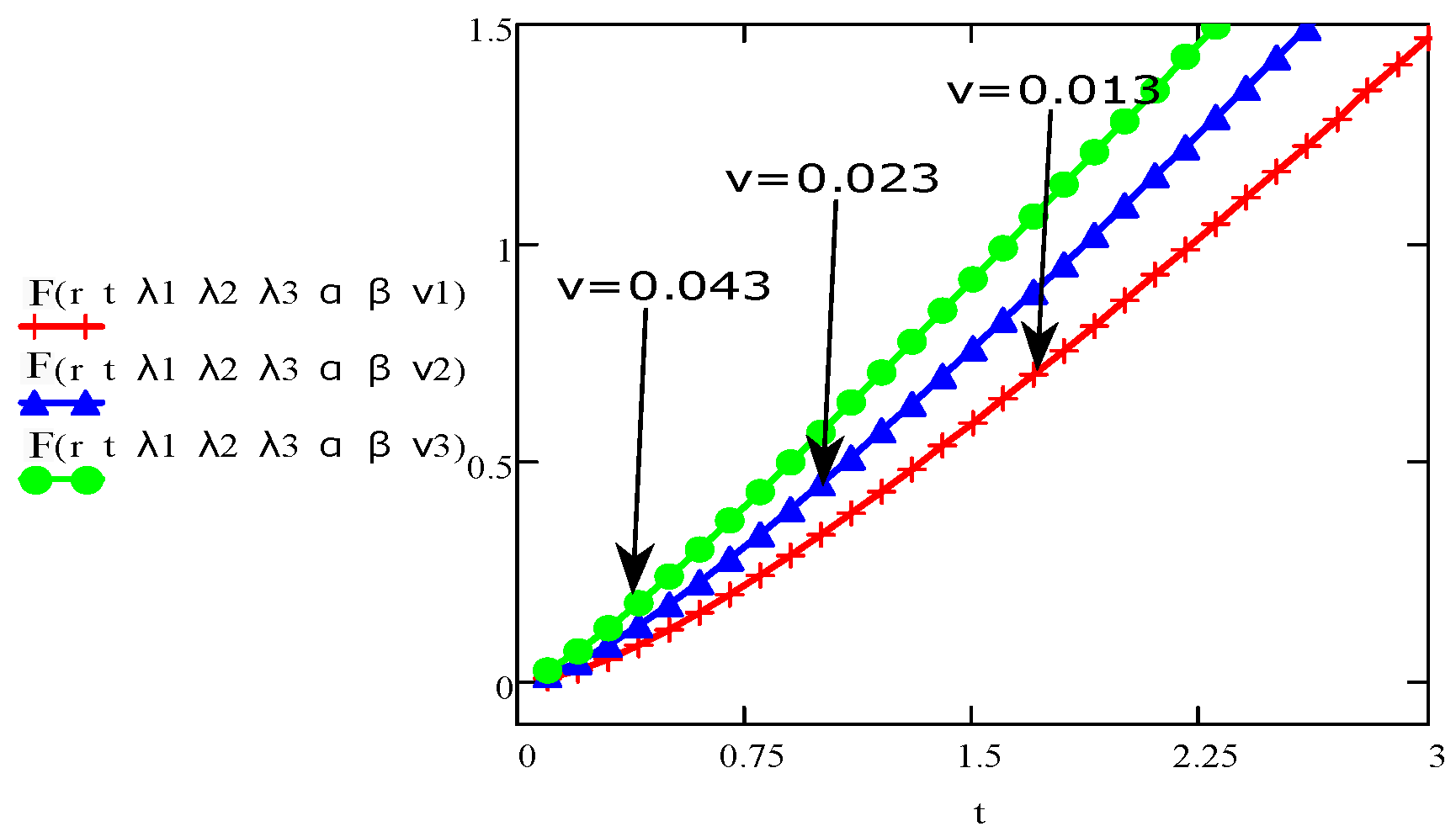
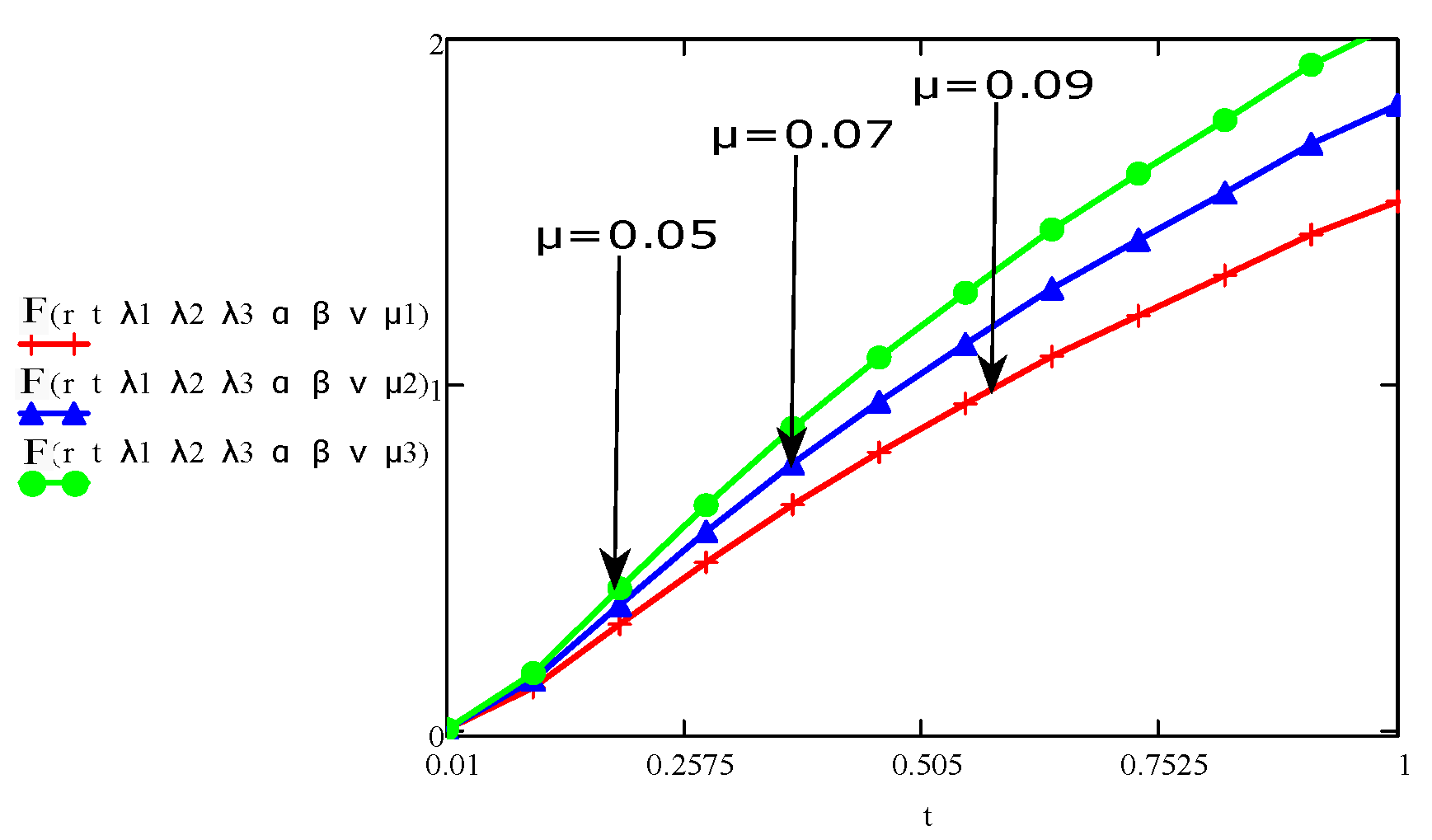
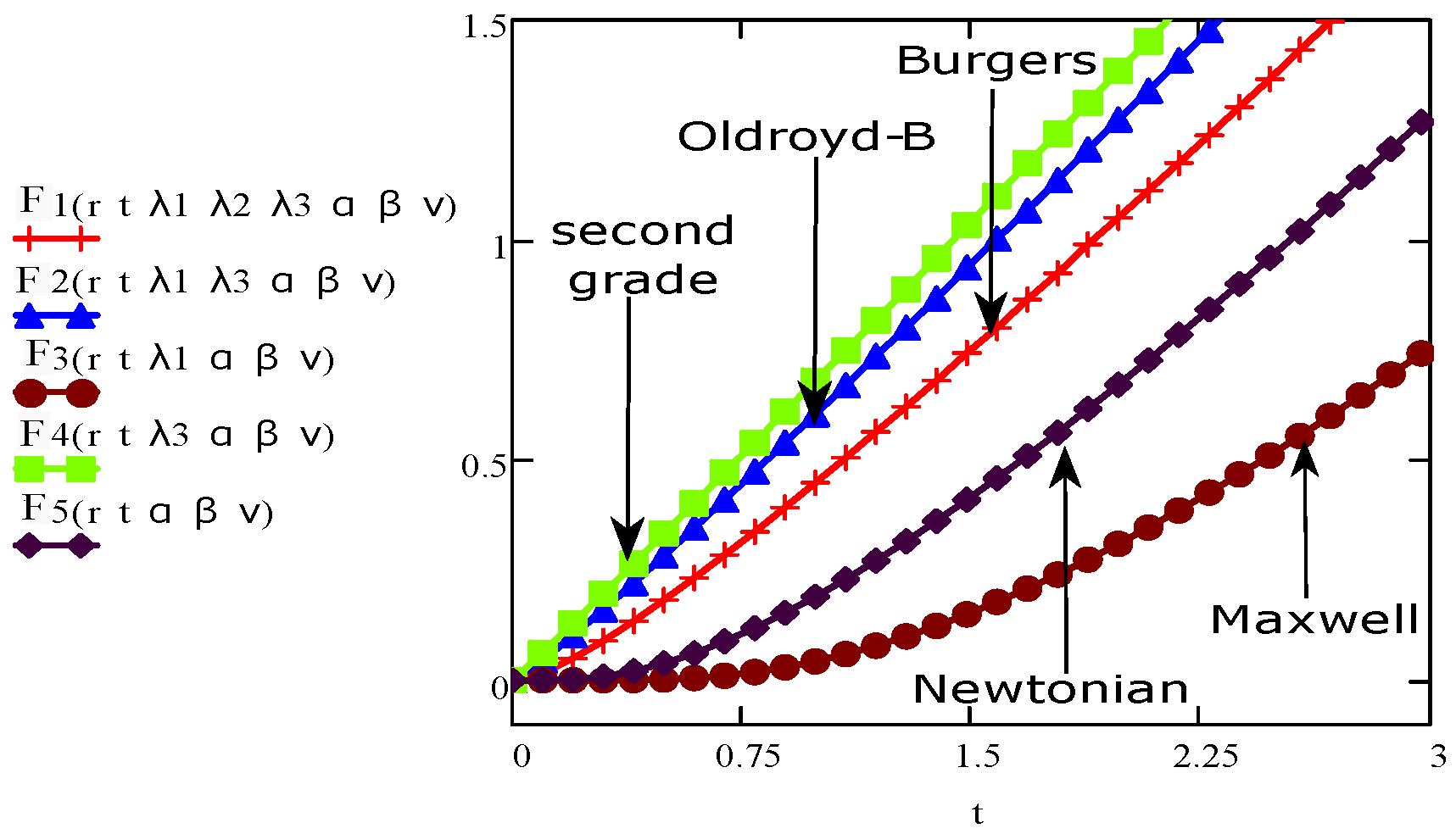
4. Results and Discussions
5. Conclusions
- The ordinary fluid have less velocity as compared to fractional order derivative fluid models. This result can be verify from the graph of fractional parameter available in Figure 12, which has decreasing altitude when the velocity is increasing.
- The velocity of the fluid increases for Burgers’ fluid model as fluid becomes more thick in this model.
- The graph of the parameters , , , t, r, and showed an increase/upward in behaviour with increase in velocity and stress function.
- The parameters , and are behaving opposite to the influence of velocity and shear stress.
- The fractional Burgers’ fluid is flowing faster than the Maxwell and Newtonian fluids.
- In future, authors will try to study the fluid motion by considering the effects of temperature and magnetic field.
Author Contributions
Funding
Conflicts of Interest
References
- Taylor, G.I. Stability of a viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1923, 223, 289–343. [Google Scholar] [CrossRef]
- Childress, S. An Introduction to Theoretical Fluid Mechanics; American Mathematical Society: New York, NY, USA, 2009; Volume 19. [Google Scholar]
- Waters, N.; King, M. The unsteady flow of an elastico-viscous liquid in a straight pipe of circular cross section. J. Phys. D Appl. Phys. 1971, 4, 204–211. [Google Scholar] [CrossRef]
- Rahaman, K.; Ramkissoon, H. Unsteady axial viscoelastic pipe flows. J. Non-Newton. Fluid Mech. 1995, 57, 27–38. [Google Scholar] [CrossRef]
- Wood, W. Transient viscoelastic helical flows in pipes of circular and annular cross-section. J. Non-Newton. Fluid Mech. 2001, 100, 115–126. [Google Scholar] [CrossRef]
- Fox, R.W.; McDonald, A.T. Introduction to Fluid Mechanics; John Wiley & Sons. Inc.: New York, NY, USA, 1994. [Google Scholar]
- Fetecau, C. Analytical solutions for non-Newtonian fluid flows in pipe-like domains. Int. J. Non-Linear Mech. 2004, 39, 225–231. [Google Scholar] [CrossRef]
- Ting, T.W. Certain non-steady flows of second-order fluids. Arch. Ration. Mech. Anal. 1963, 14, 1–26. [Google Scholar] [CrossRef]
- Srivastava, P. Non-steady helical flow of a visco-elastic liquid(Nonsteady helical flow of viscoelastic liquid contained in circular cylinder, noting occurrence of oscillations in fluid decaying exponentially with time). Arch. Mech. Stosow. 1966, 18, 145–150. [Google Scholar]
- Sherief, H.; Faltas, M.; El-Sapa, S. Pipe flow of magneto-micropolar fluids with slip. Can. J. Phys. 2017, 95, 885–893. [Google Scholar] [CrossRef]
- Fetecău, C.; Fetecău, C. On the uniqueness of some helical flows of a second grade fluid. Acta Mech. 1985, 57, 247–252. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.; Ayub, M. Some analytical solutions for second grade fluid flows for cylindrical geometries. Math. Comput. Model. 2006, 43, 16–29. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C.; Vieru, D. On some helical flows of Oldroyd-B fluids. Acta Mech. 2007, 189, 53–63. [Google Scholar] [CrossRef]
- Vieru, D.; Akhtar, W.; Fetecau, C.; Fetecau, C. Starting solutions for the oscillating motion of a Maxwell fluid in cylindrical domains. Meccanica 2007, 42, 573–583. [Google Scholar] [CrossRef]
- Nadeem, S.; Asghar, S.; Hayat, T.; Hussain, M. The Rayleigh Stokes problem for rectangular pipe in Maxwell and second grade fluid. Meccanica 2008, 43, 495–504. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, vol. 198 of Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Friedrich, C. Relaxation and retardation functions of the Maxwell model with fractional derivatives. Rheol. Acta 1991, 30, 151–158. [Google Scholar] [CrossRef]
- Tan, W.; Xian, F.; Wei, L. An exact solution of unsteady Couette flow of generalized second grade fluid. Chin. Sci. Bull. 2002, 47, 1783–1785. [Google Scholar] [CrossRef]
- Tong, D.; Shan, L. Exact solutions for generalized Burgers’ fluid in an annular pipe. Meccanica 2009, 44, 427–431. [Google Scholar] [CrossRef]
- Shah, S.H.A.M. Some helical flows of a Burgers’ fluid with fractional derivative. Meccanica 2010, 45, 143–151. [Google Scholar] [CrossRef]
- Xu, M.; Tan, W. Theoretical analysis of the velocity field, stress field and vortex sheet of generalized second order fluid with fractional anomalous diffusion. Sci. China Ser. A Math. 2001, 44, 1387–1399. [Google Scholar] [CrossRef]
- Song, D.Y.; Jiang, T.Q. Study on the constitutive equation with fractional derivative for the viscoelastic fluids–modified Jeffreys model and its application. Rheol. Acta 1998, 37, 512–517. [Google Scholar] [CrossRef]
- Wenchang, T.; Wenxiao, P.; Mingyu, X. A note on unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates. Int. J. Non-Linear Mech. 2003, 38, 645–650. [Google Scholar] [CrossRef]
- Wenchang, T.; Mingyu, X. Unsteady flows of a generalized second grade fluid with the fractional derivative model between two parallel plates. Acta Mech. Sin. 2004, 20, 471–476. [Google Scholar] [CrossRef]
- Abdullah, M.; Butt, A.R.; Raza, N.; Haque, E.U. Semi-analytical technique for the solution of fractional Maxwell fluid. Can. J. Phys. 2017, 95, 472–478. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Kamran, M.; Imran, M.; Athar, M. Exact solutions for the unsteady rotational flow of an Oldroyd-B fluid with fractional derivatives induced by a circular cylinder. Meccanica 2013, 48, 1215–1226. [Google Scholar] [CrossRef]
- Safdar, R.; Imran, M.; Sadiq, N.; Ahmad, F. Unsteady Rotational Flow of a Burgers’ Fluid through a Pipe with Non-Integer Order Fractional Derivatives. J. Appl. Environ. Biol. Sci 2018, 8, 144–156. [Google Scholar]
- Imran, M.; Athar, M.; Kamran, M. On the unsteady rotational flow of a generalized Maxwell fluid through a circular cylinder. Arch. Appl. Mech. 2011, 81, 1659–1666. [Google Scholar] [CrossRef]
| r | Exact w(r,t) [30] | Numerical V(r,t) | Error |
|---|---|---|---|
| 0 | 0.000 | 0.000 | 0.000 |
| 0.02 | 0.029 | 0.029 | 0.000 |
| 0.04 | 0.058 | 0.058 | 0.000 |
| 0.06 | 0.087 | 0.087 | 0.000 |
| 0.08 | 0.115 | 0.116 | −0.001 |
| 0.10 | 0.145 | 0.145 | 0.000 |
| 0.12 | 0.174 | 0.174 | 0.000 |
| 0.14 | 0.203 | 0.203 | 0.000 |
| 0.16 | 0.233 | 0.233 | 0.000 |
| 0.18 | 0.262 | 0.263 | −0.001 |
| 0.20 | 0.292 | 0.292 | 0.000 |
| 0.22 | 0.322 | 0.322 | 0.000 |
| 0.24 | 0.352 | 0.352 | 0.000 |
| 0.26 | 0.383 | 0.381 | 0.002 |
| 0.28 | 0.414 | 0.411 | 0.003 |
| 0.30 | 0.444 | 0.441 | 0.003 |
| 0.32 | 0.475 | 0.473 | 0.002 |
| 0.34 | 0.506 | 0.503 | 0.003 |
| 0.36 | 0.538 | 0.534 | 0.004 |
| 0.38 | 0.569 | 0.565 | 0.004 |
| 0.40 | 0.601 | 0.596 | 0.005 |
| 0.42 | 0.632 | 0.628 | 0.004 |
| 0.44 | 0.664 | 0.661 | 0.003 |
| 0.46 | 0.695 | 0.694 | 0.001 |
| 0.48 | 0.727 | 0.725 | 0.002 |
| ..... | ..... | ..... | ..... |
| r | Exact w(r,t) [29] | Numerical V(r,t) | Error |
|---|---|---|---|
| 0 | 0.000 | 0.000 | 0.000 |
| 0.02 | 0.023 | 0.023 | 0.000 |
| 0.04 | 0.046 | 0.046 | 0.000 |
| 0.06 | 0.069 | 0.069 | 0.000 |
| 0.08 | 0.093 | 0.092 | 0.001 |
| 0.10 | 0.116 | 0.115 | 0.001 |
| 0.12 | 0.139 | 0.138 | 0.001 |
| 0.14 | 0.162 | 0.161 | 0.001 |
| 0.16 | 0.185 | 0.185 | 0.000 |
| 0.18 | 0.208 | 0.208 | 0.000 |
| 0.20 | 0.232 | 0.232 | 0.000 |
| 0.22 | 0.255 | 0.256 | −0.001 |
| 0.24 | 0.279 | 0.280 | −0.001 |
| 0.26 | 0.304 | 0.304 | 0.000 |
| 0.28 | 0.329 | 0.329 | 0.000 |
| 0.30 | 0.354 | 0.354 | 0.000 |
| 0.32 | 0.379 | 0.379 | 0.000 |
| 0.34 | 0.405 | 0.404 | 0.001 |
| 0.36 | 0.431 | 0.430 | 0.001 |
| 0.38 | 0.458 | 0.456 | 0.002 |
| 0.40 | 0.484 | 0.482 | 0.002 |
| 0.42 | 0.511 | 0.509 | 0.002 |
| 0.44 | 0.538 | 0.536 | 0.002 |
| 0.46 | 0.564 | 0.564 | 0.000 |
| 0.48 | 0.591 | 0.592 | −0.001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imran, M.; Ching, D.L.C.; Safdar, R.; Khan, I.; Imran, M.A.; Nisar, K.S. The Solutions of Non-Integer Order Burgers’ Fluid Flowing through a Round Channel with Semi Analytical Technique. Symmetry 2019, 11, 962. https://doi.org/10.3390/sym11080962
Imran M, Ching DLC, Safdar R, Khan I, Imran MA, Nisar KS. The Solutions of Non-Integer Order Burgers’ Fluid Flowing through a Round Channel with Semi Analytical Technique. Symmetry. 2019; 11(8):962. https://doi.org/10.3390/sym11080962
Chicago/Turabian StyleImran, M., D.L.C. Ching, Rabia Safdar, Ilyas Khan, M. A. Imran, and K. S. Nisar. 2019. "The Solutions of Non-Integer Order Burgers’ Fluid Flowing through a Round Channel with Semi Analytical Technique" Symmetry 11, no. 8: 962. https://doi.org/10.3390/sym11080962
APA StyleImran, M., Ching, D. L. C., Safdar, R., Khan, I., Imran, M. A., & Nisar, K. S. (2019). The Solutions of Non-Integer Order Burgers’ Fluid Flowing through a Round Channel with Semi Analytical Technique. Symmetry, 11(8), 962. https://doi.org/10.3390/sym11080962





