Abstract
The basic motivation of this investigation is to develop an innovative mathematical model for electro-osmotic flow of Couette–Poiseuille nanofluids. The power-law model is treated as the base fluid suspended with nano-sized particles of aluminum oxide (Al2O3). The uniform speed of the upper wall in the axial path generates flow, whereas the lower wall is kept fixed. An analytic solution for nonlinear flow dynamics is obtained. The ramifications of entropy generation, magnetic field, and a constant pressure gradient are appraised. Moreover, the physical features of most noteworthy substantial factors such as the electro-osmotic parameter, magnetic parameter, power law fluid parameter, skin friction, Nusselt number, Brinkman number, volume fraction, and concentration are adequately delineated through various graphs and tables. The convergence analysis of the obtained solutions has been discussed explicitly. Recurrence formulae in each case are also presented.
1. Introduction
Conventional fluids like glycol, acetone, kerosene and water have low heat transfer characteristics and play an important role in laboratories and industrial engineering applications. Several experiments and procedures have been demonstrated to improve heat transfer characteristics. A significant contribution of boosting the heat transfer ability of fluids in an industrial process by the insertion of nanoparticles into the fluids was found. The pioneering work of Choi [1] led to the discovery that heat transfer rate and higher thermal conductivity can be enriched by a combination of base fluids and nanoparticles. Later, Xuan [2] experimentally investigated the enrichment of thermal conductivity in nanofluids. Some core developments have been collated in references [3,4,5,6,7,8,9].
Further, power-law fluids have attracted the attention of many scientists as the description of power-law fluids happens to be the best description of fluid behavior (with right choice of power-law index) of shear-dependent fluids. There are several more models that better describe the range of shear rates, but they do so at the cost of simplicity. For this reason, the power law is used to describe fluid behavior as compared to other fluid models. Recently, Ouyang et al. [10] proposed a two-dimensional squirmer model for power law fluids. They concluded that the selection of power law relation is the best choice to demonstrate the rheological properties of three sorts of fluids, namely: (i) Newtonian, (ii) shear-thickening, and (iii) shear-thinning fluids. Also, the exact velocity at the bottom region of shear rate cannot augur the basis of the power law model. After overcoming the insufficiency of power law, it cannot be used to find the exact velocity profile for the shear rate of the bottom and zero regions [11]. Also, power law fluid in some cases is used to describe non-Newtonian fluids [12,13]
Electro-osmotic flow, also known as electro-osmosis flow, is used in microfluidic devices and electronically controlled fluid flow or any other fluid conduit. Zhao et al. [14] have invoked electro-osmotic flow in a channel with the power law model. Das and Chakraborty [15] investigated the impact of non-Newtonian fluid on electro-osmotic flow. Several attempts regarding electro-osmosis flow can be found in references [16,17,18,19].
It is well known that magnetic fluids have significant utilization in applications such as heat transfer, cancer therapy, opto-electronic devices, sensors, cooling of nuclear reactors, liquid metal flow control, high temperature plasmas, solidification of binary alloys, drying processes etc. [20,21,22,23,24,25]. In addition, a number of researchers have conducted promising investigations on nanoparticles. Examples include the work of Malvandi et al. [26] who have studied MHD mixed convection with nanoparticle migration and Yousif et al. [27] who publicized magnetohydrodynamics (MHD) Carreau nanofluids with internal heat source/sink radiation. Further, magnetic nanofluids also exhibit interesting properties that are used in various microfluidic applications, dipolar nanoparticles, magnetic fluid hyperthermia and magnetic resonance imaging [28,29,30,31]. The existing literature bears witness that magnetic fluids with nanoparticles exhibit several interesting structural characteristics depending on the applied magnetic field strength. As a result, several studies have also been undertaken on MHD rheological fluids [32,33,34].
In recent years, prominent authors have been inspired to study entropy generation by various applications, such as diffusion and Joule heating. Entropy is caused by irreversible processes of a system and can be reduced only when it interacts with some other system whose entropy increases in the process. Bejan [35] studied the entropy generation for a flow system and discussed the main ideas to control the energy loss in flow problems and enhanced the ability of the system. Zeeshan et al. [36] discussed the radiative and electro-magnetohydrodynamic effects of a titanium dioxide/water based nanofluid on entropy generation. Ranjit and Shit [37] presented the effects of entropy generation with MHD on electro-osmotic flow. Numerical analysis for entropy generation on nanofluids with the suspension of nanoparticles (such as copper, Al2O3 and TiO3) in water as a base fluid, which passes through wavy walls, was conducted by Cho et al. [38]. Different researchers have devoted their efforts to explore the impact of entropy generation to real world problems [39,40,41,42,43].
Thus far, the simultaneous effects of entropy generation, MHD and electro-osmosis on power law nanofluid flow has not been studied. In order to fill this gap, the next section is devoted to developing a mathematical formulation of the problem, which comprises mass, momentum, and energy equations. The situation becomes difficult as the resulting equations are not only nonlinear, but also coupled. The analytical findings are developed by a homotopic tactic [44] that has been used effectively for the last two decades [45,46,47,48,49,50].
The acquired results satisfied the governing equations and boundary conditions. The physical features involve parameters which are adequately determined through various graphs and tables.
2. Problem Design
2.1. Physical Considerations
Incompressible and steady nanofluids pass through horizontal parallel plates as illustrated in Figure 1. The wall at moves with constant velocity while the second wall remains stationary at is uniform transverse magnetic field, is zeta potential at lower wall, is zeta potential at upper wall, is electric double layer potential and is the total width of the channel.

Figure 1.
Schematic representation of electro-osmotic flow of the physical problem.
2.2. Electrical Potential Distribution
During the process of electro-osmotic flow (EOF), the separation of ions takes place and an electrical double layer (EDL) forms adjacent to the channel walls, thereby developing electric potential distribution. The electric potential within the channel, described by the Poisson–Boltzmann equation [51] in the Cartesian co-ordinate system, can be calculated as:
For small values of electrical potential of the EDL, the Debye–Hückel approximation can be applied and Equation (1) becomes:
The plates of the channel are made of different materials and have different zeta potentials.
The electrical potential under the action of Equation (3) can be explored as:
The electric double layer effects are produced by the external field relation and charge density of nanoparticles. The external electric force , also called the electro-kinetic force [52,53], is generated outside of the charge particle. Along with , electric charge density is defined as:
where , , , , , and are the relative permittivity of the medium, Debye parameter, ion density of bulk liquid, valence of ions, electron charge, Boltzmann constant and absolute temperature, respectively.
2.3. Power Law Model
In the current study, the following power law fluid model [54] is used:
where is shear stresses, is the power-law or flow behavior index of the fluid and is the viscosity of the nanofluid [55] and is defined along the consistency index as:
and the viscosity of the base fluid in the current discussion is taken as:
One signifies a Newtonian fluid for whereas and respectively denote the shear-thinning and shear-thickening of fluids.
To estimate the shear stresses of a fluid, we will illustrate further investigations with shear-thinning properties. Thus, shear stress for the non-Newtonian power-law model can be written as:
2.4. Governing Equations
The electro-osmotic flow occurs in the channel due to the movement of an upper wall, whereas the flow around the channel of the walls is generated because of an applied electric field. The governing equations for the current flow phenomenon are:
where , and correspondingly represent velocity, temperature and viscous dissipation. The body force contains magnetic, electrical and buoyancy effects.
and
Under the application of Lorentz force, it produces the following Joules heating effects.
The governing Equations (10) and (12) in components form after omitting the axial heat conductions at the walls and in the fluid [54] and become:
The associated boundary conditions are:
The effective density, heat capability, and thermal and electrical conductivities of a nanofluid [55] are respectively given by:
The following dimensionless transformations
Transform Equations (16) and (17) by using (23) in the dimensionless form as:
In which
where is the electro-osmotic parameter, is density, is dynamic viscosity, is volumetric volume expansion, is Grashof number and is specific heat. Assume that is the maximum velocity between two plates, and is the ratio between electro-osmotic velocity and maximum velocity of the fluid. Thermophysical properties of alumina and the base fluid polyvinyl chloride (PVC) are illustrated below in Table 1.

Table 1.
Physical properties of PVC [56] and Al2O3 [52].
2.5. Thermophysical Relations
Skin friction is defined as:
Moreover, in the present study, different concentration of alumina particles (Al2O3) are used in the polymer solution of polyvinyl alcohol in water; consequently, different values of in correlation with nanoparticle volume fraction for different concentrations of polyvinyl alcohol are listed in Table 2.

Table 2.
Properties of the power-law equation and PVC solutions [56].
Hence, the coefficient of skin friction in the dimensionless form for both walls is:
2.6. Heat Transfer Rate
The Nusselt number is defined as:
Here, is heat transfer coefficient, is wall heat flux and is bulk mean temperature, which is given by:
The mean temperature in the dimensionless form becomes:
Therefore, the Nusselt number is:
2.7. Entropy Generation
The entropy generation of local volumetric rate can be defined as:
The characteristic entropy generation can be expressed as:
By using the transformation given in Equation (23), the non-dimensional total entropy generation may be expressed as:
where , and are respectively the magnetic field, Brinkman number, volumetric volume expansion, dimensional electric charge density, and dimensionless temperature difference. These parameters are defined as:
3. Discussion of Results
3.1. Analytic Solution
In this section, we intend to find the analytical solutions by means of the homotopy analysis method [57]. We chose the initial guesses , and linear operators , [58] as:
The deformation equations of homotopy for the zeroth-order are established as:
The nonlinear operators , are can be written as:
The solution for velocity and temperature up to -order approximation can be expressed as:
The best solutions for solving coupled differential equation can be presented as below at 20th order approximations:
The constants to and to are specified in Appendix A.
3.2. Convergence Inspection
As pointed out by Liao [59], the convergence of homotopic results can be controlled by the auxiliary parameters and . In Figure 2 and Figure 3, it is observed that the minimum error for the velocity and temperature profiles can be achieved at and .
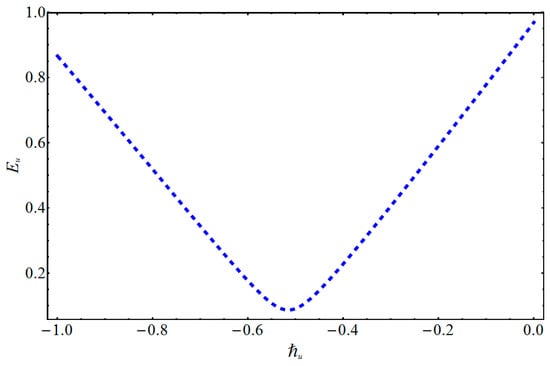
Figure 2.
Graph of residual error for .
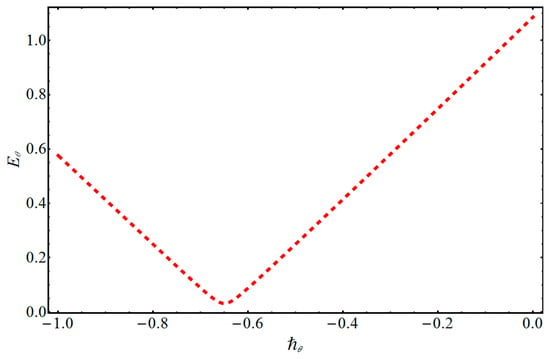
Figure 3.
Graph of residual error for .
In addition, the residual error norms have been utilized to further ensure the accuracy of the obtained series solutions. The residual errors of the velocity and temperature profiles for two succeeding approximations of temperature and velocity up to the 20th order iteration as given in Table 3 can be obtained by the following expressions:

Table 3.
Residual error of series solutions when , , , , and .
3.3. Graphical Illustration
The current research is about flow and entropy on a magnetized power law nanofluid along the horizontal walls. The effects of the nanofluid can be determined at the same pressure with the electric body force and the motion of the upper plate. Flow and entropy generation on the magnetized power law of a nanofluid in the horizontal channel are studied systematically. The lower wall is heated, and the upper wall maintains the temperature. The influence of different important parameters such as Grashof number, electro-osmosis, Reynolds number, magnetic field, Brinkman number, entropy generation, nanoparticle volume fraction and Bejan number on temperature and velocity distributions were illustrated graphically in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23. By using different parameters, we get different results which can be explained as , , , , , , , and .
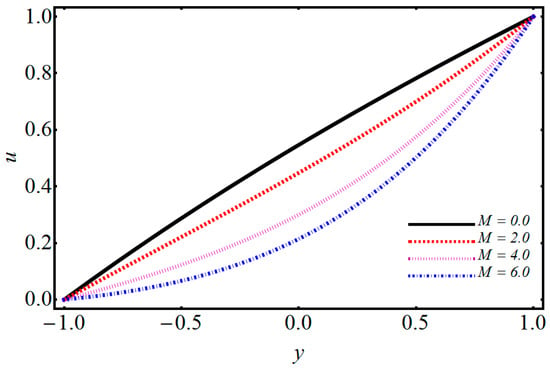
Figure 4.
Performance of M on velocity.
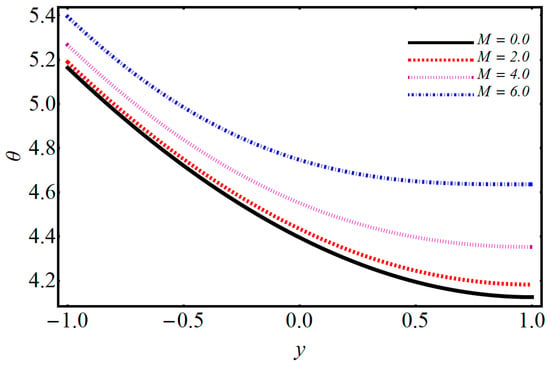
Figure 5.
Performance of M on temperature.
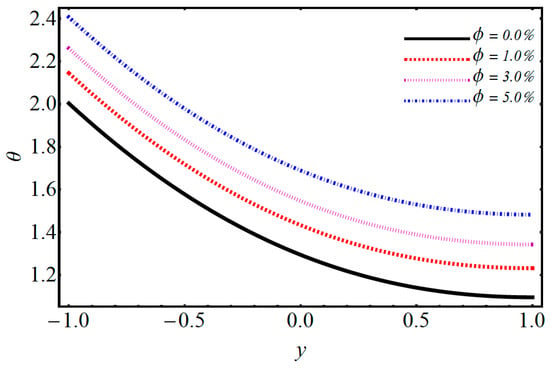
Figure 6.
Performance of on temperature.
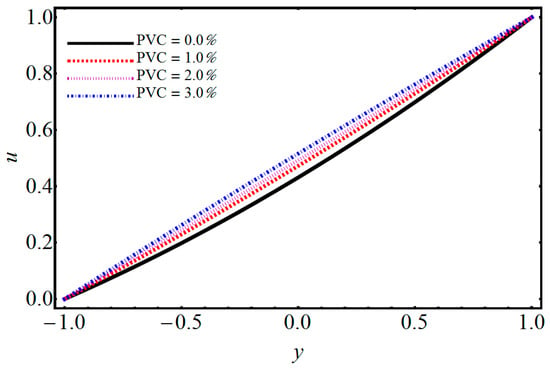
Figure 7.
Performance of PVC concentration on velocity.
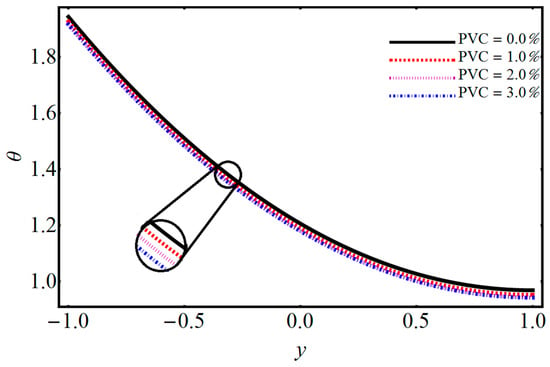
Figure 8.
Performance of PVC concentration on temperature.
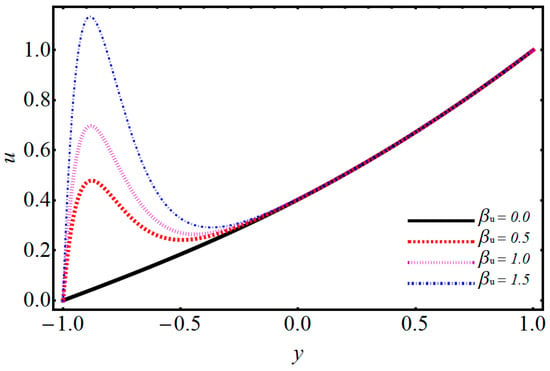
Figure 9.
Performance of on velocity.
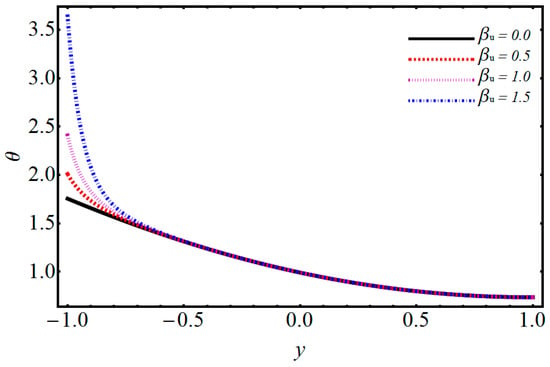
Figure 10.
Performance of on temperature.
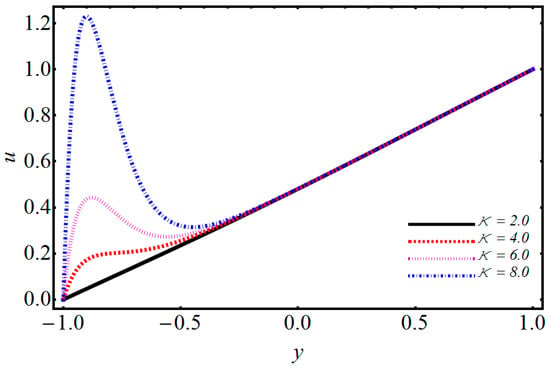
Figure 11.
Effect of the electro-osmotic parameter on velocity.
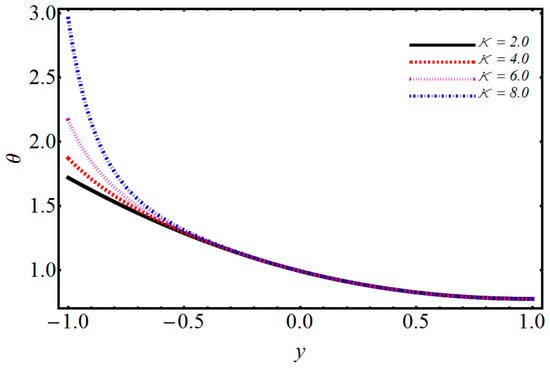
Figure 12.
Performance of the electro-osmotic parameter on temperature.
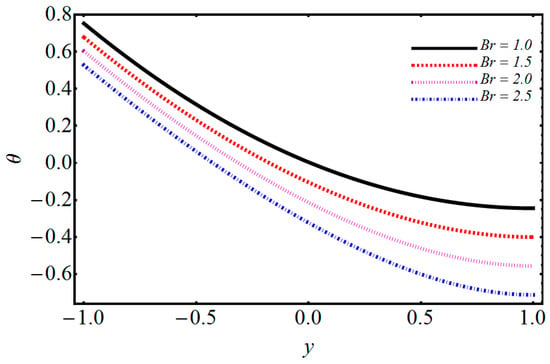
Figure 13.
Performance of Brinkman number on temperature.
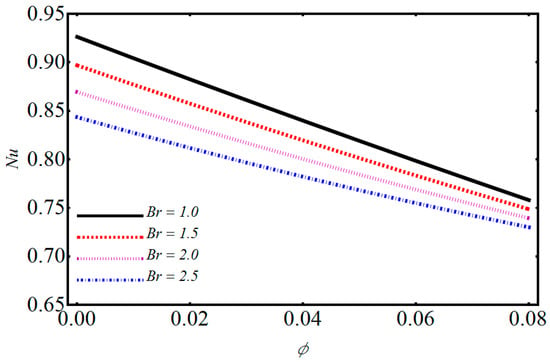
Figure 14.
Performance of w.r.t on Nusselt number.
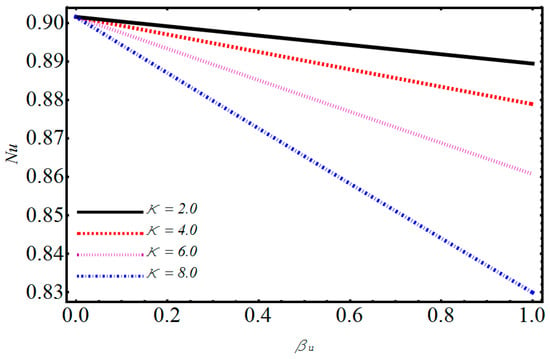
Figure 15.
Performance of w.r.t on Nusselt number.
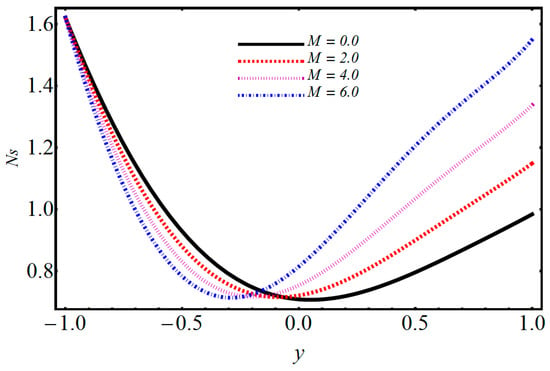
Figure 16.
Performance of the magnetic parameter on entropy generation.
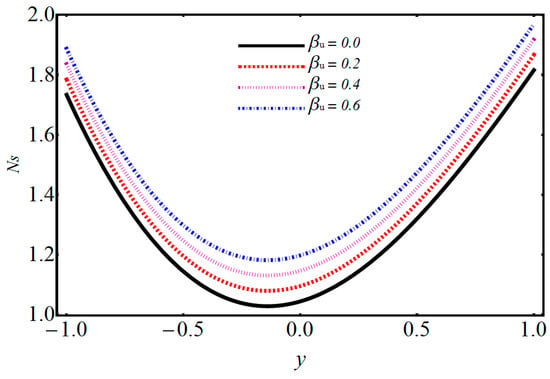
Figure 17.
Performance of β for various values on entropy generation.
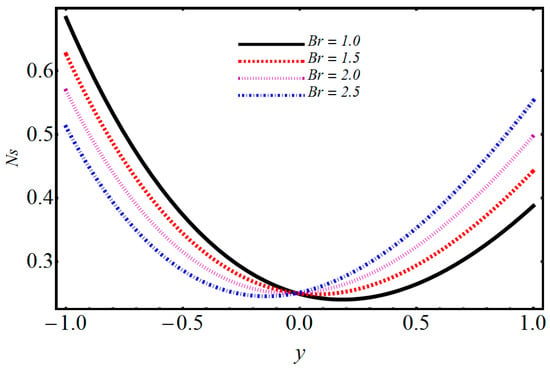
Figure 18.
Performance of Brinkman number on entropy generation.
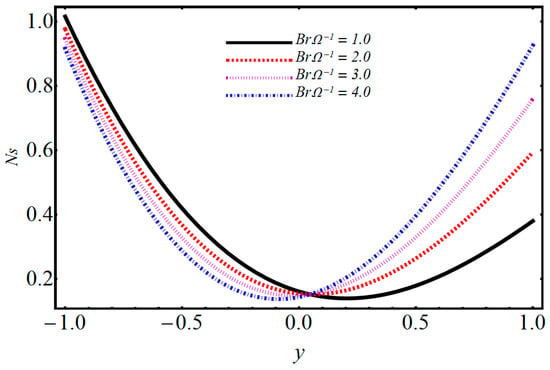
Figure 19.
Performance of on entropy generation.
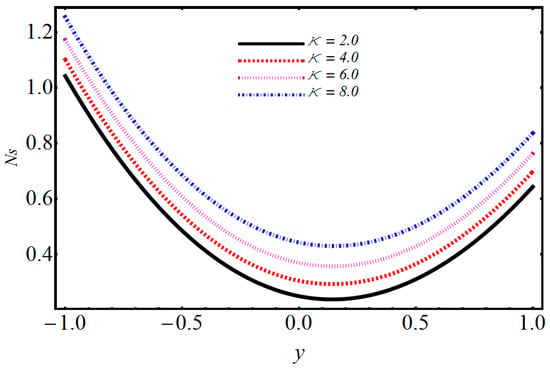
Figure 20.
Performance of on entropy generation.
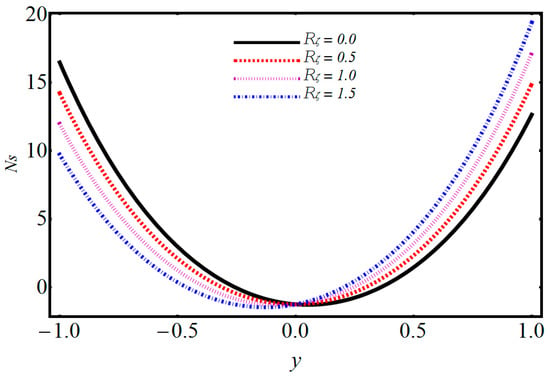
Figure 21.
Performance of on entropy generation.
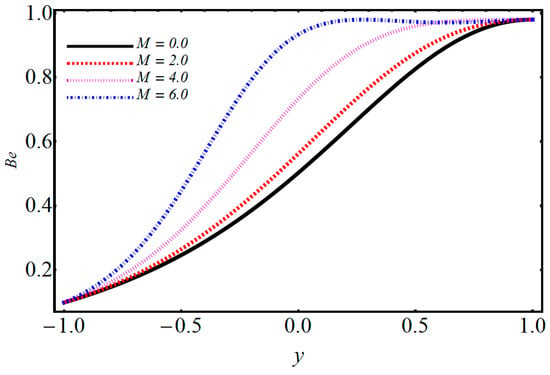
Figure 22.
Performance of the magnetic parameter on Bejan number.
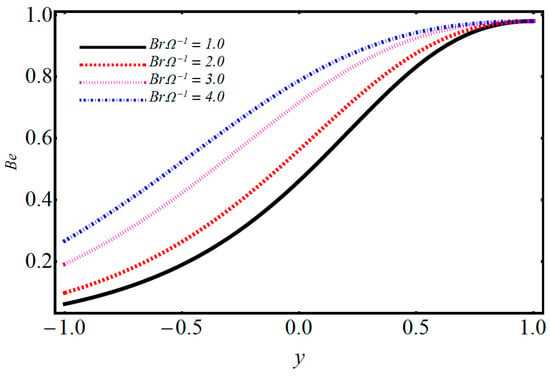
Figure 23.
Performance of on Bejan number.
The impact of on temperature and velocity is demonstrated in Figure 4 and Figure 5. They show that when the magnetic parameter increases, the velocity profile decreases while the temperature profile increases. When one applies a magnetic field on electrically treated nanofluid, then it produces a force opposite to the flow direction. Consequently, the Lorentz force increases the magnetic parameter which opposes the fluid flow, and due to that, the velocity distribution decreases and the temperature distribution upsurges. The effects of volume fraction on temperature are depicted in Figure 6. The temperature profile increases by increasing the volume fraction. Various concentrations of polyvinylchloride (PVC) on temperature and velocity are illustrated in Figure 7 and Figure 8. From Figure 7, it is observed that the velocity distribution rises with the increase of PVC. The temperature for various values of PVC are portrayed in Figure 8. It can be seen that temperature is a decreasing function between the channel. Figure 9 shows the effect of on velocity profile. can be expressed as the ratio of and of a nanofluid. Figure 9 shows that flow of a channel exceeds and gains its high value. Figure 10 reveals a minute change for increasing values of the electro-osmotic parameter for velocity and temperature. The effects of the electro-osmotic value of on temperature and velocity profile are shown in Figure 11 and Figure 12. It can be seen from Figure 11 that by increasing , the velocity profile increases. This is due to a larger value of for the velocity profiles that display EDL layers. The effect of electro-osmotic on temperature is illustrated in Figure 12, which gives the deficiency of the Joule effect. It is also noted that if the pseudo-plastic increases in electro-osmotic parameter , it results in a notable increase in temperature. The effect of on temperature is shown in Figure 13. It is perceived that by increasing , the temperature decreases, from which we conclude that increases as compared to bulk mean temperature. The effect of Brinkman number with respect to volume friction is expressed in Figure 14. It is perceived that for a developing Brinkman number with respect to volume fraction, the Nusselt number increases. Results indicate that temperature increases for higher values of nanoparticle volume fraction. The influence of and of nanofluid and on the Nusselt number are shown in Figure 15. It is seen that near the heated wall, the Nusselt number reduces; this is because first heat is moved to the fluid and then transferred into a separated plate.
The entropy generation profiles for various important parameters such as volumetric volume expansion , magnetic field , dimensionless temperature parameter , and Brinkman number are illustrated in Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. The impact of on entropy generation is displayed in Figure 16. It can be observed that when M increases, the entropy generation decreases on the left side with minimum energy loss at ; after this, increasing behavior is detected. The effect of on entropy generation is depicted in Figure 17, where it can be observed that when is increasing, the entropy generation is also increased. The energy loss on the upper wall is comparatively greater when compared to the lower wall. The significance of on entropy generation in Figure 18 shows that when increases, entropy generation decreases on the left side and has minimum energy loss at y = 0; after this, an increasing trend on the left side is seen. The influence of on entropy generation is given in Figure 19 and it is observed that entropy generation decreases on the lower wall and has minimum energy loss at . Figure 20 shows that when the electro-osmotic parameter increases, entropy generation also increases. From Figure 21, it is observed that when increases, the entropy generation at the lower wall decreases, but after , it increases at the upper wall. Figure 22 shows that when the magnetic parameter increases, Bejan number also increases. It is observed that there is a dominant effect on the lower as well as the upper wall. Figure 23 shows that when increases, the Bejan number also increases. It is noted that the Bejan number shows a dominant role on the upper wall.
The impact of the different parameters on skin friction such as the electro-osmotic parameter, the ratio between and , volume concentration, Brinkman number, and magnetic field are given in Table 4. It is found that by increasing the Brinkman number and the magnetic parameter, the skin friction decreases.

Table 4.
Coefficient of skin friction with , and along .
4. Conclusions
In this work, the effects of entropy generation on power law nanofluid through a horizontal channel in a way that one wall is movable and the other is stationary are presented. The impact of a mixed convection magnetic field and an electrical double layer has combined for momentum conduct. Flow is produced in an axial direction by the movement of the upper wall. The important findings are:
- When the magnetic parameter and nanoparticle volume fraction are increased, then the velocity of the nanofluid decreases whereas the temperature profile is increased.
- Velocity profile is increased for increasing PVC while a decrease in temperature is detected.
- Temperature and velocity demonstrate similar behavior for increasing values of and the ratio between and .
- It is observed that increases at the heated wall against higher Brinkman number and volume fraction while the reverse behavior is noted for the increasing ratio between and . The same phenomena are observed for the cases of electro-osmotic and magnetic factors.
- Skin friction is improved with increasing values of and the ratio between and , whereas it decreases with the increase in Brinkman number, volume fraction and the magnetic parameter.
- The Nusselt number escalates for a snowballing magnetic parameter but de-escalates with the increasing ratio between and , volume fraction, Brinkman number and electro-osmotic factors.
- The entropy generation increases with an increase of volumetric volume expansion , magnetic field and , while it decreases with an increase of and Brinkman number.
- A dual behavior of entropy generation is noted for decreasing and increasing values of .
- The Bejan number escalates by snowballing values of both and magnetic elements in direct relation with each other and is depicted for both of them.
Author Contributions
Conceptualization, R.E.; Writing—Review and Editing, S.M.S.; Methodology, N.S.; Investigation, N.M.
Funding
This research received no external funding.
Acknowledgments
R. Ellahi gratefully thanks to Research Institute, King Fahd University of Petroleum & Minerals, Dhahran, Saudi Arabia to honor him with the Chair Professor at KFUPM.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, San Francisco, CA, USA, 12–17 November 1995; Volume 231, pp. 99–105. [Google Scholar]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Karimipour, A.; Orazio, A.D.; Shadloo, M.S. The effects of different nano particles of Al2O3 and Ag on the MHD nanofluid flow and heat transfer in a microchannel including slip velocity and temperature jump. Physica E 2017, 86, 146–153. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Asadollahi, A. Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy. Symmetry 2019, 11, 276. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Kimiaeifar, A. Application of homotopy perturbation method to find an analytical solution for magnetohydrodynamic flows of viscoelastic fluids in converging/diverging channels. Proc. Mech. Eng. Part C J. Mech. Eng. 2011, 225, 347–353. [Google Scholar] [CrossRef]
- Safaei, M.R.; Ahmadi, G.; Goodarzi, M.S.; Shadloo, M.S.; Goshayeshi, H.R.; Dahari, M. Heat transfer and pressure drop in fully developed turbulent flows of graphene nanoplatelets–silver/water nanofluids. Fluids 2016, 1, 20. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nasiri, M.; Shadloo, M.S.; Yang, Z. Entropy generation in a circular tube heat exchanger using nanofluids: Effects of different modeling approaches. Heat Transf. Eng. 2017, 38, 853–866. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Safaei, M.R.; Goodarzi, M.; Alrashed, A.A.; Nguyen, T.K. New temperature, interfacial shell dependent dimensionless model for thermal conductivity of nanofluids. Int. J. Heat Mass Transf. 2017, 114, 207–210. [Google Scholar] [CrossRef]
- Hassan, M.; Marin, M.; Alsharif, A.; Ellahi, R. Convective heat transfer flow of nanofluid in a porous medium over wavy surface. Phys. Lett. A 2018, 382, 2749–2753. [Google Scholar] [CrossRef]
- Ouyang, Z.; Lin, J.Z.; Ku, X. The hydrodynamic behavior of a squirmer swimming in power-law fluid. Phys. Fluids 2018, 30, 083301. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow in the Process Industries, Fundamentals and Engineering Applications; Jordan Hill: Oxford, UK, 1999; pp. 206–392. [Google Scholar]
- Kakac, S.; Shah, R.K.; Aung, W. Handbook of Single-Phase Convective HEAT Transfer; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Zeeshan, A.; Bhatti, M.M.; Akbar, N.S.; Sajjad, Y. Hydromagnetic blood flow of Sisko fluid in a non-uniform channel induced by a peristaltic wave. Commun. Theor. Phys. 2017, 68, 103. [Google Scholar] [CrossRef]
- Zhao, C.; Zholkovskij, E.; Masliyah, J.H.; Yang, C. Analysis of electroosmotic flow of power-law fluids in a slit microchannel. J. Colloid Interface Sci. 2008, 326, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Chakraborty, S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal. Chim. Acta 2006, 559, 15–24. [Google Scholar] [CrossRef]
- Prakash, J.; Tripathi, D. Electroosmotic flow of Williamson ionic nanoliquids in a tapered microfluidic channel in presence of thermal radiation and peristalsis. J. Mol. Liq. 2018, 256, 352–371. [Google Scholar] [CrossRef]
- Ali, F.; Iftikhar, M.; Khan, I.; Sheikh, N.A. Atangana–Baleanu fractional model for electro-osmotic flow of viscoelastic fluids. Chaos Solitons Fractals 2019, 124, 125–133. [Google Scholar] [CrossRef]
- Mondal, A.; Shit, G.C. Transport of magneto-nanoparticles during electro-osmotic flow in a micro-tube in the presence of magnetic field for drug delivery application. J. Magn. Magn. Mater. 2017, 442, 319–328. [Google Scholar] [CrossRef]
- Shit, G.C.; Mondal, A.; Sinha, A.; Kundu, P.K. Electro-osmotically driven MHD flow and heat transfer in micro-channel. Physica A 2016, 449, 437–454. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1457. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Khan, M.I.; Alsaedi, A. Entropy generation in magnetohydrodynamic radiative flow due to rotating disk in presence of viscous dissipation and Joule heating. Phys. Fluids 2018, 30, 017101. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Qayyum, S.; Alsaedi, A. Entropy generation in flow with silver and copper nanoparticles. Colloids Surf. A 2018, 539, 335–346. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J. Colloid Interface Sci. 2017, 498, 85–90. [Google Scholar] [CrossRef]
- Goshayeshi, H.R.; Goodarzi, M.; Safaei, M.R.; Dahari, M. Experimental study on the effect of inclination angle on heat transfer enhancement of a ferrofluid in a closed loop oscillating heat pipe under magnetic field. Exp. Therm Fluid Sci. 2016, 74, 265–270. [Google Scholar] [CrossRef]
- Sohail, A.; Fatima, M.; Ellahi, R.; Akram, K.B. A videographic assessment of Ferrofluid during magnetic drug targeting: An application of artificial intelligence in nanomedicine. J. Mol. Liq. 2019, 285, 47–57. [Google Scholar] [CrossRef]
- Malvandi, A.; Safaei, M.R.; Kaffash, M.H.; Ganji, D.D. MHD mixed convection in a vertical annulus filled with Al2O3–water nanofluid considering nanoparticle migration. J. Magn. Magn. Mater. 2015, 382, 296–306. [Google Scholar] [CrossRef]
- Yousif, M.A.; Ismael, H.F.; Abbas, T.; Ellahi, R. Numerical study of momentum and heat transfer of MHD Carreau nanofluid over exponentially stretched plate with internal heat source/sink and radiation. Heat Transf. Res. 2019, 50, 649–658. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bhatti, M.M. Active method for nanofluid heat transfer enhancement by means of EHD. Int. J. Heat Mass Transf. 2017, 109, 115–122. [Google Scholar] [CrossRef]
- Tripathi, D.; Jhorar, R.; Beg, O.A.; Kadir, A. Electro-magneto-hydrodynamic peristaltic pumping of couple stress biofluids through a complex wavy micro-channel. J. Mol. Liq. 2017, 236, 358–367. [Google Scholar] [CrossRef]
- Ray, A.; Varma, V.B.; Jayaneel, P.J.; Sudharsan, N.M.; Wang, Z.P.; Ramanujan, R.V. On demand manipulation of ferrofluid droplets by magnetic fields. Sens. Actuator B Chem. 2017, 242, 760–768. [Google Scholar] [CrossRef]
- Casula, M.F.; Corrias, A.; Arosio, P.; Lascialfari, A.; Sen, T.; Floris, P.; Bruce, I.J. Design of water-based ferrofluids as contrast agents for magnetic resonance imaging. J. Colloid Interface Sci. 2011, 357, 50–55. [Google Scholar] [CrossRef]
- Makinde, O.D.; Chinyoka, T. MHD transient flows and heat transfer of dusty fluid in a channel with variable physical properties and Navier slip condition. Comp. Math. Appl. 2010, 60, 660–669. [Google Scholar] [CrossRef]
- Abro, A.K.; Khan, I. Analysis of the heat and mass transfer in the MHD flow of a generalized Casson fluid in a porous space via non-integer order derivatives without a singular kernel. Chin. J. Phys. 2017, 55, 1583–1595. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Shehzad, N.; Alamri, S.Z. Structural impact of Kerosene-Al2O3 nanoliquid on MHD Poiseuille flow with variable thermal conductivity: Application of cooling process. J. Mol. Liq. 2018, 264, 607–615. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC: Boca Raton, NY, USA, 1996. [Google Scholar]
- Zeeshan, A.; Shehzad, N.; Abbas, T.; Ellahi, R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef]
- Ranjit, K.; Shit, G.C. Entropy generation on electro-osmotic flow pumping by a uniform peristaltic wave under magnetic environment. Energy 2017, 128, 649–660. [Google Scholar] [CrossRef]
- Cho, C.C.; Chen, C.L. Natural convection heat transfer and entropy generation in wavy-wall enclosure containing water-based nanofluid. Int. J. Heat Mass Transf. 2013, 61, 749–758. [Google Scholar] [CrossRef]
- Darbari, B.; Rashidi, S.; Esfahani, A.J. Sensitivity analysis of entropy generation in nanofluid flow inside a channel by response surface methodology. Entropy 2016, 18, 52. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.-S. Numerical simulation of entropy generation with thermal radiation on MHD Carreau nanofluid towards a shrinking sheet. Entropy 2016, 18, 200. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.S.; Yang, Z. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, S.; Khan, M.I.; Khan, M.I.; Alsaedi, A. Physical aspects of irreversibility in radiative flow of viscous material with cubic autocatalysis chemical reaction. Eur. Phys. J. Plus 2019, 134, 172. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Sheikholeslami, M.; Shahid, A.; Hassan, M.; Abbas, T. Entropy generation on the interaction of nanoparticles over a stretched surface with thermal radiation. Colloids Surf. A 2019, 570, 368–376. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to Homotopy Analysis Method; Chapman & Hall: Boca Raton, FL, USA, 2003. [Google Scholar]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of spherical and nonspherical nanoparticles in mixed convection flow over a vertical stretching permeable sheet. Mech. Adv. Mater. Struct. 2017, 24, 1231–1238. [Google Scholar] [CrossRef]
- Ellahi, R.; Tariq, M.H.; Hasssan, M.; Vafai, K. On boundary layer nano-ferroliquid flow under the influence of low oscillating stretchable rotating disk. J. Mol. Liq. 2017, 229, 339–345. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R.; Vafai, K. Convective heat transfer of a nanofluid in a wavy channel: Buongiorno’s mathematical model. J. Mol. Liq. 2016, 222, 446–455. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Waqas, M.; Yasmeen, T. Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Dehghan, M.; Manafian, J.; Saadatmandi, A. Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Meth. Part Differ. Equ. Int. J. 2010, 26, 448–479. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hassan, M. Particle shape effects on Marangoni convection boundary layer flow of a nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2160–2174. [Google Scholar] [CrossRef]
- Goswami, P.; Chakraborty, S. Semi-analytical solutions for electroosmotic flows with interfacial slip in microchannels of complex cross-sectional shapes. Microfluid. Nanofluid. 2011, 11, 255–267. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R. Electroosmotic flow of MHD power law Al2O3-PVC nanofluid in a horizontal channel: Couette-Poiseuille flow model. Commun. Theor. Phys. 2018, 69, 655. [Google Scholar] [CrossRef]
- Wang, X.; Qi, H.; Yu, B.; Xiong, Z.; Xu, H. Analytical and numerical study of electroosmotic slip flows of fractional second grade fluids. Commun. Nonlinear Sci. Numer. Simul. 2017, 50, 77–87. [Google Scholar] [CrossRef]
- Aydın, O.; Avcı, M. Laminar forced convection with viscous dissipation in a Couette–Poiseuille flow between parallel plates. Appl. Energy 2016, 83, 856–867. [Google Scholar] [CrossRef]
- Maiga, S.E.B.; Palm, S.J.; Nguyen, C.T.; Roy, G.; Galanis, N. Heat transfer enhancement by using nanofluids in forced convection flows. Int. J. Heat Fluid Flow 2005, 26, 530–546. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. A study of heat transfers in power-law nanofluid. Therm. Sci. 2016, 20, 2015–2026. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Van Gorder, R.A.; Vajravelu, K. On the selection of auxiliary functions, operators, and convergence control parameters in the application of the Homotopy Analysis Method to nonlinear differential equations: A general approach. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 4078–4089. [Google Scholar] [CrossRef]
- Zhao, Y.; Liao, S.J. HAM-Based Mathematica Package BVPh 2.0 for Nonlinear Boundary Value Problems. In Advances in the Homotopy Analysis Method; World Scientific Press: Singapore, 2013. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).