Locality Sensitive Discriminative Unsupervised Dimensionality Reduction
Abstract
1. Introduction
2. Related Work
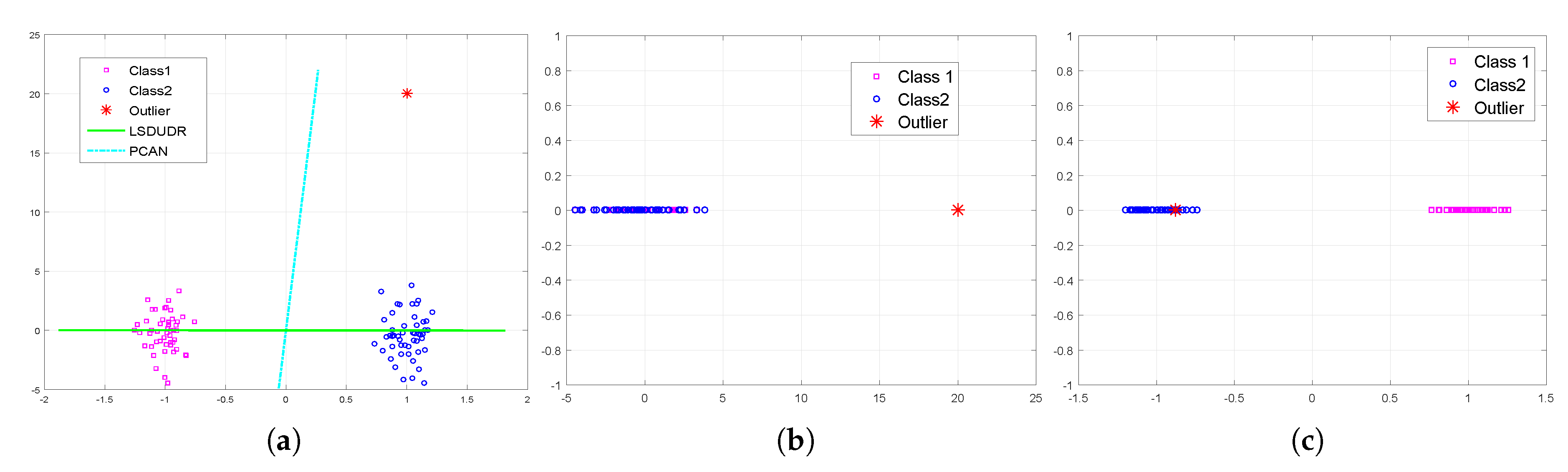
2.1. Principal Component Analysis (PCA)
2.2. Locality Preserving Projections (LPP)
2.3. Clustering and Projected Clustering with Adaptive Neighbors (PCAN)
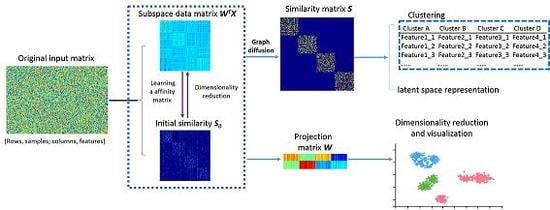
3. Locality Sensitive Discriminative Unsupervised Dimensionality Reduction
3.1. Intrinsic Structure Representation
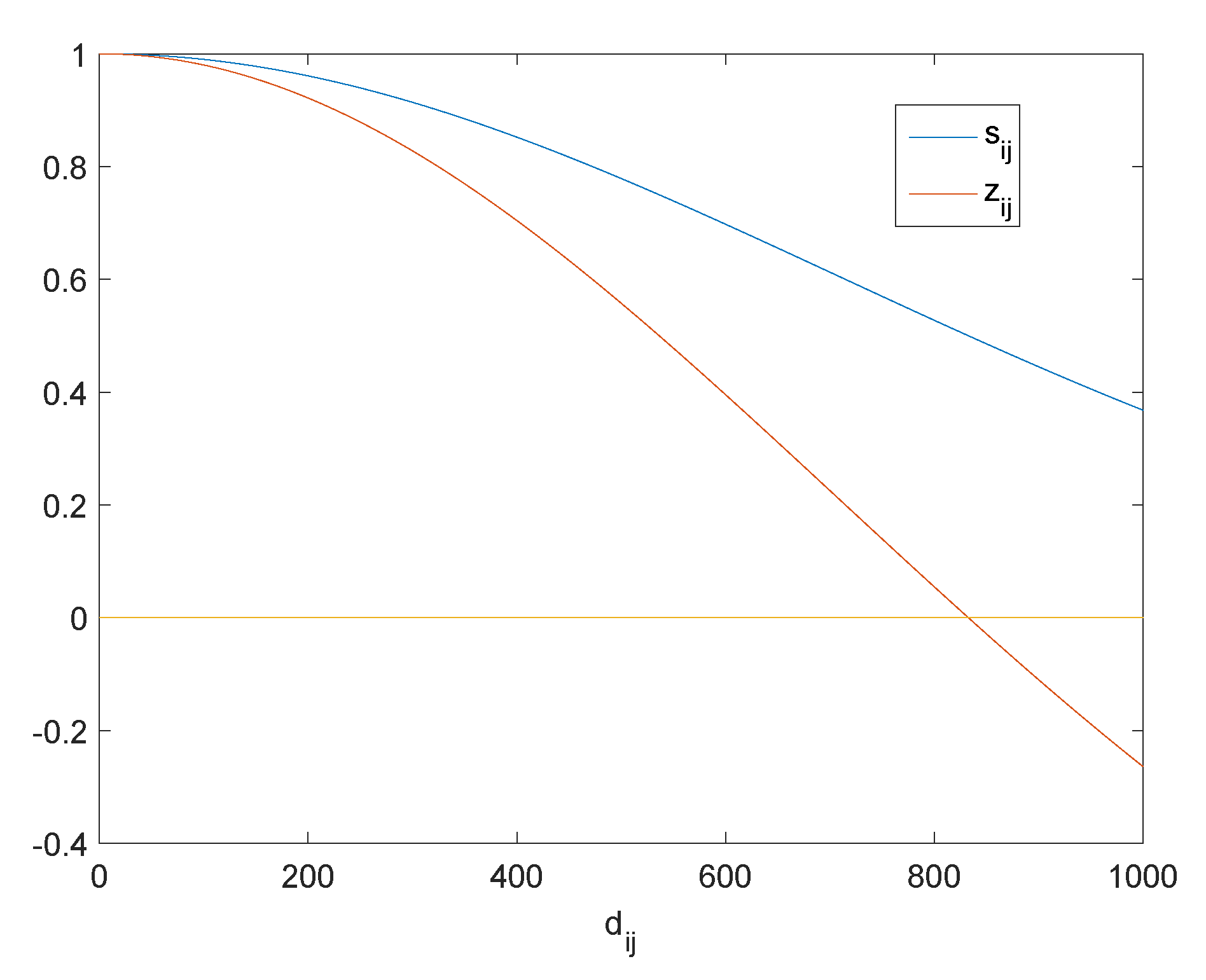
3.2. Analysis of Optimal Graph Learning
4. Optimization
4.1. Determine the Value of S, W, F
4.2. Approach to Determine the Initial Value of ,
- When the connected components are insufficient, i.e., the number of zero eigenvalues is smaller than c, we multiply by 2.
- The number of connected components could be overrun, i.e., the number of zero eigenvalues is larger than c. We divide by 2.
- If the graph has exact c connected components, then we stop the algorithm in this case and return the result.
| Algorithm 1 Framework of the LSDUDR method. |
| Require: Data , cluster number c, projection dimension m. Initialize S and V according to Equations (6) and (7). Initialize parameter and by the Equation (28). If algorithm 1 not converge: repeat 1. Construct the Laplacian matrix and . 2. Calculate F, columns of F are c eigenvectors of and are derived from the c samllest eigenvalues. 3. Calculate the projection matrix W by the m eigenvectors corresponding to the m smallest eigenvalues of the matrix: 4. Compute S by updating according to Equation (27). 5. Calculate the number of connected components of the graph, if it is smaller than c, then multiply by 2; if larger than c, then divide by 2. until Convergence End if return Projection matrix and similarity matrix . |
5. Discussion
5.1. Analysis
5.2. Convergence Study
6. Experiment
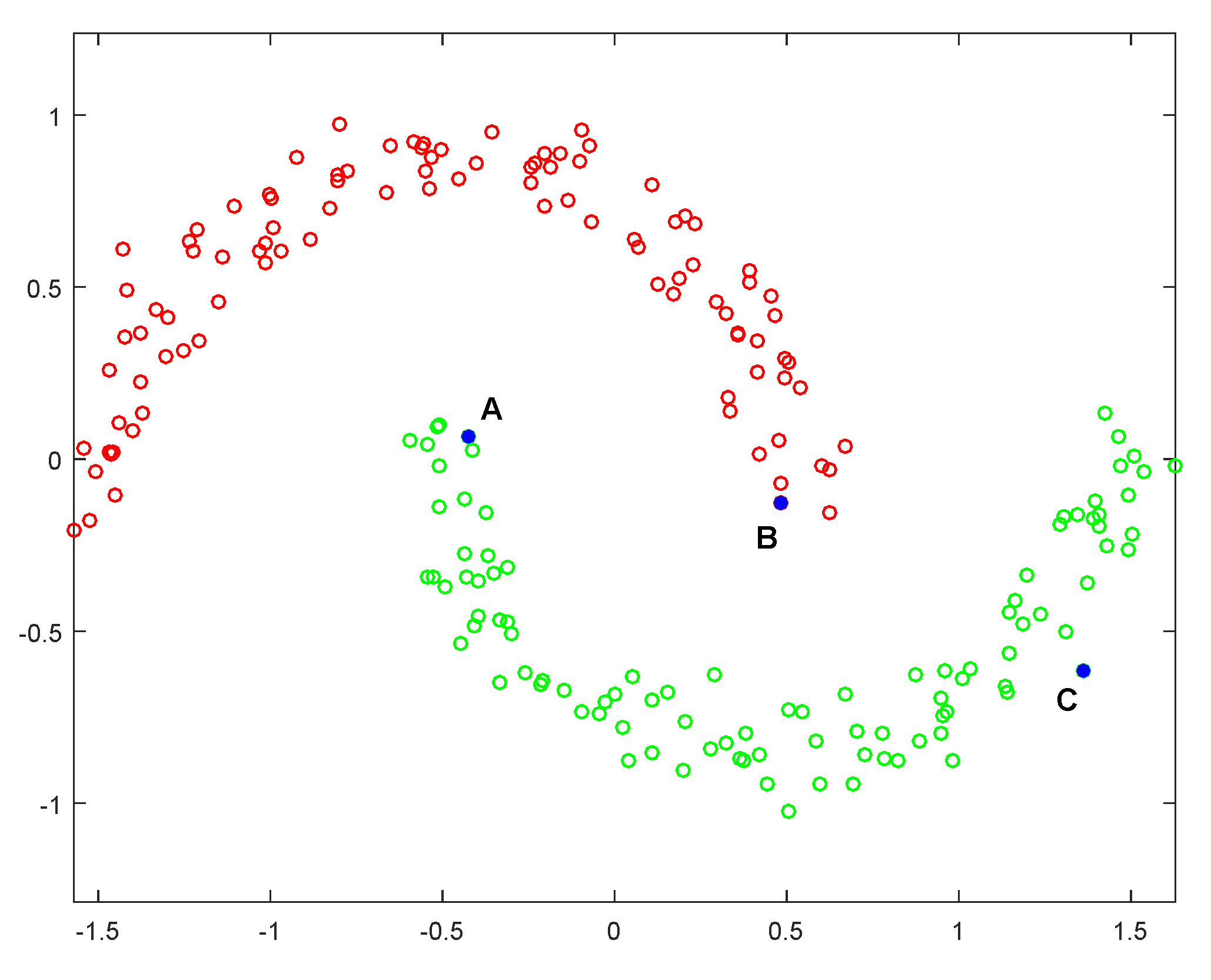
6.1. Experiment on the Synthetic Data Sets
6.2. Experiment on Low-Dimensional Benchmark Data Sets
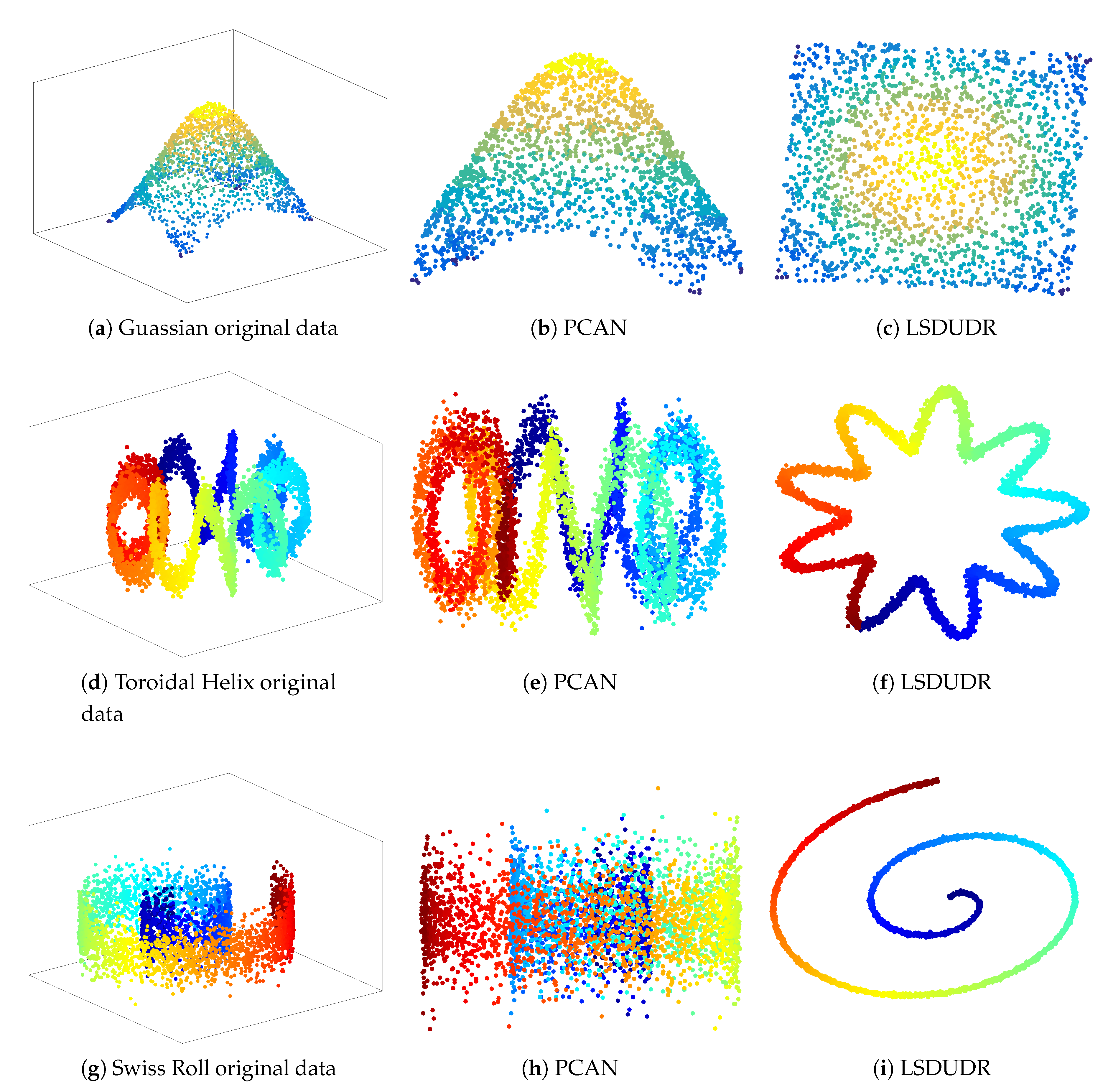
6.3. Embedding of Noise 3D Manifold Benchmarks
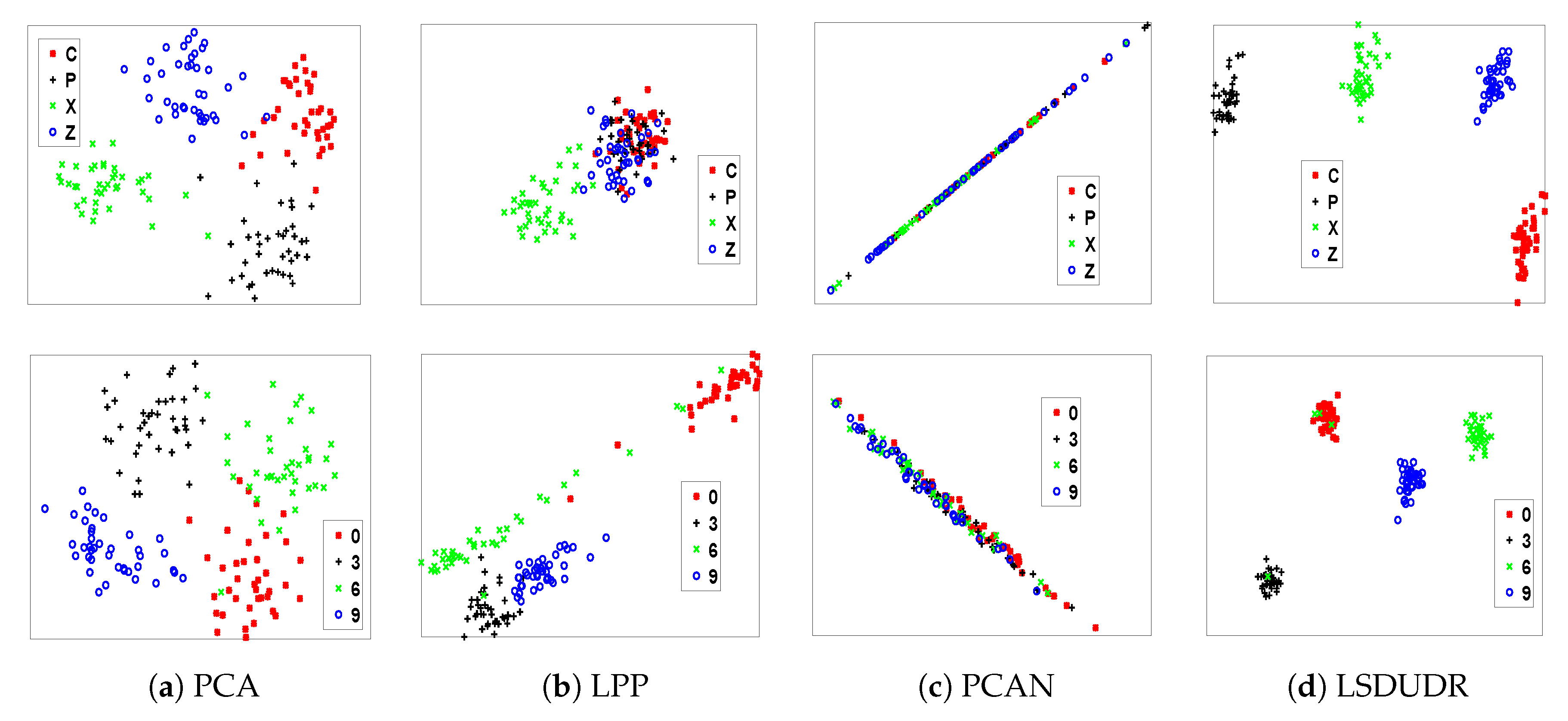
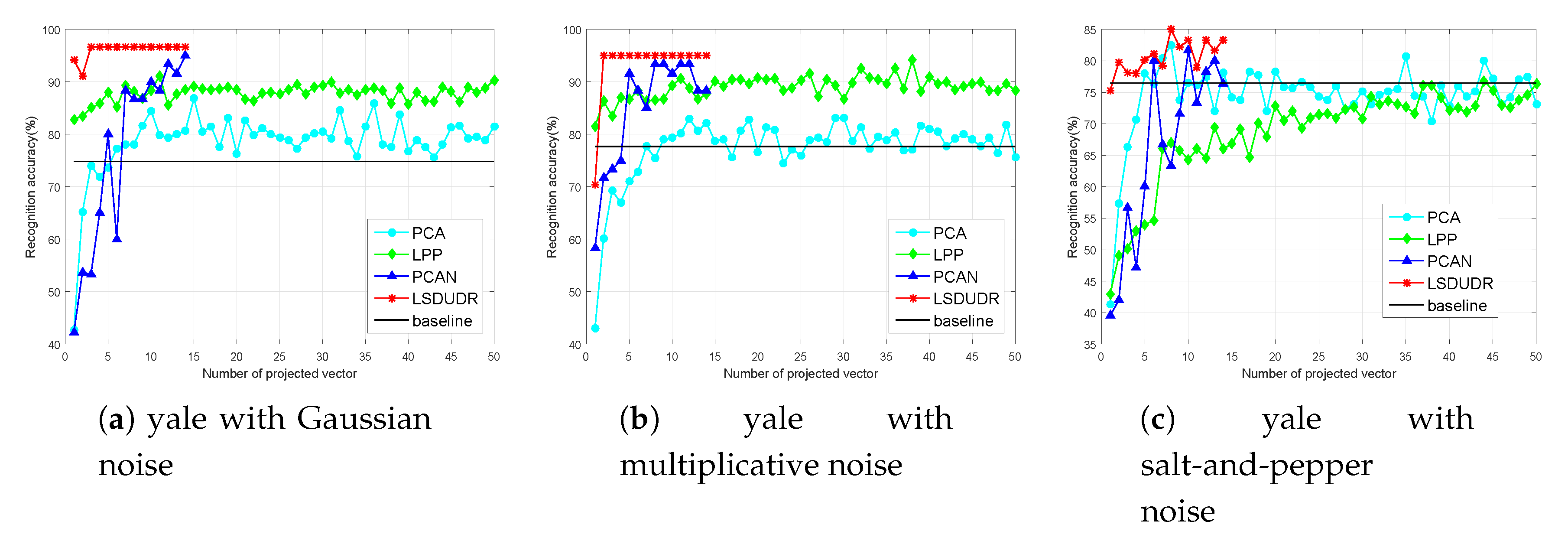
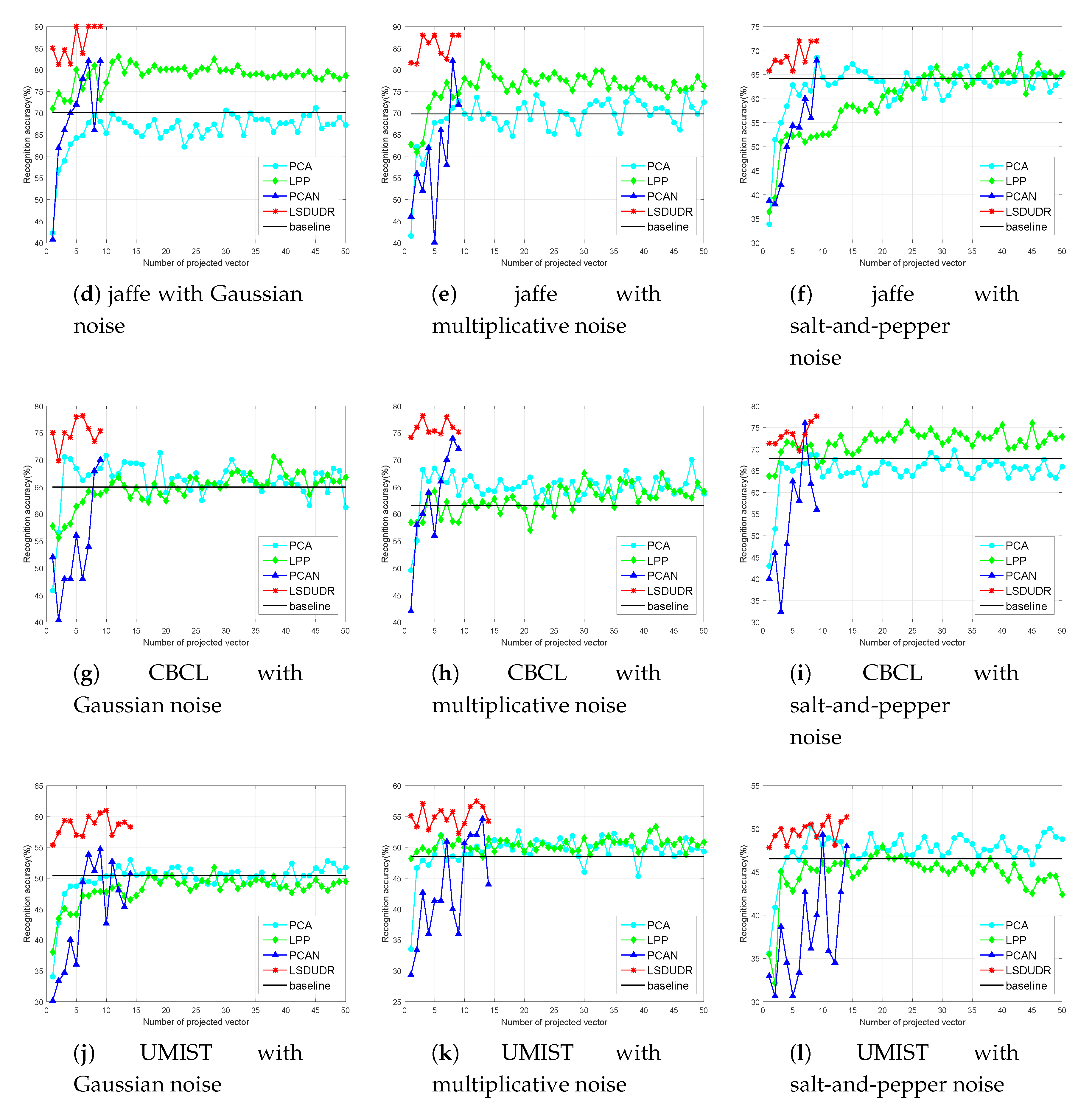
6.4. Experiment on the Image Data Sets
6.4.1. Visualization for Handwritten Digits
6.4.2. Face Benchmark Data Sets
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Everitt, B.S.; Dunn, G.; Everitt, B.S.; Dunn, G. Cluster Analysis; Wiley: Hoboken, NJ, USA, 2011; pp. 115–136. [Google Scholar]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Q.; Zhou, H.; Cheng, J. The Fisher-Markov Selector: Fast Selecting Maximally Separable Feature Subset for Multiclass Classification with Applications to High-Dimensional Data. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1217–1233. [Google Scholar] [CrossRef] [PubMed]
- Dash, M.; Liu, H. Feature selection for clustering. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Keihanna Plaza, Japan, 17–20 April 2000; pp. 110–121. [Google Scholar]
- Ben-Bassat, M. Pattern recognition and reduction of dimensionality. Handb. Stat. 1982, 2, 773–910. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- FISHER, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Hall, K.M. Anr-Dimensional Quadratic Placement Algorithm. Manag. Sci. 1970, 17, 219–229. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Luo, D.; Ding, C.; Huang, H.; Li, T. Non-negative Laplacian Embedding. In Proceedings of the 2009 Ninth IEEE International Conference on Data Mining, Miami, FL, USA, 6–9 December 2009. [Google Scholar]
- Roweis, S.T. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- He, X.; Niyogi, P. Locality preserving projections. In Advances in Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada, 2004; pp. 153–160. [Google Scholar]
- Nie, F.; Xiang, S.; Zhang, C. Neighborhood MinMax Projections. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Hyderabad, India, 8 January 2007; pp. 993–998. [Google Scholar]
- Tenenbaum, J.B. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Lu, G.F.; Jin, Z.; Zou, J. Face recognition using discriminant sparsity neighborhood preserving embedding. Knowl.-Based Syst. 2012, 31, 119–127. [Google Scholar] [CrossRef]
- Fan, Q.; Gao, D.; Wang, Z. Multiple empirical kernel learning with locality preserving constraint. Knowl.-Based Syst. 2016, 105, 107–118. [Google Scholar] [CrossRef]
- Pandove, D.; Rani, R.; Goel, S. Local graph based correlation clustering. Knowl.-Based Syst. 2017, 138, 155–175. [Google Scholar] [CrossRef]
- Feng, X.; Wu, S.; Zhou, W.; Min, Q. Efficient Locality Weighted Sparse Representation for Graph-Based Learning. Knowl.-Based Syst. 2017, 121, 129–141. [Google Scholar] [CrossRef]
- Du, L.; Shen, Y.D. Unsupervised feature selection with adaptive structure learning. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 209–218. [Google Scholar] [CrossRef]
- Nie, F.; Wang, H.; Huang, H.; Ding, C. Unsupervised and semi-supervised learning via L1-norm graph. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar] [CrossRef]
- Gao, Q.; Liu, J.; Zhang, H.; Gao, X.; Li, K. Joint Global and Local Structure Discriminant Analysis. IEEE Trans. Inf. Forensics Secur. 2013, 8, 626–635. [Google Scholar] [CrossRef]
- Nie, F.; Wang, X.; Jordan, M.I.; Huang, H. The Constrained Laplacian Rank Algorithm for Graph-Based Clustering. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1969–1976. [Google Scholar]
- Luo, D.; Nie, F.; Huang, H.; Ding, C.H. Cauchy graph embedding. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 553–560. [Google Scholar]
- Nie, F.; Wang, X.; Huang, H. Clustering and projected clustering with adaptive neighbors. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, New York, NY, USA, 24–27 August 2014; pp. 977–986. [Google Scholar] [CrossRef]
- Gao, Q.; Huang, Y.; Gao, X.; Shen, W.; Zhang, H. A novel semi-supervised learning for face recognition. Neurocomputing 2015, 152, 69–76. [Google Scholar] [CrossRef]
- Mohar, B.; Alavi, Y.; Chartrand, G.; Oellermann, O. The Laplacian spectrum of graphs. Graph Theory Comb. Appl. 1991, 2, 12. [Google Scholar]
- Fan, K. On a Theorem of Weyl Concerning Eigenvalues of Linear Transformations I. Proc. Natl. Acad. Sci. USA 1949, 35, 652–655. [Google Scholar] [CrossRef]
- Nie, F.; Xiang, S.; Jia, Y.; Zhang, C. Semi-supervised orthogonal discriminant analysis via label propagation. Pattern Recognit. 2009, 42, 2615–2627. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Hathaway, R.J. Convergence of alternating optimization. Neural Parallel Sci. Comput. 2003, 11, 351–368. [Google Scholar]
- Chen, W.; Feng, G. Spectral clustering: A semi-supervised approach. Neurocomputing 2012, 77, 229–242. [Google Scholar] [CrossRef]
- Macqueen, J. Some Methods for Classification and Analysis of MultiVariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Oakland, CA, USA, 21 June–18 July 1965; pp. 281–297. [Google Scholar]
- Hagen, L.; Kahng, A. New spectral methods for ratio cut partitioning and clustering. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1992, 11, 1074–1085. [Google Scholar] [CrossRef]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Nie, F.; Xu, D.; Li, X. Initialization Independent Clustering With Actively Self-Training Method. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 17–27. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: http://archive.ics.uci.edu/ml (accessed on 1 August 2018).
- Zelnik-Manor, L.; Perona, P. Self-tuning spectral clustering. In Advances in Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada, 2005; pp. 1601–1608. [Google Scholar]
- Chen, S.B.; Ding, C.H.; Luo, B. Similarity learning of manifold data. IEEE Trans. Cybern. 2015, 45, 1744–1756. [Google Scholar] [CrossRef]
- Roweis, S. Binary Alphadigits. Available online: https://cs.nyu.edu/~roweis/data.html (accessed on 1 August 2018).
- Har, M.T.; Conrad, S.; Shirazi, S.; Lovell, B.C. Graph embedding discriminant analysis on Grassmannian manifolds for improved image set matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
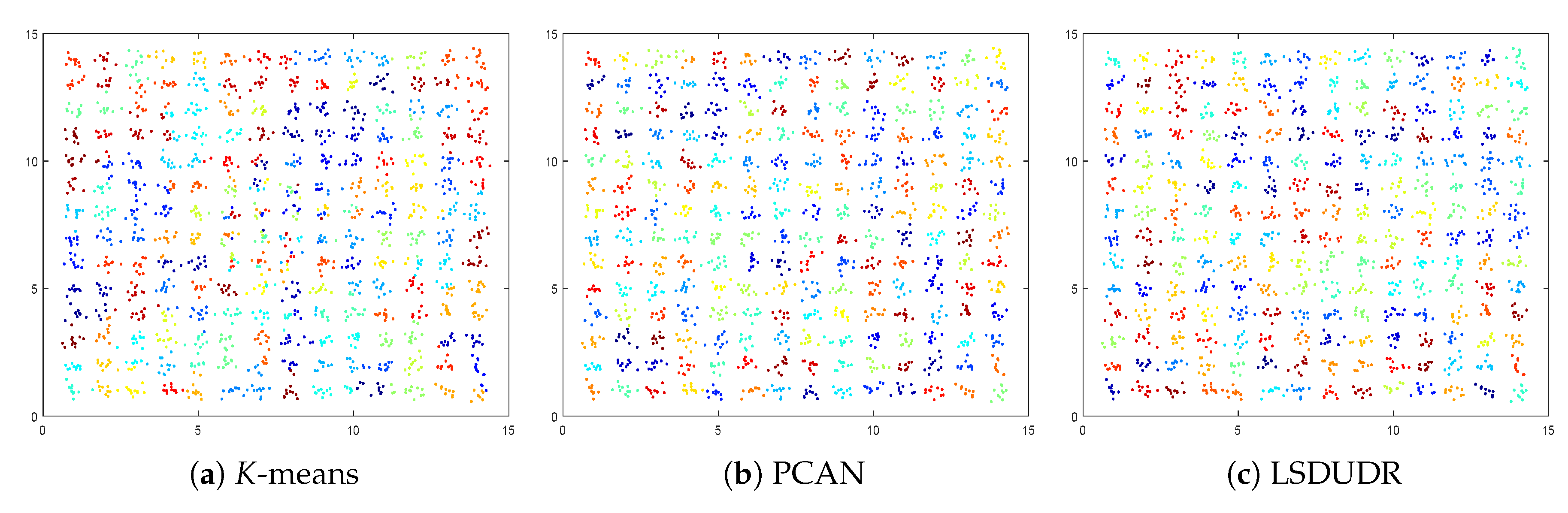
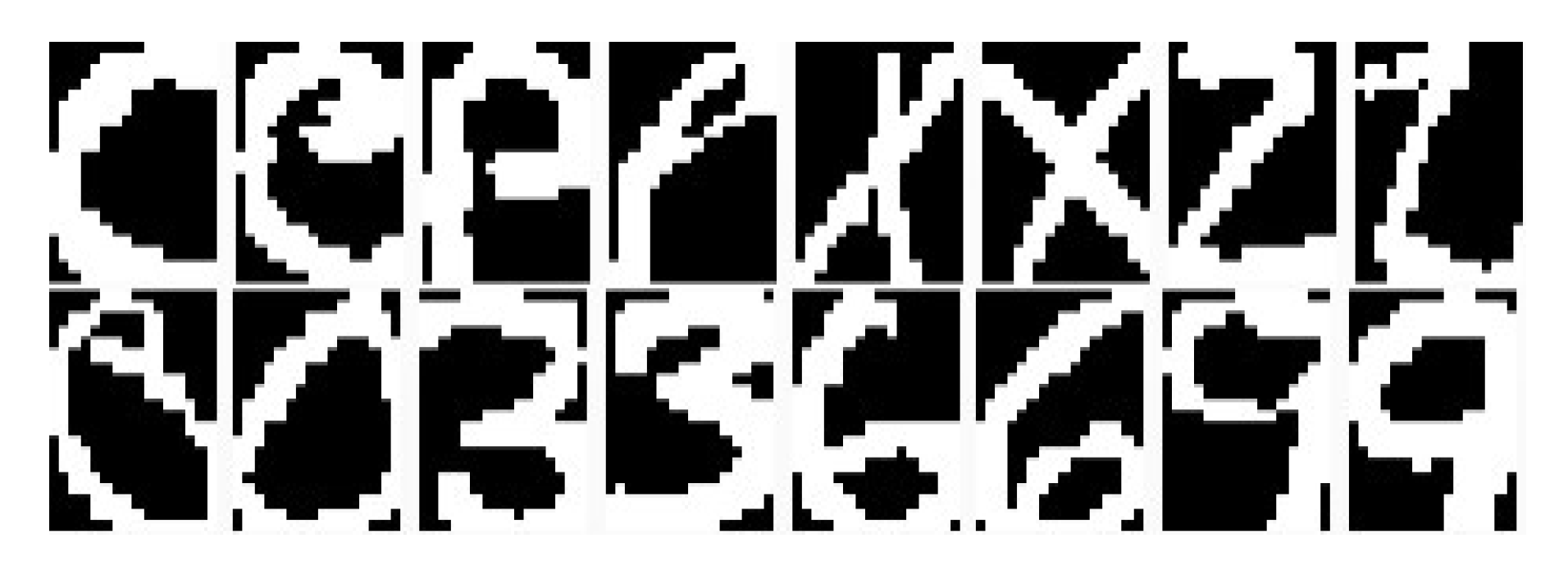

| Methods | ACC% | Minimal K-Means Objective |
|---|---|---|
| K-Means | 66.94 | 336.46 |
| PCAN | 98.62 | 107.33 |
| LSDUDR | 99.49 | 106.21 |
| Data Set | #Classes (c) | #Data Points (n) | #Dimensions (d) |
|---|---|---|---|
| Spiral | 3 | 312 | 2 |
| Pathbased | 3 | 300 | 2 |
| Compound | 6 | 399 | 2 |
| Movements | 15 | 360 | 90 |
| Iris | 3 | 150 | 4 |
| Cars | 3 | 392 | 8 |
| Glass | 6 | 214 | 9 |
| Vote | 2 | 435 | 16 |
| Diabetes | 2 | 768 | 8 |
| Dermatology | 6 | 366 | 34 |
| ACC% | K-Means | RatioCut | NormalizedCut | PCAN | LSDUDR |
|---|---|---|---|---|---|
| Spiral | 33.97 | 99.68 | 99.68 | 100 | 100 |
| Pathbased | 74.33 | 77.33 | 76.67 | 87.00 | 87.00 |
| Compound | 80.20 | 76.69 | 65.91 | 78.95 | 88.22 |
| Movements | 10.56 | 5.83 | 10.56 | 56.11 | 55.56 |
| Iris | 66.67 | 68.00 | 66.39 | 77.33 | 92.00 |
| Cars | 44.90 | 53.27 | 47.70 | 48.98 | 58.42 |
| Glass | 52.21 | 36.45 | 51.87 | 49.07 | 52.80 |
| Vote | 83.45 | 61.61 | 83.68 | 67.36 | 85.75 |
| Diabetes | 56.02 | 64.71 | 61.98 | 58.46 | 65.10 |
| Dermatology | 85.25 | 54.92 | 93.72 | 94.81 | 95.90 |
| NMI% | K-Means | RatioCut | NormalizedCut | PCAN | LSDUDR |
|---|---|---|---|---|---|
| Spiral | 12.52 | 98.35 | 98.35 | 100 | 100 |
| Pathbased | 51.33 | 54.96 | 53.10 | 75.63 | 79.27 |
| Compound | 79.74 | 71.60 | 66.32 | 77.48 | 85.16 |
| Movements | 44.11 | 15.85 | 44.91 | 84.95 | 84.17 |
| Iris | 61.68 | 61.3 | 59.05 | 61.85 | 77.52 |
| Cars | 39.10 | 21.61 | 39.06 | 39.03 | 39.39 |
| Glass | 35.83 | 35.33 | 34.88 | 35.76 | 35.90 |
| Vote | 36.58 | 30.17 | 35.66 | 35.23 | 39.37 |
| Diabetes | 52.67 | 50.02 | 61.98 | 64.01 | 68.10 |
| Dermatology | 85.20 | 41.24 | 88.43 | 91.83 | 93.53 |
| Data Sets | #Classes (c) | #Data Points (n) | #Dimensions (d) |
|---|---|---|---|
| YaleA | 15 | 165 | 3456 |
| Jaffe | 10 | 213 | 1024 |
| CBCI | 120 | 840 | 7668 |
| UMIST | 120 | 840 | 768 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.-L.; Luo, S.-Z.; Wang, Z.-H.; Chen, C.-C.; Pan, J.-Y. Locality Sensitive Discriminative Unsupervised Dimensionality Reduction. Symmetry 2019, 11, 1036. https://doi.org/10.3390/sym11081036
Gao Y-L, Luo S-Z, Wang Z-H, Chen C-C, Pan J-Y. Locality Sensitive Discriminative Unsupervised Dimensionality Reduction. Symmetry. 2019; 11(8):1036. https://doi.org/10.3390/sym11081036
Chicago/Turabian StyleGao, Yun-Long, Si-Zhe Luo, Zhi-Hao Wang, Chih-Cheng Chen, and Jin-Yan Pan. 2019. "Locality Sensitive Discriminative Unsupervised Dimensionality Reduction" Symmetry 11, no. 8: 1036. https://doi.org/10.3390/sym11081036
APA StyleGao, Y.-L., Luo, S.-Z., Wang, Z.-H., Chen, C.-C., & Pan, J.-Y. (2019). Locality Sensitive Discriminative Unsupervised Dimensionality Reduction. Symmetry, 11(8), 1036. https://doi.org/10.3390/sym11081036