Self-Consistent Two-Gap Description of MgB₂ Superconductor

Abstract

A self-consistent two-gap $\gamma$-model is used to quantitatively describe several thermodynamic properties of MgB${}_2$ superconductor. The superconducting coupling matrix, ${\nu }_{ij}$, was obtained from the fitting of the superfluid density in the entire superconducting temperature range. Using this input, temperature-dependent superconducting gaps, specific heat, and upper critical fields were calculated with no adjustable parameters and compared with the experimental data as well as with the first-principles calculations. The observed agreement between fit and data shows that $\gamma$-model provides adequate quantitative description of the two-gap superconductivity in MgB${}_2$ and may serve as a relatively simple and versatile self-consistent description of the thermodynamic quantities in multi-gap superconductors.

1. Introduction

Discovery of superconductivity in MgB${}_2$ triggered significant interest for its highest superconducting transition temperature, $T_c\approx 39.2$ K, among “conventional” superconductors with phonon-mediated pairing [1,2,3,4]. The conventional pairing mechanism was strongly supported by the Boron isotope effect [5,6,7] and exponential low-temperature attenuation of the thermodynamic quantities upon cooling indicating nodeless order parameter. Such high $T_c$ and isotropic nature of the superconducting gap offer excellent opportunities for various technological applications, including superconducting magnets, radio frequency resonance cavities for electron accelerators [8], and the next generation information technology, including high-frequency metamaterials, quantum integrated circuits, and quantum processing [9,10].

From the fundamental physics point of view, it was realized that a multi-band, multi-gap superconductivity model is required to explain the observed full-temperature range variation of thermodynamic properties. Smaller than expected for a single-gap superconductor exponential tail and a characteristic hump below $T_c$ in specific heat vs. temperature, $C\left(T\right)$, prompted the use of a well-known phenomenological $\alpha$-model, used to describe strong-coupling superconductivity [11]. In the original model, $\alpha =\Delta \left(T\right)/{\Delta }_{BCS}\left(0\right)$, where Bardeen–Cooper–Schrieffer isotropic weak-coupling single-band value is ${\Delta }_{BCS}\left(0\right)/T_c\approx 1.763$. Then $\alpha \ge 1$ was used to effectively vary the coupling strength. Indeed, this procedure is not self-consistent, but in the case of a single-band superconductor the actual temperature dependence of $\Delta \left(T\right)$ was not too far from ${\Delta }_{BCS}\left(T\right)$. In case of MgB${}_2$, two gaps were assumed to have the same, BCS temperature dependencies, but their amplitudes were taken as free parameters to fit the $C\left(T\right)$ data [12,13,14,15] and, later, London penetration depth [16,17,18]. The third parameter was the relative contributions from each band, proportional to the partial density of states and average Fermi velocities. Analysis of angle resolved photoemission spectroscopy data (ARPES) finds the difference in electron–phonon coupling between $\sigma$ and $\pi$ bands supporting two-band superconductivity in MgB${}_2$ [19,20,21].

While this simple approach “worked” in practice and has been widely used even to-date to describe multi-band superconductivity, it is not self-consistent and the obtained parameters have no physical significance. Indeed, it has been realized right away and more elaborate models were used. Whereas original $\alpha$-model used weak-coupling BCS gaps [13], later refinements used temperature dependent gaps calculated microscopically for MgB${}_2$ [22], but then again used the ratio of the gap amplitudes and the relative contributions from different bands as free parameters to fit the experimental data. While such exercise surely points toward multi-gap superconductivity in MgB${}_2$, it cannot provide information regarding superconducting pairing matrix and the success of $\alpha$-model is mostly due to the fact that thermodynamic quantities do not exhibit sharp features as a function of temperature and that in MgB${}_2$ interband coupling is quite significant.

Being clearly the case in MgB${}_2$, multiband superconductivity has received significant attention and led to the re-evaluation of known systems and looking for novel materials. Surely enough, it turned out that it is much more common if not ubiquitous with the prominent example of a diverse family of iron based superconductors [23,24,25,26], heavy fermions [27] and even elemental lead [28]. Full microscopic calculations based on multiband Eliashberg arbitrary coupling were performed, but using them to fit the experimental data was not feasible due to complexity of the realistic electronic structure as well as the number of the parameters involved [14,29,30]. Therefore, relatively simple, but self-consistent, approach was needed and such description, called the $\gamma$-model, was introduced based on Eilenberger formulation of the Gor’kov equations [31], and it provided a direct path to evaluation of the coupling constants from the data [32]. We used this model to describe multi-band superconductivity in various iron-based superconductors [24]. Originally, two isotropic s-wave gaps in the clean limit are considered. Later it was generalized for several anisotropic gaps to describe superconductivity in FeSe [33]. It can also be adopted to include scattering, but then the number of unknown parameters becomes too large. In the clean case, provided that bandstructure with Fermi velocities and partial densities of states are known, the unknown coupling matrix can be determined by fixing one of the elements to match the experimental superconducting transition temperature, $T_c$, and varying others to fit experimental quantity as a function of temperature. The quantity can be, for example, specific heat or superfluid density. Once the interaction matrix is obtained, all other thermodynamic quantities, including free energy, thermal conductivity and critical fields, can be calculated. This provides a physically meaningful way to test the model against several independent measurements.

In this work, we used a self-consistent $\gamma$-model to describe superconducting properties of MgB${}_2$ and successfully obtained the interaction matrix by fitting its normalized superfluid density measured in a purest MgB${}_2$ single crystal up to date, which was grown out of molten Mg at high pressure. The superb quality of the sample guarantees the most reliable temperature-dependent London penetration depth. Using the obtained single set of fitting parameters, the thermodynamic quantities including specific heat and upper critical field were calculated, and the temperature dependence of order parameters is in good agreement with the spectroscopic tunneling experiments.

2. Results and Discussion

Figure 1a shows temperature dependent normalized magnetic moment, $M\left(T\right)/M_{Z}FC\left(5\mathrm{K}\right)$, measured on warming after a 10 Oe magnetic field was applied at 5 K (zero-field cooling (ZFC)) and then on cooling without turning the field off (field-cooling (FC)). The normalization was performed to estimate the amount of the expelled flux from the sample interior (unknown demagnetization correction does not allow for the determination of absolute magnetic susceptibility). Figure 1b shows magnetic moment as a function of magnetic field in MgB${}_2$ crystal measured at 5 K. Sharp superconducting transition, substantial (50%) Meissner expulsion and virtually no magnetic hysteresis indicate low pinning and overall very clean superconducting nature of this sample.

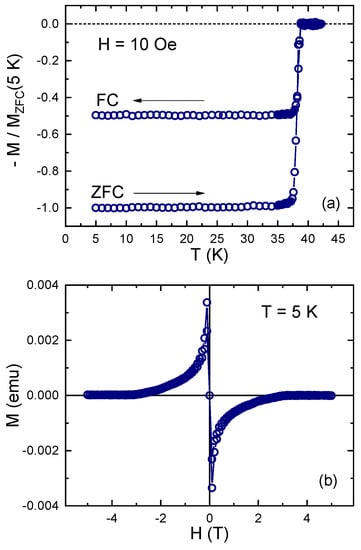
Figure 1. (a) Normalized magnetic moment, $M\left(T\right)/M_{ZFC}\left(5\mathrm{K}\right)$, measured after cooling in zero magnetic field to 5 K, applying $H_{DC}=10$ Oe and then measuring on warming (zero-field cooling (ZFC)) above $T_c$ and then on cooling (field-cooling (FC)). (b) Magnetization loop, $M\left(H\right)$, in MgB${}_2$ crystal measured at 5 K.

Figure 2 shows the temperature variation of London penetration depth $\Delta \lambda \left(T\right)$ in the same crystal of MgB${}_2$ used for the magnetic susceptibility measurements shown in Figure 1. The inset shows $\Delta \lambda \left(T\right)$ over the entire superconducting temperature range, which exhibits a sharp transition at $T_c=39$ K. In the main panel, the low temperature part of $\Delta \lambda \left(T\right)$ up to $0.3T_c$ was shown and fitted to the s-wave BCS model, $\Delta \lambda \left(T\right)=\lambda \left(0\right)\sqrt{\pi \Delta \left(0\right)/2k_{B}T}exp(-\Delta \left(0\right)/k_{B}T)$, with $\lambda \left(0\right)$ and $\Delta \left(0\right)$ being the fitting parameters. The best fitting curve shown by solid curve can be achieved with $\lambda \left(0\right)=65\pm 1$ nm and $\Delta \left(0\right)/k_B{T}_c=0.71\pm 0.01$. Although the fitting to a single-gap s-wave BCS function is reasonable, the $\lambda \left(0\right)$ obtained is much smaller than values in literature, which ranges between 84 and 116 nm [17,22,34,35]. Notably, the gap amplitude is smaller than a weak-coupling value of $\Delta \left(0\right)/k_B{T}_c=1.76$ [2], which is impossible in a single gap system. In fact, these deviations indicate either anisotropic superconducting gap or presence of multiple gaps [24,36].

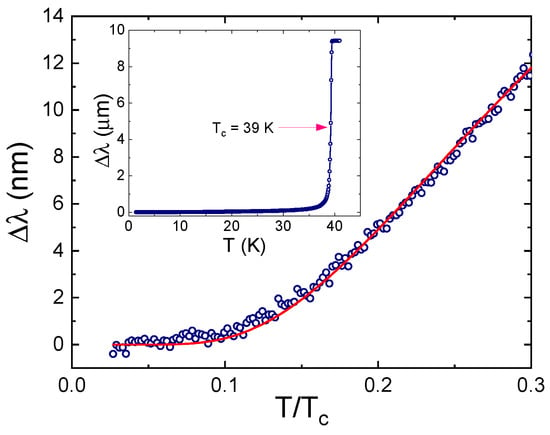
Figure 2. Temperature variation of London penetration depth $\Delta \lambda \left(T\right)$ in MgB${}_2$. Inset: $\Delta \lambda \left(T\right)$ over the full temperature range. Main panel: low-temperature part of experimental $\Delta \lambda \left(T\right)$ (symbols). Solid curve is the best fitting to a single-gap s-wave BCS asymptotic behavior, $\Delta \lambda \left(T\right)=\lambda \left(0\right)\sqrt{\pi \Delta \left(0\right)/2k_{B}T}exp(-\Delta \left(0\right)/k_{B}T)$ with $\lambda \left(0\right)$ and $\Delta \left(0\right)$ as fitting parameters within “low-temperature” range up to 0.3$T_c$.

In order to investigate the multi-gap nature in MgB${}_2$, normalized superfluid density, ${\rho }_s={\lambda }^2\left(0\right)/{\lambda }^2\left(T\right)$, was calculated using $\lambda \left(0\right)=100$ nm, approximate average from Ref. [17,22,34,35]. The experimental superfluid density shown by symbols in Figure 3a was fitted to ${\rho }_s=\gamma {\rho }_1+(1-\gamma ){\rho }_2$ by using the self-consistent $\gamma$-model [32]. Here $\gamma =n_1{v}_1^2/(n_1{v}_1^2+n_2{v}_2^2)$, where $v_1^2=$3.3$\times {10}^{15}$ cm${}^2$/s${}^2$ and $v_2^2=$2.3$\times {10}^{15}$ cm${}^2$/s${}^2$ are averages over corresponding band of the squared in-plane Fermi velocities and $n_i$ are normalized partial densities of states per spin, $n_1=$0.44 and $n_2=1-n_1$ [37]. During the fitting, one of the in-band interaction parameters, ${\lambda }_{11}$, is adjusted to produce close to experimental transition temperature, $T_c=$39 K after convergence of the fit. A phonon-mediated superconductivity with Debye temperature of 750 K was assumed in calculations of $T_c$. The only two free parameters are ${\lambda }_{12}$ and ${\lambda }_{22}$. During the fitting, superconducting gaps were obtained self-consistently. Their temperature dependence is shown in Figure 3b by solid lines. Experimentally determined gaps from tunneling spectroscopy [38] are shown by symbols for comparison.

Figure 3. (a) Fitting of the experimental superfluid density, ${\rho }_s={\lambda }^2\left(0\right)/{\lambda }^2\left(T\right)$ (symbols), to the $\gamma$-model (lines). Partial superfluid densities, $\gamma {\rho }_1$ and $(1-\gamma ){\rho }_2$ are also shown. (b) Temperature dependent superconducting energy gaps ${\Delta }_1\left(T\right)/k_B{T}_c$ and ${\Delta }_2\left(T\right)/k_B{T}_c$ calculated from the fitting procedure (lines). These results are compared with the experimental tunneling spectroscopy results [38] (purple open squares) and theoretical estimates [29] (red dashed lines), [30] (brown dotted lines).

Specific heat was deduced by using the fit parameters from the $\gamma$-model fit of superfluid density and plotted in Figure 4. It is quantitatively consistent with the experimental data [39] and estimate from the first principles calculation [30].

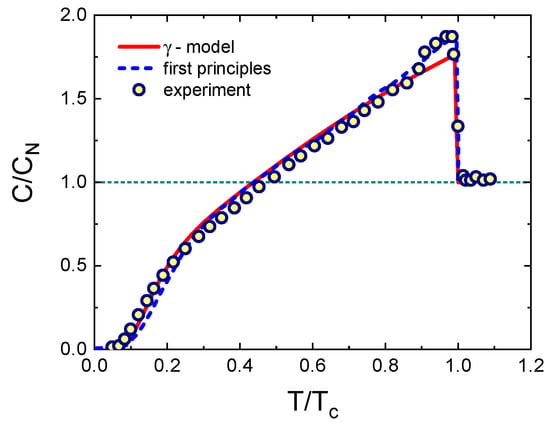
Figure 4. Temperature dependent specific heat $C/C_N$ in MgB${}_2$. Solid line and symbols represent a calculated result by using $\gamma$ model [32] and an experimental work by Putti et al. [39], respectively. The dotted line represents the estimate from first principles calculation [30].

Finally, we use parameters of the $\gamma$-model determined from the fitting of superfluid density, to calculate the upper critical field in the clean limit following ref. [40]. Temperature dependent upper critical fields were deduced for both field parallel and perpendicular to the in-plane and plotted in Figure 5. The results were quantitatively consistent with other experimental data [41,42,43].

Figure 5. (a) Temperature dependent upper critical field $H_{c2}\left(T\right)$ in MgB${}_2$ with the applied magnetic fields $H_{dc}$ along ab-axis and c-axis. (b) Temperature dependent $H_{c2}$ anisotropy $\gamma \left(T\right)=H_{c2,ab}\left(T\right)/H_{c2,c}\left(T\right)$. Solid line represent a calculated result by using $\gamma$ model [32] and symbols are experimental results by Lyard et al. (squares) [41], Karpinski et al. (triangles) [42], and Zehetmayer et al. (circles) [43], respectively.

3. Materials and Methods

High quality single crystals of MgB${}_2$ have been grown using a cubic, multianvil press, with an edge length of 19 mm from the Rockland Research Corporation (West Nyack, NY, USA). Pure distilled Mg (4 N) was squeezed so as to obtain a cylinder shaped ingot and placed into a boron nitride (BN) crucible. Enriched ${}^{11}$B powder (4 N) was added into the crucible in 0.5 to 1 ratio with Mg. The crucible was then filled with BN powder. The synthesis was carried out in a high pressure furnace at a pressure of 3.3 GPa to grow high quality of MgB${}_2$ single crystals out of the Mg solvent. The materials were heated up to 1500 ${}^{\circ }$C over 1 h and held there for 4 h. The temperature was then slowly reduced to 700 ${}^{\circ }$C at 2.7 ${}^{\circ }$C/min. The furnace was stopped resulting in a fast cooling to room temperature. After releasing the pressure, the remaining Mg was distilled and single crystals of MgB${}_2$ were obtained and manually separated from BN crystals. Typical samples are shiny platelets with dimensions of about $1\times 0.5\times 0.1$ mm${}^3$. In this paper, a sample with dimensions of $1.1\times 0.4\times 0.1$ mm${}^3$ was extracted and used for dc magnetization and the London penetration depth $\lambda$. The dc magnetization was measured in a quantum design magnetic property measurement system (MPMS) with an applied dc magnetic field of $H=10$ Oe. Temperature variation of London penetration depth $\Delta \lambda \left(T\right)$ was measured by using a tunnel-diode resonator (TDR) technique [24,44,45,46] which is mounted on a conventional ${}^3$He cryostat with a base temperature as low as $T_{\min }=0.4$ K. A $LC$ tank circuit of TDR self-resonates at a frequency about $f_0=14$ MHz with an excitation ac magnetic field of $H_{ac}=20$ mOe in the inductor coil. Placing a sample into the inductor causes the shift of the resonant frequency, $\Delta f\left(T\right)=-G4\pi {\chi }_{ac}\left(T\right)$ where G is a calibration constant determined by physically pulling the sample out of the inductor coil. With the characteristic sample size, R, $4\pi {\chi }_{ac}=(\lambda /R)tanh(R/\lambda )-1$, from which $\Delta \lambda \left(T\right)$ can be obtained [24,45,46].

4. Summary

A self-consistent $\gamma$-model with two isotropic s-wave gaps was used to describe several superconducting properties of MgB${}_2$ based on the known electronic structure and pairing matrix obtained from the least squares fit to the experimental superfluid density ${\rho }_s\left(T\right)={\lambda }^2\left(0\right)/{\lambda }^2\left(T\right)$. The temperature variation of the London penetration depth $\lambda \left(T\right)$ was measured using the tunnel diode resonator technique down to $0.01T_c$. Using the obtained single set of fitting parameters, the thermodynamic quantities including specific heat and upper critical field were calculated, and the temperature dependence of order parameters is in good agreement with the spectroscopic tunneling experiments. Our results provide solid experimental ground to using a sufficiently simple, yet self-consistent $\gamma$-model for the description of multigap superconductivity.