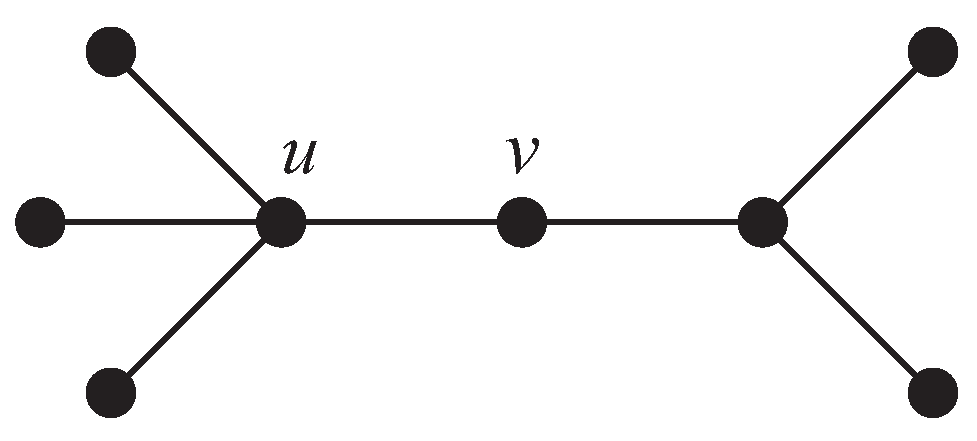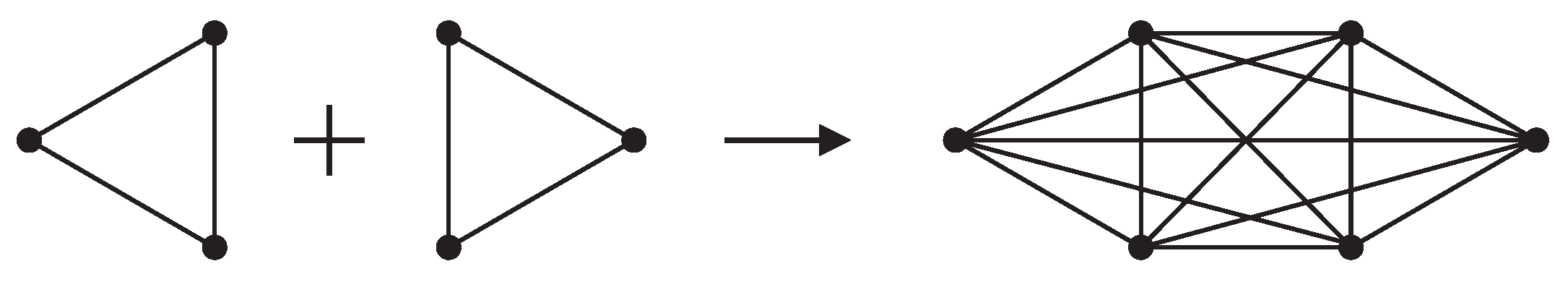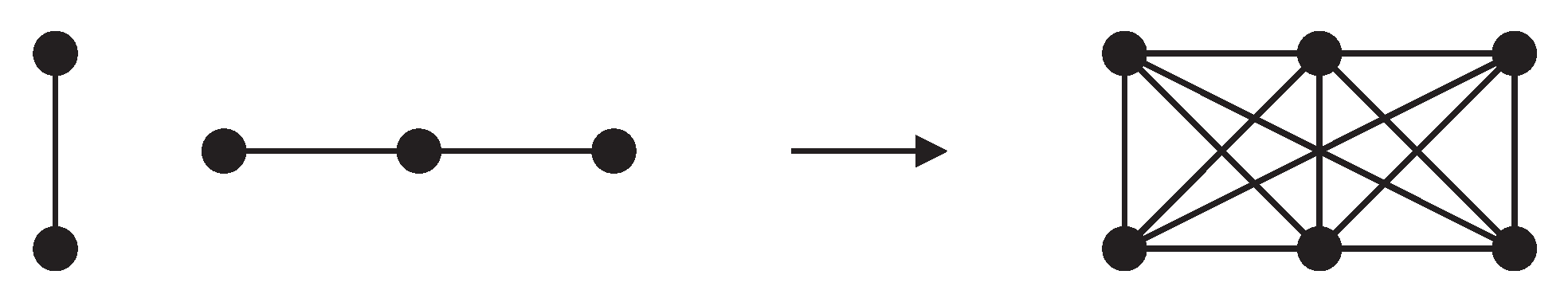The Hosoya Entropy of Graphs Revisited

Abstract

In this paper we extend earlier results on Hosoya entropy (H-entropy) of graphs, and establish connections between H-entropy and automorphisms of graphs. In particular, we determine the H-entropy of graphs whose automorphism group has exactly two orbits, and characterize some classes of graphs with zero H-entropy.

1. Introduction

Graphs and networks play an important role in many areas of study. Applications of graph theory include problems in internet-related social media, computational chemistry, genetics, data visualization, and many other domains [1,2,3,4,5,6]. Of particular interest here is research aimed at characterizing graphs numerically based on their invariants. Quantitative measures of graph structure, both information-theoretic and non-information-theoretic, have proven to be useful in various applications [7,8,9].

Graph measures based on Shannon entropy have been explored extensively. The first such measure was introduced by Rashevsky [7,9] and further investigated by Mowshowitz [7,9]. This quantitative measure, called information content, captures an important aspect of graph structure and has been characterized as an index of complexity; it is computed by applying Shannon entropy [10] to a probability distribution derived from the symmetries of a graph. More precisely, the orbits of the automorphism group of a graph form a partition of the vertices, and a natural probability distribution is obtained by dividing the size of each orbit by the number of vertices in the graph. Applying Shannon entropy to the finite probability scheme formed in this way gives the information content of the graph and such measures are useful for investigating problems in mathematical chemistry, computational physics and pattern recognition, see [1,11,12,13,14]. Graph entropy measures have now become a staple feature of network science, used to characterize networks quantitatively [7,15,16]; they have been investigated extensively and applied successfully in many different domains, see [1,2,17,18] as well as [3,4,19].

This paper explores a particular graph entropy measure introduced in [8]. The measure, called Hosoya- or H-entropy, is based on a distance-related partition of the vertices of a graph. A general framework for applying the measure is developed and applied to some specific classes of graphs such as trees and product graphs. In particular, the H-entropy measure is computed for classes of graphs with two orbits. The special case of trees with two orbits (stars and bi-stars) is examined in detail. To the best of our knowledge, this paper is the first to characterize graphs with non-zero H-entropy possessing two vertex-orbits.

2. Preliminaries on Entropy of Graphs

Given a partition of the vertices of a graph, one can define a finite probability scheme and compute its entropy. Computing group-based entropy or information content of a graph requires knowledge of the respective orbit sizes. An obvious, but generally inefficient, way to do this is first to determine the automorphism group and then to find the vertex orbits by observing the action of automorphisms on the vertices.

All graphs considered in this paper are simple, connected and finite. Let G be a graph with automorphism group $A=Aut\left(G\right)$. The vertex-orbit (or simply orbit) containing vertex $v\in V\left(G\right)$ is the set $\left\{\alpha \right(v):\alpha \in A\}$. An automorphism group $Aut\left(G\right)$ with exactly one orbit is called vertex-transitive. More formally, $Aut\left(G\right)$ is vertex-transitive if for each pair of vertices $u,v\in V\left(G\right)$ there is a $g\in Aut\left(G\right)$ such that $g\left(u\right)=v$. An edge-transitive graph can be defined similarly.

Let $G=(V,E)$ be a graph on $\left|V\right|=n$ vertices. A classical graph entropy measure, namely the topological information content elaborated by Mowshowitz [7] has been defined by

$$I_a\left(G\right)=-\sum _{i=1}^k\frac{n_i}{n}log\frac{n_i}{n},$$

(1)

where $n_i$ (1 ≤ i ≤ k) is the size of ith orbit of G. It is well-known that I${}_a$(G) reaches its maximum value if the graph has no symmetries, i.e., its automorphism group is trivial, consisting of the identity alone, see [7].

Given a graph G and vertices $u,v\in V\left(G\right)$, we say that $u,v$ are at distance r, and write $d(u,v)=r$, if the shortest path connecting them is of length r. Let G be a graph of diameter $\rho =\rho \left(G\right)$; and for $u\in V\left(G\right)$, let $S_i(G,u)$ or briefly $S_i\left(u\right)$ be the set of vertices at distance i from u. In addition, let $s_i=\left|S_i\left(u\right)\right|$. Then the distance degree sequence of a vertex v is $dds\left(v\right)=(s_0\left(v\right),s_1\left(v\right),\dots ,s_{\rho }\left(v\right))$, where $s_0\left(v\right)=1$ and $s_1\left(v\right)=deg\left(v\right)$, see [20].

Two vertices u and v are said to be Hosoya-equivalent or briefly H-equivalent if $s_i\left(u\right)=s_i\left(v\right)$, for $1\le i\le \rho \left(G\right)$, see [8]. The family of sets of H-equivalent vertices constitutes a partition of the vertices. We call this an H-partition consisting of the H-equivalence classes. Let $X_1,\cdots ,X_h$ be the set of all H-equivalence classes of G. The Hosoya entropy (or H-entropy) of G is given by [8]

$$H\left(G\right)=-\sum _{i=1}^h\frac{|X_i|}{\left|V\right|}log\left(\frac{|X_i|}{\left|V\right|}\right).$$

(2)

3. Main Results

The problem of computing H-entropy, like that of determining the information content of a graph, requires a method for finding partitions, H-partitions in this case [8,21]. In this section, we derive some basic properties of H-entropy and determine this quantity for several classes of graphs.

3.1. Properties of the H-Entropy

As mentioned earlier, this paper focuses on properties of the H-entropy of graphs related to the number of orbits of the automorphism group. The H-entropy of a graph G is based on distance between vertices. For a vertex $x\in V\left(G\right)$, the total distance of $x\in V\left(G\right)$ is defined as $D\left(x\right)={\sum }_{u\in V\left(G\right)}d(x,u)$.

Theorem 1.

If G is a vertex-transitive graph, then $D\left(u\right)=D\left(v\right)$ for all vertices $u,v\in V\left(G\right)$.

Proof. 

For any two vertices $u,v\in V\left(G\right)$, given that G is vertex-transitive, there is an automorphism $\phi \in Aut\left(G\right)$ such that $\phi \left(u\right)=v$. Hence

$$D\left(u\right)=\sum _{x\in V\left(G\right)}d(u,x)=\sum _{x\in V\left(G\right)}d(\phi \left(u\right),\phi \left(x\right))=\sum _{y\in V\left(G\right)}d(v,y)=D\left(v\right).$$

 □

Corollary 1.

Suppose u and v are in the same orbit of $Aut\left(G\right)$, then u and v are H-equivalent. If G is vertex-transitive, then $H\left(G\right)=0$.

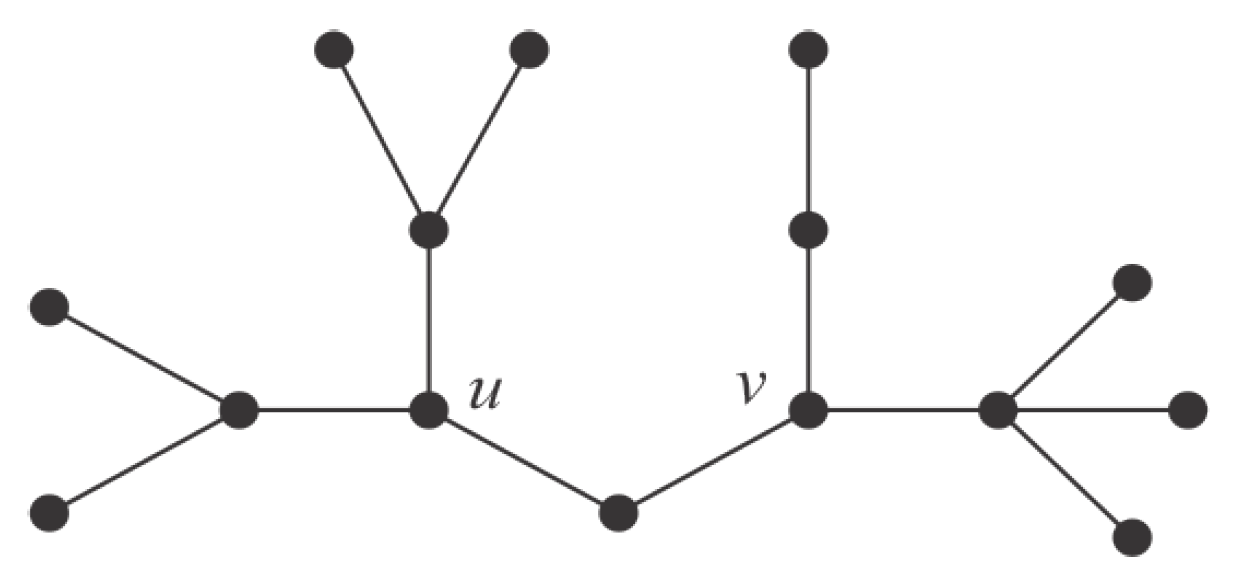
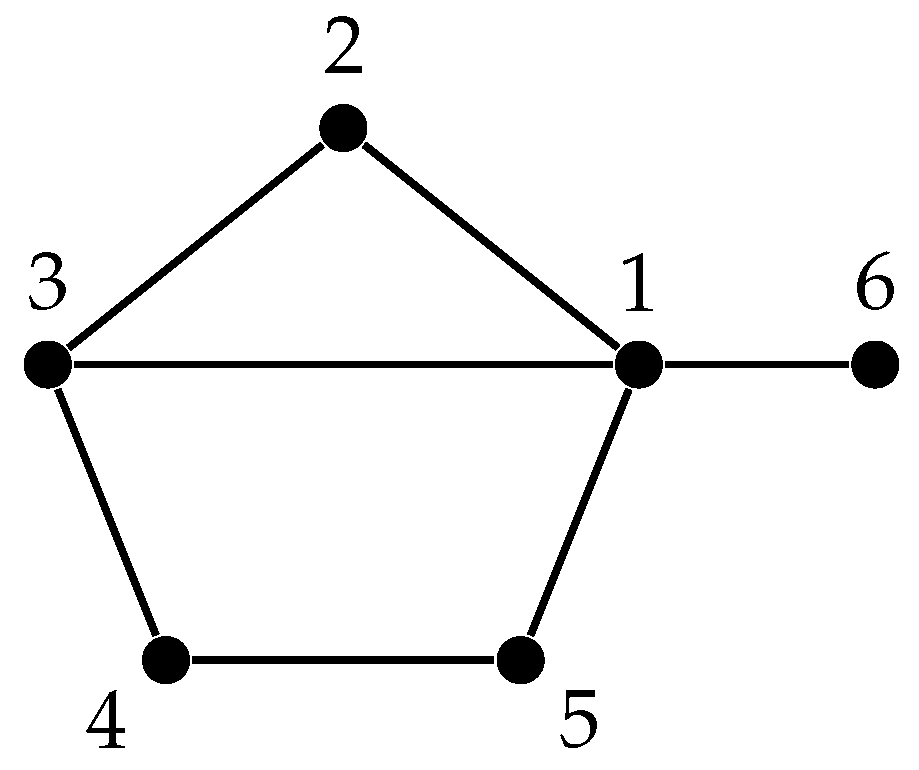
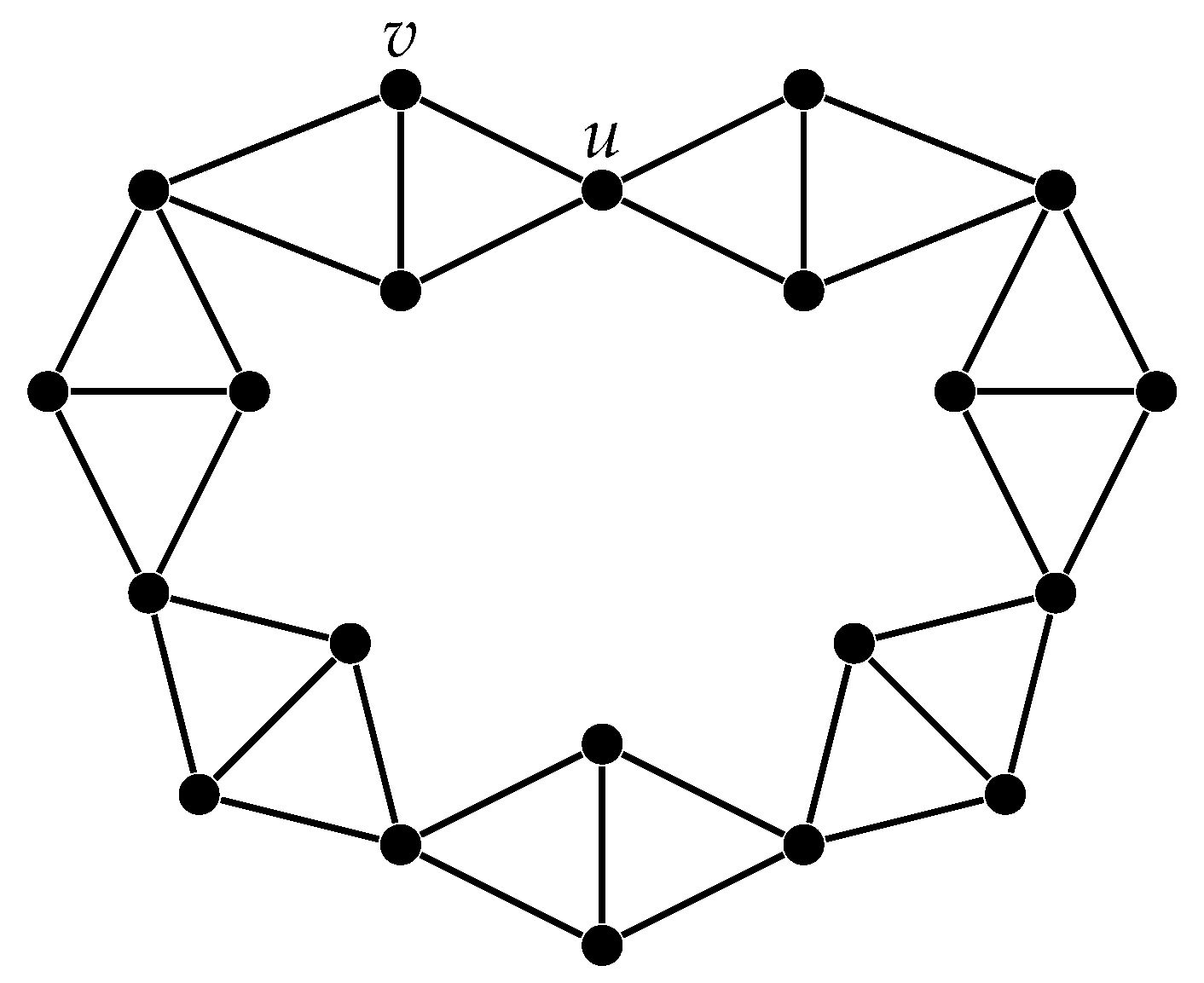
Although, each pair of similar vertices (i.e., vertices in the same orbit) are H-equivalent, the converse is not generally true. For example, the two vertices u and v shown in Figure 1 are H-equivalent, but they are in different orbits. Moreover, the condition $D\left(u\right)=D\left(v\right)$ for two arbitrary vertices $\in V\left(G\right)$ does not guarantee that they are H-equivalent. Figure 2, gives an example in which $D\left(u\right)=D\left(v\right)$, but u and v are not H-equivalent.

From Corollary 1, it is clear that if G is a vertex-transitive graph, then $H\left(G\right)=0$. However, there are many examples of non-vertex-transitive graph with zero H-entropy, see for example the graph shown in Figure 3.

Example 1.

Let G be a finite group with binary operation ☆ and $S\subseteq G$, a non-empty subset containing an inverse for every element but no identity element. The Cayley graph $X=Cay(G,S)$ is a graph with vertex set $V\left(G\right)=G$ in which any two vertices x and y are adjacent if and only if $y☆x^{-1}\in S$. Each Cayley graph is vertex-transitive and, thus, the H-entropy of X is zero. For example consider the cyclic group ${\mathcal{Z}}_4=\{e,x,x^2,x^3\}$ and suppose $S=\{x,x^3=x^{-1}\}$. The corresponding Cayley graph is isomorphic with the cycle graph $C_4$. For more details about the Cayley graphs, see [22].

Example 2.

A distance-transitive graph is defined as follows. For pairs of vertices $x,y$ and $u,v$ in $V\left(G\right)$, there exists an automorphism of the graph that carries u to x and v to y, whenever $d_G(x,y)=d_G(u,v)$.

Every distance-transitive graph G is vertex-transitive and, thus, $H\left(G\right)=0$.

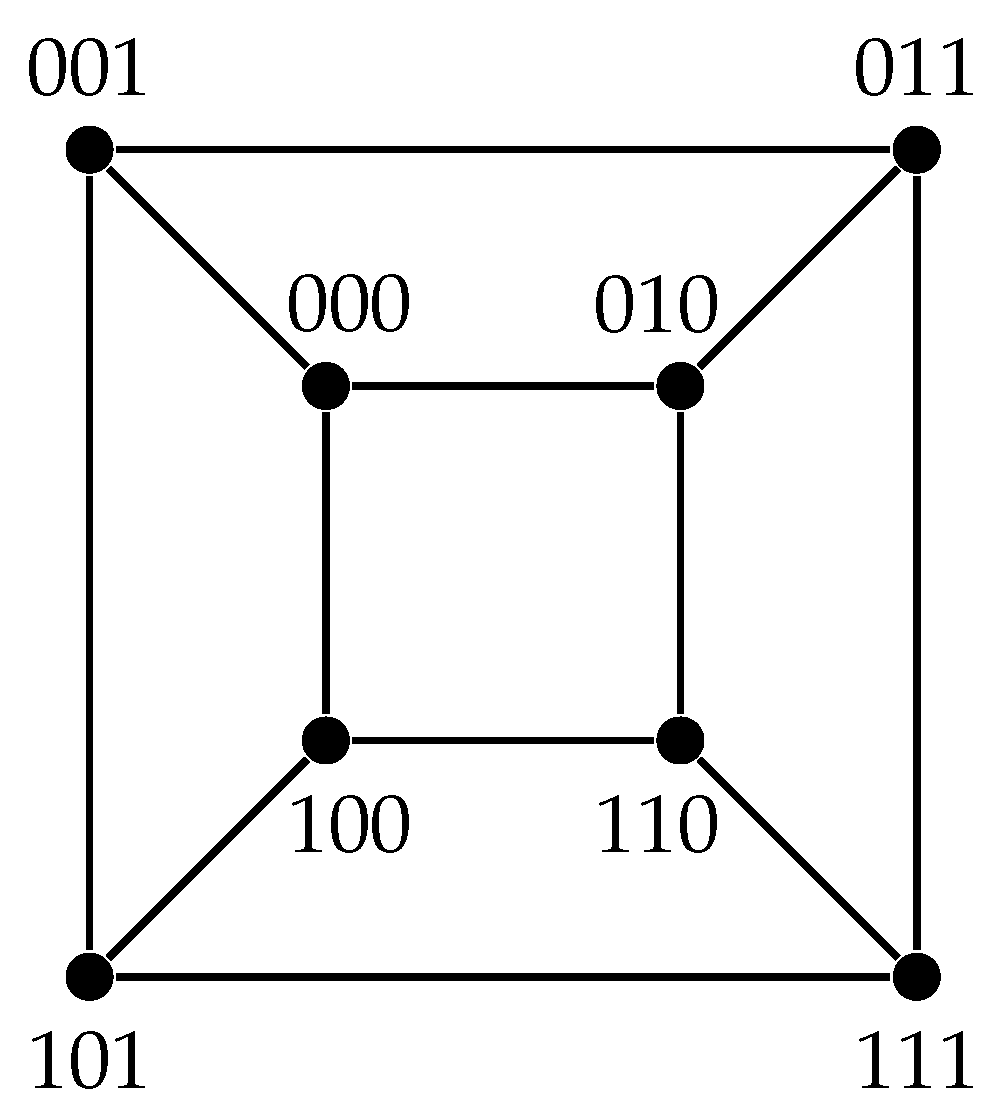
Example 3.

Hamming graphs [23] constitute a special class of graphs used in several branches of mathematics and computer science. Let S be a set of q elements and n a positive integer. The vertex set of the Hamming graph $H(n,q)$ is the set of ordered n-tuples of elements of S and two vertices $u=(u_1,\dots u_n)$ and $v=(v_1,\dots v_n)$ are adjacent if they differ in one position only. It is a well-known fact that all Hamming graphs are distance-transitive and, hence, $H\left(G\right)=0$. For example, the cube $Q_3$ is a Hamming graph, see Figure 4.

Recall the following theorem stated earlier.

Theorem 2

([8]). If G is a regular graph with diameter $\rho \left(G\right)=2$, then $H\left(G\right)=0$.

A regular graph with n vertices and degree k is said to be strongly regular if there are integers $\lambda$ and $\mu$ such that every two adjacent vertices have $\lambda$ common neighbors and every two non-adjacent vertices have $\mu$ common neighbors. The following result can be derived from Theorem 2.

Corollary 2.

If G is a strongly regular graph, then $H\left(G\right)=0$.

Proof. 

It is well-known that each strongly regular graph is regular of diameter 2. The conclusion follows from Theorem 2. □

Theorem 3.

Let G be a connected graph on n vertices with the maximum value of H-entropy. Then $Aut\left(G\right)$ consists of the identity alone.

Proof. 

Let $X_1,\cdots ,X_h$ be the set of all H-equivalence classes of G. By the definition of H-entropy one can see that

$$\begin{array}{ccc}\hfill H\left(G\right)& =& -\sum _{i=1}^h\frac{|X_i|}{\left|V\right|}log\left(\frac{|X_i|}{\left|V\right|}\right)\hfill \\ & =& -\sum _{i=1}^h\frac{|X_i|}{\left|V\right|}[log\left(|X_i|\right)-log\left(\left|V\right|\right)]\hfill \\ & =& log\left(n\right)-\frac{1}{n}\sum _{i=1}^h\left|X_i\right|log\left(|X_i|\right).\hfill \end{array}$$

Clearly, $H\left(G\right)$ reaches the maximum value $log\left(n\right)$ if $A={\sum }_{i=1}^h\left|X_i\right|log\left(|X_i|\right)=0$. Since for each $i(1\le i\le h)$, $|X_i|\ge 1$, we have $A=0$ if and only if $|X_i|=1$, for $1\le i\le h$. Hence, Corollary 1 implies that all orbits of $Aut\left(G\right)$ are singleton sets and the assertion follows. □

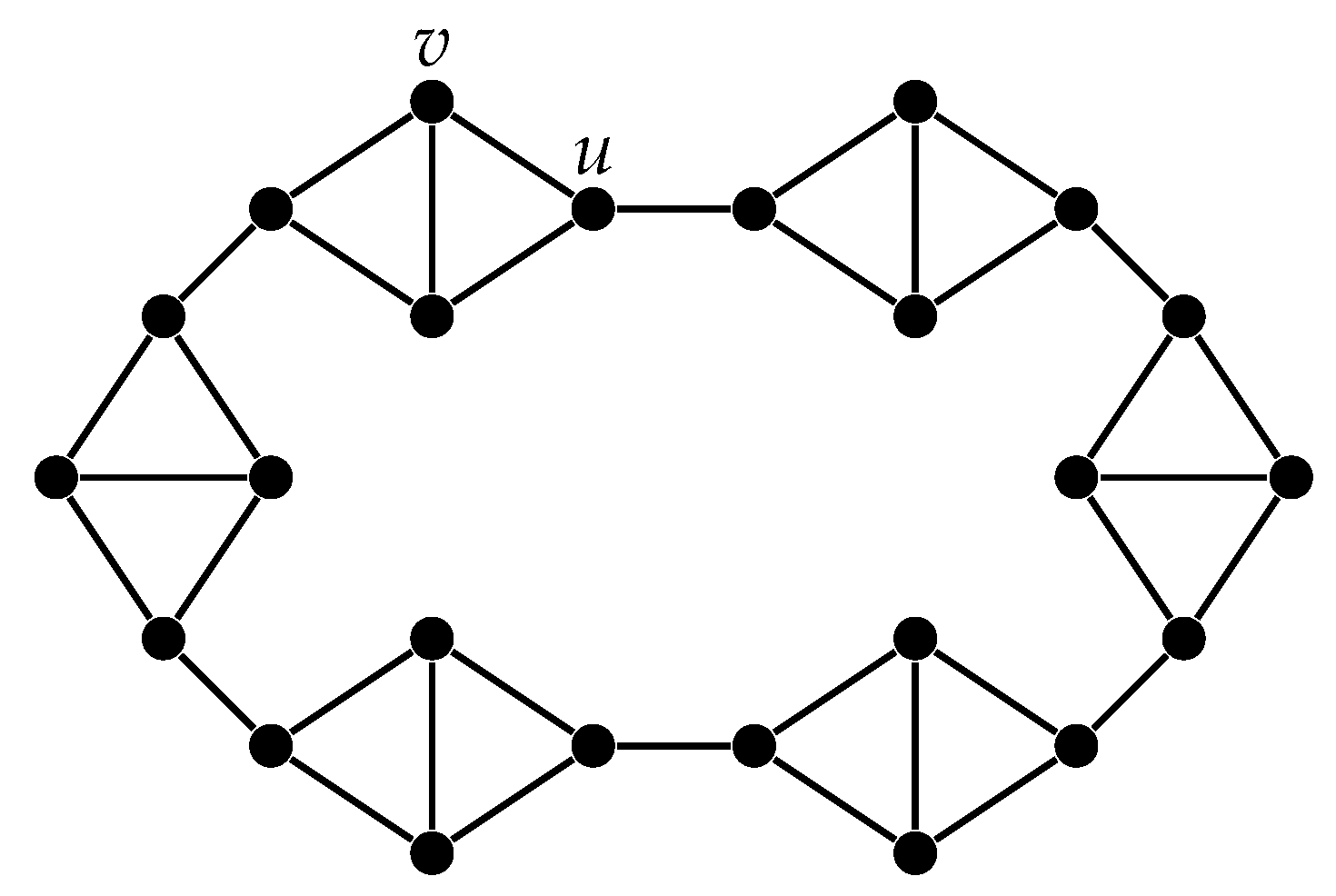
The converse of Theorem 3 is not true. For example consider the graph G shown in Figure 5. Then $Aut\left(G\right)$ consists of the identity alone, but $H\left(G\right)\ne 0$, since 2 and 5 are in the same H-partition.

Lemma 1

([8]). If G is a connected regular graph of degree greater than $n/2$, then $H\left(G\right)=0$.

Theorem 4.

Let n be an even number and G be an r-regular edge-transitive graph of order n, where $r\ge n/2$. Then $H\left(G\right)=0$.

Proof. 

If G is a regular graph of degree greater than $n/2$, then by Lemma 1 we infer $H\left(G\right)=0$. Suppose G is a regular edge-transitive graph of degree $n/2$. We claim that G is vertex-transitive. On the contrary, suppose G is not vertex-transitive. Then following [22], G is a regular bipartite graph of degree $n/2$, which implies that G is isomorphic to $K_{\frac{n}{2}.\frac{n}{2}}$, thus contradicting our hypothesis. Hence, G is vertex-transitive and the conclusion follow form Corollary 1. □

Theorem 5.

Let G be a graph with at least five vertices that is edge-transitive but not bipartite, all of whose vertices are of odd degree. Then $H\left(G\right)=0$.

Proof. 

Similar to the proof of Theorem 4, one can show that G is vertex-transitive and the result follows from Corollary 1. □

3.2. H-Entropy of Product Graphs

In this section, we derive explicit formulas for the H-Entropy of some well known graph products. Included here are the cartesian product, join, corona and lexicographic product. For detailed information about these graph products, see [24].

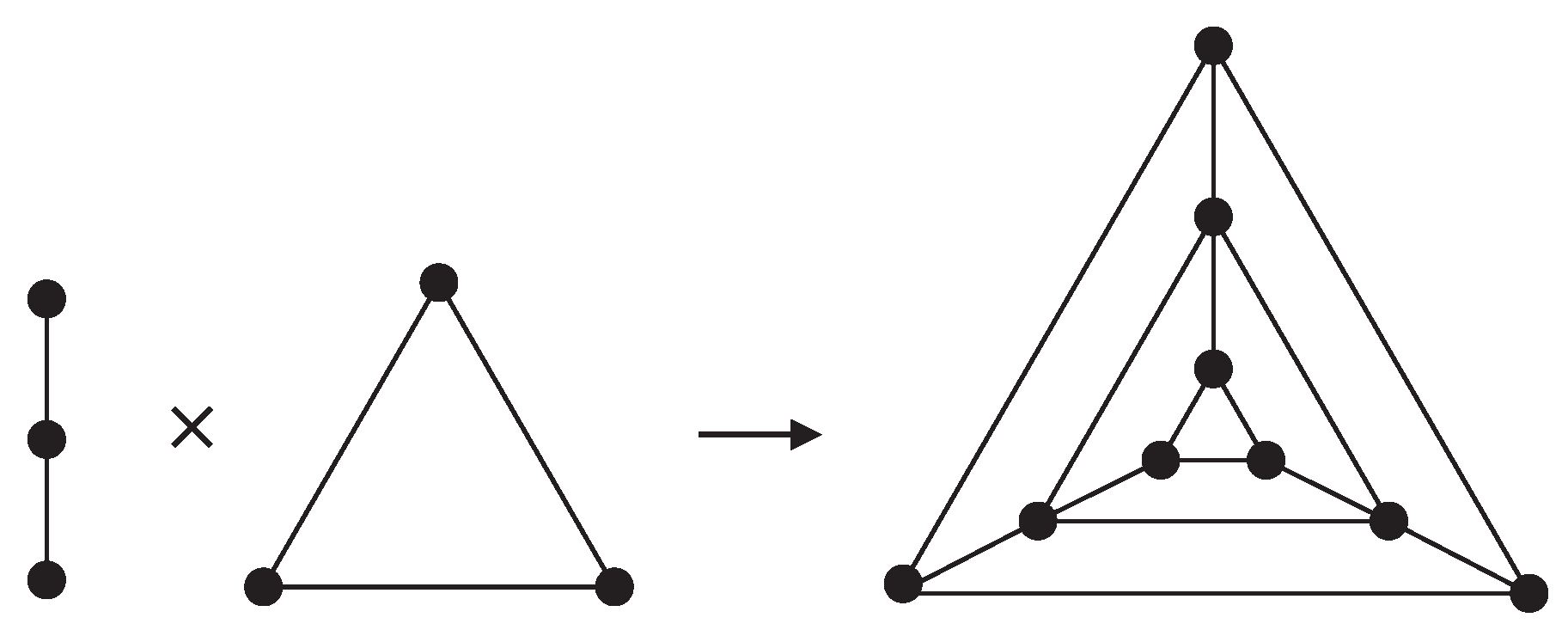
Cartesian Product.

Given graphs A and B, the cartesian product $A\times B$ is defined as the graph on the vertex set $V\left(A\right)\times V\left(B\right)$ with $u=(u_1,u_2)$ and $v=(v_1,v_2)$ adjacent if and only if either ($[u_1=v_1$ and $u_2{v}_2\in E\left(B\right)]$) or ($[u_2=v_2$ and $u_1{v}_1\in E\left(A\right)]$). This operation is illustrated in Figure 6.

Theorem 6.

Let A and B be graphs in which a and x are H-equivalent in A, and b and y are H-equivalent in B. Then $(a,b)$ and $(x,y)$ are H-equivalent in $A\times B$.

Proof. 

Appealing to the definition, we conclude

$$\begin{array}{ccc}\hfill |S_i(x,y)|& =& \left|\right\{(a,b):d_{A\times B}\left((x,y),(a,b)\right)=i\left\}\right|\hfill \\ & =& \left|\right\{(a,b):d_A(x,a)+d_B(b,y)=i\left\}\right|\hfill \\ & =& {\displaystyle \sum _{j=0}^i|S_j(A,x)|\times |S_{i-j}(B,y)|,}\hfill \end{array}$$

where for $j,i-j\ge max\left\{\rho \right(A),\rho (B\left)\right\}$ we have $|S_j\left(x\right)|\times |S_{i-j}\left(y\right)|=0.$ Since, a is H-equivalent to x, and b is H-equivalent to y, the result follows. □

Corollary 3.

Suppose $(a,x)$ and $(b,y)$ are H-equivalent in $A\times B$. If a and b are H-equivalent in A, then x and y are H-equivalent in B.

Proof. 

Suppose $(a,x)$ and $(b,y)$ are H-equivalent in $A\times B$. This means that $S_i(a,x)=S_i(b,y)$ for $1\le i\le \rho$. Then if a, b are H-equivalent in A, Theorem 6 yields that $S_i\left(x\right)=S_i\left(y\right)$ and thus x and y are H-equivalent. □

Lemma 2

([24]). Let A and B be graphs, satisfying $\left(\right|A|,|B\left|\right)=1$. Then $Aut(A\times B)$ is isomorphic to $Aut\left(A\right)\times Aut\left(B\right)$.

Theorem 7.

Let A and B be two graphs and A be vertex-transitive, where $\left(\right|A|,|B\left|\right)=1$. Then $H(A\times B)=H\left(B\right)$.

Proof. 

If A is vertex-transitive, then ${(x,y)}^{Aut(A\times B)}=V\left(A\right)\times y^{Aut\left(B\right)}$. Hence,

$${\displaystyle H(A\times B)=-\sum _{y\in V\left(B\right)}\left[\frac{\left|V\left(A\right)\right|\times |y^{Aut\left(B\right)}|}{\left|V\right(A\left)\right|\times \left|V\right(B\left)\right|}log\frac{\left|V\left(A\right)\right|\times |y^{Aut\left(B\right)}|}{\left|V\right(A\left)\right|\times \left|V\right(B\left)\right|}\right]=H\left(B\right).}$$

 □

Join

The join $G=A+B$ of graphs A and B with disjoint vertex sets $V_1$ and $V_2$ and edge sets $E_1$ and $E_2$ is the graph union $A\cup B$, where each vertex of $V_1$ is adjacent with all vertices of $V_2$, see Figure 7.

Let A and B be two r-regular graphs with n vertices. Then $A+B$ is $r+n$-regular of diameter 2 and by Theorem 2, we infer $H(A+B)=0$.

Theorem 8.

Suppose A and B are r-regular graphs. If vertices $a,b\in A+B$ are H-equivalent, then $\left|V\right(A\left)\right|=\left|V\right(B\left)\right|.$

Proof. 

By definition, we get $|S_i\left(a\right)|=|S_i\left(b\right)|$, for $i=1,2$. From $|S_2\left(a\right)|=|S_2\left(b\right)|$, we conclude that $\left|V\left(A\right)\right|-|S_1\left(a\right)|-1=|V\left(B\right)|-|S_1\left(b\right)|-1$. Finally, $|S_1\left(a\right)|=|S_1\left(b\right)|$ implies $\left|V\right(A\left)\right|=\left|V\right(B\left)\right|$. □

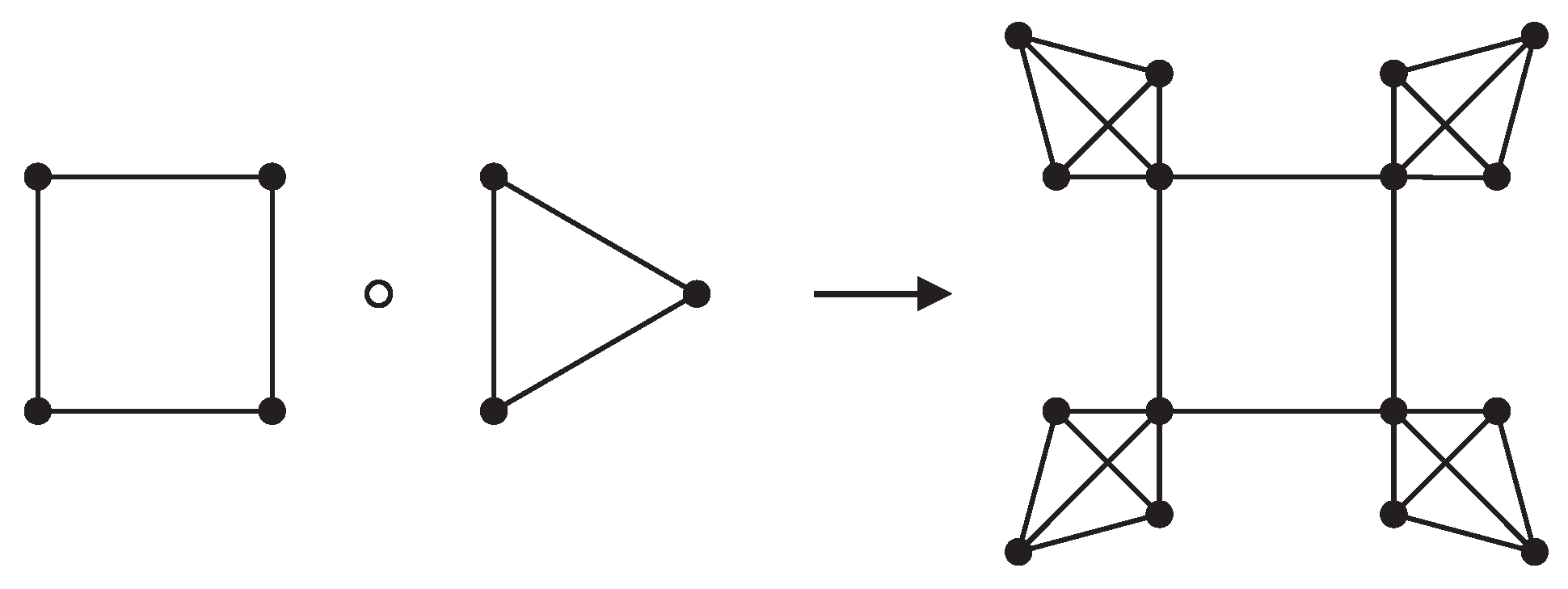
Corona

Let A and B be graphs with $n_1$ and $n_2$ vertices, respectively. The corona product $A\circ B$ is a graph obtained from A and B by taking one copy of A and $n_1$ copies of B and then joining each vertex from the ith copy of B with the ith vertex of A, see Figure 8.

Let $u_i^j$ denote the vertex in the jth copy of B corresponding to vertex $v_i\in A$, and let $B^j$ represent the jth copy of B.

Theorem 9.

Suppose A and B are two graphs with vertex sets $\{v_1,\cdots ,v_{n_1}\}$ and $\{u_1,\cdots ,u_{n_2}\}$, respectively. Then

(i) 

If $v_r,v_s\in V\left(A\right)$ are H-equivalent, then $v_r,v_s$ in $A\circ B$ are H-equivalent.

(ii) 

If $u_r,u_s\in V\left(B^i\right)$ are H-equivalent, then $u_r,u_s$ in $A\circ B$ are H-equivalent.

(iii) 

If $v_r\in V\left(A\right)$ and $u_r\in V\left(B^r\right)$, then $v_r,u_r$ in $A\circ B$ are not H-equivalent.

(iv) 

If $v_r,v_s\in V\left(A\right)$ are H-equivalent, then $u_r^r\in B^r$ and $u_s^s\in B^s$ are H-equivalent in $A\circ B$.

Proof. 

(i)

Let $v_r,v_s\in V\left(A\right)$ be H-equivalent. It is clear that $|S_1(A\circ B,v_r)|=|S_1(A,v_r)|+n_2$. For $2\le i\le \rho (A\circ B)$ and $t\ne r$, we obtain

$$\begin{array}{c}\hfill |S_i(A\circ B,v_r)|=|\{v_t\in A|d_A(v_r,v_t)=i|+|\{u_k^t\in B^t|d_A(v_r,v_t)=i-1\}|.\end{array}$$

So, $|S_i(A\circ B,v_r)|=|S_i(A,v_r)|+n_2\left|S_{i-1}(A,v_r)\right|$. This means that for $1\le i\le \rho (A\circ B)$, we have $|S_i(A\circ B,v_r)|=|S_i(A\circ B,v_s)|$.

(ii)

Let $u_r^r,u_s^r\in B^r$ be H-equivalent. Then $|S_1(A\circ B,u_r^r)|=|S_1(B,u_r^r)|+1$ and

$$|S_2(A\circ B,u_r^r)|=|S_1(A,v_r)|+n_2-\left|S_1(B^r,u_r^r)\right|.$$

If $3\le i\le \rho (A\circ B)$ and $t\ne r$, then

$$\begin{array}{ccc}\hfill |S_i(A\circ B,u_r^r)|& =& \left|\right\{v_t\in A|d_A(v_r,v_t)=i-1\}|\hfill \\ & +& \left|\right\{u_k^t\in B^t|d_A(v_r,v_t)=i-2\}|\hfill \end{array}$$

This means that, $|S_i(A\circ B,u_r^r)|=|S_{i-1}(A,v_r)|+n_2\left|S_{i-2}(A,v_r)\right|.$ Hence, for $1\le i\le \rho (A\circ B)$, $|S_i(A\circ B,u_r^r)|=|S_i(A\circ B,u_s^r)|$.

(iii)

Since the degree of each vertex in $V\left(A\right)$ is greater than the degree of vertices in $B^r$, they are not H-equivalent.

(iv)

The proof is similar to the one of $\left(ii\right)$.

 □

Corollary 4.

The H-entropy of $A\circ B$ is greater than zero.

Proof. 

By Theorem 9$\left(iii\right)$, the vertices of A are not H-equivalent to the ith copy of B and thus there are at least two vertices $a\in A$ and $b\in B^i$ such that a and b are not H-equivalent in G. Hence, $H(A\circ B)\ne 0.$ □

Lexicographic product

Let A and B be graphs having disjoint vertex sets $V_1$ and $V_2$ with $|V_1|=n_1$, $|V_2|=n_2$, and edge sets $E_1$ and $E_2$ with $|E_1|=m_1$, $|E_2|=m_2$. The lexicographic product or composition $G=A\left[B\right]$ of A and B is the graph with vertex set $V_1\times V_2$, in which $u=(u_1,v_1)$ is adjacent to $v=(u_2,v_2)$ whenever $u_1$ is adjacent to $u_2$, or $u_1=u_2$ and $v_1$ is adjacent to $v_2$, see Figure 9.

Theorem 10.

Let $u=(u_1,v_1)$ and $v=(u_2,v_2)$ be two vertices of $A\left[B\right]$. If $u_1$ and $u_2$ are H-equivalent in A and $v_1$ and $v_2$ are H-equivalent in B, then u and v are H-equivalent in $A\left[B\right].$

Proof. 

From the definition, if $u_1=u_2$ and $v_1{v}_2\in E\left(B\right)$, then $d_{A\left[B\right]}((u_1,v_1),$ $(u_2,v_2))=1$; and if $u_1=u_2$ and $v_1{v}_2\notin E\left(B\right)$, then $d_{A\left[B\right]}((u_1,v_1),(u_2,v_2))=2$. Also, if $u_1\ne u_2$, $d_{A\left[B\right]}((u_1,v_1),(u_2,v_2))=d_A(u_1,u_2).$ This implies that

$$\begin{array}{ccc}\hfill |S_1\left(u\right)|& =& n_2|S_1(A,u_1)|+|S_1(B,v_1)|,\hfill \\ \hfill |S_2\left(u\right)|& =& n_2|S_2(A,u_1)|+n_2-1-\left|S_1(B,v_1)\right|,\hfill \end{array}$$

and if $3\le i\le \rho \left(A\right[B\left]\right)$, then $S_i\left(u\right)=n_2\left|S_i(A,u_1)\right|$ and the proof is complete. □

3.3. H-entropy of Graphs with Two Orbits

In this section, we trace implications of the conditions under which a graph has two vertex-orbits and at most two H-equivalence classes.

Definition 1.

A graph G is called co-distant, if for every pair of vertices $u,v\in V\left(G\right)$, u and v have the same total distance, i.e., $D\left(u\right)=D\left(v\right)$.

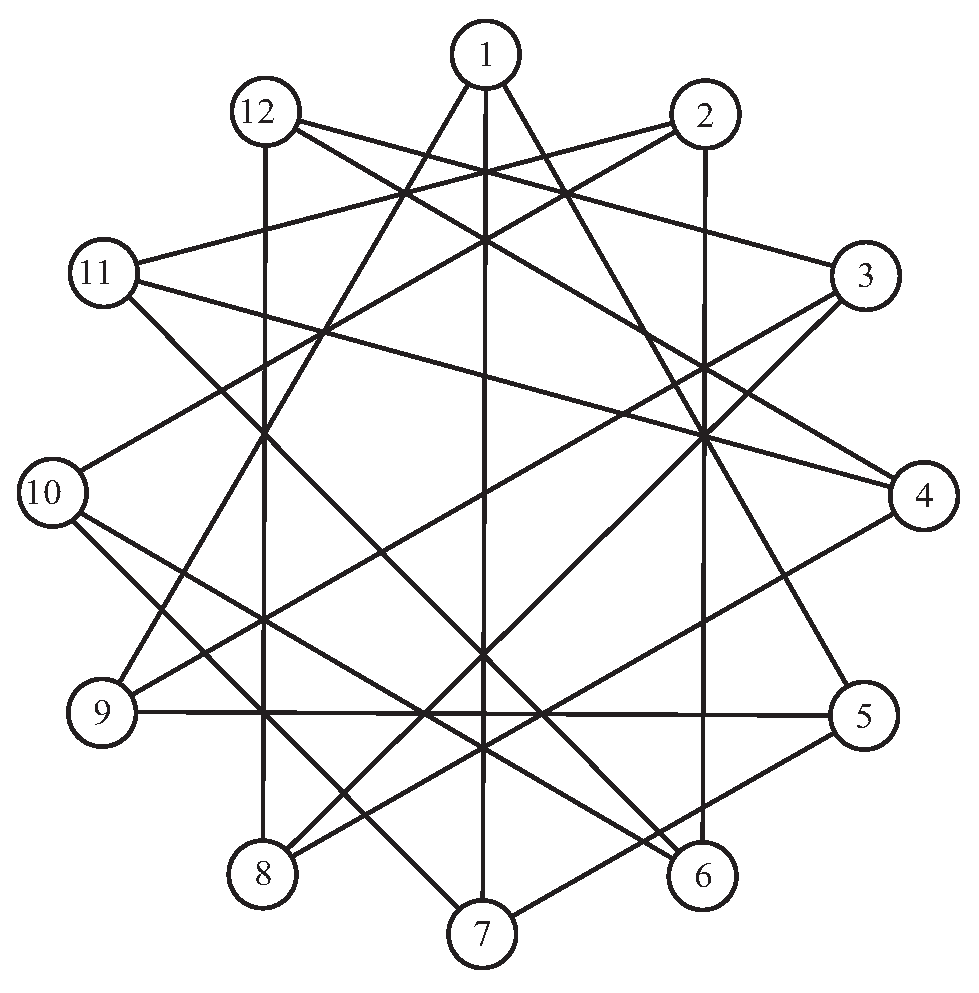
It is clear that each vertex-transitive graph is a co-distant, but there are many classes of non-transitive co-distant graphs. Consider the graph G in Figure 10. This graph has two orbits namely $V_1=\{1,2,5,6,8,12\}$ and $V_2=\{3,10,4,7,11,9\}$. The distance matrix of this graph shows that $\rho \left(G\right)=4$ and $D\left(1\right)=D\left(3\right)$ while the H-entropy of G is 1.

Theorem 11.

Let G be a graph with two orbits. Then $H\left(G\right)=0$ or $H\left(G\right)=I_a\left(G\right)$.

Proof. 

Suppose G has two orbits $V_1$ and $V_2$. If $V_1\cup V_2$ is a H-partition of G, then clearly $H\left(G\right)=-log1=0$. If $V_1$ and $V_2$ are two distinct H-partitions, then $H\left(G\right)=I_a\left(G\right)$. □

Corollary 5.

Let G be a connected edge-transitive graph but not vertex-transitive. Then $H\left(G\right)=0$ or $H\left(G\right)=I_a\left(G\right)$.

Proof. 

Under the above conditions, one can prove that if $H\left(G\right)\ne 0$, then G is bipartite and $Aut\left(G\right)$ has two orbits that form a bipartition of $V\left(G\right)$. Applying Theorem 11 concludes the proof. □

Corollary 6.

Suppose G is a graph whose H-entropy is zero. Then G is not a tree. More generally, G is a regular graph.

Proof. 

If $H\left(G\right)=0$, then by Theorem 11, H has only one H-equivalence class and thus for two arbitrary vertices $u,v\in V$, $|S_1\left(u\right)|=|S_1\left(v\right)|$. Hence G is a regular graph and this completes the proof. □

Let G be a graph with two orbits $V_1$ and $V_2$, where $|V_1|=n_1$, $|V_2|=n_2$ and $V_1$ and $V_2$ are not H-equivalent. Since $|V_2|=n_2=n-n_1$, by substituting $n_1$ and $n_2$ in Equation 2, we have

$$\begin{array}{c}\hfill H\left(G\right)={\displaystyle \frac{n_1}{n}}log{\displaystyle \frac{n}{n_1}}+{\displaystyle \frac{n-n_1}{n}}log{\displaystyle \frac{n}{n-n_1}}.\end{array}$$

(3)

Equation (3) allows for proving the following result.

Theorem 12.

Suppose G is a graph with two orbits $V_1$ and $V_2$ and with non-zero H-entropy. Then, $H\left(G\right)=1$ if and only if n is even and $|V_1|=|V_2|=n/2$.

Theorem 13.

Let G be a regular graph with two orbits $V_1=u^{Aut\left(G\right)}$ and $V_2=v^{Aut\left(G\right)}$, where the diameter of G is less than 4. If G is co-distant, then $H\left(G\right)=0$.

Proof. 

If $\rho \left(G\right)\le 2$, then according to Theorem 2, $H\left(G\right)=0$. Suppose G is an r-regular graph of diameter $\rho \left(G\right)=3$. Then the entries of the u-th and v-th rows of distance matrix are $1^r,2^a,3^b$ and $1^r,2^{a-k},3^{b+k}$, respectively, where a and b are non-negative integers such that $a+b=n-r-1$. Since $D\left(u\right)=D\left(v\right)$, we have $2(a-k)+3(b+k)=2a+3b$ which implies $k=0$. This means that the number of 2’s and 3’s in the u-th and v-th rows of the distance matrix are the same and, thus, u and v are H-equivalent. □

3.4. H-Entropy of Trees and Graphs with Two Orbits

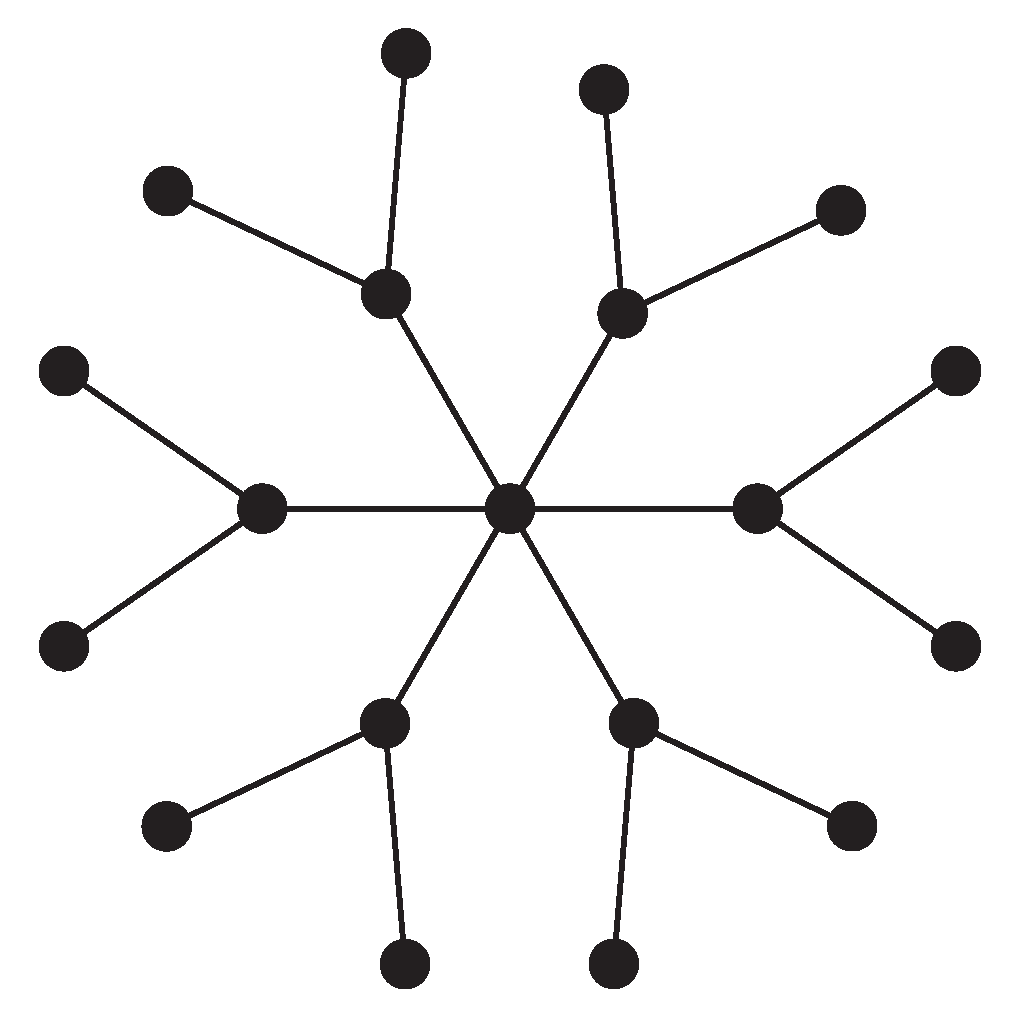
Let $S_n$ and $W_n$ be the star graph and the wheel graph on n vertices, respectively. The bi-star graph $B_{m,n}$ is a graph obtained from the union of $S_{n+1}$ and $S_{m+1}$ by joining their central vertices. Also let $S_{n,m}$ be a tree with a central vertex of degree n, n vertices of degree $m+1$ and $nm$ pendant vertices, see Figure 11. Finally, suppose, $S{B}_{m,n}$ is a graph obtained from two copies of $S_{n,m}$ by joining the central vertices.

Theorem 14

([24]). Every tree T contains an edge or a vertex that is invariant under each automorphism of T.

In what follows, a 2-graph is defined by having an automorphism group with exactly two orbits. A k-graph can be defined similarly.

Theorem 15.

Let T be a 2-tree on n vertices. Then T is isomorphic to $S_n$ or T is isomorphic to $B_{t,t}$, where $t=\frac{n}{2}-1$.

Proof. 

Suppose $Aut\left(T\right)$ has two orbits and T has a central vertex w. The central vertex forms a singleton orbit since for each automorphism $\alpha \in Aut\left(T\right)$, we have $\alpha \left(w\right)=w$. But T has only two orbits, so the other vertices are in the same orbit. Since every tree has at least two vertices of degree 1, all vertices in the second orbit are pendant and adjacent to the central vertex. This means that T is isomorphic to $S_n$. If T has a central edge, a similar argument shows that T is isomorphic to $B_{t,t}$, where $t=\frac{n}{2}-1$. □

Corollary 7.

Let T be a 2-tree on $n\ge 3$ vertices. Then one of the following cases holds:

(i) 

T is isomorphic to $S_n$ and $H\left(T\right)={\displaystyle \frac{logn}{n}}+{\displaystyle \frac{n-1}{n}}log{\displaystyle \frac{n}{n-1}}$.

(ii) 

$n=2m+2$, T is isomorphic to $B_{m,m}$ and $H\left(T\right)={\displaystyle \frac{1}{m+1}}log(m+1)+{\displaystyle \frac{m}{m+1}}log\left({\displaystyle \frac{m+1}{m}}\right)$.

Theorem 16.

Let T be a 3-tree on n vertices. Then T is isomorphic to $S_{n,m}$ or T is isomorphic to $S{B}_{n,m}$.

Proof. 

Suppose T is a tree with a central vertex w. The other vertices of T include the pendant vertices and vertices of degree i, where $i\ge 2$. We know $\left\{w\right\}$ is a singleton orbit and the vertices of degree 1 also form an orbit. Hence, the other vertices necessarily have the same degree and constitute the third orbit. This implies that T is isomorphic to $S_{n,m}$. If T has a central edge, a similar argument shows that T is isomorphic to $S{B}_{n,m}$. □

Theorem 17.

Let G be a 2-graph with non-zero H-entropy. Then $H\left(G\right)={\displaystyle \frac{logn}{n}}+{\displaystyle \frac{n-1}{n}}log{\displaystyle \frac{n}{n-1}}$ if and only if G is isomorphic to $K_1+\mathcal{H}$, where $\mathcal{H}$ is a vertex-transitive graph.

Proof. 

If $G=K_1+\mathcal{H}$, where $\mathcal{H}$ is a vertex-transitive, then G has two orbits: A singleton orbit and an orbit of size $n-1$. The conclusion follows from Equation (3). Conversely, if $H\left(G\right)={\displaystyle \frac{logn}{n}}+{\displaystyle \frac{n-1}{n}}log{\displaystyle \frac{n}{n-1}},$ then

$$\begin{array}{c}\hfill H\left(G\right)=-({\displaystyle \frac{n-1}{n}}log{\displaystyle \frac{n-1}{n}}+{\displaystyle \frac{1}{n}}log{\displaystyle \frac{1}{n}}).\end{array}$$

(4)

Since $Aut\left(G\right)$ has two orbits and $H\left(G\right)$ is non-zero, the orbits and H- partitions are the same and Equation (4) implies that $|H_1|=1$ and $|H_2|=n-1$ which completes the proof. □

4. Distance Entropy

The H-entropy of a graph G is based on the distance between the vertices of G. We examine here the well known distance-based Wiener index. This index was originally defined as one half of the sum of the distances between every pair of vertices in a graph, see [25]. More precisely, the Wiener index of a graph G is given by $W\left(G\right)=\frac{1}{2}{\sum }_{u\in V\left(G\right)}D\left(u\right).$ Hence, if G is vertex-transitive, $W\left(G\right)=\frac{n}{2}D\left(u\right)$, where $u\in V\left(G\right)$ is an arbitrary vertex.

Let G be a graph with Wiener index $W\left(G\right)$. Bonchev and Trinajstic [2] developed a distance-based entropy measure using a partition defined by sets of vertices having the same distance characteristics, as follows:

$$\begin{array}{c}\hfill I_D\left(G\right)=-\sum _{u\in V\left(G\right)}\frac{D\left(u\right)}{2W\left(G\right)}log\left(\frac{D\left(u\right)}{2W\left(G\right)}\right).\end{array}$$

Clearly, if G is vertex-transitive, then

$$\begin{array}{c}\hfill I_D\left(G\right)=-\frac{nD\left(u\right)}{nD\left(u\right)}log\left(\frac{nD\left(u\right)}{nD\left(u\right)}\right)=0.\end{array}$$

Also, if G has two orbits $V_1$ and $V_2$ where $|V_1|=n_1$ and $|V_2|=n_2$ then

$$\begin{array}{c}\hfill I_D\left(G\right)=-\frac{n_{1}D\left(u\right)}{2W\left(G\right)}log\left(\frac{n_{1}D\left(u\right)}{2W\left(G\right)}\right)-\frac{n_{2}D\left(v\right)}{2W\left(G\right)}log\left(\frac{n_{2}D\left(v\right)}{2W\left(G\right)}\right),\end{array}$$

where $u\in V_1$ and $v\in V_2$. If G is a co-distant graph, then $I_D\left(G\right)=0$ while the H-entropy is not necessarily zero. For example, consider the graph G shown in Figure 10. This graph is co-distant on 12 vertices with automorphism group $C_2\times S_4$. The automorphism group $Aut\left(G\right)$ has two orbits and G has non-zero H-entropy. In other words, the vertices 1 and 3 are not H-equivalent. Their distance degree sequences are $(0,3,2,4,1,3,1,3,1,2,4,3)$ and $(2,4,0,2,2,4,3,1,1,4,3,1)$, respectively. On the other hand, $D\left(1\right)=D\left(3\right)=27$ and its Wiener index is 162. In general, if G has n vertices, the total distance of a vertex in G is $D\left(u\right)=3n^2/16$, if 8 does not divide n, and $D\left(u\right)=3n^2/16+n/4$, if 8 divides n. Hence, the Wiener index is $W\left(G\right)=3n^3/32$ if 8 does not divide n, and $W\left(G\right)=3n3/32+n/4$, otherwise. Thus, the distance entropy of this class of graphs is zero while the H-entropy is not zero.

By exhaustive analysis, we have found that up to isomorphism, there are exactly 12 co-distant regular graphs of order at most 12 with two orbits and diameter $\rho \left(G\right)\ge 3$.

To obtain this result, we first generated all regular graph up to 12 vertices using the program of Nauty [26], and then we selected all graphs with diameter greater than 2 and less than or equal $n/2$ having two orbits. This generation process was done with an R-package [27] called igraph. Graphs with more than one H-equivalence class were then identified. The only graph in this set having non-zero H-entropy is the one labeled G in Figure 8; all the others in this set have distance entropy 0. Our results shows that when a graph is co-distant, the distance entropy does not capture enough structural information to discriminate co-distant graphs, since $I_D\left(G\right)$ is zero for all of them.

5. Numerical Results

In this section, we investigate some numerical results about the H-entropy of co-distant 2-graphs. Consider the graph G of order 24 in Figure 12. This graph has two orbits of size 12, where the orbit representatives are vertices u and v. Hence, the H-entropy is

$$\begin{array}{c}\hfill H\left(G\right)=-({\displaystyle \frac{12}{24}}log{\displaystyle \frac{12}{24}}+{\displaystyle \frac{12}{24}}log{\displaystyle \frac{12}{24}})=1.\end{array}$$

(5)

Now consider the graph G of order 21 in Figure 13. This graph has two orbits of sizes 7 and 14, where the orbit representatives are the two vertices u and v. Hence, the H-entropy is

$$\begin{array}{c}\hfill H\left(G\right)=-({\displaystyle \frac{7}{21}}log{\displaystyle \frac{7}{21}}+{\displaystyle \frac{14}{21}}log{\displaystyle \frac{14}{21}})\approx 0.92.\end{array}$$

(6)

This means that for co-distant 2-graphs of the same order, the H-entropy of a graph X with two H-equivalence classes of the same size is greater than that of a graph Y whose H-equivalence classes do not satisfy this condition. In general, the H-entropy of every graph with two H-equivalence classes can be computed by the following function:

$$\begin{array}{c}\hfill f\left(i\right)=\frac{i}{n}log\frac{n}{i}+\frac{n-i}{n}log\frac{n}{n-i},\end{array}$$

(7)

where i ($1\le i\le n-1$) and $n-i$ are the size of H-equivalence classes of G. By computing the first derivative of f in Equation (7), we conclude that $i=\frac{n}{2}$ is an extremum point and $f\left(\frac{n}{2}\right)=1$. The diagram of f for all $1\le i\le n-1$ is shown in Figure 14. In general, the following theorem holds.

Theorem 18.

Let G be a graph on n vertices with k orbits $V_1,\dots ,V_k$, where $k|n$. Then $H\left(G\right)\le logk$ and equality holds if and only if $|V_1|=\dots =|V_k|=\frac{n}{k}$.

Proof. 

Let G have k Hosoya equivalence classes $H_1,\dots ,H_k$, where $|H_j|=i_k$ and $i_1+\dots +i_k=n$. By induction on k, one can see that the function

$$f(i_1,\dots ,i_k)=\frac{i_1}{n}log\frac{n}{i_1}+\dots +\frac{i_k}{n}log\frac{n}{i_k}$$

reaches the maximum value if $i_1=\dots =i_k=\frac{n}{k}$ and hence $f(i_1,\dots i_k)=logk$, see Figure 15. □

Theorem 18 implies that among all co-distant k-graphs on n vertices, a graph whose H-equivalence classes have the same size is one with the maximum value of H-entropy. This means that the H-entropy is a powerful measure for discriminating graph structure. In contrast, the distance-entropy for all co-distant graphs is zero which means that this measure does not capture enough structural information to discriminate between co-distant graphs.

6. Summary and Conclusions

In this paper we have investigated the Hosoya-entropy of some classes of graphs such as trees and product graphs. We also characterized the H-entropy of graphs whose automorphism group possesses exactly two vertex-orbits. In particular, we have solved the problem for trees. Also, we obtained some new results regarding automorphisms of trees. We showed that up to isomorphism, there exists only one graph G of order less than or equal 12 that is regular, with diameter greater than 2, and whose automorphism group has exactly two orbits. Finally, we have investigated the topological information content $I_D\left(G\right)$ of a graph. We found that the distance-based entropy $I_D\left(G\right)$ vanishes for co-distant graphs, which suggests a need to develop further measures to discriminate co-distant graphs.

In future research, we plan to investigate the Hosoya entropy for more complex graph classes.