Cosmological Consequences of a Parametrized Equation of State
Abstract
1. Introduction
2. Dynamical Chern–Simons Modified Gravity
3. Parametrizations of Equation of State Parameter
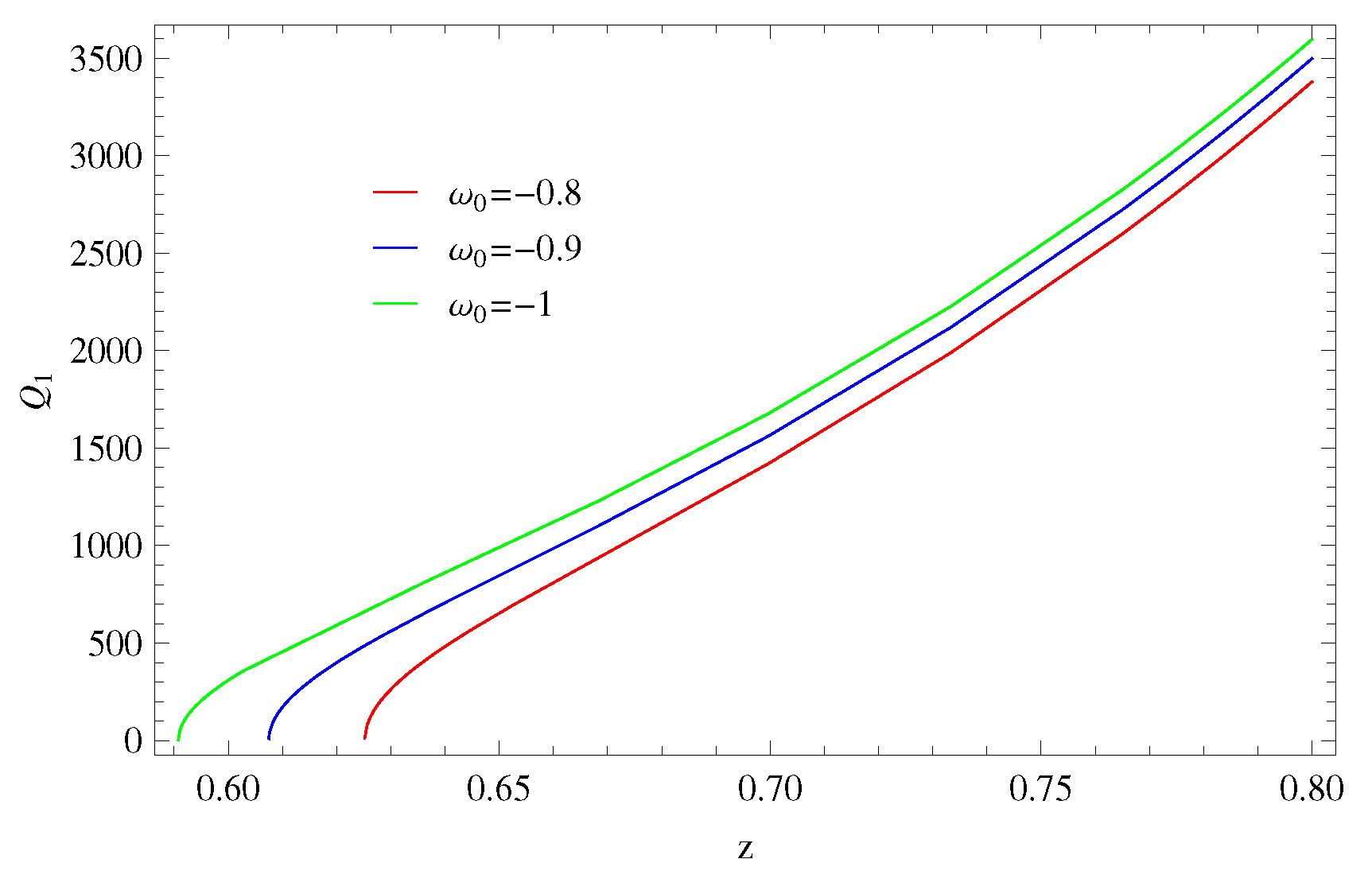
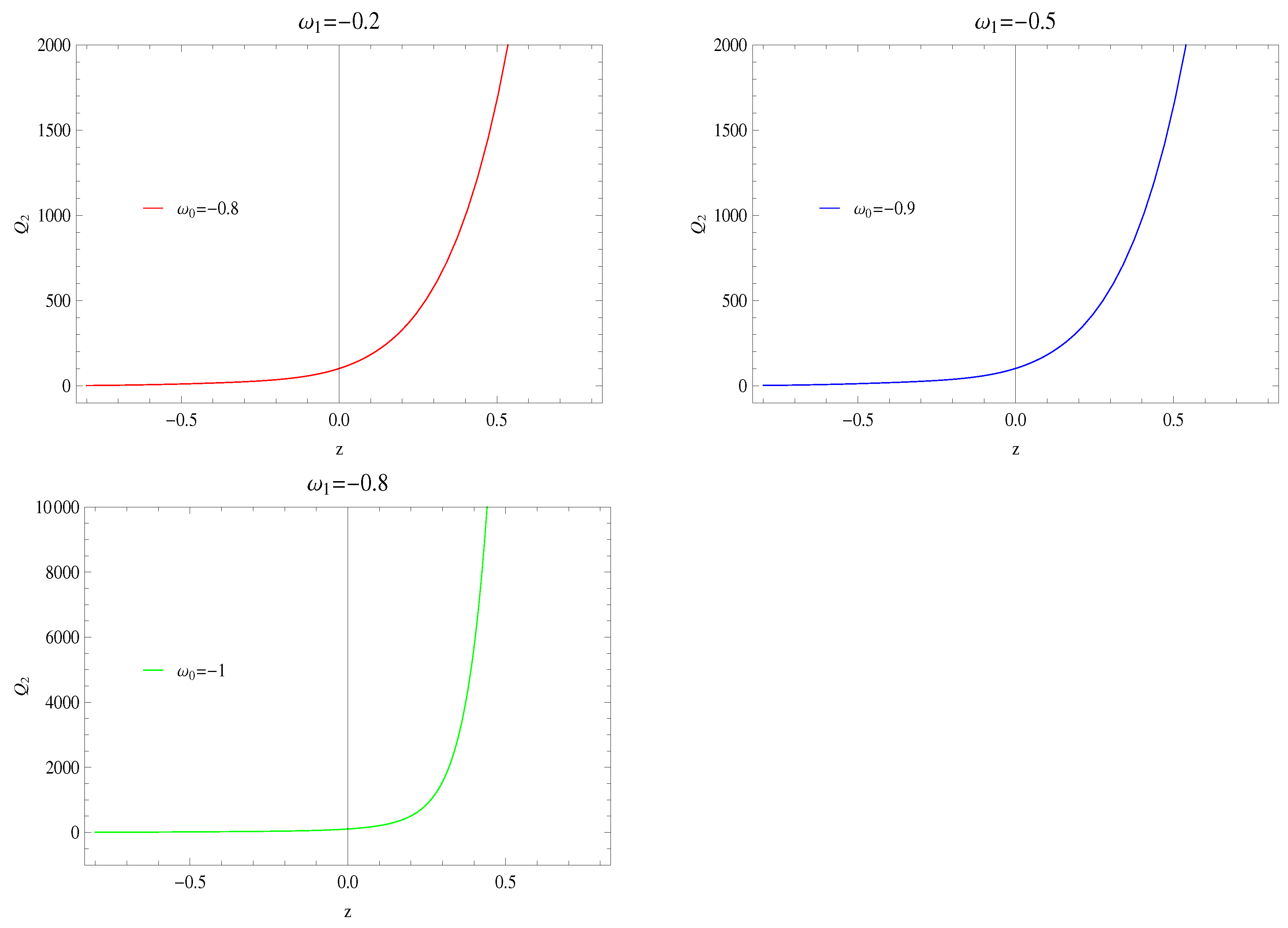
4. Cosmological Parameters
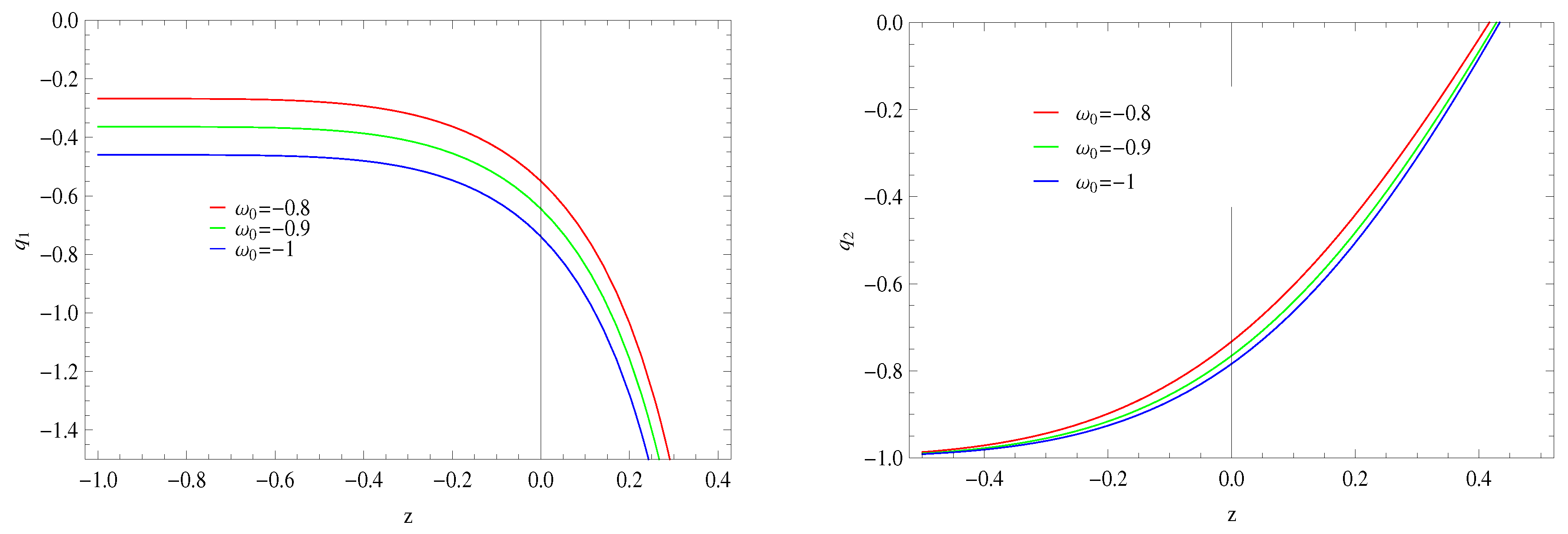
4.1. Deceleration Parameter
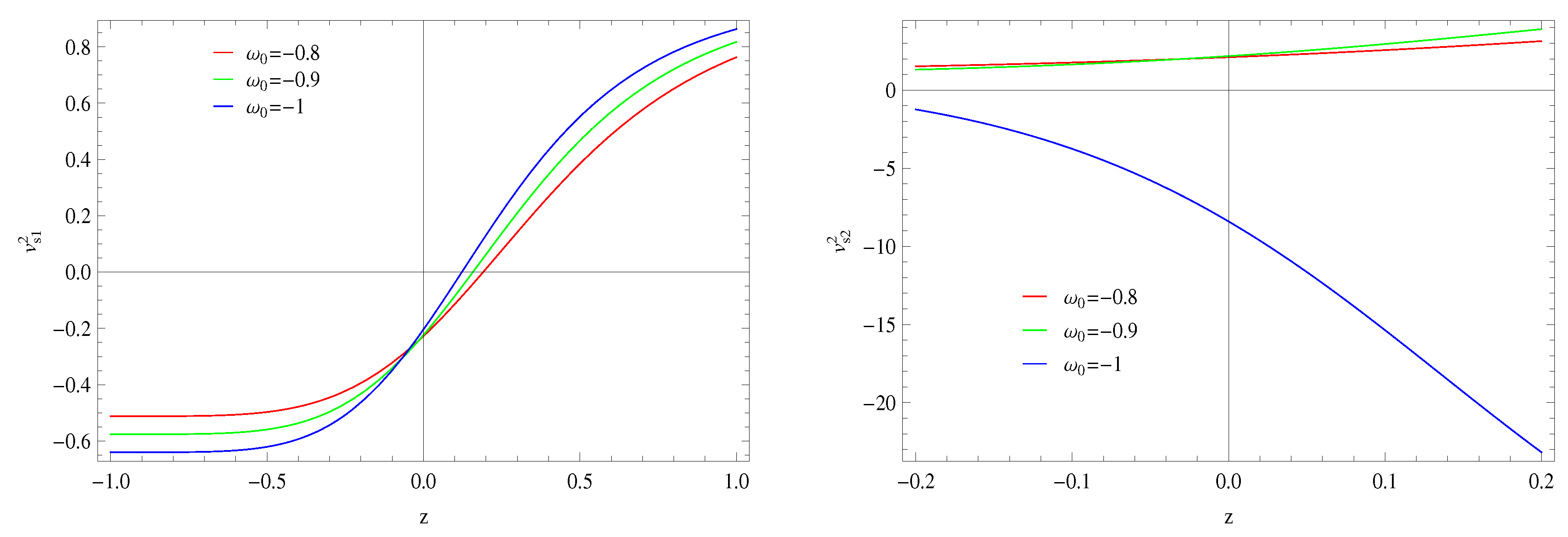
4.2. Stability Analysis
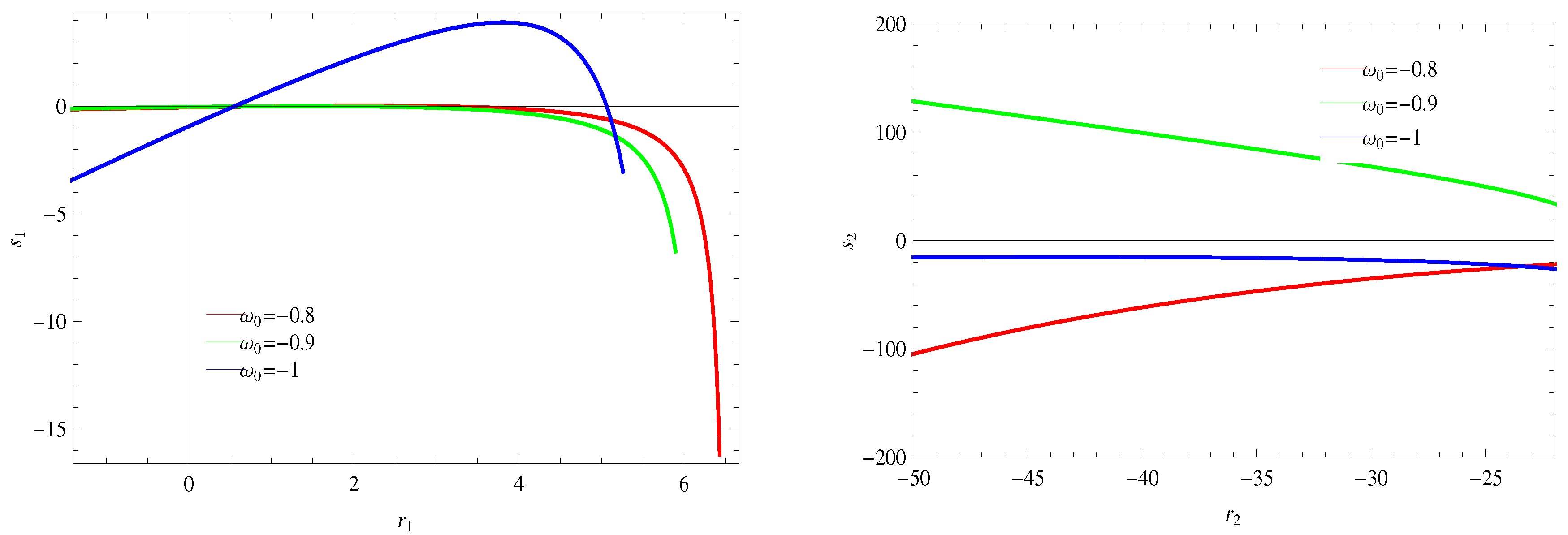
4.3. Statefinder Parameters
4.4. Om-Diagnostic
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tripathi, A.; Sangwan, A.; Jassal, H.K. Dark energy equation of state parameter and its evolution at low redshift. JCAP 2017, 06, 012. [Google Scholar] [CrossRef]
- Perlmutter, S.; Gabi, S.; Goldhaber, G.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pain, R.; et al. Measurements* of the Cosmological Parameters Ω and Λ from the First Seven Supernovae at z ≥ 0.35. Astrophys. J. 1997, 483, 565. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Astier, P.; Guy, J.; Regnault, N.; Pain, R.; Aubourg, E.; Balam, D.; Basa, S.; Carlberg, R.G.; Fabbro, S.; Fouchez, D.; et al. The Supernova Legacy Survey: Measurement of, and w from the first year data set. Astron. Astrophys. J. 2006, 447, 31–48. [Google Scholar] [CrossRef]
- Garnavich, P.M.; Jha, S.; Challis, P.; Clocchiatti, A.; Diercks, A.; Filippenko, A.V.; Gillil, R.L.; Hogan, C.J.; Kirshner, R.P.; Leibundgut, B.; et al. Supernova limits on the cosmic equation of state. Astrophys. J. 1998, 509, 74. [Google Scholar] [CrossRef]
- Tonry, J.L.; Schmidt, B.P.; Barris, B.; Candia, P.; Challis, P.; Clocchiatti, A.; Coil, A.L.; Filippenko, A.V.; Garnavich, P.; Hogan, C.; et al. Cosmological results from high-z supernovae. Astrophys. J. 2003, 594, 1. [Google Scholar] [CrossRef]
- Barris, B.J.; Tonry, J.L.; Blondin, S.; Challis, P.; Chornock, R.; Clocchiatti, A.; Filippenko, A.V.; Garnavich, P.; Holl, S.T.; Jha, S.; et al. Twenty-three high-redshift supernovae from the Institute for Astronomy Deep Survey: Doubling the supernova sample at z > 0.7. Astrophys. J. 2004, 602, 571. [Google Scholar] [CrossRef]
- Goobar, A.; Perlmutter, S.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Groom, D.E.; Hook, I.M.; et al. The acceleration of the Universe: Measurements of cosmological parameters from type Ia supernovae. Phys. Scr. J. 2000, 85, 47. [Google Scholar] [CrossRef]
- González-Gaitán, S.; Conley, A.; Bianco, F.B.; Howell, D.A.; Sullivan, M.; Perrett, K.; Carlberg, R.; Astier, P.; Balam, D.; Ball, C.; et al. The Rise Time of Normal and Subluminous Type Ia Supernovae. Astrophys. J. 2012, 745, 44. [Google Scholar] [CrossRef]
- Buckley, J.; Byrum, K.; Dingus, B.; Falcone, A.; Kaaret, P.; Krawzcynski, H.; Pohl, M.; Vassiliev, V.; Williams, D.A. The Status and future of ground-based TeV gamma-ray astronomy. A White Paper prepared for the Division of Astrophysics of the American Physical Society. arXiv 2008, arXiv:0810.0444. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Faraoni, V.; Capozziello, S. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics. Fundam. Theor. Phys. 2010, 170. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary cosmology in modified gravity theories. Symmetry 2015, 7, 220. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; Laurentis, M.D.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Pfenniger, D.; Combes, F.; Martinet, L. Is dark matter in spiral galaxies cold gas? I. Observational constraints and dynamical clues about galaxy evolution. Astron. Astrophys. 1994, 285, 79–83. [Google Scholar]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Rall, S.W.; Jones, C.; Zaritsky, D. A Direct Empirical Proof of the Existence of Dark Matter. Astrophys. J. Lett. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Alcock, C.; Allsman, R.A.; Axelrod, T.S.; Bennett, D.P.; Cook, K.H.; Freeman, K.C.; Griest, K.; Guern, J.A.; Lehner, M.J.; Marshall, S.L.; et al. The MACHO Project First-Year Large Magellanic Cloud Results: The Microlensing Rate and the Nature of the Galactic Dark Halo. Astrophys. J. 1996, 461, 84. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odinstov, S.D. Late-time cosmology in a (phantom) scalar-tensor theory: Dark energy and the cosmic speed-up. Phys. Rev. D 2004, 70, 043539. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in the (phantom) dark energy universe. Phys. Rev. D 2005, 71, 063004. [Google Scholar] [CrossRef]
- Anisimov, A.; Babichev, E.; Vikman, A. B-Inflation. J. Cosmol. Astropart. Phys. 2005, 6, 006. [Google Scholar] [CrossRef]
- Setare, M.R. Interacting generalized Chaplygin gas model in non-flat universe. Eur. Phys. J. C 2007, 52, 689–692. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P. Dynamical Solution to the Problem of a Small Cosmological Constant and Late-Time Cosmic Acceleration. J. Phys. Rev. Lett. 2000, 85, 4438. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V. k-Inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Wei, H.; Cai, R.G. A new model of agegraphic dark energy. Phys. Lett. B 2008, 660, 113–117. [Google Scholar] [CrossRef]
- Cai, R.G. A dark energy model characterized by the age of the Universe. Phys. Lett. B 2007, 657, 228–231. [Google Scholar] [CrossRef]
- Hsu, S.D.H. Entropy bounds and dark energy. Phys. Lett. B 2004, 594, 13–16. [Google Scholar] [CrossRef]
- Li, M. A model of holographic dark energy. Phys. Lett. B 2004, 603, 1–5. [Google Scholar] [CrossRef]
- Setare, M.R. The holographic dark energy in non-flat Brans–Dicke cosmology. Phys. Lett. B 2007, 644, 99–103. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Nojiri, S.; de Odintsov, S.D. Sitter brane universe induced by phantom and quantum effects. Phys. Lett. B 2003, 565, 1–9. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Quantum de Sitter cosmology and phantom matter. Phys. Lett. B 2003, 562, 147–152. [Google Scholar] [CrossRef]
- Tavayef, M.; Sheykhi, A.; Bamba, K.; Moradpour, H. Tsallis holographic dark energy. Phys. Lett. B 2018, 781, 195–200. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavon, D. Dark matter and dark energy interactions: Theoretical challenges, cosmological implications and observational signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef]
- Joan, S. Dark energy: A quantum fossil from the inflationary universe? J. Phys. A 2008, 41, 164066. [Google Scholar]
- Chevallier, M.; Polarski, D. Accelerating universes with scaling dark matter. Int. J. Mod. Phys. D 2001, 10, 213. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the Expansion History of the Universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Jassal, H.K.; Bagla, J.S.; Padmanabhan, T. Observational constraints on low redshift evolution of dark energy: How consistent are different observations? Phys. Rev. D 2005, 72, 103503. [Google Scholar] [CrossRef]
- Feng, L.; Lu, T. A new equation of state for dark energy model. JCAP 2011, 11, 034. [Google Scholar] [CrossRef]
- Efstathiou, G. Constraining the equation of state of the Universe from distant Type Ia supernovae and cosmic microwave background anisotropies. Mon. Not. R. Astron. Soc. 1999, 310, 842. [Google Scholar] [CrossRef]
- Lee, S. Constraints on the dark energy equation of state from the separation of CMB peaks and the evolution of α. Phys. Rev. D 2005, 71, 123528. [Google Scholar] [CrossRef]
- Hannestad, S.; Mörtsell, E. Cosmological constraints on the dark energy equation of state and its evolution. JCAP 2004, 9, 001. [Google Scholar] [CrossRef]
- Wang, Y.; Kostov, V.; Freese, K.; Frieman, J.A.; Gondolo, P. Probing the evolution of the dark energy density with future supernova surveys. JCAP 2004, 12, 003. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Tegmark, M. New dark energy constraints from supernovae, microwave background, and galaxy clustering. Phys. Rev. Lett. 2004, 92, 241302. [Google Scholar] [CrossRef]
- Bassett, B.A.; Corasaniti, P.S.; Kunz, M. The Essence of Quintessence and the Cost of Compression. Astrophys. J. 2004, 617, L1. [Google Scholar] [CrossRef]
- Huterer, D.; Turner, M.S. Prospects for probing the dark energy via supernova distance measurements. Phys. Rev. D 1999, 60, 081301. [Google Scholar] [CrossRef]
- Huterer, D.; Turner, M.S. Probing dark energy: Methods and strategies. Phys. Rev. D 2001, 64, 123527. [Google Scholar] [CrossRef]
- Weller, J.; Albrecht, A. Opportunities for Future Supernova Studies of Cosmic Acceleration. Phys. Rev. Lett. 2001, 86, 1939. [Google Scholar] [CrossRef]
- Pantazis, G.; Nesseris, S.; Perivolaropoulosv, L. Comparison of thawing and freezing dark energy parametrizations. Phys. Rev. D 2016, 93, 103503. [Google Scholar] [CrossRef]
- Rani, N.; Jain, D.; Mahajan, S. Transition redshift: new constraints from parametric and nonparametric methods. JCAP 2015, 12, 045. [Google Scholar] [CrossRef]
- Copel, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Elizalde, E.; Nojiri, S.I.; Odintsov, S.D. Observational constraints on dark energy with generalized equations of state. Phys. Rev. D 2006, 73, 043512. [Google Scholar] [CrossRef]
- Jackiw, R.; Pi, S.Y. Chern-Simons modification of general relativity. Phys. Rev. D 2003, 68, 104012. [Google Scholar] [CrossRef]
- Ashtekar, A.; Balachran, A.P.; Jo, S. The CP problem in quantum gravity. Int. J. Mod. Phys. A 1989, 4, 1493–1514. [Google Scholar] [CrossRef]
- Jawad, A.; Sohail, A. Cosmological evolution of modified QCD ghost dark energy in dynamical Chern-Simons gravity. Astrophys. Space Sci. 2015, 55, 359. [Google Scholar] [CrossRef]
- Jawad, A.; Rani, S. Cosmological Evolution of Pilgrim Dark Energy in f(G) Gravity. Adv. High Energy Phys. 2015, 10, 952156. [Google Scholar] [CrossRef]
- Jawad, A. Reconstruction of f() models via well-known scale factors. Eur. Phys. J. Plus 2014, 129, 207. [Google Scholar] [CrossRef]
- Jawad, A.; Majeed, A. Correspondence of pilgrim dark energy with scalar field models. Astrophy. Space Sci. 2015, 356, 375. [Google Scholar] [CrossRef]
- Jawad, A. Cosmological analysis of pilgrim dark energy in loop quantum cosmology. Eur. Phys. J. C 2015, 75, 206. [Google Scholar] [CrossRef]
- Jawad, A.; Chattopadhyay, S.; Pasqua, A. A holographic reconstruction of the modifiedf(R) Horava-Lifshitz gravity with scale factor in power-law form. Astrophy. Space Sci. 2013, 346, 273. [Google Scholar] [CrossRef]
- Jawad, A.; Chattopadhyay, S.; Pasqua, A. Reconstruction of f(G) gravity with the new agegraphic dark-energy model. Eur. Phys. J. Plus 2013, 128, 88. [Google Scholar] [CrossRef]
- Jawad, A.; Pasqua, A.; Chattopadhyay, S. Correspondence between f(G) gravity and holographic dark energy via power-law solution. Astrophy. Space Sci. 2013, 344, 489. [Google Scholar] [CrossRef]
- Jawad, A.; Pasqua, A.; Chattopadhyay, S. Holographic reconstruction of f (G) gravity for scale factors pertaining to emergent, logamediate and intermediate scenarios. Eur. Phys. J. Plus 2013, 128, 156. [Google Scholar] [CrossRef]
- Jawad, A. Analysis of QCD ghost gravity. Astrophys. Space Sci. 2014, 353, 691. [Google Scholar] [CrossRef]
- Younus, M.; Jawad, A.; Qummer, S.; Moradpour, H.; Rani, S. Cosmological Implications of the Generalized Entropy Based Holographic Dark Energy Models in Dynamical Chern-Simons Modified Gravity. Adv. High Energy Phys. 2019, 2019, 1287932. [Google Scholar] [CrossRef]
- Cohen, A.; Kaplan, D.; Nelson, A. Effective field theory, black holes, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 4971. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Jawad, A.; Rani, S. Holographic Polytropic Gravity Models. Adv. High Energy Phys. 2015, 2015, 798902. [Google Scholar] [CrossRef]
- Jawad, A.; Rani, S.; Salako, I.G.; Gulshan, F. Aspects of some new versions of pilgrim dark energy in DGP braneworld. Eur. Phys. J. Plus 2016, 131, 236. [Google Scholar] [CrossRef]
- Elizaldel, E.; Khurshudyan, M.; Nojiri, S. Cosmological singularities in interacting dark energy models with an w(q) parametrization. arxiv 2018, arXiv:1809.01961v1. [Google Scholar]
- Cruz, M.; Lepe, S. Holographic approach for dark energy–dark matter interaction in curved FLRW spacetime. Class. Quantum Gravity 2018, 35, 155013. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder—A new geometrical diagnostic of dark energy. JEPT Lett. 2003, 77, 201. [Google Scholar] [CrossRef]
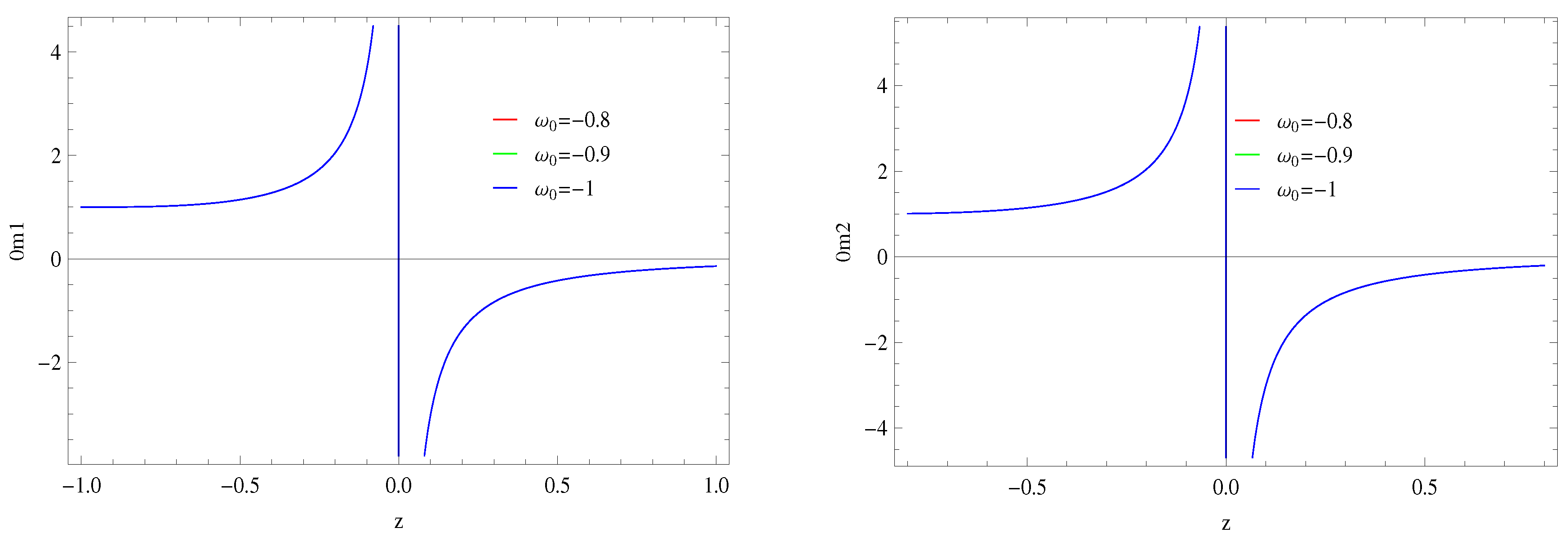
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jawad, A.; Rani, S.; Saleem, S.; Bamba, K.; Jabeen, R. Cosmological Consequences of a Parametrized Equation of State. Symmetry 2019, 11, 1009. https://doi.org/10.3390/sym11081009
Jawad A, Rani S, Saleem S, Bamba K, Jabeen R. Cosmological Consequences of a Parametrized Equation of State. Symmetry. 2019; 11(8):1009. https://doi.org/10.3390/sym11081009
Chicago/Turabian StyleJawad, Abdul, Shamaila Rani, Sidra Saleem, Kazuharu Bamba, and Riffat Jabeen. 2019. "Cosmological Consequences of a Parametrized Equation of State" Symmetry 11, no. 8: 1009. https://doi.org/10.3390/sym11081009
APA StyleJawad, A., Rani, S., Saleem, S., Bamba, K., & Jabeen, R. (2019). Cosmological Consequences of a Parametrized Equation of State. Symmetry, 11(8), 1009. https://doi.org/10.3390/sym11081009





