1. Introduction
A rich source of constructing Sasaki-Einstein (SE) metrics of positive Ricci curvature pioneered by Boyer and Galicki in Reference [
1] is via links of isolated hypersurface singularities defined by weighted homogenous polynomials. These smooth manifolds have been used to show the existence of SE metrics on many types of manifolds such as exotic spheres [
2], rational homology spheres ([
3,
4]) and connected sums of
[
1] (see Reference [
5] for more comprehensive survey.) SE manifolds are also extremely important in relation to the AdS/CFT Correspondence which is a conjecture that, in certain environments, relates Sasaki-Einstein geometries to particular superconformal theories. (See for example, Reference [
6] for recent progress in the relationship between SE geomtries and the AdS/CFT conjecture.) In general it is very difficult to determine the diffeomorphism or even homeomorphism type of a given link so determining any such geometric or topological data about the link is always helpful. Along these lines, for a given link of dimension
, Milnor and Orlik [
7] determined a formula for the
Betti number of the link and later on Orlik conjectured a formula [
8] (or see section two) for the torsion in
integral homology group. This conjecture due to Orlik regarding the torsion in integral homology of links is known to hold in certain cases. Both of these formulas have been instrumental in extracting some topological data on certain SE manifolds arising as links. For example, based on work of Cheltsov [
9], Boyer gave fourteen examples [
10] of SE 7-manifolds arising from links of isolated hypersurface singularities for which the third integral homology group is completely determined. He used Brieskorn-Pham polynomials and Orlik polynomials (see
Section 1), both of which are cases in which the aforementioned conjecture holds. Inspired by these examples, the main motivation for this article is to find other examples of SE 7-manifolds arising as links generated by Brieskorn-Pham polynomials or Orlik polynomials so that one can explicitly calculate the third integral homology group.
In general, there are obstructions to finding SE metrics (e.g., Bishop obstruction and Lichnerowicz obstruction [
11]) so it is worth finding as many examples as possible of manifolds which due admit SE metrics. Indeed, the main result of the paper is a list of ten examples (see
Section 2) of SE links defined by Orlik polynomials. Because of this, we are then able to calculate the torsion in the third integral homology group explicitly. In
Section 2, we review the necessary background and in
Section 3 we give the table of ten examples together with the third Betti number and explicit forms of
.
2. Background
Define the weighted
action on
by
where
are the weights which are positive integers and
. We use the standard notation
to denote a weight vector. In addition, we assume
Definition 1. A polynomial is weighted homogenous if it satisfiesfor any and the positive integer d is the degree of f. The link
of an isolated hypersurface singularity defined by a weighted homogenous polynomial
f with isolated singularity only at the origin is given by
where
is the weighted affine cone defined by
in
. By Milnor [
12],
is a smooth
connected manifold of dimension
.
Recall a Fano orbifold Z is an orbifold for which the orbifold anticanonical bundle is ample.
Theorem 1 [
1].
The link as defined above admits as Sasaki-Einstein structure if and only if the Fano orbifold admits a Kähler-Einstein orbifold metric of scalar curvature Note that one simply needs to rescale a Kähler-Einstein metric of positive scalar curvature to get the desired scalar curvature in the statement of the theorem. We can think of the weighted hypersurface
as the quotient space of the link
by the locally free circle action where this circle action comes from the weighted Sasakian structure on the link
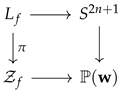
In fact this whole process is summarized in the commutative diagram [
1]
![Symmetry 11 00947 i001]()
where
denotes the unit sphere with a weighted Sasakian structure,
is weighted projective space coming from the quotient of
by a weighted circle action generated from the weighted Sasakian structure. The top horizontal arrow is a Sasakian embedding and the bottom arrow is Kähler embedding. Moreover the vertical arrows are orbifold Riemannian submersions.
Thus, a mechanism for constructing 2-connected Sasaki-Einstein 7-manifolds boils down to finding orbifold Fano Kähler-Einstein hypersurfaces in weighted projective 4-space
. Johnson and Kollár in Reference [
13] construct 4442 Fano orbifolds and of this list, 1936 of these are known to admit orbifold Kähler-Einstein metrics. Therefore, by the above construction we state a theorem of Boyer, Galicki and Nakamaye:
Theorem 2 [
3].
There exists 1936 2-connected Sasaki-Einstein 7-manifolds realized as links of isolated hypersurface singularities defined by weighted homogenous polynomials. In Reference [
3], the authors were able to determine many from the list of 1936 which yield rational homology 7-spheres and they also determined the order of
. In this paper, we identify ten links of isolated hypersurface singularities which can be given by so called Orlik polynomials, thus allowing us to calculate the third integral homology group explicitly. First, we need to define some quantities [
7]:
Let
denote a link of an isolated hypersurface singularity defined by a weighted homogenous polynomial. The formula for the Betti number
is given by:
Here the sum is over all possible subsets of
For the torsion data, Orlik conjectured [
8] that for a given link
of dimension
one has
We should now review how the
data are given, using the presentation given in Reference [
5]. Given an index set
, define
I to be the set of all of the
subsets and let us designate
J to be all of the proper subsets. For each possible subset, we must define (inductively) a pair of numbers
and
. For each ordered subset
with
one defines the set of
positive integers, beginning with
Now, to get the
:
where
Then for each
we put
Though the full conjecture is still open 45 years later, it is known to hold in certain cases. If the link is given by either of the polynomials below
then the conjecture holds [
8,
14]. The first type of polynomial is called Brieskorn-Pham and the second one is called Orlik. We will discuss these a bit more in the next section.
The formulas for the Betti numbers and torsion would indeed be quite tedious to compute by hand, especially when the degree and the weights are large. Fortunately, Evan Thomas developed a program written in C which computes the Betti numbers and the numbers
, which generates the torsion in
. Hence if the link is generated by a Brieskorn-Pham polynomial or an Orlik polynomial, then one explicitly knows the torsion in
. This program was also used extensively in References [
5,
10,
15]. I would like to thank Evan Thomas for giving me permission to use the program and to make it available. See the
Appendix A.
3. Examples
The paper of Johnson and Kollár [
13] lists (see appendix for link to list) Kähler-Einstein and Tiger of Fano orbifolds in weighted projective space
gives the weight vector
with
(which can always be done after an affine change of coordinates) and it indicates if the weighted hypersurface admits an orbifold Kähler-Einstein structure. The degree
d is given by
. It is easy to identify whether or not Kähler-Einstein orbifolds on the list come from Brieskorn-Pham polynomials since for a given weight vector
on the list, the exponents of the Brieskorn-Pham polynomial would have to be
for
and therefore one can do a computer search to see if one gets integer results for the exponents. But are there any coming from Orlik polynomials? To get some Orlik examples, one must search among the weighted hypersurfaces in the list of 1936 Kähler-Einstein orbifolds and see if the given weights can be represented by Orlik polynomials. This is more difficult than in the Brieskorn-Pham case since the constraints, given in 3.1, are more complicated. The search was done within the range
where there are 436 Fano orbifolds. Of this lot, 149 Fano orbifolds are known to admit an orbifold Fano Kähler-Einstein structure. Therefore, for a given weight vector
one needs to see if there exists exponents
, in the Orlik polynomials satisfying
The ten examples were found by hand, checking many different weights against the given conditions. Once they were found, the computer program developed by Evan Thomas was implemented to determine the Betti number and the torsion data. We now give the table of ten examples. We list the weights, the quasihomogenous polynomial generating the link, the degree and finally the third homology group. It is not claimed that this list is exhaustive. There may very well be more examples using these methods.
| (75,10,163,331,247) | z+z+z+z+z | 825 | ⊕⊕ () |
| (62,124,155,9,85) | z+z+z+z+z | 434 | () |
| (9,174,467,277,649) | z+z+z+z+z | 1575 | ( |
| (87,348,145,11,193) | z+z+z+z+z | 783 | |
| (100,350,9,113,229) | z+z+z+z+z | 800 | |
| (9,291,488,181,787) | z+z+z+z+z | 1755 | |
| (10,164,333,71,253) | z+z+z+z+z | 830 | |
| (10,540,275,163,103) | z+z+z+z+z | 1090 | |
| (32,144,11,103,31) | z+z+z+z+z | 320 | |
| (45,36,27,11,107) | z+z+z+z+z | 225 | |