Abstract
With the advent of mobile robots in commercial applications, the problem of path-planning has acquired significant attention from the research community. An optimal path for a mobile robot is measured by various factors such as path length, collision-free space, execution time, and the total number of turns. MEA* is an efficient variation of A* for optimal path-planning of mobile robots. RRT*-AB is a sampling-based planner with rapid convergence rate, and improved time and space requirements than other sampling-based methods such as RRT*. The purpose of this paper is the review and performance comparison of these planners based on metrics, i.e., path length, execution time, and memory requirements. All planners are tested in structured and complex unstructured environments cluttered with obstacles. Performance plots and statistical analysis have shown that MEA* requires less memory and computational time than other planners. These advantages of MEA* make it suitable for off-line applications using small robots with constrained power and memory resources. Moreover, performance plots of path length of MEA* is comparable to RRT*-AB with less execution time in the 2D environment. However, RRT*-AB will outperform MEA* in high-dimensional problems because of its inherited suitability for complex problems.
1. Introduction
Over the past decade, mobile robots have been effectively adapted to carry out vital unmanned tasks in various fields. Application areas of path-planning algorithms include but are not confined to security, vigilance [1], planetary exploration [2], route planning of Unmanned Aerial Vehicle (UAV) [3,4], and molecular simulation [5]. Path-planning for mobile robots deals with feasible path generation from a starting position to a goal position by avoiding collision with obstacles in an environment [6]. Canny and Reif [7] proved that global optimal motion planning is a NP-hard problem. Therefore, it is often preferred to acquire a feasible solution rather than to achieve optimality. The criteria of optimal path for mobile robots is often based on one or more features such as shortest distance, low risk, smoothness, maximum area coverage, and fewer energy requirements considering different application constraints [3,6]. One path quality may be desirable based on the type of application. For example, the shortest route would be preferred for a robotic vehicle on the road, whereas path smoothness would be required in case of rough terrain [8]. Time and memory-efficient mobile robot path-planning also saves mobile robot wear and capital expenditure [9].
Several planners have been used for mobile robots such as potential field, visibility graph, evolutionary meta-heuristic methods, sampling-based methods, and grid-based methods [3]. Each of them has their own advantages and disadvantages. Classic methods such as potential field and visibility graphs are complex, and computationally expensive to deal with real-time applications and high-dimensional problems. Nature-inspired meta-heuristic approaches such as Genetic Algorithm (GA) [10], and Artificial Bee Colony (ABC) algorithm [11] are suitable for the optimization of multi-objective planning problems. A major drawback of these approaches is pre-mature convergence, trapping in a local optimum, high computational cost, and complex mapping of data [3,11,12,13]. Recently, reinforcement learning has also emerged, but it is more suitable for robots learning new skills than for path-planning applications [14,15]. Sampling-based Planning (SBP) approaches such as RRT* (Rapidly exploring Random Tree Star) [16] are successful for high-dimensional complex problems [3]. A major limitation of sampling-based algorithms is their slow convergence rate [3,13]. RRT*-AB [12] is a recent sampling-based planner which has resolved this issue and has improved convergence rate as compared to other SBP variants [12]. Grid-based methods are another class of planning technique applicable to low-dimensional space. A* [17] is a popular grid-based algorithm and is usually preferred to solve planning problems of mobile robots in low dimensions [1,4,18,19]. However, A* does not always find the shortest path because the path is constrained to grid edges. Its memory requirements also expand vigorously for complex problems [4,6]. Memory-Efficient A* (MEA*) [20] is a variant of A* which has addressed these limitations and its performance is also comparable to A* as compared to other variants [20]. However, there is always a trade-off between processing time and robustness.
This paper is an extended version of the work presented in [20] with a detailed evaluation of performance parameters for MEA*. The purpose of this paper is to perform a comparative analysis of MEA* [20] with A*, HPA*, RRT, RRT*, and state-of-the-art sampling-based planning algorithm RRT*-AB [12] in a 2D environment as per defined metrics. The main focus of result discussion is MEA* and RRT*-AB.The assumption of application for mobile robots are as follows: 1. The environment is closed and known to the autonomous mobile robot. 2. The obstacles in the environment are stationary. 3. Planners will perform off-line, i.e., they do not rely on online sensor capabilities. The rest of the paper is as follows: Related work is described in Section 2. Section 3 presents the methodology. Section 4 describes the simulation results followed by a conclusion in Section 5.
2. Related Work
Grid-based planners map the configuration space into the grid formation by subdividing it into cells. These planners use discrete techniques for path-planning. They generate a route as a series of adjacent cells [21]. Dijkstra [22] and Extended Dijkstra [23] were early grid-based methods but they were not practical for real-time path-planning applications due to poor search efficiency [23]. Dijkstra variants led to a popular grid-based planner named A* [17]. However, efficiency of A* is highly dependent upon its heuristic cost function. Moreover, a path generated by A* can be longer than the true shortest paths in the environment because of artificially constrained headings to the edges, i.e., multiples of 45 degrees, as shown in Figure 1.
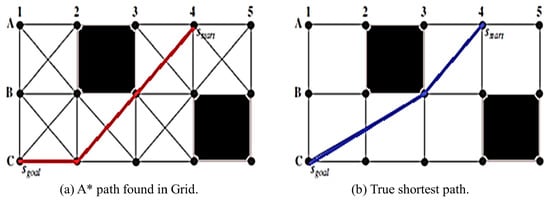
Figure 1.
Path constrained to edges vs true shortest path in grid [20].
Different variations of A* [24,25,26,27,28] have been presented to address these limitations in the advancement of grid-based heuristic planners. A variant of iterative-deepening depth-first search and A* called iterative-deepening A* (IDA*) [28] resolved the issue of large memory requirements. However, it often ends up exploring the same nodes multiple times that makes it slower than A*. Another variant Theta* [18] was proposed to address the issue of a path being constrained to grid edges. However, Theta* [18,26]-based variants consume less memory than A* but are much slower than A*. Another variant Field D* (FD*) [29] also does not constrain the path to grid edges and the generated path also comprises unnecessary turns. Two other recent variants MEA* [20] and HPA* [24] used a pruning process on a planned path. The performance of MEA* is better than A* and HPA* and it consumes less memory and computational time [20]. Optimality guarantee of grid-based algorithms such as A* is ensured up to resolution of grid. As the grid dimension increases, the run time of grid-based algorithms also increases drastically [6].
Sampling-based algorithms such as RRT [30] and RRT* [16] have gained much success due to their suitability for high-dimensional complex problems. Karaman et al. [16] proved the asymptotic optimal properties of RRT*. RRT* discovers the initial path very quickly and then enhances its quality in consecutive iterations. It produces a near-optimal path as the number of iterations approaches infinity. It has become expedient for real-time applications due to its asymptotic optimal property. However, its convergence rate is slower than basic RRT because it requires many iterations to optimize the initial path [3,13]. Another RRT* variant named RRT*-Smart [31] resolved this issue to some extent and acquired a near-optimal path in shorter time than RRT*. RRT*-AB [12] is a recent variation of RRT* which rapidly converges to an optimal or near-optimal path as compared to other RRT*-based approaches [12].
3. Methodology
MEA* and RRT*-AB along with other variations were executed in an environment cluttered with obstacles of different shapes. The operating system used for simulation was 64-bit Windows 10 on PC with 4 GB internal RAM and an Intel i5. A graphical simulation environment was built using MATLAB version 2017 to perform numerical and graphical comparison and analysis. We have compared the performance parameters of time, path length, and number of turns for MEA* [20] and RRT*-AB [12]. Both algorithms are implemented and tested in MATLAB. During tests, 2D environment maps of different cases are provided as an input to the respective planner. Algorithms of MEA* and RRT*-AB are described in the following subsections.
3.1. MEA* Algorithm
Start and goal positions are provided to planner MEA*. When the planner starts, it sets a goal state as the current node by assigning it a cost value equal to 2. Three lists are maintained during the path-finding process. contains the nodes which are unexplored. contains nodes which are already explored, whereas contains the parent of the current node. Initially, all the lists are set to empty. The is initialized with start position. Its cost function is based on
where is cost from start to current node and is the heuristic estimation of cost from current node to goal. The cost of start position is initialized with zero, and cost of every other vertex in the map is set to infinity. If is found empty, then the algorithm terminates, reporting that no path exists. If is not empty, then it originates a continuous process from goal position towards start position to build a cost matrix based on minimum Euclidean distance. In each iteration, the node with minimum cost is added in the ; this process continues until source is visited. If the visited vertex is not in goal position then it is removed from and placed in for further expansion. If the visited vertex is a goal position then the grid cells are backtracked to generate a linear piece-wise path from goal position to source position. During this backtracking, fewer grid cells are traversed and processed than previous grid-based approaches. This phenomenon leads to path generation with much improved time and memory efficiency. Long and heavily populated cost matrix in previous approaches such as A* and HPA* require planner to explore whole grid matrix during the planning process, as shown in Figure 2. However, MEA* inserts only nodes with minimum cost in the and generates a path with efficient grid matrix exploration; see Figure 3.
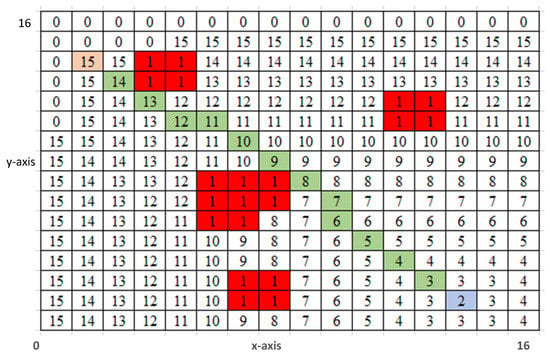
Figure 2.
Cost Matrix of A* after grid expansion [20].
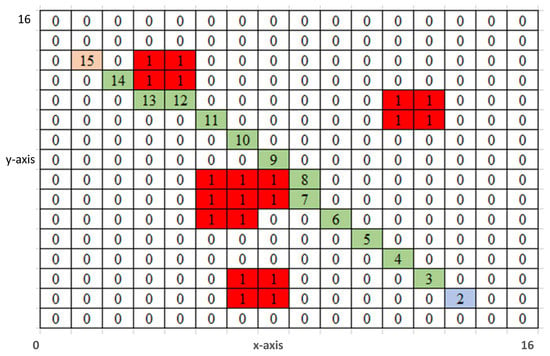
Figure 3.
Cost Matrix of MEA* after grid expansion [20].
Once a path is found, a pruning process similar to HPA* is applied to the solution path. The pruning selects points that are directly connectable by collision-free straight lines using the line-of-sight algorithm as shown in Figure 4. The final path generated after the pruning process comprises fewer waypoints than A*, see Figure 5a,b. Therefore, MEA* selects only pruned points as waypoints of the final path. This phenomenon makes the final path more efficient with respect to memory requirements and execution. Moreover, during the pruning process, a safe boundary distance is maintained according to the size of robot. The steps of MEA* are shown in Algorithm 1. The pruning algorithm is shown in Algorithm 2.
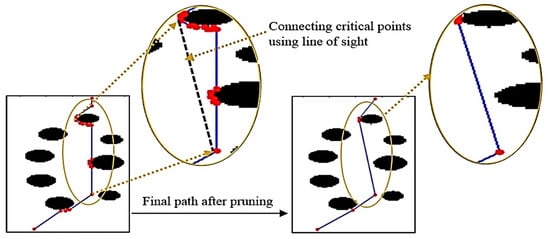
Figure 4.
Global path pruning [20].
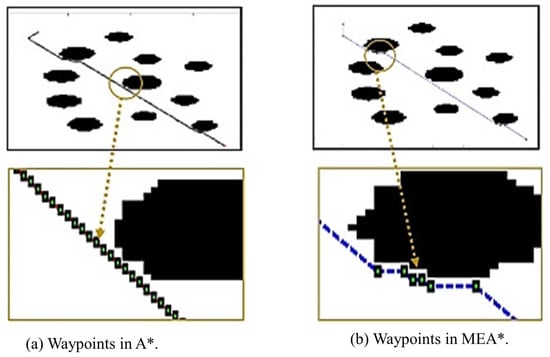
Figure 5.
Fewer waypoints in MEA* generated path than A* generated path [20].
| Algorithm 1: [20]. |
 |
| Algorithm 2: path ← postSmoothPath(pathFound) [20]. |
 |
3.2. RRT*-AB Algorithm
This section describes algorithm of RRT*-AB [12]. RRT*-AB builds a tree in obstacle-free environment space, . The tree originates from an initial state, and grows towards goal state, to find a path. It explores the environment using intelligent bounded sampling which randomly selects location points in limited region named as . maintains a search space between and using
where is expansion distance scale, S is the size of environment map and f is the expansion factor, see Figure 6c,d. Intelligent bounded sampling selects random nodes using a goal biased heuristic within the boundaries of . The tree progressively grows by adding new nodes from free space in successive iterations. During every iteration, a random node in the free space of [12] is selected. Then, a nearest node in the tree is searched, which has the smallest distance to this new random node. This search operation is performed within a circle of the area defined by
where represents the environment-based planning constant, n shows the number of nodes in the tree, and d represents the dimension of search space, [3,13]. If is connectable to the nearest node , then it is inserted in the tree as new node with nearest node as its parent in the tree. Otherwise, the planner uses a steering function to get the new node with nearest node as parent. A cost function in the planner assigns a cost value to every new node in the tree. The operation rearranges nodes to minimize the overall cost of tree. Once a goal is found, the path is formed between and within . A path cost function generates the path cost based on Euclidean distance defined by
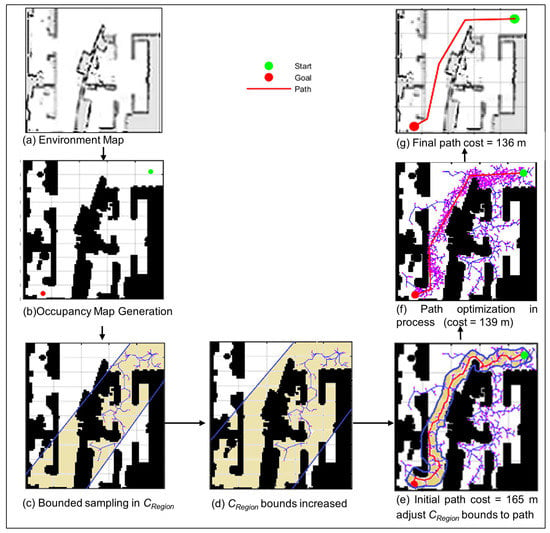
Figure 6.
Process of RRT*-Adjustable Bounds [12].
If the path is not discovered during the first scan of then is increased gradually to enhance until a path is found, as shown in Figure 6c,d. In the case of an extremely complex scenario such as a maze environment, can be increased to grow up to the full environment map. Use of the narrow makes sampling and exploration biased towards the goal as shown in Figure 6c. The final path is optimized using three more techniques called concentrated sampling, node rejection, and path pruning. A relatively narrow is acquired in the close neighborhood of the initial path for concentrated sampling. Frequent rewiring operations gradually improve the path during this process. At the same time, node rejection technique improves the path by rejecting high-cost nodes. Finally, global pruning technique [12] further optimizes the path. Steps of RRT*-AB are shown in Algorithm 3.
| Algorithm 3: [12]. |
 |
3.3. Complexity Analysis
This section describes the complexity of aforementioned approaches. Complexity of A* is highly dependent upon its heuristic function [17]. MEA* is a variation of classic A* algorithm. Complexity for the optimized path search is , where V is the total number of vertices and E is the total edges present. In our case, both vertices and edges are dependent on the size of the environment map M. Therefore, time and memory complexity for this task is . Overall, the memory and time complexity can be written as .
The space complexity of RRT*, RRT*-Smart, and RRT*-AB is as demonstrated in [12,16,31]. Time complexity of an algorithm is a measure of the amount of time required by the algorithm to execute a problem of size n. Time complexity of RRT*, RRT*-Smart, and RRT*-AB is as demonstrated in [12,16,31].
3.4. Data Set
We have used five different cases of the environment map represented by M1 to M5 as shown in Figure 7 and Figure 8. Environment maps M1 to M4 are adopted from [20,24], whereas map M5 is adopted from Intel lab data sets [32]. A description of these environments is cluttered with obstacles is as follows:
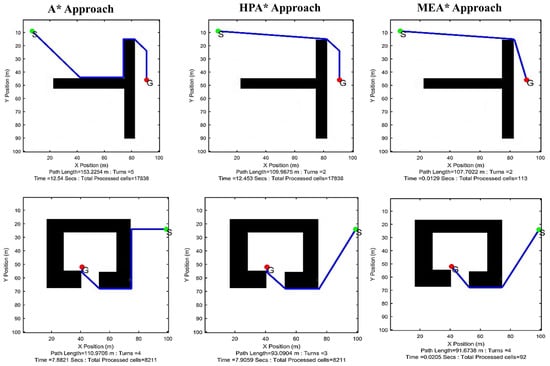
Figure 7.
Simulation comparison of planned paths for environment maps M1 and M2.
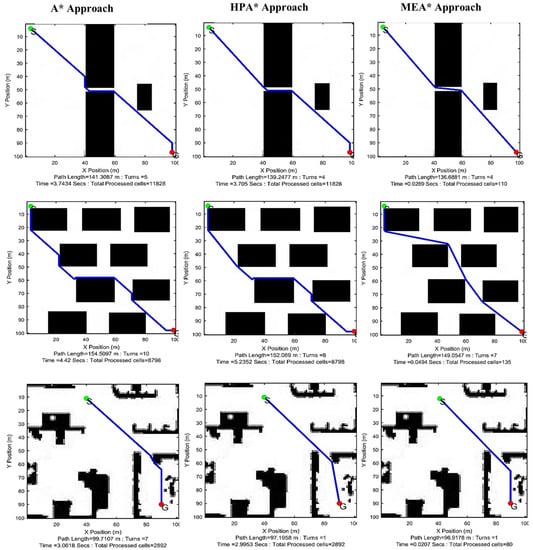
Figure 8.
Simulation comparison of planned paths for environment maps M3 to M5.
- Simple Structured Environment: M1 is the case of a structured environment map such as a turning passage.
- Concave Structured Environment: M2 represents an environment with concave shape obstacle.
- Narrow Structured Environment: M3 is the case of a narrow structured environment.
- Dense Structured Environment: M4 signifies a highly dense environment.
- Complex Unstructured Environment: M5 is an example of a complex indoor and unstructured scenario.
3.5. Performance Metrics
To evaluate the performance of the planners for known environments with varying obstacle density, the following metrics are used.
- Total Path Length: The total coverage length determines the total operational time required to perform the coverage task and the total energy consumption of the mobile robot. The path- planning algorithm is considered optimal if it generates the shortest path, thus leading to energy efficiency. Therefore, it is an important parameter for real-world solutions.
- Computational Time: The time required to compute the solution is preeminent for real-world applications. Hence, is a prominent efficiency indicator of the proposed approach.
- Memory Requirements: Memory requirements indicate the total number of vertices visited while performing the coverage task. This directly influences the total computational time required by the algorithm to find a solution.
4. Results
This section presents discussion of results and comparison of MEA* with other approaches. Results of all approaches are shown for maps M1 to M2 in Figure 7 and for maps M3 to M5 in Figure 8. Path length, execution time, total number of turns, and total number of cells processed in the grid are also shown along with visual comparison. The results show that MEA* [20] performs better than A* and HPA* based on the following parameters: number of turns, execution time, and memory requirements.
MEA* finds a collision-free path in reduced computational time as compared to previous approaches [17,24]. In addition, MEA* also eliminates any chance of multiple paths, see Figure 3. During each iteration, MEA* selects a neighboring grid cell for expansion which has minimum Euclidean distance. The expansion of cost matrix is performed using a heuristic function , which is based on selective Euclidean cost. The final path is further pruned using the line-of-sight principle.
The main factor of improved performance is that MEA* inserts only a single neighbor, which is selected based on minimum Euclidean cost in , whereas A* and HPA* insert all neighbors in openList. This makes openList short and comprising useful nodes only, thus the total number of processed grid cells and execution time both are reduced. Furthermore, MEA* traverses fewer grid cells to backtrack the path as explained in Section 1. Moreover, path length is also reduced because pruning rejects extra waypoints. Moreover, it is also obvious from results that MEA* may generate the paths of the same length or a little longer than HPA* for a densely cluttered environment M4 due to the precedence of local optimal while selecting the neighbor to insert in the list. However, in such a scenario, MEA* still gives results with minimal computational time and much fewer memory requirements. It shows a good trade-off between runtime and path length such as HPA* but with more efficient run time. MEA* is designed to improve memory and speed at the expense of path length. Therefore, it is suitable for small-scale robot applications where they have very limited memory and computational capability on board. Such applications prefer fewer memory requirements and efficient response time of the planner as optimality criteria instead of the path length. Plots of the total number of turns in the final path and processed cells in the grid are shown in Figure 9a,b for all grid-based approaches. It is obvious from plots in Figure 9 that MEA* requires minimum memory to process fewer grid cells than other grid-based approaches, i.e., A* and HPA*.
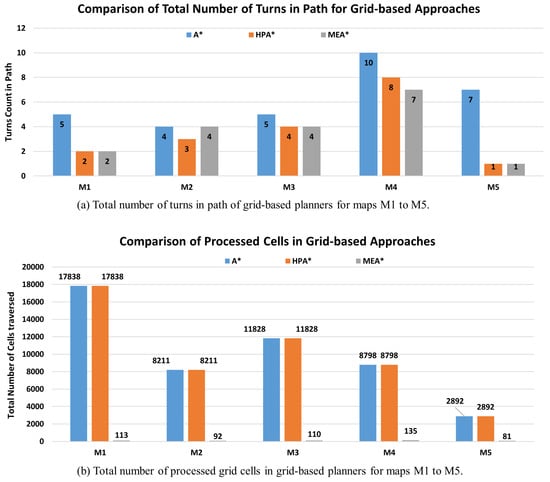
Figure 9.
Comparison of MEA * with grid-based approaches for processed grid cells and turns in the final path.
4.1. Comparison with Sampling-BASED Algorithms
In this section, simulation results of sampling-based approaches RRT [30], RRT* [16], and RRT*- AB [12] using maps M1 to M5 are presented. Simulation results of these comparisons are shown in Figure 10. Plots of path length and execution time for all planners and environment maps are shown in Figure 11. All simulations of sampling-based approaches are carried out 20 times using 3000 iterations. MEA* has generated paths of equal length or shorter length than sampling-based approaches. Keeping in view randomness of sampling-based approaches, if they are executed for more than 3000 iterations or given more time, then they may generate better path than A*. However, it is evident from plots in Figure 11 that there is a huge difference in execution time of MEA* with other planners. MEA* has generated a path in much less time compared to all approaches; also see Table 1. The path length of RRT*-AB is more comparable to the path length of MEA* than to other sampling-based approaches. If RRT*-AB is provided with enough planning iterations then it can provide a better path than MEA*. The MEA* can outperform RRT and RRT*-based state-of-the-art approaches only in low dimensions. As discussed in Section 2, RRT-based approaches are suitable for high-dimensional problems. Therefore, if complexity of the problem increases, RRT-based approaches will perform much better than grid-based approaches such as MEA*.
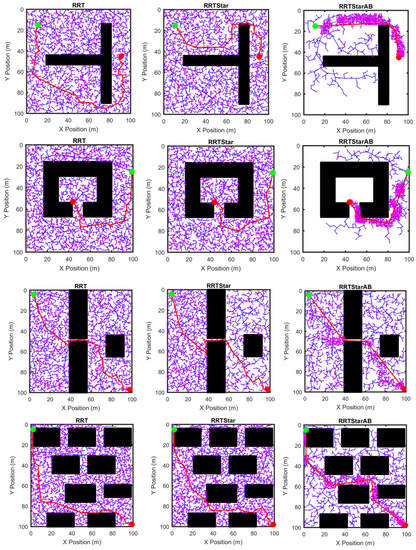
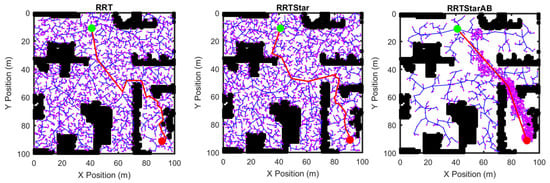
Figure 10.
Simulation results of environment maps M1 to M5 using RRT, RRT*, RRT*-AB.
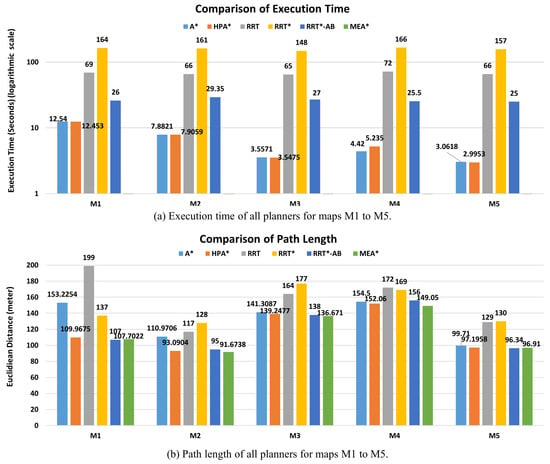
Figure 11.
Plot of path lengths and computational time of all planners for all environment maps M1 to M5.

Table 1.
Statistical results of all approaches for execution time (unit Sec).
4.2. Statistical Analysis
This section presents statistical analysis of results. Execution time and path length for all planners in all environment maps is listed in Table 1 and Table 2 respectively. Average and standard deviation values for all cases are computed to show the differences in results. Table 1 shows that on average MEA* requires minimum computational time to find the path. However, in sampling-based approaches, RRT*-AB requires minimum time. Table 2 shows that on average MEA* generated the shortest path length. However, paths generated by RRT*-AB and HPA* are comparable to it. RRT* and RRT*-AB are sampling-based randomized approaches and they gradually improve the path towards optimality if sufficient time is provided (or number of iterations are increased) [33]. They will generate a better path than MEA* if they are executed for more time. Similarly, in high-dimensional scenarios, grid-based approaches such as HPA* and MEA* will not perform well due to the exponential growth of their search space.

Table 2.
Statistical results of all approaches for path length (unit meter).
5. Conclusions
This paper presents a performance comparison of MEA* with prominent sampling-based and grid-based algorithms according to the metrics of path length and execution time. Simulation results show that the MEA* approach generates a shorter path with improved execution time and memory requirements. Though sampling-based algorithm RRT*-AB generates a better path for complex unstructured environment, MEA* still requires far less computational time. Increased computational efficiency of MEA* makes it useful for off-line application scenarios with constrained memory and computational resources in 2D. As MEA* is a grid-based approach, its search space expands exponentially when used in high-dimensional problems. However, RRT*-AB will outperform MEA* in high-dimensional problems because of its inherited suitability for complex problems. The desired future directions are motion planning using RRT*-AB in 3D-space for 6 DOF manipulator robotic arm, and use of fuzzy logic-based navigation for cooperative mobile robots in 3D-space.
Author Contributions
Conceptualization, I.N.; methodology, I.N.; software, I.N.; validation, I.N. and A.K.; formal analysis, I.N.; investigation, I.N.; resources, I.N., A.K., K.A. and Z.H.; data curation, I.N., A.K.; writing–original draft preparation, I.N.; writing–review and editing, I.N., A.K., K.A. and Z.H.; visualization, I.N.; supervision, I.N. and Z.H.; project administration, I.N.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MEA* | Memory-Efficient A* |
| RRT | Rapidly Exploring Random Tree |
| RRT* | Rapidly Exploring Random Tree Star |
| RRT*-AB | RRT*-Adjustable Bounds |
| UAV | Unmanned Aerial Vehicle |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| ACO | Ant Colony Optimization |
| SBP | Sampling-Based Planning |
| IDA* | Iterative Deepening A* |
| FD* | Field D* |
| HPA* | Hierarchical A* |
| A*PS | A* Post Smoothing |
References
- Veeraswamy, A.; Amavasai, B. Optimal path planning using an improved A* algorithm for homeland security applications. In Proceedings of the International Conference on Artificial Intelligence and Applications, Innsbruck, Austria, 13–16 February 2006; ACTA Press: Anaheim, CA, USA; pp. 50–55. [Google Scholar]
- Kuwata, Y.; Elfes, A.; Maimone, M.; Howard, A.; Pivtoraiko, M.; Howard, T.M.; Stoica, A. Path Planning Challenges for Planetary Robots. IEEE Intell. Robot. Syst. 2008, 22–27. [Google Scholar] [CrossRef]
- Noreen, I.; Khan, A.; Habib, Z. Optimal Path Planning using RRT* Based Approaches: A Survey and Future Directions. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2016, 7, 97–107. [Google Scholar] [CrossRef]
- Alejo, D.; Cobano, J.A.; Heredia, G.; Martinez-de Dios, J.R.; Ollero, A. Efficient Trajectory Planning for WSN Data Collection with Multiple UAVs. In Cooperative Robots and Sensor Networks; Springer International Publishing: New York, NY, USA, 2015; Volume 604, pp. 53–75. [Google Scholar]
- Ahmidi, N.; Hager, G.D.; Ishii, L.; Gallia, G.L.; Ishii, M. Robotic Path Planning for Surgeon Skill Evaluation in Minimally-Invasive Sinus Surgery. In Proceedings of the 15th International Conference on Medical Image Computing and Computer-Assisted Intervention, Nice, France, 1–5 October 2012; pp. 471–478. [Google Scholar]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Canny, J.; Rege, A.; Reif, J. An Exact Algorithm for Kinodynamic Planning in the Plane. Discret. Comput. Geom. 1991, 6, 461–484. [Google Scholar] [CrossRef]
- Guernane, R.; Achour, N. Generating optimized paths for motion planning. Robot. Auton. Syst. 2011, 59, 789–800. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Arora, T.; Gigras, Y.; Arora, V. Robotic Path Planning using Genetic Algorithm in Dynamic Environment. Int. J. Comput. Appl. 2014, 89, 8–12. [Google Scholar] [CrossRef]
- Liang, J.H.; Lee, C.H. Efficient Collision-free Path-planning of Multiple Mobile Robots System using Efficient Artificial Bee Colony Algorithm. Adv. Eng. Softw. 2015, 79, 47–56. [Google Scholar] [CrossRef]
- Noreen, I.; Khan, A.; Habib, Z. Optimal Path Planning using RRT*-Adjustable Bounds. Intell. Serv. Robot. 2018, 11, 41–52. [Google Scholar] [CrossRef]
- Noreen, I.; Khan, A.; Habib, Z. A Comparison of RRT, RRT* and RRT*-Smart Path Planning Algorithms. Int. J. Comput. Sci. Netw. Secur. 2016, 16, 20–27. [Google Scholar]
- Kormushev, P.; Calinon, S.; Caldwe, D.G. Reinforcement Learning in Robotics: Applications and Real-World Challenges. Robot. Auton. Syst. 2013, 2, 122–148. [Google Scholar] [CrossRef]
- Luviano-Cruz, D.; Garcia-Luna, F.; Pérez-Domínguez, L.; Gadi, S.K. Multi-Agent Reinforcement Learning Using Linear Fuzzy Model Applied to Cooperative Mobile Robots. Symmetry 2018, 10, 461. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based Algorithms for Optimal Motion Planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Daniel, K.; Nash, A.; Koenig, S. Theta Any-Angle Path Planning on Grids. J. Artif. Intell. Res. 2010, 39, 533–579. [Google Scholar] [CrossRef]
- Conlter, R.C. Implementation of the Pure Pursuit Path Tracking Algorithm; Report; The Robotics Institute, Camegie Mellon University: Pittsburgh, PA, USA, 1992. [Google Scholar]
- Noreen, I.; Khan, A.; Habib, Z. Optimal Path Planning using Memory Efficient A*. In Proceedings of the IEEE International Conference on Frontiers of Information Technology, Islamabad, Pakistan, 19–21 December 2016; pp. 142–146. [Google Scholar]
- Goerzen, C.; Kong, Z.; Mettler, B. A Survey of Motion Planning Algorithms from the Perspective of Autonomous UAV Guidance. J. Intell. Robot. Syst. 2009, 57, 65–100. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Noto, M.; Univ, K.; Sato, H. A Method for the Shortest Path Search by Extended Dijkstra Algorithm. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Nashville, TN, USA, 8–11 October 2000; Volume 3, pp. 2316–2320. [Google Scholar]
- Botea, A.; Muller, M.; Schaeffer, J. Near Optimal Hierarchical Path-Finding. J. Game Dev. 2004, 1, 1–30. [Google Scholar]
- Warren, C.W. Fast path planning using modified A* method. In Proceedings of the IEEE International Conference on Robotics and Automation, Atlanta, GA, USA, 2–6 May 1993. [Google Scholar]
- Zhang, X.; Chen, J.; Xin, B. Path Planning for Unmanned Aerial Vehicles in Surveillance Tasks Under Wind Fields. J. Cent. South Univ. 2014, 21, 3079–3091. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M.; Furcy, D. Lifelong Planning A*. Artif. Intell. 2004, 155, 93–146. [Google Scholar] [CrossRef]
- Korf, R.E. Depth-first iterative-deepening. Artif. Intell. 1985, 27, 97–109. [Google Scholar] [CrossRef]
- Ferguson, D.; Kalra, N.; Stentz, A. Replanning with RRTs. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Technical Report; Computer Science Dept., Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Nasir, J.; Islam, F.; Malik, U.; Ayaz, Y.; Hasan, O.; Khan, M.; Saeed, M. RRT*-SMART: A Rapid Convergence Implementation of RRT*. Int. J. Adv. Robot. Syst. 2013, 10, 1–12. [Google Scholar] [CrossRef]
- Stachniss, C. Robotics Datasets, University of Freiberg, 2016. Available online: http://www2.informatik.uni-freiburg.de/~stachnis/datasets.html (accessed on 14 June 2019).
- Qureshi, A.H.; Ayaz, Y. Intelligent Bidirectional Rapidly-exploring Random Trees for Optimal Motion Planning in Complex Cluttered Environments. Robot. Auton. Syst. 2015, 68, 1–11. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).