Disjunctive Representation of Triangular Bipolar Neutrosophic Numbers, De-Bipolarization Technique and Application in Multi-Criteria Decision-Making Problems
Abstract
:1. Introduction
1.1. Motivation
1.2. Novelties
1.3. Verbal Phrasesin theNeutrosophic Arena
1.4. Logical Relationship between the Objective and the Subjective Partsof this Paper
1.5. Structure of this Paper
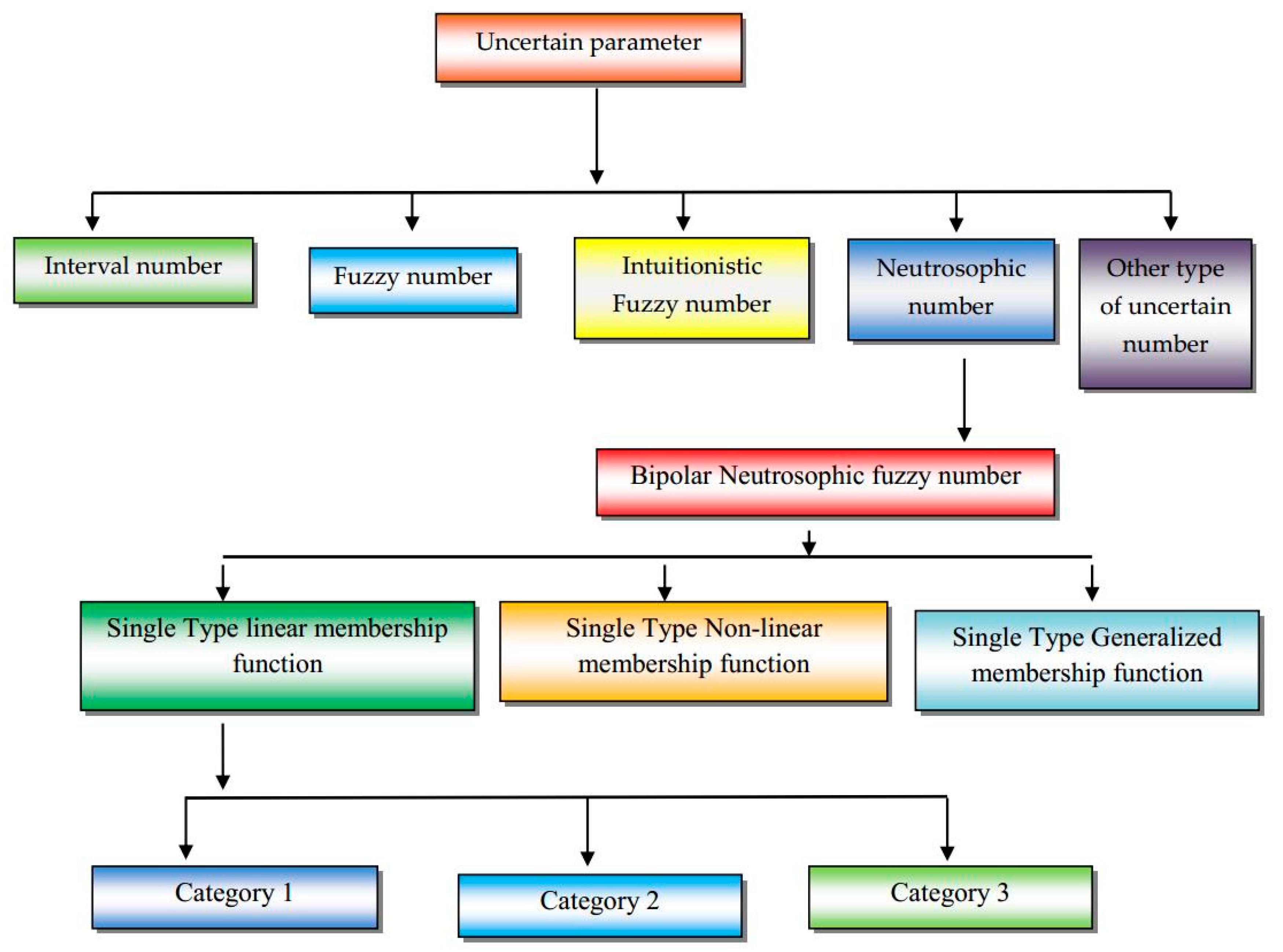
2. Preliminaries
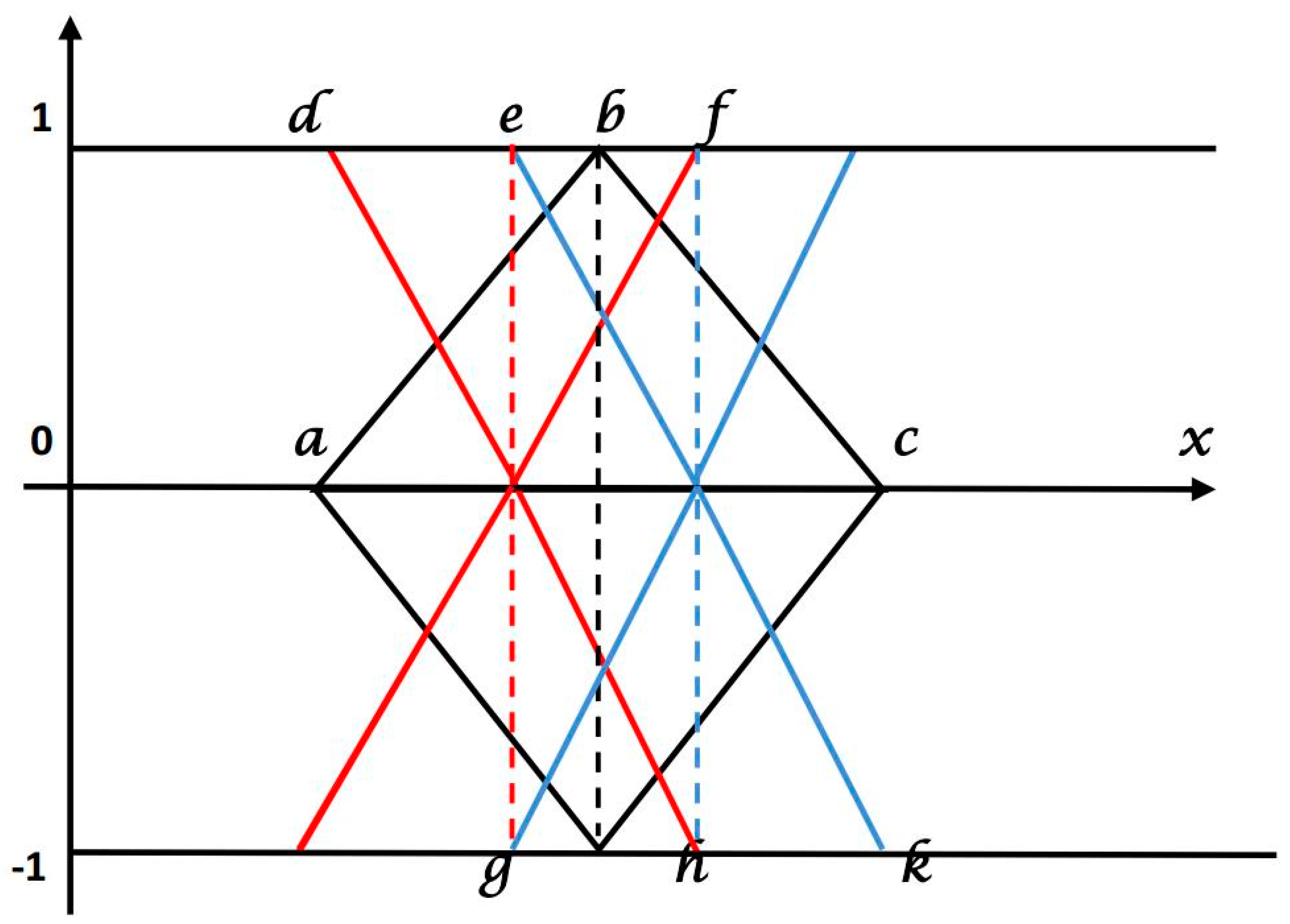
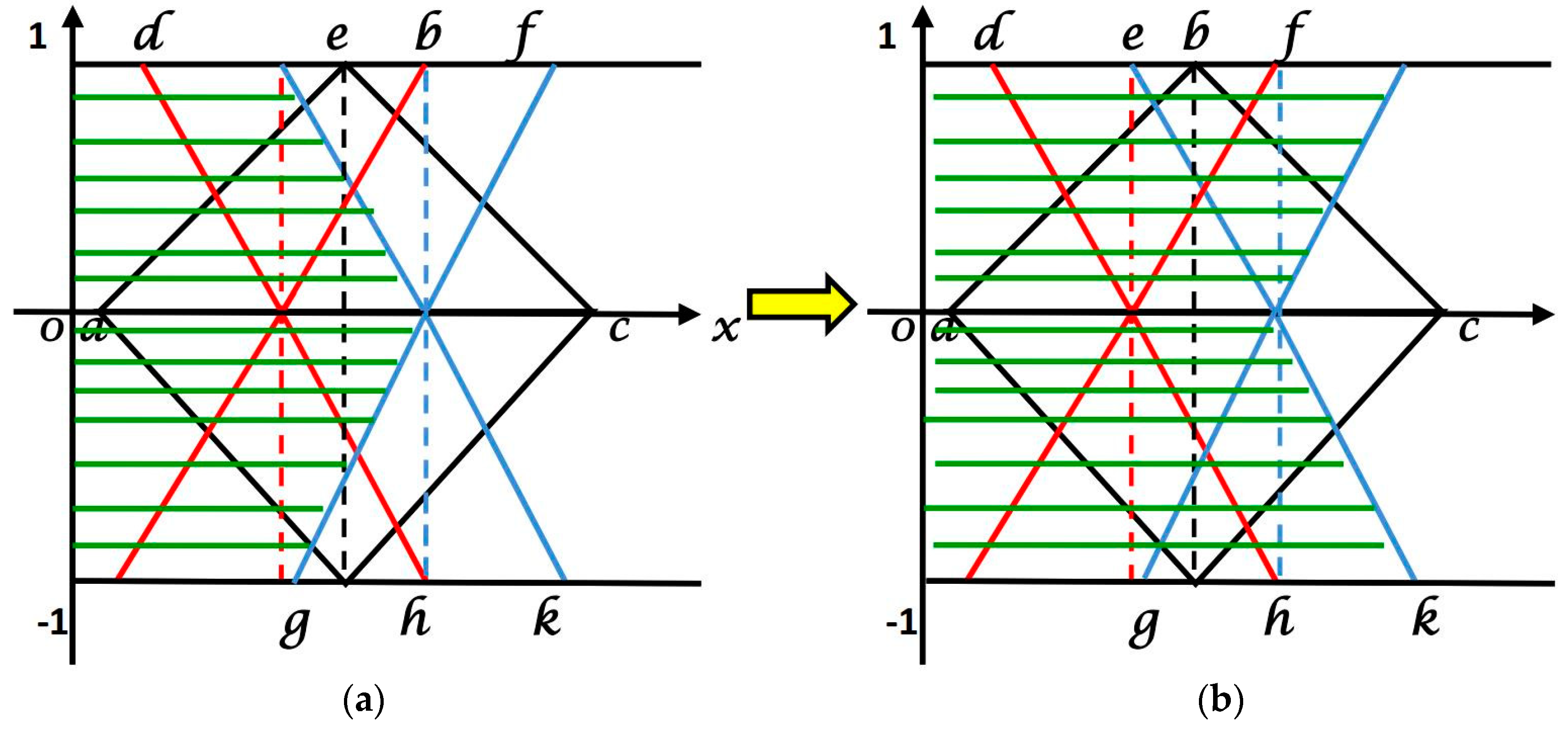
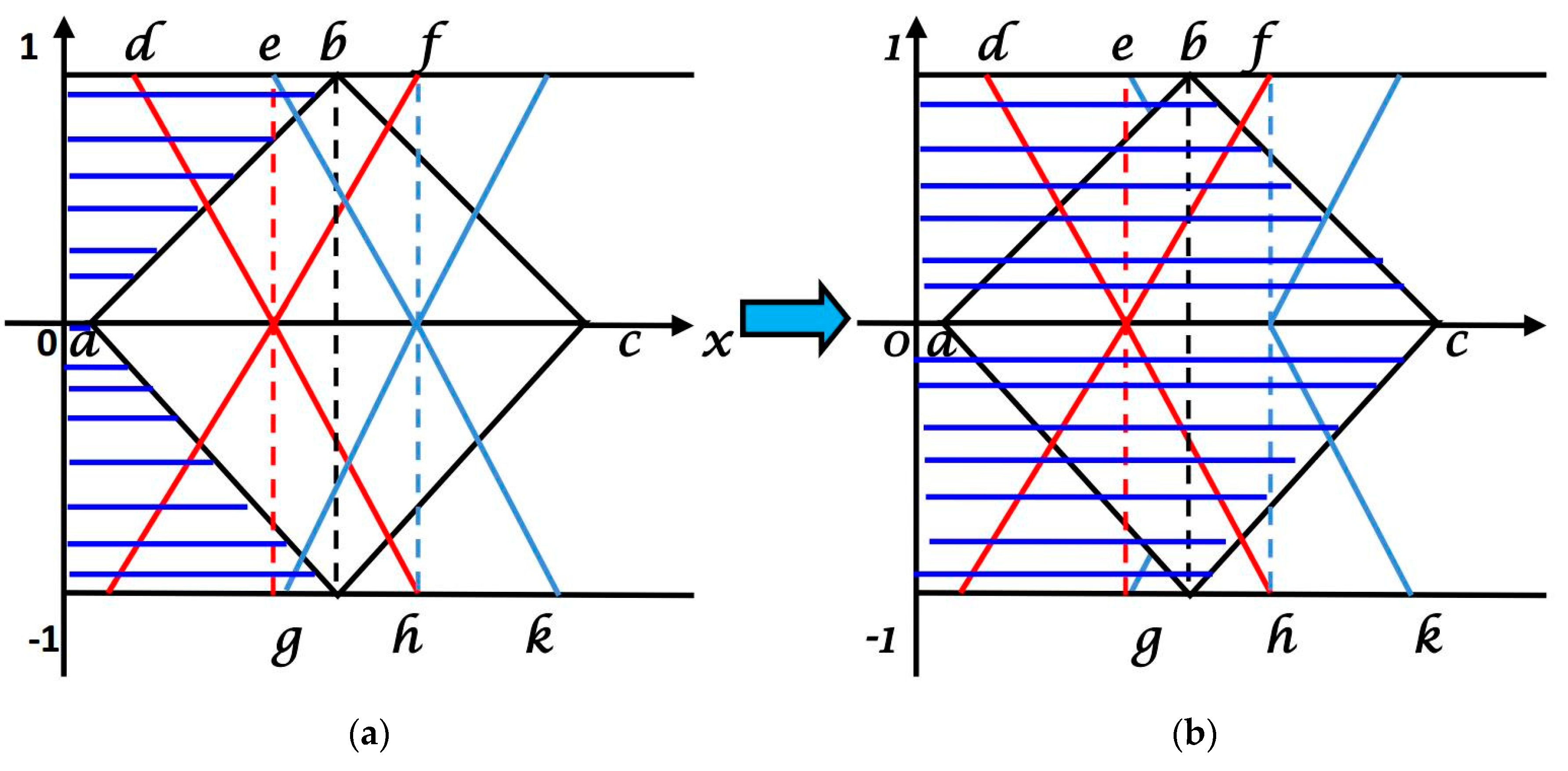
3. Single Typed Linear Triangular Bipolar Neutrosophic Number
3.1. Triangular Single Typed Bipolar NeutrosophicNumber of Category-1: The Portion of the Authenticity, Hesitation, and Untrue Are Independent
3.2. Triangular Single TypedBipolar Neutrosophic Number of Category-2: The Portion of Hesitation and Untrue Are Dependent
3.3. Triangular Single TypedBipolar Neutrosophic Number of Category-3: The Portion of the Authenticity, Hesitation, and Untrue Are Dependent
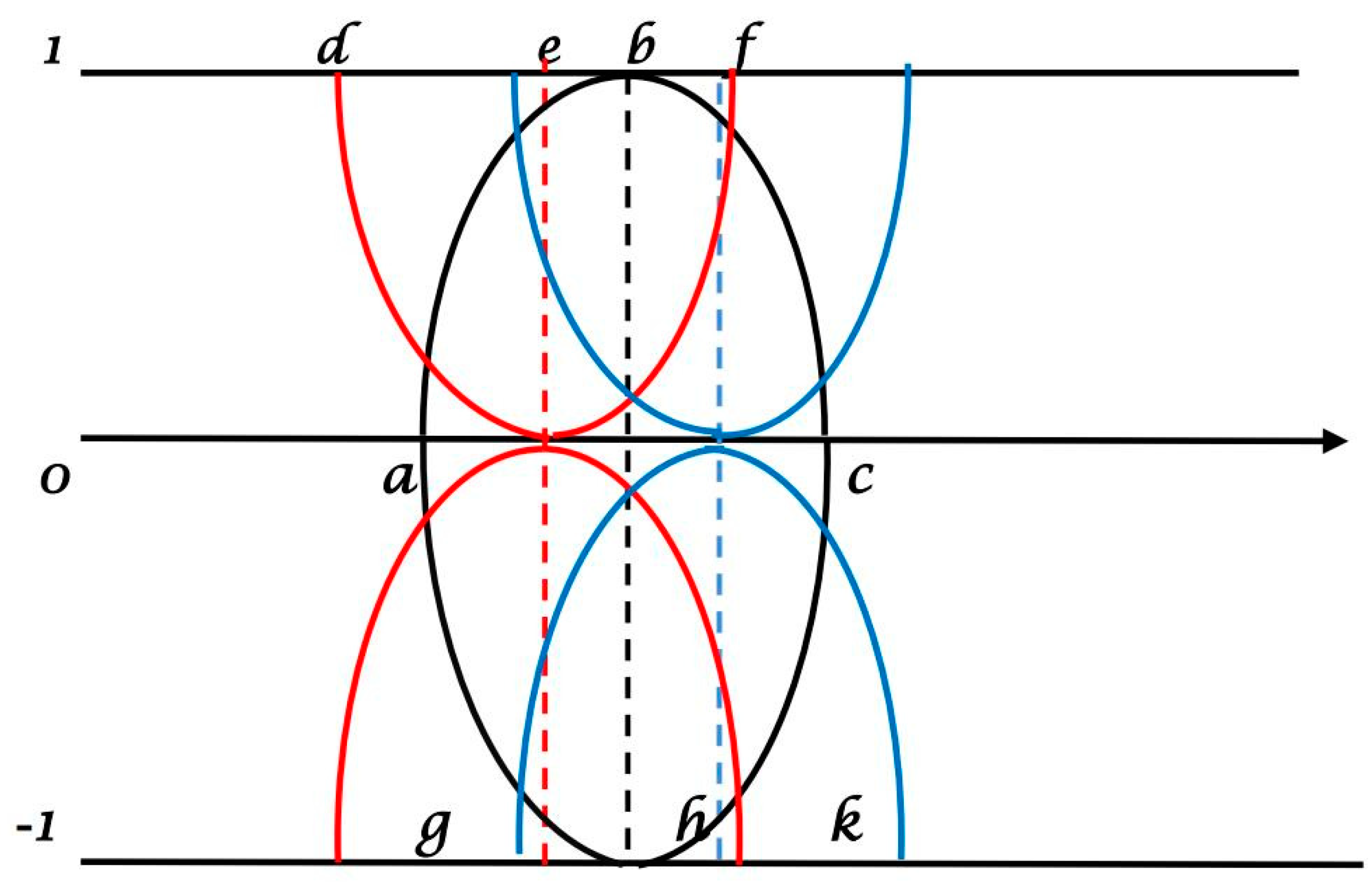
4. Single Typed Nonlinear Triangular Bipolar Neutrosophic Number
4.1. Single Typed Nonlinear Triangular Bipolar Neutrosophic Number
4.2. Single Typed Generalized Triangular Bipolar Neutrosophic Number
4.3. Single Typed Generalized Non Linear Triangular Bipolar Neutrosophic Number
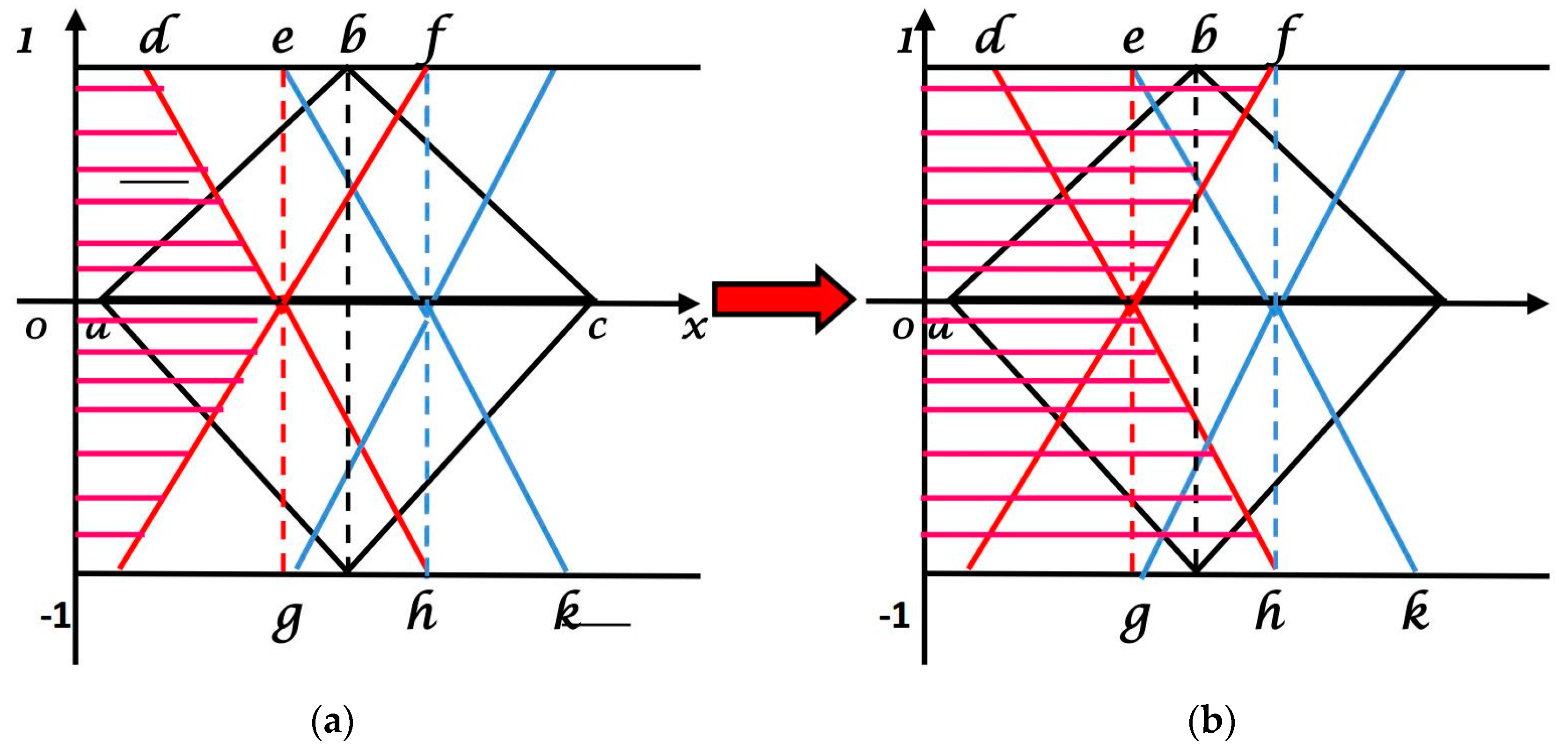
5. De-Bipolarization of a Linear Neutrosophic Triangular Bipolar Fuzzy Number
- BADD (basic defuzzification distributions)
- BOA (bisector of area)
- CDD (constraint decision defuzzification)
- COA (center of area)
- COG (center of gravity)
- ECOA (extended center of area)
- EQM (extended quality method)
- FCD (fuzzy clustering defuzzification), etc.
5.1. De-Bipolarization Using the Removal Area Method
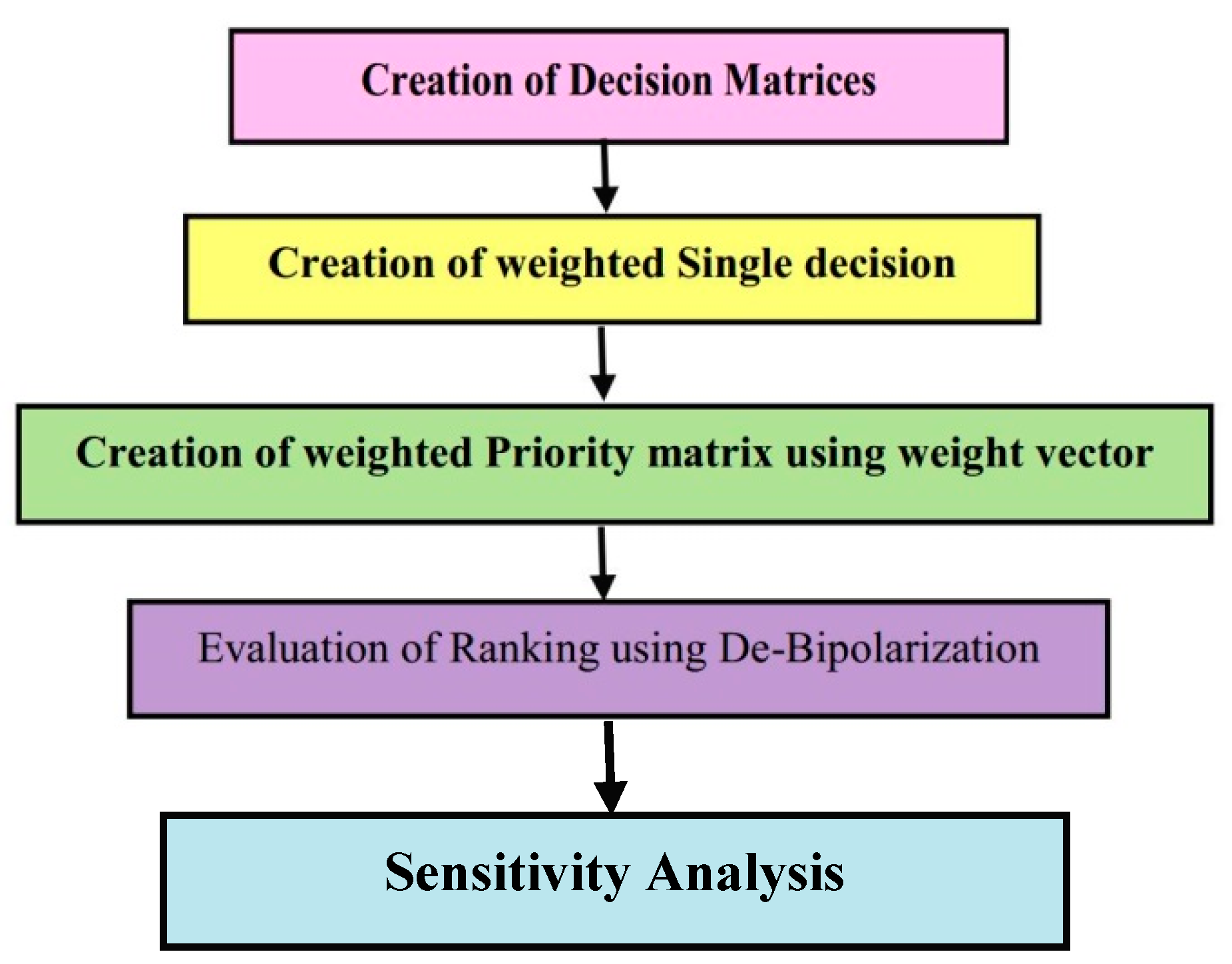
6. Multi-Criteria Decision-Making in a Triangular Bipolar Neutrosophic Fuzzy Set Environment
6.1. Illustration of the MCDM Problem
6.2. Weighted Mean and Normalisation Algorithm of the MCDM Problem
6.3. Illustrative Example
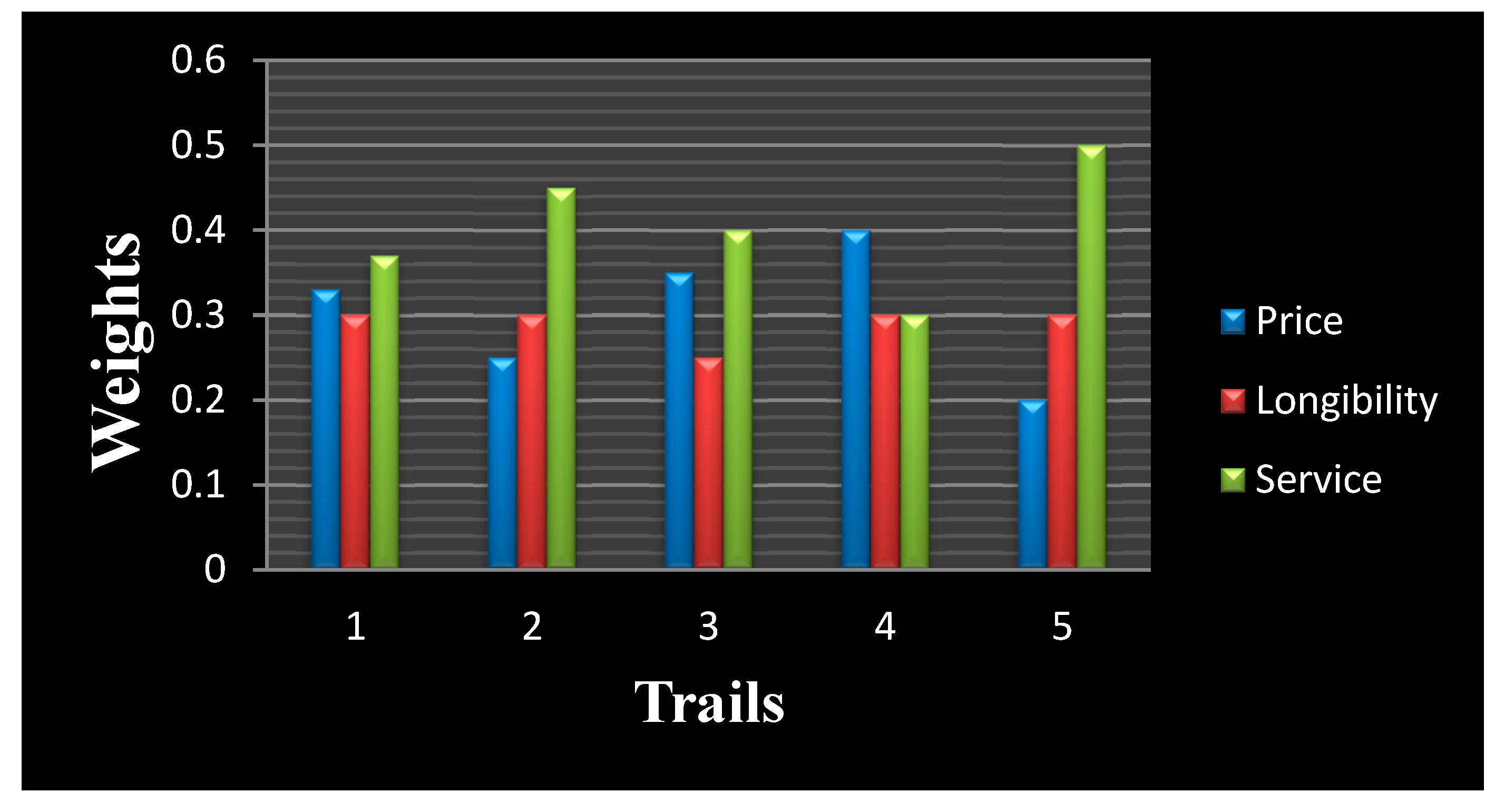
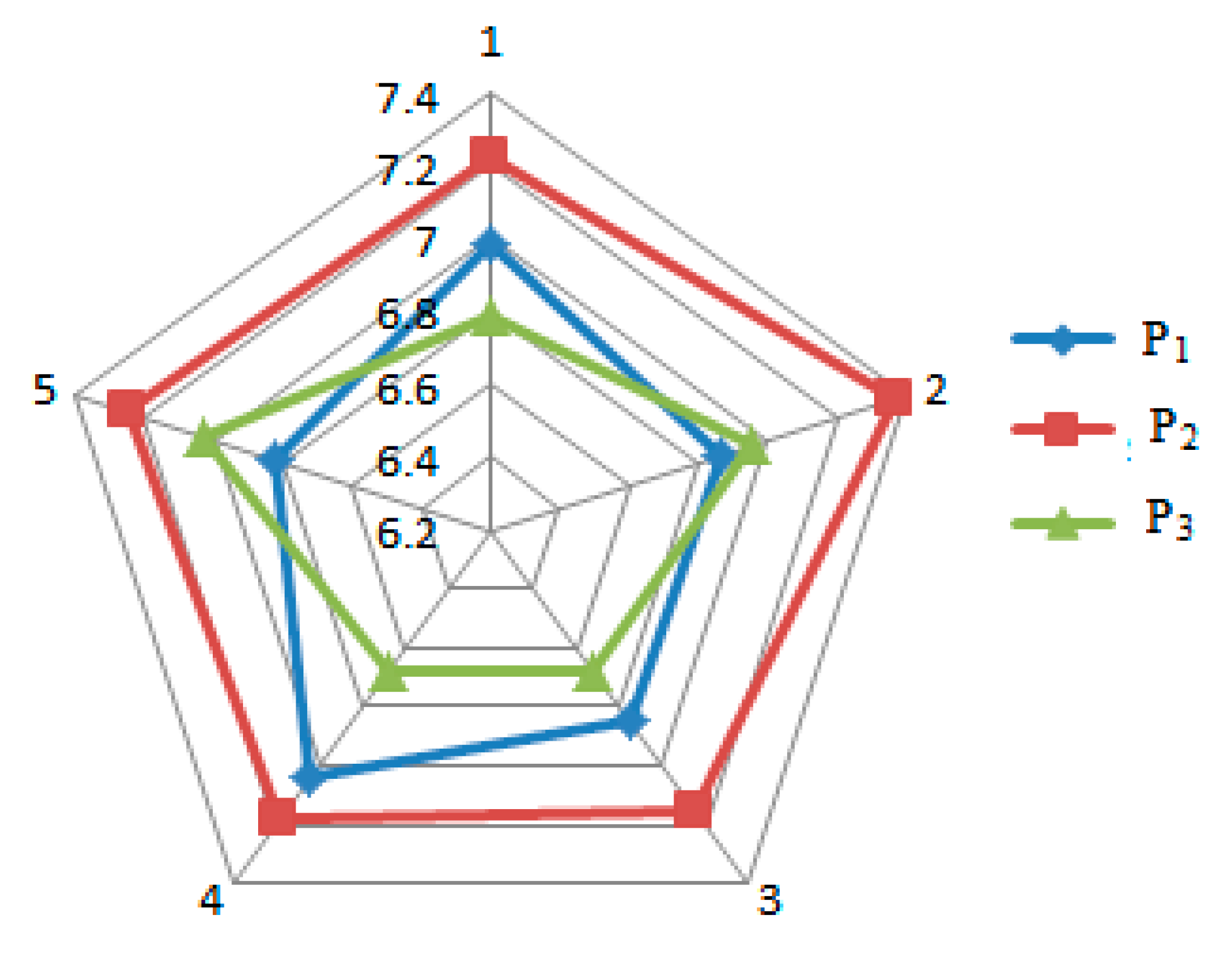
6.4. Results and Sensitivity Analysis
6.5. Comparison with Other Established Work:
7. Conclusions and Future Research Scope
Author Contributions
Funding
Conflicts of Interest
References
- Zadeh, L.A. Fuzzysets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, X.H. Fuzzy number intuitionistic fuzzy set. Fuzzy Syst. Math. 2007, 21, 88–91. [Google Scholar]
- Ye, J. Prioritized aggregation operators of trapezoidal intuitionistic fuzzy sets and their application to multi criteria decision making. Neural Comput. Appl. 2014, 25, 1447–1454. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, Delaware, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Q.; Sunderraman, R. Single valued neutrosophic sets. MultiSpace and Multistructure 2010, 4, 410–413. [Google Scholar]
- Chakraborty, A.; Mondal, S.P.; Ahmadian, A.; Senu, N.; Alam, S.; Salahshour, S. Different forms of triangular neutrosophic numbers, de-Neutrosophication techniques, and their applications. Symmetry 2018, 10, 327. [Google Scholar] [CrossRef]
- Chakraborty, A.; Mondal, S.P.; Ahmadian, A.; Senu, N.; Dey, D.; Alam, S.; Salahshour, S. The pentagonal fuzzy number: Its different representations, properties, ranking, defuzzificationand applicationin game problem. Symmetry 2019, 11, 248. [Google Scholar] [CrossRef]
- Maity, S.; Chakraborty, A.; De, S.K.; Mondal, S.P.; Alam, S. A Comprehensive Study of A Backlogging EOQ Model with Non Linear Heptagonal Dense Fuzzy Environment. Available online: https://doi.org/10.1051/ro/2018114 (accessed on 3 April 2019).
- Bosc, P.; Pivert, O. On a fuzzy bipolar relational algebra. Inf. Sci. 2013, 219, 1–16. [Google Scholar] [CrossRef]
- Lee, K.M. Bipolar-valued fuzzy sets and their operations. In Proceedings of the International Confernceon Intelligent Technologies, Bangkok, Thailand, 28–30 May 2000; pp. 307–312. [Google Scholar]
- Lee, K.J. Bipolar fuzzy sub algebras and bipolar fuzzy ideals of BCK/BCI-algebras. Bull. Malays Math. Sci. Soc. 2009, 32, 361–373. [Google Scholar]
- Kang, M.K.; Kang, J.G. Bipolar fuzzy set theory applied to sub-semi groups with operators in semi groups. J. Korean Soc. Math. Educ. Ser. B Pure Appl. Math. 2012, 19, 23–35. [Google Scholar]
- Deli, I.; Ali, M.; Smarandache, F. Bipolar neutrosophic sets and their application based on multi-criteria decision making problems. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems, Beijing, China, 22–24 August 2015. [Google Scholar]
- Broumi, S.; Smarandache, F.; Talea, M.; Bakali, A. An introduction to bipolar single valued neutrosophic graph theory. Appl. Mech. Mater. 2016, 841, 184–191. [Google Scholar] [CrossRef]
- Ali, M.; Smarandache, F. Complex neutrosophic set. Neural Comput. Appl. 2016, 25, 1–18. [Google Scholar] [CrossRef]
- Molodtsov, D.A. Soft set theory-first results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Aslam, M.; Abdullah, S.; Ullah, K. Bipolar fuzzy soft sets and its applications in decision making problem. arXiv 2013, arXiv:1303.6932v1. [Google Scholar]
- Ulucay, V.; Deli, I.; Sahin, M. Similarity measures of bipolar neutrosophic sets and their application to multiple criteria decision making. Neural Comput. Appl. 2018, 29, 739–748. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Wang, J. Frank choquet bonferroni mean operators of bipolar neutrosophic sets and their application to multi-criteria decision-making problems. Int. J. Fuzzy Syst. 2018, 20, 13–28. [Google Scholar] [CrossRef]
- Hashim, R.M.; Gulistan, M.; Smarandache, F. Applications of neutrosophic bipolar fuzzy sets in HOPE Foundation for planning to build a children hospital with different types of similarity measures. Symmetry 2018, 10, 331. [Google Scholar] [CrossRef]
- Zhang, W.R. Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multi agent decision analysis. In Proceedings of the First International Joint Conference of The North American Fuzzy Information Processing Society Biannual Conference, San Antonio, TX, USA, 18–21 December 1994; pp. 305–309. [Google Scholar]
- Zhang, W.R. Bipolar fuzzy sets. In Proceedings of the 1998 IEEE International Conference on Fuzzy Systems, Anchorage, AK, USA, 4–9 May 1998; pp. 835–840. [Google Scholar]
- Deli, I.; Broumi, S.; Smarandache, S.F. On neutrosophic refined sets and their applications in medical diagnosis. J. New Theory 2015, 6, 88–98. [Google Scholar]
- Broumi, S.; Deli, I.; Smarandache, F. Relations on interval valued neutrosophic soft sets. J. New Results Sci. 2014, 5, 1–20. [Google Scholar]
- Broumi, S.; Alkhazaleh, S.; Hazaymeh, A. N-valued refined neutrosophic soft sets and their applications in decision making problems and medical diagnosis. J. Artif. Int. Soft Comput. Res. 2018, 8, 79–86. [Google Scholar] [CrossRef]
- Ali, M.; Smarandache, F. The theory of neutrosophic cubic sets and their applications in pattern recognition. J. Intell. Fuzzy Syst. 2016, 30, 1957–1963. [Google Scholar] [CrossRef] [Green Version]
- Broumi, S.; Bakali, A.; Talea, M. Smarandache F Isolated single valued neutrosophic graphs. Neutrosophic Sets Syst. 2016, 11, 74–78. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, X.H. Simplified neutrosophic sets and their applications in multi-criteria group decision making problems. Int. J. Syst. Sci. 2015, 47, 2342–2358. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Zhang, H.Y.; Chen, X.H. The fuzzy cross-entropy for intuitionistic hesitant fuzzy sets and their application in multi-criteria decision-making. Int. J. Syst. Sci. 2014, 46, 2335–2350. [Google Scholar] [CrossRef]
- Wang, J.Q.; Peng, J.J.; Zhang, H.Y.; Liu, T.; Chen, X.H. An uncertain linguistic multi-criteria group decision-making method based on a cloud model. Group Decis. Negot. 2015, 24, 171–192. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Wang, J.; Chen, X.H. Multi valued neutrosophic sets and power aggregation operators with their applications in multi-criteria group decision-making problems. Int. J. Comput. Intell. Syst. 2015, 8, 345–363. [Google Scholar] [CrossRef]
- Wang, J.Q.; Li, X.E. The TODIM method with multi-valued neutrosophic sets. Control Decis. 2015, 30, 1139–1142. [Google Scholar]
- Garg, H. A linear programming method based on an improved score function for interval-valued pythagorean fuzzy numbers and its application to decision-making. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2018, 26, 67–80. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lee, H.S. The revised method of ranking fuzzy numbers with an area between the centroid and original points. Comput. Math. Appl. 2008, 55, 2033–2042. [Google Scholar] [CrossRef] [Green Version]
- Halgamuge, S.; Runkler, T.; Glesner, M. On the neural defuzzification methods. In Proceedings of the 5th IEEE International Conference on Fuzzy Systems, New Orleans, LA, USA, 8–11 September 1996; pp. 463–469. [Google Scholar]
- Song, Q.; Leland, R.P. Adaptive learning defuzzification techniques and applications. Comput. Math. Appl. 1996, 81, 321–329. [Google Scholar] [CrossRef]
- Yager, R.R. Knowledge-based defuzzification. Fuzzy Sets Syst. 1996, 80, 177–185. [Google Scholar] [CrossRef]
- Filev, D.P.; Yager, R.R. A generalized defuzzification method via BADD distributions. Int. J. Intell. Syst. 1991, 6, 687–697. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y. Generalized defuzzification strategies and their parameter learning procedure. IEEE Trans. Fuzzy Syst. 1996, 4, 64–71. [Google Scholar] [CrossRef]
- Ali, M.; Son, l.; Deli, I.; Tien, N.D. Bipolar neutrosophic soft sets and applications in decision making. J. Intell. Fuzzy Syst. 2017, 33, 4077–4087. [Google Scholar] [CrossRef] [Green Version]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Ali, M. Shortest path problem under bipolar neutrosphic setting. Appl. Mech. Mater. 2016, 859, 59–66. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Geng, Y. Multi-criteria decision-making method based on single-valued neutrosophic schweizer–sklar muirhead mean aggregation operators. Symmetry 2019, 11, 152. [Google Scholar] [CrossRef]
- Qamar, M.A.; Hassan, N. An approach toward a Q-neutrosophic soft set and its application in decision making. Symmetry 2019, 11, 139. [Google Scholar] [CrossRef]
- Grzegorzewski, P. On separability of fuzzy relations. Int. J. Fuzzy Logic Intell. Syst. 2017, 17, 137–144. [Google Scholar] [CrossRef]
- Saber, Y.M.; Alsharari, F. Generalized fuzzy ideal closed setson fuzzy topological spaces in sostak sense. Int. J. Fuzzy Logic Intell. Syst. 2018, 18, 161–166. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Group decision making using intuitionistic hesitant fuzzy sets. Int. J. Fuzzy Logic Intell. Syst. 2014, 14, 181–187. [Google Scholar] [CrossRef]
- Tourad, M.C.; Abdal, A. An Intelligent Similarity Model between Generalized Trapezoidal Fuzzy Numbers in Large Scale. Int. J. Fuzzy LogicIntell. Syst. 2018, 18, 303–315. [Google Scholar] [CrossRef]
- Garg, H. A novel accuracy function under interval-valued Pythagorean fuzzy environment for solving multi criteria decision making problem. J. Intell. Fuzzy Syst. 2016, 31, 529–540. [Google Scholar] [CrossRef]
| Distinct Parameter | Verbal Phrase | Information |
|---|---|---|
| Interval Number | [Low, High] | Voter will select according to their first priority within a certain range, like [2nd,3rd] candidate. |
| Triangular Fuzzy Number | [Low, Median, High] | Voter will select according to their first priority containing an intermediate candidate, like [1st,2nd,3rd] |
| Intuitionistic (Triangular) | [Standard, Median, High; Very Low, Poor, Low] | Voters will select some candidates directly and reject others immediately according to their viewpoint. |
| Neutrosophic (Triangular Bipolar) | [High, Standard, Very High; Intermediate, Average, Median; Very Low, Poor, Low] | Some voters will select some candidates directly, some will hesitate when casting their vote, and some will directly reject voting according to their viewpoint. |
| Cases | Attribute | Verbal Phrase |
|---|---|---|
| Quantitative Attributes | ||
| 1 | Price of the product | Very high (VH), High (H), Intermediate (I), Small (S), Very small (VS) |
| 2 | Legibility of the product | Very high (VH), High (H), Mid (M), Low (L), Very low (VL) |
| 3 | Service of the product | Very high (VH), High (H), Mid (M), Low (L), Very low (VL) |
| Alternatives/Attributes | C1 | C2 | C3 |
|---|---|---|---|
| A1 | L | M | H |
| A2 | VL | M | I |
| A3 | L | I | VH |
| Attribute Weight | Final Decision Matrix | Ordering |
|---|---|---|
| <(0.33,0.30,0.37> | ||
| <(0.25,0.30,0.45> | ||
| <(0.35,0.25,0.40> | ||
| <(0.40,0.30,0.30> | ||
| <(0.20,0.30,0.50> |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, A.; Mondal, S.P.; Alam, S.; Ahmadian, A.; Senu, N.; De, D.; Salahshour, S. Disjunctive Representation of Triangular Bipolar Neutrosophic Numbers, De-Bipolarization Technique and Application in Multi-Criteria Decision-Making Problems. Symmetry 2019, 11, 932. https://doi.org/10.3390/sym11070932
Chakraborty A, Mondal SP, Alam S, Ahmadian A, Senu N, De D, Salahshour S. Disjunctive Representation of Triangular Bipolar Neutrosophic Numbers, De-Bipolarization Technique and Application in Multi-Criteria Decision-Making Problems. Symmetry. 2019; 11(7):932. https://doi.org/10.3390/sym11070932
Chicago/Turabian StyleChakraborty, Avishek, Sankar Prasad Mondal, Shariful Alam, Ali Ahmadian, Norazak Senu, Debashis De, and Soheil Salahshour. 2019. "Disjunctive Representation of Triangular Bipolar Neutrosophic Numbers, De-Bipolarization Technique and Application in Multi-Criteria Decision-Making Problems" Symmetry 11, no. 7: 932. https://doi.org/10.3390/sym11070932
APA StyleChakraborty, A., Mondal, S. P., Alam, S., Ahmadian, A., Senu, N., De, D., & Salahshour, S. (2019). Disjunctive Representation of Triangular Bipolar Neutrosophic Numbers, De-Bipolarization Technique and Application in Multi-Criteria Decision-Making Problems. Symmetry, 11(7), 932. https://doi.org/10.3390/sym11070932









