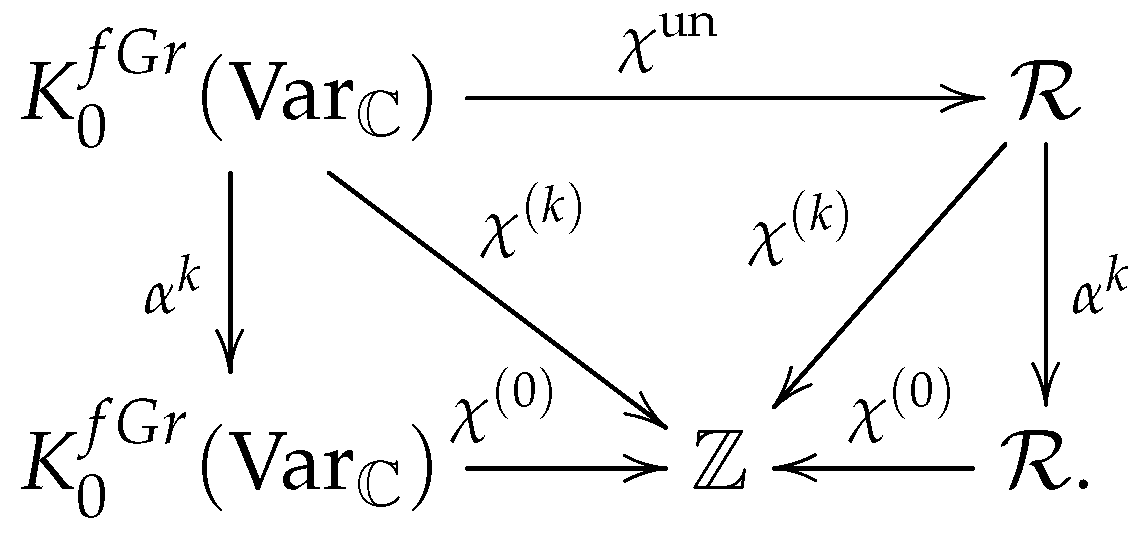Generalized Orbifold Euler Characteristics on the Grothendieck Ring of Varieties with Actions of Finite Groups

Abstract

The notion of the orbifold Euler characteristic came from physics at the end of the 1980s. Coincidence (up to sign) of the orbifold Euler characteristics is a necessary condition for crepant resolutions of orbifolds to be mirror symmetric. There were defined higher order versions of the orbifold Euler characteristic and generalized (“motivic”) versions of them. In a previous paper, the authors defined a notion of the Grothendieck ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of varieties with actions of finite groups on which the orbifold Euler characteristic and its higher order versions are homomorphisms to the ring of integers. Here, we define the generalized orbifold Euler characteristic and higher order versions of it as ring homomorphisms from $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ to the Grothendieck ring $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of complex quasi-projective varieties and give some analogues of the classical Macdonald equations for the generating series of the Euler characteristics of the symmetric products of a space.

1. Introduction

The notion of the orbifold Euler characteristic ${\chi }^{\mathrm{orb}}$ came from physics at the end of the 1980s [1] (see also [2,3]). Coincidence (up to sign) of the orbifold Euler characteristics is a necessary condition for orbifolds (or rather, for their crepant resolutions) to be mirror symmetric. Higher order Euler characteristics ${\chi }^{\left(k\right)}$ of spaces with finite group actions were defined in [2,4]. The class of a variety in the Grothendieck ring $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of complex quasi-projective varieties (being an additive invariant) can be considered as a generalized (“motivic”) Euler characteristic. Generalized versions of the orbifold Euler characteristic and of higher order Euler characteristics were defined in [5] (as a refinement of the so-called orbifold Hodge–Deligne polynomial; see, e.g., [6]) and in [7]. (They take values in the extension of the Grothendieck $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ ring of complex quasi-projective varieties by rational powers of the class of the affine line.) One has the classical Macdonald equation for the generating series of the Euler characteristics of the symmetric products of a topological space. Its versions for the orbifold Euler characteristic and for the higher order Euler characteristics were obtained in [8]. Some versions for the generalized orbifold Euler characteristic and for the generalized higher order Euler characteristics were given in [5,7].

The orbifold Euler characteristic and the higher order Euler characteristics are usually considered as functions on the Grothendieck ring $K_0^G\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of G-varieties. These functions define group homomorphisms from $K_0^G\left({\mathrm{Var}}_{\mathbb{C}}\right)$ to $\mathbb{Z}$, but not ring homomorphism. A Grothendieck ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ on which these Euler characteristics are ring homomorphisms was defined in [9]. It was called the Grothendieck ring of complex quasi-projective varieties with actions of finite groups. In [10], there was defined a notion of the universal Euler characteristic on $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$. It takes values in a ring generated, as a free Abelian group, by elements corresponding to isomorphism classes of finite groups.

Here, we define generalized orbifold Euler characteristic ${\chi }_{\mathrm{g}}^{\mathrm{orb}}$ and generalized higher order Euler characteristics ${\chi }_{\mathrm{g}}^{\left(k\right)}$ as homomorphisms from $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ to $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$. We formulate Macdonald-type equations for them in terms of $\lambda$-ring homomorphisms. There is a map $\alpha :K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ such that $p\circ {\alpha }^k={\chi }_{\mathrm{g}}^{\left(k\right)}$, where p is the natural map $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ sending the class $\left[\right(X,G\left)\right]$ of a G-variety to the class $[X/G]$ of its quotient. We prove a substitute of a Macdonald-type equation for the homomorphism $\alpha$.

2. Power Structures and the Grothendieck Ring of Varieties with Actions of Finite Groups

A power structure over a ring R (commutative, with unit) is a method to give sense to an expression of the form ${\left(A\left(t\right)\right)}^m$, where $A\left(t\right)=1+a_{1}t+a_2{t}^2+\dots \in 1+t·R\left[\left[t\right]\right]$ and $m\in R$ ([11]). It is defined by a map

$$\left(1+t·R\left[\right[t\left]\right]\right)\times R\to 1+t·R\left[\left[t\right]\right]((A\left(t\right),m)\mapsto {\left(A\left(t\right)\right)}^m),$$

which satisfies the following properties:

(1)

${\left(A\left(t\right)\right)}^0=1$;

(2)

${\left(A\left(t\right)\right)}^1=A\left(t\right)$;

(3)

${\left(A\left(t\right)·B\left(t\right)\right)}^m={\left(A\left(t\right)\right)}^m·{\left(B\left(t\right)\right)}^m$;

(4)

${\left(A\left(t\right)\right)}^{m+n}={\left(A\left(t\right)\right)}^m·{\left(A\left(t\right)\right)}^n$;

(5)

${\left(A\left(t\right)\right)}^{mn}={\left({\left(A\left(t\right)\right)}^n\right)}^m$;

(6)

${(1+a_{1}t+\dots )}^m=1+m{a}_{1}t+\dots$;

(7)

${\left(A\left(t^k\right)\right)}^m={\left(A\left(t\right)\right)}^m|{}_{t\mapsto t^k}$ for $k\in {\mathbb{Z}}_{>0}$.

Power structures over a ring are related with $\lambda$-structures on it. A $\lambda$-structure on a ring R (sometimes called a pre-lambda structure; see, e.g., [12]) is an additive-to-multiplicative homomorphism $R\to 1+t·R\left[\right[t\left]\right]$ (that is $a\mapsto {\lambda }_a\left(t\right)$, ${\lambda }_{a+b}\left(t\right)={\lambda }_a\left(t\right)·{\lambda }_b\left(t\right)$) such that ${\lambda }_a\left(t\right)=1+at+\dots$ A $\lambda$-structure on R defines a power structure over it in the following way. A series $A\left(t\right)\in 1+t·R\left[\right[t\left]\right]$ can be, in a unique way, represented as the product ${\displaystyle \prod _{k=1}^{\infty }}{\lambda }_{b_k}\left(t^k\right)$. Then one defines ${\left(A\left(t\right)\right)}^m$ as ${\displaystyle \prod _{k=1}^{\infty }}{\lambda }_{m{b}_k}\left(t^k\right)$. A power structure over R permits one to define a number of $\lambda$-structures on it: for any series ${\lambda }_1\left(t\right)=1+t+b_2{t}^2+\dots$, one can put ${\lambda }_a\left(t\right)={\left({\lambda }_1\left(t\right)\right)}^a$.

The standard power structure over the ring $\mathbb{Z}$ of integers is defined by the standard exponent of a series. A natural power structure over the Grothendieck ring $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of complex quasi-projective varieties was introduced in [11]. It is defined by the formula

$$\begin{array}{cc}& {(1+\left[A_1\right]t+\left[A_2\right]t^2+\dots )}^{\left[M\right]}=\hfill \\ =& 1+\sum _{k=1}^{\infty }\left(\sum _{\left\{k_i\right\}:\sum i{k}_i=k}\left[\left(\left(M^{{\sum }_i{k}_i}\backslash \Delta \right)\times \prod _i{A}_i^{k_i}\right)/\prod _i{S}_{k_i}\right]\right)·t^k,\hfill \end{array}$$

(1)

where $A_i$, $i=1,2,\dots$, and M are complex quasi-projective varieties, $\Delta$ is the big diagonal in $M^{{\sum }_i{k}_i}$, the group $S_{k_i}$ acts by the simultaneous permutations on the components of $M^{k_i}$ and on the components of $A_i^{k_i}$.

For a topological space X (say, a complex quasi-projective variety) with an action of a finite group G, one has the notions of the orbifold Euler characteristic ${\chi }^{\mathrm{orb}}(X,G)$ and of the (orbifold) Euler characteristics ${\chi }^{\left(k\right)}(X,G)$ of higher orders (see, e.g., [2,3,4]). They can be defined, in particular, in the following way. Let ${\chi }^{\left(0\right)}(X,G):=\chi (X/G)$, where $\chi$ is the (additive) Euler characteristic defined through cohomologies with compact support. For $k\ge 1$, let

$${\chi }^{\left(k\right)}(X,G):=\sum _{\left[g\right]\in \mathrm{Conj}G}{\chi }^{(k-1)}(X^{\langle g\rangle },C_G\left(g\right)),$$

where $\mathrm{Conj}G$ is the set of conjugacy classes of elements of G, g is a representative of the class $\left[g\right]$, $X^{\langle g\rangle }$ is the fixed point set of g, $C_G\left(g\right)$ is the centralizer of the element g in G. The orbifold Euler characteristic ${\chi }^{\mathrm{orb}}(X,G)$ is the Euler characteristic of order 1: ${\chi }^{\left(1\right)}(X,G)$.

The orbifold Euler characteristic and the Euler characteristics of higher orders can be considered as functions on the Grothendieck ring $K_0^G\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of quasi-projective G-varieties. These functions are group homomorphisms, but not ring ones. A ring on which they are defined as ring homomorphisms to $\mathbb{Z}$ was introduced in [9].

Let us consider G-varieties, i.e., pairs $(X,G)$ consisting of a complex quasi-projective variety X and a finite group G acting on X. We shall call two pairs $(X,G)$ and $(X^{\prime },G^{\prime })$ isomorphic if there exists an isomorphism $\psi :X\to X^{\prime }$ of quasi-projective varieties and a group isomorphism $\phi :G\to G^{\prime }$ such that $\psi \left(gx\right)=\phi \left(g\right)\psi \left(x\right)$ for $x\in X$, $g\in G$. If G is a subgroup of a finite group H, one has the induction operation ${\mathrm{Ind}}_G^H$, which converts G-varieties to H-varieties. For a G-variety X, ${\mathrm{Ind}}_G^{H}X$ is the quotient of $H\times X$ by the right action of the group G defined by $(h,x)*g=(hg,g^{-1}x)$. (The action of H on ${\mathrm{Ind}}_G^{H}X$ is defined in the natural way: $h_0(h,x)=(h_{0}h,x)$.)

Definition 1.

(see [9]) The Grothendieck ring of complex quasi-projective varieties with actions of finite groups is the abelian group$K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$generated by the classes$\left[\right(X,G\left)\right]$of G-varieties (for different finite groups G) modulo the relations:

(1) 

if$(X,G)$and$(X^{\prime },G^{\prime })$are isomorphic, then$\left[(X,G)\right]=\left[(X^{\prime },G^{\prime })\right]$;

(2) 

if Y is a Zariski closed G-subvariety of a G-variety X, then$\left[\right(X,G\left)\right]=\left[\right(Y,G\left)\right]+\left[\right(X\backslash Y,G\left)\right]$;

(3) 

if$(X,G)$is a G-variety and G is a subgroup of a finite group H, then$\left[({\mathrm{Ind}}_G^{H}X,H)\right]=\left[(X,G)\right]$.

The multiplication in$K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$is defined by the Cartesian product:

$$\left[(X_1,G_1)\right]\times \left[(X_2,G_2)\right]=\left[(X_1\times X_2,G_1\times G_2)\right].$$

The unit element in $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ is $1=\left[\right(Spec\left(\mathbb{C}\right),\left(e\right)\left)\right]$, the class of the one-point variety with the action of the group with one element.

Remark 1.

This ring (under the name “the Grothendieck ring of equivariant varieties”) was used in [13].

One has a natural ring homomorphism $p:K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ sending $\left[\right(X,G\left)\right]$ to $[X/G]$.

There are two (“geometric”) $\lambda$-structures on the ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$. Let X be a G-variety. The Cartesian power $X^n$ carries natural actions of the group $G^n$ (acting component-wise) and of the group $S_n$ (acting by permuting the factors in $X^n$), and therefore an action of their semi-direct product (the wreath-product) $G^n⋊S_n=G_n$.

Definition 2.

The Kapranov zeta function of$(X,G)$is

$${\zeta }_{(X,G)}\left(t\right)=1+\sum _{n=1}^{\infty }\left[(X^n,G_n)\right]t^n\in 1+t·K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\left[\left[t\right]\right].$$

In [9], it is shown that the Kapranov zeta function is well-defined for elements of the ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ and defines a $\lambda$-ring structure on it.

Another $\lambda$-structure on the ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ is defined by the generating series of classes of equivariant configuration spaces of points in X. Let ${\Delta }_G$ be the big G-diagonal in the Cartesian power $X^n$ of a G-variety X, i.e., the set of n-tuples $(x_1,\dots ,x_n)\in X^n$ with at least two of $x_i$ from the same G-orbit. The wreath product $G_n$ acts on $X^n\backslash {\Delta }_G$. Let

$${\lambda }_{(X,G)}\left(t\right)=1+\sum _{n=1}^{\infty }\left[(X^n\backslash {\Delta }_G,G_n)\right]t^n\in 1+t·K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\left[\left[t\right]\right]$$

be the generating series of classes of equivariant configuration spaces of points in X. In [9], it is shown that the series ${\lambda }_{(X,G)}\left(t\right)$ defines a $\lambda$-structure on the ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$, and there was given a geometric description of the power structure over $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ corresponding to this $\lambda$-structure. (A geometric description of the power structure over the ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ corresponding to the $\lambda$-structure defined by the Kapranov zeta function is not known.) We shall call these $\lambda$-structures (and the corresponding power structures) the symmetric product and the configuration space ones.

In [9], it was shown that the orbifold Euler characteristic and the higher order Euler characteristics of an element of $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ are well-defined (that is, ${\chi }^{\left(k\right)}({\mathrm{Ind}}_G^{H}X,H)={\chi }^{\left(k\right)}(X,G)$), and they are ring homomorphisms from $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ to $\mathbb{Z}$.

One has a ring homomorphism $\alpha :K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ defined by $\alpha \left(\left[(X,G)\right]\right)={\sum }_{\left[g\right]\in \mathrm{Conj}G}\left[(X^{\langle g\rangle },C_G\left(g\right))\right]$ (see the notations above). One can see that ${\chi }^{\left(k\right)}=\chi \circ p\circ {\alpha }^k$, where $\chi :K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)\to \mathbb{Z}$ is the usual Euler characteristic. Therefore, ${\alpha }^k$ can be considered as a sort of a generalized version of the Euler characteristic of order k with values in $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$. (In [13], the homomorphism $\alpha$ is called the inertia homomorphism.)

3. The Universal Euler Characteristic

In [10], there was defined the so-called universal Euler characteristic on the ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$. Let $\mathcal{R}$ be the subring of $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ generated by the zero-dimensional (i.e., finite) G-varieties. It can be described in the following way. Let $\mathcal{G}$ be the set of isomorphism classes of finite groups. Then $\mathcal{R}$ is the Abelian group freely generated by the elements $T^{\mathfrak{G}}$ corresponding to the isomorphism classes $\mathfrak{G}\in \mathcal{G}$ of finite groups. The generator $T^{\mathfrak{G}}$ is represented by the one-point set with the (unique) action of a representative G of the class $\mathfrak{G}$. The Krull–Schmidt theorem implies that $\mathcal{R}$ is the ring of polynomials in the variables $T^{\mathfrak{G}}$ corresponding to the isomorphism classes of finite indecomposable groups. If $(X,G)$ is a G-variety, its universal Euler characteristic is defined by

$${\chi }^{\mathrm{un}}(X,G):=\sum _{\mathfrak{H}\in \mathcal{G}}\chi \left(X^{\left(\mathfrak{H}\right)}/G\right)·T^{\mathfrak{H}},$$

where $X^{\left(\mathfrak{H}\right)}$ is the set of points $x\in X$ with the isotropy subgroup $G_x=\{g\in G:gx=x\}$ belonging to the class $\mathfrak{H}$.

Remark 2.

This characteristic can be regarded as a universal one in the topological category.

The orbifold Euler characteristic and the higher order Euler characteristics define ring homomorphisms from $\mathcal{R}$ to $\mathbb{Z}$.

One has a natural $\lambda$-ring structure on $\mathcal{R}$ defined by an analogue of the Kapranov zeta function (see [10]), and the maps ${\chi }^{\left(k\right)}$ are $\lambda$-ring homomorphisms with respect to this $\lambda$-structure.

One has the commutative diagram of ring homomorphisms

4. Macdonald-Type Equations and $\mathbf{\lambda }$-Structure Homomorphisms

The classical Macdonald equation describes the generating series of the Euler characteristics of the symmetric products of a space:

$$1+\sum _{n=1}^{\infty }\chi \left(S^{n}X\right)·t^n={(1-t)}^{-\chi \left(X\right)},$$

(2)

where X is a topological space and $S^{n}X=X^n/S_n$ is its nth symmetric product. One also has a Macdonald-type equation for the generating series of the Euler characteristics of the configuration spaces of subsets of points in X. Let $M_{n}X=(X^n\backslash \Delta )/S_n$ be the configuration space of unordered n-tuples of points in X, where $\Delta$ is the big diagonal in $X^n$. Then one has

$$1+\sum _{n=1}^{\infty }\chi \left(M_{n}X\right)·t^n={(1+t)}^{\chi \left(X\right)}.$$

(3)

There exist equations for the generating series of the Hodge–Deligne polynomials of the symmetric products of a complex quasi-projective variety and of the configuration spaces of subsets of points in it (see, e.g., [5]).

These equations are related with $\lambda$-ring homomorphisms (and therefore with power structure homomorphisms) from the Grothendieck ring $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of complex quasi-projective varieties to $\mathbb{Z}$ and to $\mathbb{Z}[u,v]$, respectively. For a ring homomorphism $\phi :R_1\to R_2$, one has a natural map (a group homomorphism) ${\phi }_{*}:1+t·R_1\left[\left[t\right]\right]\to 1+t·R_2\left[\left[t\right]\right]$ obtained by applying $\phi$ to the coefficients of a series. If $R_1$ and $R_2$ are $\lambda$-rings, a ring homomorphism $\phi :R_1\to R_2$ is said to be a $\lambda$-ring homomorphism if ${\lambda }_{\phi \left(a\right)}\left(t\right)={\phi }_{*}{\lambda }_a\left(t\right)$ for $a\in R_1$. If $R_1$ and $R_2$ are rings with power structures, $\phi :R_1\to R_2$ is a power structure homomorphism if ${\phi }_{*}\left(A{\left(t\right)}^m\right)={\left({\phi }_{*}\left(A\left(t\right)\right)\right)}^{\phi \left(m\right)}$. A $\lambda$-ring homomorphism induces a power structure homomorphism for the corresponding power structures and vise-versa.

Equations (2) and (3) are related with the following $\lambda$-ring structures on the Grothendieck ring $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ and on $\mathbb{Z}$. The Kapranov zeta function of a variety X (or of its class $\left[X\right]\in K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$) is

$${\zeta }_X\left(t\right)=1+\sum _{n=1}^{\infty }\left[S^{n}X\right]·t^n={(1-t)}^{-\left[X\right]}.$$

One can see that ${\zeta }_X\left(t\right)$ defines a $\lambda$-ring structure on $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$. Another $\lambda$-ring structure on $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ is defined by the series

$${\lambda }_X\left(t\right)=1+\sum _{n=1}^{\infty }\left[M_{n}X\right]·t^n={(1+t)}^{\left[X\right]}.$$

The corresponding $\lambda$-structures on $\mathbb{Z}$ are ${\check{\zeta }}_n\left(t\right)={(1-t)}^{-n}$ and ${\check{\lambda }}_n\left(t\right)={(1+t)}^n$, respectively. Equations (2) and (3) mean that the Euler characteristic is a $\lambda$-ring homomorphism for the corresponding $\lambda$-structures. Both $\lambda$-structures on $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ (as well as both $\lambda$-structures on $\mathbb{Z}$) induce the same power structure over $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ (over $\mathbb{Z}$, respectively). The corresponding power structure over $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ is given by Equation (1).

The Macdonald-type equations for the orbifold Euler characteristic and for the higher order Euler characteristics look like the following.

Theorem 1.

([8]) The map${\chi }^{\left(k\right)}:K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to \mathbb{Z}$is a λ-ring homomorphism for the λ-structures on the source$K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$and on the target$\mathbb{Z}$defined by the Kapranov zeta function${\zeta }_{(X,G)}\left(t\right)$and by the series

$${\lambda }_n^{\left(k\right)}\left(t\right)={\left(\prod _{r_1,\dots ,r_k\ge 1}{\left(1-t^{r_1·\dots ·r_k}\right)}^{r_2·r_3^2·\dots ·r_k^{k-1}}\right)}^n,$$

respectively, i.e.,

$${\chi }^{\left(k\right)}\left({\zeta }_{(X,G)}\left(t\right)\right)={\lambda }_{{\chi }^{\left(k\right)}(X,G)}^{\left(k\right)}\left(t\right).$$

Remark 3.

The map${\chi }^{\left(k\right)}:K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to \mathbb{Z}$is not a λ-ring homomorphism with respect to the configuration space λ-structure on$K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$.

5. Generalized Euler Characteristics of Higher Orders as Homomorphisms from ${\mathbf{K}}_{\mathbf{0}}^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$

In [9], it was shown that the orbifold Euler characteristic and the Euler characteristics of higher orders are ring homomorphism (moreover, $\lambda$-ring homomorphisms) from the Grothendieck ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ to $\mathbb{Z}$. The notions of the generalized (“motivic”) orbifold Euler characteristic and of generalized (“motivic”) Euler characteristics of higher orders were introduced by the authors in [5] (as a refinement of the orbifold Hodge–Deligne polynomial from [6]) and in [7]. They were defined as invariants of a complex quasi-projective manifold with the action of a finite group and took values in the extension of the Grothendieck ring $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of complex quasi-projective varieties by the rational powers of the class of the affine line and not defined on a ring. The generalized orbifold Euler characteristics took into account the so-called ages (or fermion shifts), which are defined by the actions of the elements of the group on the tangent spaces to their fixed points. These ages are not defined for varieties with finite group actions (or rather, for elements of the corresponding Grothendieck ring(s)). To avoid this problem, in [9], The generalized orbifold Euler characteristics were considered as functions on the Grothendieck ring of varieties with equivariant vector bundles. Here, we define versions of them (with the corresponding weight $\underline{\phi }=0$ in terms of [7,9], that is, without taking into account the ages) as ring homomorphisms from $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ to $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$.

The homomorphism $p:K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ sending the class $\left[\right(X,G\left)\right]$ to the class $[X/G$] is an additive function on $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ and, therefore, can be considered as a generalized version of the Euler characteristic. Let us call it a generalized Euler characteristic of order 0 and denote it by ${\chi }_{\mathrm{g}}^{\left(0\right)}(X,G)$. Let X be a G-variety.

Definition 3.

The generalized Euler characteristic${\chi }_{\mathrm{g}}^{\left(k\right)}(X,G)$of order k is defined by

$${\chi }_{\mathrm{g}}^{\left(k\right)}(X,G)=\sum _{\left[g\right]\in \mathrm{Conj}G}{\chi }_{\mathrm{g}}^{(k-1)}(X^{\langle g\rangle },C_G\left(g\right))\in K_0\left({\mathrm{Var}}_{\mathbb{C}}\right),$$

where the sum is over the conjugacy classes$\left[g\right]$of elements of G, g is a representative of the class$\left[g\right]$, $X^{\langle g\rangle }$is the fixed point set of g, and$C_G\left(g\right)$is the centralizer of g in G.

Proposition 1.

The generalized Euler characteristic${\chi }_{\mathrm{g}}^{\left(k\right)}$of order k is a well-defined ring homomorphism from$K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$to$K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$.

Proof. 

One has to show that ${\chi }_{\mathrm{g}}^{\left(k\right)}$ respects relations (1)–(3) of Definition 1. This obviously holds for (1) and (2). The fact that ${\chi }_{\mathrm{g}}^{\left(k\right)}$ respects condition (3) (the induction relation) can be proved by induction on k: it is obvious for $k=0$, and the statement for an arbitrary k follows from the statement for $k-1$ due to ([9], Lemma 1). □

The following statement gives a Macdonald-type equation for the generalized Euler characteristics of higher orders and is a specification of ([9], Theorem 4) or of ([7], Theorem 1).

Theorem 2.

The map${\chi }_{\mathrm{g}}^{\left(k\right)}:K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$is a λ-ring homomorphism for the λ-structures on the source$K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$and on the target$K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$defined by the Kapranov zeta function${\zeta }_{(X,G)}\left(t\right)$and by the series

$${\lambda }_X^{\left(k\right)}\left(t\right)={\left(\prod _{r_1,\dots ,r_k\ge 1}{\left(1-t^{r_1·\dots ·r_k}\right)}^{r_2·r_3^2·\dots ·r_k^{k-1}}\right)}^{\left[X\right]},$$

i.e.,

$${\chi }_{\mathrm{g}}^{\left(k\right)}\left({\zeta }_{(X,G)}\left(t\right)\right)={\lambda }_{{\chi }_{\mathrm{g}}^{\left(k\right)}(X,G)}^{\left(k\right)}\left(t\right).$$

Remark 4.

The map${\chi }_{\mathrm{g}}^{\left(k\right)}$is not a λ-ring homomorphism with respect to the configuration space λ-structure on$K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$.

One has the commutative diagram of ring homomorphisms

6. A Substitute of a Macdonald-Type Equation for the Homomorphism $\mathbf{\alpha }$

As it follows from Definition 3, the composition of the homomorphism ${\alpha }^k$ with the natural map $p:K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ coincides with the generalized (“motivic”) Euler characteristic of order k (with the generalized orbifold Euler characteristic for $k=1$) computed without the fermion shift (i.e., with $\underline{\phi }=0$ in terms of [7]). Its composition with the usual Euler characteristic homomorphism $\chi :K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)\to \mathbb{Z}$ gives the usual (orbifold) Euler characteristic of order k. One has Macdonald-type equations for the (orbifold) Euler characteristic of order k ([8]) and for the generalized Euler characteristic of order k ([7]). Here, we shall give a version of these equations for the homomorphism $\alpha$ (which reduces to the Macdonald type equations for the generalized orbifold Euler characteristic and for the orbifold Euler characteristic after applying the homomorphisms p and $\chi \circ p$, respectively). Let ${\alpha }_r:K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ be defined in the following way. Let $(X,G)$ be a G-variety. For a representative g of a conjugacy class $\left[g\right]\in \mathrm{Conj}G$, the centralizer $C_G\left(g\right)$ acts on the fixed point set $X^{\langle g\rangle }$ of the element g. Let $C_G\left(g\right)\langle a_{r,g}\rangle$ be the group generated by $C_G\left(g\right)$ and by an additional element $a_{r,g}$ commuting with all the elements of $C_G\left(g\right)$ and such that $a_{r,g}^r=g$. For $r=1$, the group $C_G\left(g\right)\langle a_{r,g}\rangle$ coincides with $C_G\left(g\right)$. One has an action of the group $C_G\left(g\right)\langle a_{r,g}\rangle$ on $X^{\langle g\rangle }$ assuming $a_{r,g}$ to act trivially. Let ${\alpha }_r:K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ be defined by

$${\alpha }_r\left(\left[\right(X,G\left)\right]\right):=\sum _{\left[g\right]\in \mathrm{Conj}G}\left[(X^{\langle g\rangle },C_G\left(g\right)\langle a_{r,g}\rangle )\right].$$

In particular, ${\alpha }_1=\alpha$.

Theorem 3.

$$\alpha \left({\zeta }_{(X,G)}\left(t\right)\right)=\prod _{r=1}^{\infty }{\zeta }_{{\alpha }_r\left(\left[\right(X,G\left)\right]\right)}\left(t^r\right).$$

(4)

Proof. 

The proof essentially follows from the description of the conjugacy classes of elements of the wreath products $G_n$ and of their centralizers from, e.g., [8] and to a big extent repeats the computations in [7]. An element of $G_n$ can be written as a pair $(\mathbf{g},s)$, where $\mathbf{g}=(g_1,\dots ,g_n)\in G^n$, $s\in S_n$. One has

$$\begin{array}{cc}& \alpha \left({\zeta }_{(X,G)}\left(t\right)\right)=\hfill \end{array}$$

(5)

$$\begin{array}{cc}=& \sum _{n\ge 0}{t}^n·\left(\sum _{\left[(\mathbf{g},s)\right]\in \mathrm{Conj}{G}_n}\left[{\left(X^n\right)}^{\langle (\mathbf{g},s)\rangle },C_{G_n}\left((\mathbf{g},s)\right)\right]\right),\hfill \end{array}$$

(6)

where the sum is over the conjugacy classes $\left[\right(\mathbf{g},s\left)\right]$ of elements of $G_n$. The conjugacy classes $\left[\right(\mathbf{g},s\left)\right]$ of elements $(\mathbf{g},s)=(g_1,\dots ,g_n;s)$ of $G_n$ are characterized by their types. For a cycle $z=(i_1,\dots ,i_r)$ (of length r) in the permutation s, its cicle product $g_{i_r}{g}_{i_{r-1}}\dots g_{i_1}$ is well-defined up to conjugacy. For $\left[c\right]\in \mathrm{Conj}G$ and for $r\ge 1$, let $m_r\left(c\right)$ be the number of r-cycles in s with the cicle product from $\left[c\right]$. One has

$$\sum _{\left[c\right]\in \mathrm{Conj}G,r\ge 1}r{m}_r\left(c\right)=n.$$

The collection ${\left\{m_r\left(c\right)\right\}}_{r,\left[c\right]}$ is called the type of the element $(\mathbf{g},s)\in G_n$. Two elements of $G_n$ are conjugate if and only if they are of the same type. Therefore, the summation over the conjugacy classes of elements of $G_n$ can be substituted by the summation over all possible types.

The fixed point set ${\left(X^n\right)}^{\langle (\mathbf{g},s)\rangle }$ can be identified with

$$\prod _{\left[c\right]\in \mathrm{Cong}G,r\ge 1}{\left(X^{\langle c\rangle }\right)}^{m_r\left(c\right)}.$$

The centralizer of $(\mathbf{g},s)\in G_n$ is isomorphic to

$$\prod _{\left[c\right]\in \mathrm{Cong}G,r\ge 1}{\left(C_G\left(c\right)\langle a_{r,c}\rangle \right)}_{m_r\left(c\right)},$$

where the definition of the group $C_G\left(c\right)\langle a_{r,c}\rangle$ and the description of its action on the fixed point set $X^{\langle c\rangle }$ are given above.

Therefore, one has

$$\begin{array}{ccc}\hfill & & \alpha \left({\zeta }_{(X,G)}\left(t\right)\right)=\sum _{n=0}^{\infty }{t}^n·\left(\sum _{\left[(\mathbf{g},s)\right]\in \mathrm{Cong}{G}_n}\left[(X^{\langle (\mathbf{g},s)\rangle },C_{G_n}\left((\mathbf{g},s)\right)\right]\right)\hfill \\ \hfill & =& \sum _{n=0}^{\infty }{t}^n·\left(\sum _{\left\{m_r\left(c\right)\right\}}\left[\prod _{\left[c\right],r}{\left(X^{\langle c\rangle }\right)}^{m_r\left(c\right)},\prod _{\left[c\right],r}{\left(C_G\left(c\right)\langle a_{r,c}\rangle \right)}_{m_r\left(c\right)}\right]\right)\hfill \\ & =& \sum _{\left\{m_r\left(c\right)\right\}}{t}^{\sum r{m}_r\left(c\right)}·\prod _{\left[c\right],r}\left[{\left(X^{\langle c\rangle }\right)}^{m_r\left(c\right)},{\left(C_G\left(c\right)\langle a_{r,c}\rangle \right)}_{m_r\left(c\right)}\right]\hfill \\ & =& \prod _{r=1}^{\infty }\prod _{\left[c\right]}\sum _{m_r\left(c\right)=1}^{\infty }\left(t^{r{m}_r\left(c\right)}\left[{\left(X^{\langle c\rangle }\right)}^{m_r\left(c\right)},{\left(C_G\left(c\right)\langle a_{r,c}\rangle \right)}_{m_r\left(c\right)}\right]\right)\hfill \\ & =& \prod _{r=1}^{\infty }\prod _{\left[c\right]}{\zeta }_{(X^{\langle c\rangle },C_G\left(c\right)\langle a_{r,c}\rangle )}\left(t^r\right)=\prod _{r=1}^{\infty }{\zeta }_{{\sum }_{\left[c\right]}\left[(X^{\langle c\rangle },C_G\left(c\right)\langle a_{r,c}\rangle )\right]}\left(t^r\right)\hfill \\ & =& \prod _{r=1}^{\infty }{\zeta }_{{\alpha }_r\left(\left[(X,G)\right]\right)}\left(t^r\right).\hfill \end{array}$$

□

The restrictions of the homomorphisms $\alpha$ and ${\alpha }_r$ to the subring $\mathcal{R}\subset K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ define the homomorphisms $\alpha$ and ${\alpha }_r$ from $\mathcal{R}$ to $\mathcal{R}.$ The homomorphism ${\alpha }_r$ acts by the formula ${\alpha }_r\left(T^{\left[G\right]}\right)={\sum }_{\left[g\right]\in \mathrm{Conj}\mathrm{G}}{T}^{\left[C_G\left(g\right)\langle a_{r,g}\rangle \right]}$.

Corollary 1.

For$a\in \mathcal{R}$, one has

$$\alpha \left({\zeta }_a\left(t\right)\right)=\prod _{r=1}^{\infty }{\zeta }_{{\alpha }_r\left(a\right)}\left(t^r\right).$$

(7)

7. Conclusions

We study generalized versions of the orbifold Euler characteristic and of higher order Euler characteristics as ring homomorphisms from the Grothendieck ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of complex quasi-projective varieties with actions of finite groups introduced in [9]. We define the generalized orbifold Euler characteristic ${\chi }_{\mathrm{g}}^{\mathrm{orb}}$ and generalized higher order Euler characteristics ${\chi }_{\mathrm{g}}^{\left(k\right)}$ as homomorphisms from $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ to the Grothendieck ring $K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ of complex quasiprojective varieties. This permits the formulation of Macdonald-type equations for them in terms of $\lambda$-ring homomorphisms. We consider a map $\alpha$ (the inertia homomorphism) from the Grothendieck ring $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)$ to itself such that the composition of its kth power with the natural map $K_0^{\mathrm{fGr}}\left({\mathrm{Var}}_{\mathbb{C}}\right)\to K_0\left({\mathrm{Var}}_{\mathbb{C}}\right)$ sending the class $\left[\right(X,G\left)\right]$ of a G-variety to the class $[X/G]$ of its quotient coincides with the generalized (orbifold) Euler characteristic of order k. We formulate and prove a substitute of a Macdonald-type equation for the homomorphism $\alpha$.