Motion Symmetry Evaluation Using Accelerometers and Energy Distribution
Abstract
:1. Introduction
2. Methods
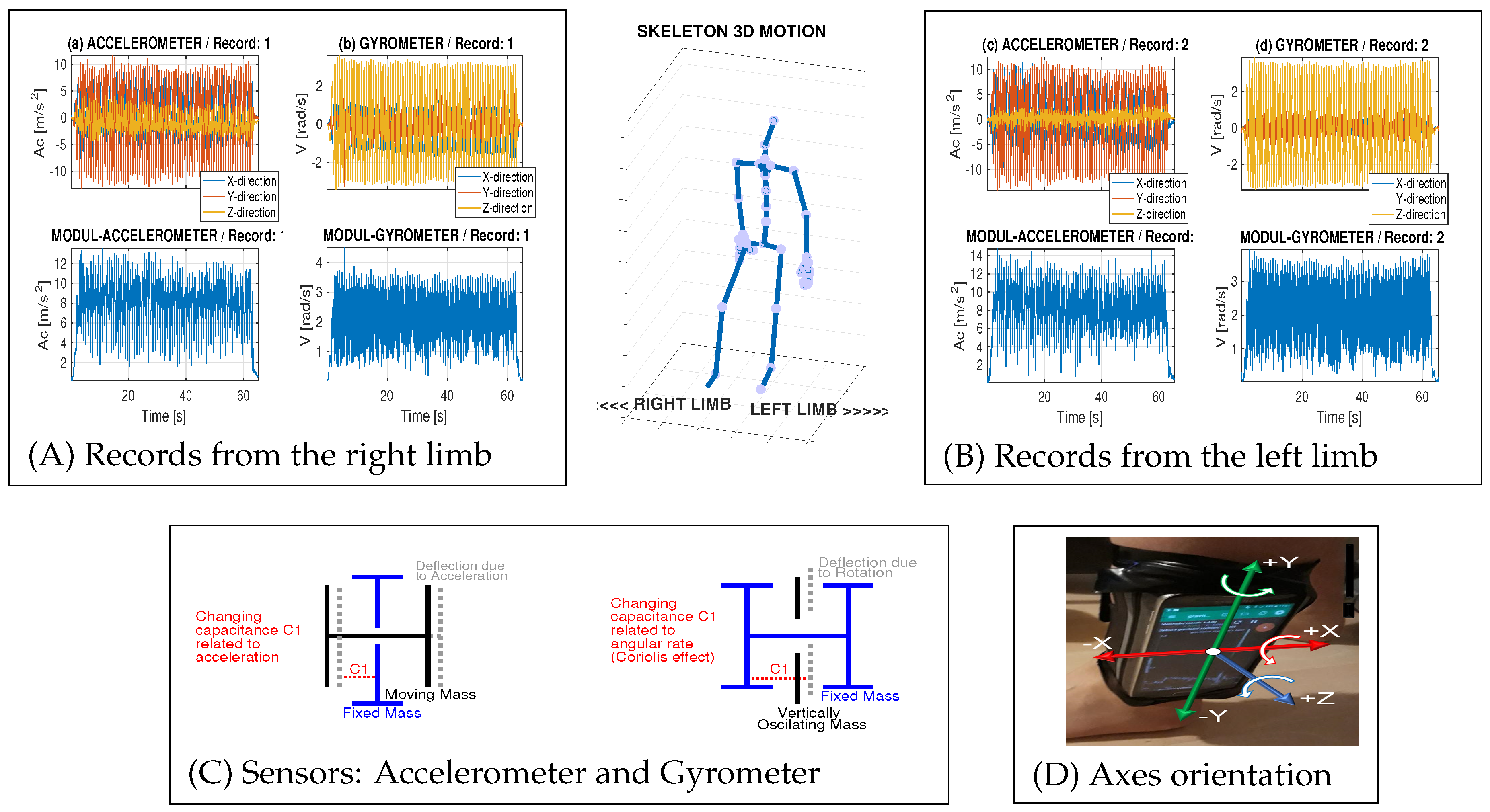
2.1. Data Acquisition
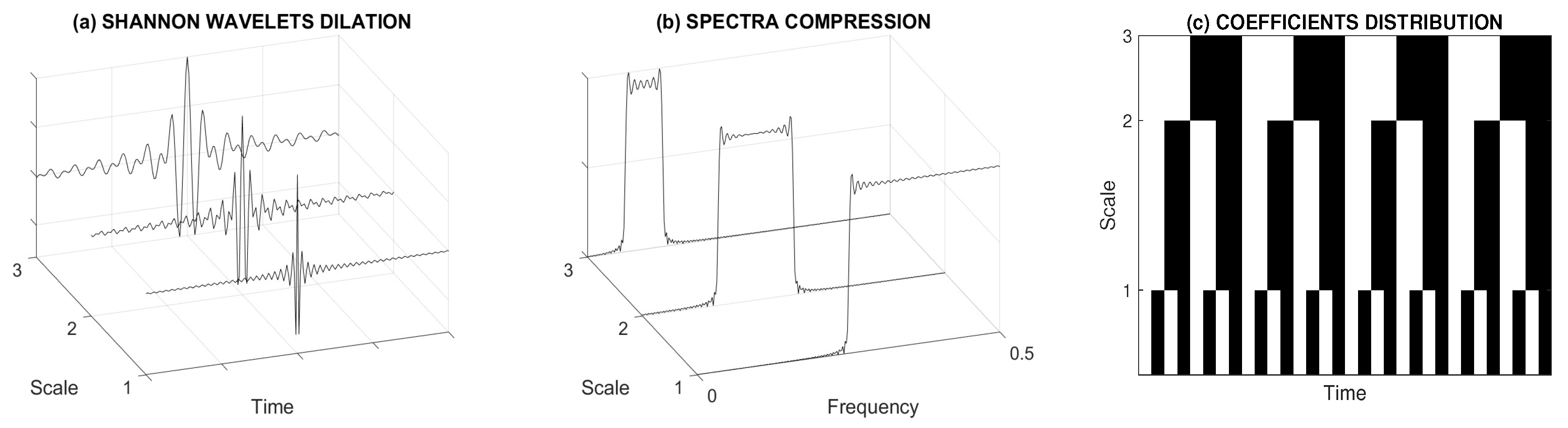
2.2. Data Processing
- relative energy components at selected wavelet decomposition levels for signals recorded by an accelerometer,
- relative energy components at selected wavelet decomposition levels for signals recorded by a gyrometer,
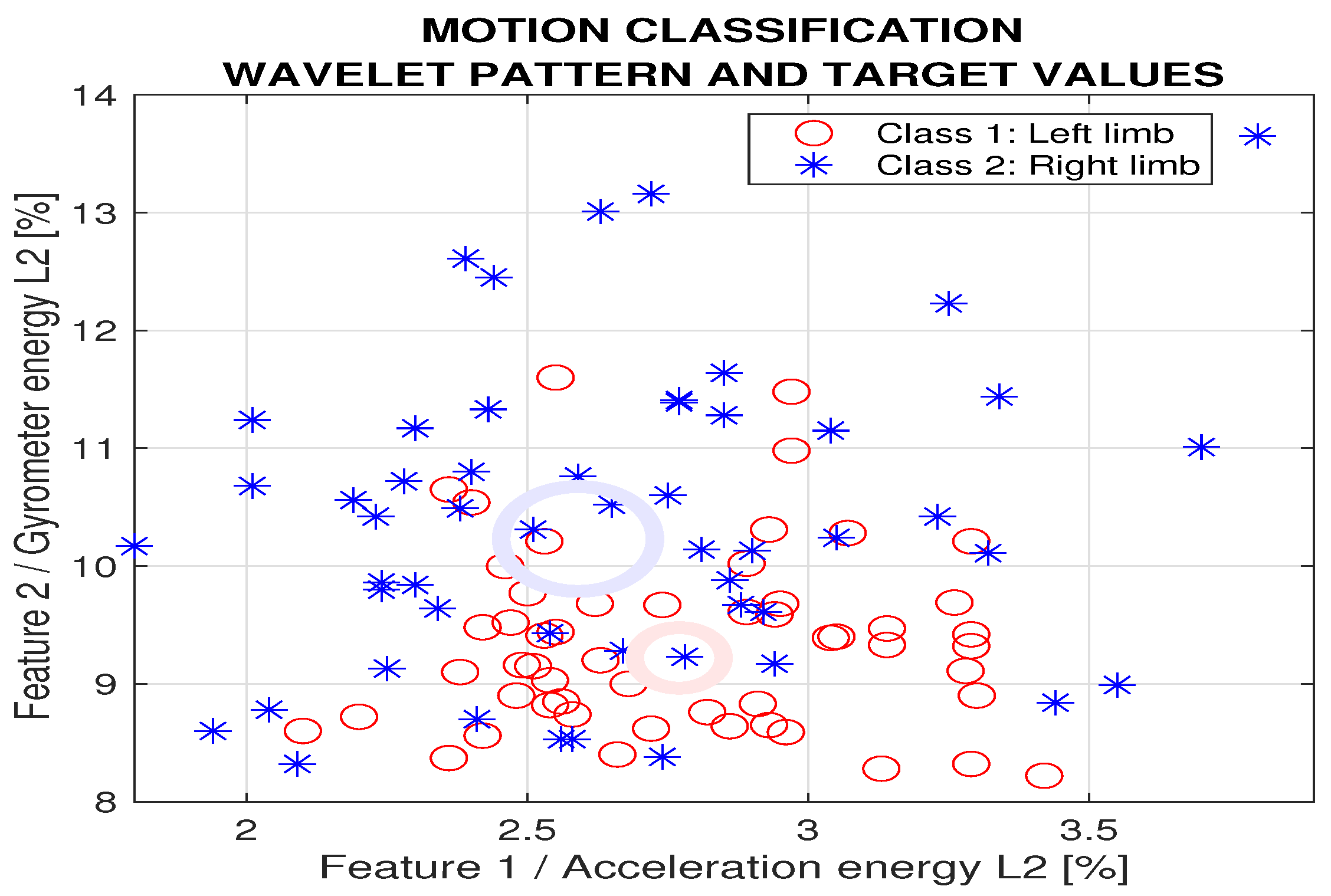
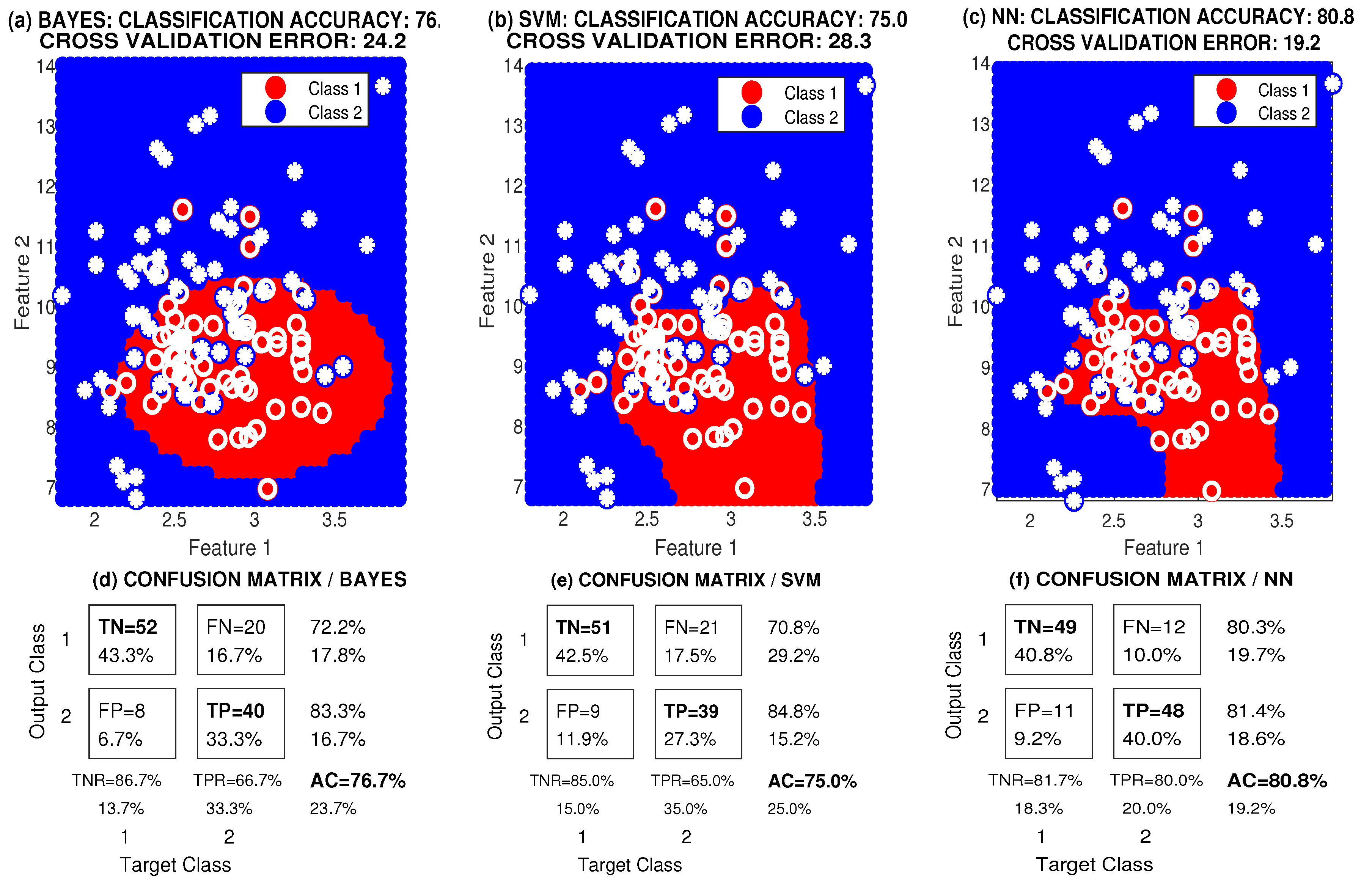
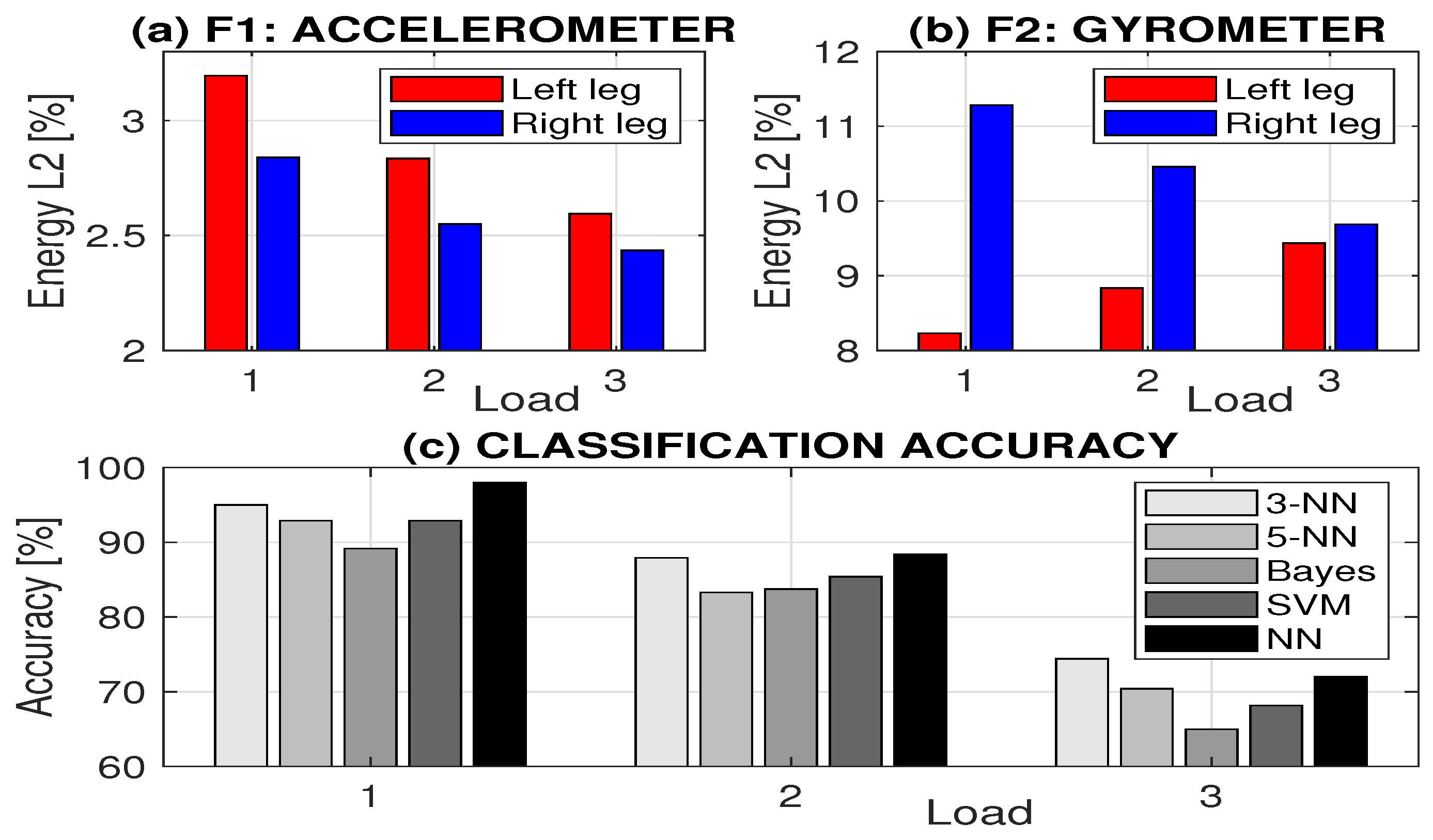
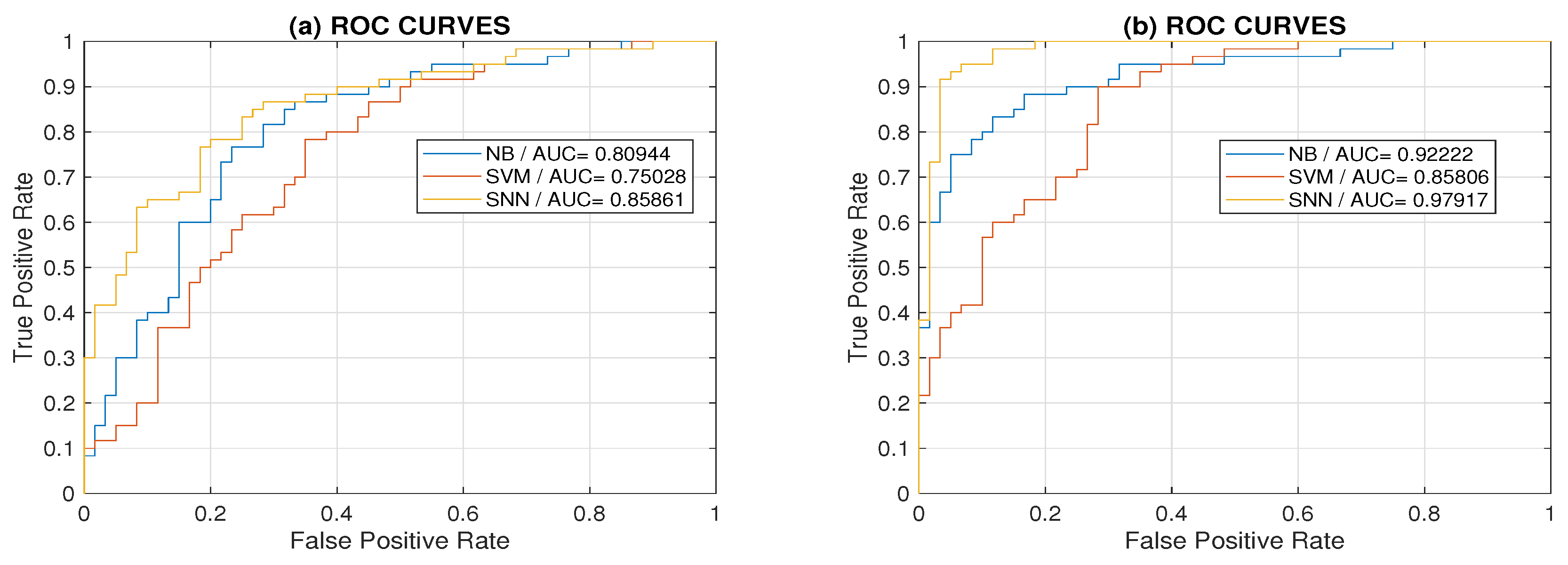
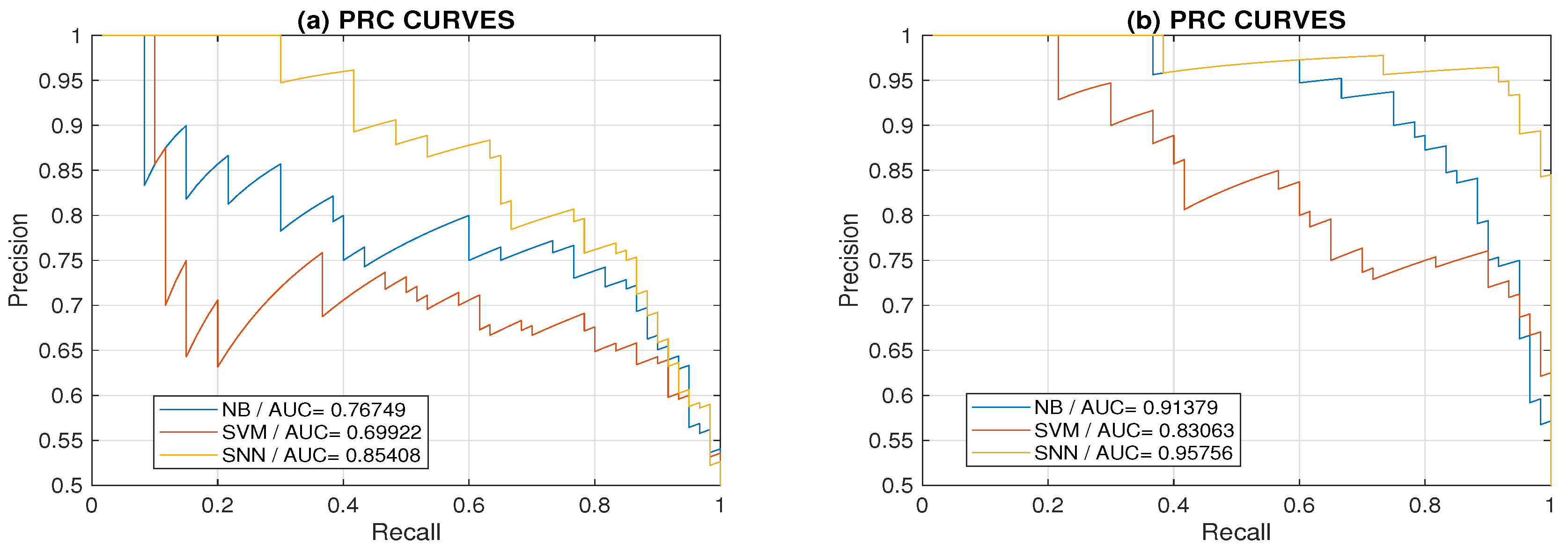
3. Results
- acquiring signals recorded by the accelerometer and gyrometer during selected physical activities using handheld devices,
- transferring signals by wired or wireless communication links to a mathematical environment (of MATLAB 2018b in this case),
- mathematical data analysis including their resampling and digital filtering,
- applying the wavelet transform and evaluating the relative signal energy at selected decomposition levels,
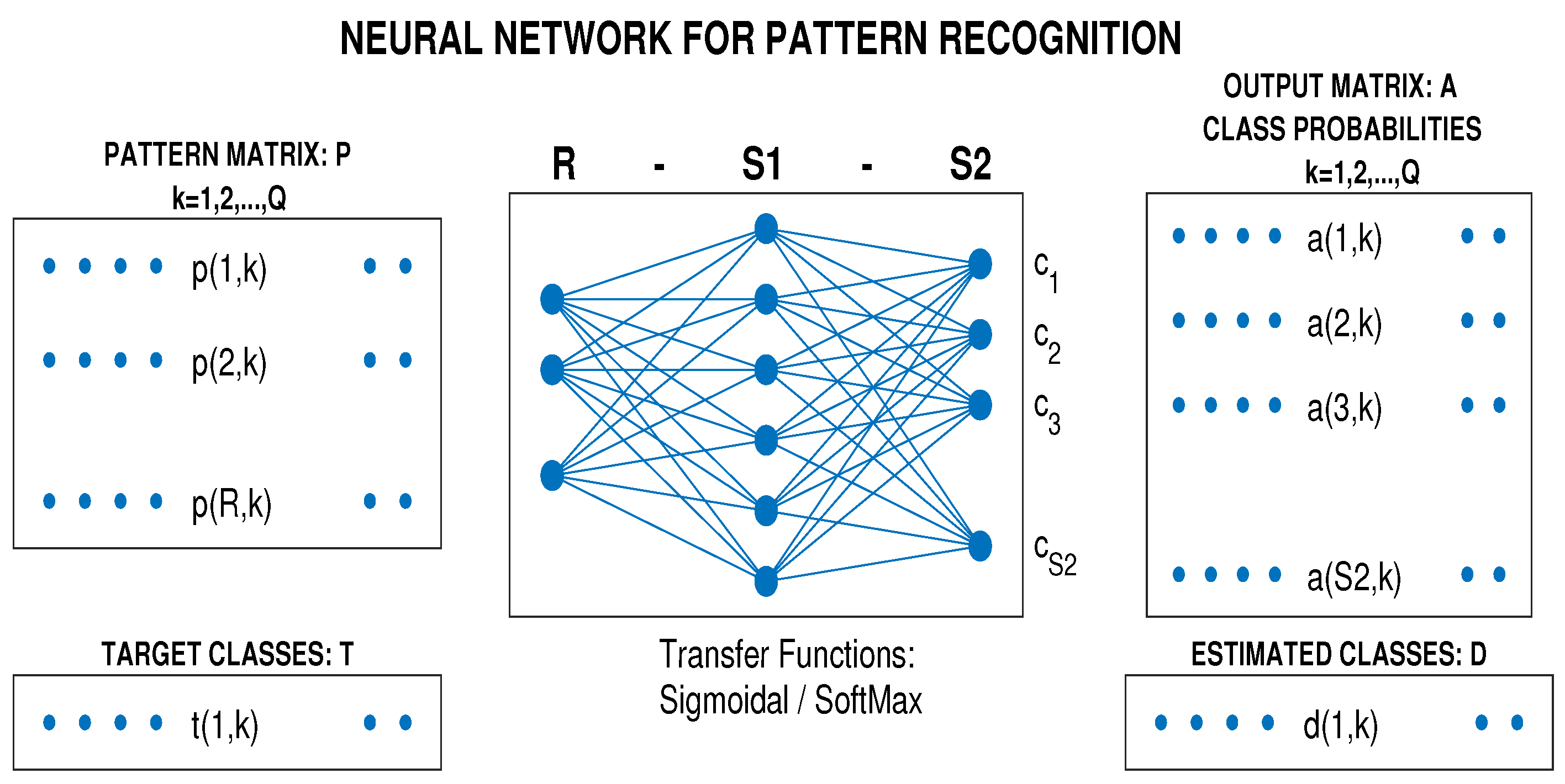
- defining a pattern matrix with Q column vectors for each signal segment and associated vector of target values,
- optimizing and then verifying the classification model.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Carpes, F.P.; Mota, C.B.; Faria, I.E. On the bilateral asymmetry during running and cycling—A review considering leg preference. Phys. Ther. Sport 2010, 11, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Hirata, K.; Kokubun, T.; Miyazawa, T.; Yokoyama, H.; Kubota, K.; Sonoo, M.; Hanawa, H.; Kanemura, N. Contribution of Lower Limb Joint Movement in Adapting to Re-establish Step Length Symmetry During Split-Belt Treadmill Walking. J. Med. Biol. Eng. 2018. [Google Scholar] [CrossRef]
- Joukov, V.; Bonnet, V.; Karg, M.; Venture, G.; Kulic, D. Rhythmic Extended Kalman Filter for Gait Rehabilitation Motion Estimation and Segmentation. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 407–418. [Google Scholar] [CrossRef] [PubMed]
- Dutta, A.; Ma, O.; Toledo, M.; Pregonero, A.; Ainsworth, B.; Buman, M.; Bliss, D. Identifying Free-Living Physical Activities Using Lab-Based Models with Wearable Accelerometers. Sensors 2018, 17, 3893. [Google Scholar] [CrossRef] [PubMed]
- Oudre, L.; Barrois-Müller, R.; Moreau, T.; Truong, C.; Vienne-Jumeau, A.; Ricard, D.; Vayatis, N.; Vidal, P. Template-Based Step Detection with Inertial Measurement Units. Sensors 2018, 18, 4033. [Google Scholar] [CrossRef] [PubMed]
- Vaughn, A.; Biocco, P.; Liu, Y.; Anwar, M. Activity detection and analysis using smartphone sensors. In Proceedings of the 2018 IEEE 19th International Conference on Information Reuse and Integration for Data Science, IRI 2018, Salt Lake City, UT, USA, 6–9 July 2018; pp. 102–107. [Google Scholar]
- Abid, M.; Renaudin, V.; Aoustin, Y.; Le-Carpentier, E.; Robert, T. Walking Gait Step Length Asymmetry Induced by Handheld Device. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 2075–2083. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhan, A.; Mohan, S.; Tarolli, C.; Schneider, R.; Adams, J.; Sharma, S.; Elson, M.; Spear, K.; Glidden, A.; Little, M.; et al. Using smartphones and machine learning to quantify Parkinson disease severity the mobile Parkinson disease score. JAMA Neurol. 2018, 75, 876–880. [Google Scholar] [CrossRef] [PubMed]
- Procházka, A.; Charvátová, H.; Vyšata, O.; Kopal, J.; Chambers, J. Breathing Analysis Using Thermal and Depth Imaging Camera Video Records. Sensors 2017, 17, 1408. [Google Scholar] [CrossRef]
- Kaneko, M.; Yamashita, Y.; Inomoto, O.; Iramina, K. Soft Neurological Signs in Childhood by Measurement of Arm Movements Using Acceleration and Angular Velocity Sensors. Sensors 2015, 15, 25793–25808. [Google Scholar] [CrossRef] [Green Version]
- Chester, V.L.; Calhoun, M. Gait Symmetry in Children with Autism. Autism Res. Treat. 2012, 2012, 576478. [Google Scholar] [CrossRef]
- Rueangsirarak, W.; Zhang, J.; Aslam, N.; Ho, E.S.L.; Shum, H.P.H. Automatic Musculoskeletal and Neurological Disorder Diagnosis with Relative Joint Displacement from Human Gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 2387–2396. [Google Scholar] [CrossRef] [PubMed]
- Filippeschi, A.; Schmitz, N.; Miezal, M.; Bleser, G.; Ruffaldi, E.; Stricker, D. Survey of Motion Tracking Methods Based on Inertial Sensors: A Focus on Upper Limb Human Motion. Sensors 2017, 17, 1257. [Google Scholar] [CrossRef] [PubMed]
- Sanei, S.; Chambers, J. EEG Signal Processing; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Nixon, M.; Aguado, A. Feature Extraction & Image Processing; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Yap, Y.T.; Gouwanda, D.; Gopalai, A.A.; Zheng, C.Y. Analysis of Instantaneous Energy Symmetry Index in Asymmetrical Gait. In Proceedings of the TENCON 2018—2018 IEEE Region 10 Conference, Jeju, Korea, 28–31 October 2018; pp. 1982–1987. [Google Scholar]
- Chen, P.; Kuang, Y.; Li, J. Human Motion Capture Algorithm Based on Inertial Sensors. J. Sens. 2016, 2016, 4343797. [Google Scholar] [CrossRef]
- Alvarez, D.; Alvarez, J.; Gonzalez, R.; Lopez, A. Upper limb joint angle measurement in occupational health. Comput. Methods Biomech. Biomed. Eng. 2015, 19, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, M.; Yamada, S.; Yamamoto, K.; Aoyagi, Y. Gait analysis in a component timed-up-and-go test using a smartphone application. J. Neurol. Sci. 2019, 398, 45–49. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Shen, C. Performance Analysis of Smartphone-Sensor Behavior for Human Activity Recognition. IEEE Access 2017, 5, 3095–3110. [Google Scholar] [CrossRef]
- Sun, B.; Wang, Y.; Banda, J. Gait Characteristic Analysis and Identification Based on the iPhone Accelerometer and Gyrometer. Sensors 2014, 18, 17037–17054. [Google Scholar] [CrossRef]
- Allseits, E.; Kim, K.; Bennett, C.; Gailey, R.; Gaunaurd, I.; Agrawal, V. A Novel Method for Estimating Knee Angle Using Two Leg-Mounted Gyroscopes for Continuous Monitoring with Mobile Health Devices. Sensors 2018, 18, 2759. [Google Scholar] [CrossRef]
- Staab, W.; Hottowitz, R.; Sohns, C.; Sohns, J.; Gilbert, F.; Menke, J.; Niklas, A.; Lotz, J. Accelerometer and Gyroscope Based Gait Analysis Using Spectral Analysis of Patients with Osteoarthritis of the Knee. J. Phys. Ther. Sci. 2014, 26, 997–1002. [Google Scholar] [CrossRef] [Green Version]
- Jang, J.; Ankit, A.; Kim, J.; Jang, Y.; Kim, H.; Kim, J.; Xiong, S. A Unified Deep-Learning Model for Classifying the Cross-Country Skiing Techniques Using Wearable Gyroscope Sensors. Sensors 2018, 18, 3819. [Google Scholar] [CrossRef]
- Ellis, K.; Kerr, J.; Godbole, S.; Lanckriet, G.; Wing, D.; Marshall, S. A random forest classifier for the prediction of energy expenditure and type of physical activity from wrist and hip accelerometers. Physiol. Meas. 2014, 35, 2191–2203. [Google Scholar] [CrossRef] [PubMed]
- Ebara, T.; Azuma, R.; Shoji, N.; Matsukawa, T.; Yamada, Y.; Akiyama, T.; Kurihara, T.; Yamada, S. Reliability of smartphone-based gait measurements for quantification of physical activity/inactivity levels. J. Occup. Health 2017, 59, 506–512. [Google Scholar] [CrossRef] [PubMed]
- Procházka, A.; Vaseghi, S.; Charvátová, H.; Ťupa, O.; Vyšata, O. Cycling Segments Multimodal Analysis and Classification Using Neural Networks. Appl. Sci. 2017, 7, 581. [Google Scholar] [CrossRef]
- Procházka, A.; Vyšata, O.; Vališ, M.; Ťupa, O.; Schatz, M.; Mařík, V. Bayesian classification and analysis of gait disorders using image and depth sensors of Microsoft Kinect. Digit. Signal Process Rev. J. 2015, 47, 169–177. [Google Scholar] [CrossRef]
- Procházka, A.; Charvátová, H.; Vaseghi, S.; Vyšata, O. Machine Learning in Rehabilitation Assessment for Thermal and Heart Rate Data Processing. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1209–1214. [Google Scholar]
- Khandoker, A.; Lai, D.; Begg, R.; Palaniswami, M. Wavelet-Based Feature Extraction for Support Vector Machines for Screening Balance Impairments in the Elderly. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 587–597. [Google Scholar] [CrossRef] [PubMed]
- Hošťálková, E.; Vyšata, O.; Procházka, A. Multi-dimensional biomedical image de-noising using Haar transform. In Proceedings of the 2007 15th International Conference on Digital Signal Processing, Cardiff, UK, 1–4 July 2007; pp. 175–179. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Antoniades, A.; Spyrou, L.; Martin-Lopez, D.; Valentin, A.; Alarcon, G.; Sanei, S.; Took, C. Detection of Interictal Discharges with Convolutional Neural Networks Using Discrete Ordered Multichannel Intracranial EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 2285–2294. [Google Scholar] [CrossRef] [PubMed]
- Carpinella, I.; Gervasoni, E.; Anastasi, D.; Lencioni, T.; Cattaneo, D.; Ferrari, M. Instrumental Assessment of Stair Ascent in People With Multiple Sclerosis, Stroke, and Parkinson’s Disease: A Wearable-Sensor-Based Approach. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 2324–2332. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Trocan, M. Deep learning of smartphone sensor data for personal health assistance. Microelectron. J. 2019, 88, 164–172. [Google Scholar] [CrossRef]
- Chambon, S.; Galtier, M.; Arnal, P.; Wainrib, G.; Gramfort, A. A Deep Learning Architecture for Temporal Sleep Stage Classification Using Multivariate and Multimodal Time Series. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 758–769. [Google Scholar] [CrossRef]
- Sadouk, L.; Gadi, T. Convolutional Neural Networks for Human Activity Recognition in Time and Frequency-Domain. Adv. Intell. Sys. Comput. 2019, 756, 485–496. [Google Scholar]
- Almaslukh, B.; Artoli, A.; Al-Muhtadi, J. A robust deep learning approach for position-independent smartphone-based human activity recognition. Sensors 2018, 18, 3726. [Google Scholar] [CrossRef] [PubMed]
- Kok, M.; Hol, J.; Schon, T. Using Inertial Sensors for Position and Orientation Estimation. Found. Trends Signal Process. 2017, 11, 1–153. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Fang, R.; Miao, M.; Zhang, Y.; Yan, Y.; Tang, X.; Lu, H.; Jin, F. Design, Fabrication, and Performance Characterization of LTCC-Based Capacitive Accelerometers. Micromachines 2018, 9, 120. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, Z.; Elfadel, I.M.; Rasras, M. Monolithic Multi Degree of Freedom (MDoF) Capacitive MEMS Accelerometers. Micromachines 2018, 9, 602. [Google Scholar] [CrossRef] [PubMed]
- Xia, A.; Yu, C.; Kong, L. The Development of Micromachined Gyroscope Structure and Circuitry Technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rezvanian, S.; Lockhart, T.E. Towards Real-Time Detection of Freezing of Gait Using Wavelet Transform on Wireless Accelerometer Data. Sensors 2016, 16, 475. [Google Scholar] [CrossRef] [PubMed]
- Glavinovitch, A.; Swamy, M.; Plotkin, E. Wavelet-Based Segmentation Techniques in the Detection of Microarousals in the Sleep EEG. In Proceedings of the 48th Midwest Symposium on Circuits and Systems, Covington, KY, USA, 7–10 August 2005; pp. 1302–1305. [Google Scholar]
- Johankhani, P.; Kodogiannis, V.; Revett, K. EEG Signal Classification Using Wavelet Feature Extraction and Neural Networks. In Proceedings of the IEEE John Vincent Atanasoff 2006 International Symposium on Modern Computing (JVA06), Sofia, Bulgaria, 3–6 October 2006; pp. 120–124. [Google Scholar]
- Dimoulas, C.; Kalliris, G.; Papanikolaou, G.; Kalampakas, A. Long-Term Signal Detection, Segmentation and Summarization Using Wavelets and Fractal Dimension: A Bioacoustics Application in Gastrointestinal- Motility Monitoring. Comput. Biol. Med. 2007, 37, 438–462. [Google Scholar] [CrossRef] [PubMed]
- Selesnick, I.; Baraniuk, R.; Kingsbury, N. The Dual-Tree Complex Wavelet Transform. IEEE Signal Process Mag. 2005, 22, 123–151. [Google Scholar] [CrossRef]
- Castellanos, N.; Makarov, V. Recovering EEG Brain Signals: Artifact Suppression with Wavelet Enhanced Independent Component Analysis. J. Neurosci. Methods 2006, 158, 300–312. [Google Scholar] [CrossRef]
- Daubechies, I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis. IEEE Trans. Inform. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Newland, D. An Introduction to Random Vibrations, Spectral and Wavelet Analysis, 3rd ed.; Longman: Essex, UK, 1994. [Google Scholar]
- Prashar, P. Neural Networks in Machine Learning. Int. J. Comput. Appl. Technol. 2014, 105, 1–3. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kusumoputro, B.; Lina, L. Infrared Face Recognition System Using Cross Entropy Error Function Based Ensemble Backpropagation Neural Networks. Int. J. Comp. Theory Eng. 2016, 8, 161–166. [Google Scholar] [CrossRef] [Green Version]
- Rimer, M.; Martinez, T. Classification-based objective functions. Mach. Learn. 2006, 63, 183–205. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C. Pattern Recognition and Machine Learning; Springer-Verlag: Berlin, Germany, 2006. [Google Scholar]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inf. 2018, in press. [Google Scholar] [CrossRef]
- Saito, T.; Rehmsmeier, M. The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [PubMed]
- Nasirzade, A.; Sadeghi, H.; Mokhtarinia, H.R.; Rahimi, A. A Review of Selected Factors Affecting Gait Symmetry. Phys. Treat. 2017, 7, 3–12. [Google Scholar] [CrossRef] [Green Version]
| Wavelet | Load | Mean Energy [%] | Standard Deviation | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Left Leg | Right Leg | Left Leg | Right Leg | ||||||
| db2 | 1a | 3.82 | 3.50 | 3.14 | 4.71 | 0.67 | 0.76 | 0.64 | 0.78 |
| 1b | 3.50 | 3.36 | 3.25 | 4.17 | 0.69 | 0.71 | 0.63 | 0.65 | |
| 2a | 3.50 | 3.32 | 2.78 | 3.93 | 0.59 | 0.56 | 0.52 | 0.52 | |
| 2b | 3.68 | 3.42 | 3.05 | 3.95 | 0.74 | 0.58 | 0.67 | 0.55 | |
| 3a | 3.34 | 3.50 | 3.07 | 3.58 | 0.63 | 0.48 | 0.41 | 0.49 | |
| 3b | 3.34 | 3.59 | 3.39 | 3.54 | 0.48 | 0.45 | 0.42 | 0.40 | |
| Haar | 1a | 3.27 | 8.33 | 2.78 | 11.90 | 0.60 | 1.10 | 0.48 | 1.55 |
| 1b | 3.12 | 8.13 | 2.90 | 10.67 | 0.54 | 1.28 | 0.55 | 1.36 | |
| 2a | 2.90 | 8.45 | 2.51 | 10.69 | 0.44 | 1.12 | 0.30 | 1.42 | |
| 2b | 2.77 | 9.22 | 2.59 | 10.23 | 0.35 | 0.88 | 0.47 | 1.66 | |
| 3a | 2.69 | 9.23 | 2.46 | 9.85 | 0.40 | 0.89 | 0.29 | 1.57 | |
| 3b | 2.50 | 9.64 | 2.51 | 8.97 | 0.37 | 1.01 | 0.33 | 1.61 | |
| Wavelet | Load | 3-NN | 5-NN | Bayes | SVM | NN | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [%] | [%] | [%] | [%] | [%] | |||||||
| db2 | 1a | 83.3 | 0.183 | 86.7 | 0.217 | 83.3 | 0.175 | 82.5 | 0.242 | 85.0 | 0.175 |
| 1b | 80.8 | 0.325 | 77.5 | 0.325 | 73.3 | 0.292 | 78.3 | 0.283 | 77.5 | 0.242 | |
| 2a | 85.8 | 0.258 | 84.2 | 0.225 | 82.5 | 0.183 | 85.8 | 0.183 | 86.7 | 0.175 | |
| 2b | 86.7 | 0.267 | 81.7 | 0.258 | 79.2 | 0.242 | 81.7 | 0.242 | 82.5 | 0.175 | |
| 3a | 76.7 | 0.475 | 72.5 | 0.433 | 65.0 | 0.383 | 70.0 | 0.392 | 72.5 | 0.308 | |
| 3b | 75.0 | 0.600 | 60.8 | 0.533 | 52.5 | 0.550 | 66.7 | 0.558 | 69.2 | 0.367 | |
| Mean: | 81.4 | 0.351 | 77.2 | 0.332 | 72.6 | 0.304 | 77.5 | 0.317 | 78.9 | 0.240 | |
| Haar | 1a | 99.2 | 0.042 | 97.5 | 0.042 | 95.8 | 0.042 | 97.5 | 0.050 | 99.2 | 0.025 |
| 1b | 90.8 | 0.150 | 88.3 | 0.167 | 82.5 | 0.192 | 88.3 | 0.167 | 96.7 | 0.058 | |
| 2a | 93.3 | 0.133 | 90.8 | 0.100 | 90.8 | 0.108 | 92.5 | 0.133 | 95.0 | 0.025 | |
| 2b | 82.5 | 0.367 | 75.8 | 0.300 | 76.7 | 0.242 | 75.0 | 0.283 | 80.8 | 0.200 | |
| 3a | 75.8 | 0.592 | 68.3 | 0.525 | 62.5 | 0.425 | 65.8 | 0.408 | 72.5 | 0.350 | |
| 3b | 73.0 | 0.495 | 72.5 | 0.470 | 67.5 | 0.330 | 70.5 | 0.333 | 71.5 | 0.320 | |
| Mean: | 85.8 | 0.297 | 82.2 | 0.267 | 79.3 | 0.223 | 82.2 | 0.229 | 86.1 | 0.163 | |
| Number of Features | Load | 3-NN | 5-NN | Bayes | SVM | NN | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| [%] | [%] | [%] | [%] | [%] | |||||||
| 1 | 95.5 | 0.096 | 92.9 | 0.105 | 89.2 | 0.117 | 92.9 | 0.109 | 97.9 | 0.042 | |
| 2 | 87.9 | 0.25 | 83.3 | 0.200 | 83.8 | 0.175 | 83.9 | 0.208 | 87.9 | 0.112 | |
| 3 | 74.4 | 0.54 | 70.4 | 0.498 | 65.0 | 0.378 | 68.2 | 0.371 | 72.0 | 0.335 | |
| Mean: | 85.8 | 0.297 | 82.2 | 0.267 | 79.3 | 0.223 | 82.2 | 0.229 | 86.1 | 0.163 | |
| 1 | 94.6 | 0.100 | 92.1 | 0.104 | 94.6 | 0.071 | 97.5 | 0.117 | 98.4 | 0.002 | |
| 2 | 90.1 | 0.188 | 85.4 | 0.221 | 88.8 | 0.137 | 90.8 | 0.283 | 92.9 | 0.088 | |
| 3 | 80.0 | 0.404 | 76.3 | 0.383 | 71.7 | 0.304 | 84.2 | 0.317 | 81.7 | 0.183 | |
| Mean: | 88.2 | 0.231 | 84.6 | 0.236 | 85.0 | 0.171 | 90.8 | 0.239 | 91.0 | 0.091 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Procházka, A.; Vyšata, O.; Charvátová, H.; Vališ, M. Motion Symmetry Evaluation Using Accelerometers and Energy Distribution. Symmetry 2019, 11, 871. https://doi.org/10.3390/sym11070871
Procházka A, Vyšata O, Charvátová H, Vališ M. Motion Symmetry Evaluation Using Accelerometers and Energy Distribution. Symmetry. 2019; 11(7):871. https://doi.org/10.3390/sym11070871
Chicago/Turabian StyleProcházka, Aleš, Oldřich Vyšata, Hana Charvátová, and Martin Vališ. 2019. "Motion Symmetry Evaluation Using Accelerometers and Energy Distribution" Symmetry 11, no. 7: 871. https://doi.org/10.3390/sym11070871
APA StyleProcházka, A., Vyšata, O., Charvátová, H., & Vališ, M. (2019). Motion Symmetry Evaluation Using Accelerometers and Energy Distribution. Symmetry, 11(7), 871. https://doi.org/10.3390/sym11070871







